Age-Related Differences in Decision-Making: Evidence Accumulation is More Gradual in Older Age

ABSTRACT

Older adults tend to exhibit longer response times than younger adults in choice tasks across cognitive domains, such as perception, attention, and memory. The diffusion model has emerged as a standard model for analyzing age differences in choice behavior. Applications of the diffusion model to choice data from younger and older adults indicate that age-related slowing is driven by a more cautious response style and slower non-decisional processes, rather than by age differences in the rate of information accumulation. The Lévy flight model, a new evidence accumulation model that extends the diffusion model, was recently developed to account for differences in response times for correct and error responses. In the Lévy flight model, larger jumps in evidence accumulation can be accommodated compared to the diffusion model. It is currently unknown whether younger and older adults differ with respect to the jumpiness of evidence accumulation. In the current study, younger and older adults (N = 40 per age group) completed a letter-number-discrimination task. Results indicate that older adults show a more gradual (less “jumpy”) pattern of evidence accumulation compared to younger adults. Implications for research on cognitive aging are discussed.

Introduction

One of the hallmark features of cognitive aging is age-related slowing, observed across many cognitive domains (Hartshorne & Germine, 2015; Jensen, 2006; Salthouse, 2010; Schaie, 2005). However, interpretation of response times is inherently challenging because response times are sensitive to multiple influences, including the speed of information processing, response criteria, and changes in sensory and motor components. This challenge is further exacerbated by well-documented age differences in speed-accuracy trade-off settings (e.g. (Starns & Ratcliff, 2010), specifically by the finding that older adults prioritize accuracy over speed to a greater extent than younger adults.

The diffusion model (Ratcliff, 1978), a sequential sampling mathematical model for two-choice decisions, provides an alternative to the classical approach of separately analyzing response times and accuracy data, and has been successfully applied in the area of cognitive aging (e.g. (Ratcliff, Thapar, & McKoon, 2004; Spaniol, Madden, & Voss, 2006)., This literature has challenged the view that longer response times in older adults reflect general age-related cognitive slowing (Salthouse, 1996). Indeed, recent meta-analytic and big-data studies confirm that simple decision tasks can reveal age differences in multiple underlying mechanisms (Theisen, Lerche, von Krause, & Voss, 2020; von Krause, Radev, & Voss, 2022).

A critical shortcoming of the basic diffusion model is that it fails to explain fast errors, which are often observed in rapid perceptual decisions (Luce, 1986). Previously, this issue was addressed by including the so-called inter-trial variability of the starting point in the diffusion process (Ratcliff & Rouder, 1998). In this account, fast errors are explained by fluctuations of expectations about the upcoming stimuli. However, the recently proposed Lévy flight model of decision-making (Voss, Lerche, Mertens, & Voss, 2019) provides an alternative explanation for fast errors: It represents shorter response times for errors by sudden changes (“jumps”) in evidence accumulation. Compared to the standard diffusion model, the Lévy flight model contains an additional parameter α, which models the impact of such “jumps” on the process of evidence accumulation. A recent study by Wieschen, Voss, and Radev (2020) suggests that individual differences in α-estimates represent trait-like characteristics of individuals. As noted by Underwood (1975), the ability to account for individual differences is a critical benchmark for psychological theories. To our knowledge, however, age differences in the parameters of the Lévy flight model, and most importantly of its additional parameter α, have not been studied so far.

The Diffusion Model

The diffusion model (Ratcliff, 1978) describes the decisions we make when presented with binary choices (e.g., is this string of letters a word or a non-word?) in terms of a continuous evidence accumulation process. The decision process takes place in a corridor between two boundaries that are each associated with one of the two possible decisional outcomes. For example, when a letter string is presented to participants in a lexical-decision task, the upper boundary could be associated with the answer “The letter string is an existing word” and the lower boundary could be associated with the answer “The letter string is a random letter string.” As soon as the process reaches one of the boundaries, the decision for the corresponding choice is made (Figure 1, Panel (a)).

Figure 1. Sample paths for the diffusion model and the Lévy flight model.

Note: Panel (a): Sample paths of the diffusion model with normally distributed noise, i.e., α = 2.Panel (b): Sample paths of a Lévy flight model with more heavy-tailed Cauchy-distributed noise, i.e., α = 1.

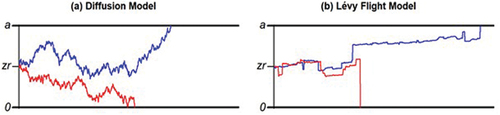
The diffusion model uses the full empirical response times distributions of correct and error responses to estimate several parameters reflecting psychologically meaningful characteristics of the decision process (Voss, Rothermund, & Voss, 2004). The model assumes that the decision process begins at a relative starting point ($z_r$) that is located between the decision boundaries. If one response is preferred a priori, e.g., because it is associated with a higher monetary reward, the starting point is shifted toward the corresponding boundary and less information has to be accumulated to make the respective decision (Voss, Rothermund, & Voss, 2004). The drift rate parameter ($v$) reflects the average speed of information accumulation. Typically, a larger drift rate (i.e., faster performance) is observed in people with high cognitive abilities (Lerche et al., 2020; Schmiedek, Oberauer, Wilhelm, Süß, & Wittmann, 2007) or in easy tasks, e.g., when non-words in a lexical-decision task are unpronounceable letter strings instead of pseudo-words that only differ from existing words by one letter (Voss, Rothermund, & Voss, 2004). The boundary separation parameter $\left(a\right)$ describes the distance between the two decision boundaries. Large values of $a$ indicate that a person adopts a conservative or careful response style, that is, they consider a lot of information before making a decision and only respond after they are quite sure about the correct answer. In addition to the evidence accumulation processes, the duration of all non-decisional processes ($t_0$) represents an additive constant to the resulting response time. These processes include perceptual encoding of a stimulus before making a decision and the motor processes involved in generating the appropriate response, such as pressing the response key, after the decision has been made (Ratcliff, 1978).

One of the key findings of cognitive aging research is an age-related increase in response times that begins in younger adulthood. Recent diffusion model analyses have suggested two mechanisms for age-related slowing (e.g. (Theisen, Lerche, von Krause, & Voss, 2020; von Krause, Radev, & Voss, 2022)., First, older adults generally need more time for non-decisional processes (i.e., perception, motor response). Second, older adults prefer a more conservative decision criterion, such that they generally consider more information for their decisions than younger adults (Dully, McGovern, & O’Connell, 2018). However, mixed findings have emerged when comparing drift rates for younger and older adults. For example, von Krause, Radev, and Voss (2022) analyzed implicit association test data from over a million participants and observed that drift rates were relatively stable up to an age of 60 years. In a recent meta-analysis, Theisen, Lerche, von Krause, and Voss (2020) found increased speed of information processing for younger adults in memory tasks and perceptual tasks, whereas speed was higher for older adults in lexical decisions. These results indicate that age-related differences in drift rate might be domain-specific rather than global.

Although diffusion model analyses shed some light on the underlying processes of an age-related cognitive slowing, the model falls short of explaining all aspects of response time distributions, as the basic version of the diffusion model is not able to account for error response times that are faster than correct response times (Voss, Nagler, & Lerche, 2013). This pattern is often observed in fast and easy perceptual tasks, such as the letter-number-discrimination tasks analyzed in the present paper (Voss, Lerche, Mertens, & Voss, 2019). Previously, fast errors have often been explained by inter-trial variabilities of the starting point (Ratcliff & Rouder, 1998; Smith, Ratcliff, & Sewell, 2014). In psychological terms, such trial-to-trial fluctuations in starting points may indicate changing expectations about the type of stimulus that will be presented in the following trial, e.g., one might expect the next stimulus in a lexical-decision task to be a word again after a longer sequence only including non-word stimuli and the starting point might move closer to the word-boundary. While the version of the diffusion model with inter-trial variabilities allows mapping data from tasks that produce fast errors, the validity of this approach is disputable. In a typical response time experiment, expectations about the next stimulus should not differ that much between similar trials. Additionally, moderate starting point variability has only a minor impact on predicted response time distributions as is evident from the fact that this parameter cannot be estimated reliably from data with typical trial numbers, which can be below 100 for parsimonious models (Boehm et al., 2018; Lerche & Voss, 2016; Lerche, Voss, & Nagler, 2017).

The Lévy Flight Model

Voss, Lerche, Mertens, and Voss (2019) proposed the Lévy flight model as a modification of the diffusion model that explains fast errors as the result of jumps in evidence accumulation. Before gaining attention in the field of cognitive processes in humans (Patten, Greer, Likens, Amazeen, & Amazeen, 2020; Rhodes & Turvey, 2007; Stephen, Mirman, Magnuson, & Dixon, 2009), the concept of Lévy flights was applied, for example, to characterize animal foraging behavior (Viswanathan et al., 1999). In this context, Lévy flights are used to describe movements of individual animals. Lévy flights involve frequent small steps that represent movements of the animal in a limited area. These movements are interrupted by infrequent large “jumps” – extended migrations to new foraging grounds (see Viswanathan et al., 1999, for further details). According to the so-called Lévy flight foraging hypothesis, this exploratory behavior is adaptive when the foraging animal has little knowledge about its surroundings (Viswanathan, Raposo, & Da Luz, 2008).¹

The information foraging theory developed by Pirolli and Card (1999) suggests that, when searching for information, humans use strategies comparable to the behavior of animals foraging for food among patches in the wild. These strategies can occur in search processes in the external world, such as searching the world wide web or searching for information in memory during cognitive processes, such as decision making (Chin, Anderson, Chin, & Fu, 2015).

While the diffusion model assumes that, in the evidence accumulation process, normally distributed noise is added to the average drift rate (Ratcliff, 1978), the Lévy flight model assumes a heavy-tailed noise distribution that allows for larger jumps. In our model, the heaviness in the tails of the noise distribution, that is, the probability of extreme jumps, is controlled by an additional stability parameter $\alpha \in \left(0;2\right]$. The normal distribution, as assumed in the diffusion model, is a special case of the Lévy alpha-stable distribution, with a stability value of α = 2.The lower the value of α, the higher the proportion of jumps in the decision-making process (Figure 1, Panels (a) and (b)). Importantly, the Lévy flight model is able to accommodate fast errors without assuming inter-trial variability of the starting point (Voss, Lerche, Mertens, & Voss, 2019). Like the parameters of the diffusion model, a person’s individual α-values are stable across tasks and across time and therefore could qualify as a trait-like characteristic (Wieschen, Voss, & Radev, 2020; Wieschen, Voss, von Krause, Vollmoeller, & Lerche, 2022).

We hypothesize that individual differences in the probability of “jumps” in the decision process represent different individual strategies on an exploration-exploitation continuum (Wieschen, Voss, von Krause, Vollmoeller, & Lerche, 2022). Thus, people with high α-values (i.e., lower probability of “jumps” in the decision-accumulation process) have a tendency to thoroughly exploit the available information and stick with one source of evidence for a long time, whereas people with low α-values (i.e., higher probability of “jumps”) prefer to quickly move on to the next patch of information when the present strategy of information accumulation becomes inefficient (Wieschen, Voss, von Krause, Vollmoeller, & Lerche, 2022).

Several previous studies (which do not apply cognitive models) have been devoted to the study of age-related differences on an exploration-exploitation trade-off. Thus, in several tasks, including a virtual fish foraging paradigm and a word search puzzle paradigm, younger adults showed more exploration whereas older adults made later decisions to stop exploiting (Chin, Payne, Fu, Morrow, & Stine‐Morrow, 2015; Mata, Wilke, & Czienskowski, 2009). This pattern has been linked to a decline in executive control in older age (Chin, Anderson, Chin, & Fu, 2015; Chin, Payne, Fu, Morrow, & Stine‐Morrow, 2015). Additionally, younger adults tend to score higher on extraversion and openness to experience – characteristics related to exploratory behavior – than older adults (e.g. (Allemand, Zimprich, & Hendriks, 2008).,

All previous studies on the Lévy flight model have included only younger adults (Voss, Lerche, Mertens, & Voss, 2019; Wieschen, Voss, & Radev, 2020; Wieschen, Voss, von Krause, Vollmoeller, & Lerche, 2022). These studies found a superior fit of the Lévy flight model, allowing for “jumps” in evidence accumulation, compared to the standard diffusion model for a number-letter-discrimination task (Voss, Lerche, Mertens, & Voss, 2019), a lexical-decision task, and a color-discrimination task (Wieschen, Voss, & Radev, 2020).

The current study is the first to estimate the parameters of the Lévy flight model, and, most importantly, the stability parameter α, in healthy younger and older adults, using data from a simple letter-number-discrimination task. We chose this task for the present study as it yields the most pronounced Lévy flight patterns in samples of younger adults (Voss, Lerche, Mertens, & Voss, 2019; Wieschen, Voss, von Krause, Vollmoeller, & Lerche, 2022). Following the previously observed age differences regarding strategies on the exploration-exploitation continuum (Chin, Anderson, Chin, & Fu, 2015; Chin, Payne, Fu, Morrow, & Stine‐Morrow, 2015; Mata, Wilke, & Czienskowski, 2009), we expected that younger participants would show an exploratory decision style characterized by more pronounced Lévy flight patterns (i.e., larger jumps in the decision-making process). For older adults, we expected that the evidence accumulation process would be characterized by normally distributed noise as assumed by the diffusion model.

A gradual evidence accumulation style might result in less flexible behavior in contexts with large uncertainty or changing circumstances, but at the same time, might be less error-prone. In the context of a simple letter-number-discrimination task, the latter decision style might therefore be associated with slower response times, but with lower proportions of fast errors. Thus, we expect the assumed age-related differences to be mirrored by lower α-values in a sample of younger compared to a sample of older adults. Additionally, we hypothesize that, in a formal model comparison, the Lévy flight model might best describe the decision-making process of most younger adults while the standard diffusion model might be superior for the majority of older adults.

Method

Participants

We recruited participants from the diverse, multiethnic urban population of the Greater Toronto Area. Participants in the final sample included 40 younger adults (27 women, 13 men; mean age = 24.0 years, range: 18–35 years) and 40 older adults (26 women, 14 men; mean age = 70.0 years, range: 63–80 years; see Table 1 for participant characteristics). An a priori power analysis with G-Power (Faul, Erdfelder, Lang, & Buchner, 2007) indicated that at least 34 participants per age group would be required to achieve 90% power for detecting a large age difference (d = 0.80) in the parameter estimates, assuming a Type I error probability of 0.05 (two-sided). We decided to increase the sample size to 40 participants per age group to be more conservative.

Table 1. Mean parameter values, response times, and accuracy rates in the letter-number-discrimination task and participant characteristics for the two age groups.

	Younger adults		Older adults				95% CI
	M	SD	M	SD	t(df = 78)	p*	LL	UL	Cohen´s d
$\alpha$	1.59	0.19	1.78	0.17	4.87	<.001	0.11	0.27	1.09
$a$	1.41	0.51	2.13	0.57	5.92	<.001	0.47	0.95	1.32
$v_n$	−3.62	1.16	−4.24	1.08	−2.47	.22	−1.12	−0.12	−0.55
$v_l$	3.49	1.04	4.23	1.07	3.14	<.05	0.27	1.21	0.70
$t_0$	0.31	0.03	0.37	0.05	6.82	<.001	0.04	0.08	1.53
$z_r$	0.52	0.08	0.51	0.05	−0.57	1.00	−0.04	0.02	−0.13
Mean RTcorrect	0.51	0.06	0.63	0.08	8.24	<.001	0.10	0.16	1.80
Mean RTerror	0.48	0.09	0.57	0.10	4.56	<.001	0.05	0.14	1.02
Accuracy	0.96	0.03	0.98	0.02	5.78	<.001	0.02	0.03	1.17
Education	15.76	1.86	16.08	2.15	0.70	1.00	−0.58	1.21	0.16
MoCA	–	–	27.73	1.34	–	–	–	–	–
Vocabulary	17.55	3.27	22.90	4.47	6.11	<.001	3.61	7.09	1.37
Speed	91.05	14.53	71.48	14.58	−6.02	<.001	−26.05	−13.10	−1.34
Pos. mood	32.00	6.09	33.21	7.46	0.80	1.00	−1.82	4.24	0.18
Neg. mood	12.58	2.91	10.43	0.87	−4.48	<.001	−3.11	−1.19	−1.00

Note: N = 40 in each group. In the older group, error response times are based on 34 participants and df = 72 for the comparison of error response times as six participants did not commit any errors. *obtained p-values are Bonferroni-corrected to account for the 14 tests presented in this table. CI = confidence interval for the mean difference; LL = lower limit; UL = upper limit; $\alpha$ = stability parameter; $a$ = boundary separation; $v_n$ = drift rate for number stimuli; $v_l$= drift rate for letter stimuli; $t_0$ = non-decisional time; $z_r$ = relative starting point; RT_correct = response times for correct responses, in seconds; RT_error = response times for error responses, in seconds. For the t-test, response times were log-transformed and accuracy was arcsin transformed. Education = years of education; MoCA = scores (maximum of 30) in the Montreal Cognitive Assessment assessed for older adults only (Nasreddine et al., 2005); Vocabulary = raw score (maximum of 33) on the Mill-Hill Vocabulary Scale (Raven, 1982); Speed = perceptual-motor speed, assessed by the number of correct responses on the Digit Symbol Task (Wechsler, 1997); Positive and Negative mood = scores (possible values 10–50) on the Positive and Negative Affect Scale (Watson, 1988).

Younger adults were recruited with flyers on the Toronto Metropolitan University campus. Older adults were recruited from the Toronto Metropolitan University Senior Participant Pool, a database of community-dwelling research volunteers. Eligibility was determined via phone or e-mail screening, with inclusion criteria including no history of cardiovascular, psychiatric, or neurological diseases or other conditions that could affect cognitive functioning. In addition, normal or corrected to normal vision, unimpaired hearing, and English language fluency were required for participation. Older participants also had to score at least 26 on the Montreal Cognitive Assessment (MoCA (Nasreddine et al., 2005),; which was administered in person during the testing session. Data from three older participants were excluded due to low scores on the MoCA. One younger adult was excluded for showing chance-level performance in the Mill-Hill Vocabulary Test (Raven, 1982). Five participants (four younger adults and one older adult) failed to complete all parts of the study. Participants whose data were excluded were replaced so that the final sample included 40 younger and 40 older adults. All participants gave written informed consent and received 20 Canadian dollars for participating. All study procedures were approved by the research ethics board at Toronto Metropolitan University under the approval number REB 2019–175.

Procedure

Participants first completed measures of verbal intelligence (Mill-Hill Vocabulary Test (Raven, 1982),; perceptual-motor speed (Digit Symbol Substitution Test (Wechsler, 1997),; and mood (Positive and Negative Affect Schedule, PANAS (Watson, 1988).; Participants then proceeded to the experimental tasks,² which were programmed in C++ and were presented on a 17-inch computer monitor. Stimuli appeared in black Arial font (20pt) against a light gray background (RGB color values: 200; 200; 200).

In the letter-number-discrimination task, numbers from “1” to “9” and letters from “A” to “I” served as stimuli and were presented one at a time. The experiment started with 12 practice trials during which participants received feedback on the accuracy of their responses. The task consisted of four blocks with 50 trials each. In each block, 25 numbers and 25 letters were presented in random order. In addition, each block included four warm-up trials that were not included in the analysis. On each trial, a fixation cross was shown for 250 ms before being replaced by a number or a letter in the middle of the screen. This stimulus remained on the screen until the participant pressed a response key (“A” for number or “L” for letter). Finally, an empty screen appeared for 1000 ms before the next trial started.

Parameter Estimation and Model Comparison

The Lévy flight model comprises six free parameters per person: Stability parameter $\alpha$, boundary separation $a$, non-decisional time $t_0$, relative starting point $z_r$, and drift rates for number and letter stimuli ($v_n$ and $v_l$, respectively). Estimating the parameters of the Lévy flight model and conducting a model comparison is challenging because the likelihood function is unknown (Voss, Lerche, Mertens, & Voss, 2019). We therefore used the BayesFlow simulation-based method, which combines Bayesian inference with normalizing flows and does not require an explicit likelihood function like other Bayesian methods (Radev, Mertens, Voss, Ardizzone, & Köthe, 2020). Parameter estimation with BayesFlow requires that a large number of synthetic data sets (up to 100,000 in the current study) is simulated using an appropriate prior distribution for each Lévy flight model parameter. Then, a combination of two neural networks is trained to learn the relationship between the raw data and the data-generating parameter values. After this training phase, the trained networks are applied to empirical data to estimate full posteriors over the model parameters. BayesFlow has the advantage that computational load is high only during the training phase, while the inference phase is very brief and the trained networks can be re-used on all data sets to estimate parameters of the same model.³

Similar to parameter estimation, the process of simulation-based model comparison is divided into a training and an inference phase. During the training phase, a permutation invariant classifier network is trained on simulated data from the candidate models of interest. It aims at approximating the posterior model probability distribution favoring simpler models. In the subsequent inference phase, the classification network, once trained, can be applied to multiple datasets to estimate model posteriors and inform model selection (Radev et al., 2021).

Results

To increase normality, response times were log-transformed and accuracy was arcsine-transformed prior to the analysis. Data from trials with log-transformed response times that fell more than 1.5 interquartile ranges below a participant’s first quartile or more than 1.5 interquartile ranges above a participant’s third quartile were removed. This procedure resulted in the exclusion of 3.64% of trials for younger adults and 3.15% of trials for older adults.

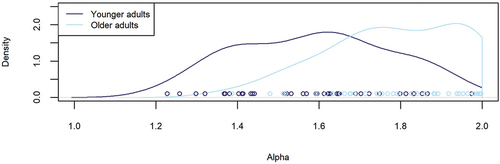
A summary of the results is presented in Table 1. Overall, older adults’ responses were slower and more accurate than those of younger adults. All model parameters, except the starting point, showed substantial age differences. As expected, older adults’ decisions were characterized by longer non-decision times and larger boundary separations (i.e., a more conservative decision strategy). Surprisingly, the absolute values of the drift rate parameter for letter stimuli were also larger for older vs. younger adults, suggesting greater cognitive speed.⁴ Most importantly, confirming the main hypothesis of this study, the stability parameter α was higher for older adults than for younger adults. Whereas for younger adults α-values were approximately normally distributed with a mean of $\alpha =1.6$, for most older adults’ α-values were close to 2.0, indicating that evidence accumulation met the assumption of the standard diffusion model in older adults, but not in younger adults (Figure 2).

Figure 2. Kernel density of mean alpha-values for the two age groups in the letter-number-discrimination task.

N = 40 in each group. Circles at the bottom represent individual α-values of the participants.

The analysis of the implied model fit showed that for the majority of participants, the Lévy flight model exhibited better goodness of fit than the diffusion model (Table 2). Moreover, mean posterior probabilities – and thus also mean Bayes factors – in favor of the diffusion model were lower for younger participants than for older participants. In the younger group, the diffusion model provided a better fit for only one out of 40 participants, whereas in the older group, the diffusion model provided a better fit for six out of 40 participants. The odds ratio comparing the odds of the diffusion model providing superior fit in older vs. younger adults was 6.88. However, the age difference was not statistically significant (95% CI [0.79, 60.06]).

Table 2. Goodness of fit for the diffusion model vs. Lévy flight model.

	Younger adults		Older adults
	M	SD	M	SD
$p_{DM}$	0.04	0.12	0.19	0.32
$B{F}_{DM}$	0.07	0.23	4.65	21.29
$N_{DM}$	1		6
$N_{LFM}$	39		34

Note: $p_{DM}=p(diffusionmodel|data)$ is the mean posterior model probability for the diffusion model given the data (i.e., the empirical response time distribution). The probability for the Lévy flight model results as $p_{LFM}=1-p_{DM}$. $B{F}_{DM}$ is the mean Bayes factor in favor of the diffusion model. $N_{DM}$ and $N_{LFM}$ give the numbers of participants for whom the diffusion model or the Lévy flight model, respectively, shows the better fit.

Discussion

A great benefit of evidence accumulator models is that they allow to disentangle different parametric components underlying age-related slowing in basic cognitive tasks. For example, previous diffusion model analyses revealed that age-related increases of response times are not primarily caused by a reduced mental speed (e.g. (Theisen, Lerche, von Krause, & Voss, 2020; von Krause, Radev, & Voss, 2022)., To our knowledge, the present study is the first to apply the Lévy flight model, a recently developed variant of the diffusion model, to study cognitive aging. In contrast to the diffusion model, the Lévy flight model explains fast errors as a result of jumps in evidence accumulation. The impact of such discontinuities in the accumulation of evidence is mapped by an additional model parameter α (Voss, Lerche, Mertens, & Voss, 2019).

In the present experiment, younger adults responded more quickly but less accurately compared to older adults. Lévy flight model analyses revealed, as hypothesized, that older adults use a more conservative decision style and need more time for non-decisional processes. Somewhat unexpected, absolute drift rates, indicating speed of information accumulation, were even higher for older adults compared to younger adults. This finding has so far mainly been observed in tasks with lexical stimuli (Theisen, Lerche, von Krause, & Voss, 2020). In the present study, this finding might have resulted from the fact that drift rates are typically more strongly associated with accuracy than with response times (Ratcliff & McKoon, 2008; Ratcliff, Thapar, & McKoon, 2004). Older adults’ high accuracy may be attributable to specific features of the sample. Older adults included in the study were likely in better physical and mental health than the general population of same-age peers. Motivational factors may also have played a role, with several older participants indicating they participated in the experiment to stay mentally active rather than to receive monetary compensation and expressing frustration when they committed an error in the task. Indeed, six out of 40 older participants did not make any mistakes across the 200 task trials, which was not the case for any of the younger adults.

The main aim of the present study was to test for qualitative differences in the type of evidence accumulation. We speculated that older adults use a more gradual way of accumulating evidence (as assumed by the diffusion model), whereas for younger adults, we expected that decision making was more strongly influenced by sudden changes (“jumps”) in evidence accumulation. Confirming these assumptions, we observed higher values of the stability parameter $\alpha$ for older adults compared to younger adults. A superior model fit of the Lévy flight model was observed for the majority of participants. However, the advantage of the Lévy flight model was especially pronounced in the younger sample.

In addition to a more conservative decision style and a longer duration of non-decisional processes, reduced proportions of “jumps” in the evidence accumulation process might contribute to the finding of increased response times in older age. Following the Lévy flight foraging hypothesis, a discontinuous information search represents an exploratory but risky behavior that can be advantageous in situations where little knowledge about the given circumstances exists (Viswanathan, Raposo, & Da Luz, 2008). However, in the context of a simple letter-number-discrimination task with little ambiguity of the presented stimulus, this strategy does not seem to lead to an advantage. It seems plausible that, in comparison to older adults, younger adults engage more in this kind of behavior as this age group typically shows a stronger tendency to adapt a more exploratory information accumulation style in various studied paradigms and shifts to unknown sources of information more quickly when the present behavioral strategy becomes inefficient (Chin, Anderson, Chin, & Fu, 2015; Chin, Payne, Fu, Morrow, & Stine‐Morrow, 2015; Mata, Wilke, & Czienskowski, 2009).

Finally, some limitations of the present study need to be addressed. Firstly, the aforementioned strict inclusion criteria for participation in the study might have resulted in a sample that is not representative of the general population. Future studies should conduct age comparisons of the Lévy flight model parameters in more representative samples. It would also be important to extend the current findings to other experimental paradigms, such as memory or lexical decision tasks. It is possible that, as in the case of the drift rate, varying patterns regarding age differences emerge depending on the stimulus content (Theisen, Lerche, von Krause, & Voss, 2020). Finally, the psychological meaning of the stability parameter α needs to be assessed in more detail. Future studies should further clarify whether an interpretation of α in the context of human decision-making is equivalent to the interpretation of an explorative behavior described in the animal foraging literature (Viswanathan, Raposo, & Da Luz, 2008), for example, by assessing possible external correlates of α. Even though the application of Lévy flights in the field of age-related differences in decision-making is still in its early stages, the present study provides a first indication that Lévy flights in this context can help gain a deeper understanding of qualitative age differences in evidence accumulation and thus, an age-related slowing of response times.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This research was supported by the Natural Sciences and Engineering Research Council of Canada under Discovery Grant 2018-04455, a grant from the German Research Foundation to Andreas Voss under Grant Nr. VO1288/5-1, a grant to the German Research Foundation´s Research Training Group “Statistical Modeling in Psychology” (SMiP; GRK 2277), a grant to Germany ́s Excellence Strategy EXC 2181/1 - 390900948 (the Heidelberg STRUCTURES Excellence Cluster) and a scholarship from the German Academic Exchange Service (DAAD) to Eva Marie Wieschen.

Notes

1. Note that the term “Lévy flights” used in the literature on animal foraging and human cognition (including the present article) refers to Lévy-like behavior that describes the behavior of agents with memory. By contrast, classic Lévy flights are memory-less.

2. In addition to the letter-number-discrimination task described here, participants completed a second unrelated experimental task. The second task is not reported here as its aims lay beyond the scope of the current article.

3. Code for applying BayesFlow is available at: https://github.com/stefanradev93/BayesFlow

4. A median split by accuracy in both age groups was conducted to further analyze the finding of higher drift rates for letter stimuli in the older group. A subsequent 2(accuracy) x 2(age group) ANOVA revealed that in addition to the main effect of age (F(1,76) = 11.30, p < .01), there was a significant main effect of accuracy (F(1,76) = 13.47, p < .001), suggesting higher drift rates for higher accuracy. Age differences in drift rate for letter stimuli are attributable to a proportion of younger adults who showed lower accuracy rates than the rest of their age group and all older adults, as indicated by a significant interaction effect (F(1,76) = 4.25, p < .05).