Production system design for quality robustness

Abstract

In automotive assembly plants, vehicles with defects are either repaired (e.g., components are exchanged, scratches are polished, etc.) or reworked (e.g., the whole vehicle is repainted) to maintain high product quality. The performance of vehicle quality is typically characterized in terms of the first time quality and also the quality buy rate. First time quality is defined as the good job ratio of all first time processing jobs, while the quality buy rate is the good job ratio of all processed jobs, including the first time jobs and reworked jobs.

In this paper, we study a repair and rework system at an automotive paint shop with random first time quality. Specifically, we show that paint quality, in terms of quality buy rate, can be described by a function of repair capacity and first time quality. Increasing the repair capacity can improve the quality buy rate and reduce unnecessary repaints. Variations in first time quality may lead to a reduction in the quality buy rate and an increase in unnecessary repaints, and consequently, a substantial waste of production capacity and materials. In addition, we observe that the average quality buy rate depends primarily on the mean and coefficient of variation of the first time quality rather than its complete distribution. Based on these results, we introduce the notion of quality robustness and show that the design of a production system should accommodate randomness in first time quality to achieve a robust quality buy rate. Finally, a case study on a repair and rework system redesign to improve paint quality is presented.

Keywords:

• Quality robustness
• first time quality
• production system design
• repair and rework
• automotive paint shops

1. Introduction

1.1. Motivation

Production system design has an impact on product quality. However, little research has been performed to address this impact explicitly. Inman et al. (2003) claim that this impact can be significant and that promising research opportunities exist in studying the coupling or interaction between production system design and product quality. This paper is intended to contribute to the research in this direction.

Specifically, we study a repair and rework system at an automotive paint shop. In these systems, to ensure quick delivery of vehicles with a high paint quality, defective jobs are repaired or reworked, depending on the type of defect. The term “repair” refers to additional work performed on jobs at a (separate) repair facility, while the term “rework” refers to total reprocessing of jobs on the main line. For example, vehicles having color defects after the coating process are either repaired at the repair facility or sent back to the painting booths for repaint. Similar systems are also typical for other large volume manufacturing industries. In printed circuit board production, a testing machine usually follows a wave soldering process to test the boards, and those which cannot pass the test are corrected in the rework center and sent back for further testing. In electronic packaging operations, imperfect packages are first cleaned up and then repackaged. Therefore, in general, repair and rework are important elements of a production system. They have attracted a considerable amount of research attention, mostly focused on performance evaluation, throughput improvement, production control or other productivity issues.

In addition to productivity, quality is another important measure of production system performance. However, the problem of the effect of system design on product quality in automotive paint shops (and other repair and rework systems) is less well addressed. In paint shops and many manufacturing facilities, product quality is typically measured in terms of first time quality (i.e., the good job ratio of all first time processing jobs) and quality buy rate (i.e., good job ratio of all processed jobs, including first time jobs and reworked jobs). Both are important quality measurements and have been widely used to characterize the quality performance. In order to achieve high paint quality in paint shops, improving first time quality is a primary objective. Substantial effort has been devoted to continuously monitoring first time quality and identifying and correcting root causes of paint defects. These include improving the environment to eliminate dirt, checking the appropriate mixture of painting materials, scheduling preventative maintenance of painting guns, etc. In addition to the above process improvement efforts, it is also important to reduce unnecessary repaints that can occur due to inadequate design of repair facilities. Such unnecessary repaints will lead to a reduction of quality buy rate and a substantial waste of production capacity and paint materials. Therefore, appropriate design of repair and rework systems in a paint shop is critical. An application study in an automotive paint shop by Li et al. (2007) shows that, for a given first time quality, the quality buy rate can be improved and unnecessary repaints reduced by increasing the repair capacity.

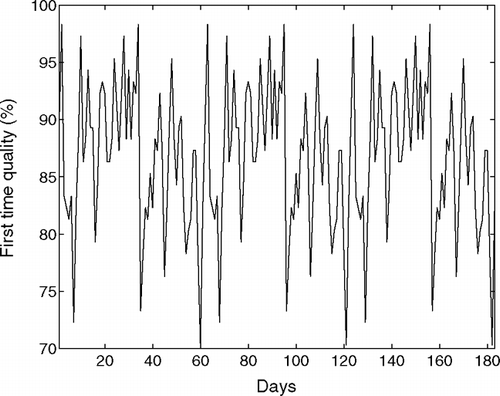
The study in Li et al. (2007) provides a reasonable guide or starting point to improve quality buy rate in paint shops. However, for complex painting processes in general, first time quality may not be constant but rather varies randomly, due to changing operating conditions. An illustration of variability in first time quality in automotive paint shop is shown in Fig. 1. (Due to confidentiality, the data shown in this paper have been modified.) Therefore, not only system design but also randomness in first time quality can affect the overall quality buy rate. To address this issue, in this paper, we extend the study in Li et al. (2007) to the case of random first time quality, and introduce the notion of quality robustness in production system design. Specifically, we study the problem of designing the repair and rework system so that the quality buy rate is robust to fluctuations in the first time quality, and we refer to this as quality robustness design.

Fig. 1 Illustration of variability of first time quality in repair and rework system in automotive paint shop.

The main contributions of this paper are as follows.

1.	In the random first time quality environment, we develop closed-form expressions to characterize the quality buy rate and number of unnecessary repaints as functions of the repair capacity, first time quality and routing parameters.
2.	We investigate how the randomness in first time quality affects the quality buy rate and number of unnecessary repaints.
3.	We observe that the first two moments, rather than the complete distribution, of first time quality have the largest effects.
4.	We introduce a case study to illustrate the design of repair capacity to achieve a robust quality buy rate.

The remainder of the paper is structured as follows. In Section 1.2, related literature is reviewed. Section 2 introduces the repair and rework system in an automotive paint shop. Section 3 presents the model and formulates the problem. The mathematical description and analysis are provided in Section 4. The effects of variability in the first time quality are introduced in this section. A case study is described in Section 5. Finally, the conclusions are formulated in Section 6. All proofs are given in the Appendix.

1.2. Literature review

As previously pointed out, little effort has been made to address the impact of production system design on product quality. Among the limited related references, Son and Park (1987) present a measure of productivity, quality and flexibility for production systems. Jacobs and Meerkov (1991) study the perturbation in the average steady-state production rate by quality inspection machines for an asymptotically reliable two-machine one-buffer line. This type of analysis is extended to a highly reliable multi-machine line by Han et al. (1998). Bulgak (1992) discusses the tradeoffs between productivity and product quality, as well as their impact on optimal buffer designs. Khouja et al. (1995) delineate the tradeoff between throughput and quality for a robot whose repeatability deteriorates with speed. Deliman and Feldman (1996) study imperfect inspection and rework of defective items in serial lines. Stochastic search techniques (generic algorithms and simulated annealing) are used by Viswanadham et al. (1996) to investigate the impact of inspection allocation in manufacturing systems (serial and non-serial) from the cost perspective. Urban (1998) analyzes the competing effects of large or small batch sizes and develops a model for the interaction between batch size and quality. In addition, Cheng et al. (2000) use quantitative measures to deduce that U-shaped lines produce better quality products. Matanachai and Yano (2001) propose a new line-balancing approach to improve quality by reducing work overload.

Inman et al. (2003) review the related literature, present evidence for the impact of production system design on quality and propose several research topics from the automotive industry perspective. Finkelshtein et al. (2005) study off-line inspection following an unreliable production process by developing a model to minimize the expected inspection and disposition error cost. Kim and Gershwin (2005) introduce an integrated model of a two-machine one-buffer line with inspection and information feedback to study both quality and quantity performance in terms of good job production rate. Li and Huang (2007) use a Markov chain model to evaluate quality performance in flexible manufacturing systems and investigate the impact of different production scheduling policies on product quality.

Repair and rework are important parts of production systems in many manufacturing industries, such as the semiconductor, electronics, packaging and process industries (e.g., Pendse et al. (1994), Nguty et al. (2000), Sha et al. (2001)), as well as the automotive industry. A lot of the effort in the areas of design and continuous improvement has been devoted to them (for instance, Lim et al. (1990), Lim and Meerkov (1993), Narahari and Viswanadham (1994), Agnihothri and Kenett (1995), Liu and Yang (1996), Narahari and Khan (1996), Yerelan and Tan (1997), Humphrey et al. (1998), Chern and Yang (1999), Li (2004a, 2004b, 2005), Li et al. (2006)). Specifically, Narahari and Viswanadham (1994) study the transient performance of manufacturing systems using unstable queueing networks with returning semi-finished part and re-entrant lines as examples. Narahari and Khan (1996) analyze a re-entrant manufacturing system with inspections, scrap and rework and present an approximate technique based on mean value analysis to predict steady-state cycle times and throughput rate. Liu and Yang (1996) consider a single-stage imperfect production system processing both new and rework jobs. An optimal control policy is presented to switch between new and rework jobs to maximize the average profit. Moreover, a threshold control policy to study a similar system is introduced by Chern and Yang (1999). Yerelan and Tan (1997) develop a flexible decomposition framework and extend it to the analysis of a work cell consisting of a workstation, a rework station and finite buffers fed by a Poisson stream of discrete parts. Humphrey et al. (1998) examine the behavior of various inventory stocking methodologies in repair and rework operations. Li (2004a) introduces overlapping decomposition to evaluate the performance of production systems with rework loops. This idea is extended in Li (2005) to the analysis of more complex production systems.

In addition to the theoretical development, several case studies have been applied in automotive paint shops. Lim et al. (1990) introduce a homogeneous, asymptotically reliable serial line model and apply it to analyze the throughput of an automotive paint shop. Lim and Meerkov (1993) extend the model to a closed serial line and optimize the number of carriers in the paint shop and the capacity of the feedback buffer, which leads to substantial improvement in the system's performance. Li (2004b) studies throughput improvement using an overlapping decomposition method in automotive paint shops where multiple rework loops exist. Finally, Li et al. (2007) investigate the impact of repair and rework system design on paint quality through an application in automotive paint shop operation. The case of constant first time quality is addressed in this work.

Although useful results have been obtained in the above studies, the coupling between production system design and product quality under the random first time quality scenario has not been studied explicitly. The goal of this paper is to develop a method to address this issue and apply it on the factory floor of an automotive paint shop.

2. Repair and rework system in automotive paint shops

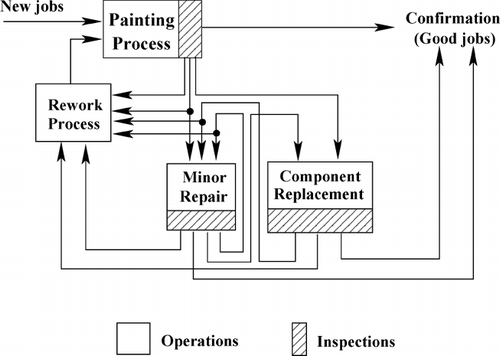
A typical repair and rework system in automotive paint shops is illustrated in Fig. 2. Jobs from painting operations (including painting booths, ovens, etc.) are checked for quality defects at painting process inspection stations. Good jobs are sent to the confirmation station. As described in Li et al. (2007), a defective job can be routed to three locations: rework (repaint), minor repair and component replacement, according to the nature and severity of the defects. Jobs with severe defects are sent back to the rework process for repaint, where the whole vehicle is painted again. Jobs with minor defects are repaired either through component replacement or by minor repair. At component replacement, one or more defective components in a job are replaced with new ones and inspected again. For instance, some panels may be exchanged. If the job quality satisfies the standard, it is routed to the confirmation station; otherwise, it is transferred to either minor repair or rework. Minor repair is used to polish light scratches, remove small dents, etc. After exiting minor repair, a good quality job is routed to the confirmation station, while jobs still with defects again have three options: to component replacement, back to minor repair again or to rework (repaint).

Fig. 2 Illustration of the job flow in the repair and rework system in an automotive paint shop.

Typically, there is no capacity constraint at component replacement, as the exchange operation is relatively quick. However, minor repair may be constrained by its capacity because many of the repairs require more floor space, involve manual operations, and are followed by baking operations, which usually take a much longer time. In addition, some paint shops keep inadequate buffers in the minor repair facility, which again limits the repair capacity. Moreover, the repair facility design in many paint shops is based on a specific value of the first time quality. In practice, this design value may not be achieved. Even if it can be achieved on average, fluctuations can still result in a lower first time quality. In either case, insufficient repair capacity may occur, which may lead to blockage of the painting process. This blockage may result in severe problems, for example, over-baking of vehicles in ovens after color coating. Therefore, to avoid blockage, a typical solution is to reroute those jobs that only need minor repair to rework instead, and these vehicles are then unnecessarily repainted.

Although rerouting jobs may solve the blockage problem, a new problem is introduced. It is quite often that the repaint quality is not as good as the first time quality. This may be due to duplication of the original painting process, where vehicles have additional exposure to a non-dirt-free environment. Therefore, a new quality problem may be encountered in addition to previous ones. In this case, rerouting the jobs for unnecessary repaints will lead to a reduction of the quality buy rate. In addition, more paint materials and production capacity are wasted. Moreover, in many automotive paint shops, vehicles are sequenced into different color batches to reduce changeovers and cost and enhance paint quality. Unnecessary repaints will cause more frequent color changes and a disruption of scheduled batches, which may increase painting cost and reduce the first time paint quality.

As a result, some questions arise. What would be a better design option to ensure a desired quality buy rate? How do we quantify the tradeoffs between repair capacity and quality buy rate? How can the system accommodate the variation in first time quality so that quality buy rate is robust? This paper is intended to provide answers to these questions.

3. Model and problem formulation

To analyze the repair and rework system discussed above, we introduce the following notation.

n	=	production capacity, i.e., number of first time jobs per day;
q(t)	=	first time quality, i.e., percentage of good jobs after first processing at painting operations in day t;
αx	=	probability a defective job should go to part exchange after painting process inspection;
αs	=	probability a defective job should go to minor repair after painting process inspection;
αr	=	probability a defective job should go to rework after painting process inspection;
βsx	=	probability a job should go to part exchange after minor repair;
βss	=	probability a job should go to minor repair again after minor repair;
βsr	=	probability a job should go to rework after minor repair;
βsg	=	probability a job has good quality after minor repair;
βxs	=	probability a job should go to minor repair after part exchange;
βxr	=	probability a job should go to rework after part exchange;
βxg	=	probability a job has good quality after part exchange;
N	=	minor repair capacity (maximum number of jobs can be repaired) per day;
Q(t)	=	quality buy rate of all jobs at painting process inspection in day t

Note that since the total probability is equal to one, the following relationship exists:

Using this notation, we introduce the following assumptions.

1.	First time quality q(t) (in day t) is a random variable taking values in (0, 1). q(1), q(2), …, is a sequence of independent identically distributed random variables. Similarly, the quality buy rate Q(t) (in day t) is also a random variable that has the range (0, 1).
2.	A job can be reworked or repaired multiple times. No scrapping of jobs is assumed.

Remark 1. In many automotive paint shops, vehicles can be repainted at most three (or, in some shops, four) times. The introduction of assumption (2) will not lead to a large discrepancy, since in most cases the defective job ratio is small and therefore the probability that a job has to be scrapped is very small. For example, if 5% of new and 10% of repainted vehicles are reworked, then roughly only 0.05% of jobs need to be repainted more than three times.

3.	All rework jobs have same probability of becoming good jobs, independent of the number of times they have been reprocessed, i.e., the good job ratio of all reprocessed jobs is the same for each day.
4.	Repaint quality, q r(t), is proportional to first time quality, i.e., q r(t) = ρ q(t), where ρ is a constant and 0 < ρ ≤ 1.
5.	All routing probabilities are constant in time. In other words, the probabilities that a defective job should go to component replacement, minor repair or rework are kept unchanged whether the job is a first time processed job or multiple time reprocessed job.

Let another random variable, n _r(t), be the number of jobs routed to rework in day t. Clearly, n _r(t) is a function of first time quality and minor repair capacity. Then, the quality buy rate, Q(t), of the painting process in day t is defined as

where the numerator is the total number of good quality jobs and the denominator is the total number of jobs processed in day t.

The problem to be addressed in this paper is: given assumptions 1–5, develop a method to analyze the quality buy rate for the painting process as a function of random first time quality and minor repair capacity.

A solution to the problem is presented below.

4. Mathematical description and analysis

4.1. Performance evaluation

Consider the repair and rework system shown in Fig. 2. Define _s(t) as the number of jobs that should be routed to minor repair in day t. Note that _s(t) includes jobs that may have previously undergone minor repair on the same day t. Then, the actual number of jobs routed to minor repair on day t, n _s(t), is equal to min { _s(t),N}. Let n _x(t) be the number of jobs routed to component replacement in day t. By conservation of flow, the following equations describe the system behavior:

Using the above equations, a closed formula to calculate quality buy rate can be derived.

Theorem 1. Under assumptions 1–5, the quality buy rate Q(t) is given by

where

Proof. See the Appendix.

Equation (5) is similar to the one developed by Li et al. (2007) for the constant first time quality case, but with randomness included. Note that in Equations (6), (7), (8), N _s(t) denotes the smallest minor repair capacity to accommodate all the jobs needing minor repair in day t, and α_s′ and α_r′ represent the actual probabilities a defective job is routed to minor repair and rework, respectively (after taking into account the defective jobs exiting from component replacement and minor repair). Clearly, when minor repair and component replacement have a 100% quality rate, i.e., β_sg = β_xg = 1, we have α_r′ = α_r and α_s′ = α_s.

Again analogous to the constant first time quality case, we have Q(t) ≤ q(t) due to ρ ≤ 1. Thus, as discussed in Section 2, when the capacity of minor repair is insufficient, rerouting the jobs needing minor repair to repaint reduces the quality buy rate of the painting process. In addition, more materials and resources are consumed during the unnecessary repaints and the throughput of the painting process is also decreased. Therefore, another important measure, which can be used to characterize the additional cost (or waste), is the number of rerouted (or unnecessarily repainted) jobs, i.e., jobs that should be routed to minor repair, but, due to capacity constraint, are rerouted instead to repaint. We denote this random variable by n _a(t).

Corollary 1. Under assumptions 1–5, the number of rerouted jobs n_a(t) can be calculated as follows:

Proof. See the Appendix.

Clearly, more rerouted jobs may lead to a smaller quality buy rate, greater loss of throughput and more waste of materials, labors, etc. Therefore, it is important to maintain sufficient minor repair capacity to ensure the desired quality buy rate and to reduce the number of rerouted jobs.

Equations (5) and (9) provide quantification of the quality buy rate and number of rerouted jobs as functions of the random first quality quality and minor repair capacity. Their expected values, and _a, are often used to evaluate system performance. These values are used as performance indices for subsequent analysis.

4.2. Structural properties

Similar to the constant first time quality case, increasing the minor repair capacity leads to improvement in the quality buy rate and reduction of number in the rerouted jobs.

Corollary 2. Under assumptions 1–5, the average value of the quality buy rate, , and the average number of rerouted jobs, _a, are monotonically increasing and decreasing functions of N, respectively.

Proof. See the Appendix.

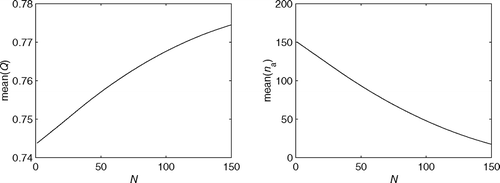
This property is illustrated in Fig. 3, where the first time quality q(t) is distributed uniformly in the interval [0.65, 0.95], and ρ = 0.6. The routing probabilities are defined as

Remark 2. In the constant first time quality case in Li et al. (2007), the quality buy rate is a constant when minor repair has sufficient capacity (greater than N _s(q), when q is a constant); however, here we observe that is monotonically increasing. Only when the minor repair capacity is so large that it is greater than N _s(min {q(t)}), would be a constant.

Fig. 3 Monotonicity of the average quality buy rate and number of rerouted jobs with respect to minor repair capacity.

In production system design practice, it is typical to use the average value of the first time quality. Let denote the expected value of the number of rerouted jobs using a random first time quality and n _a() be the number of rerouted jobs using the mean of the first time quality. We obtain the following corollary.

Corollary 3. Under assumptions 1–5,

Proof. See the Appendix.

Corollary 3 implies that if we design the system using the average value of the first time quality, we will predict a smaller number of rerouted jobs. Hence, designers may select a smaller minor repair capacity to accommodate this “smaller” number of rerouted jobs. This capacity design may lead to a smaller quality buy rate and result in a larger number of rerouted jobs, i.e., unnecessary repaints. Therefore, variability in first time quality should be taken into account in the design process.

4.3. Effect of the variability of first time quality

Intuitively, one may expect that a large variability in the first time quality may lead to a decrease in the quality buy rate, and an increase in the number of rerouted jobs per day. Using the method developed above, we provide a quantification of these effects for various values of the minor repair capacity.

To analyze the behavior of the quality buy rate and number of rerouted jobs as functions of the variability in first time quality, we assume that the first time quality can be described by a beta distribution. The reason for using this distribution is that its range of values is over a finite interval. It is therefore suitable for characterizing first time quality, which has a finite range (0–100%). In addition, it also has two parameters which enable us to place the mean and coefficient of variation (CV) with more freedom. The probability density function (pdf) of the beta distribution is

where

Consider the repair and rework system with the mean of first time quality = 0.85 and ρ = 0.6. The routing probabilities are defined according to Equation (10). To analyze the quality buy rate degradation for various minor repair capacities, we consider the minor repair capacity N to have values of 50, 100 and 150. The CV of the first time quality is selected from the range 0.025–0.4, as shown in Table 1. The constant first time quality case (CV = 0) is also included for comparison. The behavior of the average quality buy rate and average number of rerouted jobs as a function of the CV of the first time quality is shown in Fig. 4. Examining these results, we conclude the following points.

1.	For a smaller variability in the first time quality (e.g., CV ≤ 0.2), the average quality buy rate is practically insensitive to CV. However, as expected, when CV is large, the degradation of with respect to CV is significant.
2.	Compared to , the average number of rerouted jobs a is much more sensitive to variability in the first time quality. a is relatively unchanged only when CV ≤ 0.1. After that, a increases rapidly with respect to CV.
3.	Again as expected, increasing the minor repair capacity N leads to an increase in and a decrease in a. However, this improvement is very slight compared to the dramatic changes due to variations in the first time quality when CV is large.

Fig. 4 Average quality buy rate and number of rerouted jobs as a function of the coefficients of variation of the first time quality.

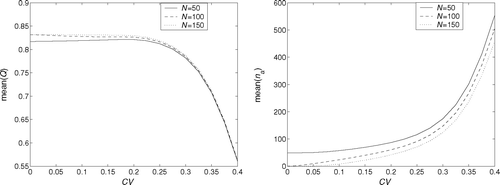
Table 1 The parameters of the considered beta distributions

	CV
	0.025	0.05	0.075	0.1	0.125	0.15	0.175	0.2	0.225	0.25	0.275	0.3	0.325	0.35	0.375	0.4
ω	42.2029	10.4382	4.5559	2.4971	1.5441	1.0265	0.7143	0.5118	0.3729	0.2735	0.2	0.1441	0.1006	0.0661	0.0382	0.0154
ν	239.15	59.15	25.8167	14.15	8.75	5.8167	4.048	2.9	2.113	1.5	1.1335	0.8167	0.5701	0.3745	0.2167	0.0875

Therefore, to ensure a desired quality buy rate and to minimize the number of rerouted jobs, reducing the variability in the first time quality is very important. Figure 4 indicates that, even if the minor repair capacity is sufficient for the average first time quality, random variations may result in a substantial number of jobs being rerouted. This validates the conclusion in Corollary 3. For example, N = 100 is sufficient when the first time quality is constant. However, when CV = 0.2, roughly on average 50 jobs will be rerouted per day. When the variation is large, the degradation in the whole system performance can be catastrophic.

Remark 3. Unexpectedly is insensitive to N when CV is large. This is due to the fact that when CV is large, in order to maintain = 0.85, there must exist many smaller values of q(t) that can lead to a dramatic decrease in Q(t) and therefore may override the effect of large repair capacity. However, n _a(t) is quite sensitive to N, which verifies that keeping an appropriate N is important to reduce the waste of materials and operating costs as well as to maintain higher throughput levels.

4.4. Performance as a function of the CV of the first time quality

The method of Section 4.1 implies that system performance (i.e., the average quality buy rate and average number of rerouted jobs) can be obtained if the distribution of the first time quality is known. However, it is difficult to determine the distribution of the first time quality on the factory floor. Below, using examples, we show that the system performance for various distributions of the first time quality remains practically the same, as long as their CVs are identical. This implies we can use any distribution to calculate and _a without sacrificing much accuracy.

The distributions we consider are the uniform, beta and power function distributions (since they all have ranges in a finite interval). Since the uniform and power function distributions cover different values of the mean and CV, we compare each one separately with the beta distribution, using different parameter sets. The pdfs, means and CVs of these distributions are shown in Table 2.

Table 2 The considered first time quality distributions

	pdf	Mean	CV
Beta	x ^ν−1(1−x)^ω−1/B(ν,ω)	ν/ν+ω	√ω/ν(ν+ω+1)
Uniform	1/b−a	a+b/2	b−a/√3(a+b)
Power function	cx ^c−1	c/c+1	1/√c(c+2)

Using the results in Section 4.1, it is possible to obtain analytical expressions for and _a for a uniformly distributed first time quality and we will use these expressions for subsequent analysis. These analytical expressions are validated by comparing with numerical solutions using q(t) randomly generated from uniform distributions. In this case, after some manipulations, we obtain the following:

Theorem 2. Under assumptions 1–5, assumes that q(t) follows uniform distribution in interval [q _a ,q _b ], the average value of quality buy rate, , can be calculated as

where

Moreover, the average number of rerouted jobs can be calculated as

Proof. See the Appendix.

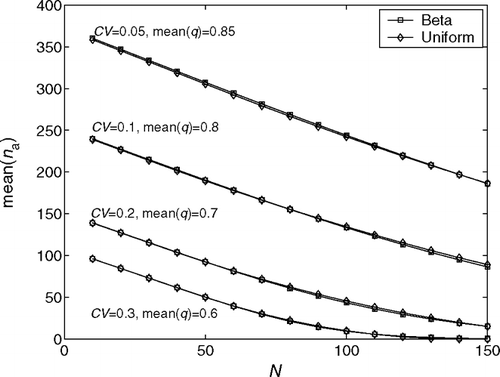
To compare the effects of distributions on the quality buy rate and number of rerouted jobs, we first consider the beta and uniform distributions, with CVs equal to 0.05, 0.1, 0.2 and 0.3. The expected values of both distributions are 0.85, 0.8, 0.7 and 0.6, respectively. Using these two pdfs, we evaluate the average quality buy rate and average number of rerouted jobs as functions of the minor repair capacity N. The results are shown in Fig. 5 and Fig. 6, respectively. As we can see, for every value of N, we obtain the almost identical and _a, as long as the CVs are the same.

Fig. 5 Effects of the beta and uniform distributions of the first time quality on the average quality buy rate.

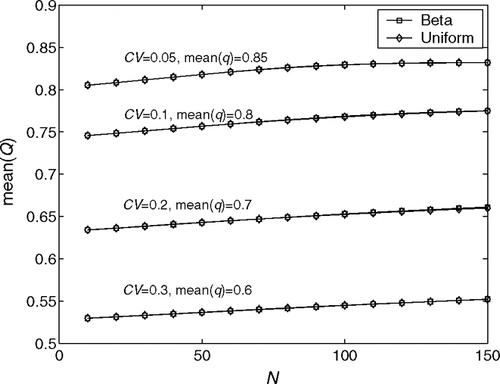
Fig. 6 Effects of the beta and uniform distributions of the first time quality on the average number of rerouted jobs.

Next we consider the beta and power function distributions. The CVs are selected as 0.1, 0.2, 0.3 and 0.4, while the expected values of the first time quality take values of 0.9005, 0.8039, 0.7127 and 0.6286, respectively. Similar results are obtained and are illustrated in Fig. 7 and Fig. 8.

Fig. 7 Effects of the beta and power function distributions of the first time quality on the average quality buy rate.

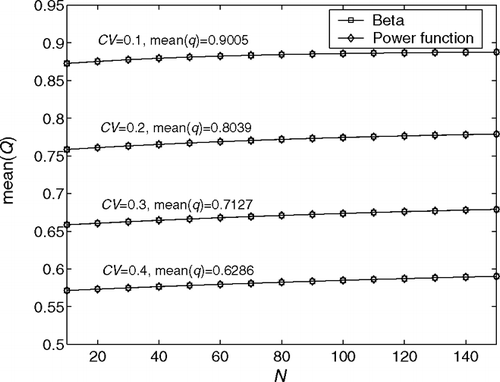
Fig. 8 Effects of the beta and power function distributions of the first time quality on the average number of rerouted jobs.

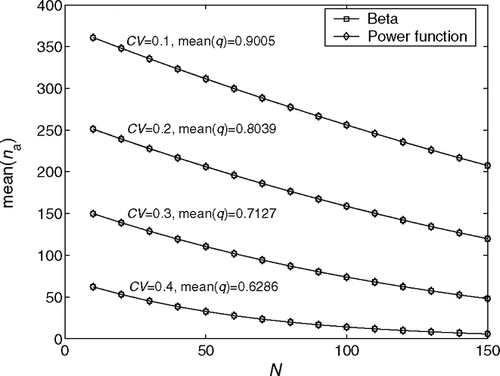
From these comparisons, we conclude that for every value of N, and _a are almost the same for all the considered pdf values as long as the CVs are identical. Then, the following hypothesis can be formulated.

Hypothesis 1. In the repair and rework system in an automotive paint shop defined by assumptions 1–5, the average quality buy rate and average number of rerouted jobs for all first time quality distributions with identical mean and coefficient of variation remain practically the same.

5. Case study

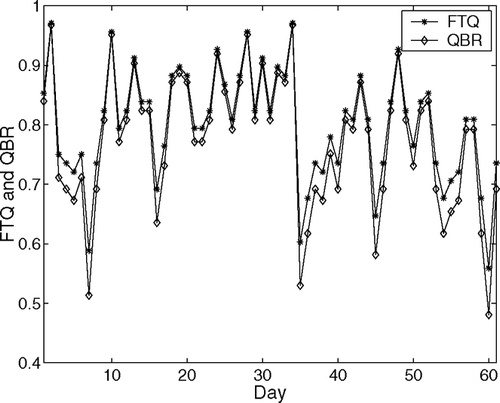
In this section, we introduce a redesign project at an automotive paint shop. Consider the repair and rework system shown in Fig. 2. The following information is collected. The routing probabilities are α_s = 0.5, α_x = 0.35, α_r = 0.15, β_xr = β_xs = β_ss = β_sr = β_sx = 0.05. The daily production volume is n = 765, and ρ = 0.5. The average first time quality is = 80% and CV = 0.116. The minor repair capacity is N = 90, which is almost sufficient to avoid rerouted jobs if the first time quality is constant. The average quality buy rate is 0.7725, and the average number of rerouted jobs is 30.83. Figure 9 illustrates the daily First Time Quality (FTQ) and Quality Buy Rate (QBR). It is clear that QBR is consistently lower than FTQ.

Fig. 9 Daily first time quality and quality buy rate.

The goal of this project is to provide recommendations to redesign the repair system to improve the QBR and reduce the number of unnecessary repaints (rerouted jobs). To do that, we first validate the model introduced in Section 4. Then, using the validated model, we discuss design options.

By assuming that the FTQ follows a beta distribution with mean and CV equal to 0.8 and 0.116, respectively, we obtain = 0.7726 and _a = 31.07. Compared with actual values, the differences are only 0.01 and 0.78%, respectively, which are within the acceptable range. Therefore, the model and analysis are validated. We will use this model to redesign the minor repair capacity.

Remark 4. Note that if a constant FTQ is used, we obtain n _a() = 6.69, which is much lower than the actual number. It verifies Corollary 3 that using a constant FTQ in the design may lead to a substantial underestimation of the number of rerouted jobs.

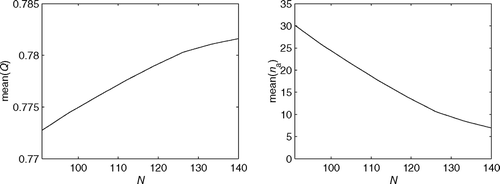
In order to make the system more robust to randomness in the FTQ, we increase the capacity of minor repair from 90 to 140. The goal is to reduce the number of rerouted jobs (for instance, close to n _a()). We obtain that and _a increase or decrease to 0.7816 and 6.95, respectively, as illustrated in Fig. 10. Therefore, the new system would be able to accommodate the variations in the FTQ to achieve a better QBR and a smaller number of unnecessary repaints. In addition, discrete-event simulations should be carried out based on this analysis to determine the details of capacity design and parameter settings, such as buffers, cycle times, etc.

Fig. 10 Illustration of the improvement in

and reduction of

_a.

Although increasing the minor repair capacity may increase investment cost and repair workforce, it improves QBR, reduces material cost by avoiding unnecessary repaints and can finally improve system throughput. For simplicity, here we only consider the cost of investment, operation and materials. Let C _se and C _so denote the unit investment cost and unit daily operation cost for increasing minor repair capacity, respectively. Also, define C _r as the daily operation cost (including labor, material, etc.) for each repainted vehicle. Then, over a long time period T, the average saving S we can obtain is

where N ₁ and N ₂ are the minor repair capacity before and after the capacity increase, respectively. Typically, the cost of repainting a vehicle is significantly higher than for repairing one, i.e., C _r ≫ C _so. Therefore, the saving we can obtain is usually much larger than the cost of increasing the repair capacity over a long time period. In addition, there would be savings of an improved QBR and FTQ, more production capacity, etc. Therefore, for systems with a large volume of production and high-profit products, the long-term impact of this improvement will be significant. The actual decisions made about the system will depend on a detailed cost analysis.

6. Conclusions

In this paper, through a case study at an automotive paint shop, we investigated the impact of production system design on product quality in a random FTQ environment. Specifically, we have shown that the quality performance of a repair and rework system in a paint shop can be improved by designing the minor repair capacity appropriately. In addition, we introduced the notion of quality robustness in production system design so that the QBR is robust to randomness in the FTQ and unnecessary repaints can be reduced. Moreover, through examples, we have shown that the system performance primarily depends on the mean and CV rather than the complete distribution of the FTQ.

Appendix

Due to space limitation, we provide here only the sketches of the proofs. The complete proof can be found in Li et al. (2005).

Proof of Theorem 1. The following two cases are considered:

•	Case 1: minor repair has sufficient capacity;
•	Case 2: minor repair does not have enough capacity.

	Case 1: When minor repair has enough capacity, no jobs needing minor repair will be rerouted to rework. Thus Substitute Equation (A2) into Equation (A3), then we have: where Therefore and Substituting into Equation (A1) we obtain: where It follows that and Finally we obtain the quality buy rate as
	Case 2: When minor repair does not have sufficient capacity, some jobs that only need minor repair will be rerouted to rework. Then we have: Substituting Equation (A11) into Equation (A12), we have that: Substituting into Equation (A10) we obtain: Therefore Finally, the quality buy rate is

Proof of Corollary 1. When minor repair has sufficient capacity, i.e., N ≥ α_s′ n(1−q(t))/1−(1−ρ q(t))α_r′, there is no job being rerouted. Thus

When minor repair does not have enough capacity, N < α_s′ n(1−q(t))/1−(1−ρ q(t))α_r′, from (A13) we have

Following from Equation (A12) we obtain:

Proof of Corollary 2. When minor repair capacity is insufficient:

Therefore, Q(t) is monotonically increasing and n _a(t) is monotonically decreasing with respect to N. As a result, and _a observe the same monotonic properties.

Proof of Corollary 3. From

we can show that

Thus, n _a(t) is a convex function. By Jensen's inequality, the conclusion is obtained.

Proof of Theorem 2. To calculate the average values, we first rewrite condition N ≥ N _s(t) in terms of q(t). From N ≥ N _s(t) we have:

which leads to

Denote q _s as the minimum first time quality necessary to avoid rerouted jobs, that is

Thus, N ≥ N _s(t) implies that q(t) ≥ q _s, i.e., q(t) ≥ (nα_s′−N(1−α_r′))/(nα_s′ +Nρα_r′). Therefore, and _a can be written as

Note that when q(t) ≥ q _s(t) (i.e., N ≥ N _s(t)), no jobs are rerouted. Then we consider the following three cases: q _a ≤ q _s ≤ q _b , q _s < q _a and q _s > q _b .

	Case 1: q a ≤ q s ≤ q b . Therefore, the average quality buy rate equals to In addition, the average number of rerouted jobs is Therefore
	Case 2: q s < q a . Replacing q s with q a in Equation (A21), we obtain: In addition
	Case 3: q s > q b . Replacing q s with q b in Equation (A22), we have:

Biographies

Jingshan Li is an Assistant Professor in the Department of Electrical and Computer Engineering and Center for Manufacturing, University of Kentucky, Lexington, KY. Before joining University of Kentucky in 2006, he was a Staff Research Engineer in Manufacturing Systems Research Lab, General Motors Research & Development Center, Warren, MI. He received a Bachelor's degree from the Department of Automation, Tsinghua University, Beijing, China, and a Master's degree from the Institute of Automation, Chinese Academy of Sciences, Beijing, China, and a PhD in Electrical Engineering—Systems, University of Michigan, Ann Arbor, MI in 1989, 1992 and 2000, respectively. He has published over 20 refereed journal articles in IIE Transactions, IEEE Transactions, Annals of Operations Research, International Journal of Production Research, etc. He is also the Associate Editor of IEEE Transactions on Automation Science and Engineering and Mathematical Problems in Engineering. He received the Best IEEE Transactions on Automation Science and Engineering Paper Award in 2005, and an IEEE Early Industry/Government Career Award in Robotics and Automation in 2006, and he was also a finalist in the Best Automation Paper Award of the 2005 IEEE International Conference on Robotics and Automation. His primary research interests are in modeling, analysis and control of complex manufacturing systems. He is a senior member of IEEE and IIE.

Dennis E. Blumenfeld is a Staff Research Scientist at the General Motors R&D Center. He previously held faculty positions at Princeton University and University College London. He has a B.Sc. in Mathematics and an M.Sc. in Statistics and Operations Research from Imperial College, London, and a Ph.D. in Civil Engineering from University College London. He is a member of the Institute for Operations Research and the Management Sciences, and a fellow of the Royal Statistical Society. He is author of a recent reference book, Operations Research Calculations Handbook, and has published articles on transportation modeling, traffic flow and queueing, inventory control and production systems. He was an Edelman Award finalist for implementation of logistics network modeling, and has served on the editorial advisory board of Transportation Research.

Samuel P. Marin is a Research Fellow and Laboratory Group Manager in the Manufacturing Systems Research Laboratory at General Motors R&D Center in Warren, MI. He is also the Co-Director of the General Motors/University of Michigan Collaborative Research Laboratory in Advanced Vehicle Manufacturing. He received a Ph.D. in Mathematics from Carnegie Mellon University and, since joining General Motors Research in 1978, has conducted and managed research programs to develop new mathematical modeling and analysis tools for application to GM's engineering, manufacturing and design operations. His published research includes papers in computer-aided design and approximation, robot path and trajectory planning, numerical solution of PDEs, and the design and modeling of manufacturing and assembly operations. He is a member of the Board of Governors of the Institute for Mathematics and Its Applications at the University of Minnesota, a past member of the Advisory Board for the Department of Mathematical Sciences at Carnegie Mellon University, and a past member of the Panel for Information Technology for the National Research Council Board of assessment of NIST Programs. He is a member of SIAM, INFORMS and Sigma Xi.

Acknowledgements

The authors thank Prof. Semyon M. Meerkov of the University of Michigan and the anonymous reviewers for their valuable suggestions and comments.