Efficient computation of Sommerfeld integral tails – methods and algorithms

Abstract

A review is presented of the most effective methods for the computation of Sommerfeld integral tails. Such integrals, which are often oscillatory, singular and divergent, commonly arise in layered media Green functions. The mathematical foundations of various pertinent methods are discussed in detail and their performance is illustrated by relevant numerical examples. The associated algorithms are given in pseudocode for their easy computer implementation.

Keywords:

• Sommerfeld integral
• Green function
• extrapolation
• double-exponential rule

1. Introduction

In a variety of applications of new and well-established technologies a need arises to compute electromagnetic fields of time-harmonic dipoles embedded in plane-stratified media. In most cases these fields may be expressed in terms of the Sommerfeld integrals (also known as Fourier–Bessel or Hankel transforms [1, p.20], [2]) of the form(1)

where the kernel comprises the appropriate spectral-domain Green function, [3,4] z and are the vertical (perpendicular to the stratification) coordinates of the field- and source-point, respectively, is the lateral (in the plane of the stratification) distance between these points, and denotes the Bessel function. [5, Section 10.2] is an even (odd) function of for even (odd) . Note that the second-order transform can always be expressed in terms of the transforms of orders 0 an 1, using the recurrence relations for the Bessel functions. [5, Section 10.6] In certain loop antenna and aperture problems the driving current is not a point source, but is distributed over a circular region of radius , which leads to a more general Sommerfeld-type integral of the form [4,6–9](2)

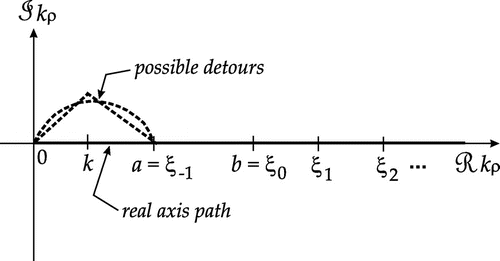
where the order may be integer or half-integer. Note that the (cylindrical) Bessel function of order is related to spherical Bessel function of order n. [5, Section 10.47] The integration path in (1(1) )–(2(2) ) follows the positive-real axis of the complex -plane, as illustrated in Figure 1. It is understood that this path should be indented to pass above any branch-point or pole singularities that may lie on or close to the positive-real axis, which may be accomplished by a path detour into the first quadrant, as also indicated in Figure 1. [9–15] Although the shape of this detour is not critical, its height is restricted by the exponential growth of the Bessel function off the real axis and the concomitant loss of accuracy when large numbers are subtracted to produce a small net result. Alternatively, one may first extract the poles [16] and keep the integration path on the real axis as(3)

and similarly for (2(2) ), where k is the branch point associated with the upper halfspace and is a suitably selected break point – for example, we may set . If the second branch point is also located on or near the real axis, the corresponding break point should be inserted between k and a. The finite-range integrals and in (1(1) ) may readily be evaluated by the Gauss–Jacobi quadrature, [17], [18–21] or by a suitable local change of the variable of integration on both sides of the singular point, [22–25] The computation of the tail integral S poses a much greater challenge, owing to the fact that typically behaves as [12](4)

Figure 1. Real axis integration path in the complex -plane, with possible detours.

where C is a constant and is a parameter related to z and – for example, in a homogeneous medium . In the above and elsewhere in this paper we utilize the “big-oh” and “little-oh” Landau symbols. [26, p.9] Hence, as long as , the integrand in (3(3) ) is oscillatory and – depending on the values of and , may be slowly convergent or may even diverge. The oscillations are only absent in the “zero offset” case. [27–29] This is why evaluating Sommerfeld integrals has been characterized as “a standard nightmare for many electromagnetic engineers”, [30] and it should not be surprising that a multitude of papers have been published – and still continue to be published – devoted to this topic. [12,15,31,45]

The purpose of the present review is to present in detail the most effective techniques and algorithms for the computation of Sommerfeld integrals along the real axis, with emphasis on the Sommerfeld tails. The mathematical foundations of the various methods are discussed in detail, with references to the relevant literature, and their performance is illustrated by representative numerical examples. In most cases algorithms are given in pseudocode for easy computer implementation. We exclude from consideration methods based on path deformation into the complex plane. [46,47] (applicable when ), as well as the complex-image and similar approximate methods. [48–51] The advantage of using the real-axis integration path is that the exact location of the poles intercepted on the proper and improper Riemann sheets need not be determined and that only Bessel functions of real arguments arise in the integral tail. The method is generally applicable, but is not recommended when the lateral distance exceeds about a hundred wavelengths, in which case the Bessel function undergoes an excessive number of oscillations in the initial interval (0, a) of the path in Figure 1. Hence, when far-zone fields are of interest, other techniques – such as numerical integration along the steepest descent path or along vertical branch cuts [52–55] – are more appropriate.

The contents of the remainder of this paper is as follows. In Section 2, we describe the DE rules and their adaptive implementation. In Section 3, we discuss sequence acceleration by extrapolation and describe and compare the performance of the most effective algorithms. In Section 4, we discuss the partition-extrapolation method for the oscillatory Sommerfeld tails and describe its efficient implementation. This method relies on the DE rules and extrapolation techniques introduced in the previous sections. In Section 5, we describe another type of DE rule applicable to oscillatory tails. In Section 6, we include sample numerical results for Sommerfeld integral tails evaluated by different methods. Finally, we end with conclusions in Section 7. Throughout the paper, we include algorithms in pseudocode, which may easily be translated into any higher level computer language, such as modern Fortran. [56]

2. Double-exponential (DE) rules

In this section, we describe efficient methods for the numerical integration over a finite or semi-infinite range of analytic functions that may be singular at one or both of the endpoints, which arise in Sommerfeld integrals. The DE rules of Takahasi and Mori [19] presented here are competitive in terms of efficiency with Gaussian quadratures, [57, Section 8.4], [58, Chapter 3] but are more versatile – as they are quite insensitive to endpoint behavior – and simple to program, since the weights and nodes (abscissae) are easily generated. Furthermore, the DE rules can be implemented in a progressive manner, with the step size halved each time the rule level is raised and reusing the function values computed on previous levels. The integral values generated at consecutive levels can be used to monitor the convergence of the quadrature. As with any other quadrature rule, singularities of the integrand near the integration path adversely affect the convergence and should preferably be extracted prior to the integration. However, any singularities on the integration path are easily treated by splitting the integration range, so that the singularities are placed at the endpoints. The development of the DE rules was motivated by the discovery by Goodwin [59] that the primitive trapezoidal rule,(5)

where is the mesh size, gives remarkably accurate results for certain functions that are analytic in a strip about the real axis. This paradox can be explained by the fact that bell-shaped functions that fall off rapidly as are well approximated by the sinc expansion, the integral of which gives exactly the rule (5(5) ) [18, p.178]. In fact, it can be shown by contour integration in the complex plane that the discretization error in (5(5) ) is as , where w is the distance from the real axis to the nearest singularity of the integrand. [60] The convergence being exponential, halving the step h doubles the number of correct figures in the result for sufficiently small values of h.

2.1. Finite intervals

To apply this method to finite-range integrals, we map the infinite interval onto using a suitable monotonic function , such that(6)

where is the Jacobian of the transformation. As indicated, the infinite sum must in practice be terminated after a finite number of terms, thus introducing a truncation error, in addition to the discretization error. The high accuracy of the rule (6(6) ) is predicted by the Euler-Maclaurin sum formula, [61, p.24], [62, p.247], [63] if the transformation results in a bell-shaped function whose derivatives all vanish at . This formula is basically a trapezoidal quadrature rule with an error term in a form of an asymptotic series, whose terms comprise the derivatives of the integrand evaluated at the endpoints of the interval of integration. Hence, a transformation that forces these endpoint derivatives to vanish results in a great enhancement of the accuracy of the trapezoidal rule. The required mapping may be effected by choosing [20](7)

where g(t) is an odd function, which leads to the trapezoidal rule approximation(8)

with the nodes and weights defined as(9)

where we have introduced(10)

It is important to code the abscissae and weights as indicated in (9(9) )–(10(10) ), since a more direct implementation of (7(7) ) would result in overflows. Using the fact that , , and , we may also express (8(8) ) in the more convenient form(11)

Although we assume in the above the standard integration interval , an arbitrary interval [a, b] may be mapped onto by the linear transformation with and , which leads to [57, p.367](12)

Hence, for an arbitrary interval [a, b] the nodes and weights become and , respectively, and (11(11) ) is transformed to(13)

We have not yet specified the function g(t) appearing in the argument of the transformation (7(7) ). Perhaps the simplest odd function choice,(14)

generates the th order tanh rule [20] which for reduces to the classical tanh rule, [64–67], whereas choosing(15)

where is a positive parameter, generates the tanh-sinh rule [19]. The Jacobians of the tanh and tanh-sinh transformations exhibit exponential and double-exponential decay, respectively, as , resulting in the desired rapid fall-off of the integrands in most cases. These Jacobians also introduce singularities in the complex plane, so that the half-width of the strip of analyticity for the tanh rule, as well as the tanh-sinh rule, provided that . The performance of the tanh-sinh rule tends to be insensitive to values of in the neighborhood of unity, hence the convenient value of has been suggested as a good practical choice [20]. Setting is counterproductive, as this causes w to decrease rapidly, with the concomitant deterioration of the convergence rate. With , the discretization error of these rules is , whereas the truncation error for a given truncation index n may be estimated as [20] For a fixed n, the truncation error grows with diminishing h, while the discretization error decreases. One can therefore estimate the optimum value of h by making the two errors equal, which leads to and for the (classical) tanh and tanh-sinh rules, respectively, assuming in the latter, and the corresponding total errors are found to be and , respectively [20]. The estimates for the higher order tanh rule are more elaborate and are also given in [20], while a more refined step size estimate for the tanh-sinh rule may be found in [63]. Although these are only crude estimates based on the assumption that the integrand function itself makes no appreciable contribution to the decay rate, they are nevertheless indicative of the performance of the two methods. In particular, we note that with a growing truncation index n the double-exponential (DE) tanh-sinh rule converges faster that the single-exponential (SE) tanh rule. One might thus expect that a triple-exponential rule would offer further improvement. It turns out, however, that beyond the double-exponential, the poles of the Jacobian come nearer to the real axis, so that the discretization error gets worse, not better [18,19,68,69]. We should mention that, from the classical point of view, the rule (13(13) ) is a strange quadrature method indeed, as it is not exact for any polynomials – not even a constant – for any h and finite n [67]. Nevertheless, it is remarkably accurate!

A salient feature of the tanh and tanh-sinh transformations is that the uniform sampling on the t-axis results in the clustering of nodes near the endpoints of the integration interval, which – in view of the rapid decrease of the weights – permits the suppression of any endpoint singularities of . This node clustering is also responsible for a pitfall in the computer implementation of (13(13) ), which may have been responsible for the initially slow rate of acceptance of the DE rules [69]. Namely, since can become very small, the round off errors in computing and may give rise to overflows as the singularities at a and b are approached. To remedy this, the function should be programmed as a two-parameter procedure f(c, d), where , or b, and , so that the singular part may be computed using d directly [20,68], [18, p.175]. For example, if the integrand comprises a term with and , this procedure should compute it as when , and as when .

In view of the indeterminate nature of the error estimates, reliance cannot be placed on a calculation of (13(13) ) for a single value of the truncation index n, and if the optimum values of the mesh size h were employed, the earlier function evaluations would usually be lost when n is increased. Hence, here we adopt the following strategy, due to Evans et al. [20]. First, with the selected starting (zero-level) mesh size h, the initial truncation index n is determined from the condition(16)

where denotes the kth term in the rule (13(13) ) and is a specified truncation error. Note that this empirical determination of the truncation index takes into account any endpoint singularities of the integrand function. In the process of computing n, the zero-level quadrature estimate is also obtained. Next, higher level estimates are computed with the number of points systematically doubled and the mesh size halved each time the level is raised, always re-utilizing in (13(13) ) the previously computed function values. The successive quadrature estimates are monitored until convergence to a specified tolerance is achieved. Since the number of correct digits approximately doubles with each iteration once the method starts converging, the actual error of the computed integral will typically be the square of the requested value [70], [18, p.178]. Accordingly, one can set to the square root of the desired precision. A posteriori error bounds for DE rules are also available, but require the computation of two derivatives of the integrand function at the sampling points [71,72].

A pseudocode implementing an automatic and progressive tanh-sinh rule is given in Algorithm 1, which comprises the main procedure and two subsidiary procedures and , as well as an auxiliary function . This algorithm closely follows the steps described above and is for the most part self-explanatory. The procedure computes the initial truncation index n and the initial quadrature estimate using the condition (16(16) ), and the procedure evaluates higher level partial sums, skipping the nodes of all previous levels. Finally, the function computes the kth term of the rsule (13(13) ). Note that the transformation (15(15) ) is implemented as

(17)

with . After some experimentation, the initial mesh size was set to and the truncation threshold in (16(16) ) to . The user-provided integrand function f should be coded as a two-parameter procedure with overflow mitigation in the case of endpoint singularities, as discussed above. Implementations of the tanh-sinh rule are also given in [73, p.312], [74,75], and [18, p.176]. The tanh rule can similarly be implemented, but the algorithm is not listed in the interest of brevity.

We now illustrate the application of the tanh-sinh rule to the integral in (3(3) ), where the integrand exhibits an inverse-square-root singularity at the upper interval end, which may be set to unity without loss of generality, since the integration variable can be normalized to the wavenumber k. Hence, we consider the integral(18)

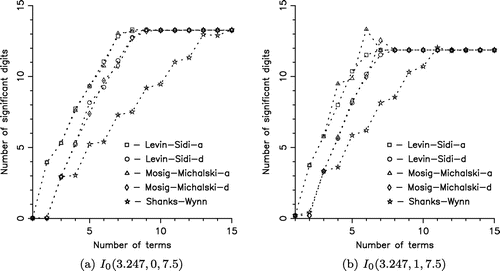
where the integrand is singular at and also oscillatory with the frequency proportional to the parameter . Applying Algorithm 1 to compute , we obtain the results listed in Table 1, where m denotes the rule level and N the cumulative number of function evaluations. A rapid convergence is observed, with the number of correct digits, which are underlined, approximately doubled each time the rule level is raised. In the last column, we include the results of the Gauss–Jacobi quadrature [17]. using the same number of nodes as in the corresponding tanh-sinh rule. The Gauss–Jacobi quadrature delivers unsurpassed accuracy, but unlike the tanh-sinh rule, is non-progressive, i.e. it cannot reuse the previously evaluated functions when the quadrature level is raised to check for convergence. For the same integral, in Tables 2 and 3, we include results obtained by the classical and fifth-order tanh rules, respectively. It is seen that although the fifth-order tanh rule requires much fewer function evaluations than the classical one, it is still inferior to the DE tanh-sinh rule.

Table 1. DE tanh-sinh rule applied to .

m	N	tanh-sinh rule	Gauss–Jacobi rule
0	7	0.649087553439706	0.636619772370296
1	13	0.636587540227121	0.636619772367582
2	25	0.636619773340205	0.636619772367581
3	49	0.636619772367581	0.636619772367581

Table 2. Classical tanh rule applied to .

m	N	tanh rule ()
0	4	0.012763231686033
1	8	0.560903906568641
2	16
3	32
4	64
5	128

Table 3. 5th-order tanh rule applied to .

m	N	tanh rule ()
0	4	0.012763231686033
1	8	0.560903906568641
2	16
3	32
4	64
5	128

Next, to examine the performance of the tanh-sinh rule in the case of highly oscillatory integrands, we evaluate with the parameter increased over fiftyfold. The results for this case are listed in Table 4, where rapid convergence is observed, but only beginning with the fourth level, after a number of nodes has been reached, sufficient to capture the oscillations of . In the last column, we again include for comparison the corresponding Gauss–Jacobi quadrature results.

Table 4. DE tanh-sinh rule applied to .

m	N	tanh-sinh rule	Gauss–Jacobi rule
0	7
1	13
2	25
3	49
4	97
5	193

To gain further insight into the performance of the tanh-sinh rule, in Figure 2(a) we plot the original integrand function of , as given by (18(18) ), and the transformed integrand .

Figure 2. Plots of the original integrand and the transformed integrand for (a) using the tanh-sinh transformation and (b) using the mixed transformation.

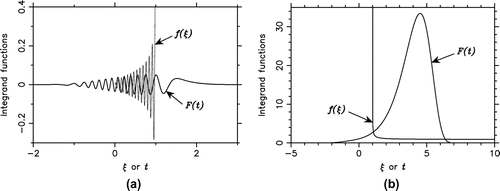
Note the singular inverse-square-root behavior of near , modulated by the oscillations of the Bessel function. In the transformed integrand, this singularity has been moved to and suppressed by the double-exponential decay of the Jacobian . Although still oscillatory, F(t) is well behaved with a rapid decay at both ends, which explains the high accuracy of the trapezoidal rule.

2.2. Semi-infinite intervals

For a semi-infinite interval , the appropriate DE transformation is [19](19)

which yields the quadrature rule(20)

with the abscissas and weights given as(21)

However, this transformation is not optimal if exhibits an exponential decay at infinity, in which case a more appropriate choice is [19](22)

Note that this is a mixed DE–SE transformation – DE at , but only SE for [18, p.176]. However, the exponential decay of at infinity results in a DE behavior at the upper integration limit also. For the mixed transformation (22(22) ), the abscissae and weights in (20(20) ) become(23)

Note that, due to the lack of symmetry in the transformations (19(19) ) and (22(22) ), the sum in (20(20) ) cannot be folded with respect to the element – as in (13(13) ), and the partial sums for negative and positive k must be evaluated separately.

A pseudocode implementing an automatic and progressive mixed rule is given in Algorithm 2, which comprises the main procedure MixedQuad and two subsidiary procedures TruncIndex and PartSum, as well as an auxiliary function Term. This algorithm is very similar to Algorithm 1 – in fact, it shares the procedures TruncIndex and PartSum with the latter. The function Term is of course different, as it implements the kth term in (20(20) ), with the abscissae and weights given by (23(23) ). The other difference is that the partial sums for negative and positive indices k must be treated separately – hence the two calls to TruncIndex and, at each level, two calls to PartSum. Note that changing to k is tantamount to the replacement . The initial truncation indices and for the negative and positive ranges of k are determined based on a condition similar to (16(16) ). As in the case of the tanh-sinh rule, the user-provided function should be coded as a two-parameter procedure , where , to facilitate overflow mitigation for integrands that have an algebraic singularity at the lower end a of the integration range.

As an example of the application of the mixed rule, consider the integral(24)

where the integrand is singular at the lower limit and exhibits exponential decay at infinity. Applying Algorithms 2 to compute for , we obtain the results listed in Table 5. Here again, once the method starts converging, approximate doubling of the number of correct digits is observed each time the rule level is raised. In this example, we specified the small value of z in order to make the integrand slowly-convergent at infinity and thus the problem more challenging. The summation limits in (20(20) ) (as determined by TruncIndex) were in this case and . It is found that increasing z ten-fold to reduces to 6 and the number of function evaluations from 57 to 45.

Table 5. Mixed rule applied to .

m	N	Mixed rule
0	15
1	29
2	57

To get more insight into the performance of the mixed rule, in Figure 2(b) we plot the original integrand function of , as given by (24(24) ), and the transformed integrand . Note the inverse-square-root singularity of at and its very slow exponential decay for large . In contrast, the transformed integrand F(t) is a smooth hat-like shaped function, with rapid decay at both ends. The singularity of the original integrand at the lower integral limit has been sent to and suppressed by the double-exponential decay of the Jacobian, and its exceedingly slow decay for has also been spectacularly accelerated, which explains the remarkable accuracy of the trapezoidal rule in this case.

The DE rules for semi-infinite ranges discussed above are not recommended in the case of slowly decaying and oscillating functions [76]. For such integrands, a special DE rule has been developed based on a different principle, which we describe in Section 5.

3. Sequence acceleration by extrapolation

Extrapolation is a powerful tool frequently employed in the efficient computation of Sommerfeld integral tails [12]. The objective of extrapolation is to accelerate the rate of convergence of a series(25)

or, equivalently, of a sequence of partial sums(26)

The sequence element may be partitioned as(27)

where is the truncation error, commonly referred to as the remainder. To accelerate the convergence of (26(26) ), we seek a transformation , such that the new sequence converges faster, i.e.(28)

where are the remainders of . Such a transformation may be viewed as an extrapolation method, since the underlying principle is to obtain better estimates from a sequence of computed values [77]. The convergence of the sequence of partial sums (26(26) ) may be characterized based on the behavior of the limits(29)

where the second equality applies with some rare exceptions [78]. If , the convergence is linear, if , it is logarithmic, if , it is hyperlinear, and if , the sequence diverges. We say that the sequence is asymptotically monotone if , and alternating if . Alternating sequences are generally the easiest to accelerate, the logarithmic convergence being the most challenging.

The most general extrapolation procedure is based on the assumption that the remainder estimates possess the asymptotic expansion(30)

where are unknown coefficients and are known, but otherwise arbitrary functions of n, with the property that . To accelerate the convergence of the sequence (26(26) ), a transformation is constructed that eliminates a number of leading coefficients from , with the number of coefficients annihilated being the order of the transformation. For many sequences encountered in practice the remainders possess a Poincaré-type asymptotic expansion [78](31)

where are the remainder estimates, which provide the structural information about the behavior of for large n, and is an auxiliary sequence of interpolation points (or nodes), such that . Note that (31(31) ) is a specialized form of (30(30) ), with the basis functions . The most powerful convergence accelerators exploit the information contained in the remainder estimates, which are obtained either numerically from the elements of the sequence, or derived analytically, based on their known asymptotic behavior. The choice of the auxiliary sequence also affects the properties of the sequence transformation. If equispaced nodes are appropriate, we may use(32)

where n is a natural number and the shift parameter is either dictated by the problem considered, or otherwise is set to 1.

3.1. The Levin transformation and the W-algorithm of Sidi

The Levin transformation is based on the remainder expansion (31(31) ) using the explicit remainder estimates . Hence, upon combining (31(31) ) and (27(27) ) and truncating the resulting asymptotic expansion after k terms, where k is the transformation order, we obtain the so-called model sequence(33)

where the remainder estimates and the interpolation points are assumed specified. The Levin transformation is constructed to be exact for this model sequence, which has unknowns, viz., the limit S and the coefficients . Thus, given a sequence of partial sums , we may use (33(33) ) to set up a system of linear equations and solve it for S using Cramer’s rule, which gives S as a ratio of two determinants. Upon expanding the numerator and denominator determinants by minors of the first column, one then finds [79, Section 10.5](34)

where(35)

In this section, we adopt the convention that the subscript of the transformation symbol refers to the sequence element index and the superscript denotes the transformation order. This notation is not always followed in the literature, where the subscripts and superscripts may have the opposite meaning, or the superscripts are dispensed with in favor of two subscripts. In the case of equispaced nodes, with given by (32(32) ), the last expression may be further specialized as(36)

where we have omitted the j-independent terms that cancel in the quotient (34(34) ), but inserted the scaling factor in the denominator to prevent overflows [18, p.214]. With properly selected reminder estimates , the values obtained from (34(34) ) with will be much closer to the limit S than the last computed partial sum . The transformation (34(34) ), which was derived by Levin [80], [5, p.94] in the special case of equispaced nodes with , will be referred to as the general Levin (GL) transformation.

The properties of the GL transformation critically depend on the choice of the remainder estimates . If the latter do not invoke the sequence elements , the transformation is linear; otherwise, it is nonlinear. For example, setting results in the Richardson extrapolation scheme [78], [77, p.72], in which case, assuming equispaced nodes , the denominator sum in (34(34) ) can be evaluated by the identity [81, p.4](37)

thus reducing (34(34) ) to the Salzer summation formula [82], [79, p.35], which is a linear transformation effective for certain logarithmically convergent sequences that are well approximated by rational functions of n [83]. However, the following remainder estimates:(38)

introduced by Levin [80] and (in the case of the d-transformation, which may be considered as a modified t-transformation) by Smith and Ford [84], give rise to the most effective extrapolation methods. There is no agreed-upon name for the modified t-transformation, which has been variously referred to as d-, -, and -transformation [18,12,78,85]. The acceleration properties of the original and modified t-transformations are similar, but the latter requires the computation of one extra term of the series for the same transformation order. Note that we may write , where denotes the forward difference operator. Hence, with the remainder estimates (38(38) ), the GL transformation is nonlinear, because depends explicitly on at least one element of . Numerical experiments [84,86] supported in some cases by rigorous analysis [79, Section 10.5], [78] indicate that the t-transformation accelerates linear convergence and is well suited for alternating series, but fails to accelerate logarithmic convergence, whereas the u- and v-transformations are more versatile, as they accelerate both logarithmic and linear convergence. The u-transformation has been pronounced “the best available across-the-board method” [84].

The GL transformation (34(34) ) is non-recursive, i.e. it has to be computed from scratch each time the order k is increased. This drawback was remedied by Fessler et al. [87], who derived a recursive scheme for the computation of (34(34) ) in the case of equidistant nodes. In the general case, the GL transformation can be efficiently computed by the recursive W-algorithm of Sidi, which utilizes the properties of the divided difference operator , defined as(39)

with [88], [89, Section 3.8], [77, Section 2.7], [90, Chapter 7]. To derive this algorithm, we rewrite (33(33) ) as(40)

and observe that the right-hand side member is a polynomial of degree in the variable . Hence, if we consider and as functions of the continuous variable x evaluated at and apply to both sides of (40(40) ), we obtain(41)

because the divided difference operator of order k annihilates polynomials of degree or less. Finally, invoking the linearity of , we may express the solution S as(42)

where, in view of (39(39) ), both the numerator and the denominator can be computed by the same recurrence formula(43)

with the staring values and , respectively. The elements connected by (43(43) ) form a triangle(44)

which suggests their arrangement in the two-dimensional table, where the subscript n is the row index and the superscript k is the column index. Assuming, for simplicity, that the acceleration commences with , the table corresponding to the transformation order k has the form(45)

where the first column comprises the starting values and the computations proceed along counterdiagonals, which are added to the table as k is increased. Since the sum of the row and column indices of the kth counterdiagonal is constant and equal to k, it is convenient to rewrite the recurrence formula (43(43) ) as [78](46)

This recursion is performed twice, to update the numerator and the denominator of (42(42) ) using the appropriate starting values, and the accelerated sequence elements are returned as . In computer implementation, the counterdiagonals can be processed in a one-dimensional array of expandable length.

A pseudocode for the GL transformation implemented via the W-algorithm is given in Algorithm 3. Here, the arrays , , and , where kmax is the maximum transformation order, store the interpolation points and the numerator and denominator counterdiagonals, respectively.

3.2. The Shanks transformation and the -algorithm of Wynn

The Shanks transformation [91] results from the choice in (30(30) ), which leads to the model sequence(47)

Essentially, this means that the limit S of the series (25(25) ) is approximated by the partial sum plus a weighted sum of the next k terms [78]. As in the case of the Levin transformation, we may use (47(47) ) to set up a system of linear equations with the limit S and the coefficients as unknowns and solve it for S using Cramer’s rule. This solution, given as a ratio of determinants, defines the Shanks transformation , which is strongly nonlinear. It follows from the model sequence (47(47) ) that the sequence elements are needed to form this solution, hence is a transformation of order 2k. The determinantal form of the Shanks transformation is computationally expensive and is never used. Instead, is computed by the so-called -algorithm of Wynn [92], which is a recursive scheme given as(48)

with the starting values and . The elements connected by the recursion (48(48) ) form a rhombus(49)

which suggests an arrangement of in a two-dimensional -table similar to (45(45) ). Wynn [92] proved that the table elements with even superscripts give the Shanks transformation, whereas the elements with odd superscripts are only auxiliary quantities. Consequently, for even , our transformation is(50)

whereas for odd , we use(51)

assuming that the extrapolation commences with the term of the sequence. The recursion (48(48) ) proceeds along the counterdiagonals of the -table, with a new counterdiagonal added when the transformation order k is incremented by one and a new sequence element (starting value) becomes available. Since the elements of the kth counterdiagonal are given as , , , it is convenient to rewrite the recurrence formula (48(48) ) as [78](52)

Here too, the counterdiagonals can be processed in an expandable one-dimensional array. However, because (52(52) ) is a rhombus, rather than a triangle scheme, two auxiliary variables are also needed to store the table elements that are required in the processing of the next counterdiagonal, but would otherwise be overwritten during the computation of the current counterdiagonal [78], [18, p.213].

A pseudocode for the Shanks transformation implemented via the -algorithm of Wynn is given in Algorithm 4. Here, the array , where kmax is the maximum transformation order, stores the counterdiagonals, and a and b are the auxiliary variables referred to above. The zero divide referred to in the comment line may occur if the algorithm is not stopped after convergence has been reached.

The Shanks transformation, or equivalently the -algorithm, is effective for alternating and linear convergence, but is unable to accelerate logarithmic convergence [86]. Since no remainder estimates are required, this algorithm is user-friendly and is implemented in some standard software libraries, such as QUADPACK [93]. Also, when applicable, the -algorithm is known to be robust in the presence of noise or irregularities in the sequence elements, and is thus frequently used as a reference benchmark method for other extrapolation techniques. Hence, a good extrapolation method should perform at least as well as the -algorithm.

3.3. The weighted-averages method and the Mosig–Michalski algorithm

Whereas the Levin and Shanks transformations are constructed to be exact for a certain model sequence, the weighted averages (WA) method belongs to the class of iterative sequence transformations, which are obtained by repeated application of some very simple transformation [78,85,94,95]. As the name indicates, the WA method is generated by a weighted mean of two consecutive partial sums [12,37,96,98]:(53)

where denotes the weight associated with . In view of (27(27) ), we may also express the above as(54)

where is the remainder of the new sequence element . Upon introducing the weights ratio coefficient(55)

into (53(53) ) and (54(54) ), we may express them as(56)

We now assume that the remainders possess the asymptotic expansion (31(31) ) and find(57)

which suggests selecting the weights ratio in (56(56) ) as(58)

With this choice of , and assuming that the denominator in (56(56) ) has the asymptotic behavior(59)

where , we find that the acceleration condition (28(28) ) is satisfied with . It can be shown that (and thus ) for all sequences other than those with logarithmic convergence, for which (). In view of (56(56) ), we conclude that the remainders have the same asymptotic form (31(31) ) as , except that the remainder estimates are now scaled by the factor . Consequently, the sequence may again be accelerated by the transformation in (56(56) ), using the properly modified in (58(58) ). We thus arrive at the recursive scheme(60)

with the starting values and the coefficients(61)

where the second expression is an asymptotic form applicable for large n. Note that with the weights ratio coefficients fixed as , (60(60) ) reduces to the so-called -transformation [99–101], which for further reduces to the classical Euler transformation [102], [103, p.124]. The power of WA derives from the fact that the coefficients are not fixed, but adaptively adjusted.

The algorithm given above is equivalent to the so-called generalized WA procedure [12], which is also referred to as the Mosig–Michalski algorithm [85]. Although the asymptotic form of the weights ratio coefficient given in (61(61) ) can hardly be justified, as the recursion is often applied beginning with and satisfactory convergence is in many cases reached before n exceeds 10, Michalski [12] observed that in practice this particular approximation results in conspicuously better performance than the exact form.

The recursion (60(60) ) is a triangle scheme similar to (43(43) ), hence the elements may be arranged in a two-dimensional table as in (45(45) ). Here again, we assume that the acceleration is applied commencing with . The first column of this table comprises the starting values and the recursion proceeds along the counterdiagonals, where the sum of the row and column indices is constant. The table is expanded by a new counterdiagonal for each new sequence element and the upper-right corner element is the best approximation of S, given the partial sums . Since the elements of the kth counterdiagonal are given as , , , we may rewrite the recurrence formula (60(60) ) in the more convenient form(62)

Similar to the W-transformation, this recursion may be processed in an expandable one-dimensional array.

A pseudocode of the WA method, implemented by a simplified Mosig–Michalski algorithm with the asymptotic weights ratio coefficients, is given in Algorithm 5. Here, the arrays and , where kmax is the maximum transformation order, store the nodes and the counterdiagonals, respectively. Recall that the coefficient should be set to 1 (for logarithmic convergence) or 2 (otherwise). The parameter , , is the ratio of the current and previous remainder estimates at the transformation order k – cf. (58(58) ). Note that is not invoked by the algorithm and may be set to zero.

Since the WA method depends on the explicit remainder estimates , it may be classified as a Levin-type transformation [85], and is thus expected to have similar properties as the GL transformation, if the same remainder estimates are employed.

3.4. Comparison of extrapolation methods

To illustrate the relative merits of the Levin–Sidi, Mosig–Michalski, and Shanks–Wynn algorithms, we compare their performance when applied to the following slowly convergent series(63) (64) (65)

which exhibit alternating, linear, and logarithmic convergence, respectively [104]. As the performance measure we use plots of the number of significant digits (defined here as , where is the relative error) in the transformed sequence vs. the number of terms evaluated. It will be recalled that the Levin–Sidi and Mosig–Michalski algorithms come in different variants – t, d, u, and v – depending on which of the numerical remainder estimates (38(38) ) is employed. We apply these methods using the equidistant interpolation points (32(32) ), with the shift parameter and without acceleration delay, i.e. the transformation commences with the partial sum . There is usually little or no advantage in delaying the commencement of acceleration, and increasing much beyond 1 slows down the convergence rate.

In Figure 3, we compare the Levin–Sidi-t, Mosig–Michalski-t, and Shanks-Wynn extrapolation algorithms for the series , , and .

Figure 3. Performance of the extrapolation methods for (a) (alternating), (b) (monotone linear), and (c) (monotone logarithmic).

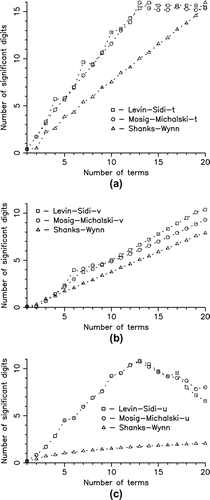
The performance of the former two methods is seen to be almost identical for the alternating series , with both reaching machine precision accuracy in under 15 iterations and outperforming the -algorithm by a significant margin. The Levin–Sidi-d and Mosig–Michalski-d algorithms perform similarly to the respective t-variants in this case. For the monotone linear series , we use the v-variants of the Levin–Sidi and Mosig–Michalski algorithms. Again, these methods perform similarly and both outperform the Shanks-Wynn algorithm, but the convergence is significantly slower than for the alternating case. For the monotone logarithmic series , we use the u-variants of the Levin–Sidi and Mosig–Michalski algorithms. The performance of these two methods is again almost identical, but the curve is not monotonic in this case, as it bends down after climbing to approximately 11 significant digits in about this many iterations. This behavior can be attributed to the numerical instability of Levin-type algorithms for high transformation orders, caused by cancellation errors that are known to occur in the monotone case [87]. The Shanks-Wynn algorithm performs poorly, as was to be expected for logarithmic convergence.

The above results confirm that the Levin–Sidi and Mosig–Michalski algorithms are among the most versatile and powerful extrapolation methods currently known. Since both algorithms are equally easy to implement, which one should be selected is largely a matter of personal preference. However, when approaching a new class of problems, one will be well-advised to try at least two different extrapolation methods, preferably including the Shanks-Wynn algorithm among them.

4. Partition-extrapolation method for oscillatory integral tails

We now describe a powerful technique for automatic integration of Sommerfeld integral tails, which combines the use of progressive quadratures, such as the DE rule, and the extrapolation methods discussed above. Hence, consider the tail integral(66)

over the real axis segment , where the integrand function is oscillatory and may be slowly decaying or even divergent, as in (1(1) ). We compute S as the limit of the sequence of the partial sums(67)

as , where and , , are suitably selected break points, e.g. the consecutive zeros of – see Figure 1. The finite-range integrals are readily computed by a low-order Gauss-Legendre quadrature. For Sommerfeld integrals, the 16th-order Gauss-Legendre rule typically yields double precision machine accuracy for the partial integrals between consecutive zeros of the Bessel function [105,106], but for greater reliability, one can resort to Gauss-Kronrod or Patterson rules [58, p.131], [107], or to the progressive Clenshaw-Curtis quadrature [108], which provide error estimates. The recursive DE tanh-sinh rule described in Section 2 can also be employed, even in the absence of endpoint singularities. Typically, the sequence is slowly convergent, hence acceleration by one of the extrapolation methods discussed in Section 3 is a good strategy. The combination of the partition of the integral in (67(67) ) with extrapolation to speed the convergence of gives rise to the partition-extrapolation (PE) method, which is the subject of many papers, including [12,15,102,109,120].

In order to effectively utilize extrapolation methods to accelerate (67(67) ), it is advisable to first investigate the behavior of the remainders(68)

Here, we assume here that for , where is a suitably selected break point, the integrand function in (66(66) ) may be expressed as(69)

where has the asymptotic expansion(70)

with the parameter , while is periodic, with half-period q, such that(71)

Consequently, we may assume equidistant break points(72)

where b is the first zero of in the range where the representation (69(69) ) is applicable. We now substitute (69(69) ) into (68(68) ) and use (70(70) ) to obtain(73)

which upon changing the variable of integration to and using (71(71) ) becomes(74)

Finally, upon expanding the inverse denominator of the integrand of (74(74) ) in a Taylor series about and integrating term-by-term, we arrive at the Poincaré-type expansion(75)

where are n-independent coefficients and are the remainder estimates, given as(76)

The break points in (75(75) )–(76(76) ) may also be replaced by the interpolation points given by (32(32) ) with the shift factor .

Based on the above analysis, we may select the most appropriate extrapolation method for the sequence of partial sums (67(67) ). Hence, upon using (75(75) ) and (76(76) ) in (29(29) ), we readily find that , which indicates that the sequence (67(67) ) is linearly convergent and alternating, and thus all four variants of the Levin-type methods, corresponding to the numerical remainder estimates (38(38) ), as well as the Shanks-Wynn algorithm, are applicable. Using the analytical remainder estimates derived above with the Levin–Sidi and Mosig–Michalski algorithms gives rise to what may be called a-variants of these methods. The parameter in the Mosig–Michalski algorithm then becomes(77)

with , and from (59(59) ) it follows that , and thus . The Levin-Sidi-a algorithm is closely related to the W-transformation of Sidi [111], while the Levin-Sidi-d algorithm is tantamount to his “user-friendly” mW-transformation [114].

As an example, consider the integral(78)

which follows from a well-known identity [81, Equation 6.623.1], [105] by splitting the integration range at an arbitrary point . For , and 2, the integrals resemble the static forms of the tail integrals that arise in the electromagnetic field computation in layered media [4]. With and the left-hand side integrals in (78(78) ) are formally divergent, but are defined in the sense of Abel summability [77, p.381], [21,105]. As the finite-range integral on the right-hand side of (78(78) ) can readily be evaluated to machine accuracy by a numerical quadrature – such as the tanh-sinh rule discussed in Section 2, the infinite integral may serve as a realistic test bed for the extrapolation methods, allowing in particular to examine the effect of changing the lower limit a. In view of the asymptotic form of the Bessel function [5, p.223](79) fits in the framework of the PE method with , , and . The natural choice of the break points for the partial integrals in (67(67) ) are in this case the consecutive zeros of (Longman partition) [102,117]. Since the exact Bessel function zeros can only be found by iterative procedures [117,121], other alternatives have been proposed, such as the asymptotic zeros based on the expansion (79(79) ) (Lyness partition) [113], or just the equidistant nodes separated by the asymptotic half-period q (Sidi partition) [111,114,122]. Still another alternative is to use the asymptotic extrema of the Bessel function, which somewhat dampens the oscillation of the partial sums and results in a modest convergence improvement of the PE method.[113] The Sidi partition method is the simplest, but it has been found unreliable, as there are certain values of for which the sequence of the partial sums (67(67) ) ceases to be strictly alternating, with the concomitant precipitous performance degradation of the PE method [12]. We have observed, however, that this problem does not occur if the lower integration limit a is always placed at the first Bessel function zero that is greater than the original a. Of course, if there is no flexibility in the choice of the lower integral limit, this shift requires an extra partial integral to bridge the gap between the original and the modified values of a. Hence, if the nth zero of is denoted by , in the modified Sidi partition we relocate a to , where m is the lowest zero index for which this condition is satisfied, and set the break points according to (72(72) ), with . We adopt this modified Sidi partition in the examples that follow. For , we use the tabulated values [123, p.409] if , and the large-n McMahon’s expansions [123, p.371] otherwise.

Figure 4. The original () and accelerated () partial sums for the integral , using the PE method with the modified Sidi partition and extrapolation by the Mosig–Michalski-a algorithm. Note that the scales of these two sequences are vastly different. Although is divergent, rapidly converges to the exact value of the integral (the antilimit), .

Figure 5. Performance of different PE methods for the integrals.

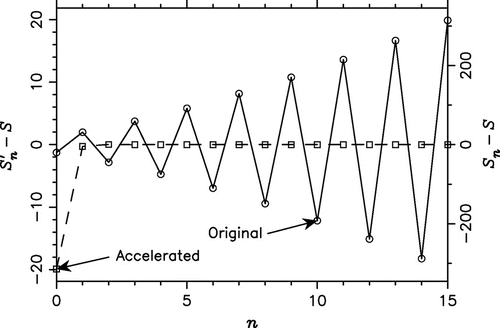
In Figure 4, we show plots of the original and accelerated partial sums for the integral , using the PE method with the Mosig–Michalski-a algorithm. Note that the chosen value of the lower limit a is the first zero of , consistent with the modified Sidi partition. The original sequence is divergent and alternating, while the transformed sequence converges rapidly to the exact integral value S – in this case to the so-called antilimit [78], [83, p.248]. In Figure 5, we compare the performance of the PE methods for the integrals and , using the modified Sidi partition and different extrapolation algorithms. The difference between these two integrals is the strong exponential decay exhibited by the integrand of the second. 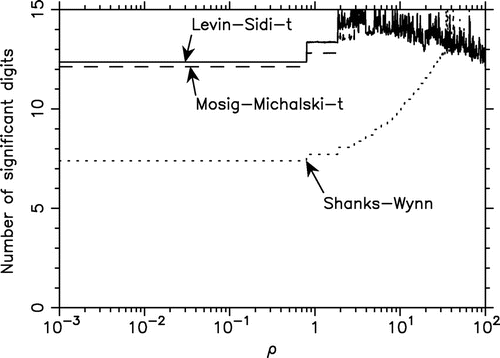Note that the chosen value is consistent with the Sidi partition. As the performance measure we use plots of the number of significant digits vs. the number of terms (partial integrals) evaluated. All computations are done using double precision arithmetic with approximately 15 significant digits. We present plots for the a- and d-variants of the Levin-type algorithms (the other variants produce very similar results) and for the Shanks-Wynn algorithm. It is noted that the Levin–Sidi and Mosig–Michalski perform similarly and both are more effective than the Shanks-Wynn algorithm. Furthermore, the a-variants, using analytical remainder estimates, have a slight advantage over the d-variants. However, the latter are more user-friendly, as no asymptotic analysis of the integrand function is required. In Figure 6, we plot the number of significant digits obtained after 9 extrapolation steps (at the cost of 10 partial integrals) for the PE method using the modified Sidi partition with the Levin–Sidi-t, Mosig–Michalski-t, and Shanks–Wynn algorithms, applied to the integral with the threshold value of and varying . Note that both Levin-type methods, using numerical remainder estimates, achieve at least 12 digits of accuracy over the five-decade -range and no breakdowns are observed. The Shanks-Wynn algorithm is competitive for large only. These plots were generated using 250 points per decade. The staircase behavior is due to the passing of the consecutive Bessel function zeros through the threshold value a and the concomitant jumps in the lower integration limit as is increased. The growing frequency of these steps is due to the logarithmic -scale used.

Figure 6. Accuracy of the PE method achieved after 9 extrapolation steps (10 partial integrals) for with varying over a five-decade range. Here a depends on consistent with the Sidi partition with the constraint .

A pseudocode for the PE method computation of tail integrals comprising Bessel functions is given in Algorithm 6, which uses the Levin-Sidi transformation implemented via the function – see Algorithm 3 of Section 3.

It is convenient in the present context to declare the array X( : ), holding the interpolation points in Algorithm 3, to have a starting index , rather than 0, so that may hold the lower integration limit a. For simplicity, we use the t-variant here, which is appropriate for alternating sequences (the u-variant can be implemented as easily by modifying just one line of the code). The modified Sidi partition is assumed, with the lower integral limit a set to a Bessel function zero and the asymptotic half-period (which is accessible as a global variable). The partial integrals are evaluated by the procedure of Section 2. Since the singularity-suppressing property of the tanh-sinh rule is not needed here, the Gauss-Legendre or Romberg quadrature may be used instead [18, p.218]. For regular integrand functions, the Gaussian quadrature is typically less costly than the tanh-sinh rule.[124] The transformation is applied recursively until the stopping rule, controlled by the relative error parameter tol, is satisfied. For simplicity, the implemented error estimate is computed as the difference between the current and the previous extrapolated results. However, to reduce the chance of false convergence, a much safer strategy is to use the maximum difference between the current and the previous two extrapolated results.[117] A pseudocode for an alternative version of the PE method, using the Mosig–Michalski Algorithm 5 of Section 3 with analytical remainder estimates (the a-variant), is given in Algorithm 7. Note that the auxiliary function implements the coefficient given by (77(77) ).

The PE method can also be used to evaluate Sommerfeld integrals, such as (2(2) ), involving a product of two Bessel functions of different orders. As an example, consider the integral [8](80)

where(81)

In the special case when , the first Bessel function in the product becomes identically 1, thus can still be computed by the PE method described above, where is now half-integer. To illustrate, in Figure 7(a) we compare the integrated and exact results for I(z, 0, 1) over a four-decade -range, with the former computed by the PE Algorithm  for , and by the mixed quadrature rule (Algorithm  of Section 2) for (where in the present case). The switching of the algorithms is beneficial, because in the latter range the behavior of the integrand function in (80(80) ) is dominated by the exponential decay, rather than the oscillations of the Bessel function.

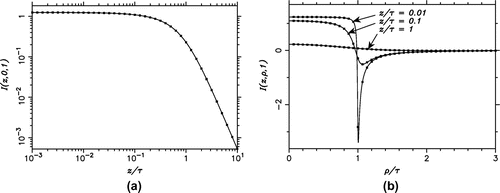
Figure 7. (a) Plot of I(z, 0, 1) vs. . The integral is computed by the PE method (Algorithm 6) for and by the mixed quadrature rule (Algorithm ) for . (b) Plot of vs. , with , 0.1, and 1, computed by the PE method (Algorithm ) with the Lucas decomposition. The integrated results are indicated by symbols and the exact results by solid lines.

In the general case, when , the integrals such as (80(80) ) are notoriously challenging to evaluate, due to the irregular oscillatory behavior of the product of the Bessel functions, which makes it difficult to devise a partition scheme that would yield a sequence of partial sums amenable to extrapolation. The method by Van Deun and Cools [105] should be mentioned here, in which the tail integral is evaluated analytically, after replacing the Bessel functions by their asymptotic expansions. In the special case where the Bessel functions have the same argument, i.e. , the modified mW-transformation of Sidi [125] may be applicable. Hence, unless , when the strong exponential decay makes the mixed rule applicable, we resort to the long-standing method of Lucas [8,106,126,127], which is based on the decomposition(82)

with(83)

where denotes the Bessel function of the second kind and order [5]. Note the analogy with the trigonometric identity . Since the large-argument form of is similar to that of , except that the cosine in (79(79) ) is replaced by a sine, it is readily found that(84)

Thus, for , both terms in the decomposition (82(82) ) approach simple sinusoids with half-periods , and for , is still asymptotically sinusoidal, but approaches a monotonically decreasing function. The splitting (82(82) ) achieves the separation of the high- and low-frequency components in the product of the Bessel functions by adding and subtracting the term . However, since Bessel functions of the second kind have large magnitudes for small arguments, to prevent the loss of accuracy due to catastrophic cancellation, the decomposition (82(82) ) should only be applied for exceeding a suitable threshold value a, where the term no longer dominates. Following Lucas [126], here we set , where denotes the first zero of . The initial zeros of are tabulated for some integer and half-integer orders [123, p.410], [123, p.467]. For the first zero, an asymptotic expansion valid for large orders is also available [123, p.371], which yields an acceptable approximation for as low as 1 [126]. Based on these considerations, we split the integral (80(80) ) into three parts as(85)

We evaluate the finite-range integral by the tanh-sinh DE rule and the two tail integrals by the PE method – except in the special case , when the integrand of ceases to be oscillatory, and we employ the mixed quadrature rule. The use of the mixed rule is justified if the integrand has some exponential decay, i.e. . Otherwise, the DE rule (20(20) )-(21(21) ) is more appropriate. Applying the PE method to , we use the modified Sidi partition and Algorithm 7 with . To find the first zero of the integrand exceeding a, we bracket it by taking a few steps of size q / 4 until a change in the sign of the function is detected, and apply the derivative-free Brent method [18, p.454]. The gap between the original and modified values of a is then bridged by another application of the tanh-sinh rule. Note that cannot be arbitrarily close to zero with this approach, as this would push the break point a towards infinity. For very small and , the integration range may have to be restricted, to prevent underflows.

To illustrate the performance of the PE method in conjunction with the Lucas decomposition, in Figure 7(b) we compare the integrated and exact results for , with varying and as a parameter (where in this case). Note the excellent agreement, even in the vicinity of , where the integral becomes singular as . Hence, the combination of the DE quadrature and a partition method with convergence acceleration by extrapolation resulted in a powerful and efficient technique, applicable for a wide range of the parameters.

5. Application of the Ogata–Sugihara DE rule

The method of Ogata and Sugihara [128–130], which extends the earlier work of Ooura and Mori [131–133], has been successfully adopted for Sommerfeld integral tails by Golubović et al. [15,41]. Whereas the conventional DE transformations make the decay of the integrand double-exponential as the variable of integration approaches , the idea here is to make the nodes of the quadrature formula approach the zeros of the Bessel function in (3(3) ) double-exponentially. In applying this method to the Sommerfeld tail(86)

we first introduce the transformation [129](87)

where and is a “mesh size” parameter, whose selection will be addressed in due course. The corresponding Jacobian is readily found as(88)

and it clearly does not possess the rapid fall-off property of the more standard DE transformations of Section 2. The integral (86(86) ) may now be expressed as [41](89)

where we have introduced(90)

and where in the second integral we have used the fact that the integrand on the left is an odd function of t. The signum function is defined as

For later reference, we note that , , and . The role of the part of the transformation (87(87) ) is to map the lower integral limit from into . The influence of this term vanishes quickly as and we find that in those limits. Consequently, the integrand function in (89(89) ) has zeros that for large t approach the values(91)

double-exponentially, where denotes the kth zero of the Bessel function of order . Hence, the second integral in (89(89) ) is amenable to the DE rule of Ogata and Sugihara [129], and we obtain(92)

where(93)

and(94)

with(95)

where are the coefficients in the Laurent series expansion of around ,(96)

In (93(93) ), denotes the Neumann function and the second expression follows upon invoking the Wronskian of and [5, Equation 10.5.2]. The zeros in (91(91) ) and (93(93) ) can be obtained using available software packages [134] or may be computed by a few Newton-Raphson iterations, using the asymptotic values as starting points. From (94(94) )–(96(96) ), we readily find that and(97)

with the higher order given by expressions rapidly increasing in complexity, which we omit to conserve space. In (97(97) ), we have used the fact that .

We still need to address the selection of the mesh size h and the truncation index n in (92(92) ). For Sommerfeld integral tails, Golubović et al. [41] recommend as the best trade-off between accuracy and computational cost. However, since it is unlikely that this particular mesh size should be suitable for all integrand functions, an algorithm for its automatic selection is desirable. If I(h) denotes the quadrature rule (92(92) ) with mesh size h, it can be shown that the discretization error is , where d is a constant. Consequently, if the mesh size is halved, the error of I(h / 2) will be approximately . Hence, we may compute a sequence of approximations , until , where is the desired error tolerance. Then, since the error of I(h / 2) will be approximately , we conclude that [135]. Although this adaptive strategy is similar to that implemented for the standard DE rules in Section 2, the Ogata–Sugihara quadrature is non-progressive, i.e. it cannot reuse the previously-computed function values each time h is halved, because the Bessel function zeros are not equidistant.

The truncation error, which depends on the truncation index n, should be kept smaller than the discretization error for any value of h. Unfortunately, it does not seem possible to derive a simple a priori formula for n satisfying this condition. A simple expedient adopted here is to continue the summation in (92(92) ) until the magnitude of the nth term falls below a small fraction, say , of the already accumulated sum. We have found that double precision arithmetic (with approximately 15 significant digits) is not sufficient for some spectral domain Green functions that grow with , in which case, when is small, the magnitude of may reach a floor value before the sum in (92(92) ) converges. On the other hand, for rapidly decreasing , its magnitude may become exceedingly small even before the first zero of the Bessel function is reached, in which case a very small mesh size h may be required to achieve the desired accuracy of the quadrature. These caveats notwithstanding, the implementation of the Ogata–Sugihara rule (92(92) ) is straightforward, hence we omit the detailed algorithm for brevity. Examples of the application of the Ogata–Sugihara rule to Sommerfeld integral tails are given in the next section.

6. Examples of automatic Sommerfeld integral tail computation

We now illustrate the application of the methods described in this paper to the automatic computation of the Sommerfeld integral tail (89(89) ) with the kernels(98)

and(99)

where(100)

with(101)

These spectral domain kernels arise in the computation of the horizontal and vertical components of the vector-potential Green functions due to a horizontal dipole radiating in air (medium 1) above a lossy halfspace (medium 2).[55] In the above, and are the reflection coefficients for TE and TM waves, respectively, looking into the lower halfspace, is the wavenumber of medium 1 and is the dielectric constant of medium 2. The complex square roots with negative imaginary parts should be selected in (101(101) ), to satisfy the radiation conditions at infinity. 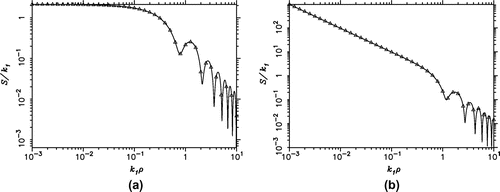In the numerical results that follow, we use , , and , where the latter is a representative value for wet soil at GHz. For the two kernels above, in Figure 8 we compare the results obtained by the automatic Ogata–Sugihara quadrature of Section 5 and the Levin-Sidi partition-extrapolation (PE) method of Section 4. The maximum discrepancy of the results is and in the cases of (98(98) ) and (99(99) ), respectively. In the case of (98(98) ), where is rapidly decreasing as a result of the vanishing for , the mesh size h as small as was required in the Ogata–Sugihara rule near the lower limit to satisfy the convergence criterion with . This example illustrates that, in view of the non-progressive nature of the Ogata–Sugihara rule, many function evaluations can be wasted in some cases before the required quadrature level is reached. The PE method does not suffer from this drawback and should thus be preferred for automatic integration of Sommerfeld tails.

Figure 8. Sommerfeld tails integrated by the automatic Ogata–Sugihara quadrature (solid line) and by the PE method (triangles) for (a) the kernel given in (98(98) ) and (b) the kernel given in (99(99) ).

7. Conclusion

A review has been presented of the most effective methods and algorithms for the computation of Sommerfeld integral tails that commonly arise in the Green functions for plane-stratified media. The mathematical foundations of these methods are discussed in detail and their performance is illustrated by relevant numerical examples. In the most challenging case of oscillatory tails, the partition-extrapolation method is the recommended approach for efficient and reliable computation of such integrals. We demonstrate the implementation of this method as a fully automatic procedure and present the associated algorithms in pseudocode, which even a novice can readily convert into a working computer program. Hence, the computation of Sommerfeld integral tails should no longer be a “cauchemar” of engineers and scientists engaged in various areas of applied electromagnetics.

Notes

No potential conflict of interest was reported by the authors.