Testing the Consensus Model: relationships among physics teachers’ professional knowledge, interconnectedness of content structure and student achievement

ABSTRACT

The structure and definition of professional knowledge is a continuing focus of science education research. In 2012, a pedagogical content knowledge (PCK) summit was held and it suggested a model of professional knowledge and skill including PCK, which was later often called the Consensus Model (Gess-Newsome, 2015. A model of teacher professional knowledge and skill including PCK: Results of the thinking from the PCK summit. In A. Berry, P. J. Friedrichsen, & J. Loughran (Eds.), Teaching and learning in science series. Re-examining pedagogical content knowledge in science education (1st ed., pp. 28–42). New York, NY: Routledge). The Consensus Model proposes a potential powerful framework for the relations among teachers’ different professional knowledge bases, but to date it has neither been investigated empirically nor systematically. In this study, we investigated the relationships suggested by the Consensus Model among different aspects of teachers’ knowledge and skill. A sample of 35 physics teachers and their classes participated in the investigation; both teachers and their students in these classes took paper-and-pencil tests. Furthermore, a lesson taught by each of the teachers was videotaped and analysed. The video analysis focused on the interconnectedness of the content structure of the lesson as representation of the in-class actions of the teachers. The interconnectedness is understood as a direct result of the application of professional knowledge of the teachers to their teaching. The teachers’ knowledge showed no significant influence on the interconnectedness of the lesson content structure. However, the results confirmed the influence of interconnectedness and certain aspects of professional knowledge on students’ outcomes. Therefore, interconnectedness of content structure could be verified as one indicator of teachers’ instructional quality.

KEYWORDS:

• Professional knowledge
• PCK
• the Consensus Model

Introduction

Professional knowledge is perceived as a requirement for effective teaching (Abell, 2007). Teachers do not only need to know their domain, but must also know about professional knowledge, for example, students’ perspectives and teaching strategies as well. Because teaching is more than just passing on knowledge, it requires a transformation of content to make it accessible for students (Duit, Gropengießer, Kattmann, Komorek, & Parchmann, 2012; Resnick, 1987).

Many studies about professional knowledge focused on model conception and clarification (e.g. Gess-Newsome & Lederman, 1999; Magnusson, Krajcik, & Borko, 1999) or the development of test instruments to measure professional knowledge (e.g. Riese, 2009). Several studies also focused on analysing the relationship between professional knowledge (or PCK in particular) and classroom actions (e.g. Alonzo, Kobarg, & Seidel, 2012; Fischer, Labudde, Neumann, & Viiri, 2014; Park & Chen, 2012). These studies have contributed further pieces of the puzzle in understanding how professional knowledge works and influences teachers in their in-class actions. It is important that researchers continue to investigate the relationship between professional knowledge and in-class actions because professional knowledge is the cornerstone of the academic education of future teachers. The education of future teachers has to put emphasis on professional knowledge which could prove meaningful for effective teaching. To achieve this goal, a common understanding of professional knowledge has to be established. In 2012, an expert group of PCK researchers met in a conference in Colorado in the USA to find a common understanding. The result of the conference of this group was the model of professional knowledge and skill including PCK (Gess-Newsome, 2015), which is now often called the Consensus Model. This model provides a potentially powerful framework for further PCK research. However, the model itself has not been empirically tested yet.

In this article, we report an empirical study in which we investigated the relationship among parts of the Consensus Model. In detail, we investigated how the professional knowledge relates to teachers’ in-class actions and whether both this knowledge and actions have an impact on student achievement.

Theory

In this section, we discuss the nature of professional knowledge and the suggestions of the Consensus Model regarding the relationship among the different knowledge bases, as well as what PCK is. Then, we discuss the results of several studies regarding the relationship of professional knowledge, especially PCK, to aspects of instructional quality and student outcomes. Finally, we ask ourselves the question of how knowledge influences the actual content taught in class and introduce the Model of Educational Reconstruction as a theoretical framework to interpret how the teachers’ knowledge influences their decision making for reconstructing the content in their lectures. A video coding instrument allows the characterisation of a lessons’ content structure through content structure diagrams. This content structure diagram was also used in this study and therefore is introduced at the end of this section.

Since Shulman (1987) categorised the knowledge of teachers, there have been several attempts to sharpen researchers’ view on professional knowledge. The common ground is that teachers need content knowledge (CK) (or often also called subject matter knowledge or SMK) of their subject. In science, CK can include ‘an understanding of science subject matter as well as research experiences within the discipline’, ‘a knowledge of science in general’ and ‘an understanding of the nature of science, including its history, philosophy, and epistemology at levels that exceed those specified in science education reform documents’ (Wenning et al., 2011, p. 4). Teaching a subject requires more than content knowledge alone. Science teachers and scientists differ in an important way: teachers have to be able to teach. On the one hand, they need general pedagogical knowledge (PK), for example, knowledge about effective classroom management or general performance assessment (Voss, Kunter, & Baumert, 2011). On the other hand, they have to transform the content into content knowledge (CK) for teaching, so that it is accessible to students and provides them learning opportunities (Duit et al., 2012; Resnick, 1987). The knowledge required for such a process is called pedagogical content knowledge (PCK) and as the word itself already implies: it is a ‘special amalgam of content and pedagogy’ (Shulman, 1987, p. 8).

Many studies focus dominantly on the research of teachers’ PCK (e.g. Park & Chen, 2012; Van Driel, Verloop, & De Vos, 1998). The broad interest in PCK has resulted in a variety of different models of PCK (e.g. Friedrichsen et al., 2008; Magnusson et al., 1999; Park & Oliver, 2008). Magnusson et al. (1999), for example, argued that CK, PK and knowledge of contexts are transformed into a new kind of knowledge: PCK. Other scholars included CK within PCK (Fernández-Balboa & Stiehl, 1995). In 2012, several research groups with a focus on PCK held a PCK summit to foster conversation, collaboration and consensus regarding PCK (Berry, Friedrichsen, & Loughran, 2015). One result of the summit was a model of teacher professional knowledge and skill including PCK (Gess-Newsome, 2015), which was often called the Consensus Model afterwards.

Figure 1 shows the Consensus Model (Gess-Newsome, 2015) which starts at teachers’ professional knowledge base (TPKB) formed by results of research and best practice. TPKB is directly related to teachers’ topic-specific professional knowledge (TSPK). This separation between these two knowledge categories has the benefits that it puts emphasis on the fact that content for teaching relates to the topic level (e.g. ‘force concept’) and not the disciplinary level (e.g. physics in general). On that level, TSPK merges with subject matter, pedagogy and context. According to the model, teachers’ beliefs and orientations also have an influence on their classroom practice. Teachers amplify or filter which knowledge they regard as important. Also, both knowledge categories mediate teachers’ in-class actions. Gess-Newsome (2015) expressed the nature of PCK as:

Unique to this model, PCK is defined as both a knowledge base used in planning for and the delivery of topic-specific instruction in a very specific classroom context, and as a skill when involved in the act of teaching. (pp. 30–31)

Figure 1. Model of teacher professional knowledge and skill including PCK and their influences on classroom practice and student outcomes (Gess-Newsome, 2015).

Furthermore, student outcomes are explicit details of the model: they are not regarded as a direct result of the teachers’ instruction but they are influenced by the students’ amplifiers and filters (Gess-Newsome, 2015).

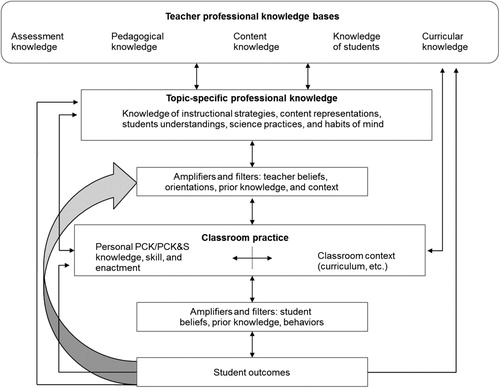
In the past years, researchers started several attempts to investigate the influence of PCK on teachers’ in-class actions. For example, Alonzo et al. (2012) made a comparison between a high-performing class and a low-performing class to investigate the difference in their teachers’ PCK-related behaviours; and they identified three types of the use of content which differed between the teachers in both classes: (a) flexible use of content, which is related to understanding what is difficult for students to understand, (b) rich use of content, which connects to teachers’ knowledge of instructional representations, and (c) learner-centeredness, which indicates that knowledge of student learning difficulties may inform the sequencing of instructional representations. Another example of these studies is the visualisation of in-class PCK expressions by a PCK map to investigate the connection of different PCK facets (Park & Chen, 2012). Park and Chen (2012) showed that, even under similar circumstances like teaching the same topic or having the same lesson plan, the resulting PCK maps differed from each other. The PCK maps provide opportunity to identify the PCK aspects that teachers lack or possess but have difficulty in their connection to other PCK aspects (Park & Chen, 2012).

There is still a lack of knowledge about the relationship between teachers’ knowledge and student achievement for learning mathematics and sciences (Abell, 2008). In mathematics teaching, the Professional Competence of Teachers, Cognitively Activating Instruction, and Development of Students’ Mathematical Literacy (COACTIV) study showed that student achievement was positively influenced by PCK, mediated by the level of cognitive activation in class (Baumert et al., 2010). Cognitive activation involves cognitively challenging tasks for students that draw on their prior knowledge by challenging their beliefs (Baumert et al., 2010). Also, a fit between topics and materials chosen by teachers is associated with the cognitive activation of the class (Baumert et al., 2010). For first- and third-grade classes, content knowledge for teaching mathematics was a significant predictor of student learning gains (Hill, Rowan, & Ball, 2005). However, in an investigation of teachers and classes of the fifth to seventh grades, no significant relations among teachers’ CK, the lesson quality and their student achievement could be found.

In physics education, the research findings are even more ambiguous. The Quality of Instruction in Physics (QuIP) project compared physics education in Finland, Germany and Switzerland (Fischer et al., 2014). Despite having the greatest learning gains in their classes, the Finnish teachers showed the lowest level of PCK (Spoden & Geller, 2014). A correlation between physics teachers’ PCK and cognitive activation in class was found for the combined subsample of Germany and Switzerland teachers without the Finnish counterparts (Ergöneç, Neumann, & Fischer, 2014).

The findings of Alonzo et al. (2012), and Park and Chen (2012) showed the influence of teachers’ professional knowledge on their in-class actions. However, as the results of the other above-mentioned studies (e.g. Baumert et al., 2010; Hill et al., 2005) showed, the influence of professional knowledge on student achievement remains unclear. Still, theoretically there is a strong connection.

In the definition of PCK, it is already stated that this knowledge is required to facilitate student learning by transforming content representations informed by teachers’ CK to a content form that is applicable for instruction. But how can such a process of making content more accessible to students be described? And finally, how is such a process influenced by the related knowledge bases of CK and PCK?

As an example, we want to imagine a lesson in the domain of mechanics. The goal of the lesson is the introduction of the ‘force’ concept. Using demonstration experiments, the teacher explains the effects of force and together with the students develops a figure on the blackboard to illustrate the effects of force.

Why do certain teachers choose to introduce the concept of force with a focus on the effects of force (e.g. acceleration)? How do they choose what they want to teach their students?

The Model of Educational Reconstruction argues that the content structure of a physics lesson is different from the content structure of physics (Duit et al., 2012). The following paragraph—if not mentioned otherwise—is based on the article of Duit et al. (2012). For clarification, there is no definite content structure of physics. Academic textbooks are possible representations. They present science in a very abstract and condensed way because they address experts or at least soon-to-be-experts. Such a representation of physics or science in general is clearly not suited for lessons at school level. Still the lessons’ content structure is based on this physics content structure. Teachers have to transform the latter into the former. To achieve this, the content structure of physics has to be elementarised first to make it accessible to students. As Duit et al. (2012) explained, there are three major facets of elementarisation: (a) Identifying the elementary principles and phenomena of a certain topic guided by the instructional goals so that students may understand them. (b) Reducing the complexity of particular science content to make it more accessible to the learners. Still, it is not about simplifying but finding a balance between scientific correctness and accessibility for students. (c) Planning student learning processes to guide them from pre-concepts towards fully developed science concepts. To make sense for the students, teachers have to enrich the elementarised ideas in the content structure by putting them into appropriate context. For both processes, knowledge about science content knowledge as well as knowledge about students’ perspectives are needed. In detail, knowledge about students’ conceptions and views about the lessons’ content as well as knowledge about their interests and science learning self-concepts are required by their teachers. Furthermore, teachers need the knowledge to initiate and support their students’ learning gains.

If these requirements of teachers for the reconstruction process described by Duit et al. (2012) are compared to the operationalisation of PCK, it becomes obvious that they are the same. For the process of educational reconstruction, teachers need to have an understanding of the subject matter (e.g. physics), which corresponds to their CK. The process itself is heavily influenced by the knowledge about students’ understanding and lesson methods, which corresponds to teachers’ PCK.

Brückmann (2009) developed a video coding manual to map a lesson’s content structure corresponding to a content structure diagram. The diagram consists of content blocks¹ and an illustration of their connections through arrows. An important measure of content structure is the interconnectedness, defined by the amount of arrows divided by the amount of content blocks. Interconnectedness shows significant influence on the learning gains of students in the domain of electricity (Müller & Duit, 2004).

Research questions: testing the Consensus Model

As discussed above, the relationship of professional knowledge to in-class actions and student achievement is not well understood. The Consensus Model proposes a powerful framework for relationships among different professional knowledge bases and how the bases are related to PCK specifically. But the proposed relationships of the Consensus Model lack a deeper empirical investigation. The Model of Educational Reconstruction in general, and the content structure diagram by Brückmann (2009) in particular, provide a strong tool to investigate the influence of knowledge on the classroom practice. According to the Model of Educational Reconstruction, the content structure is directly influenced by teachers’ decision making which requires their CK as well as PCK. Therefore, this study investigated the relationships among the different knowledge bases (as suggested by the Consensus Model) and the content structure diagrams based on these bases (as suggested by the Model of Educational Reconstruction).

Therefore, this study investigated following research questions:

RQ1: Is there a (correlational) relationship between the teacher professional knowledge (TPBK) and the topic-specific professional knowledge (TSPK)?

RQ2: Is there a (correlational) relationship among professional knowledge bases and classroom practice?

RQ3: Is there a (correlational) relationship between classroom practice and students’ outcomes?

RQ4: Is there a (correlational) relationship among professional knowledge bases and students’ outcomes?

This study was part of the second phase of a project called Professional Knowledge in Science (ProwiN II) funded by the German Federal Ministry of Education. The project had the goal to investigate the relationships among professional knowledge, in-class actions and students’ outcomes in the subjects biology, chemistry and physics. Different subprojects were performed in biology, chemistry or physics, because in Germany all three fields are separate subjects. In the first phase of ProwiN I, a model to quantify and analyse teachers’ CK, PCK and PK was developed (Kirschner, 2013; Tepner et al., 2012). The ProwiN model can be characterised as a test-development model because it focuses on certain aspects of each dimension which were assumed to be important for successful teaching. These aspects do not reflect the full width of professional knowledge (Park & Oliver, 2008), but the CK and PK can be identified as part of the TSKB of the Consensus Model. CK and PK do not represent the full spectrum of TPKB but they give a good estimate for the width of the TPKB. The PCK of the ProwiN model represents aspects of the TSPK of the Consensus Model. The PCK of the ProwiN model includes knowledge about experiments, concepts and students’ preconceptions and will be described in detail in the ‘Teacher Test’ section of this article. Even if PCK is defined rather narrowly, it represents facets of PCK which many researchers agreed to be part of (measurable) PCK (e.g. Baumert et al., 2010; Fischer et al., 2014). Additionally, these facets are part of the TSPK of the Consensus Model. The TSPK, according to Gess-Newsome (2015), includes knowledge of science practices (which would include the PCK facet ‘experiments’), content representations (which would include the PCK facet ‘concepts’) and student understanding (which would include the PCK facet ‘student preconceptions’). So, the applied PCK model may not represent the full width of TSPK of the Consensus Model but the PCK model can be used as measurement approximation of aspects which are central to TSPK.

The classroom practice is modelled on the findings of Müller and Duit (2004) where the interconnectedness of content structure diagrams is regarded as one indicator of lesson quality and effective teaching. The assumption is that teachers with higher TPKB (represented by CK and PK) and TSPK (represented by PCK) are able to apply their knowledge better in a classroom situation, and therefore, are providing a more meaningful learning environment to successfully initiate student learning.

Research focus, design and methodology

The study was conducted under a paradigm of postpositivism (Mertens, 2015). We intended to use a quasi-experimental design to capture correlational relations among the constructs we discussed above under the assumption that any correlations found in our study are no proofs but probabilities for causality. The sample of this study consisted of 35 physics teachers (34% female, M _age = 43.3 years, SD _age = 11.6 years, Min = 27 years, Max = 64 years) and their classes (N = 907 students, 55% female, M _age = 13.7 years, SD _age = 0.7 years). All classes were grade eight or grade nine at grammar schools (Gymnasium) (Wendt, Smith, & Bos, 2016) in the federal state of North Rhine-Westphalia, Germany. Following compulsory curricula of the federal state, the teachers still have freedom with regard to choosing content, objectives and teaching methods (Wendt et al., 2016). The curriculum itself follows joint national educational standards (Bildungsstandards) of the federal states of Germany (Wendt et al., 2016). The professional knowledge of the teachers and the learning achievement of the students were measured by paper-and-pencil tests which will be described in the following section. As covariates, students’ cognitive abilities were measured and the students were asked about their spoken language at home. The spoken language at home is an indicator of the migration background of the students (Quesel, Möser, & Husfeldt, 2014). The students’ answers to the home language question showed that 21% of them had a migration background. However, the percentage of students with migration background in each class varied from 0% to 48%.

The introductory lesson of each teacher on the force concept was videotaped. The lesson was part of a mechanics unit, before and after which the student outcomes were measured. Depending on the school, the length of the lesson varied: it ranged between 45 and 90 min. The reported number of lessons, of which the mechanics unit consisted, varied from 12 to 59 (standardised to 45 min per lesson). Due to this wide range of the reported number of lessons, the length of the mechanics unit was considered an additional covariate. For better comparison, the total lesson time was used, which is equal to the number of lessons multiplied by the length of a lesson in minutes.

Description of instruments

Teacher tests

The teacher tests were based on the ProwiN model of CK, PCK and PK (Tepner et al., 2012), and were developed and validated in the first project phase with regard to criterion, content and construct aspects of validity (Kirschner, 2013; Lenske, Thillmann, Wirth, Dicke, & Leutner, 2015).

In the ProwiN model, PK covers classroom management, teachings methods, individual learning processes and assessment of performance. PCK includes knowledge about experiments, concepts and students’ preconceptions. The CK of the ProwiN model differentiates among school knowledge, advanced school knowledge and university knowledge.

Kirschner (2013) developed a paper-and-pencil test for measuring physics teachers’ CK and PCK according to the model. By comparing the results of CK and PCK to the results of the ProwiN PK test, Kirschner showed that CK, PCK and PK are separable dimensions of professional knowledge. The domain-specific CK correlated more highly with PCK than with PK. Both results imply construct validity for the test instrument. To investigate content validity, the tests’ content was matched with the related curricula and literature. Furthermore, experts were consulted. Kirschner (2013) ensured criterion validity by comparing the results from different groups of teachers: physics teachers and other subject teachers as well as pre- and in-service teachers. The comparison showed the expected results: physics teachers had higher CK and PCK test scores than those of teachers of other subjects; the experienced teachers also performed better than did the pre-service teachers. A re-analyis showed that the criteria for content validity, construct validity and criterion validity were still valid in ProwiN II (Cauet, 2016).

The CK and PCK tests consisted of 12 items and 11 items, respectively. Multiple-choice and open items were used in both tests. For each item, a maximum of two points could be awarded to a correct answer.

Both tests were rated independently by two raters. Due to the fact that a bigger sample was required for the intended Rasch analysis, data collected by ProwiN I project was added to the analysis (ProwiN I: N = 79, 37% female, M _Age = 44 years, SD _Age = 10 years). The tests were coded by the two raters. Good to very good inter-rater agreements showed high reliabilities of both tests (CK: ICC _{2-fact,unjust} ≥ .96; PCK: ICC _{2-fact,unjust} ≥ .85, except for one item with ICC _{2-fact,unjust}. = .77; Wirtz & Caspar, 2002).

The PK test was developed and validated by a different ProwiN I project (Lenske et al., 2015). The PK was measured by text vignettes (Lenske et al., 2015). According to situation descriptions of concrete lesson situations or lesson planning situations, a course of action had to be selected. Each of these courses of action had to be graded by (German) school grades (1 for ‘excellent’ to 6 ‘unsatisfactory’). Pair comparisons were performed between the ranking of the teacher and a best practice ranking determined by experts (Lenske et al., 2015). The test consisted of 11 tasks with 30 items (Lenske et al., 2016). The results used a scale from 0 to 100, which corresponds to the amount of points divided by the amount of items, multiplied by 100 (Lenske et al., 2016).

The PK test was not Rasch scaled due to two reasons. The first reason was that the original test instrument was shortened (Lenske et al., 2016) and the second reason was that the construct was not one-dimensional, which is a requirement for Rasch analysis (Prenzel et al., 2006).

Student tests

The student content knowledge (SCK) test measured the domain-specific content knowledge of mechanics with special emphasis on the ‘force’ concept. The test was constructed in a multi-matrix pre–post design with two anchored test booklets. Each booklet consisted of 24 multiple-choice single-select items including nine anchor items. The total item pool consisted of 38 items. The test was taken by the students before and after the teaching of the mechanics unit.

The test was developed and validated by Cauet (2016). It included items from the Force Concept Inventory (Hestenes, Wells, & Swackhamer, 1992), the Mechanics Baseline Test (Hestenes & Wells, 1992) and Trends in International Mathematics and Science Study (TIMSS) Assessment (Olson, Martin, Mullis, & Arora, 2008). Cauet’s (2016) results showed construct and criterion validities. The curricular validity could only be shown by using the state-wide curriculum, but it could not be shown what was taught in each individual class. However, the validation results showed that, if the total lesson time as a covariate, a fair comparison among students’ results is possible and valid.

Students’ cognitive abilities were measured by the subscale N2 (A) of the Cognitive Abilities Test (CAT; Heller & Perleth, 2000). The CAT has different booklets for eighth- and ninth-grade students. Each booklet contained 25 items with 20 anchor items. In total, the item pool consisted of 30 different CAT items. The CAT is an established and validated test instrument (Heller & Perleth, 2000). However, only the N2 scale was used in this study. But, according to Heller and Perleth (2000), the N2 scale correlates strongly with general intelligence. The N2 scale also has the highest correlation with the other scales (Heller & Perleth, 2000). For these reasons, the CAT that was used can be considered as a valid indicator of the cognitive abilities of the students.

Video analysis of content structure

To analyse the content structure of the videotaped lessons, the video coding manual of Brückmann (2009) was used. In this section, we describe the video analysis procedure and then discuss its validity.

The reconstruction of content structure offered by teachers was rated by using a content-related category system. In a 10-second interval time-based coding, the rater had to make several decisions: on the broader coding level A (e.g. ‘Effects of Force’) and the corresponding finer coding level B (e.g. ‘Effects of Force on Acceleration’).

In a second coding step, the content structure diagram was reconstructed. For the coding of so-called ‘content blocks’, the video was coded a second time in 10-second intervals. In a content block, a specific content is discussed and a certain instructional strategy is used. A change of content or instructional strategy signals the change of a content block. The rater has to distinguish between two kinds of interconnection and the lack of it. The content structure of the lesson describes several characteristic traits. Special emphasis is put on the ‘interconnectedness’ which is defined by the number of arrows divided by the number of content blocks.

The interrater reliability of the content offer coding steps was determined from a double coding of intervals (N = 1412 intervals) corresponding to four lessons of the sample of 35 lessons. The Cohens Kappa values range from κ = .91 to κ = .97 over all occurring coding categories and can be interpreted as excellent. For several B categories, no instances were found; and therefore, Cohens Kappa could not be determined. For the ‘content block’ ratings, good to very good interrater reliabilities could be shown. The Cohens Kappa values ranged between κ = .77 and κ = .99 for the ratings of four double-coded lessons.

According to the students, the videotaped lessons are mostly typical for their teachers. All teachers reported that their students’ behaviours were mostly comparable to those in regular lessons. The video analysis of the lessons should therefore provide a good representation of the typical instructional offerings.

The content validity is based on the fact that the instrument was adapted from the validated instrument developed by Brückmann (2009). Preliminary work regarding the subject of content structure diagrams showed that interconnectedness is a criterion for quality of instruction (Müller & Duit, 2004). Content structure diagrams were also used in different science education studies to analyse content structures (Wüsten, Schmelzing, Sandmann, & Neuhaus, 2010). The interconnectedness of physics concepts was also shown to be a predictor of student achievement (Helaakoski & Viiri, 2014). A discriminant validation was used to show construct validity. The correlations between interconnectedness and other measures of quality, which were investigated in the ProwiN II project using the same video data, were determined. The measures were cognitive activation (Cauet, 2016) and classroom management (Lenske et al., 2016). The interconnectedness of the content structure correlated significantly with the cognitive activation, r = .38 (.15), p = .37 and the classroom management, r = .33 (.17), p = .27. The connection to classroom management can be explained by the fact that good classroom management is essential for demanding lessons (Helmke, 2015). If teachers could not be able to manage their classes properly, they would lose effective lesson time. In consequence, teachers would have less time for teaching additional content and for making connections among the content blocks they use in teaching. Overall, the correlation among the interconnectedness and two different quality measures is an indicator of the construct validity.

Rasch analyses

All Rasch analyses were performed using the R package ‘TAM’ (Kiefer, Robitzsch, & Wu, 2015). For the CK and PCK tests, a partial credit model was used. Because of their significant misfit to the Rasch model (underfit criteria: MNSQ > 1.2, ZSTD > 2; overfit criteria: MNSQ < 0.8, ZSTD > 2; Bond & Fox, 2007), one PCK item and two CK items had to be removed from the tests.

In the student test, the use of a multi-matrix design made a Rasch analysis necessary. To detect changes between the students’ abilities in the pretest and posttest, the item difficulties in both estimates had to be on the same scale. Therefore, the item- difficulty values from the posttest estimate were also used as those values for the pretest estimates. However, a potential ‘differential item functioning’ (DIF) of the items would not be detectable if they are not checked separately. Therefore, the DIF was checked separately and beforehand by building a ‘pseudo-sample’ of all the pretest and posttest booklets. For this pseudo-sample, a Rasch analysis was performed and the items checked if a DIF could be identified according to Educational Testing Service (ETS) classification (Longford, Holland, & Thayer, 1993). Five items had an ETS classification worse than ‘A’.

The Rasch analysis of the posttest data showed that three items had a significant misfit to the Rasch model (underfit criteria: MNSQ > 1.2, ZSTD > 2; overfit criteria: MNSQ < 0.8, ZSTD > 2; Bond & Fox, 2007) and had to be removed from the test. The item-difficulty estimates of the posttest were also used for the pretest analysis to ensure that the items were on the same item-difficulty scale. Exceptions were the five items classified with DIF. By using the estimates from the posttest for the pretest estimations, an under- or over-estimation of the model was possible (Linacre, 2011). In consequence, resulting misfits for items of the pretest were accepted and no further items were removed from the test.

A Rasch analysis was performed on the CAT data. Heller and Perleth (2000) recommended that even with a bad model fit no items should be removed. Six items did not fulfil the applied overfit criteria: MNSQ < 0.8, ZSTD > 2 (Bond & Fox, 2007).

Learning gains of the students

Before modelling the students’ achievement in the posttest by using multilevel models, we discuss the overall difference in class-level means as an indicator of the overall learning gains in the classes. Figure 2 shows the illustration of the differences. The plot in Figure 2 is divided in two sections. In the left section, the class IDs are shown on the x-axis and the class-level means of the person ability are shown on the y-axis. For each class, the square represents the class-level mean of the pretest, whereas the circle represents the class-level mean of the posttest. The classes are sorted by their mean differences in the pretest and posttest. To minimise an α-error-accumulation, the p-values were corrected according to Benjamini and Hochberg (1995). The error bars in Figure 2 show the standard deviation of the person-ability distribution of each class. Because a t-test is based on the standard error of the mean and not the standard deviation, a significant difference can be given even if the difference between pretest and posttest means is smaller than the standard deviation. The length of the error bars of a class indicates how heterogeneous the students were in their abilities in that class. Only 68.27% of all person-ability scores of one class are between the top and the bottom of both error bars. For double-error bars, 95% of all achieved person-ability scores are covered. The effect size d is given directly above the x-axis of each class.

Figure 2. The left side of the figure shows the distribution of average person ability of each class for the pretest and the posttest. The right side shows the distribution of the item difficulty of the SCK posttest. *p < .05; **p < .01; ***p < .001.

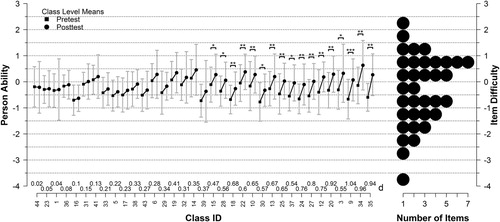
The right section of Figure 2 shows the distribution of interval-scaled item difficulties of the posttest. One property of Rasch-scaled person abilities and item difficulties is that if the ability-score distribution fits the item-difficulty distribution, the probability that a person can solve the items is 50%. In case of Figure 2, if for a class, the pretest or posttest class-level mean score distribution fits the item-difficulty distribution, the average student of this particular class has a 50% chance to solve the items. If the ability distribution is higher or lower than the item-difficulty distribution, the probability for the average student to solve the items also would be higher or lower, respectively.

Only 17 of the 35 classes showed a significant difference in their class-level person-ability means. A fraction (15.8%) of the students of each of the classes, except Classes 34 and 35, already showed better ability in their pretest than that of the average student of their class in the posttest. Under the assumption of a normal distribution of the person abilities in each class, adding one standard deviation to the pretest mean would represent the upper limit of 84.2% of all ability scores of this class. With exceptions of Classes 34 and 35, this value for each class would be higher than the class -level posttest mean.

The average learning gain was rather small for all classes. The 11 easiest items, which had an item difficulty ≤ −1, could already be answered correctly by the average student of each class with a probability of greater than 50% (depending on the difference between person ability and item difficulty). The five most difficult items with an item difficulty ≥ 1 could not be solved on average by even the best classes.

Examining the model

The Consensus Model postulates a connection or relationship among most of its main components. In the framework of the ProwiN project, it is not possible to analyse all of these relationships at once due to sample size and instrument restrictions. Additionally, as a consequence of the sample size, a structural equation model is not appropriate. The goal is therefore to focus on certain aspects of the Consensus Model by three separate analyses.

The first emphasis was on the relationship between the TPKB and the TSPK. To strengthen the statistical power and achieve more precise estimates, in addition to the 35 teachers of ProwiN II, the 79 recoded results of the ProwiN I teachers were added to the analysis. Based on this sample (N = 114), a linear model—with PCK as indicator of TSPK depending on CK, and PK as indicators of TPKB—was investigated.

The second emphasis was on the relationship among both knowledge bases and the classroom practice represented by the interconnectedness of the given lessons. Data from the video analyses were only available for the ProwiN II sample of 35 teachers. Therefore, analysis of potential mediation effects of TSPK between TPKB and classroom practice could not be conducted. Instead, a linear model among the interconnectedness (as an indicator of the classroom practice) and CK, PCK and PK (as indicators of the general professional knowledge base of teachers) was investigated.

The last focus was the investigation of the impact of classroom practice, or rather teacher knowledge, on student outcomes. The student outcomes were measured by the SCK test. The students were nested in their classes. The intraclass correlation coefficient (ICC) describes the part of total variance which is related to clustering, that is, the class dependency of each student’s achievement. An ICC value, ICC_{1-fact, unjust} = 0.09, showed that the clustering was responsible for 9% of the total variance, supporting the use of multilevel models (Shrout & Fleiss, 1979). Multilevel models—including interconnectedness on the one hand, and CK, PCK and PK on the other hand—were analysed in this study.

Results

Analysis for RQ1: the relationship between TPKB and TSPK

A linear model was found to fit the observed PCK using CK and PK as independent variables. All variables (PCK, CK and PK) were z-standardised before the analysis. Table 1 shows the results. The model showed a good fit, F(2,111) = 9.76, p < .001, but only CK with an estimate of 0.39 (SE = 0.09, CI 95% [0.18, 0.48]) showed a significant influence, t(111) = 4.42, p < .001, on PCK.

Table 1. Predictors of PCK.

Variable	PCK
	b	S.E.	CI 95%	t(111)	p(>|t|)
Constant	0	0.09	[−0.78, 0.85]	0.00	1.00
CK	0.39	0.09	[0.18, 0.48]	4.42	<0.001
PK	−0.01	0.09	[−1.15, 1.01]	−0.12	0.902
R ^2	0.15
F(2,111)	9.76
p(>|F|)	<0.001

All variables were z-standardised.

Note: N = 114. CI = confidence interval.

Analysis for RQ2: the relationship among professional knowledge bases and classroom practice

All variables (interconnectedness, PCK, CK and PK) were z-standardised before the analysis. Specifying CK, PCK and PK as independent variables, a linear model was fit to interconnectedness. Table 2 shows the results. The model showed no significant fit to the data, F(2,31) = 1.59, p = .212. However, PK with an estimate of 0.37 (SE = 0.17, CI 95% [0.02, 0.48]) showed a minor significant influence, t(31) = 2.18, p = .037.

Table 2. Predictors of interconnectedness.

Variable	Interconnectedness
	b	S.E.	CI 95%	t(31)	p(>|t|)
Constant	0.00	0.17	[−0.34, 0.34]	0.00	1.000
PCK	−0.04	0.18	[−0.40, 0.32]	−0.25	0.806
CK	0.00	0.18	[−0.35, 0.36]	0.02	0.982
PK	0.37	0.17	[0.02, 0.71]	2.18	0.037
R ^2	0.14
F(3,31)	1.59
p(>|F|)	0.212

All variables were z-standardised.

Note: N = 35. CI = confidence interval.

Analysis for RQ3 and RQ4: the relationship among classroom practice respectively professional knowledge bases and student outcomes

The success of a teaching unit is indicated by the fulfilment of learning goals and whether or not the students learn about the concept being taught between the start and the end of the unit. Regarding this study, the students’ achievement at the SCK-posttest was used to measure the learning success of the lessons taught by the teachers. In the following paragraphs, we discuss different multilevel models which predict the Rasch scaled SCK-posttest scores with predictors on the individual level (of the students) and group level (of the students’ class).

For the multilevel analysis, the R-package ‘lme4’ was used (Bates et al., 2014). Following the arguments of the package authors, we performed no significance tests for singular predictors (Bates et al., 2014). Instead, we compared different models to a covariates-only model using likelihood-ratio-tests. The explained variance in groups and between groups is reported by pseudo R ² values (Kreft & de Leeuw, 1998; Singer, 1998).

On level 1 (students), the covariates were the ability estimate of the SCK-pretest, the CAT ability estimate, the gender (0 = ♀, 1 = ♂) and the language spoken at home (0 = only German, 1 = an additional language or only a different language). On level 2 (class), the total lesson time of the whole lesson unit regarding mechanics (measured in total minutes) was used as a covariate. All covariates and predictors were z-standardised, except for the covariates gender and language spoken at home which were dichotomous.

Table 3 shows the results of the analysis. The Model Knowledge used the TPKB represented by PK and CK and the TSPK represented by PCK as predictors. The Model Interconnectedness used the interconnectedness of the lessons as a predictor. For both models, a likelihood-ratio test showed a better model fit than the covariate-only model. A likelihood-ratio test between the Model Knowledge and the Model Interconnectedness showed no meaningful difference between both models, χ ²(2) = 3.48, p = .176.

Table 3. Results of the multilevel regressions for the Model Covariates, Model Knowledge and the Model Interconnectedness.

Parameter	Model Covar.	Model Knowledge	Model Intercon.
Level 1 (Students)
SCK-Pre-Test	0.34	0.34	0.35
	(0.03)	(0.03)	(0.03)
CAT	0.18	0.17	0.18
	(0.03)	(0.03)	(0.03)
Gender	0.29	0.28	0.28
(0 = ♀)	(0.06)	(0.06)	(0.06)
Language	−0.23	−0.24	−0.22
(0 = German)	(0.07)	(0.07)	(0.07)
Residual SD	0.84	0.84	0.84
	[0.80,0.88]	[0.80,0.88]	[0.80,0.88]
Level 2 (class)
Intercept	−0.08	−0.08	−0.08
	(0.05)	(0.05)	(0.05)
Total lesson time	0.09	0.05	0.08
	(0.04)	(0.04)	(0.04)
PK		0.11
		(0.04)
CK		0.01
		(0.04)
PCK		−0.11
		(0.04)
Interconnectedness			0.12
			(0.04)
Residual SD	0.20	0.14	0.16
	[0.13,0.29]	[0.05,0.23]	[0.09,0.25]
χ ^2(1)	–	–	8.20
χ ^2(3)	–	11.68	–
p(>χ ^2)	–	0.009	.004
$R_W^2$	.23	.23	.23
$R_B^2$	.53	.77	.69

All non-dichotomous variables were z-standardized.

It is worth mentioning that CK showed no influence in the model. Furthermore, PCK showed a negative estimate and would therefore hinder the student outcomes

Discussion

Discussion of RQ1: the relationship between TPKB and TSPK

The analysis indicated that the TPKB represented by the teachers’ CK and PK showed an influence on the TSPK represented by the teachers’ PCK. However, only CK showed an overall significant influence on PCK. CK and PCK are both about how to teach physics-specific topics. In comparison, PK is mainly about the general pedagogical knowledge like classroom management which is independent of the subject.

In terms of the Consensus Model, the relationship between TPKB and TSPK could be shown in this study. However, the relationship has to be specified and not generalised. The results also showed that the model connection has to be specified more and a general connection cannot be estimated.

Discussion of RQ2: the relationship among professional knowledge bases and classroom practice

The hypothesised correlation between teachers’ knowledge and interconnectedness could not be fully verified. In the linear model, only PK showed a significant influence on interconnectedness. Lenske et al. (2016) showed that the PK test used is a strong indicator of teachers’ classroom management. As discussed above, the connection to PK and classroom management can be explained by the fact that good classroom management is essential for demanding lessons (Helmke, 2015).

According to the Model of Educational Reconstruction, the process of reconstruction starts with the content structure of physics, which corresponds to the CK of physics teachers. Furthermore, to reconstruct a content structure for a lesson, teachers need knowledge about students’ preconceptions and teaching strategies regarding physics concepts. Each of the aforementioned knowledge types is tested by the ProwiN’s CK and PCK test instruments. Yet, the teachers were not directly asked about content structure or their planning. The teachers’ decisions made regarding the content structure was not addressed by this study. Therefore, it remained unclear if the teachers made meaningful decisions about improving the interconnectedness of their lessons.

Discussion of RQ3 & RQ4: the relationship between classroom practice and student outcomes and that among professional knowledge bases and student outcomes

The multilevel analysis showed that when the interconnectedness was added to the covariate model with the other covariates (students’ prior knowledge, cognitive ability, gender, the language spoken at home and the total lesson time), the model fit could significantly be improved. The interconnectedness of content structure could be verified as an indicator of instructional quality. This result was in line with the results of Müller and Duit (2004) as well as those of Helaakoski and Viiri (2014).

However, the generalisation of the results is only valid within certain constraints. The general learning gains of the classes measured by the SCK tests were rather low. There were no significant differences between the mean Rasch-scaled ability estimates in pretests and posttests in 18 of 35 classes. These low learning gains in physics were consistent with results of studies such as PISA 2003 (Prenzel et al., 2006) or the QuIP project (Fischer et al., 2014). In 2012, the Institute for Educational Quality Improvement (IQB) conducted a comparative study between the federal states of Germany (Pant et al., 2013) and found that the students in North Rhine-Westphalia had the lowest learning gains in physics.

Further multilevel analysis showed that the regressions coefficient for PCK showed a slightly negative influence on students’ SCK posttest scores. This result indicated that the PCK test lacked prognostic validity (Vogelsang & Reinhold, 2013). A reason could be the operationalisation of the PCK test. The facets of PCK which were covered by the test instrument are widely accepted by the scientific community as a part of PCK, however, they are also normatively set (Cauet, Liepertz, Kirschner, Borowski, & Fischer, 2015).

Conclusion

Several relationships of the Consensus Model could be verified in this study. But, the results of the PCK test, or teachers’ TSPK more specifically, showed no real impact on other aspects of the model. To find the reason, we have to take a particularly closer look at the professional knowledge test instruments. The aforementioned missing aspect of predictive validity has to be taken seriously and measuring professional knowledge with paper-and-pencil tests might not be sufficient. To measure PCK or professional knowledge, which has a real impact on teachers’ in-class actions, their pedagogical reasoning has to be taken into account. Vignette tests can be one approach to measure the PCK of teachers using authentically complex teaching contexts (e.g. Brovelli, Bölsterli, Rehm, & Wilhelm, 2014).

Furthermore, one essential part of the Consensus Model was not investigated in this study which is also often neglected in similar studies (e.g. Baumert & Kunter, 2010): the amplifiers and filters. Based on their beliefs and experiences, teachers decide on which knowledge base they use in their in-class actions. Due to their past experience, teachers know what strategies and methods work or, at least they believe, to be effective. For future investigation of how teachers’ knowledge impacts their in-class actions, amplifiers and filters should not be neglected. This study could also show that higher interconnectedness measure provides better learning outcomes. However, this finding of our study does not mean that more connections in the content structure is always better for every student. Very high interconnectedness among each concept and every other concept in the lesson could cause a cognitive overload for students. A deeper investigation of the quality of content structure connections is still missing in research. The interconnection of content ideas could, for example, be analysed under the perspective of ‘pedagogical link-making’ (Scott, Mortimer, & Ametller, 2011). However, our findings are a clear indication for teachers to keep in mind that it can be beneficial to make strong connections among the concepts they are teaching.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Sven Liepertz http://orcid.org/0000-0003-3656-1742

Andreas Borowski http://orcid.org/0000-0002-9502-0420

Additional information

Funding

This work was supported by the German Federal Ministry of Education (Bundesministerium für Bildung und Forschung).

Notes

1. Inhaltsblöcke in German. This can be translated literally to ‘content blocks’ which are defined by the topic and instructional method of teachers. For example, talking about force effect on acceleration to the class would be one content block, whereas using an experiment to illustrate force effect on acceleration would be another one.