The blind side: Exploring item variance in PISA 2018 cognitive domains

ABSTRACT

Communication of International Large-Scale Assessment (ILSA) results is dominated by reporting average country achievement scores that conceal individual differences between pupils, schools, and items. Educational research primarily focuses on examining differences between pupils and schools, while differences between items are overlooked. Using a variance components model on the Programme for International Student Assessment (PISA) 2018 cognitive domains of reading, mathematics, and science literacy, we estimated how much of the response variation can be attributed to differences between pupils, schools, and items. The results show that uniformly across domains and countries, it mattered more for the correctness of an item response which items were responded to by a pupil (27–35%) than which pupil responded to these items (10–12%) or which school the pupil attended (5–7%). Given the findings, we argue that differences between items in ILSAs constitute a source of substantial untapped potential for secondary research.

KEYWORDS:

• International large-scale assessment
• item variance
• school variance components
• pupil variance components
• item variance components

International Large Scale Assessments (ILSAs), such as the Programme for International Student Assessment (PISA) by the Organisation for Economic Co-operation and Development (OECD) and the Trends in International Mathematics and Science Study (TIMSS) by the International Association for the Evaluation of Educational Achievement (IEA), have been increasingly used for comparing educational outcomes around the globe (Mullis et al., 2020; OECD, 2019). Despite the ample research opportunities the sheer magnitude of the data collected in these assessments offers, ILSA results are commonly communicated as simplified rankings of countries’ average scores on various cognitive domains. The simple average scores conceal potentially informative differences and consequently can distort our understanding of the inherent complexities of the educational processes and contexts. Secondary ILSA research is well attuned to the importance of recognising and investigating these differences between pupils, and their respective schools, as they offer valuable insight into the social, economic, and cultural contexts within which the ILSA results can be meaningfully interpreted. Rather than relying on a single average score, researchers focus on establishing the magnitude of the inter-individual differences by quantifying the variance around that average and attempting to explain said variance by considering a range of covariates (for a review, see, e.g., Hopfenbeck et al., 2018).

The countries’ average scores, however, are not only averaged across pupils and schools but also across items. Similarly to the inter-individual differences in performance between pupils (and schools), the country average obscures differences that may exist between items within a certain domain. When viewing the performance through the lens of this average, we operate under an unrealistic assumption that, for instance, in low-performing countries, the pupils score low on all of the items covering a domain. In reality, however, both higher- and lower-performing countries can have their weaknesses and relative strengths such that some items are more or less difficult for pupils.

The magnitude of the difficulty differences between items translates into systematic response variation across items (henceforth, ‘item variance’), a topic not often discussed in the current ILSA research. Driven by the prestige of examining pupil performance on blanket constructs, such as reading, mathematics, and science, we tend to take ILSA’s labelling and meaning of these constructs at their face value, without a second thought as to the items that measure them (i.e., the naming fallacy, see, e.g., Kline, 2016). The issue is further exacerbated in the secondary analysis, where the availability of the plausible values as measures of pupil achievement allows us to avoid immediate item responses altogether.

Given the breadth of the ILSAs cognitive constructs, we hypothesise that the item variance may be substantial. The reasoning behind this hypothesis is fairly intuitive. That is, the narrower a construct is, the less we would anticipate variance in the items that measure said construct. Conversely, holding test population and testing conditions equal, but moving from a narrow construct to broader constructs such as reading, mathematics, and science, a larger item variance can be expected. Such large item variance would imply substantial differences between items’ difficulties within a construct and call into question whether an average score across all items is a sufficient summary for the entire cognitive domain.

The information to be gained from quantifying the item variance and examining the factors affecting its magnitude could provide more targeted country performance profiles and align with the needs of the educators, curriculum designers, and test developers alike. The items targeting specific content, which prove to be harder or easier for most pupils, could help the educators anticipate the weaker and stronger areas in the curriculum (El Masri et al., 2017). Furthermore, the knowledge of the factors affecting item variance could help the test developers and item writers produce questions of higher validity and effectiveness in measuring the constructs (Ahmed & Pollitt, 2007; Eijkelhof et al., 2013; Le Hebel et al., 2017).

Given that the research on the item variance in ILSA is sparse, the study warrants an exploratory approach (Tukey, 1980). We do not yet intend to explain the item variation or link it to internal or external factors and item characteristics. Instead, we begin by laying the foundation by quantifying the magnitude of the item variance and identifying potential points of interest and curious patterns that will ultimately generate hypotheses for future inquiry. Using one of the most recent ILSAs, PISA 2018, as a working example, we estimate the so-called variance components or the magnitude of response variation attributable to three key sources of variation – schools, pupils, and items –, for each of the three cognitive domains – reading, mathematical, and science literacy –, in each of the participating countries. We address the following research objectives (RO).

RO1:

Describe the across-country patterns in variance component profiles.

The objective is two-fold and comprises (i) the assessment of the relative importance of response variation sources and (ii) their consistency across countries and cognitive domains. The latter helps generalise as well as identify distinct country profiles that could invite further research.

RO2:

Quantify the relative magnitude of response variation due to differences between items (i.e., differences in item difficulties) compared to that due to differences between schools and pupils.

The resulting magnitudes directly address the main concern raised in the current article. That is, the relative magnitudes of the item to person variances will put to the test our hypothesis of substantial item variance in the PISA cognitive domains and either support or oppose our call for more research into the blind side of ILSAs, the items.

Method

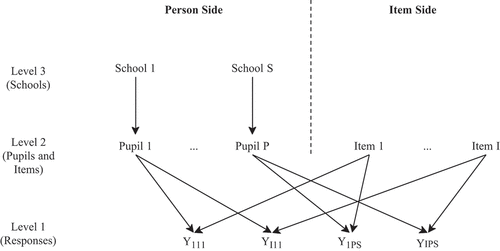
The present study viewed the total variance in a pupil’s response on a PISA 2018 cognitive domain item as a composition of two main variance sources, the person and the item. Figure 1 illustrates this notion where responses, the lower-level data units, belong to a pair resulting from crossing two higher-level data units: a tandem of pupils nested in their respective schools on the person side and items on the item side. Hence, a single response was considered a combination of both sides, with each pupil nested within one school responding to several items and each item being responded to by several pupils, reflecting the cross-classified data structure (Van den Noortgate et al., 2003).

Figure 1. PISA 2018 3-level response data structure.

Following a random-person random-item Item Response Theory (IRT) approach (De Boeck, 2008; Rijmen et al., 2003), a cross-classified mixed effects model was formulated. The total response variance was partitioned into components attributable to different sources of variation in the data structure (Briggs & Wilson, 2007). We allow the probability of a correct response to vary across pupils, schools, and items, and define the core model as

(1) $\mathrm{L}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}({\pi }_{psi})={\beta }_0+{\theta }_p+{\zeta }_s+{\beta }_i,$(1)

where ${\pi }_{psi}$ is the probability that pupil $p$ from school $s$ will answer item $i$ correctly; ${\beta }_0$ is the overall intercept (fixed effect) corresponding to the estimated logit for the probability of a correct response of an average pupil from an average school on an average item; ${\theta }_p$, ${\zeta }_s$, ${\beta }_i$ are the varying intercepts (random effects) for pupil, school, and item, respectively. The varying intercepts were assumed to follow an independent normal distribution with means fixed to zero and variances ${\sigma }_{\theta }^2$, ${\sigma }_{\zeta }^2$, and ${\sigma }_{\beta }^2$, respectively. Hence, the model effectively counted four freely estimated parameters. The three varying intercepts reflected three main effects in a variance partitioning model (i.e., one per source of variance in the data structure), indicating how responses from a specific pupil, school, or item deviated, on average, from the overall response given by an average pupil from an average school on an average item.

The model in Equation 1(1) $\mathrm{L}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}({\pi }_{psi})={\beta }_0+{\theta }_p+{\zeta }_s+{\beta }_i,$(1) implies that the total observed response variation (${\sigma }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}^2$) can be partitioned into four parts

(2) ${\sigma }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}^2=\underset{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}{\underbrace{\underset{\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{n}}{\underbrace{\underset{\mathrm{p}\mathrm{u}\mathrm{p}\mathrm{i}\mathrm{l}}{\underbrace{{\sigma }_{\theta }^2}}+\underset{\mathrm{s}\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{o}\mathrm{l}}{\underbrace{{\sigma }_{\zeta }^2}}}}+\underset{\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{m}}{\underbrace{{\sigma }_{\beta }^2}}+\underset{\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{u}\mathrm{a}\mathrm{l}}{\underbrace{\frac{{\pi }^2}{3}}}}}$(2)

where ${\sigma }_{\theta }^2$, ${\sigma }_{\zeta }^2$, ${\sigma }_{\beta }^2$ correspond to the variances of the pupil, school, and item varying intercepts, and $\frac{{\pi }^2}{3}$ is the distribution-specific residual variance from the standard logistic distribution due to the applied link function accounting for the binary nature of a response. Applying this model to the PISA 2018 item response data allowed us to derive, across countries and the PISA 2018 cognitive domains, two sets of outcome measures to address our two core research objectives: source-specific variance components and item to person variance components ratios.

Sample

The PISA 2018 item response data for the reading, mathematical and science literacy domains were used in the study. A total of over 45.5 million responses given by approximately 600,000 pupils from over 21,000 schools and 77 countries on nearly 800 items were considered.

PISA 2018 pupils and schools

Of 79 countries and economies that initially participated in the PISA 2018, the current study considered 77. Excluded were Cyprus, due to lack of available data, and Vietnam due to discrepancies in the data comparability addressed in detail in the PISA 2018 technical report (OECD, 2020). The total sample size included approximately 600,000 pupils from over 21,000 schools. The PISA 2018 sampling design prescribed to sample, population size permitting, 5250 to 6300 15-year-old pupils from a minimum of 150 schools per participating country (OECD, 2020). Country-wise sample sizes varied from 3296 pupils in Iceland to 35,943 in Spain and from 44 schools sampled in Luxembourg to 1089 schools in Spain. Tables A1, Tables A2, Tables A3 in Appendix A give pupil and school sample sizes for each of the cognitive domains and considered countries.

PISA 2018 items

PISA 2018 was primarily delivered as a computer-based (CBA) assessment. Sixty-nine countries took the CBA, whereas eight countries participated in the paper-based (PBA) version. The total number of items delivered in each country varied as a function of the administration mode and achievement domain. Table B1 gives the total numbers of items for the CBA and PBA versions, and the totals are further decomposed into the common items administered in all countries within a mode and the unique items administered only to specific subsets of countries (Appendix B). The major domain of the PISA 2018, reading literacy, included 318 CBA items and 103 PBA items. The minor domains of mathematics and science comprised 115 and 82 CBA items, respectively, and 83 PBA items each. Tables A1, Tables A2, Tables A3 in Appendix A give country-specific numbers of items across the domains. In order to reduce test length and minimise pupil fatigue, PISA implemented a rotated booklet design in which each pupil only responded to a subset of items, and each item was responded to by a subset of pupils. Subsequently, each pupil responded on average to roughly 50 items in the reading domain and 24 items in one or two of the minor domains – mathematics, science or global competence. Each reading, mathematics, and science item, on the other hand, was responded to by over 650, 420, and 550 pupils, respectively.

Outcome measures

To address the first research objective, variance components for pupils, schools, and items were computed as the ratios of the specific variance source (i.e., pupil, school or item) to the total variation defined in Equation 2(2) ${\sigma }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}^2=\underset{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}{\underbrace{\underset{\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{n}}{\underbrace{\underset{\mathrm{p}\mathrm{u}\mathrm{p}\mathrm{i}\mathrm{l}}{\underbrace{{\sigma }_{\theta }^2}}+\underset{\mathrm{s}\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{o}\mathrm{l}}{\underbrace{{\sigma }_{\zeta }^2}}}}+\underset{\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{m}}{\underbrace{{\sigma }_{\beta }^2}}+\underset{\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{u}\mathrm{a}\mathrm{l}}{\underbrace{\frac{{\pi }^2}{3}}}}}$(2) , reflecting their relative contributions to the overall response variance composition:

(3) $\mathrm{V}\mathrm{C}(\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e})=\frac{{\sigma }_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}}^2}{{\sigma }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}^2}.$(3)

To address the second research objective and showcase the magnitude of the item side variance as compared to the person side, ratios of the item to the person variance components (i.e., item to the combined pupil and school variance components) were computed:

(4) $\mathrm{V}\mathrm{C}\mathrm{R}\left(\frac{\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{m}}{\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{n}}\right)=\frac{\mathrm{V}\mathrm{C}(\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{m})}{\mathrm{V}\mathrm{C}(\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{n})}=\frac{\stackrel{\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{m}}{\overbrace{{\sigma }_{\beta }^2}}}{\underset{\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{n}}{\underbrace{\underset{\mathrm{p}\mathrm{u}\mathrm{p}\mathrm{i}\mathrm{l}}{\underbrace{{\sigma }_{\theta }^2}}+\underset{\mathrm{s}\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{o}\mathrm{l}}{\underbrace{{\sigma }_{\zeta }^2}}}}}$(4)

where the common denominators of the variance components (as seen in Equation 3)(3) $\mathrm{V}\mathrm{C}(\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e})=\frac{{\sigma }_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}}^2}{{\sigma }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}^2}.$(3) cancel out simplifying the expression to the ratio of the respective variances.

Statistical Analysis

The cross-classified mixed effects model represented in Equation 1(1) $\mathrm{L}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}({\pi }_{psi})={\beta }_0+{\theta }_p+{\zeta }_s+{\beta }_i,$(1) was fitted to each country’s item response data for each of the three cognitive domains separately (i.e., a total of $231=77\times 3$ model applications) using a marginal maximum likelihood estimation approach. The analysis was conducted using the lme4 package (Bates et al., 2015) in version 4.0.3 of the R software environment (R Core Team, 2020). Prior to model application, for 59 items across domains that allowed partial credit, partial credit was recoded into no credit, such that all the responses were dichotomously scored (i.e., correct or incorrect), facilitating comparability across items.

Variance components and variance components ratios were computed based on the models’ estimated parameters, summarised across countries, and their consistency across domains was examined. As a final step, two sensitivity analyses were performed. The first analysis addressed potential comparability issues due to country-specific item pools. All models and outcomes of interest were re-estimated using only the common-for-all-countries items. The second analysis tested the robustness of the results when taking other approaches to partial credit response handling. The alternative analyses (1) considered partial credit responses as correct, or (2) omitted partial credit items. The variance components were re-computed and compared to the original variance components (i.e., where partial credit responses were coded as incorrect). The results of the sensitivity analyses are presented in Appendix C.

Results

Tables A1, Tables A2, Tables A3 report the estimated parameters of the cross-classified mixed effects model applied to the response data of the PISA 2018 assessments of reading, mathematical, and science literacy (Appendix A). 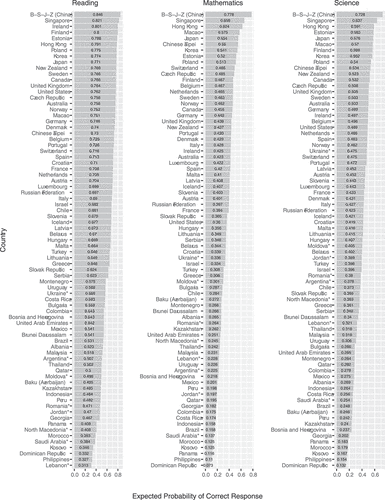Those parameters are the fixed effect intercepts (${\beta }_0$) and the variances of the pupil (${\sigma }_{\theta }^2$), school (${\sigma }_{\zeta }^2$), and item (${\sigma }_{\beta }^2$) random effects. For ease of interpretation, the initially logit-scaled intercepts from Tables A1,Tables A2,Tables A3 were converted into probabilities of a correct response, and those are visualised by domain in Figure D1 (Appendix D). The fixed intercepts’ ranks corresponded fairly closely to the PISA 2018 rankings of countries’ average scores, with Spearman’s rank correlations of 0.98, 0.97, and 0.98 for the domains of reading, mathematics, and science, respectively (OECD, 2019, pp. 57–62).

In each domain and country, the fixed effect intercepts varied over pupils and schools on the person side, and most substantially over items on the item side (Tables A1-A3 in Appendix A). The pupil, school, item, and residual variance components (see, Equation 3)(3) $\mathrm{V}\mathrm{C}(\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e})=\frac{{\sigma }_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}}^2}{{\sigma }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}^2}.$(3) computed based on said variance estimates are presented in Figures 2–4 alongside the ratios of the item to person variance components (see, Equation 4)(4) $\mathrm{V}\mathrm{C}\mathrm{R}\left(\frac{\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{m}}{\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{n}}\right)=\frac{\mathrm{V}\mathrm{C}(\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{m})}{\mathrm{V}\mathrm{C}(\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{n})}=\frac{\stackrel{\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{m}}{\overbrace{{\sigma }_{\beta }^2}}}{\underset{\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{n}}{\underbrace{\underset{\mathrm{p}\mathrm{u}\mathrm{p}\mathrm{i}\mathrm{l}}{\underbrace{{\sigma }_{\theta }^2}}+\underset{\mathrm{s}\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{o}\mathrm{l}}{\underbrace{{\sigma }_{\zeta }^2}}}}}$(4) . The residual variance uniformly constituted roughly half of the total response variance across the considered domains and countries. Its magnitude was anticipated given that PISA’s primary goal lies in assessing country-level performance rather than that of individual pupils or individual items.

Figure 2. PISA 2018 reading literacy variance components (VC) for pupils, schools and items plotted against the item to person variance components ratios (VCR).

Note. The 77 countries are arranged in descending order of variance components ratio. The 8 countries that participated in the paper-based PISA 2018 are marked by an asterisk.

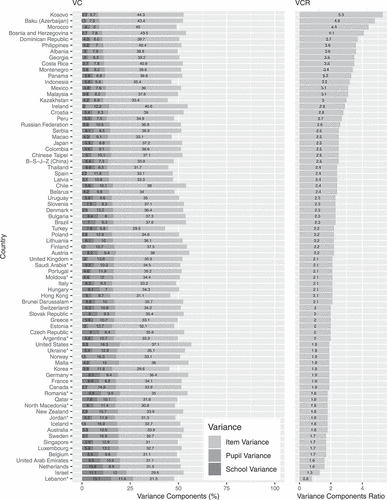
Figure 3. PISA 2018 mathematical literacy variance components (VC) for pupils, schools and items plotted against the item to person variance components ratios (VCR).

Note. The 77 countries are arranged in descending order of variance components ratio. The 8 countries that participated in the paper-based PISA 2018 are marked by an asterisk.

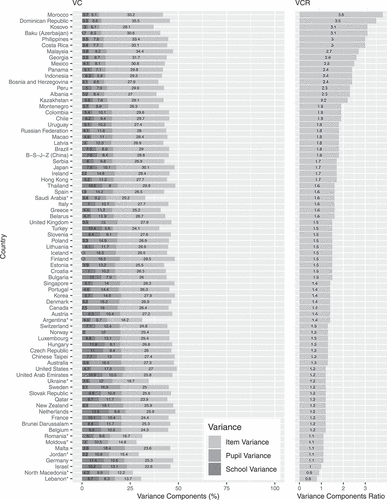
Figure 4. PISA 2018 science literacy variance components (VC) for pupils, schools and items plotted against the item to person variance components ratios (VCR).

Note. The 77 countries are arranged in descending order of variance components ratio. The 8 countries that participated in the paper-based PISA 2018 are marked by an asterisk.

Person variance component

The person variance component combines the pupil and school variance components (see, Equation 2)(2) ${\sigma }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}^2=\underset{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}{\underbrace{\underset{\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{n}}{\underbrace{\underset{\mathrm{p}\mathrm{u}\mathrm{p}\mathrm{i}\mathrm{l}}{\underbrace{{\sigma }_{\theta }^2}}+\underset{\mathrm{s}\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{o}\mathrm{l}}{\underbrace{{\sigma }_{\zeta }^2}}}}+\underset{\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{m}}{\underbrace{{\sigma }_{\beta }^2}}+\underset{\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{u}\mathrm{a}\mathrm{l}}{\underbrace{\frac{{\pi }^2}{3}}}}}$(2) to reflect the response variation due to the person side. The pupil and school variance components, in turn, each communicate the amount of the total response variation attributed to differences between pupils and between schools, respectively. The greater the variance component, the greater differences can be expected in performance between pupils within one school and between schools. For instance, in countries with a relatively larger school variance component, the school attended by a pupil may be advantageous or disadvantageous to their level of achievement.

The results show that, on average, roughly 16%, 17%, and 18% of the total response variance in the PISA 2018 reading, science, and mathematics domains, respectively, were attributed to differences between persons. Pupils accounted for about twice the amount of response variation than schools. In the mathematics domain, the average variance in pupil performance accounted for 11.7% ($\mathrm{S}\mathrm{D}=3.2\mathrm{\%}$) of the total response variance, whereas 6.5% ($\mathrm{S}\mathrm{D}=3.4\mathrm{\%}$) was due to differences between schools. The pupil and school variance components averaged 10.2% ($\mathrm{S}\mathrm{D}=2.8\mathrm{\%}$) and 5.4% ($\mathrm{S}\mathrm{D}=2.6\mathrm{\%}$) in the reading domain, and 11.1% ($\mathrm{S}\mathrm{D}=3.3\mathrm{\%}$) and 5.7% ($\mathrm{S}\mathrm{D}=3\mathrm{\%}$), respectively, in science.

Pupil variance component

The most considerable differences in pupil performance within each considered domain were systematically observed, among others, in the Nordic countries and the so-called core Anglosphere. Approximately $15-19\mathrm{\%}$ of the total response variance was due to pupils across three domains in Australia, Canada, Iceland, New Zealand, Norway, Sweden, the United States, and the United Kingdom. On the other hand, differences in pupil performance amounted to only $5-7\mathrm{\%}$ of the total response variance in Morocco, the Dominican Republic, Indonesia, Panama, and Turkey across all the domains. Moderate to high positive correlations were found between the pupil variance components and the conditional average probabilities of a correct response (i.e., on an average item for an average pupil in an average school per country) (range $r=\{0.45,0.68\}$ across domains), suggesting that, for instance, for lower-performing countries, less differences in pupil ability were observed.

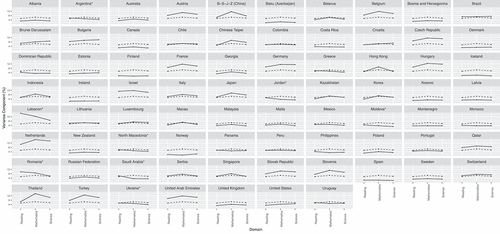
School variance component

The proportion of the school variance was approximately one-tenth of the pupil variance across domains in Denmark, Finland, Iceland and Norway (roughly $1-3\mathrm{\%}$). Other countries where achievement was also largely unaffected by the attended schools were Bosnia and Herzegovina, Canada, Ireland, Kosovo, and Spain, where $2-3\mathrm{\%}$ of the total response variation was accounted for by schools. In contrast, $10-15\mathrm{\%}$ of the total response variance was due to schools in Israel, Lebanon, Turkey and the United Arab Emirates, as well as in a range of Western and Central European countries (e.g., Belgium, Czech Republic, France, Hungary, the Netherlands).

Several system-level features have been shown to exacerbate or reduce differences between schools. Previous research on educational equity and school effectiveness identified a manifold of such factors. For instance, school differences are commonly examined in relation to the availability of early education (e.g., see, Van Huizen & Plantenga, 2018), public education expenditures, public and private schools differentiation (e.g., see, Bodovski et al., 2017), curriculum and structural school differentiation (e.g., greater school autonomy; Hanushek et al., 2017), and presence of a tracking system (Hanushek & Wöeßmann, 2006; Strello et al., 2021).

Consistency of person variance components across domains

The person variance components were consistent across the three domains (i.e., correlations between the domain-specific pupil and school variance components were between $0.85-0.96$). The average range length across the domains (i.e., the absolute difference between the highest and the lowest variance components across three domains) was 2.2% for the pupil and 1.8% for the school variance components.

The least consistent pupil variance components were found in Baku (Azerbaijan), Belarus, B-S-J-Z (China), Chinese Taipei, Macao, Portugal, and Singapore, where larger portions of the total variance could be attributed to differences between pupils in mathematics than in the other two domains (Figures 5–6). A similar tendency was noted for the school variance components across domains in the aforementioned B-S-J-Z (China), Chinese Taipei, Thailand, and Hong Kong. In these countries, not only did the pupil ability differ to a greater degree in mathematics, but so did the performance between schools. On the other hand, in the case of Lebanon (range length of 6.4%), these discrepancies in the school variance components were larger between reading and science, an inconsistency shared by other paper-based PISA 2018 participants (e.g., Romania, Saudi Arabia).

Figure 5. PISA 2018 pupil variance components by domain plotted against across-countries average pupil variance components.

Note. Countries that participated in the paper-based version of PISA 2018 are denoted by an asterisk. Country-specific variance components are shown with a solid line, and across-countries average variance components with a dashed line.

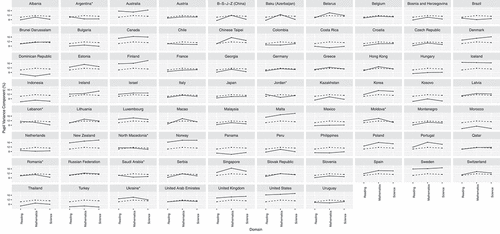
Figure 6. PISA 2018 school variance components by domain plotted against across-countries average school variance components.

Note. Countries that participated in the paper-based version of PISA 2018 are denoted by an asterisk. Country-specific variance components are shown with a solid line, and across-countries average variance components with a dashed line.

Item variance component

Figures 2–4 illustrate item to person variance components ratios (VCRs), to the right, for the PISA 2018 reading, mathematics, and science literacy domains. VCR represents the magnitude of the item side variance compared to the person side. VCR above one indicates that more response variation is ascribed to differences between items than to differences between persons. The reverse analogy holds for the VCR below one. On average, across 77 countries, item variance was roughly double the person variance (i.e., VCRs of 2.4, 2.0, and 1.7 for reading, mathematics, and science domains, respectively).

The only countries where the person variance outweighed the item variance were Lebanon in the reading and science domains (VCR = 0.8) and North Macedonia in science (VCR = 0.9). In these countries, item responses depended more on the pupils and the schools they attended than on the items to which they responded. In the B-S-J-Z (China), Chinese Taipei and Singapore in mathematics, and Israel in science, the item and person variances were balanced (i.e., VCR = 1). In the remaining countries, VCRs were consistently greater than one, in some marginally and multiple countries substantially. For example, in the reading domain, the items contributed over four times more variance than persons in Kosovo (VCR = 5.3), Baku (Azerbaijan) (VCR = 4.8) and Morocco (VCR = 4.4). In mathematics, six times more variance was due to items in the Dominican Republic (VCR = 6), and ratios over four were calculated for Costa Rica (VCR = 4.5), Panama (VCR = 4.2), and the Philippines (VCR = 4.4). Finally, over three times larger variance in science was attributed to items in the Dominican Republic (VCR = 3.5) and Morocco (VCR = 3.8).

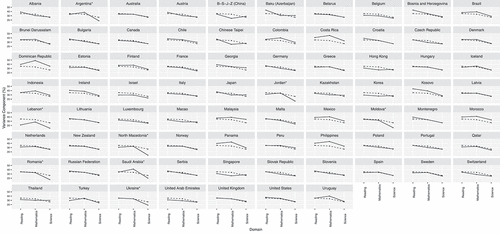
We now zoom in on the item variance components separately. The item variance component is a portion of the total response variance attributed to differences between items. In countries where this component was smaller, fewer differences between items were observed. Contrariwise, in countries with larger item variance components, the item differences were more pronounced.

The results show that, on average across 77 countries, 35.2% ($\mathrm{S}\mathrm{D}=3.7\mathrm{\%}$), 33.7% ($\mathrm{S}\mathrm{D}=4.7\mathrm{\%}$), and 26.4% ($\mathrm{S}\mathrm{D}=4.3\mathrm{\%}$) of the total response variance were due to items in the domains of reading, mathematics, and science, respectively. Items accounted for nearly half of the total mathematics domain variance in the Dominican Republic (48.7%), Costa Rica (45.7%), and the Philippines (44.3%; Figures 2–4). In reading, the largest item variance components were recorded in Kosovo (44.3%) and Bosnia and Herzegovina (43.5%). Roughly $33-35\mathrm{\%}$ of the total science literacy domain variance was due to items in the Dominican Republic, Malaysia, the Philippines, Morocco, and Costa Rica, countries which also displayed higher than average item variance in the other domains.

Less prominent, yet still sizeable, item variation was observed in Lebanon where 21.3% of the total reading domain variance was due to differences between items, and in B-S-J-Z (China) in mathematics with an item variance component of 23.9% (Figures 2–4). Markedly, in the science domain, the lowest item variance components pertained almost exclusively to the countries that participated in the paper-based PISA 2018. The item variance components in these countries were substantially lower than those of the computer-based participants situated at the lower end of the item variance component range. As such, roughly $12-15\mathrm{\%}$ of the total science domain variance was due to items in Jordan, Lebanon, Moldova, and North Macedonia, whereas $23-24\mathrm{\%}$ were attributed to items in Israel, Malta, and Qatar. One could factor in the differences in the number of science items between the two modes of administration (i.e., 115 items in CBA, 85 in PBA) as affecting the resulting variance; however, even larger item pool differences in the reading domain (i.e., 318 items in CBA, 103 in PBA, see, Table B1, Appendix B) would not support this argument.

Lastly, generally large negative correlations ($r=\{-0.72,-0.64,-0.53\}$) were found between the item variance component and the countries’ conditional average probabilities of a correct response (i.e., on an average item for an average pupil in an average school) for the domains of mathematics, science, and reading, respectively. This finding implies that more differences in item difficulty existed for low-performing participants when compared to high-performing countries.

Consistency of item variance components across domains

Compared to the pupil and school variance components, country-wise item variance components were far less consistent across domains. The amount of the item side variance appeared, to an extent, domain-specific, and its magnitude in one domain did not necessarily coincide with similar magnitudes in the remaining domains. The average range length across the domains (i.e., the absolute difference between the highest and the lowest item variance components across three domains) was approximately 10%. The most consistent item variance components were recorded in Thailand (1.8%) and Korea (2.4%). The largest discrepancies were observed almost exclusively in the PBA countries, where the differences between the item variance components across domains were around 20% due to considerably lower item variances in the science domain.

Aside from the previously mentioned PBA countries, some patterns emerged when examining the least consistent item variance components (Figure 7). First, compared to the reading and science domains, noticeably larger item variance components in mathematics (range length of around $12-13\mathrm{\%}$) were observed in several South and Central American countries such as Costa Rica, the Dominican Republic, Panama, Uruguay, and to a lesser degree, Brazil and Colombia (range length of $13-11\mathrm{\%}$ differences). Second, an inverse pattern where the mathematics domain had the least item variance compared to reading and science (range length of $10-12\mathrm{\%}$) was noted in B-S-J-Z (China) and Chinese Taipei. Finally, in the Balkans (i.e., Bosnia and Herzegovina, Croatia, Kosovo, and Montenegro), reading items exhibited more variation in their difficulty than items of the mathematics or science domains (range length of roughly 13%).

Figure 7. PISA 2018 item variance components by domain plotted against across-countries average item variance components.

Note. Countries that participated in the paper-based version of PISA 2018 are denoted by an asterisk. Country-specific variance components are shown with a solid line, and across-countries average variance components with a dashed line.

Discussion

Communication of the ILSA results is dominated by reporting countries’ average scores masking variation between pupils, their respective schools, and between items. While a great deal of secondary research focuses on examining this variation between pupils and schools, potentially informative differences between items are largely overlooked, and our knowledge of the item variance magnitude in ILSAs and the drivers behind this variance is scarce.

The present exploratory study took the initial steps towards exploring the item variance in ILSAs. Using a variance components IRT model and the PISA 2018 as a working example, we quantified the item variance in the response data for three cognitive domains of reading, mathematical, and science literacy. We estimated the total item response variance structure for each of the domains across 77 countries and divided that variance into three variance components corresponding to the portions of the total variance attributable to differences between pupils, schools, and items. The variance components computed in this study effectively demonstrated that uniformly across the three PISA 2018 cognitive domains and most of the considered countries, it mattered more which items were responded to by a pupil ($27-35\mathrm{\%}$) than which pupil responded to these items ($10-12\mathrm{\%}$) or which school the pupil attended ($5-7\mathrm{\%}$).

Given our primary focus to approach the assessment from the item side and the immense volume of existing research on the pupil and school variances, we did not anticipate our analysis to yield any novel insight into the between-pupil and -school differences. This notion held for some, yet not all, of our pupil and school findings which painted a familiar picture to those in educational research. The largest differences in the pupil performance levels were found predominantly in the economically developed educational systems, such as the Nordics and the Anglosphere. On the other hand, in economically developing educational systems, the pupil variance was far less substantial. Previous research, however, cautions against treating the low pupil variances at face value as they may indicate, among other things, the existence of a floor effect for low-performing participants (see, e.g., Rutkowski et al., 2019). Minor differences between schools were found in the Nordics, reflective of the Nordic model of education where much of the recent reforms were aimed at the provision of educational equality (see, e.g., Lundahl, 2016; Yang Hansen et al., 2014). In contrast, we observed larger school differences in some of the Western and Central European countries. These differences could stem from, for instance, socio-economic status differences, school-specific enrolment policies, greater school autonomy, and the presence of a tracking educational system in which pupils are divided based on their achievement (Strello et al., 2021).

The mentioned findings are well in line with previous research. The systematic analysis of the variance components consistency across cognitive domains, however, generated several curious results. The pupil and school variance components appeared to be relatively consistent across domains for most countries that administered the computer-based PISA 2018. For countries that took the paper-based version, however, more differences between schools were found in the reading domain compared to the other two domains. Furthermore, several countries showed higher pupil and school variances in mathematics than reading or science (e.g., B-S-J-Z (China), Chinese Taipei, Portugal, Singapore, the Netherlands). Investigating potential drivers behind these domain-specific differences at a country level could present a promising avenue for future inquiry.

One of the key outcomes of PISA is the performance profiles of each participating country. Aside from providing basic indicators of pupils’ knowledge and skills in the cognitive domains, these profiles relate the differences in the pupil and school performance (i.e., the differences we quantified on the person side) to important demographic (e.g., gender), socio-economic and educational indicators. What is lacking from said profiles is the information about countries’ relative strengths and weaknesses regarding different items or topics. Furthermore, secondary analyses using the PISA data mostly extend the knowledge on the relations between person contextual variables and pupils’ outcomes, whereas very few focus on the differences between items.

Even though we hypothesised the item variance to be substantial, we did not anticipate that it would be, with very few exceptions, at least twice the magnitude of the pupil and school variance components combined. Such magnitudes suggest that the current PISA country profiles, focusing exclusively on the person variation, explore only one side of the response data, while the potential of the other side, the item side, remains untapped. Consequently, as opposed to the pupil and school variances discussion, the systematic empirically grounded research to fall back on for potential explanations for the item variance magnitude is lacking. Therefore, the present exploratory study can be positioned as the starting point for mapping out the field and generating research questions for future inquiry. The following summarises our main findings and highlights the potential questions.

The lower item variance components were found in the domain of science ($12-24\mathrm{\%}$), while in mathematics and reading, the lowest variance components ranged $24-30\mathrm{\%}$. Markedly, lower item variance components were observed in countries that participated in the paper-based PISA 2018 science assessment ($12-20\mathrm{\%}$) than in their computer-based counterparts. More research is required to examine whether the latter stems, for example, from the existence of a mode effect, although such was not evident in the remaining domains.

The highest item variances were captured in the domains of reading and mathematics. Interestingly, some of the higher item variances clustered in certain regions. For example, nearly half of the total response variance in the reading domain could be ascribed to the items in the Balkans, and in mathematics domain in South and Central America. Furthermore, the higher item variances were observed in the lower-performing countries where more item-level differences existed than in the higher-performing countries. In the Dominican Republic, the total response variance in mathematics could be almost evenly distributed between the residual variance (44%) and the item variance (49%), whereas the pupils and schools, the areas of research that receive most of the attention, contributed only 7%. Large item variances imply that the countries’ averages are not representative of the entire cognitive domains. Rather, there are strengths and weaknesses within each domain, which, if identified and examined, could pave the ways to target and address weaker areas and consolidate the areas of strength within a country or region. These intriguing findings could also serve as motivation for researchers whose areas of interest lie in understanding regional trends in education, for example, in the context of reflecting on differences in curriculum, learning goals, and teacher training across the considered domains. PISA covering three cognitive domains allowed us to generalise our findings across the domains. Nevertheless, future research would benefit from confirming our findings across other ILSAs and multiple cycles of one or more ILSAs to study how the results generalise when a wider net is cast.

Even though we describe the item variances as lower or higher in reference to their ranges in this study, the magnitude of all the computed item variances was substantial. Suppose we were to consider the corresponding pupil and school variances as thresholds for how much variance can be treated as a wake-up call to render the country average obsolete and warrant further investigation. Then, the item variance becomes impossible to blindly ignore. That being said, our goal was by no means to undermine the research on pupil and school differences, as they are the ultimate stakeholders in education. Neither do we wish to undermine the comprehensive item-level analyses performed by PISA as means for item quality control (for an overview of the classical test theory and IRT analyses performed by PISA, see, e.g., OECD, 2020); or further between-countries comparisons drawn within the framework of Differential Item Functioning (DIF) aimed at comparing how the items perform in some countries relative to others (e.g., Zwitser et al., 2017). Instead, we argue for utilising the collected data to its fullest. Referring to the item variance in the title of this paper as the blind side, we aim to convey that there is still a great deal of untapped response variation that we don’t process on the within-country level despite its great potential to aid in producing more finely-grained country performance profiles (see, e.g., Daus et al., 2019). Lastly, we are confident that this paper presents a compelling argument for launching a series of inquiries into the item variance, be it a replication effort in other ILSAs, country-driven exploration, or further explanatory research into the covariates and moderators driving the item variance magnitude. By considering several potential predictors of the item variance on a country level (e.g., item format, item content, length of text), future research may be able to identify and highlight the challenging areas of content and item design features.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Notes on contributors

Kseniia Marcq

Kseniia Marcq received her master’s degree in Measurement, Assessment and Evaluation from the University of Oslo, Norway. She is currently a doctoral research fellow at the Centre for Educational Measurement at the University of Oslo, Norway. Her research uses exploratory and meta-analytical approaches to uncover untapped potential in the data of international large-scale assessments.

Johan Braeken

Johan Braeken is a professor of psychometrics at the Centre for Educational Measurement at the University of Oslo, Norway. His research interests are in latent variable modelling, modern test design including adaptive testing, and the information value and data quality in large-scale assessments.

Appendix A

Parameter Estimates of the Cross-Classified Mixed Effects Model

Table A1. Country-wise parameter estimates of the cross-classified mixed effects model for the PISA 2018 reading literacy domain.

Country	${\mathrm{N}}_{\mathrm{r}}$	${\mathrm{N}}_{\mathrm{p}}$	${\mathrm{N}}_{\mathrm{s}}$	${\mathrm{N}}_{\mathrm{i}}$	$b_0$ (SE)	${\sigma }_{\theta }^2$	${\sigma }_{\zeta }^2$	${\sigma }_{\beta }^2$
Albania	347,571	6341	327	308	0.09 (0.09)	0.52	0.20	2.54
Baku (Azerbaijan)	339,140	6822	197	309	−0.02 (0.10)	0.52	0.10	2.99
Argentina*	255,113	11,682	455	86	0.03 (0.16)	0.71	0.38	2.19
Australia	794,697	14,236	763	309	1.13 (0.09)	1.09	0.23	2.37
Austria	372,310	6802	291	309	0.87 (0.11)	0.70	0.60	2.81
Belgium	445,698	8460	288	309	0.98 (0.09)	0.62	0.55	2.01
Bosnia and Herzegovina	337,860	6478	213	309	0.17 (0.11)	0.56	0.19	3.11
Brazil	537,973	10,675	597	309	0.12 (0.10)	0.66	0.50	2.69
Brunei Darussalam	370,513	6821	55	308	0.16 (0.13)	0.69	0.47	2.47
Bulgaria	277,569	5279	197	309	0.24 (0.11)	0.57	0.60	2.65
Belarus	313,769	5800	234	308	0.71 (0.09)	0.62	0.26	2.15
Canada	1,223,773	22,629	821	309	1.18 (0.09)	1.01	0.19	2.30
Chile	400,308	7601	254	308	0.76 (0.10)	0.72	0.42	2.71
Chinese Taipei	410,057	7243	192	308	1.00 (0.10)	0.69	0.34	2.55
Colombia	390,308	7505	247	308	0.17 (0.10)	0.61	0.38	2.47
Costa Rica	354,675	7218	205	309	0.25 (0.10)	0.54	0.25	2.81
Croatia	364,082	6605	183	309	0.89 (0.10)	0.57	0.38	2.71
Czech Republic	386,821	7016	333	308	1.14 (0.10)	0.59	0.63	2.49
Denmark	401,867	7643	348	307	1.05 (0.09)	0.92	0.19	2.52
Dominican Republic	273,416	5672	235	308	−0.70 (0.10)	0.44	0.29	2.64
Estonia	297,711	5313	230	309	1.31 (0.09)	0.80	0.19	2.02
Finland	311,207	5647	214	309	1.39 (0.10)	1.13	0.09	2.71
France	333,574	6305	252	309	0.89 (0.10)	0.60	0.60	2.31
Georgia	275,241	5561	321	309	−0.13 (0.10)	0.55	0.20	2.60
Germany	291,620	5441	223	309	1.08 (0.11)	0.69	0.68	2.67
Greece	340,543	6399	242	308	0.61 (0.09)	0.70	0.39	2.17
Hong Kong	336,627	6024	152	309	1.27 (0.09)	0.59	0.31	1.89
Hungary	283,839	5130	238	309	0.71 (0.10)	0.46	0.60	2.27
Iceland	172,755	3294	142	308	0.74 (0.09)	1.14	0.09	2.20
Indonesia	666,995	12,080	397	304	−0.06 (0.09)	0.33	0.34	2.17
Ireland	311,077	5577	157	309	1.39 (0.10)	0.89	0.15	2.95
Israel	326,156	6618	174	318	0.76 (0.11)	0.83	0.77	2.05
Italy	639,010	11,781	542	309	0.80 (0.09)	0.60	0.40	2.13
Kosovo	272,933	5057	211	309	−0.64 (0.11)	0.40	0.18	3.07
Japan	332,520	6107	183	309	1.22 (0.10)	0.60	0.40	2.54
Kazakhstan	1,038,287	19,501	616	309	−0.06 (0.08)	0.41	0.25	1.98
Jordan*	236,070	8952	313	86	−0.12 (0.16)	0.76	0.33	1.99
Korea	379,638	6647	188	309	1.23 (0.08)	0.71	0.24	1.78
Lebanon*	120,303	5554	313	86	−0.78 (0.14)	0.72	0.95	1.34
Latvia	290,121	5302	308	309	0.72 (0.09)	0.67	0.19	2.07
Lithuania	378,840	6883	362	309	0.61 (0.10)	0.68	0.42	2.48
Luxembourg	276,049	5229	44	309	0.84 (0.13)	0.90	0.39	2.23
Macao	206,295	3772	45	309	1.10 (0.11)	0.56	0.26	2.04
Malaysia	330,482	6109	191	308	0.07 (0.10)	0.56	0.25	2.47
Malta	184,947	3360	50	309	0.68 (0.12)	1.10	0.31	2.64
Mexico	389,081	7292	286	309	0.16 (0.10)	0.52	0.33	2.65
Moldova*	129,892	5345	236	87	−0.01 (0.17)	0.80	0.30	2.30
Montenegro	350,054	6658	61	309	0.30 (0.11)	0.55	0.24	2.68
Morocco	321,293	6802	179	303	−0.44 (0.10)	0.32	0.25	2.58
Netherlands	234,688	4761	156	307	0.88 (0.11)	0.60	0.73	2.13
New Zealand	342,383	6171	192	309	1.20 (0.09)	1.09	0.20	2.35
Norway	312,974	5806	251	309	1.11 (0.09)	1.09	0.10	2.22
Panama	291,269	6263	253	309	−0.37 (0.10)	0.45	0.38	2.73
Peru	283,495	6073	340	308	−0.07 (0.09)	0.47	0.34	2.19
Philippines	384,381	7229	187	307	−0.72 (0.10)	0.48	0.29	2.75
Poland	312,194	5624	240	308	1.23 (0.09)	0.85	0.18	2.28
Portugal	321,743	5928	276	308	0.98 (0.10)	0.81	0.31	2.40
Qatar	729,462	13,820	188	309	0.00 (0.10)	0.66	0.51	2.06
Romania*	130,391	5066	170	87	−0.11 (0.18)	0.72	0.72	2.55
Russian Federation	415,796	7602	263	307	0.83 (0.10)	0.71	0.26	2.50
Saudi Arabia*	161,427	6129	234	86	−0.47 (0.17)	0.69	0.42	2.32
Serbia	347,303	6605	187	309	0.5 (0.10)	0.58	0.41	2.51
Singapore	380,970	6675	166	309	1.52 (0.10)	0.84	0.39	2.03
Slovak Republic	319,138	5955	376	309	0.51 (0.10)	0.64	0.55	2.45
Slovenia	351,454	6398	345	309	0.75 (0.10)	0.58	0.52	2.59
Spain	1,948,563	35,900	1089	309	0.91 (0.08)	0.73	0.13	2.06
Sweden	288,934	5494	223	308	1.18 (0.09)	1.09	0.21	2.23
Switzerland	315,759	5817	228	309	0.93 (0.10)	0.73	0.43	2.31
Thailand	477,619	8624	290	309	0.01 (0.09)	0.39	0.39	1.89
United Arab Emirates	1,064,061	19,261	755	309	0.17 (0.09)	0.68	0.63	2.08
Turkey	377,022	6888	186	308	0.61 (0.09)	0.34	0.45	1.70
Ukraine*	156,331	5992	250	88	0.28 (0.17)	0.91	0.38	2.47
North Macedonia*	127,965	5540	117	87	−0.37 (0.16)	0.72	0.38	1.96
United Kingdom	771,581	13,791	471	309	1.17 (0.09)	0.93	0.21	2.44
United States	268,348	4828	164	309	1.16 (0.10)	1.24	0.25	2.82
Uruguay	261,161	5255	189	308	0.28 (0.10)	0.64	0.38	2.32
B-S-J-Z (China)	690,965	12,055	361	308	1.70 (0.09)	0.46	0.40	2.13

Note. The number of responses, pupils, schools, and items used in the analysis are denoted as ${\mathrm{N}}_{\mathrm{r}}$, ${\mathrm{N}}_{\mathrm{p}}$, ${\mathrm{N}}_{\mathrm{s}}$, ${\mathrm{N}}_{\mathrm{i}}$, respectively. The estimated logit for the probability of a correct response of an average pupil from an average school on an average item is denoted as $b_0$, and its standard error is denoted as SE. The variances of the random pupil, school, and item effect are denoted as ${\sigma }_{\theta }^2$, ${\sigma }_{\zeta }^2$, ${\sigma }_{\beta }^2$, respectively. Countries that participated in the paper-based PISA 2018 are marked by an asterisk.

Table A2. Country-wise parameter estimates of the cross-classified mixed effects model for the PISA 2018 mathematical literacy domain.

Country	${\mathrm{N}}_{\mathrm{r}}$	${\mathrm{N}}_{\mathrm{p}}$	${\mathrm{N}}_{\mathrm{s}}$	${\mathrm{N}}_{\mathrm{i}}$	$b_0$ (SE)	${\sigma }_{\theta }^2$	${\sigma }_{\zeta }^2$	${\sigma }_{\beta }^2$
Albania	49,855	2593	311	69	−1.02 (0.17)	0.61	0.23	1.81
Baku (Azerbaijan)	66,981	3660	197	70	−0.98 (0.17)	0.76	0.14	1.86
Argentina*	95,657	6459	453	71	−1.24 (0.19)	0.59	0.35	2.62
Australia	153,027	7645	762	70	−0.31 (0.18)	1.04	0.34	2.37
Austria	72,523	3718	289	70	−0.40 (0.18)	0.72	0.73	2.07
Belgium	89,133	4680	287	70	−0.13 (0.18)	0.77	0.82	2.08
Bosnia and Herzegovina	60,763	3498	213	70	−1.28 (0.18)	0.65	0.21	2.24
Brazil	103,849	5672	588	70	−1.68 (0.20)	0.59	0.50	2.85
Brunei Darussalam	54,572	2805	55	69	−1.02 (0.23)	0.85	0.61	2.74
Bulgaria	54,470	2839	197	70	−0.91 (0.18)	0.59	0.63	2.08
Belarus	62,328	3131	233	70	−0.65 (0.19)	0.99	0.44	2.28
Canada	181,857	9723	805	70	−0.18 (0.18)	1.13	0.24	2.17
Chile	56,410	3101	249	70	−0.93 (0.19)	0.66	0.45	2.45
Chinese Taipei	58,986	2954	192	70	0.20 (0.16)	1.02	0.62	1.63
Colombia	57,943	3051	244	70	−1.55 (0.21)	0.65	0.42	2.90
Costa Rica	54,261	3288	205	70	−1.56 (0.22)	0.49	0.26	3.40
Croatia	49,572	2678	183	70	−0.67 (0.19)	0.67	0.41	2.26
Czech Republic	74,442	3793	333	70	−0.06 (0.18)	0.73	0.79	1.98
Denmark	81,378	4326	345	70	−0.29 (0.20)	1.07	0.23	2.60
Dominican Republic	55,535	3013	235	70	−2.53 (0.24)	0.37	0.25	3.71
Estonia	58,309	2872	229	70	0.08 (0.18)	1.03	0.24	2.24
Finland	59,518	3043	212	70	−0.13 (0.20)	1.17	0.07	2.76
France	64,694	3386	251	70	−0.43 (0.19)	0.71	0.83	2.24
Georgia	52,225	2970	317	70	−1.50 (0.18)	0.71	0.32	2.26
Germany	57,417	2992	223	70	−0.20 (0.19)	0.80	0.81	2.15
Greece	49,317	2624	237	70	−0.82 (0.19)	0.86	0.37	2.35
Hong Kong	50,358	2480	152	70	0.50 (0.17)	0.85	0.60	1.73
Hungary	55,074	2769	233	70	−0.59 (0.20)	0.56	0.89	2.38
Iceland	34,358	1782	139	70	−0.38 (0.20)	1.20	0.13	2.56
Indonesia	101,284	4936	394	70	−1.67 (0.21)	0.49	0.63	2.87
Ireland	61,461	3026	157	70	−0.30 (0.20)	0.89	0.15	2.70
Israel	51,651	2805	174	70	−0.69 (0.19)	0.95	0.85	2.16
Italy	121,867	6375	537	70	−0.29 (0.18)	0.74	0.55	2.07
Kosovo	54,222	2703	210	70	−1.95 (0.20)	0.52	0.21	2.61
Japan	65,185	3295	183	70	0.22 (0.18)	0.65	0.62	1.93
Kazakhstan	153,487	7969	607	70	−1.04 (0.17)	0.60	0.42	1.87
Jordan*	93,727	4993	313	71	−1.40 (0.18)	0.58	0.23	2.15
Korea	54,049	2729	185	70	0.16 (0.17)	0.99	0.45	1.77
Lebanon*	49,481	3108	312	70	−1.22 (0.17)	0.71	0.83	1.90
Latvia	42,769	2184	306	70	−0.37 (0.18)	0.84	0.22	2.25
Lithuania	54,525	2820	348	70	−0.62 (0.19)	0.93	0.45	2.32
Luxembourg	54,537	2821	44	70	−0.32 (0.20)	0.98	0.49	2.04
Macao	42,512	2037	45	70	0.30 (0.19)	0.90	0.46	1.86
Malaysia	69,111	3282	191	70	−1.20 (0.21)	0.73	0.35	2.81
Malta	25,892	1364	50	69	−0.37 (0.21)	1.24	0.38	2.29
Mexico	76,823	3909	280	70	−1.38 (0.21)	0.56	0.34	2.85
Moldova*	48,132	2953	235	71	−0.84 (0.18)	0.92	0.24	2.13
Montenegro	63,989	3579	61	70	−1.02 (0.19)	0.67	0.23	2.12
Morocco	48,182	2754	179	69	−1.94 (0.21)	0.49	0.26	2.86
Netherlands	49,424	2925	156	70	−0.14 (0.20)	0.61	1.12	2.40
New Zealand	65,735	3296	192	70	−0.25 (0.19)	1.22	0.25	2.34
Norway	60,287	3122	250	70	−0.15 (0.18)	1.24	0.07	2.31
Panama	41,080	2476	246	70	−2.03 (0.21)	0.39	0.34	3.05
Peru	55,494	3189	336	70	−1.40 (0.19)	0.65	0.36	2.32
Philippines	57,143	2946	187	70	−2.09 (0.22)	0.49	0.23	3.20
Poland	60,749	3014	234	70	0.05 (0.18)	1.07	0.27	2.07
Portugal	61,772	3186	276	70	−0.27 (0.18)	1.09	0.34	2.05
Qatar	143,071	7383	187	70	−1.42 (0.19)	0.81	0.66	2.30
Romania*	51,144	2834	170	71	−1.03 (0.19)	0.76	0.61	2.30
Russian Federation	60,258	3125	258	70	−0.42 (0.19)	0.82	0.34	2.28
Saudi Arabia*	65,003	3409	234	71	−1.84 (0.21)	0.61	0.25	2.94
Serbia	48,432	2698	183	82	−0.63 (0.17)	0.78	0.52	2.13
Singapore	55,921	2724	166	70	0.65 (0.17)	1.10	0.54	1.70
Slovak Republic	46,738	2504	373	70	−0.55 (0.18)	0.81	0.72	2.03
Slovenia	68,261	3515	340	70	−0.39 (0.18)	0.66	0.76	2.13
Spain	276,629	14,713	1089	70	−0.32 (0.18)	0.98	0.15	2.32
Sweden	55,857	2961	220	70	−0.15 (0.19)	1.14	0.25	2.34
Switzerland	61,662	3137	227	70	−0.02 (0.17)	0.89	0.49	1.88
Thailand	71,457	3536	286	70	−1.14 (0.18)	0.63	0.97	2.11
United Arab Emirates	213,751	10,356	747	70	−1.09 (0.17)	0.77	0.82	2.00
Turkey	74,810	3715	186	70	−0.81 (0.20)	0.47	0.91	2.50
Ukraine*	59,887	3349	250	71	−0.68 (0.19)	0.99	0.35	2.35
North Macedonia*	49,293	3101	113	71	−1.12 (0.18)	0.72	0.32	2.13
United Kingdom	139,349	7002	470	70	−0.25 (0.18)	1.00	0.29	2.31
United States	54,019	2619	163	70	−0.58 (0.20)	1.25	0.32	2.56
Uruguay	49,470	2798	189	70	−1.23 (0.21)	0.65	0.35	2.86
B-S-J-Z (China)	138,662	6505	361	70	1.25 (0.15)	0.74	0.72	1.49

Note. The number of responses, pupils, schools, and items used in the analysis are denoted as ${\mathrm{N}}_{\mathrm{r}}$, ${\mathrm{N}}_{\mathrm{p}}$, ${\mathrm{N}}_{\mathrm{s}}$, ${\mathrm{N}}_{\mathrm{i}}$. The estimated logit for the probability of a correct response of an average pupil from an average school on an average item is denoted as $b_0$, and its standard error is denoted as SE. The variances of the random pupil, school, and item effect are denoted as ${\sigma }_{\theta }^2$, ${\sigma }_{\zeta }^2$, ${\sigma }_{\beta }^2$, respectively. Countries that participated in the paper-based PISA 2018 are marked by an asterisk.

Table A3. Country-wise parameter estimates of the cross-classified mixed effects model for the PISA 2018 science literacy domain.

Country	${\mathrm{N}}_{\mathrm{r}}$	${\mathrm{N}}_{\mathrm{p}}$	${\mathrm{N}}_{\mathrm{s}}$	${\mathrm{N}}_{\mathrm{i}}$	$b_0$ (SE)	${\sigma }_{\theta }^2$	${\sigma }_{\zeta }^2$	${\sigma }_{\beta }^2$
Albania	84,282	2586	304	114	−1.00 (0.12)	0.45	0.17	1.45
Baku (Azerbaijan)	108,114	3663	197	115	−1.12 (0.12)	0.46	0.09	1.69
Argentina*	122,931	6389	452	84	−0.50 (0.10)	0.42	0.21	0.87
Australia	255,968	7698	762	115	0.01 (0.12)	1.04	0.24	1.72
Austria	119,837	3696	285	115	−0.19 (0.13)	0.64	0.57	1.68
Belgium	140,286	4696	287	115	−0.02 (0.12)	0.62	0.59	1.45
Bosnia and Herzegovina	108,054	3541	213	115	−1.17 (0.12)	0.47	0.17	1.53
Brazil	164,733	5739	591	115	−1.11 (0.13)	0.53	0.44	1.74
Brunei Darussalam	88,992	2788	55	115	−0.66 (0.15)	0.71	0.54	1.54
Bulgaria	88,520	2826	197	114	−0.92 (0.13)	0.46	0.59	1.52
Belarus	100,404	3119	233	115	−0.40 (0.12)	0.69	0.27	1.55
Canada	290,324	9716	808	115	0.09 (0.12)	0.96	0.15	1.58
Chile	93,922	3120	248	115	−0.52 (0.13)	0.56	0.37	1.79
Chinese Taipei	99,069	2963	192	115	0.14 (0.13)	0.83	0.49	1.74
Colombia	89,697	3061	244	114	−0.95 (0.13)	0.60	0.32	1.77
Costa Rica	85,268	3314	205	115	−1.07 (0.14)	0.45	0.20	1.95
Croatia	85,941	2692	183	115	−0.33 (0.13)	0.59	0.41	1.53
Czech Republic	125,876	3817	333	115	0.03 (0.13)	0.58	0.68	1.60
Denmark	130,139	4335	348	115	−0.28 (0.12)	0.99	0.20	1.65
Dominican Republic	84,389	3062	235	115	−1.88 (0.14)	0.40	0.21	2.14
Estonia	95,786	2843	226	115	0.34 (0.12)	0.76	0.23	1.46
Finland	101,217	3069	213	115	0.27 (0.13)	1.18	0.07	1.81
France	105,430	3418	252	115	−0.27 (0.12)	0.62	0.60	1.45
Georgia	87,690	3001	318	115	−1.37 (0.13)	0.51	0.20	1.86
Germany	93,085	2963	223	115	0.00 (0.13)	0.66	0.71	1.58
Greece	81,421	2618	236	115	−0.57 (0.12)	0.62	0.25	1.40
Hong Kong	79,723	2475	152	115	0.37 (0.13)	0.66	0.30	1.63
Hungary	89,933	2763	234	113	−0.38 (0.14)	0.50	0.73	1.65
Iceland	55,154	1800	132	115	−0.32 (0.12)	0.97	0.07	1.56
Indonesia	164,858	4950	396	114	−1.03 (0.12)	0.33	0.35	1.65
Ireland	99,564	2994	157	115	−0.01 (0.13)	0.89	0.13	1.71
Israel	84,244	2801	174	115	−0.42 (0.13)	0.79	0.62	1.37
Italy	201,694	6292	536	115	−0.30 (0.12)	0.60	0.42	1.65
Kosovo	86,771	2745	208	115	−1.60 (0.12)	0.32	0.16	1.47
Japan	107,444	3289	183	114	0.31 (0.14)	0.64	0.49	1.90
Kazakhstan	245,654	8001	609	115	−1.15 (0.12)	0.44	0.32	1.66
Jordan*	116,859	4995	313	85	−0.41 (0.10)	0.50	0.15	0.72
Korea	88,815	2715	187	112	0.25 (0.14)	0.93	0.36	1.78
Lebanon*	61,649	3092	308	85	−0.75 (0.10)	0.40	0.41	0.65
Latvia	69,263	2167	304	115	−0.19 (0.12)	0.70	0.17	1.53
Lithuania	90,116	2791	349	115	−0.34 (0.12)	0.70	0.37	1.60
Luxembourg	88,088	2823	44	115	−0.23 (0.15)	0.79	0.41	1.53
Macao	65,582	2032	45	115	0.28 (0.15)	0.65	0.29	1.68
Malaysia	114,175	3313	191	115	−0.77 (0.14)	0.57	0.22	2.15
Malta	43,679	1366	50	114	−0.34 (0.14)	1.12	0.23	1.43
Mexico	122,116	3920	283	115	−0.97 (0.13)	0.47	0.24	1.78
Moldova*	62,798	2979	235	85	−0.39 (0.09)	0.48	0.14	0.68
Montenegro	111,472	3592	61	115	−0.93 (0.13)	0.54	0.20	1.44
Morocco	76,093	2769	179	115	−1.52 (0.13)	0.29	0.21	1.88
Netherlands	80,459	2961	156	115	−0.06 (0.14)	0.55	0.89	1.65
New Zealand	109,081	3344	192	114	0.09 (0.13)	1.13	0.21	1.61
Norway	97,690	3127	249	115	−0.07 (0.12)	1.08	0.12	1.53
Panama	63,141	2528	250	115	−1.50 (0.13)	0.40	0.29	1.69
Peru	85,183	3254	337	115	−1.14 (0.13)	0.45	0.29	1.70
Philippines	93,618	2951	187	115	−1.70 (0.14)	0.46	0.21	1.99
Poland	101,778	3045	238	115	0.16 (0.12)	0.89	0.20	1.61
Portugal	102,897	3195	276	115	−0.11 (0.12)	0.87	0.28	1.58
Qatar	232,452	7415	187	115	−0.94 (0.12)	0.69	0.51	1.41
Romania*	63,358	2821	169	85	−0.49 (0.11)	0.41	0.29	0.80
Russian Federation	98,482	3101	262	115	−0.31 (0.12)	0.68	0.24	1.63
Saudi Arabia*	80,021	3416	234	84	−1.08 (0.11)	0.45	0.17	0.99
Serbia	80,778	2701	185	115	−0.63 (0.13)	0.56	0.34	1.55
Singapore	92,250	2756	166	115	0.56 (0.13)	0.88	0.36	1.79
Slovak Republic	77,709	2534	370	115	−0.56 (0.13)	0.66	0.60	1.57
Slovenia	114,865	3533	336	115	−0.23 (0.13)	0.56	0.58	1.69
Spain	458,655	14,637	1088	115	−0.07 (0.11)	0.81	0.11	1.52
Sweden	89,911	2956	217	115	0.01 (0.12)	1.01	0.19	1.50
Switzerland	101,256	3140	226	115	−0.10 (0.12)	0.73	0.42	1.47
Thailand	115,929	3542	283	115	−0.76 (0.14)	0.51	0.67	1.90
United Arab Emirates	352,410	10,404	748	115	−0.92 (0.12)	0.65	0.66	1.60
Turkey	121,413	3716	186	115	−0.41 (0.12)	0.31	0.57	1.33
Ukraine*	76,669	3349	250	85	−0.10 (0.11)	0.60	0.20	0.94
North Macedonia*	63,066	3072	113	85	−0.56 (0.09)	0.44	0.19	0.55
United Kingdom	234,732	7029	471	115	0.02 (0.12)	0.92	0.22	1.71
United States	86,839	2617	164	115	−0.05 (0.13)	1.13	0.30	1.75
Uruguay	80,104	2834	188	115	−0.82 (0.13)	0.59	0.29	1.58
B-S-J-Z (China)	225,216	6498	361	115	0.98 (0.13)	0.50	0.47	1.72

Note. The number of responses, pupils, schools, and items used in the analysis are denoted as ${\mathrm{N}}_{\mathrm{r}}$, ${\mathrm{N}}_{\mathrm{p}}$, ${\mathrm{N}}_{\mathrm{s}}$, ${\mathrm{N}}_{\mathrm{i}}$. The estimated logit for the probability of a correct response of an average pupil from an average school on an average item is denoted as $b_0$, and its standard error is denoted as SE. The variances of the random pupil, school, and item effect are denoted as ${\sigma }_{\theta }^2$, ${\sigma }_{\zeta }^2$, ${\sigma }_{\beta }^2$, respectively. Countries that participated in the paper-based PISA 2018 are marked by an asterisk.

Appendix B

Number of PISA Items by Domain

Table B1. Number of PISA items by domain for computer-based (CBA) and paper-based (PBA) Assessments.

Domain	Mode	Country	Items
			Unique	Common	Total
Reading	PBA	Argentina, Jordan, Lebanon,	15	$72(70{)}^a$	103
		Moldova, Romania,
		Saudi Arabia, North Macedonia
		Ukraine	16
	CBA	All CBA countries	–	$309(287{)}^b$	318
		Israel	9
Mathematics	PBA	Argentina, Jordan, Lebanon,	12	$59(58{)}^c$	83
		Moldova, Romania,
		Saudi Arabia, North Macedonia
		Ukraine	12
	CBA	$\mathrm{C}\mathrm{B}\mathrm{A}\mathrm{S}\mathrm{u}\mathrm{b}\mathrm{s}et{1}^d$	12	$58(57{)}^g$	82
		$\mathrm{C}\mathrm{B}\mathrm{A}\mathrm{S}\mathrm{u}\mathrm{b}\mathrm{s}\mathrm{e}\mathrm{t}{2}^e$	$12(11{)}^f$
Science	PBA	Argentina, Jordan, Lebanon,	–	$85(83{)}^h$	85
		Moldova, Romania,Ukraine,
		Saudi Arabia, North Macedonia,
	CBA	All CBA countries	–	$115(108{)}^j$	115

Note. All CBA countries refer to 69 out of 70 countries that took the CBA version of the PISA 2018. Excluded is Cyprus due to lack of available data.

${ }^a$ One of the common items was not administered in Jordan, Lebanon, and Saudi Arabia; one more item was not administered in Argentina.

${ }^b$ Thirty-one of the common items (one to six items per country) were not administered in one to two of the CBA countries.

${ }^c$ One of the common items was not administered in Lebanon.

${ }^d$ Baku (Azerbaijan), Brazil, Bulgaria, Chile, Colombia, Costa Rica, Dominican Republic, Kosovo, Kazakhstan, Mexico, Morocco, Panama, Peru, Philippines, Serbia, United Arab Emirates, Uruguay.

${ }^e$ Albania, Australia, Austria, Belgium, Bosnia and Herzegovina, Brunei Darussalam, Belarus, Canada, Chinese Taipei, Croatia, Czech Republic, Denmark, Estonia, Finland, France, Georgia, Germany, Greece, Hong Kong, Hungary, Iceland, Indonesia, Ireland, Israel, Italy, Japan, Korea, Latvia, Lithuania, Luxembourg, Macao, Malaysia, Malta, Montenegro, Netherlands, New Zealand, Norway, Poland, Portugal, Qatar, Russian Federation, Serbia, Singapore, Slovak Republic, Slovenia, Spain, Sweden, Switzerland, Thailand, Turkey, United Kingdom, United States, B-S-J-Z (China).

${ }^f$ One item of the subset was not administered in Albania.

${ }^g$ Three of the common items were not administered in Brunei Darussalam, Malta, and Morocco.

${ }^h$ One of the common items was not administered to Argentina, and one item was not administered to Saudi Arabia.

${ }^j$ Seven of the common items were not administered in one to two of the CBA countries.

Appendix C

Sensitivity Analysis

The first sensitivity analysis was performed to address potential comparability issues stemming from the non-uniform item pools across countries. We followed the same steps as those of the original analysis, but adjusting the item pools considered. The cross-classified model was fitted exclusively to the responses on the items which were common for all countries within each mode. The analysis considered response data on 70 PBA and 287 CBA items in the reading domain, 58 PBA and 57 CBA items in the mathematical literacy, 83 PBA and 108 CBA items in the science domain (see, Table B1). The variance components and variance components ratios were computed using the obtained variance estimates, and the observed outcome patterns in the new set of results were compared with those of the original results.

The resulting variance components and variance components ratios re-computed based on the parameter estimates of the cross-classified mixed effects model applied to the common items response data across countries and domains are presented in Table C1. Given minimal differences in the item pools in mathematics, no substantial deviations from the original results were detected in this domain. Although the re-computed variance components for the remaining domains of reading and science (Table C1) differed in their magnitude from the original results (Figures 2–4), which was anticipated considering the sensitivity analysis was performed on fewer items, the variance components did not differ in their relative proportions of the total variance structure. Moreover, if ordered by a specific variance component magnitude (i.e., pupil, school, item) or the magnitude of the variance components ratios, the countries appeared in nearly identical to the original analysis order. Finally, the re-computed correlation matrix of the outcome measures supported the associations found in the original analyses. Overall, results are fairly robust to the changes in item pools.

The second sensitivity analysis tested the robustness of the results when taking other approaches to partial credit response handling. The impact of different partial credit handling methods (i.e., partial credit responses coded as incorrect, partial credit responses coded as correct, and omitting items that allowed partial credit from analysis) appeared to be minimal. The absolute average differences in item variance components computed using the original and the alternative partial credit handling methods were 1.2–5.2%.

Table C1. Sensitivity analysis resulting country-wise variance components (VC) and variance components ratios (VCR).

Country	Reading				Mathematics				Science
	$\mathrm{V}{\mathrm{C}}_{\mathrm{p}\mathrm{u}\mathrm{p}\mathrm{i}\mathrm{l}}$	$\mathrm{V}{\mathrm{C}}_{\mathrm{s}\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{o}\mathrm{l}}$	$\mathrm{V}{\mathrm{C}}_{\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{m}}$	$\mathrm{V}\mathrm{C}\mathrm{R}$	$\mathrm{V}{\mathrm{C}}_{\mathrm{p}\mathrm{u}\mathrm{p}\mathrm{i}\mathrm{l}}$	$\mathrm{V}{\mathrm{C}}_{\mathrm{s}\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{o}\mathrm{l}}$	$\mathrm{V}{\mathrm{C}}_{\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{m}}$	$\mathrm{V}\mathrm{C}\mathrm{R}$	$\mathrm{V}{\mathrm{C}}_{\mathrm{p}\mathrm{u}\mathrm{p}\mathrm{i}\mathrm{l}}$	$\mathrm{V}{\mathrm{C}}_{\mathrm{s}\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{o}\mathrm{l}}$	$\mathrm{V}{\mathrm{C}}_{\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{m}}$	$\mathrm{V}\mathrm{C}\mathrm{R}$
Albania	8.4	3.2	38.5	3.3	10.7	3.8	29.5	2.0	8.5	3.2	27.9	2.4
Baku (Azerbaijan)	8.3	1.6	43.8	4.4	12.9	2.6	28.2	1.8	8.6	1.8	31.4	3.0
Argentina*	11.6	5.9	31.7	1.8	8.3	4.8	39.0	3.0	8.7	4.5	18.3	1.4
Australia	16.2	3.5	33.1	1.7	14.7	4.7	33.8	1.7	17.0	4.0	28.3	1.3
Austria	10.0	8.6	37.6	2.0	10.8	11.1	30.2	1.4	10.7	9.8	28.2	1.4
Belgium	10.0	8.9	30.9	1.6	11.3	11.9	29.6	1.3	10.8	10.2	25.4	1.2
Bosnia and Herzegovina	8.3	2.9	43.2	3.9	10.5	3.2	35.0	2.6	9.0	3.3	29.2	2.4
Brazil	10.1	7.6	37.6	2.1	7.7	6.4	40.9	2.9	9.1	7.5	30.2	1.8
Brunei Darussalam	10.7	7.2	35.2	2.0	11.1	7.6	35.4	1.9	12.3	8.9	26.3	1.2
Bulgaria	8.5	9.1	36.9	2.1	9.2	9.6	31.7	1.7	8.2	10.5	27.0	1.4
Belarus	10.3	4.5	34.1	2.3	13.7	5.9	32.5	1.7	12.4	4.9	27.7	1.6
Canada	15.5	2.9	33.1	1.8	16.7	3.4	31.4	1.6	16.5	2.6	27.5	1.4
Chile	10.5	6.2	37.6	2.3	9.4	6.5	36.7	2.3	9.8	6.4	31.1	1.9
Chinese Taipei	10.7	5.3	36.9	2.3	15.3	9.0	25.0	1.0	13.7	8.0	28.5	1.3
Colombia	9.5	5.9	36.6	2.4	8.4	5.5	41.3	3.0	10.4	5.7	30.2	1.9
Costa Rica	8.3	4.0	40.7	3.3	6.3	3.0	47.6	5.1	8.1	3.6	34.0	2.9
Croatia	8.6	5.7	39.1	2.7	10.1	6.1	33.8	2.1	10.6	7.3	27.4	1.5
Czech Republic	8.8	9.5	34.9	1.9	11.2	11.7	28.5	1.2	9.8	11.5	26.9	1.3
Denmark	14.0	2.9	36.3	2.1	15.0	3.1	35.4	2.0	16.9	3.4	27.4	1.3
Dominican Republic	6.9	4.7	38.8	3.3	4.3	3.1	50.7	6.9	6.9	3.7	36.5	3.4
Estonia	13.4	3.3	31.8	1.9	15.6	3.6	32.6	1.7	13.7	3.9	26.7	1.5
Finland	16.6	1.3	37.6	2.1	15.5	1.0	38.2	2.3	19.1	1.1	29.8	1.5
France	9.3	9.4	33.8	1.8	10.3	11.4	31.8	1.5	10.8	10.4	25.2	1.2
Georgia	9.0	3.3	39.0	3.2	10.9	4.8	33.8	2.2	9.2	3.5	33.0	2.6
Germany	9.9	9.9	36.1	1.8	11.3	11.7	30.3	1.3	11.0	11.8	26.2	1.1
Greece	11.2	6.2	33.0	1.9	12.9	5.4	33.6	1.8	11.7	4.7	26.1	1.6
Hong Kong	10.2	5.3	31.2	2.0	12.9	9.2	26.0	1.2	11.8	5.4	28.8	1.7
Hungary	7.4	9.9	33.9	2.0	8.2	12.4	33.2	1.6	8.3	12.1	27.6	1.4
Iceland	17.8	1.5	32.2	1.7	17.5	1.7	33.9	1.8	17.1	1.2	27.5	1.5
Indonesia	5.9	6.0	34.7	2.9	7.1	8.9	38.0	2.4	5.9	6.3	30.1	2.5
Ireland	12.7	2.2	40.0	2.7	12.6	2.1	39.1	2.7	15.2	2.3	29.3	1.7
Israel	12.7	11.7	29.4	1.2	13.6	11.8	28.5	1.1	13.4	10.6	23.6	1.0
Italy	10.0	6.8	32.9	2.0	11.4	8.4	31.1	1.6	10.4	7.3	28.6	1.6
Kosovo	6.2	3.0	44.0	4.8	7.8	2.9	39.6	3.7	6.1	3.0	28.7	3.2
Japan	9.3	6.2	36.8	2.4	10.0	9.1	29.8	1.6	10.5	8.1	30.8	1.7
Kazakhstan	7.3	4.7	33.3	2.8	9.6	6.9	30.2	1.8	7.9	5.9	30.2	2.2
Jordan*	12.2	5.1	31.2	1.8	9.6	3.8	34.8	2.6	10.8	3.2	15.6	1.1
Korea	12.2	4.1	29.9	1.8	15.1	6.4	27.6	1.3	15.0	6.0	28.4	1.4
Lebanon*	11.9	14.7	21.2	0.8	10.3	12.5	28.2	1.2	8.4	8.9	13.9	0.8
Latvia	11.4	3.2	33.4	2.3	12.7	3.3	33.7	2.1	12.8	3.1	27.3	1.7
Lithuania	10.5	6.4	35.8	2.1	13.6	6.0	32.3	1.6	11.9	6.2	28.0	1.5
Luxembourg	14.0	6.1	32.6	1.6	14.5	7.3	30.1	1.4	13.5	7.0	26.5	1.3
Macao	9.5	4.5	33.4	2.4	13.7	6.9	28.5	1.4	11.6	5.2	29.4	1.8
Malaysia	9.0	4.0	37.5	2.9	10.1	5.0	39.0	2.6	9.4	3.7	35.4	2.7
Malta	15.9	4.6	35.3	1.7	16.4	5.2	32.3	1.5	18.8	3.8	24.5	1.1
Mexico	8.0	5.1	38.7	3.0	7.6	4.8	41.8	3.4	8.4	4.3	31.9	2.5
Moldova*	12.8	4.8	34.3	1.9	14.1	3.9	32.1	1.8	10.4	2.9	15.1	1.1
Montenegro	8.8	3.9	39.5	3.1	10.8	3.5	33.1	2.3	10.4	3.8	27.6	1.9
Morocco	5.4	4.3	39.9	4.1	6.5	3.3	41.9	4.3	5.1	3.8	33.7	3.8
Netherlands	9.3	11.3	31.8	1.5	8.4	15.4	31.9	1.3	8.8	14.3	26.8	1.2
New Zealand	16.3	3.0	33.1	1.7	16.9	3.5	33.1	1.6	18.5	3.4	26.8	1.2
Norway	17.2	1.6	32.8	1.7	18.2	1.0	32.2	1.7	18.7	2.0	25.9	1.3
Panama	6.9	6.1	39.6	3.0	5.0	4.4	45.2	4.8	7.5	5.5	30.7	2.4
Peru	8.0	5.7	34.5	2.5	9.4	5.2	35.4	2.4	8.2	5.4	30.8	2.3
Philippines	7.5	4.5	38.9	3.2	6.4	3.0	46.1	4.9	8.1	3.7	33.8	2.9
Poland	13.8	3.0	34.1	2.0	16.1	4.1	31.2	1.5	15.4	3.3	28.1	1.5
Portugal	12.7	5.0	35.3	2.0	15.8	4.7	31.1	1.5	14.8	4.8	27.5	1.4
Qatar	10.9	8.3	31.3	1.6	11.5	8.9	32.3	1.6	12.1	8.9	24.7	1.2
Romania*	10.9	10.1	34.5	1.6	11.2	8.8	33.2	1.7	8.6	6.1	16.9	1.1
Russian Federation	10.9	4.1	36.9	2.5	12.3	4.9	34.0	2.0	12.0	4.2	29.0	1.8
Saudi Arabia*	10.3	5.8	35.7	2.2	8.8	3.5	43.0	3.5	9.1	3.4	20.1	1.6
Serbia	9.1	6.5	36.6	2.3	11.5	7.7	32.9	1.7	10.1	6.2	28.0	1.7
Singapore	13.6	6.2	30.7	1.6	16.9	8.0	24.5	1.0	14.5	5.9	29.6	1.5
Slovak Republic	9.5	8.3	35.1	2.0	11.8	10.4	29.0	1.3	11.2	9.9	26.5	1.3
Slovenia	8.7	7.9	37.2	2.2	10.1	11.1	30.8	1.5	9.3	9.9	28.7	1.5
Spain	12.4	2.3	32.4	2.2	14.4	2.2	35.2	2.1	14.6	2.0	27.5	1.7
Sweden	16.5	3.2	32.5	1.6	16.3	3.5	32.4	1.6	17.6	3.2	25.8	1.2
Switzerland	11.4	6.8	34.1	1.9	14.2	7.3	28.8	1.3	12.9	7.3	25.9	1.3
Thailand	6.8	7.0	31.3	2.3	8.8	13.8	30.3	1.3	8.2	10.7	30.7	1.6
United Arab Emirates	10.8	10.1	30.7	1.5	11.5	12.0	29.2	1.2	10.7	10.8	26.6	1.2
Turkey	6.0	8.3	29.5	2.1	6.9	12.4	32.9	1.7	5.8	10.8	25.2	1.5
Ukraine*	12.8	5.3	37.5	2.1	14.5	4.9	33.5	1.7	12.1	4.0	18.7	1.2
North Macedonia*	12.5	6.3	31.0	1.6	10.6	4.9	33.5	2.2	10.2	4.5	12.4	0.8
United Kingdom	14.1	3.1	34.9	2.0	14.7	4.3	33.3	1.8	15.2	3.6	29.0	1.5
United States	17.0	3.5	36.0	1.8	16.5	4.2	34.8	1.7	17.8	4.8	27.9	1.2
Uruguay	10.1	6.2	34.2	2.1	8.7	4.8	41.3	3.1	10.7	5.4	28.5	1.8
B-S-J-Z (China)	7.6	6.6	33.7	2.4	11.7	11.3	23.9	1.0	8.9	8.1	29.6	1.7

Appendix D