Scaffolding small groups at the group level: Improving the scaffolding behavior of mathematics teachers during mathematical discussions

Abstract

Background

Supporting students during collaborative learning in mathematics is challenging for teachers. We developed the Small-Group Scaffolding Tool (SGS-Tool) to assist teachers regarding how and when to offer support. The tool is based on three characteristics of scaffolding small groups at the group level: contingency to the group, phasing out content support when the group can continue independently, and transferring responsibility for learning to the group.

Method

We investigated whether the scaffolding behavior of teachers using the SGS-Tool was more adapted to the group level than that of teachers not using the tool. Participants were four teachers and their seventh grade classes. The topic was Early Algebra. We analyzed teachers’ scaffolding behavior with one group during five lessons.

Findings

The SGS-Tool offered teachers support when the groups discussed mathematics, but adaptations of the tool are needed. Overall, the SGS-Tool seems to be a promising tool for supporting mathematics teachers in scaffolding groups at the group level.

Contribution

Our study provides insight into what scaffolding small groups at the group level entails and how teachers can apply it.

Introduction

Collaborative learning can be an important means for enhancing students’ learning of mathematics (Webb, 1982). For instance, Freudenthal (1991) argued that high-quality mathematical discussions where small heterogeneous groups of students reflect on mathematical activities contribute significantly to mathematical reasoning and level raising. Mathematical discussions are therefore promoted in, for example, the Process Standards of the National Council of Teachers of Mathematics of the USA (NCTM, 2000).

However, several studies have shown that teachers experience difficulty supporting small groups during collaborative learning (Van Leeuwen et al., 2015; Webb, 2009). They face complex decisions on how and when to give support (Van de Pol et al., 2014). Three specific aspects make teacher support of small groups during collaborative learning challenging. First, teachers have to decide which type of support to provide. A second challenge is exercising the correct degree of control when giving content support. Finally, it is challenging to determine when it is time to return control over the learning process to the group.

There is a need to support teachers in guiding students through mathematical discussions (Webb & Ing, 2019). The available tools that support teachers in scaffolding students in group discussions (for example, the Contingent Teaching Model (CTM) of Van de Pol, Volman & Beishuizen, 2012) focus on individual students within a group instead of scaffolding the group as a whole. In such cases, interaction takes place between the teacher and one or two students and not with the whole group. Offering support at the group level is important to stimulate ongoing group discussion, since any discussion is a group effort. Moreover, Dekker and Elshout-Mohr (2004) found that when a teacher extensively supported one student in a group (typically a student who asked a question), other students tended to withdraw from further mathematical discussions.

We developed a tool to support mathematics teachers in scaffolding small groups at the group level. We refer to this tool as the Small-Group Scaffolding Tool (SGS-Tool). To the best of our knowledge, how teachers can scaffold small groups at the group level has not been investigated. In this explorative study, we examine whether and how the SGS-Tool helps teachers support small groups during mathematical discussions.

Theoretical framework

Challenges of guiding group work

Providing adequate support to small groups is not an easy task. Teachers have been reported to have difficulty supporting small groups during collaborative learning (Van Leeuwen et al., 2015; Webb, 2009). In their systematic review of the role of teachers in collaborative learning, Van Leeuwen and Janssen (2019) concluded that teacher support provided during collaborative learning is a complex activity requiring teachers to balance their actions carefully to be effective. We discuss here three of the aspects that make teacher support during collaborative learning so complex.

First, teachers have to decide which type of support to provide (Van Leeuwen et al., 2015). In the context of mathematical group work, mathematical content support and process support are distinguished from each other (Dekker & Elshout-Mohr, 2004). Mathematical content support involves teacher interventions in which teachers focus on mathematical content; it is concerned with students’ mathematical reasoning. Process support involves teacher interventions that stimulate mathematical discussions; it is concerned with the process of collaboration. Dekker and Elshout-Mohr (2004) developed the so-called Process Model (PM), which distinguishes different types of student interactions in mathematical discussions that teachers can encourage through process support (see the next section), and found that process support resulted in more mathematical level raising than mathematical content support. Stimulating students to share and explain their ideas to each other has also been shown to have an indirect positive influence on students’ levels of achievement through the mediating variable of student participation (Webb et al., 2019). Therefore, encouraging small groups to solve a problem by themselves, i.e., by providing process support, is an important form of support.

However, sometimes, no students in the group know the answer to a question, leaving small groups stuck, i.e., mathematical discussions come to a halt. In such cases, merely giving process support is not sufficient to put mathematical discussions back on track. Rather, mathematical content support appears to be needed. Therefore, when guiding small groups, teachers need to make careful decisions on the kind of support that is needed.

A second challenge teachers face in supporting students’ collaborative learning is exercising the correct degree of control when providing mathematical content support, i.e., deciding how much mathematical content support to provide. Taking too much control over the learning process by giving too much content support can have a negative effect on collaborative learning processes (Van Leeuwen & Janssen, 2019). For example, Dekker and Elshout-Mohr (2004) found that when a teacher provided elaborate content support to a student who asked a question, other students in the group stopped participating in the mathematical discussion. Rather than supporting the discussion, such support stops the mathematical discussion from continuing. In deciding how much support is needed, it is important to adapt the support to the students’ levels of understanding. A first step to do so is diagnosing the students’ knowledge level (Van de Pol, Volman & Beishuizen, 2012). In his investigation of mathematics teacher interventions implemented during group work, Chiu (2004) found that teachers provided less mathematical content support overall when they first diagnosed the students’ levels of understanding. Then, when mathematical content support was provided, it was built on the mathematical ideas that the students were discussing. Teachers who did not diagnose students’ levels of understanding provided the students with new information based on their own preconceived ideas. Such new information may or may not have been related to the problems that the group of students faced. This suggests that diagnosing students’ levels of understanding might not only prevent teachers from taking too much control over learning processes (providing too much content support) but also help them adapt their content support to individual students’ different levels of understanding (provide contingent content support).

Providing contingent support is one of the three key features of scaffolding (Van de Pol et al., 2010). Smit et al. (2013) defined characteristics for scaffolding of whole classes in which teachers are responsive (contingent) to what is considered the Zone of Proximal Development (ZPD) of the class as a whole. In their CTM, Van de Pol, Volman & Beishuizen (2012) describe scaffolding interactions during which teachers’ content support is adapted to the level of individual students in a small-group setting. They consider content support to be contingent when the teacher’s level of control increases after a student demonstrates a poor level of understanding and decreases after a student demonstrates a good level of understanding. The CTM involves four teaching steps. First, teachers apply diagnostic strategies to discover the current level of understanding of an individual student in the group. Second, teachers check whether their diagnosis is correct. Third, teachers provide content support adapted to the individual student’s current level of understanding (contingent content support). Finally, in the fourth step, teachers verify what the student has learned. Students were found to learn more when teachers provided contingent content support to individual students in group work settings (Van de Pol et al., 2010; Webb, 2009). However, it has been found that teachers tend to find providing contingent content support in small-group settings difficult, as it requires them to be able to diagnose how students make sense of mathematical ideas while interacting with small groups (Yackel, 2002) and because they are required to attend to the needs of all of their students at the same time (Myhill & Warren, 2005).

A third factor that makes teacher support during collaborative learning complex is determining when to return control over the learning process to the group. Diminishing content support over time (fading) and returning responsibility for learning processes to the learner (transfer of responsibility) are also described by Van de Pol et al. (2010). We define the right time to return responsibility for learning to the group as the moment when the group is able to continue mathematical discussions without content support from the teacher. In other words, it is recommended that mathematical content support be provided until the group can continue mathematical discussions independently.

Small-group scaffolding

Scaffolding small groups at the group level is important when supporting groups during discussions. Based on the preceding discussion and by combining insights from the PM (Dekker & Elshout-Mohr, 2004) and the CTM (Van de Pol, Volman & Beishuizen, 2012), we can distill three key characteristics of scaffolding small groups at the group level during mathematical discussions. In the CTM, three key characteristics of scaffolding individual students during group work have been defined as 1) contingency to individuals in the context of groupwork (adapt content support to the level of the individual student), 2) fading (phasing out content support over time), and 3) transfer of responsibility (returning responsibility for learning to the students). When we expand the notion of these characteristics from the individual to the group, the first characteristic changes from contingency to an individual student to contingency to the group at the group level, i.e., support adapted to the level of the group. This support may entail content support or process support. When dealing with a group that is stuck, i.e., the group has reached the maximum level of understanding that it can achieve together, content support adapted to this maximum level of understanding is preferred over process support since process support (encouraging students to help each other) is unlikely to help the group advance any further. When dealing with a group that has not reached its maximum level of understanding, i.e., the group is able to reach a higher level of understanding independently, process support is preferred over content support since taking too much control by offering content support might have a negative effect on the groups’ learning process (Van Leeuwen & Janssen, 2019). The second characteristic (fading), changes from phasing out content support over time, to phasing out content support when the group is able to continue on its own. Finally, the third characteristic changes from a transfer of responsibility to the student to a transfer of responsibility to the group (returning responsibility for learning to the group after the group is able to continue on its own).

Small-group scaffolding during mathematical discussions

When dealing with a group mathematical discussion, mathematical content support is considered contingent when it is adapted to the maximum level of understanding that the group can achieve together, or phrased differently, when it is in the group’s ZPD (Nyikos & Hashimoto, 1997). That means that mathematical content support needs to be given only when the group is stuck, i.e., when there is no one in the group who can come up with a solution or next step, indicating that the group has reached its maximum level of understanding.

It is recommended that all support given to a small group before the groups’ level of maximum understanding has been reached focus on stimulating the mathematical discussion. Stimulating mathematical discussions can be done by providing process support, i.e., asking students to perform interactive processes that promote the understanding of the group. The PM describes two kinds of interactive processes between students that teachers can encourage so mathematical discussions can continue (Dekker & Elshout-Mohr, 1998, 2004): 1) key activities (show/tell work, explain work, justify work, reconstruct work) and 2) regulating activities (ask students to show/tell about their work, ask them to explain their work, critique their work).

When providing contingent mathematical content support during mathematical discussion, mathematical support is no longer necessary and can be phased out when the group is able to continue the discussion by itself. In addition, returning responsibility for learning to the group can be accomplished by encouraging the group to continue the discussion (providing process support) at the moment that the group is able to continue the discussion by itself.

When scaffolding small groups during mathematical discussions, process support and content support need to be carefully combined. Process support needs to be given to stimulate the group discussion and help students share and explain their ideas (Dekker & Elshout-Mohr, 2004). Content support needs to be given only when the group is stuck, and such support needs to be adapted to the maximum level of understanding of the entire group. Therefore, teachers need to diagnose the groups’ maximum level of understanding. After diagnosing the maximal level of understanding of the group, mathematical content support can be given in what we could consider the group’s ZPD (Nyikos & Hashimoto, 1997). In a study during which teaching experiments were conducted, combined process support and content support with the use of technology during mathematical discussions showed positive effects on students’ conceptual development (Kazak et al., 2015).

Based on the above, we describe three key characteristics of small-group scaffolding at the group level during mathematical discussions as follows: 1) contingency to the group

• a. providing contingent mathematical content support at the maximum group level to the whole group when the group is stuck;

• b. providing process support when the group has not yet reached its maximum level of understanding;

• 2) phasing out mathematical content support when the group is able to continue on its own, i.e., providing contingent mathematical content support until a group is able to continue the discussion by itself; and

• 3) returning responsibility for learning to the group by providing process support at the moment that a group is able to continue the discussion by itself.

The first key characteristic “contingency to the group” addresses the first challenge teachers face when they wish to provide support to small student groups (i.e., deciding which type of support to give) by offering teachers a choice between providing process support or contingent mathematical content support. The second key characteristic “phasing out mathematical content support when the group is able to continue on its own” addresses the second challenge teachers face (exercising the correct degree of control when giving mathematical content support, i.e., deciding how much mathematical content support to give) by offering a concrete indication of when teachers can stop providing mathematical content support. The third key characteristic, “returning responsibility for learning to the group” addresses the third challenge teachers face (determining when to return control over the learning process to the group) by indicating when and how to return responsibility for learning to the group.

Based on the characteristics of small-group scaffolding during mathematical discussions, we developed a tool for supporting mathematics teachers when guiding small groups. The SGS-Tool integrates the approaches described in the PM (Dekker & Elshout-Mohr, 2004) and CTM (Van de Pol, Volman & Beishuizen, 2012). Three key characteristics of scaffolding from the CTM (contingency, fading and transfer of responsibility) were incorporated in the SGS-Tool. From the PM process support, stimulating students to share and explain their ideas was incorporated in the SGS-Tool. The SGS-Tool thus expands both models. Whereas the CTM focuses on support provided to individuals in a group work context, the SGS-Tool aims to provide support to the group as a whole, specifically by giving mathematical content support in the ZPD of the group (Nyikos & Hashimoto, 1997). Whereas the PM involves only process support, the SGS-Tool integrates process support and contingent mathematical content support.

Aims and research question

The SGS-Tool is designed to improve the scaffolding behavior of mathematics teachers during small group mathematical discussions. It meets the need described in the literature to develop tools to support the work of teachers during mathematical discussions (Webb & Ing, 2019). The tool is distinctive in that it focuses on support provided at the group level to keep mathematical discussions going. The aim of this exploratory study was to investigate whether working with the SGS-Tool offers solutions to some of the challenges that teachers face when supporting small groups discussing mathematics, particularly whether working with the tool supports teachers’ scaffolding behavior.

The following research question guided the study:

“Does working with the SGS-Tool elicit teachers’ scaffolding behavior at the group level during mathematical discussions?”

As we consider a small group to be scaffolded at the group level when a teacher provides contingent mathematical content support at the maximum level of understanding of the group as a whole or provides process support when students can be encouraged to continue their discussions to reach the maximum level of understanding of the group (the premises underlying the SGS-Tool), we expected the scaffolding behavior of the teachers working with the tool to be characterized by the following:

1. determining whether or not the group’s maximum level of understanding has been reached;

2. providing process support instead of content support when the group’s maximum level of understanding has not been reached;

3. when the maximum level of understanding has been reached, providing content support, including diagnosing the maximum level of understanding of the group, checking whether or not the diagnoses is correct, and providing contingent mathematical content support; and

4. after providing contingent mathematical content support described above, checking whether one or more students understood the support, i.e., checking whether the group can continue the discussion on its own, then phasing out content support and returning responsibility for learning to the group when the group is able to continue the discussion on its own.

As a result of this scaffolding behavior, we also expected increased student participation in the discussion (Expectation V). Furthermore, we were interested in teachers’ experiences working with the tool. Below, we explain how our operationalized expectations are related to the challenges teachers face when guiding students during collaborative learning.

Method

We conducted a study in which we analyzed the scaffolding behavior of teachers working with the SGS-Tool (SGS group) compared with the scaffolding behavior of teachers not working with the tool (non-SGS group). Teachers in both groups taught a lesson series on Early Algebra for seventh-grade students.

Small-Group Scaffolding Tool

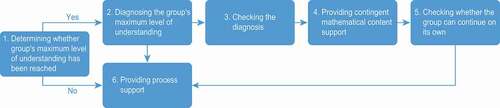
As shown in the flowchart in Figure 1, the SGS-Tool follows six steps, which are discussed below.

Figure 1. The Small-Group Scaffolding Tool for mathematical discussions.

During a mathematical discussion, when a student in the group asks the teacher a content question, the teacher faces the decision what type of support to provide. Therefore, the first step of the tool is to determine whether or not the maximum level of understanding of the group has been reached by determining whether the question is a question from the whole group or from one individual student (step 1). When the question is a question from one student and the other students have not yet shared their thoughts on the question (the maximum level of understanding has not yet been reached), the teacher is recommended to provide process support (step 6), i.e., stimulating discussions by asking the students to perform key and regulating activities as defined by Dekker and Elshout-Mohr (2004), and then end his or her interaction with the group. In cases where the question is from the whole group, the whole group is stuck, and mathematical content support from the teacher is needed for the discussion to continue. In other words, by checking whether the question is a group question, the teacher can adapt his or her support to the groups’ needs, i.e., scaffold the group at the group level.

The next step is for the teacher to diagnose the group’s maximum level of understanding by determining what mathematical ideas the group was discussing (step 2) and to give just the correct kind and degree of mathematical content support to get the discussion back on track (step 4). This diagnosis can be made by observing the group’s activities, asking questions about what the students have done so far, and/or asking them to show or explain their work. In determining the group’s level of understanding, it is important to address various students in the group. If one or more students come up with an answer during this activity (as diagnosing the group’s current level of understanding can function as a form of providing support), the teacher is asked to encourage these students to explain the answer to their fellow students, i.e., to continue the mathematical group discussion (providing process support, step 6 of the tool). If the question remains unanswered during this diagnosis phase, the teacher is recommended to check whether the diagnosis is correct (step 3 of the tool) by summarizing what the students have said and checking whether the summary is correct.

The next step (step 4) is to provide mathematical content support to the group, adapted to the group’s level of understanding as determined in step 2. Thus, this step involves giving contingent mathematical support to the group at the group level (the first key characteristic of small-group scaffolding). In step 5, the teacher checks whether at least one student in the group understands the content for which content support was provided; in other words, the teacher checks whether the group is able to continue the discussion independently (i.e., step 4 may be repeated until one or more students show understanding). At this point, teachers can stop providing mathematical content support (phasing out, the second key characteristic of small-group scaffolding) and return responsibility for learning to the group (the third key characteristic of small-group scaffolding). Returning responsibility for learning to the group can be done by providing process support (step 6 of the tool), i.e., stimulating discussions by asking the students to perform key and regulating activities and then ending his or her interaction with the group.

After developing the tool, three international experts (one on scaffolding collaborative learning, one on collaborative learning in mathematics education and one on mathematics education) were asked to provide feedback on the tool. Two experts responded via e-mail, and the first author met the first expert in person. The experts indicated that the tool addresses serious problems in mathematics education, and they endorsed the tool’s ability to improve teachers’ support for small-group discussions. They found the steps of the tool clear and emphasized the importance of not immediately providing content support when supporting small groups during mathematical discussions.

The expectations for the scaffolding behavior of teachers working with the SGS-Tool formulated above (expectation I, II, III and IV) were then operationalized (Table 1).

Table 1. Expectations and operationalized expectations for teachers working with the SGS-Tool.

Expected scaffolding behavior		Operationalized expected scaffolding behavior
I	Determining whether the group has reached its maximum level of understanding	1	Step 1: Determining whether the group’s maximum level of understanding has been reached
II	Providing process support when the group has not reached its maximum level of understanding	2	Combination of steps 1 and 6
III	Providing content support when the group reached its maximum level of understanding, including diagnosing the group’s maximum level of understanding, checking whether the diagnosis is correct, and providing contingent mathematical content support	3a	Step 4: Providing mathematical content support
		3b	Combination of steps 1 and 2: Diagnosing group’s maximum level of understanding; Step 3: Checking diagnosis
		3c	Providing contingent mathematical content support
IV	After III, checking whether one or more students understood the support (i.e., checking whether the group can continue the discussion on its own), followed by phasing out content support, and then returning responsibility for learning to the group	4a	Step 5: Checking whether the group can continue the discussion on its own
		4b	Step 6: Providing process support
		4c	Combination of steps 4, 5, and 6

Operationalized expectations 1, 2, 3a, and 3b address the first challenge for teachers when guiding small groups during collaborative learning, “deciding which type of support to provide.” Operationalized expectations 3c and 4a address the second challenge, “exercising the correct degree of control when providing mathematical content support.” Additionally, operationalized expectations 4b and 4c address the third challenge “determining when to return control over the learning process to the group.”

Participants

Participants included four teachers (3 males, 1 female) and their 109 seventh-grade students at one school in Amsterdam, the Netherlands. This school is special because it promotes collaboration between students across all school subjects, and students always sit in small, heterogeneous groups. The school delays the tracking of students until the third year of high school (grade 9), which is uncommon in the Netherlands and makes classes truly heterogeneous. Teachers working at the studied school share similar views on the importance of teaching and learning in small, heterogeneous groups. The school cooperates with the university’s research program on improving learning in small, heterogeneous groups. The four teachers volunteered to participate in this study and did not receive any compensation. They had the same teaching qualification level (for lower secondary education). Two teachers had 8 years teaching experience, and two had 35 years ($M=21.5$). To assign the teachers to one of the groups, teachers were matched into pairs by age and teaching experience. In each pair, one teacher was randomly assigned to the SGS group and the other to the non-SGS group. One teacher in each group had previously worked with the lesson series.

The teachers taught their own seventh grade class. In the SGS group, 54 students (14 groups) participated, and in the non-SGS group, 55 students (14 groups) participated. Most groups consisted of four students, while three groups consisted of three students because of class size restrictions. The groups were of mixed ability and formed by the class mentor. All students were accustomed to working in group settings. The students’ age varied from 12 to 15 years ($M=13.6$).

The aim of the study was only known to teachers of the SGS group. The importance of not revealing the nature of the study to the non-SGS teachers was explained to the SGS teachers by the researcher each time they met. The teachers assured that they had not revealed it to the non-SGS teachers. Prior to the lesson series, the SGS-Tool was explained to the two SGS teachers individually. During the lesson series, they were coached on the job by the first author so that they could make connections between their learning about working with the tool and their classroom practices (Borko et al., 2010). Directly after each lesson, the use of the tool was discussed with each teacher, and questions were answered. The focus of these conversations was on the experiences with the SGS-Tool and the observations of the first author who attended all lessons. The teachers were asked whether and how they had been able to use the tool during the lesson and whether they had encountered any difficulties in doing so.

The SGS teachers instructed their groups to work together, explain the concepts, show/tell their work to each other, ask each other about their mathematical ideas, ask each other for explanations, and critique one another’s work. The teachers who did not use the tool were instructed to execute the lesson series as they normally would. They were not familiarized with the tool.

Lesson series on Early Algebra

Students worked on a lesson series of 12 60-minute lessons on Early Algebra over five weeks. Five lessons were replaced with lessons explicitly designed to invoke mathematical discussion and to increase the students’ level of mathematical knowledge (Calor et al., 2020). The lessons involved tasks that were close to or adaptations of the regular assignments from the textbook. The tasks were developed (Calor et al., 2020) according to the design principles of Palha et al. (2013), which focus on gaining a deeper understanding of mathematics through reflection on mathematical activities (Freudenthal, 1991). Reflection, in turn, is induced by mathematical discussions (Dekker & Elshout-Mohr, 2004; Palha et al., 2013).

These design principles are as follows:

1. “the designer is guided by the learning goal of a deeper understanding of mathematics”

2. mathematics has to start at a level that is experientially real to the students and

3. reflection can be induced through mathematical discussions” (Palha et al., 2013, pp. 148–149).

In this study, the learning goal is to gain a deeper understanding of Early Algebra, particularly formulae. A reoccurring problem with learning Early Algebra is that students find it difficult to associate patterns in a situation with formulae (Kieran, 1992; Sfard & Linchevski, 1994; Van Stiphout et al., 2011). Janvier (1987) defined algebra representations, situations, graphs, tables, and formulae as describing the relation between two variables in a formula. He stated that switching between these representations is best learned in a pairwise manner. For example, students should first learn how to construct a formula from a situation, followed by constructing a situation from a formula, or vice versa. The tasks in the lessons contained all possible switches to representation formulae. If, for example, a regular task contained a switch from situations to formulae, we added a switch from formulae to situations to the adapted task. In Figure 2, we provide examples of conventional tasks (Moderne Wiskunde 1A, 2012a; Moderne Wiskunde 1B 2012b), and we provide their adapted counterparts in Figure 3.

Figure 2. Conventional task.

Figure 3. Adapted task based on conventional tasks 1 and 2.

During the five lessons, students worked collaboratively on the same assignment. Each lesson started with a 10-minute introduction provided by the teacher (all teachers were given the same instructions on how to introduce the lessons), which was followed by the students working collaboratively for 50 minutes. These lessons were used for our data collection purposes. During the remaining lessons, students sat together in the same groups and worked on regular assignments from the textbook.

All four teachers implemented the lessons as intended. An implementation check was performed by the first author or by a research assistant during the lessons (to determine whether the teachers followed the lesson plans) and afterward by reviewing a videotape of the lessons. The student groups in the SGS group and the non-SGS group were able to finish the assignments on time, and some students (from both groups) finished up to five minutes early. During the remaining time, these students chatted about personal matters that did not involve mathematics. No classroom problems occurred.

Data collection and instruments

We videotaped the interactions of each teacher with one randomly selected group in each class during the five lessons. Prior to data collection, each group was videotaped during one lesson so that students could become accustomed to being videotaped. The recordings were transcribed and divided into fragments, which were then divided into turns. An interaction fragment starts when a teacher arrives at a group and ends when the teacher leaves. Following Van de Pol (2012), a turn is defined as an utterance made by a student or teacher that lasts until another student or teacher says something. Our dataset includes 45 interaction fragments consisting of 969 turns (SGS group: 30 fragments, 683 turns, 239 of which are teacher turns; non-SGS group: 15 fragments, 286 turns, 121 of which are teacher turns).

To determine the practical usability of the SGS-Tool, we asked both teachers working with the SGS-Tool the following questions in a semistructured interview: 1) whether they found the tool usable, 2) whether they liked working with the SGS-Tool, and 3) whether they had missed any steps in the tool or found any steps unnecessary. The interviews lasted approximately one-half hour.

Analysis

Following Van de Pol, Volman, Elbers and Beishuizen (2012), who used the CTM for a qualitative description of teachers’ scaffolding behavior, we used the SGS-Tool for a qualitative description to identify what steps the teachers were and were not taking. We developed a coding scheme for coding the teachers’ turns according to the steps of the SGS-Tool (Table 2). The unit of analysis was a teacher’s turn in an interaction fragment. Since the focus of this study was on the scaffolding behavior of the teachers, we omitted student turns. We coded the turns according to the steps of the SGS-Tool as presented in Table 2.

Table 2. Coding scheme used for steps of the Small-Group Scaffolding Tool.

Steps	Description	Examples in this study
Step 1 Determining whether the group’s maximum level of understanding has been reached	Determining if the question is a question of the whole group or not	Are you asking a question of the group? Do you all think that this is correct?
Step 2 Diagnosing the group’s maximum level of understanding	Determining the group’s actual level of understanding	What has been your reasoning about your formula until now? What is your story?
Step 3 Checking the diagnosis	Checking whether the diagnosis was correct; summarizing student comments	Are you asking how you should write the arrow chain down? Do you think that it is correct to multiply the outnumber by 6 and then add 140?
Step 4 Providing contingent mathematical content support	Providing mathematical content support adapted to the group’s level of understanding	No, that 15 is my day of birth, isn’t it? So, the 15 that I added, is that the same for everyone?
		You should have an innumber and outnumber, and you should create an arrow chain that corresponds to your party.
Step 5 Checking whether the group is able to continue the discussion on its own	Checking whether at least one student has developed an understanding from the content support given	T: Did I solve the problem? S1: Yes T: Please explain it to me.
Step 6 Providing process support	Encouraging the student(s) to explain and show/tell their work to one another.	T: Have you heard what S1 said? S3 and S4: No T: S1, say it again. Leo, explain that to John.

We also coded the interactions when a teacher approached and discovered a mathematical error. Such interactions occurred 9 times between the SGS group and the non-SGS group. In such an instance, a turn was coded as step 1 when the teacher was determining whether the error was an error of the whole group. Coding a turn as step 4 (providing contingent mathematical content support) involved two steps. First, we coded a teacher turn as mathematical content support when the support involved mathematical content. Second, we used a coding scheme developed by Van de Pol (2012) to code that step 4 turn as contingent or not contingent. According to this coding scheme, a teacher’s content support is considered contingent when the level of control maintained by the teacher increases after a student demonstrates poor understanding and decreases after a student demonstrates good understanding. Control refers to the degree of regulation a teacher exercises through his or her support. The unit of analysis is a three-turn sequence (a teacher turn, a student turn, and a teacher turn). Teachers’ turns were coded according to the degree of control. The degree of control ranges from 0 to 5. A value of 0 denotes no control (the teacher is not with the group). A value of 1 (lowest level of control) is assigned when broad and open-ended questions are asked without providing new content. A value of 2 (low level of control) is assigned when a slightly more detailed question is asked without providing new content. A value of 3 (medium level of control) is assigned when a short response is elicited without providing new content. A value of 4 (high level of control) is assigned when a hint is given, when a suggestive question is asked or when new content is provided. Finally, the highest level of control, 5, is applied when the answer to a question is provided. Students’ turns were coded according to their level of understanding (poor or no understanding, partial understanding, or good understanding). Students’ mode of expression was also measured (claim vs. demonstration). See Tables A1–A3 of Appendix A for the coding scheme developed by Van de Pol (2012) for coding the teachers’ level of control, students’ level of understanding and students’ mode of expression. These coding schemes were adapted by applying examples taken from this study. Contingency was determined by using contingency rules (see Table A4 of Appendix A for the contingency rules adopted when students demonstrated their understanding, and Table 6 for a sample excerpt of the contingent mathematical support provided, including the codes used). When students claimed to understand or not understand, exceptional coding rules were used to code contingency (Van de Pol, 2012).

Table 3. Frequencies and percentages of different steps (utterances) of the SGS-Tool that teachers of the SGS and non-SGS group applied.

	SGS group		Non-SGS group
	Teacher 1	Teacher 2	Teacher 3	Teacher 4
Steps	Frequency (%)	Frequency (%)	Frequency (%)	Frequency (%)
Step 1	12 (9.2)	8 (7.3)	0 (0)	0 (0)
Step 2	22 (16.9)	11 (10.1)	12 (12.8)	1 (3.7)
Step 3	0 (0)	0 (0)	0 (0)	0 (0)
Step 4	63 (48.5)	57 (52.3)	74 (78.7)	22 (81.5)
Step 5	9 (6.9)	17 (15.6)	3 (3.2)	2 (7.4)
Step 6	24 (18.5)	16 (14.7)	5 (5.3)	2 (7.4)
Total	130 (100)	109 (100)	94 (100)	27 (100)

Step 1 (Determining whether the group’s maximum level of understanding has been reached), Step 2 (Diagnosing the group’s maximum level of understanding), Step 3 (Checking diagnosis), Step 4 (Providing contingent mathematical content support), Step5 (Checking whether the group can continue discussions on its own), Step 6 (Providing process support).

Table 4. Absolute frequencies and percentages of contingent content support provided (step 4) in both groups.

	SGS group			Non-SGS group
	Frequency (%)			Frequency (%)
	Teacher 1	Teacher 2	Total	Teacher 3	Teacher 4	Total
Contingent	30 (47.6)	31 (54.4)	61 (50.8)	36 (48.6)	4 (18.2)	40 (41.7)
Non-contingent	25 (39.7)	14 (24.6)	39 (32.5)	32 (43.2)	9 (40.9)	41 (42.7)
No Code	8 (12.7)	12 (21.1)	20 (16.7)	6 (8.1)	9 (40.9)	15 (15.6)

Table 5. Sequences of steps taken by teachers in both groups.

	SGS group		Non-SGS group
Fragment	Teacher 1	Teacher 2	Teacher 3	Teacher 4
1	144444456	1244656	44444	44
2	16	1244445554	2444444444444	4
3	24444644445	24454	444444	44444444
4	26646	1224444454	24444442444444	42
5	12245	1464	445	4
6	445	1244444454444	44444	54444
7	224	126	44444222444	4
8	124444	12444445	24444	4444
9	1244466	1244454445	266	56
10	444454644	4444	244444454	6
11	12446446	444444566	44444
12	124444444	56526	562444
13	1244544	244454666666644545465	266
14	12546445444		2444
15	26		44
16	2166666666
17	21224464
18	412
19	26
20	2224444465

Table 6. Contingent mathematical content support excerpt in the SGS group including codes for the teacher’s degree of control (TDc), student understanding (SU), student modes of expression (SM) and contingency (C).

	Turn	TDc	SU	SM	C
1	T: (The teacher has not arrived yet).	TDc0
2	T: Are you progressing?	TDc1
3	S4: No.		SU0	SM0	NC
4	S2: No.		SU0	SM0	NC
5	S3: No, we do not really have a story.		SU0	SM2	C
6	S2: We don’t have a story, but we do know the formula.		SU0	SM2	C
7	T: You know a formula?	TDc3
8	S2: Yes.		SU1	SM0	C
9	T: How does it look like?	TDc2
10	S3: Times 5 plus 20.		SU1	SM1	C
11	T: Okay, given that, what can you come up with, what kind of stories?	TDc2
12	S2: Have the handyman.		SU1	SM1	C
13	T: What?	TDcNOC
14	S2: I only have the handyman.		SU1	SM1	C
15	S1: Yes, but we also had donuts yesterday.		SU1	SM1	C
16	S4: We also have donuts.		SU1	SM1	C
17	S2: Yesterday, we had …		SUX	SM1	C
18	T: So you had that already yesterday. Okay, what kinds of examples does the textbook include?	TDc4
19	S4: People who buy donuts.		SU2	SM1	C
20	T: People who buy donuts, okay.	TDc3
21	S3: But, there it says 20 euros (pointing to 20 at the intersect of the graph with the y-axis).		SU1	SM1	C
22	S2: Yes, but …		SU1	SM1	C
23	S4: Yes, what could that 20 be for?		SU1	SM0	NC
24	S2: And who is … no …		SU1	SM1	C
25	T: But, you also had stories about a swimming pool, didn’t you?	TDc4
26	S4: No, but that is …		SUX	SM1	NC
27	S3: And golf.		SU1	SM1	C
28	T: Zoo, golf.	TDc4
29	S2: Oooooh, membership (relieved because she understands the hint about the swimming pool exercise).		SU2	SM1	C
30	T: Try to be a little creative (slowly walking backwards).	TDc3
31	S3: Why membe, membership? (S3 talks to S2, after seeing that S3 has asked S2 about the membership, for which the 20 at the intersection with the y-axis could be used; the teacher walks away).		SUX	NoCode	NoCode
32	(The teacher walks away).	TDc0

Teacher’s degree of control (TDc): TDc0 = no control; TDc1 = lowest control, TDc2 = low control, TDc3 = medium control, TDc4 = high control, TDc5 = highest control. Student’s understanding (SU): SUNOC = not on content, SU0 = poor or no understanding, SU1 = partial understanding, SU2 = good understanding. Student’s mode of expression (SM): SUNOC = none, SM0 = claim of understanding, SM1 = demonstration minimal, SM2 = demonstration extensive. Contingency (C): C = contingent, NC = not contingent, NoCode = no code (see Tables A1–A4 of the Appendix and Van de Pol, 2012).

The number of students who participated in teacher–small-group interactions during an interaction fragment was counted.

All turns were coded with the Multiple Episode Protocol Analysis software program (Erkens, 2002). The interrater reliability between two coders (first and second author) regarding teacher turns was determined (approximately 10% of the data; 70 teacher turns of the SGS group, 32 of the non-SGS group). A high level of interrater reliability agreement was observed (91%), and based on the Fleiss kappa benchmark (El Emam, 1999) a good Cohen’s kappa value was also obtained (.82). The first author independently coded the rest of the data.

For the coding of contingency for Step 4 of the SGS-Tool, interrater reliability was determined using two steps by two coders (first author and a research assistant) over 249 turns (25% of the data): 110 teacher turns and 139 student turns; 147 turns were observed in the SGS group and 102 turns in the non-SGS group. In the first step, interrater reliability was determined for the students’ mode of expression (SM), the students’ level of understanding (SU) and the teachers’ degree of control (TdC). Interrater reliability agreement percentages were measured as 79.1% (good) for SM, 79.9% (good) for SU, and 87.1% (very good) for TdC. Cohen’s kappa values were determined according to the Fleiss kappa benchmark (El Emam, 1999) and were .71 (good) for SM, .73 (good) for SU and .95 (high) for TdC. In the second phase, the two coders discussed differences in the assigned codes and reached agreement on the codes to be used. Then, interrater reliability between the two coders for contingency was determined. In total, 112 three-turn sequences were independently coded as contingent, not contingent, or impossible to code (not assigned a code). Interrater agreement was measured at 96.8% (high), and Cohen’s kappa was measured at .95 (high). The research assistant independently coded the remaining data with respect to contingency.

We tested whether mathematical content support was contingent, and used frequency analyses and relative frequency cross-table analyses to detect differences between the SGS and non-SGS group.

Results

In this section, we first describe the performance of the teachers working with the SGS-Tool on the various steps (expectations 1, 3a, 4a, and 4b) and whether they performed these steps more often than teachers not working with the tool. Next, we describe whether the content support given by SGS and non-SGS teachers was contingent (expectation 3c) and whether teachers in the SGS group gave more contingent support than non-SGS teachers. Furthermore, we describe the combination of steps as formulated in Expectations 2, 3b, and 4c. Finally, we discuss three examples of teacher–small-group interaction (two in the SGS group and one in the non-SGS group) with respect to characteristic small-group scaffolding behavior.

Performance of SGS and non-SGS teachers (expectations 1, 3a, 4a, and 4b)

In Table 3, we show the absolute frequencies and percentages of the steps of the SGS-Tool applied by teachers in both groups.

The total number of utterances differed between the teachers and varied from 27 (Teacher 4) to 130 (Teacher 1). Teachers using the SGS-Tool had turns involving the various steps, with the exception of step 3. For SGS Teacher 1 and SGS Teacher 2, step 1 occurred in approximately 9 and 7% of the contributions, step 2 occurred in approximately 17 and 10% of the contributions, step 5 occurred in approximately 7 and 16% of the contributions, and step 6 occurred in approximately 19 and 15% of the contributions, respectively. Step 4 occurred most often, marking approximately half the contributions of the SGS teachers.

Table 3 shows that the teachers of the SGS group provided more support overall than teachers who did not use the SGS-Tool. Non-SGS Teacher 4 hardly provided any support. Furthermore, the relative frequencies (percentages) suggest a similar pattern in the two SGS teachers, a pattern that was distinct from that of the non-SGS teachers. Most utterances in the SGS group were coded as step 4 (approximately 50%). However, the percentage of step 4 utterances was higher in the non-SGS group (approximately 80%). Step 1 occurred in the SGS group but not at all in the non-SGS group. Steps 2, 5 and 6 seemed to occur more often in the SGS group than in the non-SGS group. Step 3 did not occur at all. From the above, we conclude that expectations 1 (concerning step 1: determining whether the group’s maximum level of understanding has been reached), 3a (concerning step 4: providing mathematical content support), 4a (concerning step 5: checking whether the group can continue discussions on its own), and 4b (concerning step 6: providing process support) about the SGS teachers’ scaffolding were confirmed.

To determine whether the differences in the relative frequencies between the SGS group and non-SGS group were significant, we used cross-tables and calculated the two-sided $p$ values for Fisher’s exact test (Agresti, 1992). We determined whether the relative frequencies of step 1 and non-step 1 (the sum of frequencies of steps 2, 3, 4, 5, and 6), step 5 and non-step 5 (the sum of frequencies of steps 1, 2, 3, 4, and 6), and step 6 and non-step 6 (the sum of frequencies of steps 1, 2, 3, 4, and 5) differed between the two groups; see Tables B1–B3 in Appendix B for the cross-tables. The relative frequencies in the SGS group were significantly higher for step 1 ($p=.001$), step 5 ($p=.045$), and step 6 ($p=.004$) than for the non-SGS group.

We expected that teachers using the SGS-Tool would show more variation in the steps, which would result in a lower relative frequency of step 4 than that of teachers not using the SGS-Tool.

Finally, we applied a cross-table method (Table B4 in Appendix B) to determine whether the relative frequency of step 4 vs. non-step 4 (the sum of the frequencies of steps 1, 2, 3, 5, and 6) differed between the SGS and non-SGS groups. The relative frequency of step 4 was significantly lower for the SGS group ($p<.001$).

Contingency of content support of SGS and non-SGS teachers (expectation 3 c)

The analyses above revealed that teachers working with the SGS-Tool used step 1, step 5, and step 6 more often than teachers who did not use the tool. Step 4 (providing content support) occurred less often in the SGS group. The next question, however, is whether this content support was more contingent in the SGS group than in the non-SGS group (expectation 3c).

The frequencies and percentages of contingent content support given by the teachers of the SGS and non-SGS groups are shown in Table 4.

The results show that there were no large differences between the amount of contingent mathematical content support given by teachers 1, 2 and 3. Teacher 4 provided less contingent support than the other teachers.

We applied a cross-table method to determine whether the relative frequencies of contingent vs. non-contingent interactions differed between the SGS and non-SGS groups (Appendix B Table B5). The relative frequency of contingent content support was not higher in the SGS group ($p=.134$). Thus, it seems that there was no difference between the groups in terms of the amount of contingent content support given, which is not in line with expectation 3c.

Combinations of steps (expectations 2, 3b, and 4c)

Table 5 presents the sequence of the steps taken by the teachers during each interaction fragment, starting when the teacher arrived at a group and ending when the teacher left the group.

Table 5 shows considerable variation in the length of sequences (1 to 21 steps) and in the steps used. The sequences in the SGS group included more steps than the sequences in the non-SGS group, where step 4 occurred most often. In the sequences by SGS Teacher 1, step 1, step 4, step 5 and step 6 were often taken multiple times. Although the steps used by SGS Teacher 1 varied considerably, the same patterns occurred in the sequences of steps the teacher took. The sequences of SGS Teacher 2 seem similar to those of Teacher 1 but were less pronounced.

In the sequences of steps taken by non-SGS Teacher 3, step 4 occurred more often than they did with SGS teachers 1 and 2. In addition, step 1 did not occur at all. The sequences of the steps taken by non-SGS Teacher 4 were similar to those taken by non-SGS Teacher 3 but were more pronounced. Non-SGS Teacher 4 applied step 4 most often, and step 1 did not occur at all.

Sequences including only step 2 and step 4 occurred in both groups; however, they occurred less often in the SGS group. The combination of step 1, step 2, and step 3 (expectation 3b) did not occur at all, as step 3 did not occur in any group. However, the combination of step 1 and step 2 did occur in the SGS group but not in the non-SGS group. The combination of step 1 and step 6 (expectation 2), occurred in the SGS group and not in the non-SGS group. Additionally, the combination of step 4, step 5, and step 6 (expectation 4c) occurred in the SGS group but not in the non-SGS group. From the above, we conclude that, as expected, the combination of step 1 and step 6 (expectation 2) and the combination of step 4, step 5, and step 6 (expectation 4c) occurred in the SGS group. Only the first two steps in the combination of step 1, step 2, and step 3 (expectation 3b) occurred in the SGS group.

Examples of scaffolding behavior with and without the SGS-Tool

Example excerpt from the SGS group including steps 1 and 6 of the SGS-Tool

The following excerpt serves as an example of teacher support that applies step 1 (determining whether the group’s maximum level of understanding has been reached) and step 6 (providing process support) of the SGS-Tool in the SGS group, a combination shown only in the SGS group. In this example, the teacher provided process support once she had determined that the maximum level of understanding of the group had not been reached (the first characteristic of small-group scaffolding at the group level during mathematical discussions). Before student 3 asked a question, the teacher explained the concept of arrow chains using the example of the cost of a party. The students were then asked to work on an assignment in which they needed to calculate the cost of a party and create an arrow chain for the expenses. The students asked the teacher for help because they could not agree on what kind of a party to use for their assignment. The teacher explained to the group that it did not truly matter what kind of party was involved as long as they determined the cost of that party and created an arrow chain that corresponded to the expenses. The teacher also stated that the arrow chain had to contain an innumber and outnumber. As the teacher walked away, student 3 asked the teacher what an innumber was.

Student 3:

But, miss, what is an innumber?

Teacher:

Who here knows what an innumber is (pointing to students 1, 2 and 4)? [step 1]

Student 1:

5 (student 2 raises his hand).

Teacher:

Student 2, explain that to student 3. [step 6]

Student 2:

For example, if you buy 5 drinks, then the innumber is 5.

Student 4:

Is that the innumber, that 5?

Student 2:

5 is the innumber (the teacher nods and walks away).

The above excerpt serves as a good example of teacher support using step 1 and 6. The teacher first checks whether one of the other students in the group knows what an innumber is. When none of the students know what the answer is, the question is a question from the whole group and not only from student 3. By first checking whether one of the other students in the group knows what the innumber is, the teacher applies step 1 (determining whether the group’s maximum level of understanding has been reached) of the SGS-Tool. After students 1 and 2 acknowledge that they know what the innumber is, the teacher asks student 2 to explain what the innumber is to student 3. By doing so, the teacher provides process support (step 6), i.e., asking student 2 to perform the key activity of explaining the concept. When the teacher is satisfied with the explanation, she returns responsibility for learning to the group (by nodding and walking away).

Example excerpt from the non-SGS group that involves step 4 of the SGS-Tool

The following excerpt serves as an example of teacher support provided in the non-SGS group that applies step 4 of the SGS-Tool and in which steps 1 or 6 are typically not included. Two students in a group of four were working on the same assignment as the students from the previous excerpt. The other two students were not engaged with the assignment. The two working students were unsure whether their arrow chain should include more expenses than the cost of entry to the party and consumption items.

Student 4:

Teacher, do we have to incorporate more expenses than cost of entry and consumption items?

Teacher:

Well, now you can make an arrow chain. What is the innumber? [step 4]

Student 4:

Is 2 euros.

Teacher:

Number of consumption items? Times? [step 4]

Student 2:

Oh, 3, 3 consumption items.

Student 4:

3 consumption items, and the number of euros is 2.

Teacher:

No, you should leave that open, so consumption items is your innumber. Write down, number of consumption items arrows, times … [step 4]

Student 4:

2.50.

Teacher:

Times 2.50. Then, you have a betweennumber plus … [step 4]

Student 2:

Plus entrance, oh like that.

Teacher:

Look, there you have it, literally. The innumber, the arrow with multiplication, the betweennumber, and the addition. [step 4]

Student 2:

Yes (the teacher walks away).

The teacher in this excerpt only gives mathematical content support, applying step 4 of the SGS-Tool. He continues to do so until the assignment is completed. In addition, the teacher does not determine whether the question is a question of the whole group (step 1) and does not involve the other two students in the group in the mathematical discussion (step 6).

Example excerpt from the SGS group that includes step 4 (provide contingent mathematical support at the group level)

Table 6 presents an example of contingent mathematical support, including codes, in the SGS group. Four students in a group were working on an assignment in which they were asked to create a formula and come up with a story corresponding to a graph they were given. The graph includes a straight line with a slope of 5 and that intersects with the y-axis at 20. The axes were purposely left unlabeled so that students could think of their own labels when creating their story. Prior to the excerpt, all four students were engaged in a mathematical discussion about their story. They had quickly found the right formula but were struggling with the story. The students told each other the stories that they had come up with. They critiqued their own and each other’s stories. The students were not able to correctly incorporate the intersection with the y-axis at 20. One student, for example, told a story involving getting paid 5 euros for one hour of work to the other students but then quickly corrected himself by wondering out loud if one would be paid 20 euros for 0 hours of work. Another student came up with a story about gummy bears (candy) with 20 cents being paid for 0 gummy bears and 25 cents paid for 1 gummy bear. The whole group agreed that this was not possible. The mathematical discussion went on for five minutes, but the group remained stuck and could not proceed with the assignment. After a period of time, the teacher approached the group and asked how the group was progressing.

This excerpt shows that the students at several instances either partially (SM1) or extensively (SM2) demonstrated what they were thinking. In response, the teacher increased control when the students demonstrated a poor understanding, applied the same or a higher level of control when the students demonstrated a partial understanding and decreased control when the students demonstrated a good understanding. In other words, the teacher in this example mostly gave contingent mathematical content support.

The excerpt also shows that the teacher stopped providing mathematical content support (phasing out) after line 29, when it was clear that student S2 had understood the hint that the teacher provided on line 25. On line 25, the teacher reminds the students that they had previously worked with assignments from the textbook that involved stories on the costs of swimming at swimming pools. These costs included the cost of the number of swimming pool visits and of a yearly membership. Student S2 understood the hint and discovered that the intersection with the y-axis at 20 could be used in a similar way as the cost of a membership from the swimming pool assignment.

After the teacher stopped providing mathematical content support, the group’s mathematical discussion continued on line 31 when student S3 asked student S2 to explain the idea of membership. After seeing that the mathematical discussion had recommenced, the teacher returned responsibility for learning to the group by walking away.

Student participation (expectation V)

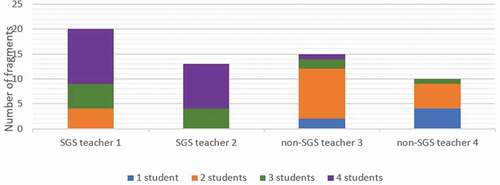
We expected that the use of the SGS-Tool would result in more students participating in the teacher–small-group interactions. Figure 4 shows the number of different students who engaged in the teacher–small-group interactions within the SGS and non-SGS groups.

Figure 4. Number of students involved in teacher–small-group interaction in both groups.

Figure 4 shows that more students were involved in the teacher–small-group interactions during a given fragment with a teacher in the SGS group than with a teacher in the non-SGS group. In the SGS group often four students participated, whereas that did not occur at all in the non-SGS group. In the non-SGS group interaction with only one student occurred, whereas that did not happen in the SGS-group.

A $t$-test that compared two averages at a 95% confidence interval was used to compare the mean number of students who participated in the teacher–small-group interaction in the SGS group and non-SGS group. The test revealed that significantly more students actively participated in the teacher–small-group interaction with the SGS teachers $(t\left(56\right)=7.96,p<.001)$ than the non-SGS teachers. The average number of students in a small group who participated in the teacher–small-group interactions during a fragment was 3.48 for the SGS group ($SD0.71$,$n=33$) and 1.96 for the non-SGS group ($SD0.73$, $n=25$).

Teacher experiences

To determine the practical usability of the SGS-Tool, we asked the teachers to describe how they viewed the tool. The teachers stated that they were able to work with the SGS-Tool, the tool was clear and quite important for supporting small groups, they had not skipped any steps within the tool, and all of the steps of the tool were necessary. Teachers also indicated that they were able to perform step 3 and determine each group’s level of understanding but that it was difficult to refrain from providing too much mathematical content support in step 4. The teachers found it especially difficult to determine what amount of support was enough and what amount was too much. Teachers stated that when they gave too much support, the discussions stopped and that when this occurred, it was easy to forget to check whether at least one of the students had understood the information provided through the support, i.e., to check whether the group could continue the discussion on its own (step 5) and encourage the students to help each other (step 6) (because there was no longer a need for these steps). The teachers also indicated that any teacher would be able to work with the tool if the teacher learned to refrain from providing answers immediately once interaction commences. In addition, the teachers stated that they were already adopting some steps of the SGS-Tool in everyday practice. For example, they reported already diagnosing individual students’ levels of understanding when the students asked questions (step 2 of the tool, but applied with individual students) and evaluating whether such diagnoses are correct (step 3 of the tool).

Conclusions and discussion

Collaborative learning is considered important for mathematics learning, but supporting students during this process is difficult for teachers (Van Leeuwen et al., 2015; Webb, 2009). This is particularly true for providing support at the group level that stimulates an ongoing discussion about a mathematical problem in the group. Support at the group level ideally involves providing mathematical content support when the group cannot continue the discussion independently but refraining from giving content support when there are members in the group who might be able to move the discussion forward, e.g., by explaining the next steps toward a solution of the problem to their fellow students. We considered three aspects that make teacher support of small groups during collaborative learning difficult. Teachers need to 1) decide which type of support to provide, 2) exercise the correct degree of control when providing mathematical content support, and 3) determine when to return control over the learning process to the group. We developed the SGS-Tool to support teachers in scaffolding small groups at the group level. The tool consists of six steps: 1) determining whether the group’s maximum level of understanding has been reached, 2) diagnosing the group’s maximum level of understanding, 3) checking the diagnosis, 4) providing contingent mathematical content support, 5) checking whether the group can continue on its own, and 6) providing process support. The steps of the SGS-Tool may help teachers decide what type of support to give (first challenge teachers face), when mathematical content support can stop (second challenge for teachers), and when and how to return responsibility for learning to the group (third challenge).

In this exploratory study, we investigated whether working with the SGS-Tool in fact helped teachers address some of the challenges they face when supporting small groups discussing mathematics. The results of a comparison between the scaffolding behavior of teachers who used the SGS-Tool and that of teachers who did not indicates the SGS-Tool offers teachers a certain degree of support in addressing such challenges by suggesting concrete steps for teachers to follow. We will first reflect on the extent to which the SGS-Tool provided assistance to teachers facing the challenges of supporting small groups during collaborative learning. Next, we present the adapted SGS-Tool. Finally, we discuss the limitations, main contribution to the field, practical implications of our study and suggest avenues for future research.

The SGS-Tool: An answer to challenges in supporting groups?

Challenge 1: Teachers have to decide which type of support to provide

The first challenge teachers face, deciding which type of support to provide, involves determining whether the group’s maximum level of understanding has been reached and then choosing to provide either process support or mathematical content support. The SGS-Tool seems to offer a degree of support regarding this challenge by suggesting whether content or process support is appropriate, whereupon the teacher can provide that type of help.

We expected that SGS teachers would determine whether the student group’s maximum level of understanding had been reached (step 1, operationalized expectation 1) because this enables them to make an informed choice between providing process support (when the maximum level of understanding has not been reached) and providing contingent mathematical content support (when the maximum level of understanding has been reached), or in other words, to be contingent on the group, the first key characteristic of small-group scaffolding at the group level. The SGS teachers indeed used step 1 significantly more than non-SGS teachers. This confirms expectation 1.

Nevertheless, a number of sequences of SGS teachers did not start with step 1 (Table 5). An explanation might be that teachers did not find this step necessary, when it was apparent to them (either by observing the activities of the group or by statements students made) whether the group had reached its maximum level of understanding. In those cases, teachers started with step 2 (diagnosing the group’s maximum level of understanding) or with step 6 (providing process support).

In addition, we expected that SGS teachers would choose to give process support when the group’s maximum level of understanding had not been reached (the combination of step 1 and step 6, operationalized expectation 2). Here, process support is preferred over content support because the group is able to reach a higher level of understanding on its own. The SGS teachers indeed used a combination of step 1 and step 6 more than the non-SGS teachers. The combination did not occur at all in the non-SGS group. However, the combination occurred only sparsely in the SGS group. A possible explanation might be that there was no need for the combination because most questions asked were questions of the entire group, i.e., the maximum level of understanding had been reached. We, therefore, confirm expectation 2.

Furthermore, we expected that the SGS-Tool would help teachers make the right choice, i.e., give mathematical content support when the maximum level of the group’s understanding had been reached (step 4, operationalized expectation 3a, including the combination of step 1, step 2, and step 3, operationalized expectation 3b). Here, content support is preferred over process support because the group is not able to reach a higher level of understanding on its own. Step 4 did occur in the SGS group, but it occurred significantly more often in the non-SGS group. This is an indicator that using the SGS-Tool might have helped the SGS teachers choose to give not only content support (step 4) but also process support (step 6), i.e., make the choice of what type of support to give. We, therefore, confirm expectation 3a. We assume that, even though step 4 occurs the most frequently in both groups, there was a qualitative difference between the groups because step 4 was more often preceded by the previous steps of the SGS-Tool in the SGS group, while these steps were omitted in the non-SGS group. The combination of step 1, step 2, and step 4 did occur in the SGS group (and not in the non-SGS group). This shows that the SGS teachers gave mathematical content support when the maximum level of understanding of the group had been reached. Step 3 did not occur at all. However, SGS teachers reported in the interviews that they often performed this step in their minds. We, therefore, confirm expectation 3b hesitantly.

Challenge 2: Exercising the correct degree of control when giving mathematical content support

Exercising the correct degree of control, i.e., deciding how much mathematical content support to give involves providing contingent mathematical content support when appropriate and phasing out mathematical content support. The SGS-Tool seems to support teachers in addressing this challenge.

We expected SGS teachers to give contingent mathematical content support (operationalized expectation 3c), i.e., build upon the mathematical ideas of the group and refrain from giving too much mathematical content support. With regard to the contingency of the content support offered, however, no differences appeared between the two groups. Therefore, our findings are not in line with expectation 3c.

We expected SGS teachers to check whether the group could continue the discussion on its own (step 5, operationalized expectation 4a). At the moment that a group can continue discussing on its own, teachers can stop providing contingent mathematical content support, i.e., mathematical content support can be phased out (the second key characteristic of small-group scaffolding at the group level). Step 5 occurred significantly more often in the SGS group. This confirms expectation 4a.

Challenge 3: Teachers have to determine when to return control over the learning process to the group

This challenge involves returning responsibility for learning to the group when a group can continue its discussion independently. The SGS-Tool seems to help teachers address this challenge.

We expected that SGS teachers would return responsibility for learning to the group (the third key characteristic of small-group scaffolding) by giving process support (step 6, operationalized expectation 4b), after providing contingent mathematical content support, checking whether the group could continue discussions on its own, and phasing out content support once the group was able to continue the discussion on its own (combination of step 4, step 5, and step 6, operationalized expectation 4c). Step 6 indeed occurred significantly more frequently in the SGS group. We, therefore, confirm expectation 4b. The combination of step 4, step 5, and step 6 occurred sparsely in the SGS group but not at all in the non-SGS group. An explanation for this sparse occurrence might be that SGS teachers reported in the interviews that they found it hard to refrain from giving too much content support and that when they did give too much content support, the discussions stopped altogether. This made it easy for them to forget to check whether the group could continue the discussion on its own and return responsibility for learning to the group because there was no need to do so anymore. We, therefore, are hesitant to confirm expectation 4c.

However, we argue that other combinations of steps and repetitions of combinations, e.g., a combination of step 4 and step 5 (providing mathematical content support and checking whether the group can continue on its own, repetition 4,454,445) and a combination of step 4 and step 6 (providing mathematical content support and providing process support, repetition 446,446), are indications of teachers determining when to return control over the learning process to the group. In addition, as illustrated in the example excerpt in Table 6, the SGS teachers stayed with the groups and listened whether the mathematical discussions indeed continued. When discussions continued, they ended the interaction, i.e., returned responsibility for learning to the group by leaving the group without providing process support (step 6). The combination of step 4 and step 5 occurred twice in the non-SGS group, but in that case, the non-SGS teacher gave mathematical content support until the problem was solved, and they did not return responsibility when it would have been possible. They also mostly gave mathematical content support to one or two students in the group, while the SGS teachers mostly gave content support to the whole group.

Reflection on the contribution of the SGS-Tool

The SGS-Tool seems to help teachers address the three challenges teachers face when guiding students during collaborative learning. As we expected, the SGS teachers determined more than the non-SGS teachers whether the student group’s maximum level of understanding had been reached. The SGS teachers also chose to give process support when the group’s maximum level of understanding of the group had not been reached, but this occurred sparsely. They provided mathematical content support (more than the non-SGS teachers) when the maximum level of understanding of the group had been reached, but failed to check the diagnosis of the maximum level of understanding. The content support the SGS teachers provided was as contingent as that of the non-SGS teachers. The SGS teachers checked whether the group could continue the discussion independently more than the non-SGS teachers. They also returned responsibility for learning to the group and phased out content support once the group was able to continue the discussion independently. However, this occurred sparsely.

We explain our findings as follows. Providing process support when the group’s maximum level of understanding had been reached might have occurred sparsely in the SGS group because the majority of questions asked were questions of the whole group (maximum level of understanding of the group had been reached). Furthermore, even though the SGS-Tool offers concrete steps for teachers to take, some aspects of the tool appeared to be more difficult for teachers to apply. First, none of the teachers verbally checked whether their diagnoses were correct (step 3), even though the teachers stated that they were able to perform step 3 and that this check was something that they normally did in their everyday practice when supporting individual students. It might be that they performed step 3 implicitly rather than verbally. Second, the teachers who worked with the SGS-Tool indicated that they found it difficult to determine the amount of contingent mathematical content support needed in step 4 to simulate the continuance of the discussion and found it hard to refrain from giving too much mathematical content support. The SGS teachers also indicated that when they did give too much content support, it was easy to forget to check whether the group could continue on its own and to provide process support to return responsibility for learning. This might explain why returning responsibility for learning by giving contingent mathematical content support, followed by checking whether the group could continue the discussion on its own and providing process support, occurred sparsely. Another explanation might be that the SGS teachers used other combinations of steps to return responsibility for learning. We argued that other (repetitions of) combinations, such as providing contingent mathematical content support and checking whether the group can continue the discussion independently, followed by listening for whether the discussion indeed continues, are also possible.

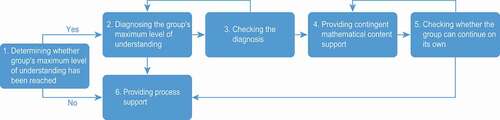
Adapted SGS-Tool

The sequences of steps the teachers took occasionally differed from the sequences outlined by the SGS-Tool. Taking this point and the preceding discussion into consideration, we adapted our SGS-Tool (Figure 5). We included loops between Steps 3 and 2 and between Steps 5 and 4. When teachers determine in Step 5 that the group cannot continue on its own, they are recommended to continue to provide contingent mathematical content support (Step 4). If the group is able to continue independently, teachers are recommended to phase out content support and return responsibility for learning to the group by providing process support (Step 6). Although Step 3 (checking the diagnosis) was not conducted by the teachers, we think it is an important step in scaffolding small groups because checking the diagnosis creates a common understanding or intersubjectivity (Van de Pol, Volman, Elbers & Beishuizen, 2012).

Figure 5. Adapted Small-Group Scaffolding Tool for mathematical discussions.

Limitations, main theoretical contribution to the field, practical implications, and future work

From the above, we conclude that the teachers’ scaffolding behavior in the SGS group differed from the teachers’ scaffolding behavior in the non-SGS group and that working with the SGS-Tool can improve teachers’ scaffolding behaviors at the group level. However, not all of our expectations were met. The fact that some of our expectations were met but others were not shows that the SGS-Tool is a contribution in this complex area but that it does not offer the final solution. It proved possible to change teacher practices with the help of the SGS-Tool in a short period of time and to improve the support they offered students during collaborative learning. Future research might focus on the scaffolding behavior of teachers who use the SGS-Tool for a longer period of time, e.g., a year. Our findings suggest that future approaches aimed at designing and implementing effective scaffolding strategies to support small groups can build on the SGS-Tool. However, more focus needs to be placed on helping teachers refrain from providing too much content support when appropriate, i.e., exercise the correct degree of control (the second challenge teachers face when guiding students during collaborative learning). Furthermore, future approaches might also focus on actions to return responsibility for learning to the group other, than those outlined by the SGS-Tool.

As this was the first exploratory study and only four teachers from one school participated, our findings need to be corroborated. Teacher 4 produced a much lower frequency of utterances than the other teachers and is something of an outlier in terms of frequency of utterances in this study. A larger sample of teachers in a replica study could shed light on whether this teacher was in fact an outlier. Furthermore, data were gathered for only one student group in the class, and teachers might have implemented the tool more strictly with this group than with the other groups. Nevertheless, our data enabled us to perform a detailed analysis of teachers’ scaffolding behavior.

With regard to the analyses, we were able to identify the steps of the tool in the teacher–small-group interactions, as the high interrater reliability showed. One drawback is that we were able to code only verbal utterances. It is possible that a teacher can utilize a particular step but not explicate it verbally, which might have been the case with checking the diagnosis in step 3. This also holds for the analysis of contingency; we could analyze only what occurred during the interactions. Previous lessons or a teacher’s knowledge of his or her students may affect a teacher’s actions but were not taken into account in this study. For this analysis, we encountered the same difficulties as those described by Van de Pol (2012). Complex contingency rules involve dealing with many different possibilities when, for example, no student understanding can be determined or when students claim that they understand but do not demonstrate their understanding. In addition, the coding scheme does not take into account whether the content of what a student has said is correct. It also does not take into account the differences among students’ difficulties or situations. Determining whether mathematical content support is contingent is complex and time consuming.

We consider our main theoretical contribution to the field of scaffolding research to be the extension of the key characteristics of scaffolding individuals in the context of group work (Van de Pol, Volman & Beishuizen, 2012) into the key characteristics of scaffolding small groups at the group level, particularly the extension of the key characteristic of contingency to an individual student to contingency to a group. We argued that contingency based on a group may entail either content support or process support, while in the literature, contingency based on an individual is only associated with content support (to be contingent upon, i.e., to adapt (or be responsive) to, the level of understanding of an individual student). In addition, content support is adapted to the maximum level of understanding of the entire group. Consequently, content support is given in what might be considered the group’s ZPD (Nyikos & Hashimoto, 1997). Furthermore, the key characteristics of fading and returning responsibility for learning to the group (instead of the individual learner) are also associated with the maximum level of understanding of the whole group. When the group is able to enhance its level of understanding on its own, content support is phased out, and responsibility for learning is returned to the group.

As far as the relevance of this work for practice is concerned, the study shows that the SGS-Tool helped teachers support groups of students during mathematical discussions, and the teachers confirmed that they felt supported/encouraged to help groups by stimulating mathematical discussions and to refrain from giving too much mathematical content support. Therefore, this work contributes to the understanding of how to help teachers implement the NCTM Process Standards (NCTM, 2000). In addition, the SGS-Tool can be used for mathematics teachers’ professionalization projects. Extra attention could be paid to the steps teachers are less inclined to conduct.

The next step would be to investigate working with the SGS-Tool on a larger scale involving more teachers, more schools, students from different grade levels, and to investigate the influence of the SGS-Tool on the quality of mathematical discussions and on students’ level of mathematical knowledge.

Acknowledgments

We give our sincere gratitude to Noreen M. Webb (Distinguished Professor, Department of Education, Graduate School of Education & Information Studies, UCLA), Alan H. Schoenfeld (Elizabeth and Edward Conner Professor of Education and Affiliated Professor of Mathematics at the University of California at Berkeley), and Janneke E. van de Pol (Assistant Professor at the Department of Education at Utrecht University, Netherlands) for providing valuable feedback on our Small-Group Scaffolding Tool. We also wish to thank the teachers and research assistant who contributed to our research. Finally, we would like to thank the editors and the anonymous reviewers of the Journal of the Learning Sciences for their constructive feedback, which enabled us to greatly improve this manuscript.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Correction Statement

This article has been republished with minor changes. These changes do not impact the academic content of the article.

Additional information

Funding

This work was supported by the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (Netherlands Organization for Scientific Research) under grant [number 023.002.088].

Appendix A

Table A1. Degree of teacher control.

Teacher degree of Control (TDc)	Description of teacher behavior	Examples taken from this study
Teacher not on content (TDcNOC)	Says something unrelated to the subject matter	Sit up straight
0 No control (TDc0)	Not with the group	Before the teacher approaches the group or after the interaction.
1 Lowest (TDc1)	Provides no new content Elicits an elaborate response Asks a broad and open question	Can you explain how you came up with this solution?
2 Low (TDc2)	Provides no new content Elicits an elaborate response, mostly for an elaboration or explanation of something (“why” questions) Asks a more detailed but still open question	Why do you think that this is the in-number?
3 Medium (TDc3)	Provides no new content Elicits a short response	Can you do that? Can you save 50 euros a week?
4 High (TDc4)	Provides new content Elicits a response Gives a hint or suggestive question	How many weeks do you think you have to save?
5 Highest (TDc5)	Provides new content Elicits no response Gives an explanation or the answer to a question	I want you to write it down with an arrow-chain. S: Am I allowed to use three things? T: No, two.

Adapted from “Scaffolding in teacher-student interaction: exploring, measuring, promoting and evaluating scaffolding.,” p. 94, by Van de Pol (2012).

Table A2. Level of student understanding.

Level of Student Understanding (SU)	Description	Examples taken from this study
Level 0 (SU0)	Poor or no understanding	T: What is the out-number? S: I have no idea. S: I don’t understand exercise 2.
Level 1 (SU1)	Partial understanding	T: If you know that the entrance fee is €10 and consumption costs €5, then you know how much a visitor must pay. S: €15. T: Yes, if you just have one drink. But if you have more drinks, you pay more.
Level 2 (SU2)	Good understanding	S: Let me see: 200, 300, 400, 500, 600, 700. That means 14 weeks (the teacher nods).
Level X (SUX)	No understanding can be determined, but the turn is about the content	There were students that thought … (the student doesn’t finish the sentence).
Not on content (SUNOC)	Student turn about, for example, organizational matters	What do you mean?

Adapted from “Scaffolding in teacher-student interaction: exploring, measuring, promoting and evaluating scaffolding.,” p.95, by Van de Pol (2012).

Table A3. Categories of student mode of expression.

Student mode (SM)	Description	Examples taken from this study
Not on content (SMNOC)	Not on content	Sir, sir, finally.
0. Claim (SM0)	Claim of understanding	I get it.
1. Demonstration minimal (SM1)	Student shows that he/she understands, but we don’t know why	1 person is €25.
2. Demonstration extensive (SM2)	Student shows that he/she understands, and we know why	Let me see: 200, 300, 400, 500, 600, 700. That means 14 weeks (the teacher nods).

Adapted from “Scaffolding in teacher-student interaction: exploring, measuring, promoting and evaluating scaffolding,” p. 95, by Van de Pol (2012).

Table A4. Contingency rules for students’ demonstrations.

	Three-turn sequence*			Contingency
	Teacher turn 1	Student turn demonstration	Teacher turn 2
First three-turn sequence	TDc0(teacher not there yet)	SU0	TDC1 or TDc2	Contingent
		SU1		Contingent
		SU2		Not contingent
Middle three-turn sequence	TDc1 to TDc4	SU0	More in control than in turn 1	Contingent
		SU1		Contingent
		SU2		Not contingent
	TDc2 to TDc5	SU0	Less in control than in turn 1	Not contingent
		SU1		Not contingent
		SU2		Contingent
	TDc2 to TDc4	SU0	Same level of control as in turn 1	Not contingent
		SU1		Contingent
		SU2		Not contingent
	TDc5	SU0	TDc5	Contingent
		SU1		Contingent
		SU2		Not contingent
	TDc1	SU0	TDc1	Not contingent
		SU1		Contingent
		SU2		Contingent
Last three-turn sequence	TDc1 to TDc5	SU0	TDc0 (teacher walks away)	Not contingent
		SU1		Not contingent
		SU2		Contingent

Teacher’s degree of control (TDc): TDc0 = no control; TDc1 = lowest control, TDc2 = low control, TDc3 = medium control, TDc4 = high control, TDc5 = highest control. Student understanding (SU): SU0 = poor understanding, SU1 = partial understanding, SU2 = good understanding.

*A three-turn-sequence consists of three subsequent turns: teacher turn-student turn-teacher turn. Reprinted from “Scaffolding in teacher-student interaction: exploring, measuring, promoting and evaluating scaffolding,” p. 96, by Van de Pol (2012).

Appendix B

Table B1. Cross-table of step 1 vs. non-step 1 for both groups.

	Non-SGS group	SGS group
	Frequency (%)	Frequency (%)
Non-step 1	121 (100)	219 (91.6)
Step 1	0 (0)	20 (8.4)
Total	121 (100)	239 (100)

Non-step 1 = sum of frequencies of step 2, step 3, step 4, step 5, and step 6.

Table B2. Cross-table of step 5 vs. non-step 5 for both groups.

	Non-SGS group	SGS group
	Frequency (%)	Frequency (%)
Non-step 5	116 (95.9)	213 (89.1)
Step 5	5 (4.1)	26 (10.9)
Total	121 (100)	239 (100)

Non-step 5 = sum of frequencies of step 1, step 2, step 3, step 4, and step 6.

Table B3. Cross-table of step 6 vs. non-step 6 for both groups.

	Non-SGS group	SGS group
	Frequency (%)	Frequency (%)
Non-step 6	114 (94.2)	199 (83.3)
Step 6	7 (5.8)	40 (16.7)
Total	121 (100)	239 (100)

Non-step 6 = sum of frequencies of step 1, step 2, step 3, step 4, and step 5.

Table B4. Cross-table step 4 vs. non-step 4 for both groups.

	Non-SGS group	SGS group
	Frequency (%)	Frequency (%)
Non-step 4	25 (20.7)	119 (49.8)
Step 4	96 (79.3)	120 (50.2)
Total	121 (100)	239 (100)

Non-step 4 = sum of frequencies of step 1, step 2, step 3, step 5, and step 6.

Table B5. Cross-table of contingent vs. non-contingent three turn (teacher-student-teacher) sequences involving content support (step 4) for both groups.

	SGS group	Non-SGS group
	Frequency (%)	Frequency (%)
Contingent	61 (61)	40 (49)
Non-contingent	39 (39)	41 (51)
Total	100 (100)	81 (100)