Teaching and Learning of Vertex Coloring Using an Inquiry-Based Approach

Abstract

Traditional lecturing is the dominant method of teaching mathematics in undergraduate mathematical courses in many countries, whereas active student-centered approaches such as inquiry-based learning have been shown in some instances to be more effective. Most teaching resources (inquiry-based tasks) available at the tertiary level are related to calculus, linear algebra, and differential equations courses. In this paper, we focus on using an inquiry-based approach to explore the teaching and learning of vertex coloring, a common topic in graph theory and undergraduate discrete mathematical courses. We designed seven inquiry-based tasks related to vertex coloring to teach vertex coloring in an undergraduate graph theory course to students majoring in mathematics. In sharing these tasks, describing students’ engagement with them, and discussing how these tasks were perceived by the students and lecturer, we hope to promote using inquiry-based tasks in undergraduate discrete mathematical courses.

KEYWORDS:

• Vertex coloring
• graph theory
• inquiry-based learning
• learning mathematics

1. INTRODUCTION

Lecturing has been the dominant part of teaching in undergraduate mathematical courses in many countries across the world. In the past few decades, tertiary mathematics education researchers call for a change to more active, student-centered approaches to teaching and learning of mathematics (e.g., [14,17]). This call has been supported by previous studies that reported active learning approaches could improve university student mathematical performance (e.g., [13,21,30]) while traditional lecturing could increase failure rates [13]. For instance, Freeman et al. [13] conducted a meta-analysis on 225 studies that compared traditional lecturing with active learning in science, technology, engineering, and mathematics (STEM) undergraduate courses and found that students who participated in classes where teaching was traditional lecturing were 55% more likely to fail compared to students who participated in courses with active learning approaches. Additionally, Theobald et al. [30] conducted Bayesian regression analyses on student examination scores and student failure rates from several studies and found that active learning approaches reduce achievement gaps for underrepresented undergraduate STEM students.

The majority of previous studies that explore how active learning approaches, such as inquiry-based learning (IBL), can be used in undergraduate mathematics courses focus on teaching and learning of calculus (e.g., [4]) and differential equations courses (e.g., [14]). However, in this study, we focus on how an IB approach can be used in a graph theory course for undergraduate students majoring in mathematics.

Graph theory is a branch of mathematics that focuses on studying different properties of graphs, where a graph can be defined as “a finite nonempty set V of objects called vertices (the singular is vertex) together with a set E of 2-element subsets of V called edges” [7, p. 27]. Simple, undirected graphs can model symmetric binary relations. Furthermore, graphs can be represented by diagrams in which the elements are shown as vertices and the binary relation as edges joining pairs of vertices. It has several applications in different disciplines, such as in chemistry, where the atoms of a compound can correspond to vertices and chemical bonds as edges (e.g., [15]) or in medical sciences, where brain analysis can be performed on graph models by considering genes (proteins) as vertices and their relationships as edges [3].

Graph theory is taught to undergraduate students majoring in mathematics and computer science as part of their discrete mathematical courses and is also included in liberal art mathematics and bridging courses. Several majors in science and engineering also include graph theory as part of their postgraduate courses. A number of studies have focused on teaching and learning graph theory based on IB approaches in undergraduate courses, both for mathematics (e.g., [27,28]) and non-mathematics majors (e.g., [10,19]). Mathematics lecturers often found teaching graph theory fun and interesting as students have “equal footing”, regardless of their knowledge and skills in other areas of mathematics such as calculus [28]. Furthermore, graph theory could be easily connected to many disciplines, and many students “feel comfortable” learning this subject [9]. In liberal art mathematics courses, for instance, Despeaux [10] investigated how a designed learning module based on Oulipo could be used to help students apply their mathematical knowledge (including their knowledge of graph theory). Furthermore, Kasman [19] discussed, among other things, how an end-of-unit writing assignment on graph coloring could be used as an assessment tool for lecturers and also as an opportunity for students to synthesize their learnt knowledge in a liberal art mathematics course.

Graph theory has also been used as a mathematical topic in a series of graded inquiry-based assignments in a bridging mathematics course to help undergraduate mathematics students develop a better understanding of how mathematical proofs are constructed and help them realize the importance of inquiry in learning mathematics [8]. Furthermore, it has been used in a “game theory and recreational mathematics” module for final-year undergraduate students to better engage with standard mathematics topics, make cross-curricular links, and create opportunities for students to enhance their problem-solving and communication in mathematics which are needed for advanced mathematics [27]. However, in the past literature, it seems there is a lack of resources on teaching an entire lesson on a mathematical concept of graph theory using an IB approach that also used problem-posing activities. Before presenting the research objectives and questions, we briefly review the importance of problem-posing activities that have been used in the design of the IB approach in this study.

2. PROBLEM POSING

Problem-posing tasks in mathematics education could be defined as tasks “which require teachers or students to generate new problems and questions based either on given situations or on mathematical expressions or diagrams” [5, p. 2]. Several benefits have been reported for using these activities in the school context, such as developing students’ mathematical understanding (e.g., [11]), mathematical creativity (e.g., [2]), and positively impact students’ attitudes toward mathematics (e.g., [11]). However, these activities have received limited attention at the tertiary level. Only recently, a number of studies focused on using such activities in tertiary mathematics education (e.g., [25,26]). For example, a recent study with undergraduate engineering students showed that many students have positive attitudes toward engaging in problem-posing activities and perceive that engaging in such activities can help them develop their conceptual understanding of mathematics [24]. Furthermore, Nedaei et al. [25] highlighted that problem-posing activities could be used as an assessment tool alongside problem-solving activities at the tertiary level to explore students’ mathematical understanding.

3. RESEARCH OBJECTIVES AND QUESTIONS

In this study, we focus on the teaching and learning of one of the common topics in graph theory called vertex coloring. We chose it as this notion has many applications in various real-life problems (see Section 4). Furthermore, vertex coloring is one of the topics the lecturer of the graph theory course recommended us to focus. He perceived that this is one of the most important topics in the introductory graph theory course, with several important and challenging theorems for undergraduate students. In this paper, we discuss seven IB tasks that we designed for teaching vertex coloring in a lesson to undergraduate students majoring in mathematics. We believe that sharing these tasks, describing how students engaged with them, and sharing students’ and the lecturer's opinions toward using these tasks could promote IBL in undergraduate discrete mathematical courses that could contribute to a more meaningful understanding of mathematics. Therefore, we address the following two research questions in this paper:

1. How do students engage with IB activities related to vertex coloring?

2. What are students’ and lecturer's opinions toward teaching and learning of vertex coloring using an IB approach?

4. VERTEX COLORING

A graph can be colored if a color has been assigned to each vertex so that adjacent vertices have different colors. In other words, the function $f\text{: }V\left(G\right)\to \{1,2,3,\dots \}$ is said to be vertex coloring, if for each edge uv$\in$ E(G), f(u)$\ne$f(v) where $V\left(G\right)$ and $E\left(G\right)$ are the set of vertices and edges of a graph, respectively. If the vertex coloring f uses only the colors {1, 2, … , k}, then f is called a k-coloring of G, and if such a k-coloring exists, then the graph G is said to be k-colorable. The smallest possible number k for which the graph G is k-colorable is the chromatic number of G and is denoted by χ(G) [1]. This mathematical concept was born when Guthrie explored whether four colors were sufficient to color the map of England's counties so that no counties sharing a common border have the same color [7]. Vertex coloring is an important concept in graph theory with a wide range of computer science and operations research applications for modeling a vast number of practical problems, such as facility location and driver scheduling problems (DSP) [7]. DSP is a model of selecting a set of duties (or assignments) for the drivers/pilots of vehicles (e.g., buses, trains, boats, or planes) working to transport passengers or goods. For example, suppose that a service company is interested in doing all the requested services with the least number of vehicles. A graph can then be constructed so that each vertex of the graph corresponds to a customer, and then there is an edge between the two vertices when the times during which service is scheduled overlaps. The chromatic number of this graph shows the minimum number of vehicles required to perform these services. Furthermore, the services corresponding to the vertices that are colored i are performed by vehicle i.

5. INQUIRY-BASED LEARNING IN UNDERGRADUATE MATHEMATICS

Inquiry-Based Learning (IBL) is a student-centered teaching strategy engaging students in sense-making activities [23] by working “on tasks that require them to solve problems, conjecture, experiment, explore, create, and communicate, all critical skills and habits of mind in which mathematicians and scientists engage regularly” [29, p. 22]. This approach focuses on students’ active participation in their knowledge development and promotes creating opportunities for students to engage in productive struggle and peer-to-peer interaction [29]. Students in an IB classroom have several responsibilities, such as

talk to each other about what they are doing and thinking, as conversations are powerful in clarifying, solidifying, and elaborating learners’ ideas. They also … provide the instructor with the feedback needed to identify fruitful next steps toward her learning goals for students. [22, p. 131]

Lecturers who use this approach design “a carefully scaffolded sequence of mathematical tasks” [12, p. 570] that help students to engage in higher-order thinking (i.e., analyzing, evaluating, and (possibly) creating mathematical objects) [22]. In this approach, the lecturer does not provide a clear path to solutions for students, but instead seeks student reasoning and guides them “via well-crafted problems and questions through an adventure in mathematical discovery while using student reasoning to advance the mathematical agenda” [29, p. 22]. Laursen and Rasmussen [22] highlighted that lecturer direct instruction/talk in this approach “is well timed and well targeted to surface and explore students’ prior knowledge, to help students organize or connect important ideas, and to support students’ changing views” [p. 131]. Such actions could help students develop a conceptual understanding of mathematics.

6. THEORETICAL FRAMEWORK

The study design is influenced by Jaworski's [16,17] developmental research approach to IBL and the first author's involvement in MatRIC¹ and PLATINUM² project activities. Building on the theory of Community of Inquiry and the concept of Critical Alignment, Jaworski has identified three inter-related layers of inquiry: Inquiry in mathematics; inquiry in mathematics teaching; and inquiry in the research process [16]. This model has been designed for working with teachers in school and recently adapted for tertiary mathematics education (see Figure 1).

Figure 1. Inquiry in the three layers at the tertiary level [17, p. 279]. (Adopted with permission from the author.)

Inquiry in mathematics focuses on developing students’ conceptual understanding of mathematics through engaging them in IB tasks in classrooms and providing opportunities for peer-to-peer interaction and questioning between students and teachers. Inquiry in mathematics teaching promotes teaching development by exploring how different approaches and tasks can foster student inquiry and engagement with mathematics. Inquiry in the research process is an analytical process in which collected data from the first two layers are analyzed to understand better how inquiries were conducted by students and teachers in the inner layers to gain a better understanding of the entire developmental process. The findings are then disseminated to the teaching team involved in the project and to the wider community involved or interested in mathematics teaching and learning [16,17]. Reflecting on her work on IB practice, we established a community of inquiry, as described in the next section.

7. THE TEACHING OF VERTEX COLORING IN THE GRAPH THEORY COURSE

Our community of inquiry consisted of an associate professor of mathematics education, an associate professor of graph theory, a postgraduate student in mathematics education, and 24 undergraduate mathematics students who were enrolled in the graph theory course and voluntarily participated in the session about vertex coloring. This graph theory course is offered by the Department of Applied Mathematics as part of the Faculty of mathematical sciences in one of the biggest public universities in Iran (20,000–25,000 students). Students could take this course after taking Introduction to Combinatorics and normally take it in the second or third year of their undergraduate study. In Iran, undergraduate study normally takes between 3.5 and 4 years of full-time study. There were 27 students enrolled in the course; however, the number of students in this course could be up to 40 students in other semesters. The class met twice a week, and each session lasted about 90 min. There were 24 sessions in the course apart from the midterm exam, and this inquiry happened in Session 12. Prior to this session, students were introduced to preliminary concepts in graph theory and topics such as connectivity, spanning trees, Hamiltonian graphs and the traveling salesman problem, Eulerian graph and the Chinese postman problem.

We design seven IB tasks related to vertex coloring (see Section 8) in consultation with a mathematics education professor and an associate professor of graph theory. We piloted these tasks with a few postgraduate students of mathematics education who had graph theory as part of their undergraduate study. The design of these tasks was mainly influenced by the first author's understanding of IBL, as mentioned earlier, his previous research about using problem-posing tasks in tertiary mathematics education (e.g., [24–26]), and his numerous past experiences teaching undergraduate mathematics courses.

Because of COVID-19 restrictions, we conducted and recorded the 150 min vertex coloring session using Adobe Connect. The associate professor of graph theory ran the session while the postgraduate student observed the session and took notes of the teaching delivery. Students participated in the IB tasks in pairs and recorded their audio communication using a smartphone. The research team then collected their written responses for further analysis. At the end of the session, the students and the lecturer individually responded to a few open-ended questions to share their views about this IB practice. The students’ open-ended questions were:

1. What is your opinion about the teaching of vertex coloring in this session?

2. In your opinion, what are the advantages and disadvantage of the teaching approach used in today's class?

3. Would you like the teaching approach to be used in the teaching of the other sessions in this course and also other mathematical courses? Please elaborate on your answer.

It is worth mentioning that traditional lecturing was mainly used to teach the course, and it was the first experience of the associate professor of using IB tasks for teaching graph theory.

8. THE INQUIRY-BASED TASKS IN RELATION TO VERTEX COLORING

We designed Task 1 (Figure 2) to motivate students to inquire how their current knowledge of graph theory can be used to solve a real-world problem. The students had no formal teaching of vertex coloring prior to this session. Similar problems are used in graph theory textbooks (e.g., [7]) to introduce vertex coloring and to provide a real-world application of this topic. Students had 20 min to work on the first task. The lecturer asked them to document their responses by taking a photo of the responses and sending the picture to the postgraduate student.

Figure 2. A contextual task to motivate students to learn about vertex coloring.

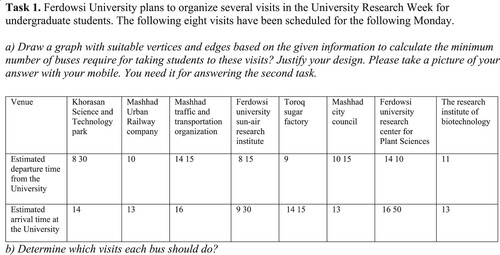
Students engaged with this task quite well, and all groups provided their responses. For instance, without receiving any help from the lecturer, Group 3 considered the intervals of departure and arrival for the venues as vertices of their graph and considered an edge between two vertices when the intervals have an overlap. In graph theory, such a graph is called an interval graph. They used the graph in Figure 3 to estimate the minimum number of buses required for the visits. Please note that students were not exposed to interval graphs when engaging with these IB tasks.

Figure 3. A simple graph constructed in response to Task 1.

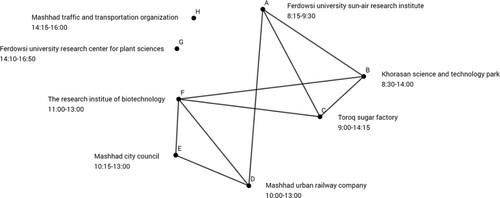
Another type of graph observed in students’ responses was a directed graph. For instance, Group 5 considered the university as the central vertex with the venues as the other vertices. Instead of assuming that a bus would remain at the venue, they constructed a directed graph by assuming that a bus would return to the University empty after dropping off the students at the venue (Figure 4). Considering this assumption, they drew a double-headed arrow from each venue to the University, and based on the departure and arrival times and their overlaps, they estimated the minimum number of buses needed for these visits.

Figure 4. A simple directed graph constructed in response to Task 1.

Without discussing the first task, the lecturer then presented Task 2 (Figure 5) to students. This was the students’ first encounter with the formal definitions related to vertex coloring. With these definitions given, the students then had a second chance to work with their graph and solution from Task 1 for another 10 min. When the groups completed Task 2 and documented their responses, Tasks 1 and 2 were discussed in the lecture, where some groups shared their responses.

Figure 5. Defining vertex coloring for students and give them the opportunity to work with Task 1 again.

Part (a) of Task 3 (Figure 6) began by giving students an opportunity to pose questions related to vertex coloring for three well-known types of graphs (i.e., tree, bipartite, and complete graphs³).

Figure 6. Providing an opportunity for students to develop their understanding of vertex coloring using a problem-posing task.

The lecturer gave students 10 min to pose their problems without informing them that they would be asked to solve their posed problems later. After they recorded their posed problem(s), the lecturer gave them 10 min to solve their posed problem(s). The majority of posed problems were related to chromatic numbers of these three graph types without referring to the term, chromatic number in the posed question (e.g., “what is the minimum number of colors for coloring trees?”; “what is the minimum number of colors for coloring complete graphs?”). A few students also posed a problem about the relationship between the vertex coloring of these three graph types (e.g., “Which pair of these three graph types has the same coloring?”; and “Is there any relationship between trees and bipartite graphs in relation to vertex coloring?”).

Immediately after completing Task 3, the lecturer gave students 20 min to complete parts (a) and (b) of Task 4 (Figure 7). This gives them more opportunities to develop their understanding of chromatic number. All groups responded correctly to the first part, and many groups were able to find the chromatic number of the graphs they constructed in part (a). After documenting their responses to parts (a) and (b), the lecturer gave students 10 min to state conjectures concerning the vertex coloring of these three types of graphs (i.e., part (c)). Several groups conjectured that “the chromatic number of trees, in general, is 2”; “the chromatic number of bipartite graphs is 2 in general”; and “the chromatic number of complete graphs is equal to the number of graph's vertex”. After documenting their conjectures, the lecturer gave students another 10 min to complete part (d) of Task 4. When the groups completed Task 4, both Tasks 3 and 4 were discussed in the lecture and some of the groups shared their responses. Afterward, students received a 10 min break.

Figure 7. Providing an opportunity for students to develop their understanding of vertex coloring.

The remaining tasks in this session were more challenging than the first four tasks, and their complexity gradually increased for students. In Task 5 (Figure 8), students were introduced to the concept of a critical graph and were given the opportunity to pose problems related to this concept. Graph coloring is computationally hard, and consequently, finding bounds even for special graphs such as critical graphs is important. Since students already knew that they would be asked to solve their posed problems, the lecturer gave students 15 min to complete both parts of Task 5.

Figure 8. Providing an opportunity for students to develop their understanding of critical graphs using a problem-posing task.

Some of the posed problems were about whether the three known graph types discussed earlier (i.e., tree, bipartite, and complete graphs) are critical graphs (e.g., “Are all elements in trees critical elements?” and “Are all elements in complete graphs critical elements?”). Other posed problems were related to the impact of removing a vertex or an edge from a graph on its chromatic number (e.g., “Does removing a vertex or an edge from a critical graph cause decreasing the chromatic number by one or more?” and “Does removing a vertex have more impact (in general) [on the chromatic number of a graph] or an edge?”).

After students documented their responses to Task 5, the lecturer gave students 15 min to complete Task 6 (Figure 9). This task gave students more opportunities to develop their understanding of critical graphs in preparation to prove the theorem given in Task 7 (Figure 10). The NP-hardness of computing chromatic numbers justifies efforts to study them for particular classes of graphs. The students had 15 min to complete Task 7. Once groups completed Task 7, Tasks 5–7 were discussed in the lecture, and some groups shared their responses. The majority of groups were successful with part (a) of Task 6 and made the conjecture that “each complete graph with k vertices is k-critical”. However, other conjectures, such as “k-critical graphs are derived by removing a vertex from complete graphs” were also observed. More than half of the groups respond correctly to parts (c) and (d). Finally, for part (e), three groups conjectured $\delta \left(G\right)\ge k-1,$ and two groups conjectured $\delta \left(G\right)=k-1$. The remaining groups left this part blank. In the given short time, only one group was able to prove the given theorem, and two other groups were able to realize that proof by contradiction and proof by induction should be used here.

Figure 9. Providing more opportunities for students to inquire about critical graphs.

Figure 10. A theorem related to k-critical graph.

9. STUDENTS’ AND LECTURER'S FEEDBACK ON THE INQUIRY-BASED PRACTICE

The majority of students who participated in this session (22 out of 24 (92%)) enjoyed engaging with these IB tasks. They highlighted different reasons for their perceptions,⁴ including helping students develop a conceptual understanding of mathematics (54%), giving them the opportunity to work with their peers solving problems using different strategies (33%), constructing their knowledge step-by-step (8%), and having the opportunity to pose problems (4%). Some students (12%) also highlighted that they did not notice how much time elapsed during the session, which could indicate that they enjoyed engaging with these IB tasks. Two students (8%) also appreciated that the teaching were started with a real-world problem. Two sample responses were:

The teaching today was very interesting and enjoyable. If all the sessions in different [mathematical] courses are designed in this way, the lectures can be more productive … Also, in terms of learning, it was meaningful and more lasting in mind.

This method, in which the student starts by just reading the definitions and posing a question and then answering it himself and finds the connection between the problems, is very useful because it makes the problems last longer in mind, and the student becomes more familiar with how to do research and solve problems.

While most students enjoyed engaging with these IB tasks, some students raised a few concerns. Some students (21%) believed more time should be allocated for group work, and one student (4%) mentioned that more time could be considered for whole classroom discussion. Two students (8%) also found it hard to communicate with each other through the online format. Two students (8%) also highlighted that less content could be covered in such practice than in traditional lecturing. A sample response was

The teaching method was good on the one hand and was bad, on the other hand. It was good that the teaching was not lecture-centered, and we did group works. However, on the other hand, if we had traditional lecturing, more content could be taught, and we did not spend much time on each task.

After the session, the lecturer also agreed that more time could be given to students for these IB tasks, so if readers are interested in using these (or similar) IB tasks in their courses, they need to consider giving more time to students to work together than what was offered in our study. Considering it was his first experience of using IB practice, the lecturer mentioned that he might be a bit distracted when orchestrating the classroom discussion, and that might cause the lecturer to lose some of his attention on the content. Despite these disadvantages, he highlighted the advantages of IB practice, helping students develop their mathematical thinking, reasoning, and communicational skills, and it is more enjoyable for students than traditional lecturing. After the semester completed, we approached the lecturer again and asked his opinion about the teaching of vertex coloring using this IBL approach compared to his traditional lecturer-centred approach in the past over several years. He mentioned again that this approach is time-consuming but highlighted: “It had a positive impact. I do not mean that their grades necessarily improved. I mean, students were able to make a better connection with the topic and therefore develop a deeper understanding of these concepts.”

Our observation of this IB practice was also in line with what the students and the lecturer shared. For instance, as we expected, Task 1 motivated students to learn more about vertex coloring, and students appreciated the opportunity to engage with problem-posing tasks and make conjectures about different properties of graphs. However, we need to highlight that Task 7 was challenging for many groups, and engaging with the previous tasks, mostly Task 5 and 6, were not enough for these groups to help them overcome the challenge of proving the theorem in the limited time given to students. Therefore, in future work, to help students develop their proving skills in relation to concepts in graph theory, other approaches could be investigated, particularly reflecting on the literature regarding learning to prove (e.g., [20]).

10. DISCUSSION AND CONCLUSIONS

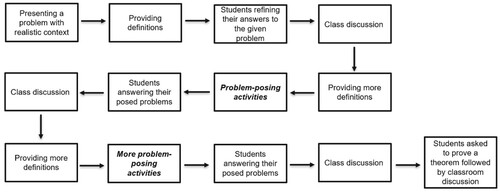
This paper focused on a set of seven inquiry-based tasks intended to introduce the concept of vertex coloring, a topic covered in introductory graph theory courses. What distinguishes this report from the past literature on IBL is the combination of IBL together with problem-posing activities to introduce a mathematical concept at the undergraduate level. The process into the discovery of the concept proposed here (i.e., Figure 11) could be used to introduce other mathematical concepts at the undergraduate level. Our inquiry into the teaching and learning of vertex coloring shows that many students enjoyed working with IB tasks and perceived that IB practice could help them develop their conceptual understanding of mathematics. Furthermore, the problem-posing activities gave students the opportunities to lead their inquiry in mathematics and such tasks could be used more often in undergraduate courses as also suggested in the literature (e.g., [25]). The results from our inquiry suggest that such practices could be used in teaching graph theory courses, even when mathematics teaching at the university level is still dominantly taught through traditional lecturing. While the majority of students and the lecturer had positive perceptions toward the IB tasks, both agreed that less content could be covered using an IB approach as such an approach is time-consuming. We expected to receive such a comment from the lecturer considering his teaching environment and background; however, it was interesting that students also raised this issue by taking a critical stance toward mathematics teaching [14].

Figure 11. An integration of IBL with problem-posing activities to introduce a mathematical concept at the undergraduate level.

Blending IB practice with a flipped-classroom approach [6,23] can help lecturers reduce the content pressure in their mathematical courses. However, it is worth highlighting recent studies (e.g., [18]) suggest that the teaching approach lecturers use in their practice is dependent on their personal beliefs, such as their perceptions of the effectiveness of lecturing. For instance, Johnson et al. [18] reported that lecturers who use lecturing more than 75% of the time had the highest agreement with statements such as I think lecture is the best way to teach and I think lecture is the only way to teach that allows me to cover the necessary content. Johnson et al. [18] further suggested that

Meeting instructors where they are, and introducing behaviors that are commensurate with their beliefs, may be an entry point for supporting them in transitioning to more research- and evidence-based instructional practice. That is, identifying pedagogical changes that are broadly consistent with instructors’ current practice and beliefs may provide the “activation energy” for a self-reinforcing cycle of changes in practice and belief leading to more student-centered instructional practices [p. 20]

We agree with this point of view and hope that sharing IB practices, similar to what we shared in this paper, will encourage more mathematics lecturers to use student-centered approaches in their teaching.

DISCLOSURE STATEMENT

No potential conflict of interest was reported by the author(s).

Additional information

Notes on contributors

Farzad Radmehr

Dr. Farzad Radmehr holds two PhDs in mathematics education from Ferdowsi University of Mashhad, Iran (2014), and Victoria University of Wellington, New Zealand (2016). Currently, he is an Associate Professor of Mathematics Education at Norwegian University of Science and Technology, Norway. Farzad's research focuses on improving the teaching and learning of mathematics at upper secondary and tertiary levels. He is also interested in mathematical modeling, networking learning theories, and task design in mathematics education.

Khaled Tohidinasab

Mr. Khaled Tohidnasab is a postgraduate student of mathematics education at Ferdowsi University of Mashhad. His research focuses on using inquiry-based learning to improve teaching and learning of mathematics at the university level. Khaled also teaches upper secondary mathematical courses as a certified mathematics teacher.

Mostafa Tavakoli

Dr. Mostafa Tavakoli received his M. Sc. from the University of Tehran under the supervision of professor Hassan Yousefi-Azari, and his Ph. D. at the Ferdowsi University of Mashhad under the supervision of professor Freydoon Rahbarnia. He is currently an Associate professor of mathematics at the Ferdowsi University of Mashhad. His research focuses on graph products, metric graph theory, combinatorial optimization, and applications of graph theory.

Notes

1 https://www.matric.no/.

2 https://platinum.uia.no/.

3 Please note that students are already familiar with these types of graphs from previous lectures.

4 The following percentages do not add up to 100% as some students mentioned more than one reason for their perceptions.