Parabolic Degrees and Lyapunov Exponents for Hypergeometric Local Systems

Abstract

Consider the flat bundle on ${\mathbb{P}}^1-\{0,1,\infty \}$ corresponding to solutions of the hypergeometric differential equation

$${\prod }_{i=1}^n(\mathrm{D}-{\alpha }_i)-z{\prod }_{j=1}^n(\mathrm{D}-{\beta }_j)=0,\text{where\hspace{0.5em}}\mathrm{D}=z\frac{\mathrm{d}}{\mathrm{d}z}$$

For α_i and β_j real numbers, this bundle is known to underlie a complex polarized variation of Hodge structure. Setting the complete hyperbolic metric on ${\mathbb{P}}^1-\{0,1,\infty \},$ we associate n Lyapunov exponents to this bundle. We study the dependence of these exponents on parameters ${\alpha }_i,{\beta }_j$ through algebraic computations and numerical simulations, and point out new equality cases of the exponents with parabolic degrees of these bundles.

Keywords:

• hypergeometric functions
• Higgs bundle
• variation of Hodge structure
• parabolic degree
• Lyapunov exponent

MATHEMATICS SUBJECT CLASSIFICATION:

• 34D08; 37D50; 14D07; 33C20; 22E40

1. Introduction

Oseledets decomposition of flat bundles over an ergodic dynamical system is often referred to as dynamical variation of Hodge structure. In the case of Teichmüller dynamics both Oseledets decomposition and a variation of Hodge structure (VHS) appear. Two decades ago it was observed in [Kontsevich 97] that these structures are linked, some of their invariants are related: the sum of the Lyapunov exponents associated to a Teichmüller curve equals the normalized degree of the Hodge bundle. This formula was studied extensively and extended to strata of abelian and quadratic differentials from then (see [Bouw and Möller 10, Eskin et al. 14, Forni et al. 14, Krikorian 03–04]). Soon this link was observed in other settings: in [Kappes and Möller 16] it was used as a new invariant to classify hyperbolic structures and distinguish commensurability classes of Deligne–Mostow’s non-arithmetic lattices in $\text{PU}(2,1)$ and $\text{PU}(3,1);$ in [Filip 14] a similar formula was observed for higher weight variation of Hodge structures. The motivation of the present work is the study of the relationship between these two structures in a broad class of examples with arbitrary weight. The examples will be given by hypergeometric differential equations which yield a flat bundle endowed with a variation of Hodge structure over the 3-punctured sphere. A recent article [Eskin et al. 16] shows that the degrees of holomorphic flags of the Hodge filtration bound by below the partial sums of Lyapunov exponents. Our study will start by computing these degrees in Sections 2 and 3. After presenting an algorithm to approximate Lyapunov exponents in Section 4, we then explore the behavior of Lyapunov exponents and their distance to the latter lower bounds in Section 5. This will enable us to bring out some simple algebraic relations under which there is a conjectural equality.

1.1. Hypergeometric equations

Let ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n$ and ${\beta }_1,{\beta }_2,\dots ,{\beta }_n$ be two disjoint sequences of n real numbers. We define the hypergeometric differential equation corresponding to those parameters (1–1) $$\prod _{i=1}^n(\mathrm{D}-{\alpha }_i)-z\prod _{j=1}^n(\mathrm{D}-{\beta }_j)=0,\text{where\hspace{0.5em}}\mathrm{D}=z\frac{\mathrm{d}}{\mathrm{d}z}$$(1–1)

This equation originates from a large class of special functions called generalized hypergeometric functions which satisfy it. These functions have a lot of interesting properties and there is a very rich literature about them. For an introduction to the subject see for example [Yoshida 97].

Equation (1–1)(1–1) $$\prod _{i=1}^n(\mathrm{D}-{\alpha }_i)-z\prod _{j=1}^n(\mathrm{D}-{\beta }_j)=0,\text{where\hspace{0.5em}}\mathrm{D}=z\frac{\mathrm{d}}{\mathrm{d}z}$$(1–1) is an order n differential equation with three singularities at 0, 1, and $\infty$ hence its space of solutions defines locally a dimension n vector space away from singularities and can be seen in a geometric way as a flat bundle over ${\mathbb{P}}^1-\{0,1,\infty \}.$ This flat bundle is completely described by its monodromy matrices around singularities. We will denote monodromy matrices associated to simple closed loop going counterclockwise around 0, 1, and $\infty$ by M₀, M₁, and $M_{\infty }.$ We obtain a first relation between these matrices observing that composing the three loops in the same order will give a trivial loop: $M_{\infty }{M}_1{M}_0=\text{Id}.$ The eigenvalues of M₀ and $M_{\infty }$ can be expressed with respect to parameters of the hypergeometric equation (1–1) and M₁ has a very specific form as stated in the following proposition.

Proposition 1.1.

For any two sequences of real numbers ${\alpha }_1,\dots ,{\alpha }_n$ and ${\beta }_1,\dots ,{\beta }_n,$

• M₀ has eigenvalues $e^{2i\pi {\alpha }_1},\dots ,e^{2i\pi {\alpha }_n}$

• $M_{\infty }$ has eigenvalues $e^{-2i\pi {\beta }_1},\dots ,e^{-2i\pi {\beta }_n}$

• M₁ is the identity plus a matrix of rank one

Proof.

See Proposition 2.1 in [Fedorov 15] or alternatively Proposition 3.2 and Theorem 3.5 in [Beukers and Heckman 89].□

This proposition determines the conjugacy class of the representation associated to the flat bundle ${\pi }_1\left({\mathbb{P}}^1-\{0,1,\infty \}\right)\to G{L}_n\left(\mathbb{C}\right)$ thanks to the rigidity of hypergeometric equations (see [Beukers and Heckman 89]). These classes are given explicitly in Section 4.3.

1.2. Lyapunov exponents

We now endow the 3-punctured sphere with its hyperbolic metric. As this metric yields an ergodic geodesic flow g_t, to any integrable norm $\Vert ·\Vert$ on the flat bundle E of dimension n we associate, using Oseledets theorem, real numbers ${\lambda }_1\ge \cdots \ge {\lambda }_n,$ and a flag decomposition of E in subbundles above almost every point, $$E={\mathcal{V}}^{\le {\lambda }_1}\supseteq \cdots \supseteq {\mathcal{V}}^{\le {\lambda }_n}\subset 0$$ such that for any vector $v\in {\mathcal{V}}^{{\lambda }_i}\backslash {\mathcal{V}}^{{\lambda }_{i+1}},$ $$\Vert G_{t}v\Vert =\hspace{0.17em}\text{exp}\hspace{0.17em}\left({\lambda }_{i}t+o\left(t\right)\right)$$ where $G_{t}v$ is the flow induced by g_t on E by the parallel transport for the flat connection. This is usually called the Oseledets flag decomposition. The λ_i are the Lyapunov exponents and correspond to the growth rate of the norm of a generic vector in each of these flags while transporting it along with the flat connection.

A complete explanation of the existence of these Lyapunov exponents in our setting can be found in [Eskin et al. 16]. Moreover, it is proved in Theorem 2.1 of this article that there exists a canonical family of integrable norms on the flat bundle associated to the hypergeometric equation which will produce the same flag decomposition and Lyapunov exponents. They call this family the admissible norms. In particular, the harmonic norm (see Remark in Section 2.1) induced by a VHS is admissible.

Figure 2. Geometric representation of middle convolution action on f.

For numerical simulations, the most convenient norm to compute Lyapunov exponents is the constant norm. Consider a norm on the fiber in E over some base point in the base curve ${\mathbb{P}}^1-\{0,1,\infty \},$ and extend it by parallel transport on a maximal simply connected subspace. The maximal domain is chosen to be the complement of a finite collection of closed path. Then this norm is not continuous across the boundaries, and depends on the choice of the domain, but define Lyapnunov exponents independently according to the following proposition.

Proposition

(2.2 in [Eskin et al. 16]). Any constant norm on a flat bundle in the case defined above is also integrable and computes the same Lyapunov exponents as any admissible norm.

1.3. Parabolic degree bound

Let $\mathcal{V}$ be a dimension k holomorphic vector subbundle of the Deligne extension of E (defined in Section 2.3), we can define its parabolic degree as in Definition 2.2 that we denote by ${\mathrm{deg}}_{\mathit{par}}(\mathcal{V}).$ It can be through of as a generalization of the degree of holomorphic bundles on compact complex varieties to the case were these varieties are punctured. The main theorem in [Eskin et al. 16] states that, in our setting, (1–2) $$\sum _{i=1}^k{\lambda }_i\ge 2{\mathrm{deg}}_{\mathit{par}}\left(\mathcal{V}\right).$$(1–2)

The motivation of the present work is to explore the equality cases for this inequality. In the case of examples coming from hypergeometric equations, there are several such holomorphic vector subbundles that will be induced by an extra algebraic structure: the variation of Hodge structure.

The present work will consist, first, in computing the parabolic degrees for these induced holomorphic vector subbundles, second, to compare them with sum of Lyapunov exponents.

1.4. Variation of Hodge structure

Hypergeometric equations on the sphere are well known to be physically rigid (see [Beukers and Heckman 89] or [Katz 96]) and this rigidity together with irreducibility is enough to endow the flat bundle with a (complex) VHS (see Definition in Section 2.1) using its associated Higgs bundle structure (see [Fedorov 15] or directly Corollary 8.2 in [Simpson 90]). Using techniques from [Katz 96] and [Dettweiler and Sabbah 13], Fedorov gives in [Fedorov 15] an explicit way to compute the Hodge numbers for the underlying VHS. We extend this computation and give a combinatoric point of view that will be more convenient in the following to express parabolic degrees of the Hodge flag decomposition.

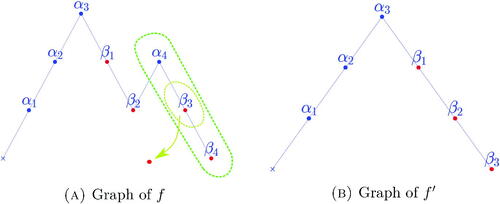
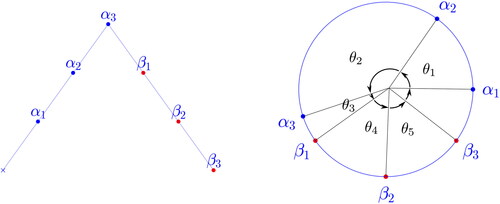
Let α and β be two sets of n points on the circle $\mathbb{R}/\mathbb{Z}.$ Starting from any of these points, we browse the circle counterclockwise (or in the increasing direction for $\mathbb{R}$) and enumerate the points in $\alpha \cup \beta$ by order of appearance ${\eta }_1,{\eta }_2,\dots ,{\eta }_{2n}.$ Let us now define $\tilde{f}:\mathbb{Z}\cap [0,2n]\mapsto \mathbb{Z}$ recursively by the following properties,

• $\tilde{f}(0)=0,$

• $\tilde{f}(k)=\tilde{f}(k-1)+\{\begin{array}{cc}1& \text{if}{\eta }_k\in \alpha \\ -1& \text{if}{\eta }_k\in \beta \end{array}.$

We denote by f the function defined for any ${\eta }_k\in \alpha \cup \beta$ by $f({\eta }_k)=\tilde{f}(k).$ This definition depends up to a shift on the choice of starting point. For a canonical definition, we shift f such that its minimal value is 0. Which is equivalent to starting at a point of minimal value. This defines a non-negative function f that we will call the intertwining diagram of the equation (Figure 1).

Figure 1. Example of computation of f.

For every integer $1\le i\le n$ we define $$h_i:=\#\{\alpha |f(\alpha )=i\}=\#\{\beta \left|f\right(\beta )=i-1\}$$

Then we have the following theorem from [Fedorov 15],

Theorem

(Fedorov). The $h_1,h_2,\dots ,h_n$ are the Hodge numbers of the VHS after an appropriate shifting.

Remark.

If the αs and βs appear in an alternate order then $f(\alpha )\equiv 1$ and $f(\beta )\equiv 0$ thus there is just one element in the Hodge decomposition and the polarization form is positive definite. In other words the harmonic norm is invariant with respect to the flat connection. This implies that Lyapunov exponents are zero.

In general, this Hodge structure endows the flat bundle with a pseudo-Hermitian form of signature (p, q) where p is the sum of the even Hodge numbers and q the sum of the odd ones. This gives classically the fact that the Lyapunov spectrum is symmetric with respect to 0 and that at least $|p-q|$ exponents are zero (see Appendix A in[Forni et al. 14]).

Pushing further methods of [Fedorov 15] and [Dettweiler and Sabbah 13], we compute the parabolic degrees of the sub Hodge bundles in the hypergeometric frame. This computation was done with the help of computer experiments in Section 5.2 which yielded a conjectural formula for these degrees. Besides from the intertwining diagram, another quantity appears. Let us relabel α and β by order of appearance after choosing α₁ such that $f({\alpha }_1)=1,$ then take the representatives of α and β in $\mathbb{R}$ which are included in $[{\alpha }_1,{\alpha }_1+1[$ for an arbitrary representative of α₁, and define $\gamma :=\sum \beta -\sum \alpha .$ The formula will depend on the floor value of γ. As $0<\gamma <n$ we have n possible values $0\le [\gamma ]<n.$

Theorem 1.2.

Let E a flat bundle over ${\mathbb{P}}^1-\{0,1,\infty \}$ defined by hypergeometric differential equations, and let $E={\oplus }_{p=1}^n{\mathcal{E}}^p$ a Hodge decomposition for its VHS. For all $1\le p\le n$ we denote by δ^p the degree of the Deligne compactification of ${\mathcal{E}}^p$ over the sphere. Then,

• if $p=[\gamma ]+1,$ $${\mathrm{deg}}_{\mathit{par}}\left({\mathcal{E}}^p\right)={\delta }^p+\{\gamma \}+\sum _{f(\alpha )=p}\alpha +\sum _{f(\beta )=p-1}1-\beta ;$$

• otherwise, $${\mathrm{deg}}_{\mathit{par}}\left({\mathcal{E}}^p\right)={\delta }^p+\sum _{f(\alpha )=p}\alpha +\sum _{f(\beta )=p-1}1-\beta .$$

The proof of this theorem is given in Section 3. In Algorithm 1 we present a general way to compute δ^p.

1.5. Observed new phenomenon

Generalizing an example of [Eskin et al. 16] coming from families of Calabi–Yau varieties, we exhibit in Section 5.1 new examples which satisfy conjecturally an equality in formula (1–2) and whose monodromy groups have a particular algebraic behavior.

2. Degree of Hodge subbundles

2.1. Variation of Hodge structure

We start recalling the definition of a polarized complex variations of Hodge structures (VHS).

A VHS on a curve C consists of a complex flat bundle $(E,\nabla )$ together with an Hermitian form h and a h-orthogonal decomposition $$E=\underset{p\in \mathbb{Z}}{\oplus }{\mathcal{E}}^p$$ into $C^{\infty }$-subbundles. We write the induced flag filtrations by ${\mathcal{F}}^p:=\underset{i\ge p}{\oplus }{\mathcal{E}}^i$ and $\overline{{\mathcal{F}}^p}:=\underset{i\le p}{\oplus }{\mathcal{E}}^i.$ The following conditions are satisfied:

• The decreasing filtration ${\mathcal{F}}^{•}$ is holomorphic, and the increasing filtration ${\overline{\mathcal{F}}}^{•}$ is anti-holomorphic.

• The connection shifts the grading by at most one, i.e. $$\nabla \left({\mathcal{F}}^p\right)\subset {\mathcal{F}}^{p-1}\otimes {\Omega }_{\mathcal{C}}^1\text{and}\nabla \left(\overline{{\mathcal{F}}^p}\right)\subset \overline{{\mathcal{F}}^{p¯1}}\otimes {\Omega }_{\mathcal{C}}^1$$

• h is positive definite on ${\mathcal{E}}^p$ if p is even; negative definite if p is odd.

Up to a shift, we can assume that there is a n such that ${\mathcal{E}}^i=0$ for i < 0 and i > n. We call n the width of the VHS.

Remark.

We can define a canonical norm by taking $\pm h$ on spaces ${\mathcal{E}}^p$, such that it is positive definite on each of these spaces. This norm is called the harmonic norm.

2.2. Decomposition of an extended holomorphic bundle

Let $\mathcal{C}$ be a complex curve, we assume that its boundary set $\Delta :=\overline{\mathcal{C}}\backslash \mathcal{C}$ is an union of points. Consider $\mathcal{E}$ an holomorphic bundle on $\overline{\mathcal{C}}.$ We introduce structures which will appear on such holomorphic bundle when they are obtained by canonical extension when we compactify $\mathcal{C}.$ The first one will take the form of filtrations on each fibers above points of Δ.

Definition 2.1

(Filtration). A $[0,1)$-filtration on a complex vector space V is a collection of real weights $0\le w_1<w_2<\cdots <w_n<w_{n+1}=1$ for some $n\ge 1$ together with a decreasing filtration of subvector spaces $$G^{•}:V=V^{\ge w_1}⊋V^{\ge w_2}⊋\cdots ⊋V^{\ge w_{n+1}}=V^{\ge 1}=0$$

The filtration satisfies $V^{\ge \nu }\subset V^{\ge \omega }$ whenever $\nu \ge \omega$ and the previous weights satisfy $V^{\ge w_i+ϵ}⊊V^{\ge w_i}$ for any $ϵ>0.$

We denote the graded vector spaces by ${\text{gr}}_{w_i}:=V^{\ge w_i}/V^{\ge w_i+ϵ}$ for ϵ small. The degree of such a filtration is by definition $$\mathrm{deg}\left(G^{•}\right):=\sum _{i=1}^n{w}_i\dim \left({\text{gr}}_{w_i}\right)$$

This leads to the next definition,

Definition 2.2

(Parabolic structure). A parabolic structure on $\mathcal{E}$ with respect to Δ is a couple $(\mathcal{E},G^{•})$ where $G^{•}$ defines a $[0,1)$-filtration $G^{•}{\mathcal{E}}_s$ on every fiber ${\mathcal{E}}_s$ for any $s\in \Delta .$

A parabolic bundle is a holomorphic bundle endowed with a parabolic structure. The parabolic degree of $(\mathcal{E},G^{•})$ is defined to be $${\mathrm{deg}}_{\mathit{par}}(\mathcal{E},G^{•}):=\mathrm{deg}\left(\mathcal{E}\right)+\sum _{s\in \Delta }\mathrm{deg}\left(G^{•}{\mathcal{E}}_s\right)$$

2.3. Deligne extension

In the following we consider $\mathbb{V}$ a local system on ${\mathbb{P}}^1-\{0,1,\infty \}$ associated to a monodromy representation with eigenvalues of modulus one. We denote by $\mathcal{V}$ the associated holomorphic vector bundle.

We recall the construction of Deligne’s extension of $\mathcal{V}$ which defines a holomorphic bundle on $\overline{\mathcal{C}}$ with a logarithmic flat connection. We describe it on a small pointed disk centered at $s\in D^{*}$ (the full disk is denoted $D$). Let ρ be a ray going outward of the singularity, then we can speak of the vector space of flat sections along the ray $L(\rho )$ which has the same rank r as $\mathcal{V}.$ As all the $L(\rho )$ are isomorphic, we choose to denote it by V⁰. There is a monodromy transformation $T:V^0\to V^0$ to itself obtained after continuing the solutions. This corresponds to the monodromy matrix in the given representation. For every $\alpha \in [0,1)$ we define $$W_{\alpha }=\{v\in V^0:{(T-{\zeta }_{\alpha })}^{r}v=0\}\text{where}{\zeta }_{\alpha }=e^{2i\pi \alpha }$$

These vector spaces are nontrivial for finitely many ${\alpha }_i\in [0,1).$ We define $$T_{\alpha }={\zeta }_{\alpha }^{-1}{T}_{|W_{\alpha }}\text{and}{N}_{\alpha }=\hspace{0.17em}\text{log}\hspace{0.17em}{T}_{\alpha }$$

Let $q:\mathbb{H}\to D^{*},q(z)=e^{2i\pi z}$ be the universal cover of $D^{*}.$ Choose a basis $v_1,\dots ,v_r$ of V⁰ adapted to the generalized eigenspace decomposition $V^0=\underset{\alpha }{\oplus }{W}_{\alpha }.$ We consider $v_i(z)$ as the pull back of v_i on $\mathbb{H}.$ If $v_i\in W_{\alpha },$ then we define $${\tilde{v}}_i\left(z\right)=\hspace{0.17em}\text{exp}\hspace{0.17em}(2i\pi \alpha z+z{N}_{\alpha })v_i$$

These sections are equivariant under $z\mapsto z+1$ hence they give global sections of ${\mathcal{V}}_{\mathcal{C}}(D^{*}).$ The Deligne extension of ${\mathcal{V}}_{\mathcal{C}}$ is the vector bundle whose space of section over D is the ${\mathcal{O}}_{\mathcal{D}}$-module spanned by ${\tilde{v}}_1,\dots ,{\tilde{v}}_r.$ This construction naturally gives a filtration on V⁰.

In general, we can define various extensions ${\mathcal{V}}^a\subset {\mathcal{V}}^{-\infty }\subset j_{*}\mathcal{V}$ where j is the inclusion $j:D^{*}\to D,{\mathcal{V}}^{\infty }$ is the Deligne’s meromorphic extension and ${\mathcal{V}}^a$ (resp. ${\mathcal{V}}^{>a}$) for $a\in \mathbb{R}$ is the free ${\mathcal{O}}_{\overline{\mathcal{C}}}$-module on which the residue of $\nabla$ has eigenvalues α in $[a,a+1)$ (resp. $(a,a+1]$). The bundle ${\mathcal{V}}^{•}$ is a filtered vector bundle in the definition of [Eskin et al. 16].

If we have a VHS $F^{•}$ on $\mathcal{V}$ over $\mathcal{C},$ it induces a filtration of every ${\mathcal{V}}^a$ simply by taking $$F^p{\mathcal{V}}^a:=j_{*}{F}^p\mathcal{V}\cap {\mathcal{V}}^a$$ this is a well-defined vector bundle thanks to nilpotent orbit theorem ([Schmid 73] (4.9)).

In general for $\mathcal{C},$ we define on fibers over any singularity $s\in \Delta ,$ for $a\in (-1,0]$ and $\lambda =\hspace{0.17em}\text{exp}\hspace{0.17em}(-2i\pi a),$ $${\psi }_{\lambda }\left({\mathcal{V}}_s^{-\infty }\right)={\text{gr}}_{{\mathcal{V}}_s}^a={\mathcal{V}}_s^a/{\mathcal{V}}_s^{>a}$$

Definition 2.3

(Local Hodge data). For $a\in [0,1),\lambda =\hspace{0.17em}\text{exp}\hspace{0.17em}(2i\pi a)$ and $p\in \mathbb{Z}$, we set for any singularity $s\in \Delta$

• ${\nu }_{\alpha }^p=\dim {\text{gr}}_F^p{\psi }_{\lambda }({\mathcal{V}}_s)$ also written $h^p{\psi }_{\lambda }({\mathcal{V}}_s)$

• $h^p(\mathcal{V})=\sum _{\alpha }{\nu }_{\alpha }^p({\mathcal{V}}_s)$

According to Riemann–Hilbert theorem, for any local system with all eigenvalues of the form $\text{exp}\hspace{0.17em}(-2\pi i\alpha )$ at the singularities endowed with a trivial filtration we associate a filtered ${\mathcal{D}}_{\overline{\mathcal{C}}}$-module with residues and jumps both equal to α (see for example synopsis of [Simpson 90]). Thus the sub ${\mathcal{D}}_{\overline{\mathcal{C}}}$-module corresponding to the residue α has only one jump of full dimension at α, and (2–3) $${\mathrm{deg}}_{\mathit{par}}\left({\text{gr}}_F^p\mathcal{V}\right)={\delta }^p\left(\mathcal{V}\right)+\sum _{s\in \Delta ,\alpha }\alpha {\nu }_{\alpha }^p\left({\mathcal{V}}_s\right)$$(2–3) where we choose $\alpha \in [0,1)$ and where ${\delta }^p(\mathcal{V})$ is the degree of $j_{*}\mathcal{V}.$

2.4. Acceptable metrics and metric extensions

The above Deligne extension has a geometric interpretation when we endow $\mathcal{C}$ with an acceptable metric K. If V is a holomorphic bundle on $\mathcal{C},$ we define the sheaf $\Xi {(V)}_{\alpha }$ on $\mathcal{C}\cup \left\{s\right\}$ as follows. The germs of sections of $\Xi {(E)}_{\alpha }$ at s are the sections s(q) in $j_{*}V$ in the neighborhood of s which satisfy a growth condition; for all $ϵ>0$ there exists $C_{ϵ}$ such that $$\left|s\right(q){|}_K\le C_{ϵ}|q{|}^{\alpha -ϵ}.$$

In general this extension is a filtered vector bundle on which we do not have much information, but the metric is called acceptable if it satisfies some extra growth condition on the curvature, and if it induces the above Deligne extensions.

Lemma 2.4

(Theorem 4 [Simpson 90]). The local system $\mathbb{V}$ with non-expanding cusp monodromies has a metric which is acceptable.

Proof.

For completeness, we reproduce the construction of [Eskin et al. 16]. The idea is to construct locally a nice metric and to patch the local constructions together with partition of unity. The only delicate choice is for the metric around singularities. We want the basis elements ${\tilde{v}}_i$ of the α-eigenspace of the Deligne extension to be given the norm of order $|q{|}^{\alpha }$ in the local coordinate q around the cusp and to be pairwise orthogonal. Let M be such that $e^{2i\pi M}=T,$ where T is the monodromy transformation. Then the Hermitian matrix $\text{exp}\hspace{0.17em}(\hspace{0.17em}\text{log}\hspace{0.17em}|q|\overline{M^t}M)$ defines a metric such that the element ${\tilde{v}}_i$ has norm $\left|q{|}^{\alpha }\right|{\tilde{v}}_i|.$ □

Corollary 2.5.

When the monodromy representation goes to identity, the parabolic degree goes to zero.

Proof.

In the proof above, it appears that $T\to \text{Id}$ implies that the matrix $M\to 0$ and that the metric goes to the standard hermitian metric locally. The curvature goes to zero around singularities and its integral on any subbundle goes to zero. This is its analytic degree, and it is equal to the parabolic degree we are considering (Lemma 6.1 [Simpson 90]). □

3. Proof of Theorem 1.2

3.1. Local Hodge invariants

Our purpose in this subsection is to show the following relation on local Hodge invariants, which will imply Theorem 1.2 according to formula (2–3). The proof will be given in Section 3.2.

Theorem 3.1.

The local Hodge invariants for equation (1–1) are:

1. at z = 0, $${\nu }_{{\alpha }_m}^p=\{\begin{array}{c}1\text{if}p=f\left({\alpha }_m\right)\hfill \\ 0\text{otherwise}\hfill \end{array}$$

2. at $z=\infty ,$ $${\nu }_{-{\beta }_m}^p=\{\begin{array}{c}1\text{if}p-1=f\left({\beta }_m\right)\hfill \\ 0\text{otherwise}\hfill \end{array}$$

3. at z = 1, $${\nu }_{\gamma }^p=\{\begin{array}{c}1\text{if}p=[\gamma ]+1\hfill \\ 0\text{otherwise}\hfill \end{array}$$

Remark.

Computations of (1–1) and (1–2) are done in [Fedorov 15, Theorem 3]. We give a similar proof with an alternative combinatoric point of view.

Recall that the monodromy at z = 1 has all eigenvalues but one equal to one. The last one is equal to $e^{2i\pi \gamma }.$

3.2. Computation of local Hodge invariants

In the following, we denote by M the local system defined by the hypergeometric equation (1–1) in the introduction. The point at infinity plays a particular role in middle convolution, thus we apply a biholomorphism to the sphere which will send the three singularity points $0,1,\infty$ to $0,1,2.$ Hereafter, M will have singularities at 0, 1, 2.

Similarly $M_{k,j}$ corresponds to the hypergeometric equation where we remove terms in α_k and β_j, $$\prod _{m\ne k}(D-{\alpha }_m)-z\prod _{n\ne j}(D-{\beta }_n)=0$$

Let $L_{k,j}$ be a flat line bundle above ${\mathbb{P}}^1-\{0,2,\infty \}$ with monodromy $E\left({\alpha }_k\right)$ at 0, $E\left(-{\beta }_j\right)$ at 2 and $E\left({\beta }_j-{\alpha }_k\right)$ at $\infty .$ Similarly $L{\prime }_{k,j}$ is defined to have monodromy $E\left(-{\beta }_j\right)$ at 0, $E\left({\alpha }_k\right)$ at 2 and $E\left({\beta }_j-{\alpha }_k\right)$ at $\infty .$

The two key stones in the proof are Lemma 3.1 in [Fedorov 15] and Theorem 3.1.2 in [Dettweiler and Sabbah 13]:

Lemma 3.2

(Fedorov). For any $k,j\in \{1,\dots ,n\}$ we have, $$M\simeq {\text{MC}}_{{\beta }_j-{\alpha }_k}\left(M_{k,j}\otimes L{\prime }_{k,j}\right)\otimes L_{k,j}$$

In the following theorem, we modify a little bit the formulation of [Dettweiler and Sabbah 13], taking $\alpha =1-\alpha$ so that the condition becomes $1-\alpha \in (0,1-{\alpha }_0]\iff \alpha \in [{\alpha }_0,1).$

Theorem 3.3

(Dettweiler-Sabbah). Let ${\alpha }_0\in (0,1)$, for every singular point in $\Delta$, every $\alpha \in [0,1)$ and any local system M, we have, $${\nu }_{\alpha }^p\left({\text{MC}}_{{\alpha }_0}\left(M\right)\right)=\{\begin{array}{cc}{\nu }_{\alpha -{\alpha }_0}^{p-1}\left(M\right)\hfill & \text{if}\alpha \in \left[0,{\alpha }_0\right)\hfill \\ {\nu }_{\alpha -{\alpha }_0}^p\left(M\right)\hfill & \text{otherwise}\hfill \end{array}$$ and, $${\delta }^p\left({\text{MC}}_{{\alpha }_0}\left(M\right)\right)={\delta }^p\left(M\right)+h^p\left(M\right)-{\sum }_{\underset{\{-\alpha \}\in [0,{\alpha }_0)}{s\in \Delta }}{\nu }_{s,\alpha }^{p-1}\left(M\right)$$

3.2.1. Recursive argument

We apply a recursive argument on the dimension of the hypergeometric equation. Let us assume that $n\ge 3$ and that Theorem 3.1 is true for n – 1.

Figure 3. The Farey’s tessellation.

For convenience in the demonstration, we change the indices of α and β such that α_i (resp. β_i) is the ith α (resp. β) we come upon while browsing the circle to construct the function f. For $x,y,z$ in $\mathbb{R}/\mathbb{Z}$ we write $x\prec y\prec z$ if there are three real $\widehat{x},\widehat{y},\widehat{z}$ which represent x, y, z such that x < y < z and $z-x<1.$

We apply Lemma 3.2 with α_k and β_j such that ${\alpha }_k\le {\beta }_j.$ Let us describe what happens to the combinatorial function f after we remove these two eigenvalues. We denote by $f\prime$ the function we obtain (Figure 2).

Removing α_k will make the function decrease by one for the following eigenvalues until we meet β_j, thus for any $\tau \ne {\alpha }_k,{\beta }_j,$ $$f(\tau )=\{\begin{array}{cc}f\prime (\tau )\hfill & \text{if}\tau \prec {\alpha }_k\prec {\beta }_j\hfill \\ f\prime (\tau )+1\hfill & \text{if}{\alpha }_k\prec \tau \prec {\beta }_j\hfill \end{array}$$

We apply Theorem 3.3 with ${\alpha }_0={\beta }_j-{\alpha }_k.$ It yields that we have for all $m\ne k,$ at singularity zero, $${\nu }_{1+{\alpha }_m-{\alpha }_k}^p\left(M\otimes L_{k,j}^{-1}\right)=\{\begin{array}{cc}{\nu }_{{\alpha }_m-{\beta }_j}^{p-1}\left(M_{k,j}\otimes L{\prime }_{k,j}\right)\hfill & \text{if}\{{\alpha }_m-{\alpha }_k\}<{\beta }_j-{\alpha }_k\hfill \\ {\nu }_{{\alpha }_m-{\beta }_j}^p\left(M_{k,j}\otimes L{\prime }_{k,j}\right)\hfill & \text{otherwise}\hfill \end{array}$$ which can be written in a simpler form $${\nu }_{{\alpha }_m-{\alpha }_k}^p\left(M\otimes L_{k,j}^{-1}\right)=\{\begin{array}{cc}{\nu }_{{\alpha }_m-{\beta }_j}^{p-1}\left(M_{k,j}\otimes L{\prime }_{k,j}\right)\hfill & \text{if}{\alpha }_k\prec {\alpha }_m\prec {\beta }_j\hfill \\ {\nu }_{{\alpha }_k-{\beta }_j}^p\left(M_{k,j}\otimes L{\prime }_{k,j}\right)\hfill & \text{if}{\alpha }_m\prec {\alpha }_k\prec {\beta }_j\hfill \end{array}$$

In terms of M and $M_{k,j},$ $${\nu }_{{\alpha }_m}^p\left(M\right)=\{\begin{array}{cc}{\nu }_{{\alpha }_m}^{p-1}\left(M_{k,j}\right)\hfill & \text{if}{\alpha }_k\prec {\alpha }_m\prec {\beta }_j\hfill \\ {\nu }_{{\alpha }_m}^p\left(M_{k,j}\right)\hfill & \text{if}{\alpha }_m\prec {\alpha }_k\prec {\beta }_j\hfill \end{array}$$

For any integer i, j we denote by $\delta (i,j)$ the function which is 1 when i = j and is zero otherwise. $${\nu }_{{\alpha }_m}^p\left(M\right)=\{\begin{array}{cc}\delta \left(p-1,f\prime \left({\alpha }_m\right)\right)\hfill & \text{if}{\alpha }_k\prec {\alpha }_m\prec {\beta }_j\hfill \\ \delta \left(p,f\prime \left({\alpha }_m\right)\right)\hfill & \text{if}{\alpha }_m\prec {\alpha }_k\prec {\beta }_j\hfill \end{array}=\delta \left(p,f\left({\alpha }_m\right)\right)$$

Similarly for all $m\ne j,$ at singularity 2, $$\begin{array}{c}{\nu }_{-{\beta }_m}^p\left(M\right)=\{\begin{array}{cc}{\nu }_{-{\beta }_m}^{p-1}\left(M_{k,j}\right)\hfill & \text{if}{\alpha }_k\prec {\beta }_j\prec {\beta }_m\hfill \\ {\nu }_{-{\beta }_m}^p\left(M_{k,j}\right)\hfill & \text{if}{\alpha }_k\prec {\beta }_m\prec {\beta }_j\hfill \end{array}\\ {\nu }_{{\beta }_m}^p\left(M\right)=\{\begin{array}{cc}\delta \left(p-1,f\prime \left({\beta }_m\right)\right)\hfill & \text{if}{\alpha }_k\prec {\beta }_j\prec {\beta }_m\hfill \\ \delta \left(p,f\prime \left({\beta }_m\right)\right)\hfill & \text{if}{\alpha }_k\prec {\beta }_m\prec {\beta }_j\hfill \end{array}=\delta \left(p,f\left({\beta }_k\right)\right)\end{array}$$ And at 1, we set $$\tilde{\gamma }:=\gamma -{\beta }_j+{\alpha }_k=\sum _{m\ne j}{\beta }_m-\sum _{m\ne k}{\alpha }_m,$$ $$\begin{array}{c}{\nu }_{\gamma }^p\left(M\right)=\{\begin{array}{cc}{\nu }_{\tilde{\gamma }}^{p-1}\left(M_{k,j}\right)\hfill & \text{if}\{\gamma \}<{\beta }_j-{\alpha }_k\hfill \\ {\nu }_{\tilde{\gamma }}^p\left(M_{k,j}\right)\hfill & \text{otherwise}\hfill \end{array}\\ {\nu }_{\gamma }^p\left(M\right)=\{\begin{array}{cc}\delta \left(p-1,\left[\tilde{\gamma }\right]+1\right)\hfill & \text{if}\{\gamma \}=\left\{\tilde{\gamma }\right\}+{\beta }_j-{\alpha }_k-1\hfill \\ \delta \left(p,\left[\tilde{\gamma }\right]+1\right)\hfill & \text{if}\{\gamma \}=\left\{\tilde{\gamma }\right\}+{\beta }_j-{\alpha }_k\hfill \end{array}=\delta \left(p,[\gamma ]+1\right)\end{array}$$

If we pick ${\beta }_n>{\alpha }_n$ for the computation, we have Hodge invariants for all values except for α_n and β_n. We then perform the computation for ${\alpha }_1<{\beta }_1,$ from which we deduce the invariants at β_n and α_n. Yet, we should keep in mind that the previous computations are always modulo shifting of the VHS. That is why we need to have dimension at least 3, since in this case α₂ will appear in both computations and will show there is no shift in our formulas.

3.2.2. Initialization for n = 2

We use the computations performed in the previous part for α₂ and β₂. To do so, remark that the unique (complex polarized) VHS on $M_{2,2}$ is defined by $h^p\left(M\right)=\delta (p,1)$ and the only non-zero local Hodge invariants are $$\begin{array}{ccc}{\nu }_{{\alpha }_1}^1\left(M_{2,2}\right)\hfill & =1\hfill & \text{at}\text{singularity}0\hfill \\ {\nu }_{-{\beta }_1}^1\left(M_{2,2}\right)\hfill & =1\hfill & \text{at}\text{singularity}\infty \hfill \\ {\nu }_{{\beta }_1-{\alpha }_1}^1\left(M_{2,2}\right)\hfill & =1\hfill & \text{at}\text{singularity}1\hfill \end{array}$$ which corresponds to the definition of $\delta (p,f\prime ({\alpha }_1))$ for the first two, and to $\delta (p,[\gamma ]+1)$ for the last one.

Using the previous subsection, we deduce $$\begin{array}{ccc}{\nu }_{{\alpha }_1}^p\left(M\right)\hfill & =\delta (p,f({\alpha }_1\left)\right)\hfill & \text{at}\text{singularity}0\hfill \\ {\nu }_{-{\beta }_1}^p\left(M\right)\hfill & =\delta (p,f({\alpha }_1\left)\right)\hfill & \text{at}\text{singularity}\infty \hfill \\ {\nu }_{\gamma }^p\left(M\right)\hfill & =\delta (p,[\gamma ]+1)\hfill & \text{at}\text{singularity}1\hfill \end{array}$$

According to [Fedorov 15], the Hodge numbers of M are $$h^1=\{\begin{array}{cc}1\hfill & \text{if}{\alpha }_1\prec {\alpha }_2\prec {\beta }_1\prec {\beta }_2\hfill \\ 2\hfill & \text{if}{\alpha }_1\prec {\beta }_1\prec {\alpha }_2\prec {\beta }_2\hfill \end{array},h^2=\{\begin{array}{cc}1\hfill & \text{if}{\alpha }_1\prec {\alpha }_2\prec {\beta }_1\prec {\beta }_2\hfill \\ 0\hfill & \text{if}{\alpha }_1\prec {\beta }_1\prec {\alpha }_2\prec {\beta }_2\hfill \end{array}$$

Using the fact that $\sum _{\alpha }{\nu }_{\alpha }^p=h^p,$ we can deduce the other Hodge invariants. $$\begin{array}{cc}{\nu }_{{\alpha }_2}^2=1\hfill & \text{if}{\alpha }_1\prec {\alpha }_2\prec {\beta }_1\prec {\beta }_2\hfill \\ {\nu }_{{\alpha }_2}^1=1\hfill & \text{if}{\alpha }_1\prec {\beta }_1\prec {\alpha }_2\prec {\beta }_2\hfill \end{array}$$

We conclude that ${\nu }_{{\alpha }_2}^p\left(M\right)=\delta (p,f({\alpha }_2))$ and similarly ${\nu }_{-{\beta }_2}^p\left(M\right)=\delta (p,f({\alpha }_2)).$

3.3. Continuity of the parabolic degree

To compute ${\delta }^p(V)$ in equation (2–3), we show in the following Lemma that they are locally constant on a given domain.

Lemma 3.4.

For all hypergeometric systems belonging to ${\alpha }_1,\dots ,{\alpha }_m,{\beta }_1,\dots ,{\beta }_n$ all distinct modulo one the δ^p’s only depend on the intertwining diagram and the integer part of γ.

Proof.

The main idea here is that rigidity implies that the holomorphic structure of the Higgs bundles is locally constant.

Let L and $L\prime$ be the flat bundles of solutions of equation (1–1) for eigenvalues α, β and $\alpha \prime ,\beta \prime$ as in the Theorem with the same intertwining diagram and integer part of γ. We endow these flat bundles with a trivial filtration. To L and $L\prime$ correspond some Higgs bundle $(E,\theta )$ and $(E\prime ,\theta \prime )$ together with parabolic structures at singularities (see [Simpson 90]).

Now consider $(E,\theta )$ filtered with the weights $\alpha {\prime }_1\le \cdots \le \alpha {\prime }_n$ at 0 where we take ${\mathcal{E}}^{\ge \alpha {\prime }_i}={\mathcal{E}}^{\ge {\alpha }_i}.$ Similarly at $\infty$ and we keep the same filtration above 1. The monodromy matrices of the flat bundle associated to this new filtered Higgs bundle have the same eigenvalues as $L\prime$ according to the table in the Synopsis of [Simpson 90] (p. 720) and no nilpotent part. Thus its monodromy matrices are conjugate locally with the ones of $L\prime$ and by rigidity is isomorphic to $L\prime .$

We conclude using uniqueness of system of Hodge bundle associated to a stable rigid Higgs bundle with given weights. □

Together with Corollary 2.5 it will be enough to compute ${\delta }^p(V).$ We fix an intertwining diagram and a floor value for γ and make the α and βs go to 0 or 1. At the limit, the parabolic degree is zero and we can deduce ${\delta }^p(V)$ from the Theorem 3.1 as described in the next subsection.

Figure 5. Crossings of a given geodesic.

3.4. Algorithm to compute δ^p

Algorithm 1.

Computation of δ^p

function degree($\alpha ,\beta ,p$)

if $p\le 1$ then return 0

else if LENGTH $(\alpha )=1$ then

if p > 1 then return 0

else return –1

end if

end if

relabel $(\alpha ,\beta )$

$p\leftarrow \mathrm{SORT}(\alpha ·\beta )$

$G_{\alpha }\leftarrow [\varnothing ],G_{\beta }\leftarrow [\varnothing ]$

$c\leftarrow 0,p\prime \leftarrow p$

for $1\le i\le 2n$ do

if $p_i\in \alpha$ and $p_{i+1}\in \beta$ then

$G_{\alpha }\leftarrow G_{\alpha }·[p_{i+1}-p_i]$

end if

if $p_i\in \beta$ and $p_{i+1}\in \alpha$ then

$G_{\beta }\leftarrow G_{\beta }·[p_{i+1}-p_i]$

end if

end for

$G_{\beta }\leftarrow p_{2n}-p_1$

$({\alpha }_i,{\beta }_j)\leftarrow \mathrm{SMALLEST}(G_{\alpha })$

$({\beta }_k,{\alpha }_l)\leftarrow \mathrm{SMALLEST}(G_{\beta })$

if ${\beta }_j-{\alpha }_i<{\alpha }_l-{\beta }_k$ then

$\alpha \prime \leftarrow \alpha \backslash {\alpha }_i$

$\beta \prime \leftarrow \beta \backslash {\beta }_j$

${\beta }_k^{\prime }\leftarrow {\beta }_k+{\beta }_j-{\alpha }_i$

if $f({\beta }_j)=p-1$ then

$c\leftarrow -1$

end if

else

$\alpha \prime \leftarrow \alpha \backslash {\alpha }_l$

$\beta \prime \leftarrow \beta \backslash {\beta }_k$

${\alpha }_i^{\prime }\leftarrow {\alpha }_i+{\alpha }_l-{\beta }_k$

if $f({\beta }_k)=p-1$ then

$c\leftarrow -1$

end if

end if

if $\min f(\beta \prime )>0$ then

$p\prime \leftarrow p-1$

end if

return $c+\mathrm{DEGREE}(\alpha \prime ,\beta \prime ,p\prime )$

end function

Using the previous lemma, we present an algorithm to compute δ^p for a given set of α and β. We let the monodromy matrices go to identity while keeping the intertwining diagram and γ unchanged. Corollary 2.5 states that the parabolic degree at the limit will be zero, thus we can deduce δ^p from the formula for the corresponding parabolic degree at the limit.

Assume $f({\alpha }_1)$ is a minimal value of $f(\alpha ),$ then γ is computed for representatives of the α and β in the interval $[{\alpha }_1,{\alpha }_1+1)$ for any representative of α₁ in $\mathbb{R}.$ We shift everything so that we can assume ${\alpha }_1=0$ — this process of relabeling and shifting is done by the function Relabel in Algorithm 1.

Remark that we can deform the set of points continuously such that two consecutive α and β get infinitely close from one another without changing the quantity γ, their value do not interfere any further in the degree formula. Indeed, as they are consecutive points, they will always appear substracted one to the other in the formulas, we can thus shift them together freely without changing neither the intertwining diagram, the value of γ, nor the parabolic degrees. We can then concentrate on the remaining points.

This implies an induction process on the dimension of the bundle to compute δ^p. Consider the gaps between two consecutive points that are not both α or both β. Let α_i and β_j be the two points with a minimal such gap—this is returned by the function Smallest in Algorithm 1. If α_i comes before β_j in the cyclic order, pick another β_k such that the next point is some α, and shift simultaneously α_i and β_k by ${\beta }_j-{\alpha }_i.$ We make a symmetric process in the opposite case. This reduces the problem to one dimension lower, without α_i and β_j.

In the case ${\alpha }_i={\alpha }_1,$ when we let β_j go to α₁, the quantity ${\alpha }_i+1-{\beta }_j\to 0.$ Otherwise, ${\alpha }_i+1-{\beta }_j\to 1.$ This is why we add the variable c to the recursive result in the algorithm when these two points appear in the formula of the parabolic degree, i.e. when $f({\beta }_j)=p-1.$

Finally, in some cases the intertwining diagram on the induced set of α and β will be shift by one, compared to the initial one. This is why we need to compare the minimum of the function f one the new set of points, and modify the value of p accordingly.

4. Algorithm

In this section, we describe the algorithm used to compute the Lyapunov exponents. We start by simulating a generic hyperbolic geodesic and following how it winds around the surface, namely the evolution of the homology class of the closed path. Finally we compute the corresponding monodromy matrix after each turn around a cusp.

4.1. Hyperbolic geodesics

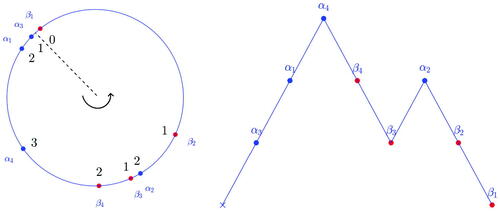
The first question that arise when trying to compute Lyapunov exponents is how to simulate a generic hyperbolic geodesic. We find an answer in a beautiful theorem proved by Caroline Series in [Series 85] which relates hyperbolic geodesics on the Poincaré half-plane and continued fraction development of real numbers. We follow here the notations of [Dal’Bo 07] (see part II.4.1).

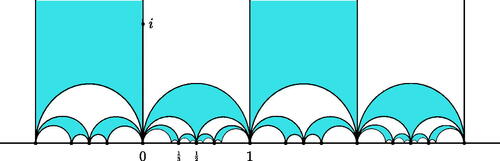
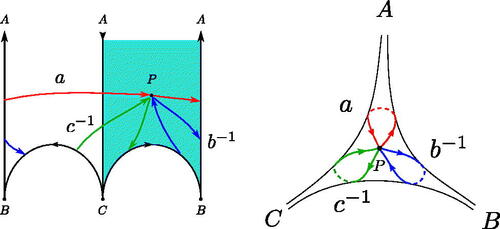
Let us consider the Farey tessellation of $\mathbb{H}$ (see Figure 3). It is invariant with respect to the discrete subgroup of index 3 in $\text{PSL}\left(\mathbb{Z}\right)$ generated by $$〈\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right),\left(\begin{array}{cc}1& 0\\ 1& 1\end{array}\right)〉.$$

The tessellation yields fundamental domains for the action of this group. The sphere minus three points endowed with its complete hyperbolic metric is a degree two cover of the surface induced by the quotient of $\mathbb{H}$ by this group. This is why we represent the tessellation with two colors: a fundamental domain for the sphere is given by any two adjacent triangles of different colors. Thus it will be easy once we understand the geodesics with respect to this tessellation to see them on the sphere.

Let us consider a geodesic going through i. It lands on the real axis at a positive and a negative real number. The positive real number will be called x, this number determines completely the geodesic since we know two distinct points on it.

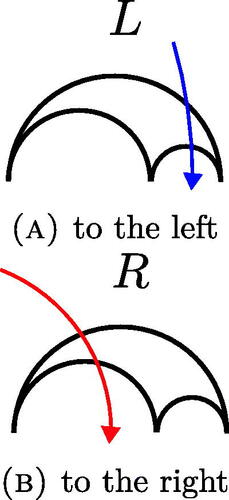
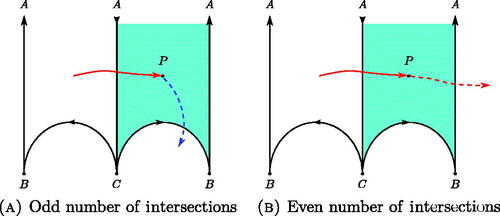
We associate to this geodesic a sequence of positive integers: consider the sequence of hyperbolic triangles the geodesic crosses. For each one of those triangles, the geodesic has two ways to cross them (see Figure 4). Once it enters it, it can leave it crossing either the side of the triangle to its left (a) or to its right (b).

Figure 4. Two ways to cross an hyperbolic triangle.

Remark.

The vertices of hyperbolic triangles are located at rational numbers, so this sequence will be infinite if and only if x is irrational (see [Dal’Bo 07] Lemme 4.2).

We have now for a generic geodesic an infinite word in two letters L and R associated to a geodesic. For example the word associated to the geodesic in Figure 5, is of the form $\mathit{LLRRLR}\cdots =L^2{R}^2{L}^{1}R\cdots .$ We can factorize each of these words and get $$R^{n_0}{L}^{n_1}{R}^{n_2}{L}^{n_3}\cdots$$

Except for n₀ which can be zero the n_i are positive integers.

Theorem 4.1.

The sequence $(n_k)$ is the continued fraction development of x. In other words, $$x=n_0+\frac{1}{n_1+\frac{1}{n_2+\frac{1}{n_3+\cdots }}}$$

The measure induced on the real axis by the measure on $T^1\mathbb{H}$ dominates Lebesgue measure.

See [Dal’Bo 07] II.4 or [Series 85] for a proof.

Remark.

This theorem states exactly that to study a generic geodesic on the hyperbolic plane, we can consider a Lebesgue generic number in $(0,\infty )$ and compute its continued fraction development.

As explained in the introduction, we consider the Lyapunov exponents induced by the flat connection on the hypergeometric functions bundle. They are defined for almost every points in the unit tangent bundle of the base space (here ${\mathbb{P}}^1-\{0,1,\infty \}$) as the growth of transported vectors along the hyperbolic geodesic flow. Thus to compute these Lyapunov exponents, we need to estimate the parallel transport induced by the flat connection along the hyperbolic flow. So we need to understand how a generic hyperbolic geodesic winds around the cusps, and compute the product of the corresponding monodromy matrices for the flat connection. By the previous theorem we can simulate a generic cutting sequence of a hyperbolic geodesic in the Farey’s tessellation of $\mathbb{H}.$ Our goal now will be to associate to such a sequence a product of monodromy matrices keeping track of its homotopy class.

There is a representation of the hyperbolic structure on ${\mathbb{P}}^1-\{0,1,\infty \}$ given by two ideal triangles in the hyperbolic half-plane $(0,1,\infty )$ and $(-1,0,\infty )$ glued together as in Figure 6. The three cups of this representation are denoted by A, B, and C. They can be permuted by an isometry which preserves or reverses orientation whenever the permutation preserves or changes the cyclic order of the cups. This representation is constructed with two copies of a fundamental domain for Farey’s tessellation, thus the cutting sequence of a generic geodesic against these two cells is encoded as previously by the continued fraction expansion of a generic real number.

Figure 6. Homology marking.

In this representation, let P be a point inside the triangle $(0,1,\infty ).$ Let us assume the first side crossed by the geodesic in $(1,\infty ),$ and the next number in the coding N describes how many times the geodesic will cross the left sides of the triangle after the first crossing. Observe that after one crossing we are back to P and the geodesic made a loop in the direct (counter-clockwise) direction around the cusp A. Each pair of crossing to the left adds one loop around A. At the end of this sequence of crossings we must discriminate two cases:

• If N is even, the geodesic makes $N/2$ direct loops around A, and the next crossing will be along $(1,\infty ).$

• If N is odd, the geodesic makes $(N+1)/2$ direct loops around A. The next crossing is given by one unit of the next number of crossings to the right and will be along (0, 1).

The remaining part of the trajectory of the geodesic is now described by the next numbers of the coding. The one following N, $N\prime$ now describes how many times the geodesic crosses the right side of the triangles. We now apply an orientation reversing isometry (such that left and right will be switched) on the representation to reduce the problem to the previous case, where the geodesic starts by crossing the geodesic $(1,\infty )$ and the number N describes how many times it will cross the left side (Figure 7).

Figure 7. Crossings after N steps.

• In the first case, we invert 1 and $\infty$ (A and B), and $N:=N\prime .$

• In the second case, we invert 0 and $\infty$ (C and A), and $N:=N\prime -1.$

There is a last point to consider, since we want to compare the growth of the norm with regards to the geodesic flow, we need to follow the length of the latter. Here we have a discretized description of the geodesic flow, at each time it returns to the fundamental domain. We can with this description fully describe the homology of the flow, but its length will a priori not correspond to the number of iterations of our algorithm. Its speed is given by the first Lyapunov exponent of the Gauss map, as explained in [Zorich 96] Appendix 10. It is equal to Lévy’s constant $\gamma =\frac{{\pi }^2}{12\hspace{0.17em}\text{log}\hspace{0.17em}2}.$

4.2. Pseudo-code

Based on the previous subsection, we now formulate in Algorithm 2 the pseudo-code of an algorithm to computing the Lyapunov exponents of a local system over ${\mathbb{P}}^1-\{0,1,\infty \},$ for given monodromy matrices at cusps.

Let us start with a random vector ($\mathit{random}\_\mathit{vector}$) in the local system and follow its parallel transport along a random hyperbolic geodesic. This random geodesic is coded by a random number in the interval $x\in [0,1]$ with respect to the invariant Gauss measure ($\mathit{random}\_\mathit{gauss}$). Namely, it is coded by the continued fraction development $x=[0:x_1,x_2,\dots ].$

As explained in the previous subsection, we start in a ideal triangle $(0,1,\infty )$ in the fundamental domain, and mark the cusp at the top with the variable $\mathit{cusp}=\infty .$ The geodesic $(1,\infty )$ will be the first one to be crossed by the cutting sequence.

The orientation alternates after each step, so it will be read out of the parity of i. Moreover, when the number of cuttings determined by x_i is odd, we use one cutting from the next sequence $x_{i+1}$ to reduce to the previous case. We keep track of this phenomenon with a penalty variable p.

The key point of the algorithm is to keep track of which cusp is placed at $\infty$ in the given representation. The other two cups will be determined by the orientation, that is why we use maps next and previous which browse through this cyclic ordering of the cusps fixed at the beginning, here $0\to 1\to \infty \to 0.$

Algorithm 2.

Simulation of hyperbolic flow

$v\leftarrow \mathit{random}\_\mathit{vector}()$

$x\leftarrow \mathit{random}\_\mathit{gauss}()$ ⊳ $x=[0:x_1,x_2,\dots ]$

$p\leftarrow 0,\mathit{cusp}\leftarrow \infty$

for $1\le i\le K$ do

$N\leftarrow x_i-p$

if N is even and i is odd then

$v\leftarrow M_{\mathit{cusp}}^{N/2}·v$

$\mathit{cusp}\leftarrow \mathit{next}(\mathit{cusp})$

$p\leftarrow 0$

end if

if N is even and i is even then

$v\leftarrow M_{\mathit{cusp}}^{-N/2}·v$

$\mathit{cusp}\leftarrow \mathit{previous}(\mathit{cusp})$

$p\leftarrow 0$

end if

if N is odd and i is odd then

$v\leftarrow M_{\mathit{cusp}}^{(N+1)/2}·v$

$\mathit{cusp}\leftarrow \mathit{previous}(\mathit{cusp})$

$p\leftarrow 1$

end if

if N is odd and i is even then

$v\leftarrow M_{\mathit{cusp}}^{-(N+1)/2}·v$

$\mathit{cusp}\leftarrow \mathit{next}(\mathit{cusp})$

$p\leftarrow 1$

end if

end for

We apply this algorithm to n random vectors v, after a large number of iterations K we orthogonalize the family of vectors using Gram–Schmidt process. Let $z_1,\dots ,z_n$ the norms of these orthogonal vectors. Then the Lyapunov exponents λ_i can be estimated with the formula $$\frac{1}{\gamma }·\frac{z_i}{K}\approx {\lambda }_i.$$

4.3. Monodromy matrices

In the introduction, Proposition 1.1 gives a set of properties on the monodromy matrices for hypergeometric differential equations with two distinct sequences of real parameters. The following theorem of Levelt (see Theorem 3.2.3 in [Beukers 09] for a proof) gives a rigidity property for these matrices together with a very useful specific form for them.

Theorem 4.2

(Levelt). Assume $e^{2i\pi {\alpha }_1},\dots ,e^{2i\pi {\alpha }_n}$ and $e^{2i\pi {\beta }_1},\dots ,e^{2i\pi {\beta }_n}$ are two disjoint sequences. Then $M_0{M}_{\infty }$ is a reflection and the pair $M_0,M_{\infty }$ is uniquely determined up to conjugation by $$M_0=\left(\begin{array}{ccccc}0& 0& \dots & 0& -A_n\\ 1& 0& \dots & 0& -A_{n-1}\\ 0& 1& \dots & 0& -A_{n-2}\\ ⋮& & & 0& ⋮\\ 0& 0& \dots & 1& -A_1\end{array}\right)M_{\infty }^{-1}=\left(\begin{array}{ccccc}0& 0& \dots & 0& -B_n\\ 1& 0& \dots & 0& -B_{n-1}\\ 0& 1& \dots & 0& -B_{n-2}\\ ⋮& & & 0& ⋮\\ 0& 0& \dots & 1& -B_1\end{array}\right)$$

With $$\begin{array}{c}\prod _i(X-e^{2i\pi {\alpha }_i})=X^n+A_1{X}^{n-1}+\cdots +A_n\\ \prod _i(X-e^{2i\pi {\beta }_i})=X^n+B_1{X}^{n-1}+\cdots +B_n\end{array}$$

5. Observations

5.1. Calabi–Yau families example

A first family of examples is coming from 14 1-dimensional families of Calabi–Yau varieties of dimension 3. The Gauss–Manin connection for this family on its Hodge bundle gives an example of the hypergeometric family we are considering. The monodromy matrices were computed explicitly in [Van Enckevort and Van Straten 08] and are parametrized by two integers C and d. We introduce the following monodromy matrices, $$T=\left(\begin{array}{cccc}1& 0& 0& 0\\ 1& 1& 0& 0\\ 1/2& 1& 1& 0\\ 1/6& 1/2& 1& 1\end{array}\right)S=\left(\begin{array}{cccc}1& -C/12& 0& -d\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$$

In the previous notations, $M_0=T,M_1=S,M_{\infty }={(\mathit{TS})}^{-1}.$ These matrices satisfy relation $M_{\infty }{M}_0{M}_1=\text{Id}.$ We see that $M_1-\text{Id}$ has rank one and eigenvalues of M₀ and $M_{\infty }$ have modulus one thus correspond to hypergeometric equations. In this setting, T has eigenvalues all equal to one and eigenvalues of ${(\mathit{TS})}^{-1}$ are symmetric with respect to zero, we denote them by ${\mu }_1,{\mu }_2,-{\mu }_2,-{\mu }_1$ where ${\mu }_1,{\mu }_2\ge 0.$

The parabolic degree of the holomorphic Hodge subbundles are given by,

Theorem

[Eskin et al. 16]. Suppose $0<{\mu }_1\le {\mu }_2\le 1/2$ then the degree of the Hodge bundles are $${\mathrm{deg}}_{\mathit{par}}{\mathcal{E}}^{3,0}={\mu }_1\text{and}{\mathrm{deg}}_{\mathit{par}}{\mathcal{E}}^{2,1}={\mu }_2$$

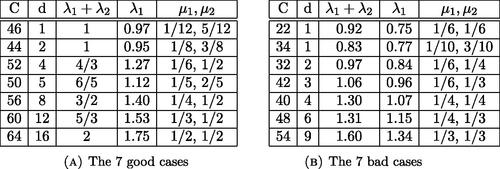
Thus according to the same article, we know that $2({\mu }_1+{\mu }_2)$ is a lower bound for the sum of Lyapunov exponents. We call good cases the equality cases and bad cases the cases where there is strict inequality.

There are 14 different couples of values for C and d where the corresponding flat bundle is an actual Hodge bundle over a family of Calabi–Yau varieties. These examples where computed few years ago by M. Kontsevich and were a motivation for this article. We list them in Figure 8.

Figure 8. Experiments.

Figure 9. Difference between sum of Lyapunov exponents and parabolic degree for a generalization of the 14 families in [Eskin et al. 16].

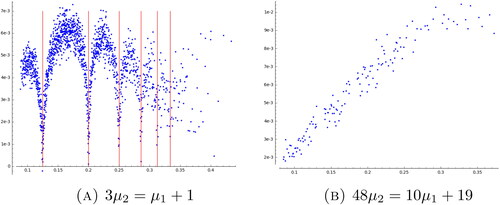
To see what happens in a similar setting for more general hypergeometric equations, we vary C, d and compute the corresponding eigenvalues μ₁ and μ₂ as well as the Lyapunov exponents. In Figure 9(a) we drew a blue point at coordinate $({\mu }_1,{\mu }_2)$ if the sum of positive Lyapunov exponents are as close to the parabolic degree $2({\mu }_1+{\mu }_2)$ as the precision we have numerically and we put a red point when this value is outside of the confidence interval.

Figure 10. Restriction on the blue line in Figure 9a.

Note that according to Figure 9(a) it seems that all points below the line of equation $3{\mu }_2={\mu }_1+1$ are bad cases. In Figure 9(b), we represent the distance of the sum of the Lyapunov exponents to the expected formula. We see that this gives a function that oscillates above zero. More precisely, it seems that good cases are outside of some lines passing through $(1/2,1/2).$

To push the numerical simulations further, we consider what happens on lines of equation $3{\mu }_2={\mu }_1+1$ (Figure 10(a)) and $48{\mu }_2=10{\mu }_1+19$ (Figure 10(b)) both passing through $(1/2,1/2)$ and a point corresponding to one of the previous good cases.

Figure 11. Sum of positive Lyapunov exponents in a subfamily of hypergeometric equation of order 2.

We observe that on the graph (Figure 10(b)) there is only one good case which corresponds to $({\mu }_1,{\mu }_2)=(1/10,3/10)$ in the previous list of good cases. In the graph (Figure 10(a)), there are good cases at points $({\mu }_1,{\mu }_2)=(1/8,3/8),(2/10,4/10)$ which were also on the previous list but other points appear such as $(3/12,5/12),(4/14,6/14),(5/16,7/16),(6/18,8/18).$

Remark that these all have the form $$(\frac{k-3}{2k},\frac{k-1}{2k})$$ we checked it numerically for all $4\le k\le 10,$ we conjecture that this phenomenon appears for every $k\ge 4.$

According to [Brav and Thomas 14] and [Singh and Venkataramana 14], the 7 good cases correspond to cases where the monodromy group of the hypergeometric local system is of infinite index in $\mathit{Sp}(4,\mathbb{Z}),$ which is commonly called thin. In the other cases the group is of finite index and is called thick. The new conjectural good cases we found by ways of Lyapunov exponents do not seem to have a representation with integers or even rational C and d. A lot of questions arise about these points, for example can we find a number-theoretic interpretation of their equality as in Conjecture 6.5 in [Eskin et al. 16], or is there a specific property on the monodromy group in these cases.

Yuri Manin pointed out a possible interpretation in cosmology of the Lyapunov exponents in our setting, and a probable relation to Kasner exponents using time complexification; compare to [Manin and Marcolli 14] and [Manin and Marcolli 15].

5.2. Examples for n = 2

As we have seen in the introduction the two Lyapunov exponents are symmetric λ₁ and $-{\lambda }_1.$ The sum of the positive Lyapunov exponents is just λ₁. The parameter space we have for these 2-dimensional flat bundles are ${\alpha }_1,{\alpha }_2,{\beta }_1,{\beta }_2.$

The Lyapunov exponents are invariant through translation of the set of parameters. Indeed, we can consider the bundle with $e^{\delta }{M}_0$ and $e^{-\delta }{M}_{\infty }$ monodromies, it will have the same set of Lyapunov exponents since both scalar will appear with the same frequency and its parameters will be ${\alpha }_1+\delta ,\dots ,{\alpha }_h+\delta ,{\beta }_1+\delta ,\dots ,{\beta }_h+\delta$ hence without loss of generality we can assume ${\beta }_1=0.$ Moreover the parameters are given as a set, the order does not matter.

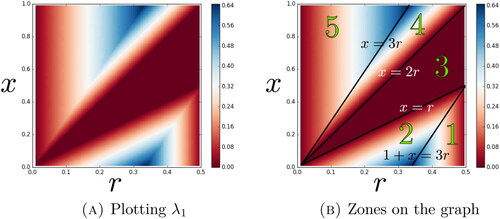
In the following experiments we will consider a set of parameters where the βs will be equidistributed and the αs will be shifted with respect to them. Here we represent the value of the Lyapunov exponent for ${\alpha }_1=r,{\alpha }_2=2r,{\beta }_1=0,{\beta }_2=x$ and we have by definition $\gamma =x-3r$ (Figure 11).

Figure 12. Intertwining diagrams in the zones of Figure 11b.

Remark.

We first notice that the zone where the Lyapunov exponent is zero corresponds to the setting where the parameters are alternate and where there is a positive definite bilinear form invariant by the flat connection (see Section 1). This will be true whenever the VHS has weight 0.

Another noticeable fact is that zones are delimited by combinatorics of α and β, and of $[\gamma ]$ introduced in the introduction.

Remark that $[\gamma ]$ is 0 in zones 1, 4, and 1 in zones 2, 5. In the following table, we give a relation binding ${\lambda }_1,r,x$ obtained by linear regression. The other column is the formula for the parabolic degree in the given zone (Figure 12).

In this case, the VHS is of weight $\le 1$ and thus is in the setting of [Kontsevich 97]. In consequence, we have the equality $${\lambda }_1=2\frac{{\mathrm{deg}}_{\mathit{par}}{\mathcal{E}}^1}{\chi \left(S\right)}$$ where ${\mathrm{deg}}_{\mathit{par}}$ is the parabolic degree of the holomorphic bundle and $\chi (S)=1$ the Euler characteristic of S.

This is a good test for our algorithm and formula on degree. More generally, for any dimension n, this formula will hold as long as the weight is equal to 1.

Figure 13. Intertwining diagram and parameters for a family with weight 2 VHS.

5.3. A peep to weight 2

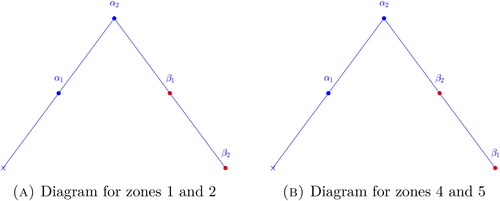
Let n be equal to 3. In this case, there will be three Lyapunov exponents ${\lambda }_1,0,-{\lambda }_1.$ As explained in the previous subsection, if the weight of the VHS is 0, ${\lambda }_1=0;$ if it is 1, λ₁ is equal to twice the parabolic degree of ${\mathcal{E}}^1.$ We consider configurations where the weight is 2. Assume ${\alpha }_1=0,$ the only cyclic order in which the VHS is irreducible and of weight 2 is for, $$0={\alpha }_1<{\alpha }_2<{\alpha }_3<{\beta }_1<{\beta }_2<{\beta }_3<1$$

We parametrize these configurations with 5 parameters which will correspond to the distance between two consecutive eigenvalues: ${\theta }_1={\alpha }_2-{\alpha }_1,{\theta }_2={\alpha }_3-{\alpha }_2,{\theta }_3={\beta }_1-{\alpha }_3,{\theta }_4={\beta }_2-{\beta }_1,{\theta }_5={\beta }_3-{\beta }_2$ (Figure 13).

Figure 14. Difference between the sum of Lyapunov exponents in a family of weight 2.

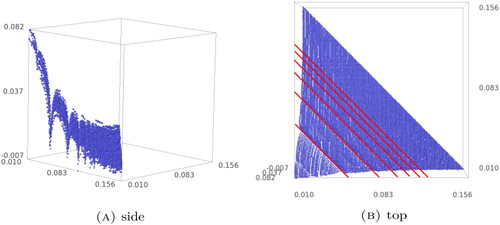
Using a Monte-Carlo process, we found some values in this configuration for which there is equality with twice the parabolic degree of ${\mathcal{E}}^2\oplus {\mathcal{E}}^1.$ We remarked that several parameter points where there is equality satisfy ${\theta }_1={\theta }_2$ and ${\theta }_4={\theta }_5.$ This motivated us to consider the 2 dimensional subspace of parameters $$({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5)=(x,x,1/2,y,y)$$

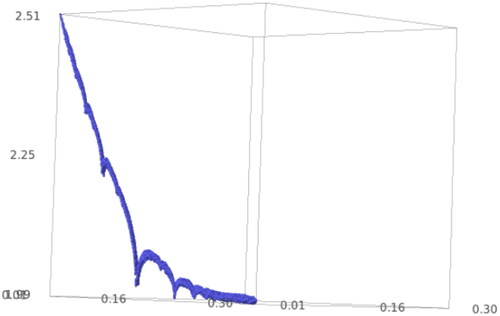
For these parameters we can observe a remarkable phenomenon; the difference between the Lyapunov exponent and the formula with parabolic degrees depends only on x + y. We plot this difference in Figure 14 and see that for some values of x + y there is equality.

Figure 15. Another example of weight 2.

We computed that for $x+y=1/10,1/12,1/18$ the formula holds.

Remark that $${\mathrm{deg}}_{\mathit{par}}{\mathcal{E}}^1\otimes {\mathcal{E}}^2=2(-1+{\alpha }_1+{\alpha }_2+1-{\beta }_2+1-{\beta }_3+\{\gamma \left\}\right)$$

Yet ${\alpha }_1=0,{\alpha }_2=x,$ ${\beta }_2=1/2+2x+y,{\beta }_3=1/2+2x+2y$ and $\gamma =3y+3/2+3x>1.$ Hence $${\mathrm{deg}}_{\mathit{par}}{\mathcal{E}}^1\otimes {\mathcal{E}}^2=1$$

There is equality when ${\lambda }_1=1.$

Moreover ${\mathrm{deg}}_{\mathit{par}}{\mathcal{E}}^1=2(0+{\alpha }_1+1-{\beta }_3)=1-4(x+y)=3/5,2/3,7/9$ in the three previous cases.

We try now another family with an irrational parameter, $$({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5)=(x,x,\frac{1}{2\sqrt{2}},y,y)$$

Again we observe that the difference between the Lyapunov exponent and the formula with parabolic degrees depends only on x + y (Figure 15).

We observe that the difference goes to zero at $x+y=0.22978$ which does not seems to be rational as before. Moreover, in this case, $\gamma =3y+\frac{3}{2\sqrt{2}}+3x$ and $${\mathrm{deg}}_{\mathit{par}}{\mathcal{E}}^1\otimes {\mathcal{E}}^2=\frac{1}{\sqrt{2}}$$ and $${\mathrm{deg}}_{\mathit{par}}{\mathcal{E}}^1=2-\frac{1}{\sqrt{2}}-4(x+y)=0.37377$$

Acknowledgments

These experiments were suggested by Maxim Kontsevich, I am very grateful to him for suggesting this problem, sharing his initial experiments, and for his involvement. I thank dearly Jeremy Daniel for his curiosity to the subject and his answer to my myriad of questions as well as Bertrand Deroin; Anton Zorich for his flawless support and attention, Martin Müller and Roman Fedorov for taking time to explain their understanding of the parabolic degrees and Hodge invariants at MPIM in Bonn. I am also very thankful to Carlos Simpson for his kind answers and encouragements, and to Yuri Manin for pointing out a possible link to cosmology.