Numerical Verification of the Birch and Swinnerton-Dyer Conjecture for Hyperelliptic Curves of Higher Genus over ℚ up to Squares

Abstract

The Birch and Swinnerton-Dyer conjecture has been numerically verified for the Jacobians of 32 modular hyperelliptic curves of genus 2 by Flynn, Leprévost, Schaefer, Stein, Stoll and Wetherell, using modular methods. In the calculation of the real period, there is a slight inaccuracy, which might give problems for curves with non-reduced components in the special fiber of their Néron model. In this present article, we explain how the real period can be computed, and how the verification has been extended to many more hyperelliptic curves, some of genus 3, 4, and 5, without using modular methods.

Keywords:

• Birch-Swinnerton-Dyer conjecture
• Jacobians
• curves

2010 AMS Subject Classification:

• 11G40
• 11G10
• 11G30
• 14H40

1. Introduction

In [Birch and Swinnerton-Dyer 65], Birch and Swinnerton-Dyer first stated their famous conjecture, based on computations with elliptic curves. Later, in [Tate 66], Tate generalized the conjecture to abelian varieties of higher dimension.

Conjecture 1

(BSD, [Hindry and Silverman 2000, Conj. F.4.1.6, p. 462]). Let $A/\mathbb{Q}$ be an abelian variety of dimension d and algebraic rank r. Let L(A, s) be its L-function, $A^{\vee }$ its dual, R_A its regulator, $Ш(A)$ its Tate-Shafarevich group and P_A its period. For each prime p, let c_p be the Tamagawa number of A at p. Then L(A, s) has a zero of order r at s = 1 and $$\underset{s\to 1}{\lim }{(s-1)}^{-r}L(A,s)=\frac{P_A{R}_A·|Ш(A\left)\right|·\prod _p{c}_p}{\left|A{\left(\mathbb{Q}\right)}_{\text{tors}}\right|·\left|A^{\vee }{\left(\mathbb{Q}\right)}_{\text{tors}}\right|}.$$

Remark 2.

In Tate’s original version, [Tate 66], the period, Tamagawa numbers and discriminant are put in the normalization of the L-function.

Tate stated the conjecture for abelian varieties over number fields. However, in [Milne 72], Milne proved that the conjecture is compatible with Weil restriction, so BSD holds for all abelian varieties overall number fields if and only if it holds for all abelian varieties over $\mathbb{Q}.$

Due to work of Kolyvagin [Kolyvagin 89, Kolyvagin 91] and others, a weak version of BSD has been proven for elliptic curves over $\mathbb{Q}$ with analytic rank at most 1. More precisely, we know that in these cases the algebraic rank equals the analytic rank. On the other hand, on the numerical side, in [Flynn et al. 01] Flynn et al. numerically verified BSD for the Jacobians of 32 hyperelliptic curves of genus 2 with small conductor, using modular methods for their calculations.

There is, however, a slight inaccuracy in [Flynn et al. 01]. In the calculation of the real period, calculations seem to be done inside the sheaf of relative differentials, while they should be done inside the canonical sheaf. For curves whose Néron model has non-reduced fibers, this could cause a problem. For the curves considered, it did not seem to invalidate the final results.

The goal of this article is twofold. On the one hand, we will give a more explicit algorithm to compute the real period, or more specifically, a Néron differential, along with the theoretical foundations that are needed for this. On the other hand, we will present how we extended the numerical verification of BSD to the Jacobians of many more hyperelliptic curves of genus 2, 3, 4, and 5 without using modular methods. As far as the author is aware, this is the first time BSD has been numerically verified for the Jacobians of curves of genus 3, 4, and 5.

We did not compute, however, the order of $Ш(A).$ Moreover, the verification is only provable up to squares. That is, all terms but $|Ш(A)|$ are computed, of which some are only provably correct up to squares. Then it is verified that the conjectural order of $Ш(A),$ as predicted by the conjecture, up to a certain high precision, is a rational square or two times a rational square, in accordance with the criteria described in [Poonen and Stoll 99, Sect. 8, pp. 1125–1126].

The structure of this article is as follows. First we present our verification results. Then we discuss the computation of the real period and the theoretical background needed. Then in the last part we briefly discuss the computation of the other terms in the BSD formula.

2. Results

For the Jacobians of the curves listed below, we numerically verified BSD in the following sense. We numerically determined the algebraic and analytic rank, the special value of the L-function, the regulator (provably only up to squares), the real period, the Tamagawa numbers, and the size of the torsion subgroup of the Jacobian, assuming some conjectures mentioned below. Then the BSD formula was used to calculate a conjectural order for $Ш,$ and it was verified that it is a rational square (which it should be according to the criteria in [Poonen and Stoll 99]).

In practice this meant that the conjectural order for $Ш$ was less than ${10}^{-9}$ away from an integer. Moreover, for all but one of the curves of genus 2, this conjectural order was actually equal to 1.000000000.

The conjectural results that we assume to hold for the verification include the analytic continuation, and the correctness of the functional equation of the L-function (see [Hindry and Silverman 2000, Conj. F.4.1.5, p. 461]). When we computed the analytic rank, we did this by numerically checking whether the L-function and its derivatives up to certain order, vanish at 1. Even though this does not prove that these functions vanish, we do assume this to be true. Moreover, we assume the correctness of Ogg’s formula for the computation of the 2-part of the conductor (for more details, see Remark 15). In a certain sense, one could say that our verification also provides evidence for these conjectures.

List of curves

• All elliptic curves of the form $y^2=x^3+\mathit{ax}+b$ with $a,b\in \{-15,\dots ,15\},$ and compared it with the outcomes of already existing algorithms in Magma.

• All hyperelliptic curves from [Flynn et al. 01], comparing it with the outcomes given in that article.

• All 300 hyperelliptic curves C of genus 2, of the form $$y^2=x^5+a{x}^4+b{x}^3+c{x}^2+\mathit{dx}+e,$$

up to isomorphism, with $a,b,c,d,e\in \{-10,\dots ,10\}$ and $\Delta (C)\le {10}^5.$ About one third of them have rank 1, the rest are of rank 0. They are all contained in the LMFDB, cf. [Booker et al. 16].

• All six hyperelliptic curves of genus 3, of the form $$y^2=x^7+a{x}^6+b{x}^5+c{x}^4+d{x}^3+e{x}^2+\mathit{fx}+g,$$

with $a,b,c,d,e,f,g\in \{-3,\dots ,3\}$ and $\Delta (C)\le {10}^6,$ that is, we checked BSD, up to squares, for

• $H_1:(a,b,c,d,e,f,g)=(1,-3,2,2,-3,0,1,0),$

• $H_2:(a,b,c,d,e,f,g)=(1,-2,-1,2,2,-1,-1,0),$

• $H_3:(a,b,c,d,e,f,g)=(1,0,-3,-2,2,3,1,0),$

• $H_4:(a,b,c,d,e,f,g)=(1,0,-1,0,-2,3,-1,0),$

• $H_5:(a,b,c,d,e,f,g)=(1,1,-2,-2,1,2,-1,0),$

• $H_6:(a,b,c,d,e,f,g)=(1,-3,2,0,1,0,-1,0),$

and, in order to have an example of rank 1, the curve

• $H_7:(a,b,c,d,e,f,g)=(1,-3,1,3,-2,0,1,0).$

As far as we are aware these are the first examples of curves of genus 3 for which BSD has been numerically verified. These were the invariants we found:

Table

	r	$\underset{s\to 1}{\lim }\dots$	PA	RA	cp	$\left|A{(\mathbb{Q})}_{\text{tors}}\right|$	$|Ш{|}_{\text{an}}$
H1	0	0.8006061	51.23879	1	$c_2=c_5=c_{23}=1$	8	1.000000
H2	0	0.7636550	48.87392	1	$c_2=c_5=c_{23}=1$	8	1.000000
H3	0	0.9275079	59.36050	1	$c_2=c_5=c_{23}=1$	8	1.000000
H4	0	0.8087909	51.76262	1	$c_2=c_5=c_{31}=1$	8	1.000000
H5	0	0.9784790	62.62265	1	$c_2=c_5=c_{23}=1$	8	1.000000
H6	0	0.4310775	55.17793	1	$c_2=2,c_5=c_{23}=1$	16	1.000000
H7	1	1.953631	50.85263	0.6146799	$c_2=c_5=c_{11}=1$	4	1.000000

For the torsion and regulator, points were searched up to a certain height on the Jacobian. This maximum search height is considerably smaller than the height given by the various height bounds in the literature. It is possible that the size of the torsion subgroups and the regulator is incorrect, but this would only cause a rational square error factor for the value of $|Ш{|}_{\text{an}}.$

• The curve $$y^2+(x^5+x^2)y=x^8+x^7+x^6+4x^5+3x^4+2x^3+4x^2+2x$$ of genus 4, with discriminant -1,064,000, which was found by Harrison [Harrison 18]. It has Mordell-Weil rank 0. We found $L(A,1)\approx 0.09889146,P_A\approx 178.0046,c_2=2,$ c_p = 1 for all other p, and $\left|A{(\mathbb{Q})}_{\text{tors}}\right|=60,$ yielding $|Ш{|}_{\text{an}}=1.0000000.$ Again the torsion is not computed in a provable way. However by reducing modulo 3, we found that the torsion is a divisor of 180. As far as we are aware this is the first example of a curve of genus 4 for which BSD has been numerically verified.

• The curve $$y^2+(x^6+x^4+1)y=x^4+x^2$$ of genus 5, with discriminant 116,985,856, found in the aforementioned list. It has Mordell-Weil rank 0. We found $L(A,1)\approx 0.1002872,P_A\approx 579.2589,$ c_p = 1 for all p, and $\left|A{(\mathbb{Q})}_{\text{tors}}\right|=76,$ yielding $|Ш{|}_{\text{an}}=1.0000000.$ As this curve does not have a rational Weierstraß point (which we actually do assume for most of the article), the search for torsion points was much more cumbersome, due to the Mumford representation not behaving well in this case. Again it is not provable; the best upper bound for the torsion that we found is 304. As far as we are aware this is the first example of a curve of genus 5 for which BSD has been numerically verified.

Remark 3.

It could be the case that some of these curves have isomorphic (or isogenous) Jacobians. Then we actually verified BSD two times for the same abelian variety. In the verification process, we did not check for this.

Remark 4.

Even though for all our curves the verification went well, it should be remarked that problems are to be expected when trying to verify BSD for Jacobians of curves with higher discriminant (or rather, higher conductor). The computation of the L-function takes much longer in these cases. Also the computation of the regulator will be harder, as the heights of the points involved might increase, in particular in case the Mordell-Weil rank is higher.

It should be feasible to carry out the verification for more of the small examples from Harrison’s list, [Harrison 18] of genus 4, as long as the maximum bad prime is small enough. We also tried the verification for some more examples of genus 5, but in these cases the computation of the special value of the L-function was taking hours and the computation of the regular model sometimes did not seem to finish in reasonable time.

3. Theory of differentials

Let $C/\mathbb{Q}$ be a smooth, geometrically irreducible, projective curve of genus g over $\mathbb{Q}.$ Let $J/\mathbb{Q}$ be its Jacobian. The goal of this section is to define the period of J, and to describe a way to compute it in the case C is hyperelliptic. We will be following the algorithm described in [Flynn et al. 01, sect. 3.5].

First we will discuss both the theoretical considerations that are needed for this algorithm.

Throughout the section p will be a prime and S will be the scheme $\text{Spec}({\mathbb{Z}}_{(p)}).$ The generic point of S is called η and the special point p.

3.1. Preliminaries

First, for completeness, we will recall the following definition.

Definition 5

([Bosch et al. 90, p. 166]). A (relative) curve $\mathcal{C}$ over S is a normal, proper, flat S-scheme, such that for all $t\in S,$ the fiber ${\mathcal{C}}_t$ is of pure dimension 1. A model of C over S is a relative curve $\mathcal{C}$ over S together with an isomorphism ${\mathcal{C}}_{\eta }\cong C.$

Remark 6.

Without the normality assumption, the special fiber of a curve over S could have embedded components. In order to be able to use the results from [Bosch et al. 90], which have been partially derived from [Raynaud 70], it is necessary to not have embedded components.

Let $\mathcal{J}$ be a Néron model of J over S, and let $\mathcal{C}/S$ be a regular model of C. Assume that the geometric multiplicities of the irreducible components of ${\mathcal{C}}_p$ in ${\mathcal{C}}_p$ have greatest common divisor 1.

Theorem 7

([Bosch et al. 90, Thm. 4(b), sect. 9.5, p. 267]). Under these conditions, ${\text{Pic}}_{\mathcal{C}/S}^0$ is a separated scheme and ${\text{Pic}}_{\mathcal{C}/S}^0$ coincides with the identity component of $\mathcal{J}.$

From [Raynaud 70, Prop. 5.2, p. 46], it now follows that $\mathcal{C}/S$ is cohomologically flat, which we will need for the next part.

3.2. Differentials of Jacobian and regular model

A classical theorem (see e.g. [Milne 86, Prop. 2.2, p. 172]) relates the differentials on the Jacobian of a smooth curve over a field with the differentials on the curve itself. We will generalize this to $\mathcal{J}$ and $\mathcal{C}.$

Definition 8

([Liu 02, Def. 4.7, sect. 6.4.2, p. 239]). Let Y/T be a quasi-projective locally noetherian scheme. Let $i:Y\to Z$ be an immersion into a smooth scheme Z/T. Then the canonical sheaf of Y/T is defined to be the ${\mathcal{O}}_Y$-module $${\omega }_{Y/T}:=\det {\left(i^{*}\right(\mathcal{I}/{\mathcal{I}}^2\left)\right)}^{\vee }{\otimes }_{{\mathcal{O}}_T}{i}^{*}\left(\det {\Omega }_{Z/T}^1\right),$$ where $\mathcal{I}$ is the sheaf of ideals defining Y in an open $Z\prime \subset Z$ containing Y as closed subset. This is independent of the choice of Z and i, see loc. cit.

The following lemma generalizes the aforementioned theorem.

Lemma 9.

There are canonical isomorphisms of ${\mathcal{O}}_S$-modules

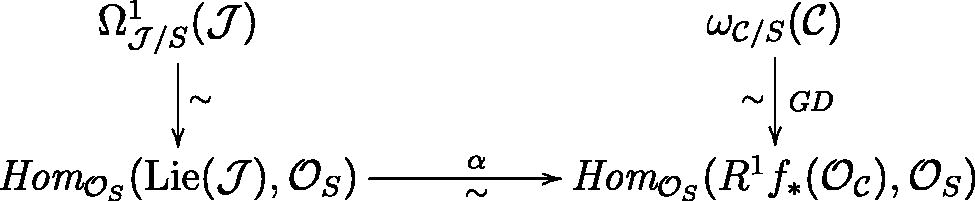
Proof.

The right hand isomorphism is given by Grothendieck duality, see [Liu 02, Sect. 6.4.3, p. 243]. The bottom isomorphism, α, is from [Bosch et al. 90, Thm. 8.4.1, p. 231] (here we use that $\mathcal{C}/S$ is cohomologically flat). Getting the left hand isomorphism is a little bit more involved.

First remark that global differentials on an abelian variety are translation invariant. As the image of J is dense in $\mathcal{J},$ also the differentials in ${\Omega }_{\mathcal{J}/S}^1(\mathcal{J})$ are translation invariant. Combining this with [Bosch et al. 90, Prop. 4.2.1, p. 100], we get (3–1) $${\Omega }_{\mathcal{J}/S}\left(\mathcal{J}\right)={\Omega }_{\mathcal{J}/S}^1{\left(\mathcal{J}\right)}^{\text{inv}}=e^{*}{\Omega }_{\mathcal{J}/S}^1\left(S\right),$$(3–1) where $e:S\to \mathcal{J}$ is the unit section. Now, by [Liu 02, Prop. 6.1.24, p. 217], we get an exact sequence of ${\mathcal{O}}_S$-modules $$\mathfrak{m}/{\mathfrak{m}}^2\to e^{*}{\Omega }_{\mathcal{J}/S}^1\to {\Omega }_{S/S}^1=0,$$ where $\mathfrak{m}$ is the ideal of the schematic image of e inside $\mathcal{J}.$ As both $\mathfrak{m}/{\mathfrak{m}}^2$ and ${\Omega }_{\mathcal{J}/S}^1,$ and hence $e^{*}{\Omega }_{\mathcal{J}/S}^1$ are locally free of rank g (as $\mathcal{J}$ is regular), we get that the kernel of $\mathfrak{m}/{\mathfrak{m}}^2\to e^{*}{\Omega }_{\mathcal{J}/S}^1$ is torsion. As ${\mathcal{O}}_S$ is torsion-free in our case, and hence the locally free module $\mathfrak{m}/{\mathfrak{m}}^2$ is torsion-free, we find a canonical isomorphism of ${\mathcal{O}}_S$-modules $$e^{*}{\Omega }_{\mathcal{J}/S}^1=\mathfrak{m}/{\mathfrak{m}}^2=\text{Hom}{ }_{{\mathcal{O}}_S}\left(\text{Lie}\right(\mathcal{J}),{\mathcal{O}}_S),$$ which gives, by taking global sections and composing with Equation (1–3), the construction of the left hand isomorphism in the diagram. □

Remark 10.

Under the natural identifications ${\Omega }_{\mathcal{J}/S}^1(\mathcal{J}){\otimes }_{{\mathbb{Z}}_{(p)}}\mathbb{Q}={\Omega }_{J/\mathbb{Q}}^1(J)$ and ${\omega }_{\mathcal{C}/S}(\mathcal{C}){\otimes }_{{\mathbb{Z}}_{(p)}}\mathbb{Q}={\Omega }_{C/\mathbb{Q}}^1(C),$ the isomorphism ${\Omega }_{\mathcal{J}/S}^1(\mathcal{J})\cong {\omega }_{\mathcal{C}/S}(\mathcal{C})$ in the lemma above is compatible with the aforementioned classical isomorphism ${\Omega }_{J/\mathbb{Q}}^1(J)\cong {\Omega }_{C/\mathbb{Q}}^1(C).$

3.3. Algorithm for the real period

Suppose that ${\omega }_1,\dots ,{\omega }_g\in {\Omega }_{C/\mathbb{Q}}^1(C)$ are such that, for every prime p, they form a ${\mathbb{Z}}_{(p)}$-basis of ${\omega }_{\mathcal{C}/S}(\mathcal{C}),$ under the identification ${\omega }_{\mathcal{C}/S}(\mathcal{C}){\otimes }_{{\mathbb{Z}}_{(p)}}\mathbb{Q}={\Omega }_{C/\mathbb{Q}}^1(C).$ In other words, cf. Lemma 9, suppose that ${\omega }_1,\dots ,{\omega }_g$ correspond to generators of ${\Omega }_{{\mathcal{J}}_{\mathbb{Z}}/\mathbb{Z}}^1({\mathcal{J}}_{\mathbb{Z}}),$ where ${\mathcal{J}}_{\mathbb{Z}}/\mathbb{Z}$ is a Néron model of J over $\text{Spec}\mathbb{Z}.$ Moreover, let ${\gamma }_1,\dots ,{\gamma }_{2g}\in H^1(C,\mathbb{Z})$ form a symplectic basis for the homology. Then the real period can be defined as follows.

Definition 11.

The real period of J is the covolume of the lattice $$\mathbb{Z}(a_1+\overline{a_1})+\dots +\mathbb{Z}(a_{2g}+\overline{a_{2g}})\subset {\mathbb{R}}^g,$$ where $a_i={({\int }_{{\gamma }_i}{\omega }_j)}_{j=1}^g\in {\mathbb{C}}^g$ for $i=1,\dots ,2g.$

Now suppose that we are working with a hyperelliptic curve given by $y^2=f$ for some $f\in \mathbb{Q}[x].$ Then, due to Van Wamelen there is a procedure in Magma to compute a symplectic basis of $H^1(C,\mathbb{Z})$ as mentioned before, and the integrals ${\int }_{{\gamma }_i}\frac{x^{j-1}·\mathit{dx}}{y}$ for all $i=1,\dots ,2g$ and $j=1,\dots ,g.$

In order to compute the real period, we only need to find a basis ${\omega }_1,\dots ,{\omega }_g$ as above in terms of the differentials $\frac{x^{j-1}·\mathit{dx}}{y}.$ For our purpose, the calculation can be done for each prime p separately. Fortunately for us, due to Donnely, Magma also has an algorithm to compute explicit equations for a regular model $\mathcal{C}$ of C over S. It will represent $\mathcal{C}/S$ by giving charts, each of which is a relative complete intersection. The following lemma explicitly gives the isomorphism ${\omega }_{\mathcal{C}/S}(\mathcal{C}){\otimes }_{{\mathbb{Z}}_{(p)}}\mathbb{Q}\cong {\Omega }_{C/\mathbb{Q}}^1(C)$ that we need to compute whether a certain differential is vanishing or having a pole on one of the components of the special fiber (Step 5 and 6 in Algorithm 13).

Lemma 12.

Let $\mathcal{X}\subset {\mathbb{A}}_S^n=\text{Spec}({\mathbb{Z}}_p[x_1,\dots ,x_n])$ be regular, flat, and of relative dimension 1 over $S=\text{Spec}{\mathbb{Z}}_{(p)}$. Suppose that $\mathcal{X}$ is a relative complete intersection inside ${\mathbb{A}}_S^n$, given by equations $g_1=\dots =g_{n-1}=0$, with $g_i\in {\mathbb{Z}}_{(p)}[x_1,\dots ,x_n]$. Moreover, suppose that the generic fiber ${\mathcal{X}}_{\eta }$ is smooth over $\mathbb{Q}.$

Then, on the one hand, after possibly reordering $x_1,\dots ,x_n$, we may and will assume that ${\Omega }_{k({\mathcal{X}}_{\eta })/\mathbb{Q}}^1$ is a $k({\mathcal{X}}_{\eta })$-vector space of dimension 1 generated by dx_n. This space contains ${\Omega }_{{\mathcal{X}}_{\eta }/\mathbb{Q}}^1({\mathcal{X}}_{\eta })$. On the other hand, we can define ${\omega }_{\mathcal{X}/S}$ using this immersion into ${\mathbb{A}}_S^n$ (cf. Def. 8). Then ${\omega }_{\mathcal{X}/S}$ is free of rank 1 and generated by an element, which we will denote by ${(g_1\wedge \dots \wedge g_{n-1})}^{\vee }\otimes d{x}_1\wedge \dots \wedge d{x}_n$. Then there is a canonical isomorphism of $\mathbb{Q}$-vector spaces $${\Omega }_{{\mathcal{X}}_{\eta }/\mathbb{Q}}^1\left({\mathcal{X}}_{\eta }\right)\stackrel{\sim }{\to }{\omega }_{\mathcal{X}/S}\left(\mathcal{X}\right){\otimes }_{{\mathbb{Z}}_{\left(p\right)}}\mathbb{Q},$$ which is given by $$f·d{x}_n\mapsto f·\det {\left(\begin{array}{c}\partial g_i/\partial x_j\end{array}\right)}_{i,j=1}^{n-1}·{(g_1\wedge \dots \wedge g_{n-1})}^{\vee }\otimes d{x}_1\wedge \dots \wedge d{x}_n.$$

Proof.

On the one hand, we can consider ${\mathcal{X}}_{\eta }\subset {\mathcal{X}}_{\eta },$ on the other hand, we have an embedding ${\mathcal{X}}_{\eta }\subset {\mathbb{A}}_{\mathbb{Q}}^n.$ Both give us a way to construct ${\Omega }_{{\mathcal{X}}_{\eta }/\mathbb{Q}}^1,$ and [Liu 02, Lem. 6.4.5, p. 238] gives an explicit natural isomorphism between them. What is left to check, is that this isomorphism is exactly the one described in the statement of Lemma 12.

We will break down the proof of [Liu 02, Lem. 6.4.5, p. 238] to find the map explicitly. In this lemma, we will take $X=Z_1={\mathcal{X}}_{\eta },Y=\text{Spec}\mathbb{Q}$ and $Z_2={\mathbb{A}}_{\mathbb{Q}}^n,$ and we let $i_2:{\mathcal{X}}_{\eta }\to {\mathbb{A}}_{\mathbb{Q}}^n$ be the map induced by the embedding of $\mathcal{X}$ into ${\mathbb{A}}_S^n.$ The two exact sequences, induced by [Liu 02, Cor. 6.3.22, p. 233] are $$0\to 0\to {\mathcal{C}}_{{\mathcal{X}}_{\eta }/W}\to i_2^{*}{\Omega }_{{\mathbb{A}}_{\mathbb{Q}}^n/\mathbb{Q}}^1\to 0\hspace{1em}\hspace{1em}\text{and}\hspace{1em}\hspace{1em}0\to {\mathcal{C}}_{{\mathcal{X}}_{\eta }/{\mathbb{A}}_{\mathbb{Q}}^n}\to {\mathcal{C}}_{{\mathcal{X}}_{\eta }/W}\to {\Omega }_{{\mathcal{X}}_{\eta }/\mathbb{Q}}^1\to 0,$$ where $W={\mathcal{X}}_{\eta }{\times }_{\mathbb{Q}}{\mathbb{A}}_{\mathbb{Q}}^n,$ and the map $h:{\mathcal{X}}_{\eta }\to W$ is given by $({\text{id}}_{{\mathcal{X}}_{\eta }},i_2),$ and ${\mathcal{C}}_{{\mathcal{X}}_{\eta }/W}=h^{*}{\mathcal{I}}_h/{\mathcal{I}}_h^2$ and ${\mathcal{C}}_{{\mathcal{X}}_{\eta }}/{\mathbb{A}}_{\mathbb{Q}}^n=i_2^{*}{\mathcal{I}}_{i_2}/{\mathcal{I}}_{i_2}^2$ with ${\mathcal{I}}_h$ and ${\mathcal{I}}_{i_2}$ the sheaf of ideals on W and ${\mathbb{A}}_q^n$ respectively, defining ${\mathcal{X}}_{\eta }.$

We will make the maps in these exact sequences explicit, starting with the first sequence. Let $p_1:W\to {\mathcal{X}}_{\eta }$ and $p_2:W\to {\mathbb{A}}_{\mathbb{Q}}^n$ be the two projections. We know that ${\Omega }_{{\mathbb{A}}_{\mathbb{Q}}^n/\mathbb{Q}}^1$ is a free sheaf generated by n elements $d{x}_1,\dots ,d{x}_n.$ Now ${\Omega }_{W/{\mathcal{X}}_{\eta }}^1$ is identified with $p_2^{*}{\Omega }_{{\mathbb{A}}_{\mathbb{Q}}^n/\mathbb{Q}}^1,$ and in this identification the differential dx_j is mapped to dz_j, where $z_j=p_2^{*}{x}_j.$ By pulling back along h, we get an identification $h^{*}{\Omega }_{W/{\mathcal{X}}_{\eta }}^1=i_2^{*}{\Omega }_{{\mathbb{A}}_{\mathbb{Q}}^n/\mathbb{Q}}^1.$

Now the isomorphism ${\mathcal{C}}_{{\mathcal{X}}_{\eta }/W}\to h^{*}{\Omega }_{W/{\mathcal{X}}_{\eta }}^1$ is ultimately coming from [Liu 02, Prop. 6.1.8, p. 212]. The sheaf ${\mathcal{I}}_h/{\mathcal{I}}_h^2$ is generated by $z_j-y_j,$ for $j=1,\dots ,n-1,$ where $y_j=p_1^{*}{i}_2^{*}{x}_j.$ These are mapped to $d(z_j-y_j)=d{z}_j$ in $h^{*}{\Omega }_{W/{\mathcal{X}}_{\eta }}^1$ or to dx_j in $i_2^{*}{\Omega }_{{\mathbb{A}}_{\mathbb{Q}}^n/\mathbb{Q}}^1.$

To understand the morphism ${\mathcal{C}}_{{\mathcal{X}}_{\eta }/{\mathbb{A}}_{\mathbb{Q}}^n}\to {\mathcal{C}}_{{\mathcal{X}}_{\eta }/W}$ in the second sequence, we have to go back to [Liu 02, Cor. 6.3.22]. The sheaf ${\mathcal{I}}_{i_2}/{\mathcal{I}}_{i_2}^2$ is generated by the functions $g_1,\dots ,g_{n-1}.$ Following the proof of the aforementioned corollary, we consider the following Cartesian diagram.

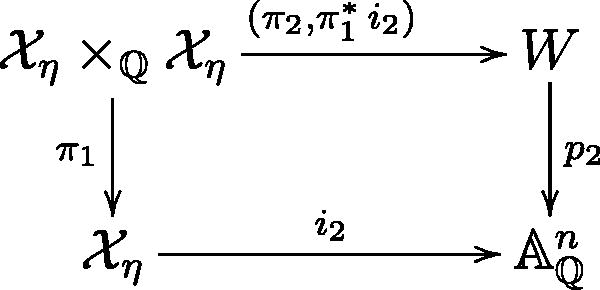
Here π₁ and π₂ are the first and second coordinate projections ${\mathcal{X}}_{\eta }{\times }_{\mathbb{Q}}{\mathcal{X}}_{\eta }\to {\mathcal{X}}_{\eta }.$ The map $h:{\mathcal{X}}_{\eta }\to W$ from the bottom left to the top right, using the universal property of the product, gives rise to the diagonal section $\Delta :{\mathcal{X}}_{\eta }\to {\mathcal{X}}_{\eta }{\times }_{\mathbb{Q}}{\mathcal{X}}_{\eta }$ of π₁. Then, there is the identification $${\mathcal{C}}_{{\mathcal{X}}_{\eta }/{\mathbb{A}}_{\mathbb{Q}}^n}={\Delta }^{*}{\pi }_1^{*}{\mathcal{C}}_{{\mathcal{X}}_{\eta }/{\mathbb{A}}_{\mathbb{Q}}^n}={\Delta }^{*}{\mathcal{C}}_{{\mathcal{X}}_{\eta }{\times }_{\mathbb{Q}}{\mathcal{X}}_{\eta }/W},$$ identifying the functions g_i in ${\mathcal{C}}_{{\mathcal{X}}_{\eta }/{\mathbb{A}}_{\mathbb{Q}}^n}$ with the functions $p_2^{*}{g}_i$ in ${\Delta }^{*}{\mathcal{C}}_{{\mathcal{X}}_{\eta }{\times }_{\mathbb{Q}}{\mathcal{X}}_{\eta }/W}.$ In other words, if you express the g_i in terms of the variables x_j on ${\mathbb{A}}_{\mathbb{Q}}^n,$ then you get $p_2^{*}{g}_i$ by replacing all the x_j’s by z_j’s.

The map ${\mathcal{C}}_{{\mathcal{X}}_{\eta }/W}\to {\Omega }_{{\mathcal{X}}_{\eta }/\mathbb{Q}}^1$ is constructed in an analogous way to the construction of the map ${\mathcal{C}}_{{\mathcal{X}}_{\eta }/W}\to i_2^{*}{\Omega }_{{\mathbb{A}}_{\mathbb{Q}}^n/\mathbb{Q}}^1.$ It sends $z_j-y_j$ to $-d{w}_j,$ where $w_j=i_2^{*}{x}_j,$ on ${\Omega }_{{\mathcal{X}}_{\eta }/\mathbb{Q}}^1.$

Now the isomorphism $$\begin{array}{c}\det {\mathcal{C}}_{{\mathcal{X}}_{\eta }/{\mathbb{A}}_{\mathbb{Q}}^n}\otimes \det {\Omega }_{{\mathcal{X}}_{\eta }/\mathbb{Q}}^1\to \det {\mathcal{C}}_{{\mathcal{X}}_{\eta }/W}\to \det i_2^{*}{\Omega }_{{\mathbb{A}}_{\mathbb{Q}}^n/\mathbb{Q}}^1\\ (g_1\wedge \dots \wedge g_{n-1})\otimes d{w}_n\mapsto p_2^{*}{g}_1\wedge \dots \wedge p_2^{*}{g}_{n-1}\wedge d{w}_n\mapsto d{g}_1\wedge \dots \wedge d{g}_{n-1}\wedge d{x}_n\end{array}$$ is constructed cf. [Liu 02, Lem. 6.4.1, pp.. 236–237]. Of course, $$d{g}_1\wedge \dots \wedge d{g}_{n-1}\wedge d{x}_n=\det {\left(\begin{array}{c}\partial g_i/\partial x_j\end{array}\right)}_{i,j=1}^{n-1}·d{x}_1\wedge \dots \wedge d{x}_n.$$

Recall that ${\omega }_{\mathcal{X}/S}=\det {({\iota }^{*}{\mathcal{I}}_{\iota }/{\mathcal{I}}_{\iota }^2)}^{\vee }{\otimes }_S {\iota }^{*}\det {\Omega }_{\mathcal{X}/S}^1,$ where $\iota :\mathcal{X}\to {\mathbb{A}}_S^n$ is the embedding, and ${\mathcal{I}}_{\iota }$ is the sheaf of ideals on ${\mathcal{O}}_{{\mathbb{A}}_S^n}$ defining $\mathcal{X}.$ After base change to $\mathbb{Q},$ this becomes ${(\det {\mathcal{C}}_{{\mathcal{X}}_{\eta }/{\mathbb{A}}_{\mathbb{Q}}^n})}^{\vee }{\otimes }_{\mathbb{Q}}\det i_2^{*}{\Omega }_{{\mathbb{A}}_{\mathbb{Q}}^n/\mathbb{Q}}^1.$ The result now follows immediately. □

Altogether, this leads to the following algorithm.

Algorithm 13.

Input: monic polynomial $f\in \mathbb{Z}[X]$ of degree $2g+1$ describing a hyperelliptic curve C of genus g over $\mathbb{Q}.$

Output: the real period Ω of its Jacobian J.

Step 1: calculate the so-called big period matrix ${({\int }_{{\gamma }_i}{\omega }_j)}_{i=1,\dots ,2g, j=1,\dots g}$ of J, where the notation is as before, using the Magma command BigPeriodMatrix (due to Van Wamelen).

Step 2: for each subset $I\subset \{1,\dots ,2g\}$ with $\left|I\right|=g,$ calculate the covolume $P_I:=\left|\det {\left({\int }_{{\gamma }_i}{\omega }_j+\overline{{\int }_{{\gamma }_i}{\omega }_j}\right)}_{i\in I, j=1,\dots ,g}\right|.$

Step 3: use Euclid’s algorithm to find a generator P for the lattice spanned by the P_I.

Step 4: for each bad prime p, calculate a regular model $\mathcal{C}/{\mathbb{Z}}_{(p)}$ of C, using the Magma command RegularModel. This will give us a representation of $\mathcal{C}$ by charts which are relative complete intersections.

Step 5: for each of the differentials ${\omega }_1,\dots ,{\omega }_g,$ check if it has a pole on any of the irreducible components of the special fiber of $\mathcal{C}.$ If so, adjust the basis by multiplying the differential having a pole with p to get a new basis $\underset{¯}{\omega }\prime$ and apply Step 5 again (until the basis is not changing anymore).

Step 6: for each ${(c_j)}_{j=1}^g\in {\{0,\dots ,p-1\}}^g\setminus \{(0,0,\dots ,0)\},$ check if $\sum _j{c}_j{\omega }_j$ vanishes on the whole special fiber of $\mathcal{C}.$ If so, adjust the basis $\underset{¯}{\omega }\prime$ by replacing one of the ω_j such that $c_j\ne 0$ with $\frac{1}{p}\sum _j{c}_j{\omega }_j,$ then apply Step 6 again (until the basis is not changing anymore).

Step 7: for each bad prime p compute $p^{a-b},$ where a is the number of basis adjustments done in Step 5, and b is the number of basis adjustments done in Step 6 (this is also the determinant of the change of basis matrix whose columns express $\underset{¯}{\omega }\prime$ in terms of $\underset{¯}{\omega }$). Then take the product W over p of these determinants, and output $W·P.$

End.

4. Computation of other terms in BSD formula

Throughout this section, we will use the following notation.

Notation 14. We define $H/\mathbb{Q}$ to be a hyperelliptic curve of genus g. When a prime p is introduced, $\mathcal{H}/{\mathbb{Z}}_{(p)}$ is a regular model of H over ${\mathbb{Z}}_{(p)}.$ The Jacobian of H is denoted by J, and the Néron model of J over $\mathbb{Z}$ is called $\mathcal{J}.$

Moreover, we will assume that H is given by a model of the form $y^2=f(x),$ where the input polynomial f(x) has odd degree. The reason we assume f(x) to have odd degree, is twofold. On the one hand, the existence of a rational Weierstraß point ensures the conditions of Theorem 7 are met. On the other hand, the Jacobian arithmetic has not been fully implemented in Magma for hyperelliptic curves without rational Weierstraß point.

4.1. Torsion subgroup and rank

In order to compute the torsion group and algebraic rank of J, we will be computing upper and lower bounds.

For the torsion, upper bounds are given by considering the reduction of J at good primes. For the algebraic rank, upper bounds are given by considering 2-Selmer groups. This is already implemented in Magma by Stoll.

To get lower bounds, we try to find as many points as possible on J. For genus 2, this is already implemented in Magma. For genus 3, 4, and 5, the author implemented a simple search algorithm for points, using the Mumford representation that Magma is using to represent points on J.

In fact, for Jacobians of curves J and $J^{\vee }$ are isomorphic. Hence, in order to verify the BSD conjecture up to squares in this case, it is actually not necessary to know the size of the torsion subgroup at all.

4.2. L-function

In this section, we will briefly discuss the computation of the special value of the L-function associated to the Jacobian of a hyperelliptic curve. For a complete definition and theoretical background on the L-function, see [Serre 70].

The idea used to compute the L-function is as follows. The local L-factors at the good primes p > 2 can be found by counting points in $\mathcal{J}({\mathbb{F}}_{p^m})$ for sufficiently many $m\ge 1.$ In order to find the local L-factors at the bad places, one uses the functional equation. The idea is to guess, in a clever way, the conductor and, for the bad primes, the local L-factors, in such a way that the L-function obtained satisfies the conjectural functional equation, see also [Booker et al. 16, sect. 5, pp. 243–245].

Remark 15.

To guess the 2-part of the conductor, the following naive version of Ogg’s formula is used: $$f^{\text{guess}}=v(\Delta )-n+1.$$

Here, $v(\Delta )$ is the valuation of the (naive) minimal discriminant, n is the number of geometrically irreducible components in a minimal regular model, and $f^{\text{guess}}$ is our guess for the 2-valuation of the conductor. The formula, in this shape, does not give the correct 2-valuation of the conductor in general. For curves of genus 2 over a Henselian discrete valuation ring with algebraically closed residue field, we can deduce the formula $$f=v(\Delta )-n+1-11·c\left(X\right),$$ from [Liu 94], where c(X), as defined in loc. cit., is a non-negative integer. Over general discrete valuation rings, the discriminant could change after a quadratic field extension, cf. [Liu 96, Prop. 4, p. 4595]. In this case, it drops by $2(2g+1).$ So, for genus 2, in case $v(\Delta )<10,$ the discriminant will apparently not change anymore, and c(X) = 0 must hold for the 2-valuation f of the conductor to not become negative. Hence, the naive version of Ogg’s formula holds in this case.

In [Dokchitser 04], Tim Dokchitser describes a trick with an inverse Mellin transform in order to actually evaluate the L-function. This has been implemented by him, together with Vladimir Dokchitser, in Magma. This is the method we used for our calculations. However, it is useful to remark that the runtime increases quickly when the conductor increases and that this could probably by remedied by using the methods from [Harvey et al. 16].

4.3. Regulator

Using the points on J that we found when computing the algebraic rank, we will compute the regulator. In order to do that, we need to calculate the height pairing for several pairs of points.

Due to work of Holmes [Holmes 12] and Müller [Müller 14] it is now known how arithmetic intersection theory could be used to do this calculation. This has also been implemented in Magma for Jacobians of hyperelliptic curves by Müller, and works in practice for genus up to 10.

In many cases, especially in genus 3, 4, and 5, the height bound we use for point finding is not high enough to provably compute the regulator. The upper bounds for difference between the naive and canonical height are quite big in some cases, see for example [Müller and Stoll 16] for genus 2. In that case, we can only obtain a finite index subgroup of the Mordell-Weil group. Therefore, the regulator that we get might be a square multiple of the actual regulator of J. Hence, the conjectural order of $Ш,$ assuming BSD, might be a multiple of the order that we compute.

4.4. Tamagawa numbers

Suppose that we have a regular model ${\mathcal{H}}^{\text{hens}}$ of H over the strict henselization of ${\mathbb{Z}}_{(p)}.$ Then in [Bosch and Liu 99, Thm. 1.1, p. 277], Bosch and Liu give an exact sequence $$0\to \text{Im}\overline{\alpha }\to \ker \overline{\beta }\to {\varphi }_A\left(\overline{{\mathbb{F}}_p}\right)\to 0$$ of $\text{Gal}(\overline{{\mathbb{F}}_p}/{\mathbb{F}}_p)$-modules. Here ${\varphi }_A(\overline{{\mathbb{F}}_p})$ is the geometric component group of the Néron model of $\mathcal{J}.$ The map $\overline{\alpha }:{\mathbb{Z}}^{\overline{I}}\to {\mathbb{Z}}^{\overline{I}},$ with $\overline{I}$ indexing the components $\{{\Gamma }_i:i\in I\}$ of the special fiber of ${\mathcal{H}}^{\text{hens}},$ maps each component Γ_j to $\sum _{i\in \overline{I}}{e}_i^{-1}〈{\Gamma }_j,{\Gamma }_i〉·{\Gamma }_i,$ where $〈·,·〉$ is the intersection pairing and e_i is the geometric multiplicity of Γ_i (in itself, which is 1 in our case). The map $\overline{\beta }:{\mathbb{Z}}^{\overline{I}}\to \mathbb{Z}$ maps each component Γ_j to $d_j{e}_j,$ where d_j is the multiplicity of Γ_j in the special fiber. Here, the Galois group $\text{Gal}(\overline{{\mathbb{F}}_p}/{\mathbb{F}}_p)$ acts on ${\mathbb{Z}}^{\overline{I}}$ by its natural action on the components of the special fiber.

Due to Donnely, Magma is able to compute this geometric component group using this theorem, and moreover, because explicit equations exist for a regular model $\mathcal{H}$ of H over ${\mathbb{Z}}_{(p)},$ we are able to compute the action of Frobenius on $\text{Im}\overline{\alpha }$ and $\ker \overline{\beta }.$

The way regular models are constructed in Magma is by repeatedly blowing up non-regular points until the fibered surface is regular. To compute the Galois action on the components of the special fiber, we traced down this blow-up procedure, and in each step we computed the action of Galois on the points blown-up, and on the new components which appeared in the special fiber on the new blown-up charts.

The result is an implementation of a Magma package on top of the existing regular models package, which computes the action of the Galois group on ${\varphi }_A(\overline{{\mathbb{F}}_p}),$ and then computes the Tamagawa number, the order of ${\varphi }_A({\mathbb{F}}_p).$ The source code for this package will be released together with this article. It has been used to compute Tamagawa numbers for the Jacobians associated to almost all of the 66,158 genus 2 curves present in [LMFDB 00] (see also [Booker et al. 16]). This computation was finished within a few hours.

4.5. Tate-Shafarevich group

For our calculations, we do not calculate the order of the Tate-Shafarevich group. Instead, we only check whether the conjectural order, given by the BSD conjecture, is (up to a certain precision) a rational square or two times a rational square (with a small denominator) according to the criteria described in [Poonen and Stoll 99].

Acknowledgements

The author wishes to thank his supervisors David Holmes and Fabien Pazuki. Moreover, Tim Dokchitser and Steffen Müller are thanked for their advise and insight, Carlo Pagano is thanked for helping with the proof of a lemma, and anonymous referees are thanked for the comments they provided to improve this article.