Gaps Between Consecutive Primes and the Exponential Distribution

Abstract

Based on the primes less than $4\times {10}^{18}$, Oliveira e Silva et al. (Math. Comp., 83(288):2033–2060, 2014) conjectured an asymptotic formula for the sum of the kth power of the gaps between consecutive primes less than a large number x. We show that the conjecture of Oliveira e Silva holds if and only if the kth moment of the first n gaps is asymptotic to the kth moment of an exponential distribution with mean $\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n$, though the distribution of gaps is not exponential. Asymptotically exponential moments imply that the gaps asymptotically obey Taylor’s law of fluctuation scaling: variance of the first n gaps ∼ (mean of the first n gaps)². If the distribution of the first n gaps is asymptotically exponential with mean $\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n$, then the expectation of the largest of the first n gaps is asymptotic to ${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$. The largest of the first n gaps is asymptotic to ${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$ if and only if the Cramér-Shanks conjecture holds. Numerical counts of gaps and the maximal gap G_n among the first n gaps test these results. While most values of G_n are better approximated by ${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$ than by other models, seven exceptional values of n with $G_n>2e^{-\gamma }{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$ suggest that $\underset{n\to \infty }{\mathrm{\text{lim sup}}}{G}_n/[2e^{-\gamma }{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2]$ may exceed 1.

2020 MATHEMATICS SUBJECT CLASSIFICATION:

• Primary: 11A41
• 11N05

KEYWORDS:

• Cramér-Shanks conjecture
• Firoozbakht’s conjecture
• fluctuation scaling
• gap between consecutive primes
• largest prime gap
• Maier’s theorem
• prime gap
• power variance function
• Taylor’s law
• variance function

1 Introduction

The gaps between consecutive prime numbers have been studied mathematically, numerically, and statistically by many people for centuries [4, 8–10, 13, 16, 17, 19–21, 23–25, 28, 29, 32, 38–42]. This list of references is far from complete. Many questions remain open. Throughout, we use gap to mean a difference, denoted d, between consecutive primes, including $d_4:=p_5-p_4=11-7=4$ and excluding $p_4-p_2=7-3=4$, where p_n is the nth prime, $p_1=2$.

We do not attempt to summarize here everything that is currently known about the distribution of prime gaps. Some selected recent results and conjectures are pertinent. Heath-Brown [21, p. 87] conjectured a simple asymptotic expression for the sum of the squares of the gaps of the primes not exceeding a large real x (OEIS A074741). Wolf [39, Conjecture 5] conjectured an alternative asymptotic form and compared the two alternatives numerically. Based on a detailed numerical study of the primes less than $4\times {10}^{18}$, Oliveira e Silva [28, p. 2056] conjectured a simple asymptotic formula for the sum of the kth power of the gaps of primes less than x as $x\to \infty$, for every $k=1,2,\dots$. Wolf [41] refined and extended the conjectured asymptotic expressions of Oliveira e Silva and compared the alternatives analytically and numerically. Firoozbakht conjectured that the sequence ${(p_n^{1/n})}_{n\in \mathbb{N}}$ decreases as n increases [38]. The conjecture holds for all primes less than $2^{64}\approx 1.84\times {10}^{19}$ as of April 2024 [38]. Kourbatov [23] showed that Firoozbakht’s conjecture implies an upper bound on all gaps. Maier [24] showed that chains of consecutive large gaps exist, and that average gaps of primes in short intervals do not converge (contrary to previous conjecture) but have a limsup strictly greater than the liminf [25].

What is new here? We consider the first $n=1,2,\dots$ gaps instead of the gaps of primes less than large x (Section 3). This change of scale enables us to show (Theorem 3) that the conjecture of Oliveira e Silva holds if and only if, for every $k=1,2,\dots$, the kth moment of the gaps (that is, the sum of the kth power of the first n gaps, divided by n) is asymptotically (as $n\to \infty$) the kth moment $k!{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^k$ of an exponential distribution with mean $\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n$.

Obviously the distribution of gaps is not exponential because an exponential random variable has a continuous density function on $[0,\infty )$, whereas gaps are positive integers only and all gaps except $d_1=p_2-p_1=3-2=1$ are even integers. Gaps are also not geometrically distributed (the integer-valued analog of the exponential) because a geometric distribution would give positive probability to all odd positive integers. Despite these deviations from the exponential distribution at a microscopic scale, the numerically supported conjecture that the kth moment of the first n gaps is asymptotically the kth moment $k!{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^k$ of an exponential distribution with mean $\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n$ has interesting consequences, as we now summarize and then show in detail.

From Theorem 3, it follows (Corollary 4) that, as $n\to \infty$, the ratio of the variance of the first n gaps to the square of the mean of the first n gaps converges to 1 (Section 4). Thus the gaps have a power-law asymptotic variance function [1, 2, 11, 34–36] or, equivalently, asymptotically obey Taylor’s law of fluctuation scaling: variance of the first n gaps ∼ square of the mean of the first n gaps [4, 6, 7, 12, 14, 33]. Moreover (Section 6), Taylor’s law (with a different coefficient and a different exponent) also describes the variance function of the maximal gap among the first n gaps if the maximal gap may be modeled as the largest order statistic of n observations of an exponential distribution with mean $\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n$: variance of the maximal order statistic $\sim ({\pi }^2/6)\times$ mean of the maximal order statistic. These (conjectured) scaling laws do not appear to have been noticed previously.

The Cramér-Shanks conjecture (Cramér [8, pp. 24, 27], Shanks [32, p. 648, his Eq. (5)(5) $$\pi (x)\sim \frac{x}{\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x}\text{ as }x\to \infty \text{ or equivalently }{p}_n\sim n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n\text{ as }n\to \infty .$$(5) ], Granville [17, p. 21, his Eq. (14)(14) $$\mathrm{\text{Pr}}\{X_{(n)}\le x\}={(1-\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(-\lambda x))}^n,x\ge 0.$$(14) ]) proposes that the maximal gap of primes less than x is asymptotic to ${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^2$ as $x\to \infty$ (Section 6). Using the exponential distribution as a heuristic model of the gaps, we show (Theorem 5) that the Cramér-Shanks conjecture holds if and only if the largest of the first n gaps is asymptotic (as $n\to \infty$) to the expectation ${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$ of the largest order statistic of a sample of n independent observations from an exponential distribution with mean $\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n$. However, the $(1-1/n)$-quantile of the largest order statistic of a sample of n independent observations from an exponential distribution with mean $\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n$ yields $2{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$ as an asymptotic estimate of the largest of the first n gaps. This estimate exceeds the Cramér-Shanks conjecture and Kourbatov’s bound [23] on gaps derived from Firoozbakht’s conjecture.

In the concluding Section 7, we compare asymptotic expressions (derived from the exponential model of prime gaps and from other conjectures) for moments and maximal gaps with exact numerical results derived from public sources. Numerical evidence supports the moments of an exponential distribution with mean $\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n$ as models of the moments of the first n gaps and questions ${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$ as an asymptotic description of the largest of the first n gaps.

2 Definitions and background

For any natural number $n\in \mathbb{N}:=\{1,2,\dots \}$, let p_n be the nth prime starting from $p_1=2,p_2=3$ (OEIS A000040). Let $\mathbb{P}:=\{p_1,p_2,\dots \}$ be the set of primes. Define the nth gap d_n between consecutive primes (OEIS A001223) and the sum $D_k(x)$ of the kth power, $k\in \left\{0\right\}\cup \mathbb{N}$, of the gaps between consecutive primes that do not exceed real x to be (1) $$d_n:=p_{n+1}-p_n,n\in \mathbb{N},$$(1) (2) $$D_k(x):=\sum _{p_{n+1\le x}}{d}_n^k.$$(2)

We shall say that d_n is the gap of p_n if and only if (1(1) $$d_n:=p_{n+1}-p_n,n\in \mathbb{N},$$(1) ). For example, the gap of 17 is 2.

Let $\pi (x):=\#\{p\in \mathbb{P}|p\le x\}$ be the number of primes that do not exceed real $x\ge 2$ (OEIS A000720 gives $\pi (x)$ evaluated at positive integral values of x). Obviously $\pi (p_n)=n$ and $p_{\pi (x)}=\mathrm{\text{max}}\{p_n\in \mathbb{P}|p_n\le x\}$. For $2<a<b$, the number of primes in the interval $(a,b]$ equals $\pi (b)-\pi (a)$. Those primes are $p_{\pi (a)+1},\dots ,p_{\pi (b)}$ and the gaps of those primes are $d_{\pi (a)+1},\dots ,d_{\pi (b)}$. Then (3) $$d_{\pi (a)+1}+\cdots +d_{\pi (b)-1}:=L_1<L:=b-a<L_2:=d_{\pi (a)+1}+\cdots +d_{\pi (b)}.$$(3)

Some authors define the number of the gaps of the primes in $(a,b]$ to be $N_1:=\pi (b)-\pi (a)-1$ (excluding gap $d_{\pi (b)}$ because $p_{\pi (b)+1}>b$) and some authors define it to be $N_2:=\pi (b)-\pi (a)$ (including gap $d_{\pi (b)})$. Asymptotically, the difference in these definitions is immaterial.

If f(x) and g(x) are real-valued functions of real x and g(x) > 0 for all x sufficiently large, define $f(x)\sim g(x)$ to mean that $f(x)/g(x)\to 1$ as $x\to \infty$. In Riesel’s [29, p. 61] cautious notation, define $f(x){\sim }_{c}g(x)$ if $f(x)\sim g(x)$ is conjectured but not proved. Likewise, ${=}_c$ will denote a conjectured but unproved equality.

Oliveira e Silva [28, p. 2056] conjectured that (4) $$D_k(x){\sim }_{c}k!x{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^{k-1},\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}k\ge 1.$$(4)

The prime number theorem states: (5) $$\pi (x)\sim \frac{x}{\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x}\text{ as }x\to \infty \text{ or equivalently }{p}_n\sim n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n\text{ as }n\to \infty .$$(5)

Because $\pi (x)\sim x/\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x$ if and only if $\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x\sim x/\pi (x)$, and because $x/\pi (x)$ is asymptotic to the average gap of the primes $\le x$, the prime number theorem (5) implies that the average gap of the primes $\le x$ is asymptotic to $\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x$. (Why? Because x is asymptotic to the sum of gaps of the primes $\le x$. Also $\pi (x)$ is asymptotic to the number of gaps of the primes $\le x$, by either definition of that number N₁ or N₂ above. By definition, the average of the gaps of the primes $\le x$ is the sum of gaps of the primes $\le x$ divided by the number of gaps of the primes $\le x$. That ratio is asymptotic to $x/\pi (x)=\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(x)$.) As $n\to \infty$, (5(5) $$\pi (x)\sim \frac{x}{\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x}\text{ as }x\to \infty \text{ or equivalently }{p}_n\sim n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n\text{ as }n\to \infty .$$(5) ) implies that $p_n/n\to \infty$. Taking logs of both sides gives $\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_n-\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n\to \infty$ but $\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_n/\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n\sim (\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n+\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)/\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n\to 1$.

Wolf [41] remarked that, when k = 0, the right side of conjecture (4(4) $$D_k(x){\sim }_{c}k!x{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^{k-1},\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}k\ge 1.$$(4) ) becomes $x/\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x$ as in the prime number theorem in (5(5) $$\pi (x)\sim \frac{x}{\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x}\text{ as }x\to \infty \text{ or equivalently }{p}_n\sim n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n\text{ as }n\to \infty .$$(5) ). When k = 1, (2(2) $$D_k(x):=\sum _{p_{n+1\le x}}{d}_n^k.$$(2) ) simplifies to $D_1(x)=p_{\pi (x)}-2$ and (4(4) $$D_k(x){\sim }_{c}k!x{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^{k-1},\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}k\ge 1.$$(4) ) asserts that $D_1(x)\sim x$, which is well known and, in any case, follows from Lemma 1. For k > 1, (4(4) $$D_k(x){\sim }_{c}k!x{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^{k-1},\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}k\ge 1.$$(4) ) apparently remains unproved, though well supported numerically [28, 41].

We shall use some elementary consequences of the prime number theorem (5).

Lemma 1.

The prime number theorem (5) implies (6) $$\underset{n\to \infty }{\mathrm{\text{lim}}}\frac{p_{n+1}}{p_n}=1,$$(6) (7) $$\underset{x\to \infty }{\mathrm{\text{lim}}}\frac{x}{p_{\pi (x)}}=1,$$(7) (8) $$\underset{x\to \infty }{\mathrm{\text{lim}}}\frac{\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}\pi (x)}{\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x}=1.$$(8)

Proof.

By (5(5) $$\pi (x)\sim \frac{x}{\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x}\text{ as }x\to \infty \text{ or equivalently }{p}_n\sim n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n\text{ as }n\to \infty .$$(5) ), (9) $$\frac{p_{n+1}}{p_n}\sim \frac{(n+1)\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(n+1)}{n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n}\sim 1·1=1.$$(9)

This proves (6(6) $$\underset{n\to \infty }{\mathrm{\text{lim}}}\frac{p_{n+1}}{p_n}=1,$$(6) ). To prove (7(7) $$\underset{x\to \infty }{\mathrm{\text{lim}}}\frac{x}{p_{\pi (x)}}=1,$$(7) ), observe that $p_{\pi (x)}\le x<p_{\pi (x)+1}$, hence $1\le x/p_{\pi (x)}<p_{\pi (x)+1}/p_{\pi (x)}$. As $x\to \infty$, also $\pi (x)\to \infty$, so (6(6) $$\underset{n\to \infty }{\mathrm{\text{lim}}}\frac{p_{n+1}}{p_n}=1,$$(6) ) implies (7(7) $$\underset{x\to \infty }{\mathrm{\text{lim}}}\frac{x}{p_{\pi (x)}}=1,$$(7) ). To prove (8(8) $$\underset{x\to \infty }{\mathrm{\text{lim}}}\frac{\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}\pi (x)}{\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x}=1.$$(8) ), take logarithms of (5(5) $$\pi (x)\sim \frac{x}{\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x}\text{ as }x\to \infty \text{ or equivalently }{p}_n\sim n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n\text{ as }n\to \infty .$$(5) ): $\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}\pi (x)\sim \hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x-\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x\sim \hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x$ as $x\to \infty$. □

Now we define an exponentially distributed random variable and state, mostly without proof, several of its well known properties. Let X be a nonnegative real-valued random variable with cumulative distribution function (cdf) $F(x):=\mathrm{\text{Pr}}\{X\le x\},x\ge 0$. If there exists some $\lambda >0$ such that $F(x)=1-\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(-\mathit{\lambda x})$, then X is exponentially distributed with scale parameter λ and we write $X\stackrel{d}{=}\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(\lambda )$.

Lemma 2.

Assume $\lambda >0$. For n > 1, let X and $X_1,\dots ,X_n$ be independently and identically distributed (iid) $\mathrm{\text{Exp}}(\lambda )$ random variables. Then:

1. For any real c > 0, $\mathit{\text{cX}}\stackrel{d}{=}\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(\lambda /c)$.

2. For real $r>-1$, the rth moment of X is $E(X^r)=\Gamma (r+1)/{\lambda }^r$ [26, p. 28, Eq. (5)(5) $$\pi (x)\sim \frac{x}{\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x}\text{ as }x\to \infty \text{ or equivalently }{p}_n\sim n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n\text{ as }n\to \infty .$$(5) ]. When $r\in \mathbb{N}$, then $\Gamma (r+1)=r!$. Hence the expectation or mean of X is $1/\lambda$ and the variance of X is $1/{\lambda }^2$.

3. Let the order statistics of $X_1,\dots ,X_n$ be $X_{(1)}\le \cdots \le X_{(n)}$. Then [30, p. 343] for $i=1,\dots ,n$, (10) $$E(X_{(i)})=\frac{1}{\lambda }\sum _{j=1}^i\frac{1}{n-j+1}=\frac{1}{\lambda }\sum _{j=n-i+1}^n\frac{1}{j},$$(10) (11) $$\mathit{\text{Var}}(X_{(i)})=\frac{1}{{\lambda }^2}\sum _{j=1}^i\frac{1}{{(n-j+1)}^2}=\frac{1}{{\lambda }^2}\sum _{j=n-i+1}^n\frac{1}{j^2}.$$(11)

4. The cumulative distribution function (cdf) of the smallest order statistic $X_{(1)}$ is (12) $$\mathrm{\text{Pr}}\{X_{(1)}\le x\}=1-\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(-\mathit{n\lambda x}),x\ge 0,$$(12) i.e., $X_{(1)}\stackrel{d}{=}\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(\mathit{\lambda n})$. For $0<q<1$, let y₁ be the $(1-q)$-quantile of $X_{(1)}$. By definition, y₁ satisfies $q=\mathrm{\text{Pr}}\{X_{(1)}>y_1\}=1‐\mathrm{\text{Pr}}\{X_{(1)}\le y_1\}=\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(-\mathit{n\lambda }{y}_1)$. Then (13) $$y_1=-(1/[\mathit{n\lambda }])\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}q<+(1/[\mathit{n\lambda }])(1/q-1).$$(13) In particular, if $q=1/n$, then $y_1=+(1/[\mathit{n\lambda }])\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n$.

5. The cdf of the largest order statistic $X_{(n)}$ is (14) $$\mathrm{\text{Pr}}\{X_{(n)}\le x\}={(1-\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(-\lambda x))}^n,x\ge 0.$$(14) For $0<q<1$, let y_n be the $(1-q)$-quantile of $X_{(n)}$. By definition, y_n satisfies $\mathrm{\text{Pr}}\{X_{(n)}>y_n\}=1‐\mathrm{\text{Pr}}\{X_{(n)}\le y_n\}=q$. Then (15) $$y_n=-(1/\lambda )\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(1-{(1-q)}^{1/n})<+(1/\lambda )(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n-\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}q).$$(15) Proof. $q=1-{(1-\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(-\lambda y_n))}^n$, hence $1-\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(-\lambda y_n)={(1-q)}^{1/n}$ and then $-\lambda y_n=\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(1-{(1-q)}^{1/n})$. The inequality follows from ${(1-q)}^{1/n}<1-q/n$. □

6. [18, p. 324, Ex. 9] By Lemma 2.1, $\lambda X_n\stackrel{d}{=}\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(1)$. Then (16) $$\mathrm{\text{Pr}}\left\{\underset{n\to \infty }{\mathrm{\text{lim sup}}}\frac{\lambda X_n}{\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n}=1\right\}=1.$$(16)

7. Let $S_n:=X_1+\cdots +X_n$. Let random variables $U_1,\dots ,U_{n-1}$ be iid uniformly on $[0,1]$ and let $U_0:=0,U_n:=1$ with probability 1. Then $(X_1/S_n,X_2/S_n,\dots ,X_n/S_n)\stackrel{d}{=}(g_1,g_2,\dots ,g_n):=(U_{(1)}-U_{(0)},U_{(2)}-U_{(1)},\dots ,U_{(n)}-U_{(n-1)})$ ([15, p. 75, III.3(e)] and [18, p. 302, Ex. 42]).

8. [27] Large deviations: When $a>1/\lambda$, then (17) $$\mathrm{\text{Pr}}\left\{\frac{X_1+\cdots +X_n}{n}>a\right\}\approx \hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(-(\mathit{a\lambda }-1-\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}\lambda -\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}a)n).$$(17)

3 Asymptotic moments of first n gaps are exponential

Define the kth moment ($k>-1$) of the first n gaps to be (18) $${\mu }_{k,n}^{\prime }:=\frac{1}{n}\sum _{j=1}^n{d}_j^k.$$(18)

Thus if $\pi (x)=n$, then (2(2) $$D_k(x):=\sum _{p_{n+1\le x}}{d}_n^k.$$(2) ) and (18(18) $${\mu }_{k,n}^{\prime }:=\frac{1}{n}\sum _{j=1}^n{d}_j^k.$$(18) ) give ${\mu }_{k,n}^{\prime }=D_k(x)/n$.

Theorem 3.

The conjecture (4(4) $$D_k(x){\sim }_{c}k!x{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^{k-1},\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}k\ge 1.$$(4) ) of Oliveira e Silva [28, p. 2056] holds for each $k\in \left\{0\right\}\cup \mathbb{N}$ if and only if the kth moment of the first n gaps is asymptotic to the kth moment of the exponential distribution $\mathrm{\text{Exp}}(1/\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)$ with mean $\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n$: (19) $${\mu }_{k,n}^{\prime }{\sim }_{c}k!{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^k,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}n\to \infty .$$(19)

Proof.

The cases $k=0,k=1$ are known to be true. Assume (4(4) $$D_k(x){\sim }_{c}k!x{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^{k-1},\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}k\ge 1.$$(4) ) for k > 1. Using the definition (2(2) $$D_k(x):=\sum _{p_{n+1\le x}}{d}_n^k.$$(2) ) and Lemma 1, replace x by $p_{n+1}$ in (4(4) $$D_k(x){\sim }_{c}k!x{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^{k-1},\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}k\ge 1.$$(4) ) to get (20) $$D_k(p_{n+1}){\sim }_{c}k!n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n))}^{k-1}=k!n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n+\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^{k-1}\sim k!n{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^k.$$(20)

Dividing both sides by n gives (19(19) $${\mu }_{k,n}^{\prime }{\sim }_{c}k!{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^k,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}n\to \infty .$$(19) ).

Conversely, suppose the kth moment of the first n gaps is asymptotic to the kth moment of the exponential distribution $\mathrm{\text{Exp}}(1/\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)$. Then, working backward through the calculation in (20(20) $$D_k(p_{n+1}){\sim }_{c}k!n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n))}^{k-1}=k!n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n+\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^{k-1}\sim k!n{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^k.$$(20) ), (21) $$\begin{array}{c}n{\mu }_{k,n}^{\prime }:=\sum _{j=1}^n{d}_j^k\sim k!n{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^k\sim k!n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n+\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^{k-1}\\ =k!n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n))}^{k-1}{\sim }_c{D}_k(p_{n+1}).\end{array}$$(21)

Again using Lemma 1 to replace $p_{n+1}$ by x and $n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n\sim p_n\sim p_{n+1}$ by x gives (22) $$k!x{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^{k-1}{\sim }_c{D}_k(x).$$(22) □

4 Asymptotic variance function obeys Taylor’s power law

For $n\in \mathbb{N},n\ge 2$, define the mean and variance of the first n gaps as (23) $$m_n:=\frac{1}{n}\sum _{j=1}^n{d}_j={\mu }_{1,n}^{\prime },$$(23) (24) $$v_n:=\frac{1}{n-1}\sum _{j=1}^n{(d_j-m_n)}^2=\frac{n}{n-1}\left(\frac{1}{n}\sum _{j=1}^n{d}_j^2-m_n^2\right)=\frac{n}{n-1}({\mu }_{2,n}^{\prime }-{({\mu }_{1,n}^{\prime })}^2).$$(24)

The central equality in (24(24) $$v_n:=\frac{1}{n-1}\sum _{j=1}^n{(d_j-m_n)}^2=\frac{n}{n-1}\left(\frac{1}{n}\sum _{j=1}^n{d}_j^2-m_n^2\right)=\frac{n}{n-1}({\mu }_{2,n}^{\prime }-{({\mu }_{1,n}^{\prime })}^2).$$(24) ) holds because ${\sum }_{j=1}^n{(d_j-m_n)}^2={\sum }_{j=1}^n(d_j^2-2d_j{m}_n+m_n^2)={\sum }_{j=1}^n{d}_j^2-2{\sum }_{j=1}^n{d}_j{m}_n+n{m}_n^2={\sum }_{j=1}^n{d}_j^2-2(n{m}_n)m_n+n{m}_n^2={\sum }_{j=1}^n{d}_j^2-n{m}_n^2.$

The variance function of gaps is the function f that satisfies $v_n=f(m_n)$ [1, 2, 11, 34–36]. The asymptotic variance function of gaps is a (not unique) function f that satisfies $v_n\sim f(m_n)$.

Corollary 4.

Conditional on the conjectures of Heath-Brown [21], Wolf [39], and (4(4) $$D_k(x){\sim }_{c}k!x{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^{k-1},\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}k\ge 1.$$(4) ) of Oliveira e Silva [28, p. 2056], (25) $$\underset{n\to \infty }{\mathrm{\text{lim}}}\frac{v_n}{m_n^2}{=}_{c}1.$$(25)

Proof.

From (19(19) $${\mu }_{k,n}^{\prime }{\sim }_{c}k!{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^k,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}n\to \infty .$$(19) ), (26) $$\frac{{\mu }_{2,n}^{\prime }}{{({\mu }_{1,n}^{\prime })}^2}{\sim }_{c}2.$$(26)

Hence (27) $$v_n\sim {({\mu }_{1,n}^{\prime })}^2\left(\frac{{\mu }_{2,n}^{\prime }}{{({\mu }_{1,n}^{\prime })}^2}-1\right){\sim }_c{({\mu }_{1,n}^{\prime })}^2(2-1)=m_n^2.$$(27)

□

This power-law asymptotic variance function is the special case $c=1,b=2$ of Taylor’s law of fluctuation scaling $v_n\sim c{m}_n^b,c>0$ [4–7, 12, 14, 33]. These parameter values $c=1,b=2$ are consistent with the exponential distribution, in which the variance equals the square of the mean. However, a variance asymptotic to the squared mean does not imply an exponential distribution (e.g., a normal distribution with mean μ and variance ${\mu }^2$ has a variance equal to the squared mean).

5 An asymptotically exponential distribution of gaps is plausible

In a heuristic and numerical exploration, Yamasaki and Yamasaki [42] “assume that the exponential distribution can be applied to the gaps of prime numbers. But the gaps [except for $d_1=1$] are always even integers, so do not distribute continuously on $[0,\infty )$.” They proposed adjustments to the exponential distribution.

Conditional on a uniform version of the unproved prime r-tuple conjecture of Hardy and Littlewood [20], Gallagher [16] showed that, for $\lambda >0,h\sim \lambda \hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}N$, and $n\le N$, as $N\to \infty$, the distribution of the values of $\pi (n+h)-\pi (n)$ converges to the Poisson distribution with parameter λ. Thus λ is the expectation and the variance of the number of primes over the interval $(n,n+\lambda \hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}N]$ of length $\lambda \hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}N$, so the average gap is asymptotically $\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}N$. If the Poisson-distributed number of primes arrived in the interval $(n,n+\lambda \hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}N]$ according to a Poisson process, then the inter-arrival interval between successive primes (that is, the gap) would be exponentially distributed [15, pp. 188, 378], $\mathrm{\text{Exp}}(1/\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}N)$.

Wolf [40] gave strong numerical evidence [40, p. 3, his Figure 1] and a heuristic argument [40, p. 2, his Eq. (7)(7) $$\underset{x\to \infty }{\mathrm{\text{lim}}}\frac{x}{p_{\pi (x)}}=1,$$(7) ] that an exponential distribution with mean $\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n$ asymptotically approximates the distribution of the first n gaps. To circumvent the difficulty that the exponential distribution lacks the discreteness of the natural numbers, Wolf [40, his Eq. (19)(19) $${\mu }_{k,n}^{\prime }{\sim }_{c}k!{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^k,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}n\to \infty .$$(19) , his Figure 5] proposed a rescaling that turns the discrete d_n into a continuous variable.

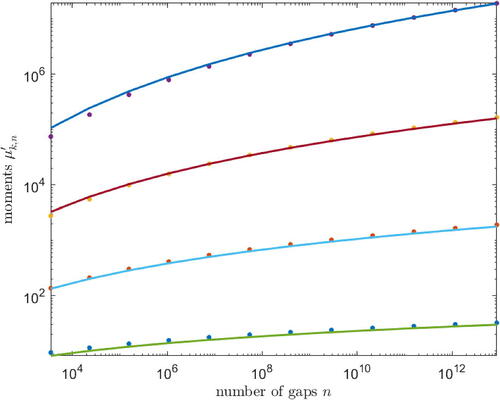
Fig. 1 Moments ${\mu }_{k,n}^{\prime }(k=1,2,3,4)$ of the first n gaps between consecutive primes (solid dots) from k = 1 (bottom row) to k = 4 (top row); and corresponding kth moments $(k=1,2,3,4)$ of exponential distributions $\mathrm{\text{Exp}}(1/\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)$ (solid lines). The dots and the lines are calculated independently with no adjustment of parameters.

Our finding that, conditional on the conjecture (4(4) $$D_k(x){\sim }_{c}k!x{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^{k-1},\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}k\ge 1.$$(4) ) of Oliveira e Silva [28, p. 2056], the moments of the first n gaps are asymptotic to the moments of the exponential distribution, even though the gaps are not continuously distributed, is consistent with T. Stieltjes’s discovery in 1894 that the moments of the lognormal distribution do not uniquely specify the continuous probability distribution that produced the moments [31, pp. 17–18, section 2.1].

We suggest it is plausible that the moments (18(18) $${\mu }_{k,n}^{\prime }:=\frac{1}{n}\sum _{j=1}^n{d}_j^k.$$(18) ) of the first n gaps are asymptotic to the moments of $\mathrm{\text{Exp}}(1/\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)$. First, the primes that do not exceed x are asymptotically uniformly distributed on $[0,x]$ as $x\to \infty$ [4]. To see why, choose any $0<r<1$. Then, for large x, the number of primes not exceeding rx divided by the number of primes not exceeding x is asymptotically, by the prime number theorem (5), $\pi (\mathit{\text{rx}})/\pi (x)\sim \underset{x\to \infty }{\mathrm{\text{lim}}}(\mathit{\text{rx}}/\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(\mathit{\text{rx}}))/(x/\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)=r$. (From a more general perspective, the asymptotic counting function $\pi (x)\sim x/\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x$ of primes is regularly varying [3] with exponent 1.)

Assume $U_1,\dots ,U_n$ are iid uniform on $[0,x]$. The finding that the primes are asymptotically uniformly distributed on $[0,x]$ [4] suggests the order statistics $U_{(1)}\le \cdots \le U_{(n)}$ of $U_1,\dots ,U_n$ as a stochastic model of the asymptotic distribution of the primes on $[0,x]$ and suggests the n “spacings” [5, 22] $g_i:=U_{(i)}-U_{(i-1)},i=1,\dots ,n$, with $U_{(0)}:=0$ almost surely, as a stochastic model of the first n gaps. The spacings are exponentially distributed (Lemma 2.7) and their average size is asymptotically $\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n$. So the gaps between consecutive primes $\le x$ are plausibly distributed as the spacings between consecutive order statistics of $\pi (x)$ iid uniform random variables on $[0,x]$, and these spacings are distributed as $\mathrm{\text{Exp}}(1/\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)$.

This stochastic model of the primes and gaps intentionally omits the discreteness of integers and the lack of independence of primes.

6 The largest of the first n gaps

What would the exponential model of gaps predict about the asymptotic behavior of the maximal gap, $G_n:=\mathrm{\text{max}}\{d_1,\dots ,d_n\}$, among the first n gaps? Here we consider two possible answers.

Theorem 5.

For fixed n > 1, let $X_i\stackrel{d}{=}\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(1/\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n),i=1,\dots ,n$, be iid. Let $\gamma \approx 0.5772$ be the Euler-Mascheroni constant, $\zeta (·)$ the zeta function, and ${\pi }^2/6\approx 1.6449$. Then the mean and variance of the largest order statistic $X_{(n)}$ are (28) $$E(X_{(n)})=(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)\sum _{j=1}^n\frac{1}{n-j+1}\sim (\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)(\gamma +\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)\sim {(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2,$$(28) (29) $$\mathit{\text{Var}}(X_{(n)})={(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2\sum _{j=1}^n\frac{1}{{(n-j+1)}^2}\sim {(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2\zeta (2)={(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2\frac{{\pi }^2}{6}.$$(29)

Thus $\mathit{\text{Var}}(X_{(n)})/E(X_{(n)})\to {\pi }^2/6>1$ and $\mathit{\text{Var}}(X_{(n)})\sim ({\pi }^2/6)E(X_{(n)})$. The maximal gap illustrates Taylor’s law with $c={\pi }^2/6,b=1$.

Proof.

From Lemma 2.3, (30) $$E(X_{(n)})=(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)\left(1+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}\right)\sim (\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)(\gamma +\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)\sim {(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2,$$(30) (31) $$\mathit{\text{Var}}(X_{(n)})={(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2\left(1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots +\frac{1}{n^2}\right)\sim {(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2\zeta (2)={(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2\frac{{\pi }^2}{6}.$$(31) □

The Cramér-Shanks conjecture may be stated as (32) $$\underset{p_j\le x}{\mathrm{\text{max}}}(p_{j+1}-p_j){\sim }_c{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^2\sim {(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_{\pi (x)})}^2.$$(32)

See Cramér [8, pp. 24, 27], Shanks [32, p. 648, his Eq. (5)(5) $$\pi (x)\sim \frac{x}{\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x}\text{ as }x\to \infty \text{ or equivalently }{p}_n\sim n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n\text{ as }n\to \infty .$$(5) ], and the very helpful Granville [17, p. 21, his Eq. (14)(14) $$\mathrm{\text{Pr}}\{X_{(n)}\le x\}={(1-\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(-\lambda x))}^n,x\ge 0.$$(14) ].

Theorem 6.

The Cramér-Shanks conjecture (32(32) $$\underset{p_j\le x}{\mathrm{\text{max}}}(p_{j+1}-p_j){\sim }_c{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^2\sim {(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_{\pi (x)})}^2.$$(32) ) holds if and only if the maximal gap $G_n:=\mathrm{\text{max}}\{d_1,\dots ,d_n\}$ satisfies (33) $$G_n{\sim }_c{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2.$$(33)

Proof.

If there are n primes less than or equal to x, then the largest of these is $p_n\sim n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n\sim x$, using Lemma 1. Thus, translated from the scale of primes not exceeding x to the first n gaps, the Cramér-Shanks conjecture (32(32) $$\underset{p_j\le x}{\mathrm{\text{max}}}(p_{j+1}-p_j){\sim }_c{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^2\sim {(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_{\pi (x)})}^2.$$(32) ) becomes (33(33) $$G_n{\sim }_c{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2.$$(33) ) because (34) $$\underset{1\le j\le n}{\mathrm{\text{max}}}{d}_j{\sim }_c{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n))}^2={(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n+\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2\sim {(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2.$$(34)

Conversely, if ${\mathrm{\text{max}}}_{1\le j\le n}{d}_j{\sim }_c{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$, then ${\mathrm{\text{max}}}_{1\le j\le n}{d}_j={\mathrm{\text{max}}}_{p_j\le p_n}{d}_j\sim {\mathrm{\text{max}}}_{p_j\le x}{d}_j$ and $\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x\sim \hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)\sim \hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n+\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n\sim \hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n$, so ${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^2\sim {(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$ and (32(32) $$\underset{p_j\le x}{\mathrm{\text{max}}}(p_{j+1}-p_j){\sim }_c{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^2\sim {(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_{\pi (x)})}^2.$$(32) ) holds. □

Theorems 5 and 6 suggest that ${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^2$ in the Cramér-Shanks conjecture (32(32) $$\underset{p_j\le x}{\mathrm{\text{max}}}(p_{j+1}-p_j){\sim }_c{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^2\sim {(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_{\pi (x)})}^2.$$(32) ) is too small asymptotically. In the model of Theorem 5, the largest gap is likely to be larger than the expectation of the largest gap because the variance of the largest gap is of the same order of magnitude as the expectation of the largest gap. To the extent that the above conjectures are correct that gaps have exponential moments asymptotically, it would be surprising if the largest of the first n gaps did not exceed ${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^2$.

These suggestions indirectly challenge Firoozbakht’s conjecture [38]. Kourbatov [23] showed that Firoozbakht’s conjecture implies that $d_n:=p_{n+1}-p_n{<}_c{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_n)}^2-\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_n-1$ for all n > 9 and is implied by $d_n{<}_c{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_n)}^2-\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_n-1.17$ for all n > 9. These upper bounds are stronger than the Cramér-Shanks conjecture (32(32) $$\underset{p_j\le x}{\mathrm{\text{max}}}(p_{j+1}-p_j){\sim }_c{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^2\sim {(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_{\pi (x)})}^2.$$(32) ), and lower than the dominant term ${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_n)}^2\sim {(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$ (see Theorem 6) by amounts that increase without limit as n increases. To the extent that our Theorems 5 and 6 suggest that ${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^2$ in the Cramér-Shanks conjecture (32(32) $$\underset{p_j\le x}{\mathrm{\text{max}}}(p_{j+1}-p_j){\sim }_c{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^2\sim {(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_{\pi (x)})}^2.$$(32) ) is too small asymptotically, our results suggest even more that Kourbatov’s upper bounds on gaps are likely to be too small. Kourbatov [23] discusses many related inequalities and conjectures concerning prime gaps.

Granville [17, p. 24] reviewed results that suggest, contrary to the Cramér-Shanks conjecture (32(32) $$\underset{p_j\le x}{\mathrm{\text{max}}}(p_{j+1}-p_j){\sim }_c{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^2\sim {(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_{\pi (x)})}^2.$$(32) ), that (35) $$\underset{p_j\le x}{\mathrm{\text{max}}}{d}_j{\stackrel{>}{\sim }}_{c}2e^{-\gamma }{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^2\sim 2e^{-\gamma }{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_{\pi (x)})}^2,$$(35) where $2e^{-\gamma }\approx 1.1229$. Translating from the scale of x to the scale of the number of gaps $n=\pi (x)$ by $x\sim p_n\sim n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n$ so that ${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^2\sim {(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n))}^2\sim {(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$ gives the proposal that (36) $$G_n{\stackrel{>}{\sim }}_{c}2e^{-\gamma }{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2.$$(36)

These observations motivate another estimate of the largest of the first n gaps, namely, the $(1-1/n)$-quantile of the largest order statistic $X_{(n)}$. We now determine the value of y such that, in a sample of size n from $\mathrm{\text{Exp}}(1/\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)$, as in Theorem 5, the probability that the largest order statistic $X_{(n)}$ exceeds y is $1/n$.

Theorem 7.

In a sample of size k > 1 from $\mathrm{\text{Exp}}(1/\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)$, let y_k be the $(1-1/k)$-quantile of the maximal order statistic $X_{(k)}$. Then $y_k\sim 2(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}k)$ as $k\to \infty$. If $k\sim \mathit{\text{tn}}$ for some t > 0, then $y_k\sim 2{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$ as $n\to \infty$.

Proof.

Using Lemma 2.5, (13(13) $$y_1=-(1/[\mathit{n\lambda }])\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}q<+(1/[\mathit{n\lambda }])(1/q-1).$$(13) ), with $\lambda =1/\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n$ gives (37) $$y_k=-(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(1-{(1-1/k)}^{1/k}).$$(37)

Repeated applications of l’Hopital’s rule as $k\to \infty$ shows that $-\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(1-{(1-1/k)}^{1/k})\sim (2\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}k)$ and hence that (38) $$y_k\sim +2(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}k).$$(38) □

Wolf [40, his Eq. (15)(15) $$y_n=-(1/\lambda )\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(1-{(1-q)}^{1/n})<+(1/\lambda )(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n-\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}q).$$(15) ] argued heuristically for the conjecture that, as $x\to \infty$, (39) $$G_W(x):=\underset{p_n<x}{\mathrm{\text{max}}}(p_n-p_{n-1}){\sim }_c\frac{x}{\pi (x)}(2\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(\pi (x))-\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(x)+c),$$(39) where $c\approx 0.2778769$. Here $c:=\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(C_2)$ and $C_2:=2\prod _{p>2}(1-(p-1{)}^{-2})$ is known sometimes as the twins constant and sometimes as twice the twins constant. The product in C₂ is taken over all positive odd primes. Replacing x by $p_n+\epsilon$ and letting $\epsilon \downarrow 0$ gives the equivalent conjecture, as $n\to \infty$, (40) $$G_W(p_n){\sim }_c\frac{p_n}{n}(2\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(n)-\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)+c)\sim {(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2.$$(40)

7 Numerical illustrations

For moments and maximal gaps, we compare exact numerical results derived from public sources with asymptotic expressions derived from the exponential model of prime gaps and from other conjectures.

7.1 Moments

To illustrate Theorem 3, we compare exact computations of the moments of the first n gaps with the moments of an exponential distribution with mean $\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n$ as given by (19(19) $${\mu }_{k,n}^{\prime }{\sim }_{c}k!{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^k,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}n\to \infty .$$(19) ). Wolf [40] generously made public extensive numerical results at http://pracownicy.uksw.edu.pl/mwolf/gapstau.zip. Wolf [40, p. 2, his Eq. (2)(2) $$D_k(x):=\sum _{p_{n+1\le x}}{d}_n^k.$$(2) ] defined, for large real x and even $d\in \mathbb{N}$, (41) $${\tau }_d(x):=\#\left\{p_{n+1}\right|p_{n+1}<\mathit{x\hspace{1em}}\text{and}\hspace{1em}{p}_{n+1}-p_n=d\}$$(41) and, for every odd $d\in \mathbb{N},{\tau }_d(x):=0$. In words, when d is even, ${\tau }_d(x)$ is the number of pairs of consecutive primes such that the larger prime is less than x and such that their difference equals d; and for odd d, ${\tau }_d(x):=0$. This definition and my subsequent analyses exclude ${\tau }_1(x)=1,x\ge 3$, representing the single gap $p_2-p_1=3-2$ of size d = 1. Wolf collected the non-zero values of ${\tau }_d(x)$ in 34 text files, one file for each of the 34 values of $x=2^t,t=15(1)48$. (Approximately, $2^{48}\approx 2.8147\times {10}^{14}$.) Each file has two columns, the first listing values of d such that ${\tau }_d(x)>0$, and the second listing the corresponding non-zero values of ${\tau }_d(x)$.

First, using MATLAB Version 9.13.0.2049777 (R2022b), I calculated ${\tau }_d(x)$ directly for all primes less than 2²⁰. My results agreed exactly with those in Wolf’s file tau20s.dat. For example, Wolf and I independently found ${\tau }_2(2^{20})=8535$ gaps of size d = 2; the maximal gap size, d = 114, occurred once: ${\tau }_{114}(2^{20})=1$.

Having partially verified Wolf’s results, I analyzed Wolf’s 12 files with values of $x=2^t,t=15,18,21,24,27,\dots ,48$. For each such file separately, Table 1 gives t; the number of gaps $n=\sum _{d\in \mathbb{N}}{\tau }_d(x)$ where $x=2^t$ (not counting the first gap d = 1); the first four integer moments ${\mu }_{k,n}^{\prime },k=1,2,3,4$ from (18(18) $${\mu }_{k,n}^{\prime }:=\frac{1}{n}\sum _{j=1}^n{d}_j^k.$$(18) ); and the maximal gap G_n. Figure 1 compares ${\mu }_{k,n}^{\prime }$ with $k!{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^k$, which is asymptotic to the corresponding moments of samples of size n from an exponential distribution $\mathrm{\text{Exp}}(1/\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)$, as conjectured in (19(19) $${\mu }_{k,n}^{\prime }{\sim }_{c}k!{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^k,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}n\to \infty .$$(19) ). Visually, the agreement in Figure 1 between the exact moments and the asymptotic moments of $\mathrm{\text{Exp}}(1/\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)$ is remarkable.

Table 1 For each upper limit $x=2^t$, this table shows the exponent t of 2, the number n of gaps between consecutive primes (not counting the odd first gap), the moments ${\mu }_{k,n}^{\prime }(k=1,2,3,4)$, and the maximal gap G_n .

			Moments
row	t	n	k = 1	k = 2	k = 3	k = 4	G n
1	15	3510	9.3293	136.2017	2.7818e + 03	7.4292e + 04	72
2	18	22998	11.3982	210.7095	5.5060e + 03	1.8546e + 05	86
3	21	155609	13.4770	304.1124	9.8914e + 03	4.2503e + 05	148
4	24	1077869	15.5652	412.7866	1.5776e + 04	7.8862e + 05	154
5	27	7603551	17.6520	539.4491	2.3885e + 04	1.3864e + 06	222
6	30	54400026	19.7379	683.2373	3.4423e + 04	2.2806e + 06	282
7	33	393615804	21.8231	844.1273	4.7670e + 04	3.5440e + 06	354
8	36	2.8744e + 09	23.9074	1.0222e + 03	6.3972e + 04	5.2773e + 06	464
9	39	2.1152e + 10	25.9908	1.2173e + 03	8.3638e + 04	7.5819e + 06	532
10	42	1.5666e + 11	28.0736	1.4296e + 03	1.0699e + 05	1.0574e + 07	652
11	45	1.1667e + 12	30.1560	1.6590e + 03	1.3435e + 05	1.4377e + 07	766
12	48	8.7312e + 12	32.2379	1.9056e + 03	1.6603e + 05	1.9127e + 07	906

7.2 Maximal gaps

We compare the first 80 known maximal gaps (now including the initial gap of size 1) [37] with four asymptotic models: (32, 33, 36), and (35(35) $$\underset{p_j\le x}{\mathrm{\text{max}}}{d}_j{\stackrel{>}{\sim }}_{c}2e^{-\gamma }{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}x)}^2\sim 2e^{-\gamma }{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_{\pi (x)})}^2,$$(35) ). These results on maximal gaps are more extensive and more detailed than those in Table 1. The tabulation lists three sequences:

1. the indices of primes after which a maximal gap occurs

   $n=1,2,4,9,24,30,99,154,189,217,1183,\dots$ (OEIS A005669),

2. the corresponding maximal gaps

   $G_n:=p_{n+1}-p_n=1,2,4,6,8,14,18,20,22,34,36,\dots$ (OEIS A005250), and

3. the primes after which a maximal gap occurs

   $p_n=2,3,7,23,89,113,523,887,1129,1327,9551,\dots$ (OEIS A002386).

I partially verified the Wikipedia tabulation in two ways. First, Marek Wolf (personal communication, 2022-11-10) generously sent me his tabulation of the first 74 maximal gaps G_n (not including G₁), their indices n, and their beginning primes p_n. Second, using MATLAB, I calculated these three sequences directly for all primes less than 10⁶. My results and Wolf’s agreed exactly, as far as they went, with the Wikipedia tabulation [37].

Figure 2 plots, as a function of n, the maximal gap size G_n among the first n gaps; and the values of the four conjectured asymptotic expressions ${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$; ${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_n)}^2$; $2e^{-\gamma }{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$, where $2e^{-\gamma }\approx 1.1229$; and $2e^{-\gamma }{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_n)}^2$. The majority of points $(n,G_n)$ (blue solid dots in Figure 2) fall slightly below the conjectured asymptotic behavior $(n,{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2)$ (solid black line in Figure 2) derived here from the conjectured asymptotically exponential distribution of gaps. The form of Wolf’s conjecture in (40(40) $$G_W(p_n){\sim }_c\frac{p_n}{n}(2\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(n)-\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(n\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)+c)\sim {(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2.$$(40) ) falls slightly below $(n,{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2)$ and often closer to the points $(n,G_n)$ than $(n,{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2)$. However, the seven exceptional values of n with $G_n>2e^{-\gamma }{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$ in Table 2 suggest that $\underset{n\to \infty }{\mathrm{\text{lim sup}}}{G}_n/[2e^{-\gamma }{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2]$ may exceed 1. The available numerical results neither confirm nor reject the suggestion implied by Theorem 7 that $\underset{n\to \infty }{\mathrm{\text{lim sup}}}{G}_n$ might be asymptotic to $2{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$. The asymptotic behavior of G_n remains to be determined.

Fig. 2 Maximal gap G_n (solid blue dots) among the first n gaps and four conjectured models: ${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$ (solid black line); ${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_n)}^2$ (solid black line with + markers); $2e^{-\gamma }{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$ (dashed purple line), where $2e^{-\gamma }\approx 1.1229$; and $2e^{-\gamma }{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_n)}^2$ (dashed purple line with + markers). The dots and lines are calculated independently with no adjustment of parameters. While the great majority of the values of G_n are better approximated by ${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$ (solid black line) than by the other models, the seven exceptional values of n with $G_n>2e^{-\gamma }{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$ in Table 2 suggest that $\underset{n\to \infty }{\mathrm{\text{lim sup}}}{G}_n/[2e^{-\gamma }{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2]$ may exceed 1.

Table 2 Seven maximal gaps G_n that exceed ${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$ and $2e^{-\gamma }{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$, the index n of the prime p_n that begins the maximal gap, the prime p_n that begins the maximal gap, ${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_n)}^2$, and $2e^{-\gamma }{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_n)}^2$.

row	n	Gn	pn	${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$	${(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_n)}^2$	$2e^{-\gamma }{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}n)}^2$	$2e^{-\gamma }{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_n)}^2$
1	1	1	2	0	0.4805	0	0.5395
2	2	2	3	0.4805	1.2069	0.5395	1.3553
3	4	4	7	1.9218	3.7866	2.1580	4.2520
4	9	6	23	4.8278	9.8313	5.4212	11.0398
5	30	14	113	11.5681	22.3482	12.9901	25.0952
6	217	34	1327	28.9433	51.7058	32.5010	58.0614
7	49749629143526	1132	1693182318746371	994.6470	1229.6	1116.9	1380.7

Only for n = 1 and n = 2 is $G_n>2e^{-\gamma }{(\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}{p}_n)}^2$.

Acknowledgments

J.E.C. thanks Andrew Granville, D. R. Heath-Brown, Tomás Oliveira e Silva, and Marek Wolf for very helpful guidance to relevant references; Marek Wolf for sharing numerical results analyzed here; and Roseanne Benjamin for assistance during this work. Two helpful reviewers provided constructive suggestions.

Declaration of Interest

The author reports there are no competing interests to declare.