What's Brewing? A Statistics Education Discovery Project

ABSTRACT

We believe that students learn best, are actively engaged, and are genuinely interested when working on real-world problems. This can be done by giving students the opportunity to work collaboratively on projects that investigate authentic, familiar problems. This article shares one such project that was used in an introductory statistics course. We describe the steps taken to investigate why customers are charged more for iced coffee than hot coffee, which included collecting data and using descriptive and inferential statistical analysis. Interspersed throughout the article, we describe strategies that can help teachers implement the project and scaffold material to assist students who may have gaps in their mathematical background and offer suggestions if using the lesson with students who are mathematically stronger. Students were highly motivated and enthusiastic to work on a problem with a rich, readily understood context. This article provides teachers with an alternative way to assess student learning, and gives students the opportunity to work the way statisticians work.

KEYWORDS:

• Coffee prices
• Course project
• Data collection
• Descriptive statistics
• Paired t-test
• Statistics education
• Teaching statistics

1. Introduction and Rationale

In our data-driven world, interest in studying statistics has been growing at a rapid rate as the importance of collecting and analyzing data play key roles in providing evidence on which to make decisions. According to the American Statistical Association (ASA), from 2010 to 2013, the number of undergraduate statistics degrees awarded increased by 95%, which made the field of statistics the fastest growing science, technology, engineering, and mathematics (STEM) field (Meyers 2015). Also, a recent study by Logue, Watanabe-Rose, and Douglas (2016) showed that students designated in need of remediation in mathematics were more likely to successfully complete a credit-bearing statistics course with a required developmental math workshop than to complete the typical college quantitative pathway of enrolling in a noncredit remedial elementary algebra course. Based on this study, some colleges that require all students take a credit bearing mathematics course to fulfill a general education requirement have started giving nonstem students the option to take an introductory statistics course in place of the combination of remedial algebra followed by College Algebra. These results suggest that in addition to advanced undergraduate statistics courses for statistics majors, there may be a need to offer more introductory undergraduate statistics courses for nonmajors.

The growth in popularity of statistics may be due, in part, to the fact that in students' professional and personal lives outside of school, important decisions often rest on one's ability to use, understand, and interpret data. By contrast to what is taught in mathematics classes, wherein students are frequently encouraged to master abstract concepts before learning applications (Madison 2004), in introductory statistics classes, applications play a more central and critical role. Therefore, the ability to “think statistically,” can differ from the ability to “think mathematically.” Accordingly, to learn how to “think statistically” context is essential to facilitate the development of the habits of the mind for modeling the way statisticians work and to recognize how data and statistics are used to answer questions posed (Garfield and Ben-Zvi 2008). That is, to develop statistical reasoning skills, students need to learn that the strength of the evidence supporting or refuting a claim is influenced by the quality of the data (Sole 2015) and that data can be used to assess the validity of a claim being made (Ben-Zvi and Garfield 2004). They need to learn how to formulate researchable questions (Chance 2002), and to select the appropriate statistical methods to explain the sources of variation present in the data (Wild and Pfannkuch 1999). They also need to communicate the results. The full process of posing researchable questions, collecting and cleaning data, selecting and applying appropriate statistical tools to answer those questions, and interpreting results within the context of the problem are all key elements of statistical thinking. In alignment with the tenets of constructivism, which stress giving students the opportunity to have a meaningful learning experience by raising questions, seeking patterns, and being actively engaged (Smith 1998; Twomey Fosnot 2005; Libman 2010; Neumann, Hood, and Neumann 2013; Thompson 2013), this article describes a successfully implemented project that uses real data (Neumann, Hood, and Neumann 2013; Sole 2016a) that students themselves collect (Smith 1998) to answer a question that is meaningful to them. It also supports their construction of knowledge (Neumann, Hood, and Neumann 2013) by having them analyze and report their findings (Fillebrown 1994) in a way that models how research is done in practice (Libman 2010).

2. The Larger Context

As appropriate to an introductory undergraduate statistics course, the project entailed the exploration and analysis of real-world data via the construction of histograms and boxplots, and the application of inferential methods such as confidence intervals and paired t-tests. Extensions are suggested to make the project more challenging. Because the project was implemented in a statistics course for students who do not have the typical prerequisite skills of college algebra, time was devoted, as needed, throughout the semester to teach or refresh students' basic algebra skills. In addition, in line with an approach taken by Fillebrown (1994), students were taught how to input formulas into Excel, obtain results, and compare those results to those obtained using Excel's drop-down menu of built-in formulas.

Following the work of Hmelo-Silver, Duncan, and Chinn (2007) on the importance of scaffolding, the project was subdivided into smaller segments so that students' understanding could be built upon and extended, which helped students to more easily grasp some of the more complex material.

3. Stimulating Interest in the Project

This project was motivated by the article, “With Coffee, Icy Means Pricey” (Kadet 2014), which explains why customers might be charged $4 or even $5 for a cup filled with ice and very little coffee. To stimulate student interest and enthusiasm, and serve as a motivation for this investigation, one small cup of hot coffee and one small cup of iced coffee were brought to class and placed on the desk at the front of the room. The following two questions were posed: (1) Do you think these two drinks cost the same? (2) If not, which drink do you think costs more and why? A lively debate ensued. Because the majority of students were familiar with the price of different types of coffee drinks, they were not shy about offering answers to these questions.

Relying on personal experience, the vast majority of students “predicted” that iced coffee costs more than hot coffee. Students selected the hypothesis test to be performed based on the prediction their group had made. They were not so sure, however, about the reasons for the price difference as a variety of explanations were offered, including the following: the cost of producing ice; the time and effort required to produce the iced drink; the larger cup size and different material used for iced coffee; the use of additional flavors or special coffee in iced coffee; a higher demand for cool drinks in warm weather that leads stores to inflate the price of iced coffee artificially. Although showing creativity and thought, as it turned out, none of the proposed explanations reflected the real reason for the price difference. Because many students believed that the reason for the difference would be uncovered through the analysis of the prices themselves, a good lesson was learned when they realized that a thorough statistical analysis left them with unanswered questions. Seeking out and interviewing an individual with expertise in the subject matter provided “extra-statistical” information (Weinberg and Abramowitz 2016a, 2016b) to shed light on the results.

Having introduced the problem, made predictions about which drink would cost more, and engaged the students further by asking them to propose reasons for the predicted price difference, they were now motivated to begin to find the true answers to the questions posed.

4. Rules of the Road: Collaborative Group Learning and Grading

This project was designed to model the collaborative way in which statisticians work in the real world and, at the same time, to offer students the opportunity to learn from their peers within a working group setting. Although assigning students to work in groups has been shown to be beneficial, the extent to which it is beneficial has been shown to depend upon the nature of the group dynamic (Garfield 1995, 2013; Roseth, Garfield, and Ben-Zvi 2008). To increase the likelihood of creating a positive group dynamic so that the members of each group work cooperatively to complete the task, students had the opportunity to select the students with whom they would like to work or, if no selection was made, to inform the instructor confidentially if they would prefer not to work with a particular student or students in the class. Because the class was told that all members of the same group would receive the same grade based on the satisfactory completion of the project, students understood that their individual success was linked to the success of their peers. Understanding this fact was important in helping to facilitate teamwork and a mutually beneficial working relationship among members of the same group. In an effort to engender an even more harmonious group dynamic, immediately after being given the assignment, students were encouraged to discuss how the work might be divided among group members. Twenty minutes of class time was allotted to allow groups to create detailed project plans including how each student would contribute uniquely to the project and how each student would support the other members of the group.

It should be noted that in lieu of this approach, each group member could have been asked to grade each of the other members in the group based on their unique contributions to the work (Bailey, Spence, and Sinn 2013).

Teaching Tip: Detailed project plans can further increase the likelihood that groups are productive and minimize the chance that conflicts arise. Plans could delineate that part of the project on which each person would take the lead and that part on which he/she would play a secondary role in completing. They also could describe how group members would communicate with each other over the course of the project (phone, in-person, text, google document, email, frequency of communication, etc.), and include a tentative timeline for completing the project.

5. Phase I: Data Collection

Educators and educational organizations have strongly encouraged using real data to perform authentic investigations (Singer and Willett 1990; National Council of Teachers of Mathematics [NCTM] 2000; Franklin et al. 2007; Sole 2015, 2016a; Carver et al. 2016; Weinberg and Abramowitz 2016a, 2016b). Using real-world, readily understood data has been shown to help make statistics accessible, relevant, and even enjoyable. Students also need to have the opportunity to collect or generate data to answer a question posed as it is crucial for students to understand potential problems that might arise in the data collection phase (e.g., the presence of duplicate, inaccurately recorded, or missing data).

However, because exercises in textbooks are frequently accompanied by real datasets (Hogg 1991; Sole 2015; Weinberg and Abramowitz 2016a, 2016b), and because it is difficult and often time-consuming to collect one's own data (Sole 2015), some instructors may be deterred from having students collect their own data for class assignments or projects. For students to understand the full enterprise of what it means to be an empirical researcher, and what constitutes an evidence-based inquiry, this project was designed to engage students not only in a data analysis phase, but also in the critical data collection phase (Woodard and McGowan 2012; Sole 2015).

For this class of 24 students, eight working groups of size three were formed. Because the project was assigned before the course withdrawal deadline, potentially some students could withdraw from the course before the first part of the project was completed. The size of the groups and amount of data to be collected were designed to keep groups on track even if they lost a member. Students were asked to collect data from selected coffee shops and/or casual restaurants (hereinafter, called “cafés,” for brevity).

To facilitate the selection of cafés, and to avoid potential selection overlap, the instructor suggested that students map out several paths from school that led in different directions and contained cafés along the way. In addition, students divided other areas near the school or their place of work into blocks, shopping malls, and train stations, and selected all of the cafés they came upon within those selected areas. As the school is in a large city, the job of data collection was not overwhelming or difficult and most students viewed it as a fun adventure. Because many cafés post their menus online, students could also be encouraged to collect their data online from cafés in the vicinity of the school or their place of work. To achieve a large enough sample of observations, each group was asked to collect the coffee data from 45 coffee shops and/or casual restaurants. As coffee is frequently sold in small, medium, and large sizes rather than by the number of ounces, students were instructed to collect data on iced and hot coffee relative to a particular sized coffee cup, deemed by the café as being small, medium, or large even if the number of ounces was different.

After the data were collected, each group was asked to inspect their data and to raise questions about anomalous or otherwise problematic data points. For example, one group realized that two of the students in its group collected data from the same coffee shop chain, although at different locations, and understood that those two sources of data really were one source only, and that the two sets of values were duplicates of each other. Rather than two independent observations of hot coffee and of iced coffee, these two sets of values represented only one observation of each coffee type. This discussion gave students a glimpse into the important task of inspecting and cleaning one's data as precursors to analyzing it.

Teaching Tip: Discussing potential problems can help ensure that the data is of a good quality and, at the same time, satisfies the assumptions underlying the analyses to be undertaken. Instructors may want to alert students to the fact that an underlying assumption of many of the hypothesis tests they will be learning is the independence of observations. Observations that duplicate one another because they arise from virtually the same source represent a violation of the assumption of independence.

Teaching Tip: For larger classes, this project could be assigned using the already collected data as the basis for one of several capstone-type group projects to be handed in or presented in class at the end of the semester. In this case, groups of students could prepare a report in traditional or power point format that uses the appropriate statistical tools to address the questions posed.

6. Professional Portfolios: Showcasing Students' Work

Electronic portfolios are used at the college where this project was implemented. During orientation, students learn how to set up and post content on their own e-portfolio sites and, during the year, learn how to submit assignments confidentially. For work that is posted online, students can designate whether the content they post can be seen only by the site owner, by all people at the college, or by anyone browsing the web.

To help students manage their time in connection with this project, it was broken down into three smaller assignments to be submitted biweekly. Confidence was built as components were completed successfully, and having the components broken down in this way prevented students from feeling overwhelmed. After each group submitted a hard copy of his/her dataset and a written description of the data collection approach used, each student uploaded the data to his or her electronic portfolio (e-portfolio) site under the statistics course header.

Mathematics portfolios contain a collection of the student's work in mathematics. Portfolios, whether kept electronically or not, are a valuable means to assess students work (Fukawa-Connelly and Buck 2010; Sole 2012). Portfolios allow students to monitor their progress and build confidence in their ability to carry out the work assigned (Sole 2012).

Electronic portfolios have the added benefit of being able to be viewed by one's peers and used by a department or institution to assess student learning. E-portfolios have been shown to benefit both the student and the institution (Miller and Morgaine 2009; Gambino 2014) by providing a rich, archived record of each student's work for sharing with peers or prospective employers. They also provide a way for students to see how their skills have developed over their college careers and for institutions to assess students' progress in a more authentic and thorough way.

Teaching Tip: If using e-portfolios, to deter cheating, students should be asked to upload their work to their own e-portfolio sites to share with the college community and prospective employers only after each member of the class has submitted their work to the instructor.

7. Tools for Analysis

Although a variety of software packages could have been used, such as SPSS, SAS, or Stata, students were required to use the Data Analysis Toolpak in Microsoft Excel for analyzing the data for this project. Links to online Excel tutorials from YouTube and other resources as well as course updates were posted continually throughout the semester on the course e-portfolio site.

Teaching Tip: Maintaining a brief list of daily topics covered on-line in an e-portfolio site with links to relevant on-line resources can be a valuable reference tool for larger projects which can help students work independently.

8. Phase II Descriptive Analysis: Summary Statistics, Frequency Tables, and Graphical Displays

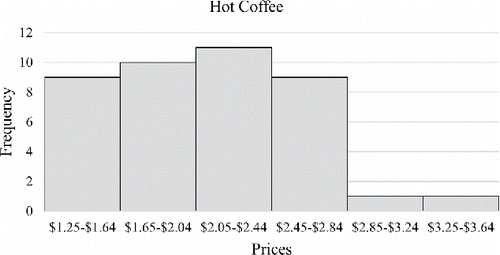
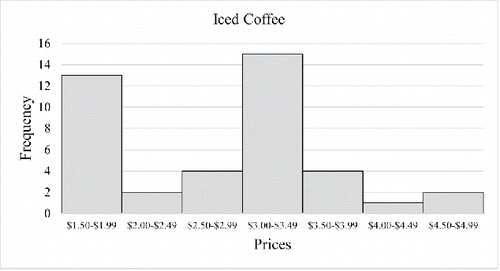
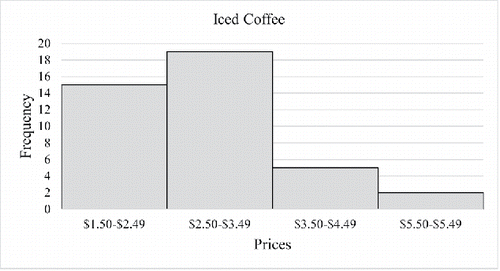
After students submitted and uploaded their datasets, they were asked to produce the following descriptive statistics for both hot and iced coffee: the means, medians, first and third quartiles, minima, maxima, standard deviations, interquartile ranges, and ranges (see Table 1). They also were asked to produce frequency and relative frequency tables, histograms, boxplots, and to comment on the shape of the distribution and the presence of univariate outliers (see Tables 2–4 and Figures 1–5). Because communication of results to individuals with little knowledge of statistics is a critical part of the job of a statistician, students were encouraged to present their results in a formal, yet jargon-free manner so that they could be understood by a general audience who has not necessarily taken a course in statistics as they now have.

Teaching Tip: This project could have been presented in a more open-ended way simply by asking students to apply what they learned in the course to compare the price of hot and iced coffee and interpret their findings. With the appropriate audience, there are many benefits of projects that are more open-ended (Silver1997; Cifarelli and Cai 2005; Sole 2016b). For example, they give students the opportunity to be creative in the type of approach to sampling and data collection and analysis used (Silver 1997; Sole 2016a). In addition, because they are not proscriptive, they better represent the type of problems encountered in the real-world (Cline 2005; Sole 2016a, 2016b). Given the level of the students in this course, however, providing more specific directions in a stepwise fashion was viewed as more appropriate.

Table 1. Summary statistics for medium-sized coffee by type.

Coffee Type	Sample size	Minimum	Q1	Median	Q3	Maximum	Mean	Std. Dev.	Range	IQR
Hot	41	$1.25	$1.70	$2.10	$2.50	$3.50	$2.07	$0.52	$2.25	$0.80
Iced	41	$1.50	$1.80	$3.00	$3.19	$4.65	$2.73	$0.85	$3.15	$1.39

Table 2. Frequency and relative frequency distribution of medium-sized hot coffee prices.

Prices	Frequency	Relative frequency
$1.25–$1.64	9	0.22
$1.65–$2.04	10	0.24
$2.05–$2.44	11	0.27
$2.45–$2.84	9	0.22
$2.85–$3.24	1	0.02
$3.25–$3.64	1	0.02

Table 3. Frequency and relative frequency distribution of medium-sized iced coffee prices.

Prices	Frequency	Relative frequency
$1.50–$1.99	13	0.32
$2.00–$2.49	2	0.05
$2.50–$2.99	4	0.10
$3.00–$3.49	15	0.37
$3.50–$3.99	4	0.10
$4.00–$4.49	1	0.02
$4.50–$4.99	2	0.05

Table 4. Frequency and relative frequency distribution of medium-sized iced coffee prices using a larger bin size.

Prices	Frequency	Relative frequency
$1.50–$2.49	15	0.37
$2.50–$3.49	19	0.46
$3.50–$4.49	5	0.12
$5.50–$5.49	2	0.05

Figure 1. Histogram of medium-sized hot coffee prices.

Figure 2. Histogram of medium-sized iced coffee prices.

Figure 3. Histogram of medium-sized iced coffee prices using a larger bin size.

Figure 4. Boxplot of medium-sized coffee prices by type.

Figure 5. Differences in price between medium-sized iced and hot coffee.

The Excel output obtained from the data collected and analyzed in this class is shown in Table 1.

Teaching Tip: If presenting this work in class rather than assigning it as a project, students could be asked to use the summary statistics to predict and compare the shapes of the histograms. An important idea worth exploring is attempting to predict the shape of the distribution before data are collected and connecting the prediction to the sampling technique used. For example, students might predict that the price distribution of each type of coffee would be bimodal if they collected data from two neighborhoods that had very different socioeconomic statuses.

There is no consensus on the exact number of bins a frequency table should have. Some books recommend having between 5 and 20 classes (Triola 2014) while others recommend about 10 classes (Gravetter and Wallnau 2016), and still others leave it up to the judgment of the researcher, pointing out that too few classes may not show the shape of the distribution and using too many classes is cumbersome (Weinberg and Abramowitz 2016a, 2016b). Some students had a preference for “nice” class widths such as $1 or $0.50, which determined the number of classes rather than adhering to recommended guidelines. If done in class, comparing Figure 2 and Figure 3, it is valuable to illustrate that the histogram can appear either bimodal or right skewed depending on the class widths. The change in the shape of a distribution can help students understand and appreciate that data can be presented in multiple ways.

Teaching Tip: Students could be asked to explore whether the choice of bin size has an impact on the shape of the distribution. After confirming that bin size does in fact impact the distribution shape, students could be asked which histogram they believe best represents the underlying shape of the distribution.

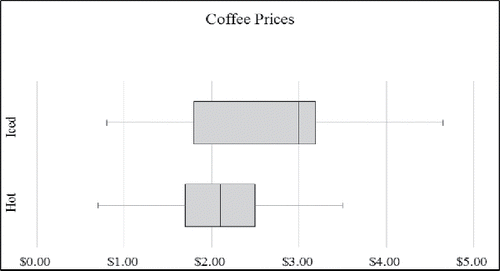
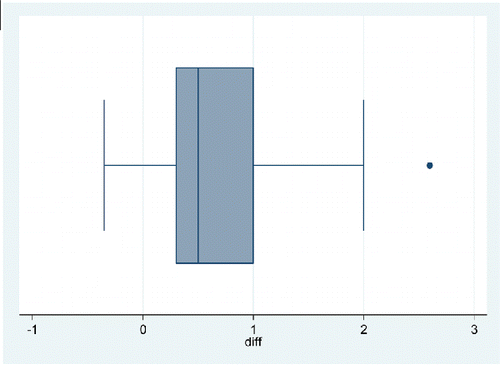
In addition to the histogram, box-and-whiskers plot also may be used to represent the two sets of data graphically in one display as in Figure 4.

Comparing the two boxplots, the distribution of iced coffee prices appears to have greater variability than that of hot coffee prices. Both the range and IQR of iced coffee prices are larger. The median price of iced coffee is higher than the median price of hot coffee. Although the distribution of hot and iced coffee prices appear to be positively skewed in the histograms of Figures 1 and 3, the middle 50% of prices represented by the boxplots of Figure 4 shows the distribution of hot coffee prices to be reasonably symmetric and the distribution of iced coffee prices to be negatively skewed. This apparent contradiction is perhaps due to the fact that unlike histograms, boxplots depict only five summary statistics of a distribution, the minimum, maximum, and Q₁, Q₂ (median), and Q₃. Summary statistics for iced and hot coffee are shown in Table 1.

Students were asked to consider whether any of the observations were potential univariate outliers. Students should be encouraged to determine the reasons for the outliers, if there are any. Possible reasons might include having one piece of data from a street vendor, rather than a café, or misinterpreting the size of the coffee cup when drinks have different names such as “Tall” or “Grande.”

Teaching Tip: The boxplots, constructed in Excel, do not display any outliers, (i.e., points that are smaller than Q₁-1.5 interquartile ranges or larger than Q₃+1.5 interquartile ranges from the median). Where outliers do exist, they are represented in a boxplot by symbols (e.g., an asterisk or dot) beyond the minimum and maximum values displayed as the ends of the two whiskers attached to the middle box.

Because each pair of hot and iced coffee prices comes from the same café, this example gives students an opportunity to learn the difference between paired (dependent) and unpaired data, as well as to learn how to compute difference scores using Excel. Using the difference scores, students could be asked to construct a boxplot that gives a more explicit comparison of the coffee price differences. For the graphic of Figure 5, we computed the difference as hot coffee price minus iced coffee price. Because the median is positive, we know that, on average, iced coffee costs more than hot coffee. We also may note the positively skewed distribution of differences in price with one outlier at approximately 2.6. Table 5 presents summary statistics for the price difference.

Table 5. Summary statistics for the price differences.

Price difference
Mean	0.66
Standard error	0.09
Median	0.50
Mode	1.00
Standard deviation	0.55
Sample variance	0.31
Kurtosis	2.97
Skewness	1.34
Range	2.95
Minimum	−0.35
Maximum	2.60
Sum	27.19
Count	41.00
Confidence level (95.0%)	0.17

9. Inferential Analysis: Confidence Intervals and A Hypothesis Test

After students submitted and uploaded the set of descriptive statistics and graphics, they were asked to consider the dataset as a “random” sample of hot and iced coffee prices selected from a defined population of locations and to draw conclusions about the population based on sample findings. To do so, students were asked to find the 95% confidence interval about the mean price difference between hot and iced coffee and to use the confidence interval to perform a hypothesis test on the mean price difference between iced and hot coffee (see Table 6). Once results were obtained, students were asked to interpret the findings.

Teaching Tip: To increase the level of rigor and better model the way statisticians work in the real world, the question could be presented in an open-ended manner, asking students to select the appropriate test to compare the prices. To help students select the appropriate test, during the semester, it might be beneficial to have students develop a spreadsheet that lists different statistics tests, for each test a sample question that could be answered by applying the test, key features of the test, and characteristics of independent and dependent variables.

Table 6. t-Test results for the price of hot coffee versus Iced coffee.

t-Test: Paired two sample for means
	Iced coffee	Hot coffee
Mean	2.7322	2.0690
Variance	0.7163	0.2680
Observations	41.0000	41.0000
Pearson correlation	0.7743
Hypothesized mean difference	0.0000
df	40.0000
t Stat	7.6790
P(T< = t) one-tail	0.0000
t Critical one-tail	1.6839
P(T< = t) two-tail	0.0000
t Critical two-tail	2.0211

We noted that because the distribution of price differences had a skewness of 1.34, it was unlikely that the distribution of price differences was normal in the population. However, the sample size is n = 41 pairs. According to the central limit theorem, for sample sizes that exceed 30, the sampling distribution of sample means (e.g., sample mean differences), will be approximately normally distributed. Therefore, we considered the assumption of normality underlying the construction of the confidence interval for the mean price difference to be viable, which enabled us to proceed with the following inferential analysis.

The 95% confidence interval about the mean price difference that was obtained using the summary statistics was $0.49 to $0.83

Students interpreted this to mean that they were highly confident that the interval from $0.49 to $0.83 contains the true mean price difference between iced and hot coffee. Since zero is not included in the interval, we know that, on average, it would be very unusual to observe a mean difference this large if there really was not a difference between iced coffee and hot coffee prices. Furthermore, because we subtracted hot coffee prices from iced coffee prices, the positive values of the confidence interval indicate that the mean price of iced coffee is statistically significantly higher than the mean price of hot coffee.

Teaching Tip: If presenting this work in class rather than assigning it as a project, students could be asked to anticipate the results of the hypothesis test given the confidence interval. This could help students understand the connection between confidence intervals and hypothesis tests. To be conservative and reinforce the agreement between the confidence interval and hypothesis test, students could be asked to carry out a nondirectional hypothesis test of the price difference. For a good explanation of the connection between confidence intervals and nondirectional hypothesis tests, the reader is referred to Weinberg and Abramowitz (2016a, 2016b).

Each group of students compared these results with their original predictions made before data were collected. Most of the groups predicted correctly that iced coffee would cost more than hot coffee on average. The observed test-statistic had p-value of < 0.0001, indicating that on average, the price of iced coffee is statistically significantly higher than the price of hot coffee. This was the result the class expected based on the initial class discussion.

10. Pedagogical Practice

Although the results clearly showed that iced coffee costs more, on average, than hot coffee, students had no more insight into why there was a price difference. In their final write up, some students suggested that the preparation of iced coffee was “a more complex process,” but did not elaborate. Often students do not fully understand the need to obtain additional information in order to present a more comprehensive understanding of the phenomenon being studied. After students submitted the final part of the project, the class took a trip to a coffeehouse and had the chance to interview a coffee manager. Only then did they learn that typically to produce iced coffee grounds are steeped in cold water for a day. Using this process to produce a drink that is less acidic, more beans were needed to make iced coffee, which led to the drink having a higher price—a surprising fact no student had guessed. Other variables that could have been collected to explain the variation in price difference are whether the café was centrally located on a busy thoroughfare, whether the café was part of a chain, the number of ounces in a typical iced or medium-sized hot coffee, and the temperature outside (iced coffee would likely be more in demand during the hot summer months).

11. Teaching Reflection: Goals and Discussion

This project was designed to scaffold learning, model the way statisticians work, and increase students' understanding of statistics in the context of a problem that is meaningful to them. Pedagogical strategies were put in place to help groups work together effectively and to manage the project. These strategies could be used by students in other courses or in the workforce. Reflecting on the use of pedagogical techniques, students appeared to gain confidence as they completed each component of the project. By breaking down the project and scaffolding topics, work that otherwise might have felt overwhelming, seemed to be viewed by students as manageable. By creating project plans before the work began, each of the groups appeared to enjoy a harmonious and mutually beneficial group dynamic.

The project began with a familiar real-world question which increased the relevancy of the problem and students' motivations to find an answer to the question posed. Having students collect their own data allowed students to see firsthand how difficult it could be to obtain good data and how important it is for the data to be inspected and cleaned before analyses are undertaken, a point that usually receives little time and attention in statistics courses. The benefits we found in using real-world data within a constructivist perspective (Smith 1998; Libman 2010; Neumann, Hood and Neumann 2013; Thompson 2013) are in line with the recommendations of other researchers (Singer and Willett 1990; Garfield and Ben-Zvi 2008; Neumann, Hood, and Neumann 2013; Sole 2016a) who advocate that students should not merely be passive recipients of knowledge, but rather, active participants, who are fully engaged in the process from start to finish.

By first getting to know the dataset using both graphics and descriptive statistics, students obtained a good understanding of whether the dataset supported the prediction they were testing before they turned to inferential statistics to test out a hypothesis that they intuitively believed to be true, but awaited empirical evidence to confirm.

Students were adept at finding the confidence intervals, performing the hypothesis test, and interpreting the results. Unexpectedly, many students had assumed that the statistical analysis would reveal why iced coffee cost more than hot coffee. Inferential statistics and seeking the advice of an expert to shed light on the findings gave students an in-depth understanding of how statisticians work in practice and an opportunity to think statistically.

12. Conclusion

The main goal of this article is to encourage, by example, other instructors to consider incorporating similar projects into their courses. For instructors who would prefer not to have their students collect data or do not have the time to devote to data collection, we have provided the dataset. As described, with the appropriate guidance, encouragement, and scaffolding of material, such projects can offer students a successful, enjoyable, and confidence-building experience.

Supplemental Material

Supplementary files for this article are available on the publisher's website.