Kinetic Considerations of Texture Softening in Heat Treated Root Vegetables

Abstract

Cylindrical pieces of turnip (Brassica napobbrassica) and beet root (B. vulgaris L) were heated at temperatures ranging from 70–100°C for different time intervals. Texture values of heat-treated products were evaluated by a computer-interfaced compression testing machine using a single-cycle deformation test. The force-to-deformation ratio was taken as a measure of sample firmness; the stress-to-strain ratio (modulus of deformability) as a measure of the sample stiffness; and the percentage of recoverability of input energy (percentage ratio of the area under the force-to-deformation curve during relaxation in relation to the total area) as a measure of sample springiness. The thermal softening behavior represented by all three measured parameters were found to follow the same trend of the pseudo first-order kinetic theory based on two substrates, one softening faster than the other. The softening rate for the rapid (first) mechanism was up to 100 times faster than for the slower (second) mechanism. The softening rate for turnip was up to 15 times faster than for the beet. While turnip pieces indicated a higher associated activation energy (141–167 kJ/mol) for the rapid mechanism compared to the slower mechanism (60–83 kJ/mol), the beet root showed a closer range of activation energy (82–92 kJ/mol) for the two mechanisms. The results obtained are useful in thermal processing applications to improve the quality of root vegetables.

Keywords:

• Texture
• Kinetics
• Root vegetables
• Heat treatment

INTRODUCTION

Plant roots constitute an important category of foodstuffs in terms of consumption, nutritional contribution and sensory attributes.[1,2] These vegetables are subjected to thermal processing in order to destroy micro-organisms that cause spoilage, so that they can be consumed long after they have been harvested. Heat treatment also causes significant quality degradation, especially regarding thermolabile nutrients and organoleptic factors.[4] Changes in mechanical properties and softening of the tissue in vegetables are major limiting factors for heat treatment. These changes are important because they are related to the textural and sensorial characteristics of the food, and consequently, with the quality and acceptance of the product by the consumer.[5] Softening of the tissue has been related to the loss of turgor pressure, uptake, or adsorption of water during thermal processing, which can reduce the cohesiveness of the matrix and soften the cell wall, and to the chemical, enzymatic, and non-enzymatic changes in pectin presented in the cell wall and middle lamella in the plant foodstuffs.[6–9] Cell wall softening and disruption has been found after heating, freeze-thawing, brining, air drying, and osmotic dehydration.[5,8,10–15]

Improvement of quality factors have been made possible by the increase in knowledge of the kinetics of food deterioration, advanced analytical methods, and availability of different numerical methods and powerful computers that can simulate the behavior of complex systems.[5,16] The analytical approach to food quality deterioration allows a wider scope of investigation which may provide alternative processes, different conditions, or more efficient operation, in order to minimize undesired changes and optimize quality retention. It also provides a deeper understanding of the mechanisms controlling the processes studied.[4,8,17]

A number of chemical changes take place when foods are subjected to a thermal process. Because of the complex chemical composition of foods, it has not been possible to quantify all the changes taking place as a result of heating, and to relate, in a quantitative manner, the chemical changes to physical changes, such as softening. A simple and useful approach in softening studies has been to express data in terms of either apparent reaction rate constants or, analogous to microbial death kinetics, in terms of D-values.[15]

For an optimization of the sensory quality in thermal processing, the temperature dependence of the sensory quality in various foods should be known with a fair degree of accuracy.[8,18] The chemical reactions in foods have a temperature dependency that can be described by a z-value of 33°C.[3] The z-value corresponds to the temperature shift needed for a tenfold change in the rate of a chemical reaction or biological inactivation. The inactivation of bacterial spores, with a z-value of around 10°C, is however generally the basis for the duration of the sterilization.[18,19] The differences in the temperature dependence between bacteriological inactivation and chemical and sensory quality changes imply that an optimization of the quality retention is possible.[20] Therefore, knowledge of the time and temperature relationship for the changes during thermal processing is necessary. In addition, the sensory quality is evaluated as a volume-averaged value, whereas the spore inactivation is considered only at its minimum value.

The objectives of this study were, therefore, firstly to evaluate the effects of cooking on the textural properties (firmness, stiffness, and springiness) of turnip and beet roots, for the purpose of gathering data to be used in predicting the texture loss of roots subjected to thermal processing; and secondly to determine whether cooking of these root vegetables yields two simultaneous first-order kinetic reactions, which have been observed with the thermal softening behavior of some other vegetables.

MATERIALS AND METHODS

Sample Preparation

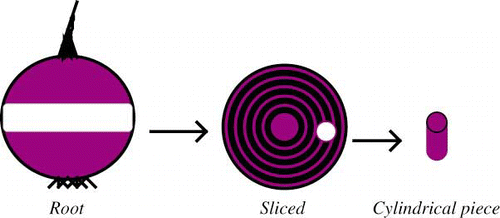
During a period covering six harvest dates, a total of 80 kg of regular turnip, and red beet roots of medium diameter (8–10 cm), were obtained from an orchard located on Ile-Perrot, Quebec, Canada. Beet and turnip roots were packaged in vented, polyethylene bags (5 kg) to maintain high humidity, and stored at 4°C until use.[21,22] For each temperature treatment, a 5 kg bag of beets or turnips was used, and textural properties were measured on the same day. Beet and turnip roots were first sliced (turnips 20 mm and beets 10-mm thick) using an electrical slicer. Later, each slice was punched out by two cork borers to provide cylindrical pieces of turnips (20 mm thick × 18 mm diameter) and beets (10 mm thick × 9 mm diameter). Cylindrical specimens were placed in sealable polyethylene bags to prevent moisture loss prior to further experiments. Figure 1 illustrates the sample preparation of these root vegetables.

Figure 1 Steps in sample preparation of root vegetables.

Heat Treatment

Two metal cans (211 × 400 picnic type) were first perforated around the body for ease of hot water circulation around the food particles (∼100g). The main purpose of using a perforated can was to hold the particles in place. The cylindrical pieces of each sample were then placed in cans and immersed in a well-circulated water bath (THERMOMIX 1480, B. Braun Co., Melsungen, Germany) for selected times (1–80 min). Five bath temperatures (70, 80, 90, 95, and 100°C ± 0.7°C) were employed to heat treat the samples. After heat treatment, samples were cooled by immersion in a cold water tank, drained for two minutes, and then placed in polyethylene sealable bags to prevent moisture loss during texture measurement. Each temperature treatment and texture measurement was performed on the same day.

Texture Evaluation

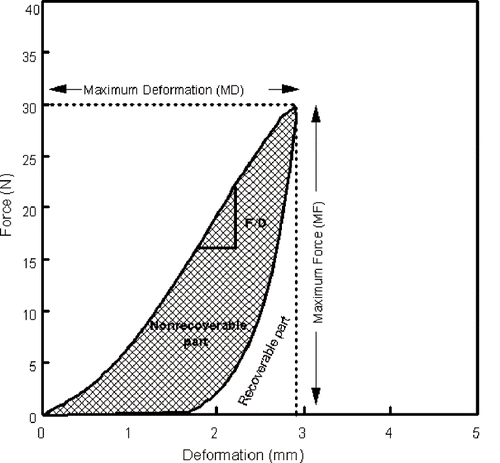
Evaluation of textural properties was performed using a Universal Testing Machine (Lloyd Model LRX - 2500 N; Lloyd Instruments Ltd., Fareham, Hans, UK). The cylindrical pieces of beet and turnip roots were compressed under a constant force of 30 N in a single cycle compression-decompression test, using a 50 N load cell and a 50-mm diameter circular probe, with 10 mm/min as a rate of deformation. Several parameters were derived from the deformation curves (Figure 2) as indicators of physical properties, based on the following definition: firmness as the force-to-deformation ratio (N/mm), stiffness as the stress-to-strain ratio (modulus of deformation; N/mm²),

(1)

(2)

Figure 2 Typical plot of compression-decompression test used to calculated texture parameters.

where F/D is the slope of the linear section.

(3)

Each test was replicated five times (6 measurements per replicate) and their mean values were used as indicators of the textural properties of these selected vegetables.

Kinetic Considerations

A first-order model was assumed for the texture softening kinetics. The first-order model is shown in Eq. (4), indicating that the rate of reaction at any time is directly proportional to the existing concentration:

(4)

where C is the concentration of the reactant at time t and k is the rate constant. Integrating and transposing yields:

(5)

where C_o is the concentration of that reactant at zero time. A plot of ln C versus time is linear and the negative slope of the line gives the rate constant k, while the intercept on the ordinate at time zero gives ln C_o. The decimal reduction time (D-value), also a measure of the reaction rate, is the time required at a particular temperature to result in one decimal reduction in the texture value (firmness, stiffness or springiness), which can be calculated using Eq. (6):

(6)

The temperature dependence of k and D can be obtained by the Arrhenius equation as shown below:

(7)

where E_a is the activation energy, R is the gas constant, T is the absolute temperature and A is a constant. In the Arrhenius model, the plot of ln k vs 1/T is linear and the activation energy, E_a, can be calculated from the slope (=E_a/R) of the line. The temperature dependence can also be obtained from the z-value, which is obtained from the plot of log D vs T. Based on a two point approach; z can be obtained using Eq. (8):

(8)

where D₁ and D₂ are the decimal reduction times at temperatures T1 and T₂, respectively; these can also be obtained as the negative reciprocal of the regression slope. The z-value represents a temperature range resulting in a 10-fold change in the D-values. In simple terms, the D-value goes up ten times as the temperature is decreased by one z–value, and goes down to one-tenth if the temperature goes up by one z-value.

Several researchers who studied the rate of thermal softening of vegetables tissues have found a good fit of their experimental data to the first-order kinetic model. Many of the processes do not arise from simple first-order chemical reactions; the chemistry of the process may also be unclear. Generally, the slope of the log (concentration) versus time plot is called the apparent first-order rate constant. The modifying adjective “pseudo or apparent” is used to signify that the process is not truly first-order in the chemical sense, but that the experimental data gives a good fit to the first-order chemistry model.

From analogy with kinetic theory for two apparent first-order processes, it can be postulated that the texture of vegetable tissue is composed of two substrates, “a” and “b”, and that substrate “a” softens by a rapid Mechanism 1, while substrate “b” softens by a slower Mechanism 2.[23–25] Based on the assumption that the faster mechanism ceases to be significant after a reasonably long time, the rate constant for the slower mechanism can be obtained from the latter portion of the curve. Then, the linear portion of this slower mechanism is extrapolated back to zero cooking time, and this extrapolated line is subtracted from the points above it to get more realistic data for the rapid mechanism. For instance, in this study, seven different heating times were selected at each heating temperature. The resulting texture values (each point representing 12 measurements for 2 replicates) were then plotted in an Excel worksheet. All softening curves indicated a curvature shape. The log of the last four measuring points (Mechanism 2) were selected and extrapolated back to zero, leaving three new points below the first three measurement points. These points were then subtracted from the above points, leaving another straight line which represented Mechanism 1. The derived line using the modified data was then used to calculate the apparent rate constant for this mechanism. This procedure was reported for describing the cooking behavior with other legumes by Huang and Bourne[23] and Bourne.[24,25] Thus, assuming two simultaneous first-order processes, the texture softening kinetics are represented by two equations as shown below:

(9)

where “a” is the firmness contributed by the first substrate and “b” by the second substrate, t is the time, k₁ is the apparent rate constant for Mechanism 1 (substrate a) and k₂ for Mechanism 2 (substrate b) when the tissue is heated. Integration and transposing in the usual manner gives:

(10)

where a_o and b_o are the firmness contributed by substrates “a” and “b”, respectively, at zero cooking time. At any cooking time, the total firmness is a + b, and this value can be calculated when a_o, K_a, b_o and K_b are known. Since “a” has a high softening rate, its contribution to firmness becomes inconsequential after a prolonged heating time.

Temperature Correction for Kinetic Parameters

The time-temperature profile at the center of prepared vegetable pieces was measured during the heat treatment. A semi-rigid CNS copper-constantan thermocouple (Ecklund-Harrison Technologies, Cape Coral. FL) placed in the bath was used for measuring the bath temperature, and a flexible thermo-couple (24 AWG Copper Constantan, Omega Engineering Co., Stamford, CT) attached to the center of a test particle placed in the perforated can was used to measure the particle temperature during the treatment.

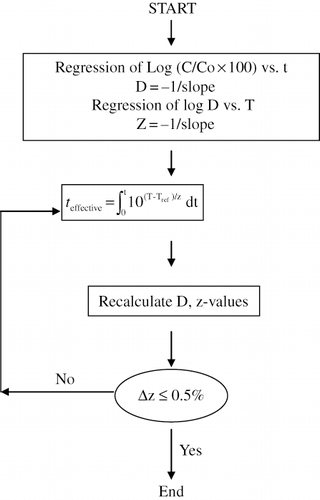
During the kinetic experiments, the prepared vegetables take a certain time to come up to the bath temperature (come-up time). The treatment during this come-up time will be less effective than at a similar time after the come-up or hold time. For this reason, the come-up time needs to be corrected and added to the hold time. Alternatively, the entire time-temperature combination during the treatment can be integrated to get the effective time, as in the case of thermal processing. Procedures for obtaining the effective time and for correcting the kinetic data have been reported in the literature.[26,27] Consistent with thermal processing concepts, the effective time at the bath temperature (T_ref) can be computed in a manner similar to the computation of thermal time or process lethality:

(11)

This requires knowledge of the z-value, which can be calculated as a first estimate from the uncorrected log D versus T data, and then used to get the first estimates of effective time. Using these effective times, new D-values are then computed and, subsequently, using these, a new z-value is obtained. This calls for the computation another set of effective time, D–value, and z-value.[28] The procedure is repeated several times for convergence of the z-value (27). A schematic flow chart of calculation steps is shown Fig. 3.

Figure 3 Typical force-deformation curves for beet and turnip before and after cooking at 100°C.

RESULTS AND DISCUSSION

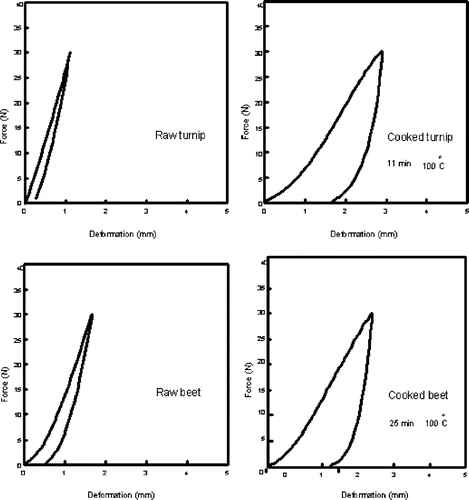
Typical force-deformation curves for turnip test samples both prior and after cooking at 100°C are shown in Fig. 4. Plots for other heat-treated samples were similar except for the fact that the associated deformations were smaller, indicating higher texture values. The graphs of cooked samples showed a larger deformation which is associated with lower texture values; also, raw beet had a lower texture value as compared with raw turnip. This is due to the fact that the dimensions of turnip cylinders were two times larger (height and diameter) than those of the beets. The differences arising from small dimensional variations generally get normalized when texture values are calculated in the form of firmness, stiffness or springiness.

Figure 4 Measured textural parameters as a function of heating time at 80°C.

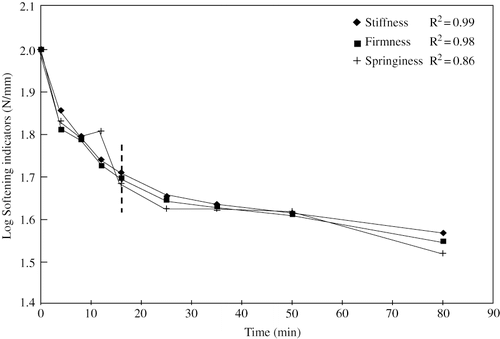
A plot of the three measured parameters, firmness, stiffness (modulus of deformability) and springiness, as a function of heating time at 80°C for beet root, are shown in Fig. 5. All measured textural properties were found to decrease with an increase in the exposure to heat. Loading and unloading of biological materials for several cycles has shown the reduction of residual deformation and strain hardening phenomena.[29] However, when the slope of the unloading curves for the first and subsequent cycles was compared, no change in slope was detected. For calculation of stiffness and firmness, force and the corresponding elastic deformation, F/D, was obtained from the single loading and unloading cycle. Each point on the curves represents the mean of five measurements in a single-cycle loading and unloading test. A comparison between three textural characteristics of thermal softening of beet root at 80°C indicates a good similarity. Although not clearly evident, the springiness values sometimes deviated from the other two in both vegetables. Such behavior, as has been pointed out by Mohsenin,[29] may be due to some residual deformation after the first loading and unloading cycle. None of the biological materials tested so far showed perfect springiness. The major part of the residual deformation is due to initial settings, which may be caused by the presence of pores or air spaces, weak ruptured cells on the surface, microscopic cracks in brittle materials, or other discontinuities, which may exist in the structure of the material.

Figure 5 Softening curves for turnip at selected temperatures.

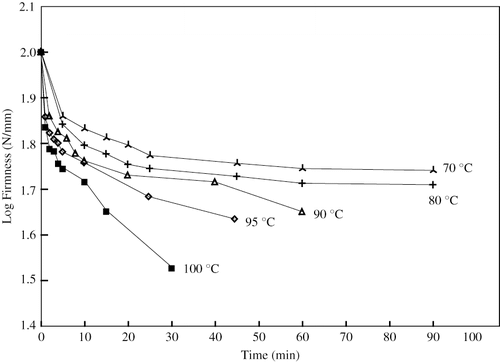
Since, in general, the study showed a similar pattern in the softening curves for both products, a detailed description is given only with respect to firmness for the sake of brevity. Figure 6 is a plot of log compression force versus cooking time for beet root cooked at 70 to 100oC. The general shape of this curve is typical for both root vegetables that were studied. The softening curve is characterized by an initial rapid decrease in firmness, and then a subsequent slower change. This is consistent with the findings of the apparent first-order softening kinetics in other studies demonstrating biphasic behaviors.[23] Following the first rapid decrease, the rate of texture loss gradually diminished in the second phase, with a shallower slope and longer processing times. Since a first-order process is represented by a rectilinear plot on a semi-logarithmic scale, it is quite clear that simple apparent first-order kinetics cannot apply to long cooking times. Although inconsistent with a simple apparent first-order process, this relationship is entirely consistent with two pseudo first-order processes with different rate constants occurring simultaneously, one process being rapid and the other process slow.

Figure 6 Typical plot for characterization of softening behaviour in root vegetables.

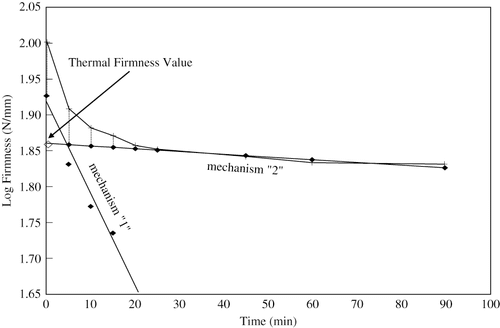
As detailed in the methodology, in order to characterize the softening behavior, the rate constant for the second or slower softening mechanism was first evaluated as the negative slope of the linear portion of the curve. This linear portion was then extrapolated backwards to zero cooking time and the values from the extrapolated line subtracted from the experimental data above it (Fig. 7). A typical heat curve for the test samples indicated a come-up lag of about 3 min to reach the bath temperature. The transient time-temperature data (including the come-up and hold periods; cooling ignored since it was very rapid) were integrated to obtain the effective time using Eq. (11), and uncorrected z-values were obtained by D-value data from uncorrected heating times. This correction only affected the D-value of softening parameters for Mechanism 1, since Mechanism 2 involved longer heating times, in which the sample temperatures had already reached the bath temperature. It must be emphasized that the initial thermal lag effect will depend not only on the size of the particle but also on the food under investigation. For these reasons, correction for thermal lag must be determined for each test.

Figure 7 Typical heat penetration curve for the beet root during come-up time.

The rate constants associated with the three texture parameters, calculated from regression, are summarized in Tables 1 and 2 for beet and turnip. The results generally confirm the first-order nature for both softening mechanisms, as indicated by their associated high R² values (0.82–0.99) in selected vegetables and their textural characteristics. Springiness in turnip and beet is the only one which indicated a lower R² in comparison with the other properties. This difference could be attributed to the residual deformation in biological materials, as was previously indicated. D-values associated with the slow mechanism (Mechanism 2), which varied between 67 to 1826 min and 71–693 min for beet and turnip, respectively, in the temperature range 70–100°C, were nearly 50 to 100 times larger than the range of values for the rapid mechanism. The values of the reaction rate constant (k) showed more similar trends to the higher values associated with the rapid mechanism than the slower one (obvious since k is reciprocally related to D). The results, again, indicated that softening by the rapid mechanism 1 is at least 50 times faster than the slower mechanism 2.

Table 1 Kinetic parameters for thermal softening of beet root

Property	Temperature (°C)	Mechanism 1			Mechanism 2
		K (min^−1)	D (min)	R^2	K (min^−1)	D (min)	R^2
A. Firmness	70	0.134	17.2	0.95	0.00126	1826	0.82
	80	0.157	14.6	0.95	0.00348	662	0.99
	90	0.355	6.48	0.91	0.00638	360	0.90
	95	0.621	3.71	0.76	0.00784	293	0.95
	100	1.42	1.61	0.75	0.0190	120	0.97
B. Stiffnes
	70	0.114	20.0	0.92	0.00168	1373	0.84
	80	0.150	15.3	0.99	0.00316	728	0.99
	90	0.374	6.15	0.92	0.00557	413	0.95
	95	0.615	3.74	0.75	0.00746	308	0.93
	100	1.77	1.29	0.75	0.0228	101	0.98
C. Springiness
	70	0.142	16.1	0.98	0.00255	902	0.75
	80	0.157	14.6	0.78	0.00459	501	0.86
	90	0.399	5.76	0.98	0.0154	149	0.82
	95	0.908	2.54	0.75	0.0167	137	0.96
	100	1.86	1.23	0.87	0.0343	67	0.91

Table 2 Kinetic parameters for thermal softening of turnip

Property	Temperature (°C)	Mechanism 1			Mechanism 2
		K (min^−1)	D (min)	R^2	K (min^−1)	D (min)	R^2
A. Firmness	70	0.17	13.28	0.83	0.00333	692	0.98
	80	0.29	7.94	0.75	0.00486	474	0.91
	90	1.23	1.87	0.76	0.01049	219	0.95
	95	3.10	0.74	0.83	0.2203	104	0.97
	100	11.70	0.20	0.93	0.0321	71	0.91
B. Stiffness
	70	0.169	13.6	0.81	0.00332	693	0.98
	80	0.288	7.99	0.77	0.00480	479	0.91
	90	1.25	1.84	0.75	0.01048	219	0.96
	95	2.25	1.02	0.92	0.0226	102	0.98
	100	10.87	0.212	0.80	0.0322	71	0.91
C. Springiness
	70	0.136	16.9	0.78	0.00395	582	0.84
	80	0.330	6.97	0.75	0.00841	273	0.90
	90	1.17	1.95	0.88	0.01407	163	0.75
	95	2.42	0.953	0.93	0.1719	133	0.94
	100	25.9	0.088	0.83	0.03065	75	0.99

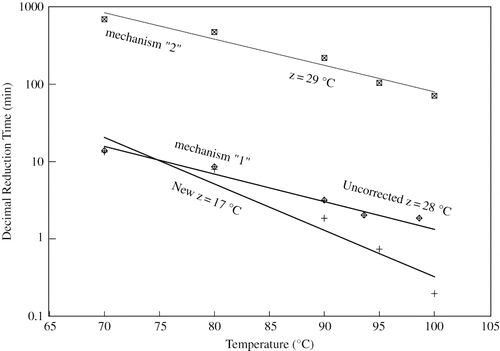
Figure 8 illustrates the z-value plot for turnip before and after correction for thermal lag for the firmness parameter, with similar plots for the other two parameters. The results showed no effect of corrected time for kinetic values and their dependence on temperature (z and E_a) for the heat resistant fraction (Mechanism 2). A comparison between the rate of softening of turnip and beet at any selected temperature shows that cooking causes softening of turnip tissue much faster than that of beet root. The activation energies (E_a) and z-values calculated from regression for both mechanisms of softening properties in turnip and beet are presented in Table 3. These data further show that temperature-dependence parameters (E_a and z) of softening rates for the first mechanism in turnip are much different from that of the second mechanism, while they are in the same range for beet root. This may be attributed to structural or compositional differences between these two biological materials.

Table 3 Calculated activation energies (Ea) and temperature dependence of softening rate (z value) for turnip and beet root

Property →	Firmness				Stiffness				Springiness
Product ↓	Ea (kJ/mole) (k100)	R^2	z (C°) (D100)	R2	Ea (kJ/mole) (k100)	R2	z (C°) (D100)	R2	Ea (kJ/mole) (k100)	R2	z (C°) (D100)	R2
Turnip Mech. 1	146 (1.6862)	0.92	17 (1.33)	0.93	141 (1.6916)	0.91	17 (1.32)	0.92	167 (1.6829)	0.87	22 (1.26)	0.98
Turnip Mech. 2	83 (0.0279)	0.95	29 (80)	0.96	83 (0.0281)	0.95	29 (79)	0.95	60 (0.0256)	0.97	36 (84)	0.98
Beet Mech. 1	81.7 (0.7088)	0.88	30 (3.16)	0.92	92 (0.8225)	0.89	30 (2.71)	0.93	92 (0.8279)	0.88	26 (2.70)	0.89
Beet Mech. 2	87 (0.0150)	0.96	28 (148)	0.96	82 (0.0146)	0.90	29.6 (152)	0.91	92 (0.0301)	0.97	27 (74)	0.97

Figure 8 Change in z vale before and after correction for thermal lag for turnip.

The thermal firmness value is obtained as the intercept of the extrapolated rate curve for the slower mechanism (Figure 7). The calculated log mean thermal firmness values and the percentage residual texture values for beet and turnip are shown in Table 4. The thermal firmness value, or the residual firmness value, is important with respect to the quality of vegetables following thermal treatments such as canning, since it is this value that can be best preserved from optimization techniques. The results generally indicate 46–59% residual firmness and stiffness and 49–72% residual springiness for turnip and beet. The larger magnitude of springiness, as was discussed before, may refer to residual firmness after loading of the sample. The result, however, showed no difference between thermal firmness values obtained from cooking at different temperatures, except for springiness of turnip which had a relatively lower value when cooked at 100°C.

Table 4 The log mean thermal firmness values for root vegetables

Temperature (°C)	Turnip			Beet
	Firmness	Stiffness	Springiness	Firmness	Stiffness	Springiness
70	1.70	1.70	1.86	1.74	1.75	1.70
80	1.67	1.67	1.85	1.73	1.73	1.69
90	1.68	1.68	1.85	1.74	1.71	1.74
95	1.72	1.72	1.84	1.72	1.72	1.73
100	1.69	1.69	1.80	1.77	1.75	1.71

Since the majority of texture contributed by the substrate responsible for the rapid softening mechanism is lost quickly, its consideration may play a role only in mild heat treatment applications such as blanching. From a thermal processing (canning) point of view, searching for a way to slow the apparent rate constant k1 (rapid mechanism) can only provide a small gain, due to the fact that the texture loss is so fast that even reducing the rate constant by 50% may have little net effect on texture after a commercial process.

CONCLUSIONS

The kinetic evidence given above pointing to two softening mechanisms indicates that any attempt to specify the textural quality of vegetables cannot employ simple first-order kinetics, except for very short heating times. Of practical interest is the fact that an extension of heating past a certain time slows further deterioration of textural properties. The softening process follows two simultaneous pseudo first-order rate softening mechanisms, one more rapid than the other. The dominant factor which determines residual firmness in thermally treated samples is the slower mechanism since the substrate responsible for the rapid mechanism could be lost during a short exposure to 100°C.