Rheological Properties of Cabbage Pulp

Abstract

The rheological behavior of cabbage pulp was determined using a computer controlled rotational rheometer at a temperature range of 20, 30, 40, and 50°C. The flow behavior of pulp was pseudoplastic and fitted well to the Casson model. In all the cases, the effect of soluble solids on apparent viscosity was more pronounced than the effect of temperature. The combined effect of temperature and soluble solid content on viscosity was also given. The activation energy value of 3–6°Brix cabbage puree varied from 7 to 12.6 kJ/mol when shear rate increased from 1 to 10 s⁻¹. The exponential model developed had an excellent fit (r² > 0.87) and would be useful for the engineering applications.

Keywords:

• Cabbage pulp
• Rheology
• Power law
• Herschel-Bulkley
• Casson model

INTRODUCTION

Cabbage (Brassica oleracea L.var.capitata(L.)) is a world wide grown vegetable and rich in nutrition. Dietary intake of cabbage can reduce incidence of cancer. Spray drying fresh cabbage into powder can extend its shelf life and become a convenient solid beverage. In processing cabbage powder, cabbage pulp is concentrated usually under vacuum to improve efficiency of spray drying.

Knowledge of the flow behavior of fluid is useful in engineering applications that are related to the proper design and unit operations, as well as for the understanding of the transport processes.[1–3] The rheological properties of cabbage pulp play an important role in the processing, such as agitation, feed-in of spray drying. Temperature and concentration are the variables, which considerably affect rheological properties. The yield stress is just as important as the shear-stress against shear–rate relationship in the design of equipment for processing purees.[4] Concentration of dissolved solids, particle size distribution and shape, and mode of interaction of suspended particles can have remarkable effect on the flow behavior of fruit purees.[5–7] Studies on the flow behavior of cabbage pulp are scarce.

Many authors made use of models to describe the flow behavior.[8–12] Most fluid foods do not have the simple Newtonian rheological model; in other words, their viscosities are independent of shear rate or shear stress and not constant with temperature. The non-Newtonian models in Eqs.(1) –(3) were considered for their suitability in describing the flow of cabbage pulp. The powder law model is perhaps the most widely employed model for non-Newtonian liquids and is used extensively to describe the flow properties of liquids in theoretical analysis as well as in practical engineering applications.[13] The power law model of the form was used to describe the shear stress and shear rate data. The k value corresponds to the viscosity of Newtonian fluids.

(1)

The Herschel-Bulkey model[14,15] (Eq. 2) and Casson's equation[16] (Eq. 3) is derived from the power-law model by adding a yield stress term (σ₀):

(2)

(3)

The Casson model has been applied a wide range of food products such as molten chocolate, fruit purees, gums and tomato products.[17] This model was originally derived by Casson[18] for the prediction of the flow behavior of pigment-oil suspensions. Unlike the Power Law model, this model is based on a structural model of the interactive behavior of solid and liquid phases of a two phase suspension. The objective of this study was (a) to determine the rheological behavior of cabbage pulp as affected by soluble solid concentration range of 3–6% and temperature range of 20–50°C, (b) to evaluate the influence of temperature and soluble solid on its apparent viscosity.

MATERIALS AND METHODS

Preparations of Cabbage Pulp

Figure 1 shows the preparations of cabbage pulp. Soluble solids concentration of cabbage pulp was in the range 3–6°Brix, and pH value was 5.5–6.5. The cabbage pulp was consisted of particles of irregular shape about 200 mesh.

Figure 1 Production of cabbage pulp from fresh cabbage.

Rheological Measurements

The rheological measurements were performed using AR1000 rheometer (TA Instruments, UK) with commercial computer software (Rheology Advantage Analysis Software Version. 4.1, TA Instruments). The experiments were carried out in the controlled stress mode. A flat plate geometry (radius 4 cm) was used to measure the viscosity of the pulps. The viscosities of the pulps were measured at temperatures between 20 and 50°C (±0.1°C) and with shear rate range 0.1–20 s⁻¹. The samples were adequately mixed using a magnetic stirrer to achieve uniform consistency before loading into the rheometer.

RESULTS AND DISCUSSION

Influence of Temperature and Solids Content on Apparent Viscosity

The plot of ln at shear rate from 0.1 to 20 s⁻¹ versus ln η at two temperatures, 20 and 50°C, is illustrated in Fig. 2. Similar flow diagrams were also obtained for other temperature. The flow behavior characteristic of cabbage pulp was influenced by dissolved solids concentration and temperature. It is evident that the log of apparent viscosity at shear rate from 0.1 to 20 s⁻¹ decreased for all the soluble solids and increased by increasing the dissolved solids concentration at any given shear rate. The effect of soluble solids on apparent viscosity was more pronounced than the effect of temperature.

Figure 2 Effect of ln on the lnηof cabbage pulp at different concentrations (a) 20°C, and (b)50°C. °Brix level: (△)6°Brix, (▲)5 °Brix, (□)4°Brix, and (■)3°Brix.

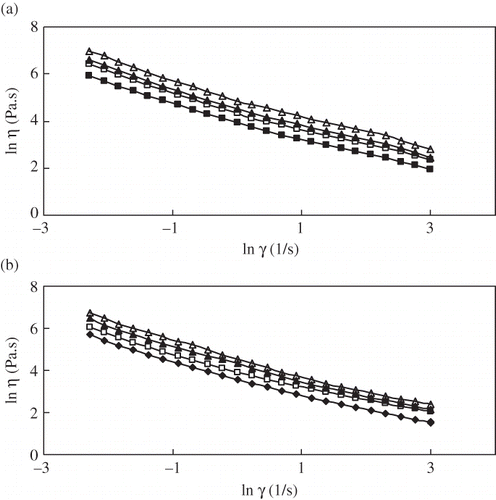
Linear regression analysis was performed on the data to find consistency coefficient (k), flow behavior index (n), and correlation coefficient (r ²), the results of which are summarized in Table 1. n values ranged from 0.22 to 0.33 under different conditions of temperature and soluble solids, demonstrating a shear thinning (pseudoplastic) behavior. The flow behavior index n did not change with the temperature, which was also observed in tamarind juice concentrates.[19] Consistency coefficient k is an indicator of the viscous nature of the system. The magnitude of k decreased with temperature and increased with soluble solids. Raising the temperature from 20 to 50°C considerably decreased the k value.

Table 1 Influence of temperature and concentration on Power law parameters

T/°C	°Brix	n	k/Pa· s^n	r ^2
20	3	0.305±0.012	54.5±0.9	0.9775
	4	0.298±0.009	83.8±1.2	0.9669
	5	0.312±0.010	99.8±2.2	0.9692
	6	0.276±0.007	145.6±3.4	0.9706
30	3	0.290±0.009	48.4±1.3	0.9456
	4	0.310±0.011	69.1±1.6	0.9442
	5	0.300±0.008	86.5±1.9	0.9537
	6	0.300±0.010	130.3±1.7	0.9541
40	3	0.318±0.013	42.2±1.2	0.9299
	4	0.304±0.005	61.9±1.1	0.9378
	5	0.301±0.007	81.3±1.6	0.9654
	6	0.294±0.008	115.4±2.5	0.9485
50	3	0.280±0.012	37.6±1.1	0.9543
	4	0.330±0.009	54.3±1.3	0.9580
	5	0.230±0.007	77.4±1.7	0.9299
	6	0.220±0.008	99.7±1.6	0.8906

Effect of Temperature and Solids Content on Stress

Figure 3 shows the shear rate from 0.1 to 20 s⁻¹ versus shear stress at two temperatures, 20°C and 50°C. Similar flow diagrams were also obtained for other temperature. The stress of cabbage pulp at 10 s⁻¹ decreased by about 43.4 Pa as the temperature increased at 3°Brix from 20 to 50°C, however, at 20°C, it increased by about 179.4 Pa as the dissolved solids content increased from 3 to 6 °Brix, indicating a greater influence of concentration on stress.

Figure 3 Effect of shear rate on the shear stress of cabbage pulp at different concentrations (a) 20°C, and (b) 50°C.°Brix level: (△)6°Brix, (▲)5°Brix, (□)4°Brix, and (■)3°Brix.

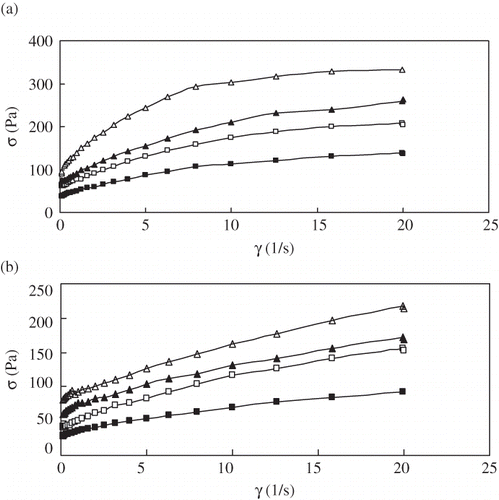
The three models, namely, Power Law (Eq. 1), HB model (Eq. 2), and Casson model (Eq. 3) were used to fit the measured data to determine the one that best described the flow behavior of cabbage pulp over the studied temperature and concentration ranges. The flow curves for cabbage pulp all showed yield stress, indicating that the Power Law model was not most suitable for describing their rheological behavior. The coefficients of Casson and HB models at 50°C are illustrated in Table 2. The yield stress (σ₀) increased with solids content as expected. For the range of temperatures investigated, the 6°Brix cabbage pulp showed yield stress values that are three times more than the 3°Brix pulp. Casson model appears to be suitable for describing the flow behavior of cabbage pulp in the solids content range as indicated by higher determination coefficient (r ² > 0.99) values, while HB model gave a little good fit for the cabbage pulp. However, it is important to note that most authors used either the Power Law or HB model to determine the rheological parameters. As demonstrated by Mizrahi,[7,20] the yield stress values are strongly dependent on the shear rate range, type of model, and shape and size of particles forming the purees.

Table 2 Regression parameters for different rheological models at 50°C

	HB model				Casson model
°Brix	σ0/Pa	k/Pa·s^n	n	r ^2	σ0/Pa	η0/Pa·s	r ^2
3	24.28	10.87	0.61	0.9173	24.91	1.07	0.9989
4	32.64	17.59	0.65	0.9056	34.34	1.53	0.998
5	52.92	15.87	0.66	0.9084	47.68	1.3	0.9979
6	69.10	13.18	0.78	0.9388	71.26	1.4	0.9952

Combined Effect of Temperature and Soluble Solids on Viscosity Model

Both temperature and soluble solids had an important effect on cabbage apparent viscosity. For engineering applications, it is very useful to obtain a simple equation describing the combined effect of temperature and soluble solids on the cabbage pulp. The following models have been used by Kaya et al.[20]:

(4)

(5)

Equations (4) and (5) were linearized in order to obtain their parameters. The values of these constants are summarized in Tables 3 and 4. Results showed that the activation energy decreased as the shear rate increased. The value of activation energy varied from 7 to 12.6 kJ/mol when shear rate increased from 1 to 10 1/s. A multiple regression analysis on the apparent viscosity-temperature-concentration data showed Eq. (5) better described the combined effect of temperature and soluble solids, which had higher r ².

Table 3 The combined effect of temperature and soluble solids on the apparent viscosity of cabbage pulp [fitted model Eq. (4)]. apparent viscosity of cabbage pulp [fitted model Eq. (4)]

	η1/Pa.s	a 1	Ea/kJ/mol	r ^2
1.001	0.017	1.167	12.644	0.8776
1.26	0.026	1.168	12.323	0.8735
1.584	0.034	1.153	11.877	0.8770
1.995	0.045	1.164	11.608	0.9077
2.51	0.062	1.155	11.155	0.9111
3.162	0.101	1.151	10.257	0.9222
3.98	0.129	1.134	10.022	0.9204
5.012	0.236	1.130	8.868	0.9253
6.308	0.347	1.156	8.387	0.9277
7.947	0.545	1.136	7.628	0.9268
9.989	0.830	1.239	7.039	0.9744

Table 4 The combined effect of temperature and soluble solids on the apparent viscosity of cabbage pulp [fitted model Eq. (5)]

	η2(Pa s)	a 2	Ea(kJ/mol)	r ^2
1.001	0.029	0.271	12.644	0.8826
1.26	0.042	0.272	12.323	0.8803
1.584	0.056	0.268	11.877	0.8831
1.995	0.074	0.270	11.608	0.9133
2.51	0.101	0.269	11.155	0.9185
3.162	0.165	0.267	10.257	0.9244
3.98	0.210	0.263	10.022	0.9253
5.012	0.388	0.262	8.868	0.9265
6.308	0.567	0.267	8.387	0.9261
7.947	0.895	0.263	7.628	0.9264
9.989	1.366	0.285	7.039	0.9640

CONCLUSIONS

The flow behavior of cabbage pulp was found to be pseudoplastic and fitted well to the Casson model. Dissolved solids content had a greater influence on flow behavior than temperature. The consistency coefficient decreased with temperature and increased with soluble solids. The value of activation energy varied from 7 to 12.6 kJ/mol when shear rate increased from 1 to 10 1/s. The exponential model developed had an excellent fit and would be useful for the engineering applications.

NOMENCLATURE

σ	=	shear stress, Pa
k	=	consistency coefficient, Pa· sn
	=	shear rate, s−1
n	=	flow behavior index, dimensionless
Ea	=	activation energy, kJ/mol
R	=	gas constant, 8.314 J/ mol K
T	=	temperature, K
η	=	apparent viscosity, Pa· s
η1	=	constant in Eq. (4), Pa· s
η2	=	constant in Eq. (5), Pa· s
a 1	=	constant
a 2	=	constant