Experimental Study on Thermal Conductivity of Orange Juice Using Probe System

Abstract

An improved thermal conductivity probe system consisting of a probe heater, control circuits and data test system was developed and described. It has the merits of the short duration of the experiments, simplicity, high accuracy, and relatively small sample requirement. The measurement time is about 20 s. The effective volume of sample is 50 ml. Calibration of the probe with glycerin and ethanol in this work exhibits an accuracy of 1.4% and 1.9%, respectively. The probe system was used to measure the thermal conductivity of orange juice. The measured thermal conductivity values were linearly dependent on the concentration and temperature of the orange juice. A decrease in the concentration of orange juice and an increase in the temperature resulted in an increase in the values of thermal conductivity. However, the influence of concentration on the thermal conductivity of orange juice was stronger than that of temperature. An empirical model for the thermal conductivity of orange juice as a function of concentration and temperature was obtained.

Keywords:

• Orange juice
• Thermal conductivity
• Temperature
• Concentration
• Probe system

NOMENCLATURE

C	=	Instrument constant of the probe, Ω/m K s
E	=	Electric voltage of power supply, V
K	=	Thermal conductivity, W/m K
L	=	Effective length of the probe, m
Q	=	Heat input per unit length, W/m
R	=	Electric resistance values, Ω
R0	=	Electric resistance value of the copper electric resistance at 0°C, Ω
s	=	Concentration of the orange juice (°Brix)
T	=	Temperature of the copper wire, K
t	=	Temperature of the orange juice, °C
U	=	Electric voltage, V
△R	=	Electric resistance rise of copper wire in probe, Ω
△V	=	Output electric voltage of the electric circuit, V
Greek Symbols	=
α0	=	Copper electric resistance's temperature coefficient at 0°C, 1/K
θ(τ i )	=	Initial temperature, K
θ(τ)	=	Temperature difference, K
θ	=	Temperature of the copper wire of probe, K
	=	Average temperature of the copper wire of probe, K
τ	=	Heating time, s
τ i	=	Initial time, s
Subindexes	=
s	=	Resistance box
p	=	Thermal probe

INTRODUCTION

Thermal conductivity of fruit juice is one of the important thermal properties used to estimate the rate of heat transfer during processes, such as preservation, transportation and freezing. Orange juice is one of the most important commodities in the Chinese market; it contains sugar, carotenoid, citric acid, malic acid, pectin, and a complex mixture of vitamins. Most especially, orange juice contains a large amount of vitamin C. Measurement of the thermal conductivity of every product under every conceivable condition would be an enormous task, so the use of models to predict thermal conductivity using other more easily measured properties, such as concentration and temperature, appears to be the best way to assure the availability of data. Mathematical models that express the dependence of thermal conductivity on temperature and concentration are a very appealing alternative to experimentation, and they are a useful tool for the implementation of computer-aided procedures for equipment design and process automation.

Many thermal conductivity values for food are available in the literature.[1–5] Generally, an extensive review of existing methods of measuring thermal conductivity of food has been carried out.[6–11] Some investigators reported the experimental values of thermal conductivity of orange juice as well as the mathematical models for their calculations.[12,13]

Several techniques including steady and non steady state methods have been used to evaluate the conductivity of food systems.[5] The line heat source thermal conductivity probe is recommended for most food applications because it is simple, fast, convenience, low cost and suitable for small sample size.[14] In this work, an improved thermal conductivity probe system was used to determine the thermal conductivity of orange juice. Advantages of this system are the short duration of the experiments, simplicity, high accuracy, and relatively small sample requirement. The measurement time is about 20 s. The effective volume of sample is 50 ml. Calibration of the probe with glycerin and ethanol in this work exhibits an accuracy of 1.4% and 1.9%, respectively. The specific objectives of this research were (1) to elaborate a specifically designed probe system for thermal conductivity of orange juice; and (2) to develop prediction equations for thermal conductivity of orange juice as functions of concentration and temperature.

MATERIALS AND METHODS

Sample Preparation

Orange juice (66°Brix) was supplied by SanMenXia Lake Juice Company, Henan Province, China. All the orange juice samples were mixed with the ultra pure water with an electric resistance rate of 18.2 MΩ cm to obtain various concentrations of 5°Brix, 10°Brix, 20°Brix, 30°Brix, 40°Brix, 50°Brix, and 66°Brix. The concentrations of orange juice were determined using an Abbe Refractometer (2WAJ, Shanghai Precision & Scientific Instrument Company, China) with ±0.1°Brix precision at 20°C. The prepared samples were put into several identical cylindrical glass holders (effective volume 50 ml) with a diameter of 50 mm and height of 60 mm. The samples were equilibrated to the desired temperature by a constant temperature cabinet with ±0.5°C precision.

Thermal Conductivity

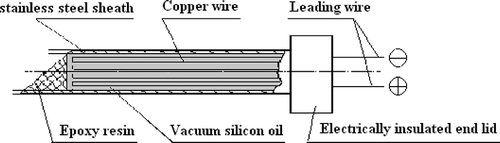
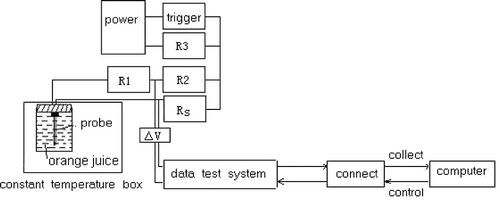
In this experiment, a specifically designed thermal conductivity probe system was used to measure thermal conductivities of juice samples by an idealized transient heat conduction model.[11,15,16] In the system, a probe was made of a stainless steel needle; its length was 32 mm, outside diameter of 0.7 mm and inside diameter 0.3 mm. Paint-wrapping copper wire was used to coat the inside of the needle. The probe was full of vacuum silica gel, which had good heat conduction and electricity insulation. Both of the probe ends were sealed with epoxide resin glue (Fig. 1).

Figure 1 Structure of the probe.

During the measurement of thermal conductivity, the probe was inserted into samples that filled the sample holder. The samples were equilibrated to the desired temperature by a constant temperature cabinet. Then the thermal conductivity of the sample (k) was calculated from the slope of average temperature () against logarithmic time (lnt) and power input (q) according to Eq. (1) given by Carslaw and Jaeger[17]:

(1)

where k is thermal conductivity (W/m K); q is heat input per unit length of the line heat source (W/m); is average temperature (K); and _τ is heating time (s). The measurement system is shown in Fig. 2. The electric resistance values of R₁ and R₂ were almost equal and the temperature coefficient was identical. The electric resistance values of R₁ , R₂ , and R₃ were far bigger than that of resistance box (R_S ) and thermal probe (R_p ).[18] In this system, R₁ = R₂ = R₃ = 10⁴Ω and the electric resistance values of R_S , R_p were decided according to the experimental measurement. When the sample temperature was uniform, the copper wire of the probe was supplied with a constant voltage E. According to the high correlation between the copper electric resistance value and temperature, the electric resistance value of the heated copper wire of the probe would rise up gradually. A weak electric voltage signal would be produced from the controlled electric circuit, which would be amplified by the data test equipment and imported by a computer; a linear relation equation of electric voltage against logarithmic time could be obtained.

Figure 2 Diagram of the measurement system of orange juice.

Before the probe was heated, the resistance box's value (R_S ) was adjusted to be equal to the electric resistance value of the probe (R_p ). Thus the electric voltage of the probe (U_p ) and the resistance box's (U_s ) were also equal according to the principle of Wheatstone bridge (Eq. (2)). In the course of heating the copper wire of the probe was heated, and the electric resistance had an increment, which was expressed with △R, and then the probe's electric resistance (R_p ) could be expressed in Eq. (3).

(2)

and

(3)

where, E is the electric voltage of power (V); △V is the two-side electric voltage increment of probe for heating (V). According to the temperature characteristic of the copper electric resistance, the relation between electric resistance value and temperature within the scope of 0–100°C can be expressed as:

(4)

(5)

If ΔV << E, Eqs. (3) and (5) could become Eqs. (6) and (7), respectively.

(6)

(7)

Equations (4) and (6) were differentiated and integrated:

(8)

Then the thermal conductivity of the sample could be obtained as Eq. (9) after turning Eqs. (7) and (8) into (1).

(9)

Or

(10)

Equation (10) was the basis of the thermal conductivity measurement. In Eq. (10), C = α ₀R₀ /64πL was named instrument constant of the probe, Ω/m K s; which only related with the probe material, length and had nothing with the heating power, testing temperature of the testing system, △V was the output electric voltage of the electric circuit, V; τ was heating time(s). k was the thermal conductivity of sample, W/m K. E was the electric voltage of power supply, V. R_s was the initial electric resistance value of probe, Ω.

Firstly, the probe should be calibrated. The probe was inserted directly into ultra pure water with a cyclindrical glass holder, whose electric resistance rate was 18.2 MΩ cm and thermal conductivity was known in the literature.[19] Secondly, the electric voltage signals tested by the data measurement system and heating time were fed into a computer. Thirdly, the curve of ΔV-ln τ could be drawn. Finally, according to the least-squares method, the slope of d(ΔV)/d(ln τ) could be obtained. And this should be repeated eight times to obtain the slope average. Then the instrument constant of the probe could be obtained by Eq. (10). Using this method the thermal conductivities of glycerin, ethanol and orange juice with different concentrations of 5°Brix, 10°Brix, 20°Brix, 30°Brix, 40°Brix, 50°Brix, 60°Brix and 66°Brix under the environment temperature of 0°C, 10°C, 20°C, 30°C, 40°C, 50°C, 60°C, and 70°C could be measured, respectively. According to the obtained instrument constant of the probe, thermal conductivities of 48 samples could be calculated.

RESULTS AND DISCUSSION

Calibration of Instrument Constant Value

The ultra pure water was used to calibrate the probe. The test data for ultra pure water at 20°C is shown in Table 1. During the test run, the heating time was no more than 20 seconds and the temperature rise was no more than 1°C, which could weaken convection effects. The linear correlation degree of d(ΔV)/d(ln τ) curve was more than 0.9999 and the relative deviation was less than 2%. The reproducibility was better than 2%. From Table 1, the average value of d(ΔV)/d(ln τ) can be calculated. According to Equation (10), the demarcation value of the instrument constant of the probe can be obtained, and it was C = 0.0355 Ω/m K s.

Table 1 Measured Data of ultra pure water at 20°C

Test number	Electric voltage of power (V)	Initial electric resistance value of probe (Ω)	test time (s)	Maximal voltage difference ΔVmax (mV)	Maximal temperature rise (℃)	dΔV/dlnt (mV/s)	Relative deviation	Linear correlation degree (R)
1	3.05	64.9	18	1.37	0.46	0.000395	0.77%	0.9999541
2	3.05	64.9	20	1.26	0.42	0.000397	1.28%	0.9999454
3	3.05	64.9	19	1.27	0.43	0.00039	−0.51%	0.9999696
4	3.05	64.9	20	1.06	0.35	0.000397	1.28%	0.9999242
5	3.05	64.9	20	1.57	0.53	0.000387	−1.28%	0.9999468
6	3.05	64.9	20	1.4	0.47	0.000386	−1.53%	0.9999860
7	3.05	64.9	20	1.37	0.46	0.000399	1.79%	0.9999192
8	3.05	64.9	20	1.39	0.47	0.000387	−1.28%	0.9999919

Thermal Conductivities of Glycerin and Ethanol

In order to check the accuracy of this method, the thermal conductivities of glycerin (purification degree of more than 99%), ethanol (purification degree of more than 99.7%), were measured in a constant temperature cabinet in the laboratory at 15°C ± 0.5°C. Each sample was measured 6 times under the same conditions and the average was calculated. The experimental results are listed in Table 2. The relative errors with reference values[19] were within 2% and every sample's maximal deviation to the mean tested thermal conductivity to be within 2%.

Table 2 Thermal conductivity values of some liquids

Sample	k (Measured value at 15°C) (W/m K)	k (reference value) (W/m K)	Difference (%)	Maximal deviationc (%)
Glycerin	0.29	0.286	0.9	1.4
ethanol	0.175	0.17	1.8	1.9

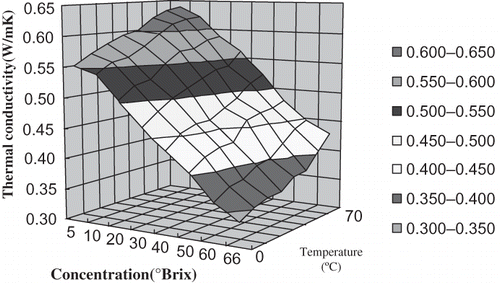
Influence of Concentration on the Thermal Conductivity of Orange Juice

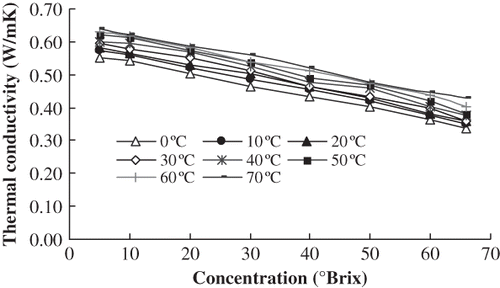
The thermal conductivities of orange juice with 5°Brix, 10°Brix, 20°Brix, 30°Brix, 40°Brix, 50°Brix, 60°Brix and 66°Brix were determined at 0°C, 10°C, 20°C, 30°C, 40°C, 50°C, 60°C, and 70°C, respectively. Figure 3 shows that there was a high negative correlation between concentration and thermal conductivity at the same temperature. Using Excel and linear regression analysis, the regression equations ① between concentration (s) and thermal conductivity (k) were established. The six equations had high significance according to the Fisher test (α = 0.01). Therefore, it was suitable to represent the relation between thermal conductivity and concentration at the same temperature. The regression equations are shown in Table 3.

Figure 3 Change of thermal conductivities of orange juice with concentration.

Table 3 Regression equations and variance analysis describing relations between concentration, temperature, and thermal conductivity

		Regression equation	Linear correlation	F value	F0.01	Significance
Temperature	0°C	k ＝ －0.0035s + 0.5735^①	0.9985	107	4.03	**
	10°C	k ＝ －0.0036s + 0.5926^①	0.9979	104	4.03	**
	20°C	k ＝ －0.0036s + 0.6036^①	0.9963	110	4.03	**
	30°C	k ＝ －0.0038s + 0.6203^①	0.9949	156	4.03	**
	40°C	k ＝ －0.0038s + 0.6332^①	0.9871	192	4.03	**
	50°C	k ＝ －0.0039s + 0.6485^②	0.9913	112	4.03	**
	60°C	k ＝ －0.0037s + 0.6537^①	0.9968	125	4.03	**
	70°C	k ＝ －0.0035s + 0.6583^①	0.9978	143	4.03	**
Concentration	5°Brix	k ＝ 0.0012t + 0.5570^②	0.9865	11	4.03	**
	10°Brix	k ＝ 0.0012t + 0.5433^②	0.9755	22	4.03	**
	20°Brix	k ＝ 0.0012t + 0.5088^②	0.9609	16	4.03	**
	30°Brix	k ＝ 0.0013t + 0.4714^②	0.9770	18	4.03	**
	40°Brix	k ＝ 0.0012t + 0.4342^②	0.9664	9	4.03	**
	50°Brix	k ＝ 0.0011t + 0.4065^②	0.9543	30	4.03	**
	60°Brix	k ＝ 0.0012t + 0.3605^②	0.9776	25	4.03	**
	66°Brix	k ＝ 0.0011t + 0.3344^②	0.9175	24	4.03	**
**Difference at the level of 0.01.

Influence of Temperature on the Thermal Conductivity of Orange Juice

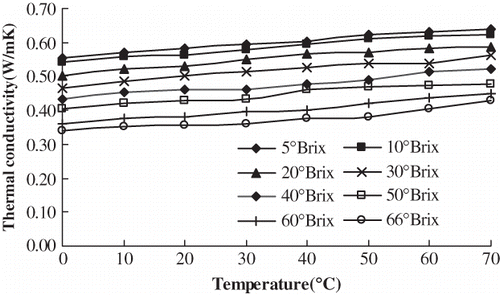
The thermal conductivities of orange juice with 5°Brix, 10°Brix, 20°Brix, 30°Brix, 40°Brix, 50°Brix, 60°Brix, and 66°Brix were determined at 0°C, 10°C, 20°C, 30°C, 40°C, 50°C, 60°C, and 70°C, respectively. Figure 4 shows that there was a high positive linear correlation between temperature and thermal conductivity of orange juice at the same concentration. Using Excel and linear regression analysis, the regression equations ② between temperature (t) and thermal conductivity (k) were established. They had high significance according to the Fisher test (α = 0.01). Therefore, it was suitable to predict the thermal conductivity of orange juice at the same concentration at different temperature conditions. The regression equations are shown in Table 3.

Figure 4 Change of thermal conductivities of orange juice with temperature.

Prediction Equation of Thermal Conductivities of Orange Juice with Temperature and Concentration

Data Processing System software was used to process the experimental data. The double-factors regressive equation of thermal conductivities of orange juice with temperature and concentration could be obtained:

(11)

where, k is the thermal conductivity of orange juice, W/m K; s is the concentration of the orange juice (°Brix) and t is the temperature of the orange juice, °C. Figure 5 shows that there was a high positive linear correlation between the temperature and thermal conductivity of orange juice and a high negative linear correlation between concentration and thermal conductivity. Double-factors variance analysis shows that temperature and concentration were both the main influencing factors of thermal conductivities of orange juice. However, their interaction was tiny, and so it could be neglected. The two equations were very efficient. Through this equation, the thermal conductivity of different concentrations of orange juice under the temperature from 0 to 70°C could be predicted. The obtained equation of thermal conductivities of orange juice with temperature and concentration were compared with prediction equation existing in the literature.^[12] The experimental data and calculated from Eq. (11) were compared with the calculated from Telis's formula (Figs. 6, 7). The results show Eq. (11) was fitted with the experimental data.

Figure 5 A 3D scatter of thermal conductivities of orange juice with temperature and concentration.

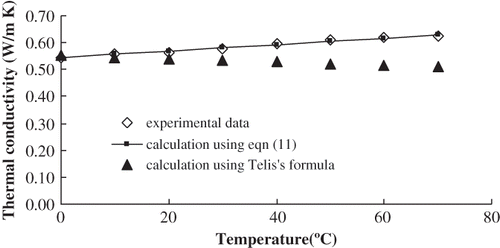
Figure 6 Comparison of thermal conductivity calculated from Eq. (11) and in literature at 10°C.

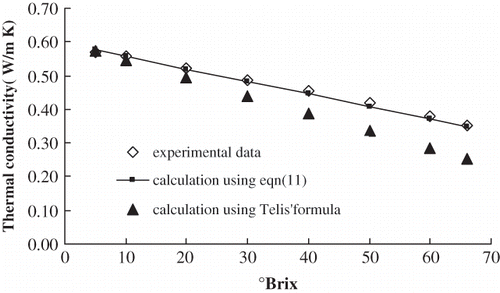
Figure 7 Comparison of thermal conductivity calculated from Eq. (11) and in literature at 10°Brix.

CONCLUSIONS

The effects of concentration in the range of 5–66°Brix and temperature in the range of 0–70°C on the thermal conductivity of orange juice were determined in this study. The thermal conductivity probe system was proposed, which needs short duration of the experiments, simplicity, high accuracy, and relatively small sample requirement. The system worked satisfactorily and its application could be extended to measure thermal conductivities of other solid and liquid foods. The thermal conductivity of orange juice decreased with an increase in concentration, while it increased with an increase in temperature. In addition, the influence of concentration on the thermal conductivity of orange juice was stronger than that of temperature. An empirical correlation for the thermal conductivity of orange juice as a function of concentration and temperature was obtained. The results of this work have direct application as predictive equations for fruit juice processes of heat transfer.

ACKNOWLEDGMENTS

This work is supported by the Natural Science Foundation of China, Grant No 30771245.