Surface Area and Volume Modeling of the Williams Pear (Pyrus Communis)

Abstract

Two methods for estimation of the surface area and volume of a Williams pear quarter provides the focus of this study. The heat energy needed for the drying process depends, in part, on the surface area. The first method involved multiplying the number of pears by the average surface area or volume. The second method involved calculating the surface area and volume of each pear quarter based on the pear length only, as described in the proposed algorithm. It was based on significant correlation between pear length and points on the upper bounder of the pear as well as on integral calculus.

Keywords:

• Surface area
• Pear
• Volume

INTRODUCTION

Shape, surface area, and volume are physical properties with a dominant role in many processes of heat exchange as well as other processes in biomaterial handling.[1] Shape and size should be described when seeds and grains are sorting or cleaning or when fruits and vegetables are drying or cooling.[2–6] Fruits, including pears, are dominantly irregular in shape. In general, their shape can be descriptively expressed^[1] as oblate, oblong, ovate, elliptical, spherical, or truncated. Full characterization of their shape demands a certain number of measurements. Usually, surveying three mutually perpendicular axes offers enough information for further volume or surface area modeling. Measuring fruits in three dimensions can be done by hand with calipers or by tracing using a photographic enlarger.^[1]

Bovi and Spiering[7] used both methods to determine the surface area of the peach palm. The fruit's length and width were measured by calipers and by tracing the halved fruit on paper. The images were digitized using black and white colors and were processed with Corel Photo Paint (Corel Corp., Ottawa, ON, Canada). Three measurements were used for the surface area calculation using Area version 2.1 software.[8] These authors concluded that a linear regression exists between the measurements obtained by the gravimetric (caliper) method and the image digitalization method. The regression equation indicates a high correlation (R = 0.99). The peach palm's surface area (Y) was obtained as a function of the product of the fruit's length and width (X). They also noticed that the best model was an exponential function of X:

A micrometer was used to measure the dimensions of apricot stones and kernels with different moisture contents in order to establish the correlation between these physical properties.[9] A digital camera and the Sigma Scan Pro 5 program (Systat Software, Inc., San Jose, CA, USA) were used for evaluating the projected area. The authors concluded that the length, width, and thickness of the stone and kernel as well as the projection area were increasing with increasing moisture content. The relationship between the projection area and the stone and kernel moisture content was determined by equations.

Some well known geometric shapes[1] (e.g., sphere, prolate, oblate, cone, and cylinder) can approximate the irregular shape of fruit. All three fruits' dimensions are necessary for such a procedure, and it is also necessary to perform actual measurement of the surface area or volume in order to determine correction factors. Calculation of the sphericity of sphere, cubes, rectangular solid, and cylinder was given by Bayram.[10] The researchers, Kabas et al.,[11] were looking to define the relationship between physical properties and the moisture content of the fruit. They found that linear dimensions (length, width, and thickness) and shapes (geometric mean diameter, sphericity, and surface area) linearly decreased with moisture content. A fruit's surface area and volume are closely related to moisture content: when the moisture content decreases, the surface area and volume linearly decrease as well.

The average volume, surface area, and sphericity of almond cultivars and effects of compression on these variables were investigated in a previously published article.[12] The resemblance between irregular fruit body shapes and spheres was presented by Ochoa et al.[13] The volumes of individual cherries were measured via the picnometric method and on the basis of gravimetric measurements with a micrometer on two main axes. Surface area was evaluated from the gravimetric measurements and by calculating the approximate surface area of an equivalent sphere that had the same volume as a real cherry. The surface area and volume of a seedless grape were approximated with an ellipsoid and cylinder.[14] The calculations were compared with the results of surveying done by using a grid paper counting method. The authors assumed that the results of the grid paper method were representing the actual surface area. In that case, the ellipsoid model overestimates the surface area by 6.3%, whereas the cylinder model overestimates by 81.8%.

Pear dimensions were evaluated daily during processing.[15] Those data were used to calculate the pear's volume and surface area. Cut pears were photographed vertically and horizontally against a millimeter-scaled paper, and dimensions were read directly from the scale. The geometry of the whole pear was replaced with two regular bodies, a cone and half of a sphere. Another article[16] reviewed moisture transfer mechanisms, models developed to predict moisture transfer, measurement of effective moisture diffusivity and advanced measurements of moisture profiles to quantify and validate predictive models.

An image processing-based method[17] was developed to measure the volume and surface area of ellipsoidal agricultural products like eggs, lemons, limes, and peaches. This method assumed that each product exhibits an axi-symmetric geometry, which was not the case for pears. Use of digital images as a basis for further analysis is necessary when color is an important factor.[18,19] Optimization of digital images was studied.[20,21] Some mechanical properties of pears have been examined.[22] The aim of this study was a development of the mathematical expression for the surface area and volume estimation for a Williams pear quarter. The ultimate object of this study was to create an algorithm that, with sufficient accuracy, predicts the surface area and volume on the basis of as few measurements as possible. The pear's border line is complex, so seven characteristic points were chosen to serve as an outline of a pear quarter. Our final step was to develop an algorithm permitting calculation surface area and volume of whole or quartered pears based on the pear's length only. The measurement in two perpendicular axes would be necessary. This surveying method should be a non destructive one.

MATERIAL AND METHODS

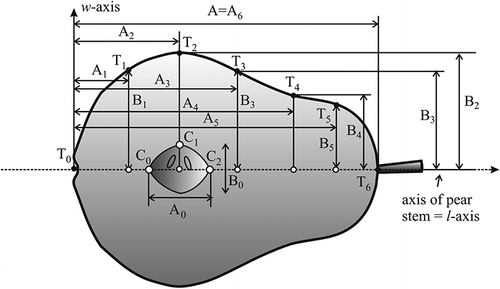
The Williams pear was the object of this study. Thirty fruits were randomly selected and halved through the longitudinal axis. Then, each half was split along the same axis to generate two equal pieces (thus creating pear quarters). The core and seeds were removed. Half of a pear was placed in a two-axis system, such that the zero point was at the bulbous end of the pear (Fig. 1). The length (L) of the pear was on l-axis, and width (W) was on the w-axis. The measurement of those two dimensions of the pear is sufficient for further analysis, because the pear quarters can be used to represent part of a rotating body. The pear's third dimension, thickness, had the same value as the pear's width. Seven distinctive points were marked on the upper bounder of the pear as T_i , i = 0, 1, … , 6. The assumption was that the coordinates of these seven points would give us enough information for further mathematical modeling of the pear's boundary line.

Figure 1 The pear outline and points T_i (A_i , B_i ), i = 0, … , 6.

The coordinates of the points T_i (A_i , B_i ), i = 1, … , 6 were measured using hand calipers (Table 1). At the point T ₂, half of the maximum width was reached (Fig. 1). The point T ₄ represents the location on the pear edge curve where the shape is changing; therefore, the appropriate length is denoted as A ₄ and the width as B ₄. The total fruit length A ₆ (= L) was measured at the point T ₆. The remaining length values A ₁, A ₃, and A ₅ were calculated as the mean values of the measured data:

Table 1 The length and width of the pear and pear core

The pear half length (mm)						The pear half width (mm)					Core with seeds (mm)
A 6	A 1	A 2	A 3	A 4	A 5	B 1	B 2	B 3	B 4	B 5	A 0	B 0
87	15.5	31.0	46.0	60.0	74.0	28.0	34.0	30.0	24.0	18.5	27.0	21.0
80	13.4	27.0	41.0	55.0	67.5	27.5	31.5	28.0	22.0	19.0	25.0	21.5
81	13.8	27.5	41.8	56.0	68.5	30.0	35.0	33.5	23.0	20.0	24.0	19.0
85	14.5	29.0	45.8	62.5	73.8	28.5	32.0	27.0	22.5	19.5	28.0	22.0
86	15.0	30.0	43.5	57.0	71.5	28.0	33.0	29.5	23.5	18.5	27.0	20.0
87	15.0	31.5	48.3	65.0	76.0	28.0	33.0	32.0	23.5	17.5	28.0	21.5
88	15.0	30.0	48.5	67.0	77.5	29.0	33.0	28.0	22.0	21.0	26.0	21.0
88	15.0	28.0	44.8	61.5	74.8	28.0	31.5	27.0	20.0	18.0	26.0	20.0
90	16.5	33.0	47.3	61.5	75.8	30.0	33.0	28.5	23.0	19.0	28.0	25.0
92	16.0	28.0	44.0	60.0	76.0	30.5	32.0	30.0	20.0	17.0	24.5	22.0
73	12.0	26.4	44.5	60.0	66.5	15.4	29.7	27.5	16.5	14.3	24.0	22.0
79	13.0	27.0	40.5	54.0	65.0	26.0	30.0	27.0	21.0	18.0	25.0	21.0
80	13.5	27.5	41.0	56.3	68.2	29.0	35.0	32.0	23.0	20.0	23.5	19.0
84	14.0	28.0	45.0	61.0	72.5	27.0	31.0	26.0	22.0	19.0	27.0	21.0
66	12.0	24.0	39.3	54.5	60.3	14.0	27.0	25.0	15.0	13.0	22.0	20.0
87	16.0	32.0	48.0	64.0	75.5	28.0	33.0	32.0	25.0	17.5	28.0	21.5
89	16.0	32.0	47.0	67.0	78.0	29.0	33.0	28.0	24.0	21.0	26.0	21.0
88	14.0	28.0	44.4	61.5	75.0	29.0	31.5	30.0	21.0	19.0	25.0	19.0
89	15.0	33.0	47.5	62.0	77.0	30.0	33.0	29.0	23.0	20.0	28.5	24.0
92	16.0	29.0	45.0	61.0	76.5	31.0	32.0	30.0	21.0	18.0	24.5	22.0
68	12.0	25.0	41.0	55.0	61.5	16.0	28.0	25.0	17.0	14.0	22.0	20.0
81	14.3	28.5	41.0	55.0	68.0	26.4	31.1	28.0	22.0	19.0	25.0	21.5
81	13.8	27.5	43.0	56.0	68.5	30.0	35.0	31.0	23.0	20.0	24.0	19.0
85	14.4	28.8	45.7	62.5	73.8	29.0	32.0	27.0	21.0	20.0	28.0	22.0
86	14.0	30.0	43.5	57.0	71.5	28.0	33.0	30.0	22.3	18.0	27.0	20.0
86	15.8	31.5	48.3	65.0	75.5	28.0	32.4	32.0	23.0	17.0	28.0	22.0
87	14.5	29.0	48.0	67.0	77.0	29.0	33.0	28.0	22.5	21.0	26.0	21.0
85	14.0	28.0	44.0	60.0	72.5	28.0	31.2	27.0	20.0	18.0	26.0	20.0
89	16.1	32.2	45.6	59.0	74.0	30.0	33.0	28.5	21.0	18.0	28.0	24.0
89	16.0	28.0	43.0	58.0	73.5	30.5	32.0	30.0	19.0	16.0	25.0	22.0
A 6	A 1	A 2	A 3	A 4	A 5	B 1	B 2	B 3	B 4	B 5	A 0	B 0
84.3	14.5	29	44.5	60.0	72.2	27.4	32.1	28.9	21.5	18.3	25.9	21.2
6.3	1.3	2.3	2.7	3.9	4.7	4.3	1.8	2.2	2.3	2.0	1.8	1.5

Pear width (B ₁, B ₂, B ₃, B ₄, and B ₅) is also presented in Table 1 as the second coordinate of the points T_i , i = 1, … , 5. The mean values of each recording were calculated and marked as A ₆ (= L ), A ₁, A ₂, … , B ₅ (next to last row in Table 1) as well as its standard deviation (last row in Table 1 ). Variability of length and width of the examined pears was 7 and 6%, respectively. The simple procedure of shape variability (applicable also for pears) was described.[23] The dimensions of the core and seeds were measured with length A ₀ and width B _0, and their mean values A ₀ and B ₀ were also presented in Table 1. Standard mathematical and statistical methods, including the least square method and integral calculus, were employed when processing the measurement values.

RESULTS AND DISCUSSION

It was assumed that the pear had a distinctive symmetrical shape,[24] i.e., the width and thickness were almost equal; and, therefore, the pear could be described as a body rotating around a stem axis. A similar conclusion could be drawn for the seed core. It is obvious that the outline of a pear is more complex, so an appropriate polynomial function needs to pass through seven points (T_i , i = 0, 1, … , 6). On the other hand, the simplicity of a shape allows us to approximate the core outline with a polynomial function that passes through just three points (C ₀, C ₁, and C ₂; Fig. 1). The formulas for the surface area, S, and volume, V, of the rotating body within the interval (a, b), where a is the starting point on the x-axis and b the last point on the same axis, for a non negative period of function f(x) are given:[25]

(1)

and

(2)

In order to obtain formulas for the surface area and volume of an average pear, program Mathematica 6 was employed.[26] The function f(x) in (1) and (2) must pass through all seven points on the pear edge. It was necessary to obtain a model that will describe the pear's shape in as much detail as possible. So, it used a polynomial fit to obtain a polynomial function passing through all seven points (T_i ( A _i , B _i ), i = 0, … , 6) as follows:

(3)

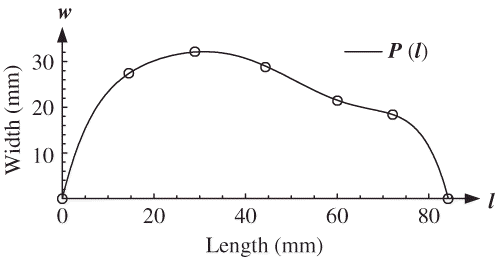
where l [0, 84.3]. The graphical interpretation of Eq. (3) is presented in Fig. 2 as a continuous line, whereas the dots represent the average measured values of the pear. The average pear length is marked as L and the average pear width as W = 2 B ₂. The average surface of a whole William's pear (S_PEAR ) can be calculated by inserting the function (3) and its first derivative:

Figure 2 Function P(l) for a pear outline.

into (1):

(4)

After solving this integral in Mathematica 6, the result is S_PEAR (P(l), 0 mm, 84.3 mm) = 14,749.5 mm². Analogously, the average volume of a whole pear (V_PEAR ) is

(5)

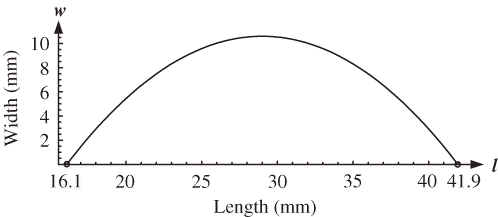
Again, after solving the integral in Eq. (5), the result is V_PEAR (P(l), 0 mm, 84.3 mm) = 159,518.1 mm³. The pear core was removed during the process; therefore, its surface should not be calculated in the surface area of a pear quarter. The core length and width are presented in Table 1. Based on the average values for pear length and width and the fact that the core middle is under point T ₂ (Fig. 1), the coordinates of the core outline C₀(l ₀, w ₀), C₁(l ₁, w ₁), and C₂(l ₂, w ₂) were calculated as:

This is shown in Table 2. The polynomial of the second order provides an adequate expression for describing the pear core outline. Mathematica 6 gives us the desired polynomial:

Table 2 Average coordinates of points C _i , i = 0, 1, 2 on the core outline

li (mm)	wi (mm)	Ci (li , wi )
16.1	0.0	C 0(l 0, w 0)
29.0	10.6	C 1(l 1, w 1)
41.9	0.0	C 2(l 2, w 2)

(6)

for l ϵ[l ₀, l ₂] = [16.1, 41.9]. The graph is shown in Fig. 3. The core can be approximated using a rotating body with a boundary line described by the polynomial L_CORE (l). The whole mean surface of a core (S_CORE ) was calculating based on Eq. (1):

(7)

Figure 3 The graph of the second-order polynomial function for the pear core outline.

Then, S_CORE  = 1,401.67 mm². Using Eq. (2), one can calculate the average volume of a core (V_CORE ) as:

(8)

which is V_CORE  = 4,866.48 mm³. The quarter of one pear is bounded with two lateral flat surfaces. FS denotes one lateral flat surface bounded by the x-axis and f(x). Then, one has to use the formula,

for f(x) ≥ 0, x ϵ (a, b). In this particular case, the flat surface of the pear quarter is equal to

or

(9)

After solving integrals in Eq. (9), the result is FS_FLAT  = 1,780.07 mm². Finally, the total average surface area (S_TOTAL ) of one quarter of a Williams pear is:

or S_TOTAL = (14,749.5 mm² + 1,401.67 mm²)/4 + 3,580.14 mm² = 7,597.93 mm². Of course, the total volume (V_TOTAL ) of one quarter of a pear is

or

Putting n pears through the drying process, then the total surface of the pear quarters can be approximated by 4n·S_TOTAL ; the total volume of the pear quarters can be approximated by 4n·V_TOTAL . On the other hand, since many factors significantly influence the size of a fruit, the average dimensions of pears from another sample may differ from any given dimension in this article. Because of that, an algorithm that provides the surface area and volume of a pear quarter based on the pear length only, was proposed.

ALGORITHM FOR EVALUATING THE SURFACE AREA AND VOLUME OF A WILLIAMS PEAR BASED ON FRUIT LENGTH ONLY

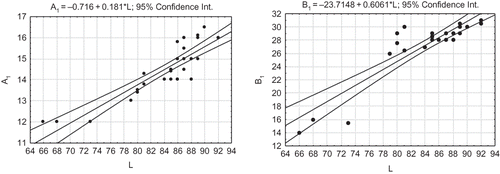
It is more suitable to use only one dimension to model the surface area and volume of a pear. Therefore, statistical analysis has to be employed to determine the mutual relationship between pear length (A_i ) and width (B_i ), i = 1, … , 6. Part of the corresponding correlation matrix is presented in Table 3. Given correlations are statistically significant at the 5% error level. There is a strong correlation between pear length and width. This will be useful for further simplification of the mathematical expression for border shape determination. The point T ₁(A ₁, B ₁) is very significant for the border curve approximation. The coordinates A ₁ (for R ² = 0.79) and B ₁ (for R ² = 0.77) can be expressed as a linear function of pear length L, as in Eq. (10). Both expressions hold for the 95% confidence interval (Fig. 4):

Table 3 Correlation matrix, significance level p < 0.05

A 1	A 2	A 3	A 4	A 5	B 1	B 2	B 3	B 4	B 5
0.89	0.74	0.66	0.59	0.93	0.88	0.62	0.41	0.61	0.57	L = A 6

(10)

Figure 4 Correlations between coordinates A ₁ and L, and B ₂ and L with a 95% confidence interval.

The Mathematica 6 package was employed to calculate the surface area and volume of a pear quarter (without pear core) based on the pear length only. The steps of the algorithm are as follows:

1.	Input the pear length L.
2.	Calculate A*1 (= A 1(L)) and B*1 (= B 1(L)) using Eq. (10), and then calculate the percentages pA and pB of coordinate change using the following relations:
3.	Calculate the coordinates of the border line points according to the values of pA and pB :
4.	Determine the new polynomial P*(l) through the points T 0*(0, 0); T 1*(A 1*, B 1*), T 2*(A 2*, B 2*), T 3*(A 3*, B 3*), T 4*(A 4*, B 4*), T 5*(A 5*, B 5*), and T 6*(L, 0).
5.	Use (1) to calculate the total surface area of a pear after replacing f(x), f'(x), a and b with P*(l), P*(l)', 0 and L, respectively.
6.	Use (2) to calculate the total volume of a pear after replacing f(x), a and b with P*(l), 0 and L, respectively.
7.	Quantify the surface area of a flat pear quarter using numerical integration and formula (9). Replace P(l) with P*(l) and L = 84.3 with the new measured value for L. The result should be multiplied by eight.
8.	Adopt the surface area SCORE and volume V CORE of a pear core as constant values.
9.	Calculate the sum of the surfaces found in steps 5, 7, and 8. This gives us the surface area of a Williams pear quarter.
10.	The total pear volume from step 6 minus the pear core volume from step 8 gives us the volume of a pear quarter.

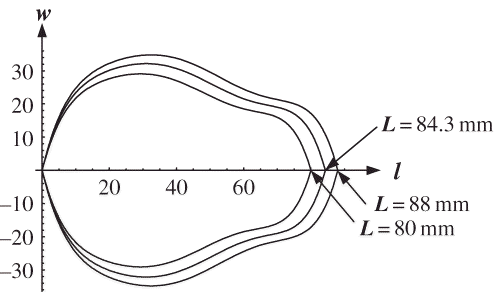
Further simplification can be done using the assumption that the surface area and volume of the core have constant values of 1,401.67 mm² and 4,866.48 mm³, respectively. The dimensions of the core are almost equal for pears with different lengths, and they strongly depend on the worker who removes the pear core. Thus, the core size appears to be a subjective factor. In that case, the whole method lies upon a non destructive procedure. The main advantage of this algorithm is that only one measurement is sufficient to estimate the surface area and volume of a pear or pear quarter. The algorithm was tested for two different pear length values (L). With a pear length of L = 80 mm, S_TOTAL  = 6,476.38 mm² and V_TOTAL  = 29,709 mm³; with a length of L = 88 mm, S_TOTAL  = 8,630.72 mm² and V_TOTAL  = 47,583.8 mm³ (Fig. 5).

Figure 5 Pear outlines based on pear length.

CONCLUSION

The surface area and volume of a Williams pear quarter were observed. On the outline of the pear quarters, seven characteristic points were identified. The length and width of the pear quarters were measured within a sample of 30 Williams pears. The polynomial function for the pear border line is:

for l ϵ [0, L ], where L stands for the average pear length. The assumption was made that pear quarters were part of a rotating body; therefore, the external pear surface could be calculated according to Eq. (1) and the volume according to Eq. (2). A second-order polynomial function (6) was developed to describe the shape of the pear core, which is usually removed during processing. The surface area and the volume of the core (as a rotating body) were also calculated along with two flat boundary surfaces. The correlation matrix confirmed the existence of strong relationships between the pear length and one point on the pear outline. Therefore, all characteristic points on the boundary curve can be expressed as a function of pear length. This process provided the first step for making a more efficient model. The second step involved adopting the assumption that the surface and volume of a pear core had constant values. The final achievement was the creation of a mathematical model and algorithm for the estimation of a pear quarter's surface area and volume on the basis of just the pear's length. From an engineering point of view, this mathematical model, based on non destructive measurements, is useful for storage and handling equipment design for this fruit.

ACKNOWLEDGMENT

This research was realized in the framework of the Ministry of Sciences and Environmental Protection, Republic of Serbia, Project “The Quality of Dried Fruits,” No. BTR20065. The article was financed the Ministry of Education and Science, the Republic of Serbia, Grant No. TR-31058, TR-31046, 2011–2014.