A suggested method for dispersion model evaluation

Abstract

Too often operational atmospheric dispersion models are evaluated in their ability to replicate short-term concentration maxima, when in fact a valid model evaluation procedure would evaluate a model's ability to replicate ensemble-average patterns in hourly concentration values. A valid model evaluation includes two basic tasks: In Step 1 we should analyze the observations to provide average patterns for comparison with modeled patterns, and in Step 2 we should account for the uncertainties inherent in Step 1 so we can tell whether differences seen in a comparison of performance of several models are statistically significant. Using comparisons of model simulation results from AERMOD and ISCST3 with tracer concentration values collected during the EPRI Kincaid experiment, a candidate model evaluation procedure is demonstrated that assesses whether a model has the correct total mass at the receptor level (crosswind integrated concentration values) and whether a model is correctly spreading the mass laterally (lateral dispersion), and assesses the uncertainty in characterizing the transport. The use of the BOOT software (preferably using the ASTM D 6589 resampling procedure) is suggested to provide an objective assessment of whether differences in model performance between models are significant.

Implications:

Regulatory agencies can choose to treat modeling results as “pseudo-monitors,” but air quality models actually only predict what they are constructed to predict, which certainly does not include the stochastic variations that result in observed short-term maxima (e.g., arc-maxima). Models predict the average concentration pattern of a collection of hours having very similar dispersive conditions. An easy-to-implement evaluation procedure is presented that challenges a model to properly estimate ensemble average concentration values, reveals where to look in a model to remove bias, and provides statistical tests to assess the significance of skill differences seen between competing models.

Introduction

For more than 30 years the following conclusions regarding air quality models have been known and are still accepted today (e.g., Venkatram, 1979; Fox, 1984; Weil, 1985; Weil et al., 1992; Stein and Wyngaard, 2001). Most operational atmospheric simulation models are deterministic. They provide estimates of the average time and space variations in the conditions (e.g., a mesoscale meteorological model), or they provide estimates of the average effects of such time and space variations (e.g., a dispersion model). The observations used to test the performance of these models are individual realizations (which can be envisioned as coming from some ideal ensemble), and are affected by stochastic variations unaccounted for within the simulation model. Air-quality dispersion models predict the mean concentration for a given set of conditions (i.e., an ensemble average), whereas observations are individual realizations drawn from various ensembles.

The comparison of short-term (1 hr or less) model predictions with observations, taken under supposedly the same conditions, will reveal large deviations between that which is predicted and that which is observed. The deviations have a mean (or model bias) and a variance. Given unbiased model inputs, the bias is due solely to internal model errors (e.g., physics, parameterizations, etc.), whereas the variance is due to four factors: (1) uncertainty in model input variables, (2) errors in the concentration measurements, (3) internal model errors, and (4) natural or inherent variability (see Weil, 1985; Fox, 1984, Venkatram, 1979). Bias in the model inputs might occur and thereby bias the model estimates if the meteorology or emissions are consistently mischaracterized, but biased model inputs are unlikely when using intensive tracer field experiment data, as discussed and used in this paper.

If we believe dispersion models provide estimates of the ensemble average concentration values, then it makes sense to ask the models to replicate average patterns seen in the observations, but it does not make sense to ask the models to replicate exactly what is seen in any one observation period, which contains the effects of stochastic variations unaccounted for within the simulation model (maxima, minima, or total variance as seen in the observations, etc.). Thus, we are faced with two basic tasks in order to develop a performance evaluation strategy: In Step 1 we should analyze the observations to provide average patterns for comparison with modeled patterns, and in Step 2 we should account for the uncertainties inherent in Step 1 so we can tell whether differences seen in a comparison of performance of several models are statistically significant.

Within the American Society for Testing and Materials (ASTM), a standard guide, D6589 (2010), was developed to address these two steps to foster development of objective statistical procedures for comparing air quality dispersion simulation modeling results with tracer field data. In contrast to a direct comparison of observations and modeling results, D6589 recommends that comparisons be made of some average characteristic of the observed and modeled concentration pattern. To illustrate how this might work, an example procedure was provided for evaluating performance of models to estimate the average maximum ground-level centerline concentration. In the example procedure, evaluation data having similar meteorological and physical conditions are grouped together. Grouping the data together provides a way for us to compute an average centerline maximum concentration for the group for comparison with what the model simulates (on average) for the same group. Comparison of these averages over a series of groups provides a means for assessing modeling skill (Step 1). In order to place confidence bounds on conclusions reached, bootstrap sampling was used (Step 2).

The example procedure outlined in D6589 is nontrivial to implement, and, as discussed in the following, may not be that informative. The goal is to compare some feature (or features) that (1) informs us as to how well the model is doing in estimating the ensemble average centerline concentration values and (2) reveals trends in model bias in such a manner that we have clues to where to look in the modeling algorithms to improve model performance. It can be easily shown that the modeled centerline concentration value, C_max, is:

1

where C_y is the crosswind integrated concentration, σ_y is the lateral dispersion, and C_max, C_y, and σ_y are all ensemble average values. The crosswind integrated concentration, C_y, is a function of the release height, plume rise, vertical dispersion, and the reflections with the surface and any interactions at the top of the convective mixed layer. The lateral and vertical dispersion are mostly a function of the travel downwind and stability, and to a lesser extent of buoyant plume rise and interactions at the top of the convective mixed layer. Lastly, the lateral dispersion is known to increases as sampling time increases.

There are three ways to estimate the correct value for C_max: (1) estimate the correct values for C_y and σ_y, (2) overestimate the values of C_y and σ_y by the same amount, and (3) underestimate the value of C_y and σ_y by the same amount, and only one of these ways is accomplished by good model performance. This suggests that the comparison of observed and modeled average centerline concentration values as promoted by D6589 may reveal overall model performance, but will not reveal whether the model is providing the correct values of C_max by properly estimating C_y and σ_y. So, why structure a model evaluation strategy on C_max? We suggest that a starting point for a better evaluation strategy is to compare observed and estimated group averages values of C_y and σ_y.

In the following discussion, we demonstrate how dispersion model performance can be assessed using group average values of C_y and σ_y. The procedure is fairly easy to implement, makes good use of full-scale intensive tracer field data, and seems to provide insight into a model's performance.

Field Data and Analyses

The site of the Kincaid plant is approximately 15 miles southeast of Springfield, IL and is surrounded generally by flat farmlands. The surface roughness varies from 7 cm to 15 cm, depending on time of year and wind direction. During two periods (April 20–August 29, 1980, and May 9–June 1, 1981), Sulfur hexafluoride (SF₆) tracer gas was injected into the ductwork of the 187-m stack, and 1-hr samples were collected. Approximately 200 sampling sites were activated for a period of 6 to 9 hr in a sector chosen on the basis of the expected meteorological conditions. The network design consisted of concentric circles at average radial distances of 0.5, 1, 2, 3, 5, 7, 10, 15, 20, 30, 40, and 50 km from the power plant, using the existing roadway network, and the downwind distance to an arc varied as much as 20% of the mean distance (Bowne et al., 1983; Liu and Moore, 1984; Hanna and Paine, 1989). An analysis of the Kincaid data determined there were 676 arcs with at least 5 or more nonzero concentration values, and with a maximum concentration within the middle third of the nonzero receptors. Of the 676 arcs, we selected initially the 546 arcs at downwind distances of 3, 5, 7, 10, 15, and 20 m, as there were almost 60 or more arcs for analysis at each downwind distance. Of these 546 arcs, we lost 78 arcs for lack of meteorological data to drive the models or one of the models assumed the plume rise had punched through the elevated unstable mixing height, resulting in simulating zero concentrations at the surface. This left 478 Kincaid arcs for analysis.

The steps in the analysis of the observations consisted of (1) selecting receptors for analysis with concentration values that were greater than or equal to zero (i.e., ignoring receptors with missing values); (2) computing the lateral dispersion, σ_y, as

, where C_i is the concentration at the ith receptor, and y_i is the distance along the arc in a clockwise sense from the first receptor with a valid concentration value; (3) computing the crosswind integrated concentration, C_y, by trapezoidal integration; and (4) computing the Gaussian-fit centerline concentration using σ_y, C_y, and eq 1. In listing out the results, C_y and C_max were converted to micrograms per cubic meter and then the values were divided by the assumed emission rate of 1000 g/s.

Model Simulations and Analyses

We used model simulation results from two dispersion models (ISCST3 version 02035 and AERMOD version 12345).

The Industrial Source Complex Short-Term model (ISCST3) has a long history of use in the United States, as it was designated by the U.S. Environmental Protection Agency (EPA) as preferred model for use for State Implementation Plan (SIP) revisions for existing sources and for New Source Review (NSR) and Prevention of Significant Deterioration (PSD) programs (U.S. EPA, 1978). ISCST3 is a steady-state Gaussian plume model for continuous source emissions to compute ground-level concentration from stack, volume and area sources. The Briggs equations are used to compute plume rise as a function of stack emission characteristics, stack top wind speed, and downwind distance. The wind speed is adjusted using a stability-dependent power law. The vertical and lateral dispersion are estimated using the Pasquill–Gifford curves (U.S. EPA, 1995).

In 1991, the American Meteorological Society (AMS) and the U.S. Environmental Protection Agency (EPA) initiated a formal collaboration with the designated goal of introducing recent advances in boundary layer meteorology into regulatory dispersion models. A working group (AMS/EPA Regulatory Model Improvement Committee, AERMIC) was formed with a goal to provide a complete replacement for ISCST3 by (1) adopting ISCST3’s input/output computer architecture; (2) updating antiquated ISCST3 model algorithms with newly developed or current surface-layer and planetary boundary layer modeling techniques; and (3) insuring that all processes then modeled by ISCST3 would be handled by the AERMIC Model (AERMOD). Relative to ISCST3, AERMOD currently contains new or improved algorithms for (1) dispersion in both the convective and stable boundary layers; (2) plume rise and buoyancy; (3) plume penetration into elevated inversions; (4) computation of vertical profiles of wind, turbulence, and temperature; (5) the urban nighttime boundary layer; (6) the treatment of receptors on all types of terrain from the surface up to and above the plume height; (7) the treatment of building wake effects; (8) an improved approach for characterizing the fundamental boundary layer parameters; and (9) the treatment of plume meander (U.S. EPA, 2004; U.S. EPA, 2012a; Cimorelli et al., 2005; Perry et al., 2005).

The meteorology for each model was generated with the AERMET version 12345 (U.S. EPA, 2012b) meteorological processor, using the Springfield, IL, hourly National Weather Service (NWS) weather observations, and Peoria, IL, twice daily NWS upper air observations, to characterize the meteorological conditions for the tracer dispersion site. The AERMET meteorology and mixing heights were used by both models. For ISCST3, the AERMOD Monin–Obukhov length, L, was converted to a Pasquill stability category by assuming a surface roughness that varied by season and wind direction but was generally on the order of 15 cm, and using the Golder (1972) relationships listed in Irwin (1979).

Receptors were generated for each experiment, where we had observation results, assuming the wind was coming from the west, covering a 150-degree sector with receptors spaced at 0.5 degree. In default mode, AERMOD's plume meander will compute nonzero concentrations essentially in all directions, which does not realistically replicate the coherent plumes seen in all of the Kincaid intensive field experiments. So we used the nondefault model option LOWWIND1 to turn off AERMOD's plume meander. All AERMOD input files contained the following statement:

MODELOPT BETA CONC NOCHKD FLAT LOWWIND1. The modeled concentrations along each arc were analyzed in the same way as the observations, and C_y and C_max were divided by the assumed emission rate of 1000 g/s.

Grouping Data

It was suggested in the introduction that comparison of averages of a group of observations and modeled values might provide a more meaningful comparison. In this section we outline our reasoning for this conclusion.

The observed concentrations can be envisioned as (Venkatram, 1988):

2

where α are the model input parameters, β are the variables needed to describe the unresolved transport and dispersion processes, the overbar represents an average over all possible values of β for the specified set of model input parameters α, represents the effects of measurement uncertainty, and represents our ignorance of β (unresolved deterministic processes and stochastic fluctuations). Since is an average over all β, it is only a function of α.

The modeled concentrations, , are envisioned as:

3

where represents the effects of uncertainty in specifying the model inputs, and f represents the effects of errors in the model formulations. Of the components making up a modeled concentration, only is affected by stochastic effects.

A comparison of the observed maximum concentration along an arc (often called arc-maxima) with the modeled centerline concentration is suggesting that “good model performance” occurs when eq 2 equals eq 3, which can only happen fortuitously if the random effects and happen to equal and. If anything, we should expect from eq 3 that a model with no bias, f , and negligible input uncertainty, , will consistently underestimate the ‘arc-maxima.’ So why are such comparisons in the literature? The answer is likely that various regulatory agencies use the model (inappropriately) as if they can simulate “arc maxima.” Such comparisons reveal how well the model performs an “inappropriate” task, but do not tell us much about how well the model is performing its true tasks, namely, simulating ensemble average concentration values. If we truly wish to model short-term observed concentration values, then we would need to add to eq 3 a term to simulate the stochastic effects of , and such a model would then express its estimates in a probabilistic fashion.

One way to perform a valid evaluation of modeling skill is to separately average the observations and modeling results over a series of nonoverlapping limited ranges of α. Averaging the observations provides an empirical estimate of what the model is attempting to simulate, . A comparison of the respective averages over a series of α-groups provides an empirical estimate of the combined deterministic error associated with input uncertainty and formulation errors. These averages can consist of any definable feature or characteristic in the concentration pattern (e.g., lateral extent, centerline concentration maximum, variance of centerline concentrations). This process is not without problems. The variance due to natural variability is of order of the magnitude of the ensemble averages (Hanna, 1993; Irwin and Hanna, 2005; Irwin et al., 2007), and hence small sample sizes in the groups can lead to large uncertainties in the estimates of the ensemble averages. The variance due to input uncertainty could be quite large—see Irwin et al. (1987)—and hence small sample sizes in the groups can lead to large uncertainties in the estimates of the deterministic error in each group. Grouping data together for analysis requires large data sets, of which there are few.

In spite of the problems noted, this process does avoid making physically inappropriate comparisons to determine modeling skill. From eqs 2 and 3, we can conclude that the modeled and observed concentrations (unaveraged) have different sources of variance. Therefore, unless one happens to be working with one of the very few models that attempts to simulate the total variability, any agreement in the upper (or lower) percentile values of the respective cumulative frequency distributions (or Quantile–Quantile plots) can be attributed to happenstance—that is, the effects of Δα’ and f(α) are compensating for the lack of any characterization of C’(α,β) in the modeling. So it is concluded that grouping the data for determination of average patterns has merit, but it comes at the price of developing grouping and analysis strategies.

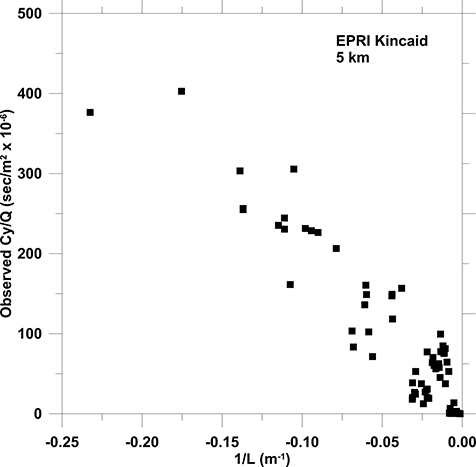
Generally, concentration values decrease as the distance downwind increases and stability effects are seen at a fixed distance downwind (Figure 1). Thus, the distance downwind and surface-layer atmospheric stability are two obvious criteria for sorting observed and modeled values into groups for analysis and comparison. For each downwind arc, the observed and modeled C_y, σ_y, and C_max values were sorted by stability (AERMOD 1/L values, where L is the Monin–Obukhov length). Ten values to a group were defined going from most unstable towards stable, until we did not have sufficient data to form a 10-value group. Initially we computed arithmetic averages for each group. It was discovered that the computed C_max using eq 1 and arithmetic averages for C_y and σ_y did not agree with the 10-value arithmetic average C_max. It was then determined that the computed C_max using eq 1 and geometric averages for C_y and σ_y, did agree with the 10-value geometric average C_max.

Figure 1. Kincaid 5-km observed crosswind integrated concentration values versus AERMOD 1/L values.

Step 1: Comparison of Group Averages

The numbers of arcs to sort into 10-value groups for analysis at each Kincaid distance were 3 km (58), 5 km (90), 7 km (105), 10 km (82), 15 km (79), and 20 km (54), so the numbers of groups for each distance were 5, 9, 10, 8, 7, and, 5 respectively, and the stability ranges are unique for each distance.

In the following analyses, we have chosen to place the observations on the y-axis, as least-square fits assume that random noise effects are most apparent in the y-values. In the plots to be shown, the dotted line is a least-square fit with the intercept forced through the origin (which usually provides a first-order estimate of overall bias). The open symbols denote daytime unstable/neutral conditions, and the solid symbols denote daytime neutral conditions. The first number in the symbol label indicates downwind distance (1 being nearest to the release) and the decimal number indicates stability (1 being most unstable). A symbol label of 1.1 indicates a result for 3 km downwind for the most unstable group, and a label of 1.5 indicates a result for the 3 km downwind for the most stable group.

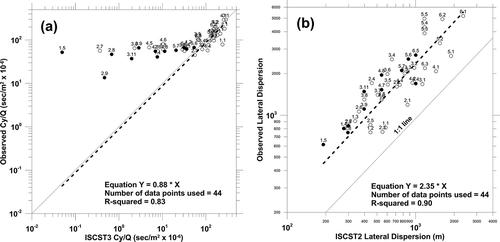
The ISCST3 results shown in Figure 2a show that as we go from unstable to neutral conditions, C_y is increasingly underestimated. The results shown in Figure 2b show that the ISCST3 model is consistently underestimating σ_y by over a factor of 2. As discussed in Pasquill (1976), the Pasquill–Gifford lateral dispersion curves have an averaging time of approximately 3 min, while the Kincaid sampling time was 1 hr. A simplistic adjustment for averaging time effects on lateral dispersion is (Turner, 1970):

4

where is the ISCST2 averaging time of 3 min, is the Kincaid sampling time of 60 min, and γ is between 0.17 and 0.20. This means we should expect ISCST3 estimates of lateral dispersion to be about 1.66 to 1.82 smaller than that observed during the Kincaid intensive experiments.

Figure 2. (a) Comparison of Kincaid observed and ISCST3 modeled crosswind integrated concentration values. (b) Comparison of Kincaid observed and ISCST3 modeled lateral dispersion values.

A visual inspection of AERMOD's results shown in Figures 3a and 3b suggests that AERMOD is estimating C_y fairly well and is slightly underestimating σ_y. It would also appear that the bias in the estimates of C_y may be related to downwind distance, and the bias in the estimates of σ_y may be related to stability.

Figure 3. (a) Comparison of Kincaid observed and AERMOD modeled crosswind integrated concentration values. (b) Comparison of Kincaid observed and AERMOD modeled lateral dispersion values.

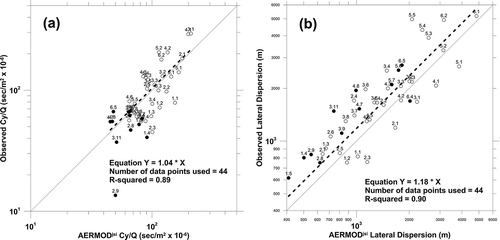
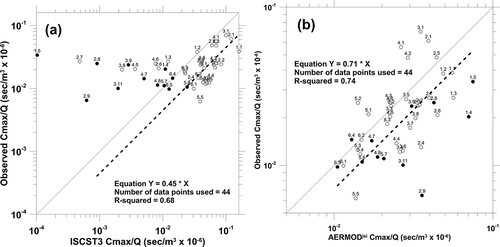
Figures 4a and 4b illustrate how the biases seen in C_y and σ_y affect the estimates of the Gaussian-fit centerline concentration value (C_max). From Figures 2a and 2b it was seen that ISCST3 was underestimating C_y for near-neutral conditions and was nearly unbiased for unstable conditions, while ISCST3 was consistently underestimating σ_y by more than a factor of 2. Thus, the overestimates shown for ISCST3 C_max in Figure 4a are resulting from a bias to underestimate σ_y. For AERMOD (Figures 3a and 3b) it was seen that the estimates of C_y were nearly unbiased and the estimates of σ_y were slightly underestimated, and yet it appears AERMOD is overestimating the group-average centerline concentration values by about 40%, which we explore in the following discussion.

Figure 4. (a) Comparison of Kincaid observed and ISCST3 modeled average centerline concentration values. (b) Comparison of Kincaid observed and AERMOD modeled average centerline concentration values.

Figure 5a provides a way to examine whether the bias in AERMOD's C_y estimates might be related to distance downwind. The overall average and geometric mean of the ratio values shown in Figure 5a are nearly one. As shown in Figure 5a, AERMOD's estimates of C_y are larger than that observed for the 3-km and 5-km arcs. For transport beyond 7 km, it appears that AERMOD's estimates of C_y may be slightly underestimated on average. Thus, the bias in AERMOD's estimates of C_y is seen to vary in a predictable way with distance downwind. It is seen in Figure 5b that the bias in AERMOD's estimates of σ_y is mostly a function of stability, with AERMOD overestimating σ_y for unstable conditions and increasingly underestimating σ_y as conditions become more stable. If we delve a bit further for the 3-, 5-, and 7-km distances, the ratios of AERMOD estimates divided by that observed for C_max, C_y, and σ_y are 1.60, 1.33, and 0.81 (geometric means of the twenty-four 10-group averages, respectively). Thus AERMOD is overestimating C_max by overestimating C_y and underestimating σ_y. For the 10-, 15-, and 20-km distances, the ratios of AERMOD estimates divided by that observed for C_max, C_y, and σ_y are 1.07, 0.88, and 0.80 (geometric means of the twenty 10-group averages, respectively). Thus AERMOD is very slightly overestimating Cmax by underestimating σ_y more so than it underestimates C_y.

Figure 5. (a) The ratio of C_y estimated by AERMOD divided by C_y observed as a function of distance downwind. (b) The ratio of σ_y estimated by AERMOD divided σ_y observed as a function of AERMOD 1/L values. The solid and dashed lines connect distance groups 1 and 3, respectively, as a function of stability.

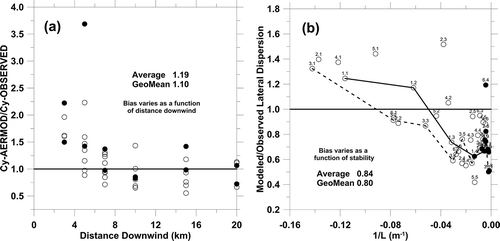
Figure 5 and the preceding discussion reveal how the bias in AERMOD's estimates of C_y and σ_y varies by distance and stability, and combined such that AERMOD's estimates of C_max are strongly overestimated at 3, 5, and 7 km, while further downwind the C_max estimates are nearly unbiased (through a combination of underestimates in C_y and σ_y). Hopefully this discussion further confirms the usefulness of using C_y and σ_y to discern dispersion model performance, and how difficult it is to deduce performance from only a comparison of observed and estimated centerline concentration values.

Step 2: Bootstrap Sampling

If one compares Figures 3a and 4a it is obvious that ISCST3 is not performing as well as AERMOD in estimating the group-average crosswind integrated concentration values (C_y). We really do not need a statistical significance test to confirm what our eyes can see. Likewise, if you compare Figures 3b and 4b, it is obvious that ISCST3 is not performing as well as AERMOD in estimating the group average lateral dispersion (σ_y). That said, whether the differences in performance are statistically significant in future evaluations using different models (or new versions of existing models) may not be as clear. Hence, we recommend that all model evaluations include tests to assess whether differences in performance are statistically significant.

Outline of procedure

To review, we are recommending comparison of observed and modeled group averages of some feature in the concentration pattern, so the question becomes how best to assess differences in performance when the observed and modeled averages are themselves uncertain. Standard D-6589 addressed this concern directly, and recommended a procedure that used bootstrap sampling.

Bootstrap sampling is used to generate estimates of the sampling error in the statistical metric computed, (e.g., Hanna and Paine, 1989; Cox and Tikvart, 1990; Efron and Tibshirani, 1993). The distribution of some statistical metrics is not necessarily easily transformed to a normal distribution, which is desirable when performing statistical tests to see if there are statistically significant differences in the observed and modeled values computed of some concentration feature.

Following the description provided by (Efron and Tibshirani, 1993), suppose one is analyzing a data set x₁,x₂,…x_n, which for convenience is denoted by the vector x = (x₁,x₂,…x_n). A bootstrap sample x* = (x₁*,x₂*,…x_n*) is obtained by randomly sampling n times, with replacement, from the original data points x = (x₁,x₂,…x_n). For instance, with n = 7 one might obtain x* = (x₅,x₇,x₅,x₄,x₇,x₃,x₁). From each bootstrap sample one can compute some statistics (say the observed and modeled averages). By creating a number of bootstrap samples, B, one can compute the mean, , and standard deviation, , of the statistic of interest. For estimation of standard errors, B typically is on the order of 500 or more. The bootstrap sampling procedure often can be improved by blocking the data into groups, where each group has distinctly different descriptive factors; the data within a group have similar characteristics, and the number of values within each group is similar.

When performing model performance evaluations, for each hour there are not only the observed concentration values, but also the modeling results from all the models being tested. In such cases, the individual members, x_i, in the vector x = (x₁,x₂,…x_n) are in themselves vectors, composed of the observed value and its associated modeling results (from all models, if there are more than one); thus, the selection of the observed concentration x₂ also includes each model's estimate for this case. This is called “concurrent sampling.” The purpose of concurrent sampling is to preserve correlations inherent in the data (Cox and Tikvart, 1990). These temporal and spatial correlations affect the statistical properties of the data samples. One of the considerations in devising a bootstrap sampling procedure is to address how best to preserve inherent correlations that might exist within the data.

For assessing differences in model performance, one often wishes to test whether the differences seen in a performance metric computed between Model 1 and the observations is significantly different when compared to that computed for another model using the same observations. For testing whether the difference between statistical metrics is significant, the following procedure is recommended by D6589 and is diagramed in Figure 6.

Figure 6. Diagram of bootstrap sampling procedure. In this depiction there are R regimes and each regime has N_i observed and modeled values for some feature in the concentration distribution (e.g. crosswind integrated concentration). The number N_i does not have to be the same, from one regime to the next, but it is suggested to keep the N_i values at least similar. The number of bootstrap samples (e.g., loops) is usually on the order of 500 or more.

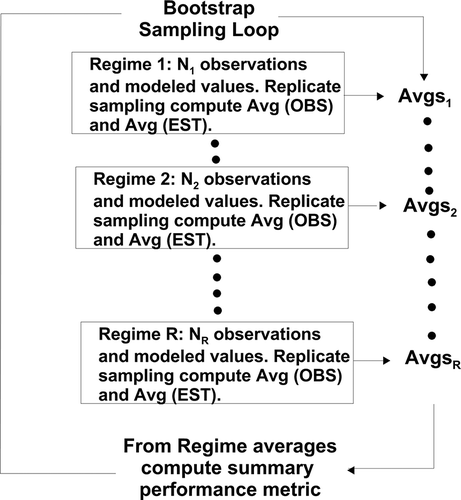
Let the results from each bootstrap (loop) be denoted, x^*b, where * indicates this is a bootstrap sample and b indicates this is sample b of a series of bootstrap samples (where the total number of bootstrap samples is B). For this discussion, assume we are asking whether the geometric mean bias, , computed for one model, MG₁, is significantly different from that computed for another model, MG₂, where C_p and C_o are the modeled and observed regime averages of say the crosswind integrated concentration values, and the overbar denotes an average over all R regimes. From each bootstrap sample, x^*b, one computes the respective values for MG₁ ^b and MG₂ ^b. The difference ∆Δ^*b = MG₁ ^*b – MG₂ ^*b then can be computed. Once all B samples have been processed, compute from the set of B values of Δ* = (Δ^*1, Δ^*2,… Δ^*B) the average and standard deviation, and . The null hypothesis is that is greater than zero with a stated level of confidence, η, and the t-value for use in a Student's t-test is:

5

For illustration purposes, assume the level of confidence is 90 % (η = 0.1). Then, for large values of B, if the t-value from eq 5 is larger than Student's t _η/2 equal to 1.645, it can be concluded with 90% confidence that is not equal to zero, and hence, there is a significant difference in the MG values for the two models being tested.

Example results

The scatter-plot comparisons previously shown used regimes defined in terms of downwind distance and stability with 10 values in each regime. The freely available BOOT software (Chang and Hanna, 2005) provides a means to assess whether differences in performance between two or more dispersion models are statistically significant, has been in use since 1991, and was updated in 2005 to include the ASTM D6589 resampling procedure. There are a number of performance measures one can choose from, but the geometric mean bias, MG, is easy to understand and suitable for demonstration purposes. If MG is less than 1, then the model is overestimating this feature in the concentration pattern, and if MG is greater than 1, then the model is underestimating this feature in the concentration pattern.

There were 440 values sorted into forty-four 10-value regimes (“blocks” in BOOT nomenclature). The input file to BOOT has basically two parts. The first part provides a means to define how many values, number of models, number of regimes, number of values in each regime, and names for the regimes and models. The second part is a listing of the values. The key inputs to the BOOT software were setting IMENU = 4 (which provides MG results), saying “yes” to use of the ASTM procedure, and saying “yes” to bootstrap resampling. The BOOT software uses 1000 boot samples.

For the comparisons of crosswind integrated concentration values, MG was 0.9 and 2.7 for AERMOD and ISCST3, respectively. For comparisons of lateral dispersion, MG was 1.2 and 2.5 for AERMOD and ISCST3, respectively. For AERMOD, the slight overestimation of the crosswind integrated concentration is actually amplified by the underestimation of the lateral dispersion, to result in overestimation of the regime-average centerline concentration values. ISCST3 is underestimating both the crosswind integrated concentration values and the lateral dispersion, which combine to result in over-estimation of the regime-average centerline concentration values. Not surprisingly, the differences in model performance between AERMOD and ISCST3 (as determined by MG) were determined to be statistically significant both for the crosswind integrated concentration values and the lateral dispersion values.

Transport Direction

Irwin and Hanna (2005) suggested a lower bound estimate of the uncertainties associated in wind transport through an analysis of well-controlled tracer experiments from low-level releases. The lower bound uncertainty in wind speed was of the order 0.5 m/s, and the lower bound uncertainty in the wind direction was of the order 10 degrees. At Kincaid we are dealing with a tall stack with buoyant plume rise, so we might expect larger transport uncertainties.

During the Kincaid tracer experiments there was a 100-m meteorological mast 645 m east of the Kincaid stack, with hourly-averaged direction measurements at heights above ground of 10, 30, 50, and 100 m. Of the 440 arcs used in previous analyses, we had onsite wind directions for 404 arcs. Table 1 summarizes the comparison of the observed transport direction (defined as the bearing from the stack to the center of mass along an arc), with the transport defined by the Springfield NWS observations and the wind directions observed by the Kincaid meteorological mast at different heights. The median and averages are similar suggesting single-mode distributions that are somewhat Gaussian. The standard deviations are so large that the average transport differences are easily shown to be not statistically significant. An F-test shows that the standard deviation in differences using NWS data (36 degrees) is significantly different (from a statistical viewpoint) as compared to the standard deviations seen in the differences using onsite wind directions; however, the transport uncertainties are sufficiently large regardless of what wind directions are used to preclude confidently simulating the plume position for any one hour.

Table 1. Summary of differences seen in simulated transport versus that deduced from sampled concentration values along arcs. The “observed” transport was defined as the center of mass of the observed concentration values along an arc. The difference was defined as the observed transport minus that simulated by NWS wind directions or Kincaid wind directions (e.g., observed onsite from the 100-m meteorological mast). All values shown are in degrees

		Kincaid wind direction measurement height
	NWS	100 m	50 m	30 m	10 m
Median	4.57	4.51	1.97	2.78	5.98
Average	2.36	4.22	2.01	2.57	5.80
Standard Deviation	36.00	24.42	24.58	24.67	25.30
Number	404	404	404	404	404

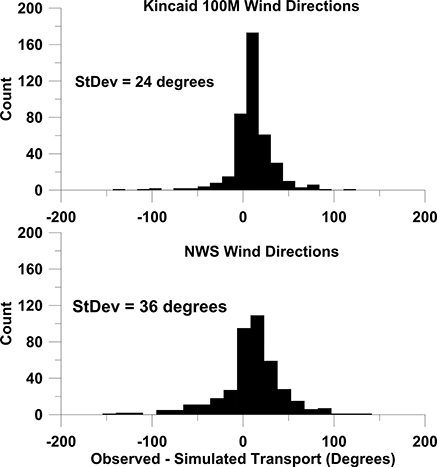
Figure 7 depicts the histogram of observed transport minus simulated transport using NWS wind directions versus Kincaid 100-m wind directions. There is a shift in the transport to the right of the simulated wind directions of order 2 to 10 degrees, depending on which wind direction is used (see Table 1). The histograms generated using 10-, 30-, and 50-m Kincaid wind directions are very similar to that depicted in Figure 7 for the Kincaid 100-m results.

Figure 7. Histograms of differences seen in transport observed and simulated using Kincaid 100-m versus NWS wind directions. The standard deviation of differences (StDev) is a measure of the uncertainty in simulated transport. While the difference in standard deviation values is found to be statistically significant, it is of little practical importance in helping to significantly improve model performance in locating the dispersing plume's position.

The observed average lateral dispersion was on the order of 10 degrees, hence the uncertainty in transport of at least 20 or more degrees (as suggested by the standard deviations listed in Table 1), confirm the findings of Weil et al. (1992) who analyzed nine periods from the EPRI Kincaid experiments, where each period was about 4 hr long. They concluded that for short travel times (where the growth rate of the plume's width is nearly linear with travel time), the uncertainty in the plume transport direction is of the order of one-fourth of the plume's total width. Farther downwind, where the growth rate of the plume's width is less rapid, the uncertainty in the plume transport direction is larger than one-fourth of the plume's total width.

It is concluded that although use of onsite wind directions slightly reduces the uncertainty in the transport versus using offsite NWS wind directions, the improvement is of little practical importance. Our results confirm previous findings that transport uncertainties are sufficiently large that at best we can only estimate within about 25 degrees where a plume is positioned on any given hour.

Conclusion

A missing element in past model evaluations is an accurate consideration of the fact that current dispersion models provide hourly estimates of the deterministic portion of the observed concentration time series (namely, the ensemble average). Lack of consideration of what models truly are capable of providing likely comes from various regulatory agencies erroneously treating hourly concentration estimates as if they are monitored (observed) values. Treating model estimates as if they are hourly “observations” has resulted in assessments that test a model's ability to replicate hourly maxima (sometimes referred to as “arc-maxima”), which (as discussed in the Grouping Data section) is a misinterpretation of what dispersion models provide. While regulatory agencies can accept modeling results to suit their purposes, this does not mean that useful model evaluation can be constructed by testing a model's ability to be misused.

We define a useful model evaluation procedure as one that (1) informs us as to how well the model is doing in estimating the ensemble-average concentration values; (2) reveals trends in model bias in such a manner that we have clues to where to look in the modeling algorithms to improve model performance; and (3) uses objective statistical tests to assess whether differences in performance between two or more dispersion models are statistically significant.

We have demonstrated a candidate model evaluation procedure that assesses whether a model has the correct total mass at the receptor level (crosswind integrated concentration values), is correctly spreading the mass laterally (lateral dispersion), and assesses the uncertainty in transport. We argue for the use of the BOOT software (preferably using the ASTM D6589 resampling procedure) to provide an objective assessment of whether differences in model performance between one or more models are significant.

The observed Kincaid concentration values have a 1-hr averaging time. Thus, we can attribute the underestimation of σ_y by ISCST3 to the fact that the averaging time of the lateral dispersion estimates by ISCST3 is 3 min versus the 1-hr averaging time associated with the Kincaid observations (Pasquill, 1976). AERMOD is using theoretical fits to experimental field observations to estimate the lateral and vertical turbulence, and to characterize the growth of the lateral and vertical dispersion as a function of transport downwind. Hence the averaging time to be associated with AERMOD's lateral and vertical dispersion parameters is not clear, and may deserve further investigation.

Improvements in AERMOD's estimates have been made in the past with comparisons primarily of observed arc-maxima and estimated centerline concentration values. This discussion argues that future improvements in model performance can be achieved by a forensic analysis of observed and estimated crosswind integrated concentration values and lateral dispersion values, by recognizing that models provide estimates of hourly ensemble average concentration values, and by including in all evaluations objective statistical tests to assess whether differences in performance between two or more dispersion models are statistically significant.

Acknowledgment

This paper results from Gale Hoffnagle's kind invitation to provide a luncheon presentation at the 2013 A&WMA Specialty Conference Guideline on Air Quality Models: The Path Forward. Joseph C. Chang provided me with all of his Kincaid data files, which we have come to understand were likely created by someone working for SAI, many years ago. Gary Moore provided me with all of his Kincaid data files, which are 61 archive 1-week files. Through a series of e-mails, Norman Bowne, Roger Brode, Steve Hanna, Jayant Hardikar, Russ Lee, Douglas R. Murray, Helge Olesen, Bob Paine, James Paumier, Don Shearer, and Dave Strimaitis have all tried to help me decipher the available data files. As you can see, I have had lots of help, and I am honored that so many have offered their help.