Is counting hindering learning? An investigation into children’s proficiency with simple addition and their flexibility with mental computation strategies

ABSTRACT

There is a growing awareness that many children are not developing fast and accurate retrieval-based strategies for solving single-digit addition problems. In this study we individually assessed 166 third and fourth grade children to identify a group of children (called accurate-min-counters) who frequently solved simple single-digit addition problems using a min-counting strategy and were accurate using it. We investigated if these children were adaptive when it came to using retrieval for simple addition and if they were disadvantaged when it came to demonstrating mental computational flexibility with multi-digit addition. We found accurate-min-counters represented over 30% of participants. These children were often incorrect when they were required to use retrieval for simple addition and were less flexible than most peers with mental computation strategies. The findings indicate that educators should be concerned about the prevalence of accurate-min-counting and call into question the widely held view that it is mostly children with a mathematics learning disability (or persistent low achievement) who display the protracted use of counting-based strategies for simple addition. Further research is needed to investigate if, and how, current teaching approaches are encouraging children to rely on counting beyond a time when it is advantageous to do so.

KEYWORDS:

• Counting
• retrieval
• mental computation
• flexibility
• addition

Counting and arithmetic development

Counting is foundational for learning about number (Fuson, 1988; Jordan et al., 2006; Krajewski & Schneider, 2009) and plays an important role in early arithmetic development. Children use a variety of counting-based strategies for solving simple (single-digit) addition problems, with the mix of strategies changing with increasing knowledge (Carpenter & Moser, 1984; Goldman et al., 1988; Gray, 1991; Siegler & Jenkins, 1989). Counting-based strategies include, (i) a count-all strategy, where children start the count at one (e.g., 3 + 5 = 1, 2, 3; 4, 5, 6, 7, 8); (ii) a count-from-first strategy, where they count on from the first operand (e.g., 3 + 5 = 3; 4, 5, 6, 7, 8); and (iii) the min-counting strategy, where they count on from the larger operand (e.g., 3 + 5 = 5; 6, 7, 8). The min-counting strategy (sometimes abbreviated to min-counting) is considered the most efficient counting strategy since it requires the fewest counts.

While counting-based strategies for solving simple addition problems are emphasized in mathematics curricula around first grade, children are expected to use fast and efficient retrieval-based strategies by second or third grade (Australian Curriculum, Assessment and Reporting Authority, 2010; Department for Education, 2013; NCTM, 2000). Both retrieval and decomposition are often classified as retrieval-based strategies (Canobi, 2009; Geary, 2011a). Retrieval refers to the direct retrieval of an answer from a store of facts held in long term memory (Ashcraft, 1995). It has been hypothesized that retrieval is made possible when problem-answer associations are strengthened in memory through the correct application of back-up strategies, including counting strategies (Shrager & Siegler, 1998; Siegler & Araya, 2005; Siegler & Shrager, 1984)¹. If the associative strength exceeds an individual’s response threshold representing a confidence criterion, the answer will be retrieved and stated (Siegler & Shrager, 1984). Decomposition strategies are strategies that make use of retrieved facts (Siegler, 1987), for example, the bridging ten strategy (e.g., 7 + 4 = 7 + 3 + 1 = 10 + 1 = 11) and the near-ties strategy (7 + 8 = 7 + 7 + 1 = 14 + 1 = 15).

Traditionally, researchers have viewed the protracted use of counting-based strategies for simple addition as being uniquely characteristic of students with a mathematics learning disability (MLD) or students who display persistent low achievement in mathematics (e.g., Geary et al., 1991; Geary, et al. 2012; Jordan et al., 2003; Ostad & Sorensen, 2007). Children with MLD have been compared to average achieving peers and found to be delayed in using the min-counting strategy and more likely to make counting errors (Geary et al., 2004). Such counting errors make them more likely to err when they do use the min-counting strategy (Geary et al., 2000; Jordan & Hanich, 2000) and make them less likely to encode and/or retrieve basic addition facts (e.g., Geary, 2011b; Jordan & Hanich, 2000; Ostad & Sorensen, 2007). Geary (2011b) reported that around 7% of students have MLD and another 10% show persistent low achievement in mathematics.

There is a growing awareness, however, that it is not just students in the lowest achievement group who are exhibiting difficulties with retrieval. Cowan et al. (2011) reported that many second and third grade children in the UK were not using retrieval when solving simple addition problems. Rhodes et al. (2019) highlighted the frequent use of min-counting by adolescent students in the United States. In an Australian study involving 200 students in seventh grade, Hopkins and Bayliss (2017) found fewer than half the cohort relied on retrieval-based strategies for simple addition. Students who were proficient with simple addition were distinguished from students who were almost proficient and from students who frequently used min-counting. Students who frequently used min-counting were classified into accurate-min-counters and inaccurate-min-counters. Accurate-min-counters represented a sizable group (35% of participants) and exhibited lower math achievement than their peers who usually used retrieval-based strategies, but not so low as to suggest a prominent learning difficulty. Very little is known about the learning difficulties faced by this group of students who have largely gone unnoticed by the mathematics education research community.

The present study

The present study had two main purposes. The first purpose was to determine if accurate-min-counters were adaptive in their use of retrieval with simple addition. Children are said to make adaptive strategy choices when they choose (consciously or unconsciously) a strategy from a variety of strategies according to one of three factors: (i) what works best for them on a particular problem (learner characteristics) – best in terms of speed and accuracy; (ii) what is efficient in terms of the characteristics of the problem, for example, the size of the operands, and/or (iii) what is considered appropriate and wise by influential others (sociocultural context) (Verschaffel et al., 2009). In this paper we use the term adaptive strategy choices (or adaptiveness) to refer specifically to choices that are influenced by learner characteristics (in line with Siegler & Lemaire, 1997), and flexible strategy choices (or flexibility) to refer to choices that are influenced by problem characteristics (in line with Blöte et al., 2000).

Generally, children make increasingly adaptive strategy choices when solving single-digit addition problems; this means they become more likely to select the fastest and most accurate strategy they know for solving a particular problem (Torbeyns et al., 2004). Strategy choice is thought to be influenced by knowledge that is encoded as a result of previous experience, such that each time a strategy is used, information about the success and efficacy of (i) the strategy in general, (ii) the strategy on specific problem types, and (iii) the strategy on specific problems, is encoded in memory (Shrager & Siegler, 1998; Siegler & Araya, 2005; Siegler & Shrager, 1984). Consequently, while young children frequently use different strategies to solve the same problem on different occasions, as they encode more information about the efficacy of a range of strategies, they become increasingly likely to select the strategy that has worked best for them in the past to solve a particular problem or type of problem (Siegler, 1996).

In this study we investigated if accurate-min-counters were making adaptive strategy choices or not. Accurate-min-counters could be fast and accurate with retrieval but not oriented toward using retrieval for currently unknown reasons (Carr et al., 1999). To investigate this possibility, we assessed accurate-min-counters as they solved single-digit addition problems in a choice condition, where they were free to select a preferred strategy, and in a no-choice condition, where time restraints encouraged their use of retrieval. We reasoned that if accurate-min-counters were just as accurate in the no-choice condition as in the choice condition, then these children were not making adaptive choices, since retrieval is generally faster than min-counting. On the other hand, if accurate-min-counters were less accurate in the no-choice condition than the choice condition, this would suggest that accurate-min-counters were making adaptive strategy choices in often selecting min-counting rather than retrieval.

The second purpose of the study was to evaluate the extent to which accurate-min-counters were disadvantaged in terms of developing mental computation flexibility. Mental computation encompasses arithmetic calculations that are predominantly carried out ‘in the head’ or ‘with the head’; that is, without relying on external tools such as pen and paper (Thompson, 1999). The term “predominantly” is an important one, as jottings may be used to support the mental calculation, for example, writing down the answer to an intermediate step (De Smedt et al., 2010).

To the best of our knowledge, no studies have related the strategies children use for simple addition to their proficiency at mental computation with multi-digit numbers. Carr and Alexeev (2011) found that children’s speed at solving simple addition and subtraction problems in first grade predicted growth in the use of more advanced strategies for solving multi-digit addition and subtraction problems during second and third grade. However, these authors did not distinguish between children’s use of mental strategies and their use of standard written algorithms. The strategies children use for simple addition are more likely to impact their proficiency with mental computation than written algorithms, since mental computation places greater demands on working memory resources, and retrieval places fewer demands on working memory resources than counting strategies (Imbo & Vandierendonck, 2007). Furthermore, Carr and Alexeeve looked only at speed and not at strategy when examining simple addition performance. Strategy (rather than speed) may be the more important factor when considering proficiency with mental computation. For example, the time taken to make two counts to solve a problem like 2 + 7 using a min-counting strategy (2 + 7 = 7; 8, 9) would not differ much from the time taken to retrieve the answer nine, and might not impinge on children’s ability to quickly and correctly solve a problem like 22 + 17 = 39 using the standard written algorithm. Yet retrieval may be a critical factor when it comes to being able to correctly solve this same problem mentally using a standard partitioning strategy (i.e., 22 + 17 = 20 + 10 + 2 + 7 = 30 + 9). In other words, retrieval may be a determinant of being able to recognize the efficiency of a standard partitioning strategy for solving such a problem.

Elementary school children are expected to not only develop accurate strategies for mental computation with multi-digit numbers but also to make flexible choices and select efficient strategies according to problem characteristics (Blöte et al., 2000). Procedural flexibility is an important aspect of mental computation proficiency (NCTM, 2014). Therefore, to examine the possible disadvantages of accurate-min-counting relative to consistent use of retrieval, we designed a new measure of children’s flexible use of mental computation strategies and compared the performance of accurate-min-counters and their peers using this measure.

Methods

A within-subjects design was utilized. Data were collected from participants as they solved simple addition problems in a choice condition and a no-choice condition. Participants also completed an assessment designed to measure flexibility with mental computation strategies.

Participants

Participants were 166 children (mean age 9.0 years, SD = 0.5; 84 boys and 82 girls), 81 in Grade 3 and 85 in Grade 4, from three public primary schools in Melbourne, Australia. Based on the Index of Community Socio-Educational Advantage (ICSEA), which sets the mean at 1000 for all Australian school communities, one school community was relatively advantaged (ICSEA = 1145), and two schools were similar to the Australian average (ICSEA = 1027; ICSEA = 1046). Participation rates in the schools were 51%, 38% and 71%. All data were collected in Terms 2 and 3 of the school year. (There are four terms in the Australian school year.)

Materials and procedure

Participants were individually brought from their classroom to a nearby room to complete an assessment of single-digit addition under two conditions: a choice condition, where they were free to select any strategy, and a no-choice condition, where they were asked to retrieve the answer. Participants then completed a group-administered, written assessment of mental computational flexibility with addition, in class, under test conditions.

Assessment of single-digit addition in the choice condition

Each participant worked alongside a researcher (the second author) to complete the assessment of single-digit addition on a computer. The researcher explained to the participant that an addition problem would be displayed on the computer screen and that after s/he stated an answer, he would ask them how they solved the problem before showing them the next problem. An example problem was provided for practice.

The assessment under choice conditions included 36 single-digit addition problems with addends 2 to 9. For all problems, the first addend was less than or equal to the second addend to allow discrimination between a min-counting strategy and a count-from-first strategy. Problems were written in a horizontal format (e.g., 3 + 4 =) and presented in random order.

The procedure for collecting data was as follows. The researcher pressed the space bar on the computer to display the first problem. At the same time, a timer was started (unbeknownst to the child). Immediately after the child stated the answer, the researcher pressed the space bar to stop the timer and remove the problem from the screen. The researcher then entered the given answer into the computer and asked, ‘How did you do it?’ After the child gave his/her explanation, the researcher recorded the self-reported strategy as being either retrieval (often reported as “just knew it”), counting, something else, or don’t know. If it was not obvious to the researcher what counting strategy the child had used, he asked the child to describe the counting and then recorded the counting strategy (min-counting, count-from-first or count-all). On trials where the child reported ‘something else’, the researcher took notes describing the strategy. The large majority (88.4%) of strategies initially coded as ‘something else’ were decomposition strategies and were therefore classified as such.

Children’s reports of counting were usually consistent with behaviors observed by the researcher. For example, children were observed using their fingers or bobbing their head when they reported counting. On the rare occasion when these sources of information contradicted each other, the researcher asked the child if s/he was sure that they had used that particular strategy. If the child was sure or gave a corrected self-report, the child’s reported strategy was recorded. If the child became unsure, it was recorded as ‘don’t know’. Once the strategy was recorded, the next problem was displayed. Thus, strategy use was based on self-report and observation, with data collected on a trial by trial basis, as recommended by Siegler (1987). This approach has been used extensively in the field (e.g., Canobi, 2009; Geary et al., 2000; Vanbinst et al., 2015) and has been shown to be both reliable and valid (Reed et al., 2015; Siegler, 1987).

Cluster analysis, a common procedure for categorizing children’s mathematical behavior (e.g., Bartelet et al., 2014; Reeve et al., 2012; Vanbinst et al., 2015) was used to categorize strategy use under choice conditions. In such analyses, the number of clusters can be determined by characteristics of the data or predetermined using a K-means analysis (Jain, 2010). The latter approach was used here to replicate the steps used by Hopkins and Bayliss (2017) to distinguish four groups of students: proficient, almost-proficient, accurate-min-counters and inaccurate-min-counters.

Assessment of retrieval in the no-choice condition

After completing the assessment of single-digit addition in the choice condition and having a short break (around five minutes), participants completed the assessment of single-digit addition in the no-choice condition. The choice/no-choice approach was first used to study adults’ strategy adaptiveness with multiplication (Siegler & Lemaire, 1997) and has since been applied to study strategy adaptiveness in many domains, including simple and complex addition (e.g., Green et al., 2007; Imbo & Vandierendonck, 2007; Torbeyns et al., 2004) and computational estimation (e.g,, Imbo et al., 2007). This approach often involves comparing the accuracy and/or speed of an individual solving the same problem under two conditions: when they are free to choose any strategy and when they are required to utilize a particular strategy (Luwel et al., 2009).

To fully implement the choice/no-choice method, the number of no-choice conditions needs to be the same as the number of strategies available in the choice condition. In the present context, this would have required restricting the range of strategies children could use in the choice condition (as in Torbeyns et al., 2004). A drawback of such an approach is that restricting the range of strategies allows only a simplified picture of strategy choice to emerge (Luwel et al., 2009). Therefore, instead of having five no-choice conditions (retrieval, decomposition, min-counting, count-from-first, and count-all), we had only one no-choice condition – retrieval – similar to others who have used choice/no-choice designs (Geary et al., 2000; Geary, et al.2012; Hanich, Jordan, Kaplan, & Dick; 2001; Hecht, 2006). As noted by Luwel et al. (2009), “limiting the number of no-choice conditions to one may sometimes be sufficient for testing a particular hypothesis concerning the nature of people’s strategy choice” (p. 355).

In the retrieval no-choice condition, participants solved the same 36 problems presented in the choice condition, but problems were displayed on the computer screen at a rate of three seconds per problem, and participants were asked to state the answer within the three seconds. Although this did not rule out the possibility of using strategies other than retrieval, it would have been very difficult. Response times of three seconds and under, are often used to infer retrieval (Cowan et al., 2011; Jordan et al., 2003).

Problems were organized into four sets of nine problems. Within a set, problems were presented with no breaks between problems; problems sets were separated by a five-second break. Problems were organized into sets such that each set contained similar types of problems (i.e., the same number of tie problems and the same number of problems with small and large sums). Within each set, problems were ordered from easiest to hardest. A problem with one as an operand was included at the end of each set, to ensure that children finished each set successfully before beginning the next set, but data for these problems were not analyzed. Problems were organized in this way to maximize children’s opportunity to retrieve answers that they knew.

To investigate whether accurate-min-counters chose strategies adaptively, their difference in accuracy under choice and no-choice conditions was compared to differences in accuracy among children in the other groups. Also, for each group, the percentage of trials on which retrieval was used to solve a problem in the choice condition was correlated with the percentage of correct trials on that problem in the no-choice condition. The strength of the correlation was viewed as a measure of adaptiveness. This approach has been common in previous uses of the choice/no-choice method (e.g, Luwel et al., 2009; Siegler & Lemaire, 1997).

Assessment of mental computation flexibility

Descriptions of the mental computation strategies children use for multi-digit addition problems are generally consistent in the literature, although different labels have been used (Blöte et al., 2000; Fuson et al., 1997; Heirdsfield & Cooper, 2002; Reys et al., 1995; Torbeyns et al., 2006). Among the common approaches are standard partitioning strategies, nonstandard partitioning strategies, compensation strategies, and noticing strategies. Standard partitioning strategies involve partitioning numbers according to place value to make adding easier. They include split strategies (partitioning two or more operands [e.g., 34 + 48 = (30 + 40) + (4 + 8)] and jump strategies (partitioning one operand [e.g., 76 + 13 = (76 + 10) + 3]). Nonstandard partitioning strategies make use of facts involving tie problems [e.g., 25 + 26 = (25 + 25) + 1] or facts involving multiples of 10 [e.g., 47 + 6 = (47 + 3) + 3]. Compensation strategies involve adding to or subtracting from one operand to make use of a known fact, and then compensating for this change. Compensation strategies include an overshoot strategy [e.g., 17 + 9 = (17 + 10) – 1 = 27–1] and an equalizing strategy [e.g., 17 + 9 = (17–1) + (9 + 1) = 16 + 10]. Noticing strategies involve changing the order of which three (or more) operands are summed (e.g., 18 + 5 + 2 = 20 + 5).

To measure mental computation flexibility, Beishuizen (1993) recorded self-reports of children’s strategy use as they mentally solved two-digit addition and subtraction problems, and compared groups using measures of strategy frequency and accuracy. While this approach provided informative data about individual differences, it was not able to provide a clear overall picture of which groups showed stronger mental computational performance.

To pursue a similar goal, Klein et al. (1998) utilized the Arithmetic Scratch-Paper Test, which included three addition problems given in numerical context (57 + 36, 42 + 43, 54 + 39) and three addition problems in a problem/worded context (48 + 37, 33 + 34, 54 + 29), with problems in each context designed to evoke one of three strategies (a jump, split, or overshoot strategy). These authors considered that a child who correctly used all three strategies was more flexible than a child who used only one or two of them. However, rather than using each child’s number of strategies as a measure of that child’s flexibility of strategy use, Blöte et al. relied on visual inspection to compare stacked bar graphs for groups of children showing the frequency of each of the three strategies and finding one group was more flexible than the other. In another study, Blöte et al. (2001)² did score children’s flexibility based on their performance on The Arithmetic Scratch-Paper Test, but the way in which scores were assigned was not clear – except that the data were analyzed as categorical data.

Using a similar approach to Blöte et al. (2001); Torbeyns et al. (2006) compared the strategy repertoire of high, above-average, and below-average achievers based on the number of children in each group who solved a set of problems using the jump strategy only, the split strategy only, or both the jump and split strategy. To limit the number of possible combinations, problems that evoked the use of other strategies were deliberately excluded (for example, problems with a 9 in the digit position were excluded in order to prevent the use of a compensation strategy). Differences were analyzed using a non-parametric test (Chi-square) since strategy repertoire was measured at the categorical level.

Current assessments designed to capture children’s flexible use (or repertoire) of mental computation strategies are limited in that they produce only categorical data, thereby restricting the types of analyses permitted. In addition, they do not make use of the full range of strategies children commonly use. For these reasons, we designed a new instrument to measure mental computation flexibility, which we called the test of Mental Computation Flexibility with addition (MCF-A).

The MCF-A requires children to recognize strategies used by Emma (a fictitious student). Children were introduced to the assessment as follows:

Emma is good at adding numbers. She uses clever strategies to make adding easier. Your job is to try and think like Emma. Explain what Emma did to get the number in the box. For example, to solve 3 + 4, Emma thinks, that is the same as 6 + 1. What numbers did Emma add together to get 6?

After working through this example as a group, children individually completed the MCF-A comprising 16 items, with each item written in a table format as shown in Figure 1.

Figure 1. An example showing the format of items on the MCF-A.

Responses were scored as correct if they represented an efficient step in solving the original problem. For the example shown in Figure 1, children are expected to recognize that Emma added 28 + 10 to get 38, representing a step involved in applying a jump strategy. A response like 30 + 8 would not be scored as correct, since it does not make sense in light of the original problem. MCF-A items are listed in Appendix 1, along with the strategy Emma used and the correct response.

A pilot test of the instrument employing Rasch analysis (Andrich, 2016) produced a 16-item test. The modified version (called the MCF-A here) was found to produce scores that (i) fit the Rasch model (indicating it produced continuous data, measured at the scale level), and (ii) represented a uni-dimensional measure of performance (Hopkins et al., 2019).

The MCF-A is an assessment of strategy flexibility, as it captures in a single measure children’s ability to recognize efficient strategies based on problem characteristics. The instrument produced data for the study cohort with suitable properties: scores ranged from 0% to 93.8%, with M = 46.7%, SD = 28.7, skewness = −0.2 (SE = 0.2) and kurtosis = −1.2 (SE = 0.4). Chronbach’s alpha indicated strong reliability (α = 0.9).

Results

For validation purposes, RTs collected during the choice condition were analyzed and were found to be consistent with the strategies children reported: RTs for correct trials were fastest for retrieval (M = 2.4s, SD = 1.5, n = 2767 trials) and generally under three seconds, followed by RTs for decomposition (M = 5.1s, SD = 4.4, n = 1817 trials), min-counting (M = 6.4s, SD = 5.0, n = 933 trials), count-from-first (M = 9.4s, SD = 4.8, n = 58) and count-all (M = 18.4s, SD = 15.6, n = 51). Moreover, on min-counting trials, RTs mostly increased by 1–2 seconds per count (See Appendix 2), a rate consistent with past studies (e.g., Siegler, 1987). Trials executed within three seconds in the choice condition were also examined and included trials solved using retrieval (75.6%), decomposition (18.8%) and min-counting (5.3%). The three second time limit imposed in the no-choice condition to encourage retrieval therefore appeared to be appropriate: it was not too restrictive (retrieval times were generally, but not always, under three seconds), nor was it too lenient (problems solved in under three seconds were predominantly, but not always, solved using retrieval).

Identifying groups and group differences

In the choice condition, participants most commonly used retrieval (M = 47.2%, SD = 17.7), decomposition (M = 31.8%, SD = 18.7), and min-counting (M = 16.8%, SD = 21.3) to solve single-digit addition problems. Performance was quite accurate (M = 94.9%, SD = 10.5). Given considerable variation in strategy use, it was appropriate to try to cluster participants into groups with distinct profiles.

Six children who used a count-from-first strategy or counting-all strategy to solve more than a third of the problems formed the inefficient counting group. (The use of inefficient strategies could not be included in the cluster analysis since few participants used these strategies). The remaining children were clustered into four groups based on how frequently they used retrieval, how accurate they were when using it, and how accurate they were when using a min-counting strategy. Fifty participants, who only used retrieval and decomposition strategies formed the proficient group. Forty-eight participants, who predominantly used retrieval and decomposition strategies but with some min-counting, and were mostly accurate when using retrieval and min-counting, formed the almost-proficient group. Nine participants who predominantly used retrieval and decomposition strategies with some min-counting, and displayed poor accuracy with min-counting, formed the inaccurate-min-counting group. Fifty-three participants who frequently used min-counting and were relatively accurate with min-counting, formed the accurate-min-counting group. The five performance groups and key features of each are detailed in Table 1.

Table 1. Mean percentage (SD) for strategy frequency and accuracy by group

		Strategy
		Retrieval	Decomposition	Min count	Count from first	Count all
Proficient (n= 50)	Frequency	59.4 (16.2)***	39.8 (16.5)**	0***	0	0
	Accuracy	99.7 (1.2)**	97.9 (6.2)**	-	-	-
Almost-proficient (n= 48)	Frequency	54.5 (11.2) **	31.3 (14.8)	13.3 (12.4) **	0.1 (0.8)	0.3(1.6)
	Accuracy	98.5 (3.3)	95.2 (11.6)	98.4(4.2) **
Inaccurate-min-counting (n= 9)	Frequency	48.5 (13.1)***	30.2 (18.6)	15.1 (9.8) ***	1.9 (4.6)	1.5 (4.6)
	Accuracy	92.6 (6.2)	90.3 (10.6)	56.2 (14.2) ***
Accurate-min-counting (n= 53)	Frequency	32.0 (8.6)	28.4 (20.4)	37.7 (23.2)	0.6 (2.4)	0.2 (0.8)
	Accuracy	97.1 (6.4)	89.6 (17.6)	94.1 (7.6)
Inefficient-counting (n= 6)	Frequency	19.9 (15.0)	0.9 (2.3)	3.2 (4.1)	30.6 (34.8)	28.7 (34.4)
	Accuracy	96.6 (5.8)			43.8 (51.5)	40.6 (46.9)

Note. Groups are ordered according to frequency of retrieval (descending order) and this order is kept constant in all tables. Data are not shown for strategy accuracy if strategy frequency was ≤5%. Children in the inefficient-counting group responded with ‘don’t know’ on 16.7% of trials. *Results of planned comparisons between the accurate-min-counting group and the proficient, almost-proficient and inaccurate-min-counting group (***p < 0.001, **p < 0.01)

To test the distinctiveness of these groups, the frequency and accuracy of retrieval, min-counting and decomposition were compared across the five groups using ANOVAs. Main effects were found for (i) the frequency of retrieval [F(4, 161) = 42.98, p <.001, η² = 0.52]; (ii) the accuracy of retrieval [F(4, 161) = 5.88, p < .001, η² = 0.13]; (iii) the frequency of decomposition [F(4, 161) = 8.08, p < .001, η² = 0.17]; (iv) the accuracy of decomposition [F(4, 150) = 6.11, p < .001, η² = 0.14]; (v) the frequency of min-counting [F(4, 161) = 43.29, p < .001, η² = 0.52]; and (vi) the accuracy of min-counting [F(3, 109) = 92.63, p < .001, η² = 0.82]. T-tests were used to test differences in these measures (and other measures used in this study) between the accurate-min-counting group and the proficient, almost-proficient and inaccurate-min-counting groups. The distinct strategy mix of children in the inefficient-counting group made statistical comparisons superfluous. A Bonferroni correction was applied to reduce the likelihood of Type I errors when conducting multiple t-tests (adjusted α level = 0.05/3 = 0.017). Effect size was calculated using Cohen’s d for planned comparisons between groups, except when comparing accurate-min-counters with inaccurate-min-counters, where Hedges’ g was calculated instead due to difference in the sizes of these groups. It should be noted that a non-significant finding resulting from comparing measures for the accurate-min-counting group with the inaccurate-min-counting group should be interpreted with caution, since the small number of children in the inaccurate-min-counting group rendered the power of the analysis insufficient for detecting differences.

As indicated in Table 1, children in the accurate-min-counting group were clearly distinguishable by their relative infrequent use of retrieval (32% of trials) in the choice condition, compared to children in the proficient group (59%); t(101) = 10.82, p < .001, d = 2.11, almost-proficient group (55%); t(99) = 11.42, p < .001, d = 2.25, and inaccurate-min-counting group (49%); t(60) = 4.92, p < .001, Hedges’ g = 1.77. Correspondingly, children in the accurate-min-counting group were clearly distinguishable by their frequent use of min-counting (38% of trials) from children in the proficient group (0%); t(101) = 11.46, p < .001, the almost-proficient group (13%); t(99) = 6.47, p < .001, d = 1.31, and the inaccurate-min-counting group (15%), t(60) = 2.85, p < .01, Hedges’ g = 1.03. Further, the accuracy with which min-counting was executed clearly distinguished children in the accurate-min-counting group (94% accuracy) from those in the inaccurate-min-counting group (56% accuracy), t(60) = 12.0, p < .001, Hedges’ g = 4.33. The frequency of decomposition discriminated between children in the accurate-min-counting group (28.4%), and those in the proficient group (39.8%), t(101) = 3.13, p < .01, d = 0.61. Also, accuracy with decomposition discriminated between children in the accurate-min-counting group (90% accuracy) and those in the proficient group (98% accuracy), t(96) = 3.16, p < .01, d = 0.62. Frequency of use and accuracy of decomposition strategies did not discriminate between children in the accurate-min-counting group and the other three groups.

Differences in speed

To investigate differences in speed, 405 trials (6.8% of trials) for which children generated extreme RTs (±3 x IQR) were excluded from analysis. Descriptive statistics for RTs for the problem set (correct trials only) for each performance group were generated and compared.

Differences in RTs across groups were significant for the combined problem set [F(4,5320) = 243.44, p < .001, η² = 0.15]. Children in the accurate-min-counting group took more time on average (M = 4.3s SD = 2.7) to solve a problem than children in the proficient group (M = 2.7s, SD = 1.7), t(3381) = 20.87, p < .001, d = 0.71, and almost-proficient group (M = 3.3s, SD = 2.3), t(3229) = 10.87, p < .001, d = 0.38, but not more time than children in the inaccurate-min-counting group (M = 4.1s, SD = 3.5), t(1878) = 0.89, ns. Children in the inefficient-counting group took the longest time (M = 8.9s, SD = 6.3). These findings provide converging evidence for our interpretation of the clusters; children in them showed patterns of speed consistent with the strategies that were reported most often in the different clusters. They also ruled out the possibility that accurate-min-counters were particularly fast at counting.

Comparing accuracy in the choice and no-choice conditions

Descriptive statistics for the percentage of problems solved correctly by each group, in each condition, are displayed in Table 2.

Table 2. Percent correct by condition and group, and differences in accuracy between conditions for each group

	Choice M (SD)	No choice M (SD)	Difference M (SD)
Proficient	98.7 (3.4)	89.1 (11.4)	9.6 (9.4)
Almost-proficient	97.7 (3.6)	76.6 (16.3)	21.1 (15.4)
Inaccurate-min-counting	84.9 (8.5)	54.3 (18.5)	30.5 (14.3)
Accurate-min-counting	94.0 (6.4)	58.2 (19.0)	35.7 (17.8)
Inefficient-counting	63.9 (36.5)	21.8 (16.0)	42.1 (29.2)

A repeated measures ANOVA was conducted to examine differences in accuracy across conditions for each group, to investigate the extent to which using a strategy of choice resulted in more or less accurate performance than using retrieval in the no-choice condition. The results indicated a significant difference in children’s accuracy across conditions, Wilks’ Λ = 0.40, F(1, 164) = 244.12, p < .001, η² = .60. Children were less accurate in the no-choice condition compared to the choice condition. A significant condition by group effect was also evident: Wilks’ Λ = 0.65, F(4,161) = 21.69, p < .001, η² = .35. Planned comparisons indicated that accuracy scores in the no-choice condition were further below those in the choice condition for accurate-min-counters, compared to children in the proficient group, t(101) = 9.25, p < .001, d = 1.83, and almost-proficient group, t(99) = 4.39, p < .001, d = 0.88.

Given that accurate-min-counters did not fare well in the no-choice condition, it appears that their choice to not use retrieval was adaptive. Comparing differences in accuracy across groups and conditions suggested that accurate-min-counters were at least as adaptive as those of other groups. These results highlight how adaptive strategy choices under choice conditions can mask differences in knowledge between groups that are apparent when students perform under time constraints. When children had a choice of which strategy to use, accurate-min-counters were almost as accurate as children in the proficient and almost-proficient groups, and considerably more accurate than children the inaccurate-min-counting group. On the other hand, when children needed to retrieve in the no-choice condition, accurate-min-counters were no better than inaccurate-min-counters and much worse than the two high performing groups.

To compare the adaptiveness of accurate-min-counters with that of other groups on a problem-by-problem basis, we examined the strength of the correlation between retrieval use in the choice condition and accuracy of performance in the no-choice condition. For each problem, we correlated the percentage of trials where retrieval was used in the choice condition with the percentage of trials that were correctly solved in the no-choice condition. A strong, positive correlation (between retrieval choice and retrieval accuracy) would indicate highly adaptive behavior. Corresponding scatterplots (shown in Figure 2) were examined to reveal possible differences in adaptiveness at the problem level. Since we could not label each problem in these scatterplots, we coded problems into one of three subsets: Subset 1 included non-tie problems with sums less than ten, Subset 2 included non-tie problems with sums more than ten, and Subset 3 included all tie problems and problems with sums equal to ten.

Figure 2. Association between percentage correct retrieval in choice condition and percentage correct in no-choice condition by groups. N = 36 problems for each scatterplot. ***p < .001. Problem Key: ●Subset 1 ▲Subset 2 * Subset 3.

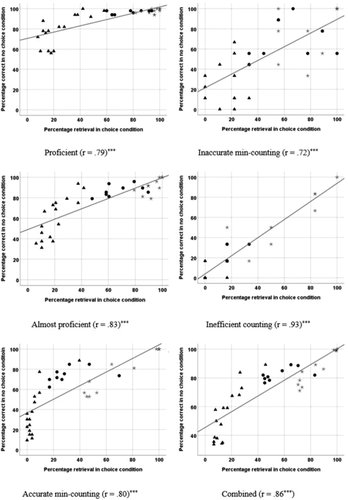
As shown in Figure 2, a strong correlation between percentages retrieved in the choice condition and percentages correct in the no-choice condition was evident for children in each of the five groups. More specifically, the strength of the correlation for children in the accurate-min-counting group was similar to that calculated for children in the almost-proficient group and proficient group (r ≈ 0.8). In other words, for these groups, the frequency with which retrieval was chosen to solve a given problem predicted around 64% of variance in the accuracy with which that problem was solved (arguably with retrieval) in the no-choice condition.

These scatterplots display two features of performance that require further scrutiny. First, accuracy in the no-choice condition was generally higher than expected given the frequency of retrieval in the choice-condition. For example, for the combined group, problems that were solved accurately in the no-choice condition around 80% of the time, were solved only around 50% of the time using retrieval in the choice condition. This feature could reflect the fact that problems solved in the no-choice condition were not always solved using retrieval, or that students’ confidence with retrieval restricts their use of retrieval. Second, non-linear patterns were evident. Non-linearity indicates that some problems were more conducive to adaptive strategy choices than others. Given that adaptiveness develops as children gain experience with a range of strategies, the non-linear feature of these graphs, which appear to be related to problem type (subset), suggest that children’s experiences using multiple strategies are not equivalent across problem type.

Comparing groups on the MCF-A

The distribution of scores on the MCF-A for each group are displayed in Figure 3. Mean scores differed across groups, F(4, 161) = 10.94, p < .001, η² = 0.21.

Figure 3. Distribution of scores on the assessment of mental computation flexibility with addition (MCF-A) by group.

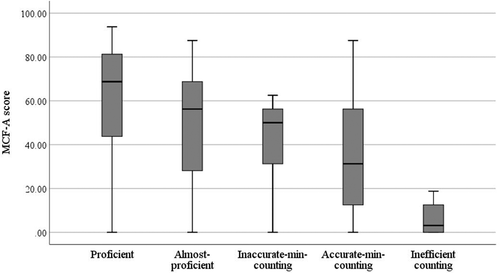
Children in the accurate-min-counting group scored significantly lower on the MCF-A assessment (M = 35.4, SD = 25.9) than children in the proficient group (M = 61.8, SD = 27.7), t(101) = 4.99, p < .001, d = 0.98, and children in the almost-proficient group (M = 50.0, SD = 25.0), t(99) = 2.88, p < .01, d = 0.57. There was no difference in mean scores between children in the accurate-min-counting group and the inaccurate-min-counting group (M = 38.9, SD = 23.3), t(60) = 0.38, ns. Unsurprisingly, children in the inefficient-counting group scored lowest on the assessment (M = 6.3, SD = 7.9).

Discussion

In this study, 166 8- and 9-year-olds were individually assessed to ascertain for single-digit addition how often they used different strategies, how long they took to apply each strategy, and how accurate they were with each strategy. Children used retrieval most often (48% of trials), followed by decomposition strategies (32%), and the min-counting strategy (17%). Overall accuracy was high (95% correct). The frequency of min-counting for simple addition reported here for elementary school students was similar to that found by Rhodes et al. (2019) for middle school students (20%). Whereas Rhodes et al. modeled individual differences to investigate variations in aggregate measures, we clustered individuals into groups that displayed similar performance characteristics. Our goal was to identify a group of children who used min-counting frequently and accurately, to investigate if these children were adaptive in their use of retrieval, and to determine if they were disadvantaged in terms of mental computation flexibility.

Our findings indicated that there were a substantial number of accurate-min-counters, identifiable by their relatively frequent and accurate use of min-counting (38% of trials, 94% correct) and, complementarily, their relatively infrequent use of retrieval (32%). The prevalence of accurate-min-counters in this study represented 32% of children in Grade 3 and 4, a comparable figure to that reported by Hopkins and Bayliss (2017) for Grade 7 students (35%). An important difference in findings between the two studies was that decomposition strategies were used more frequently by participants in this study (32%), compared to the earlier one (10%). Children in the earlier study might have had less exposure to decomposition strategies as data reported in that study were collected in 2009, which meant participants would have been in third grade in 2003, a time when there was less emphasis on teaching ‘thinking’ strategies and mental computation in Australian schools than at present (McIntosh, 2005). Despite differences in decomposition use, and perhaps in exposure to decomposition, a similar proportion of accurate-min-counters was found in both studies.

The prevalence of accurate-min-counting when children are in third and fourth grade, and the relatively infrequent use of retrieval among accurate-min-counters, should raise concerns among educators given the strong association between retrieval use and mathematics achievement (Geary, 2011a). However, these findings by themselves may not elicit such reactions for two reasons. First, it is not clear if accurate-min-counters choose their best strategy. To address this possibility, we compared how accurately these children solved the same set of simple addition problems in a no-choice condition, where time limits required them to retrieve. Second, the relation between simple addition strategy choice and mental computational proficiency has not been examined previously. To address this gap in the literature, we developed the MCF-A and compared measures of flexibility across groups, clustered according to simple addition performance.

Our findings revealed that children in the accurate-min-counting group were particularly inaccurate when it came to solving single-digit addition problems in the no-choice condition with time limits that strongly encouraged use of retrieval: their accuracy decreased from 94% in the choice condition to 58% in the no-choice condition. Moreover, a strong association (r ≥ 0.8) was evident between percentage of trials on which each problem was retrieved in the choice condition and percentage of trials on which each problem was correctly solved in the no-choice condition. These relations were strong both overall and for children in the accurate-min-counting group. The findings are consistent with theories of strategy choice (Siegler & Lemaire, 1997), which posit that people choose adaptively among problem-solving strategies. The results also extended previous findings documenting children’s adaptive choices among strategies for simple addition (Torbeyns et al., 2004) to children who display the accurate-min-counting profile.

Some limitations of using a cutoff response time to create a no-choice condition for retrieval need to be noted. The decision to display problems in the no-choice condition at a rate of three seconds per problem was based on previous analyses of retrieval times (e.g., Cowan et al., 2011; Jordan et al., 2003) as well as our own prior findings regarding response times on correct retrieval trials (Hopkins & Bayliss, 2017). As it turned out, children in this study had somewhat longer response times on correct retrieval trials (M = 2.4s, SD = 1.5) compared to the older children in the earlier study (M = 1.8s, SD = 0.8). This meant that the rate at which problems were displayed could have made retrieval difficult for some children. While a longer time constraint might have made retrieval easier, it also would have increased the likelihood that strategies other than retrieval would be used in the no-choice condition.

Additionally, our findings indicated that accurate-min-counters were relatively weak in mental computation flexibility. On the MCF-A, the mean score for children in the accurate-min-counting group (35%) was lower than that for children in the proficient group (62%) and the almost-proficient group (50%). Taken together with earlier findings (Hopkins & Bayliss, 2017), these results suggest that helping children who demonstrate the accurate-min-counting pattern to gain greater mental computation flexibility is a worthwhile goal for instruction.

Implications

The present findings, as well as ones from Hopkins and Bayliss (2017), challenge the long held view in the field of mathematics learning disability that only a small number of children display protracted use of counting-based strategies for simple addition (e.g., Geary, 2011b). If these results are representative, then in addition to children who display inefficient and inaccurate counting strategies, there is a substantial group of children (around 10 children in a typical class of 30) who frequently and accurately use the min-counting strategy instead of retrieval-based strategies for simple addition. Children in this study and its predecessor were from predominantly middle-class areas; the percentage of children who do not consistently use retrieval to solve simple addition problems might well be even higher in lower-income areas.

The prevalence of accurate-min-counting signals the need for explanations of retrieval difficulties to move beyond the notion of cognitive deficits (Geary, 2011b). When an issue affects over one-third of a class, broader explanations and more practical ways of addressing this problem are needed than removing children from their classrooms for special instruction. It may be that these children need more opportunities to develop number sense (Baroody et al., 2009), including an understanding of part-part-whole relations among numbers (Cheng, 2012; Gaidoschik, 2019; Sun et al., 2019). Alternatively (or in addition), it may be that the development of retrieval is hindered by the overuse of standard problem types during practice (Chesney et al., 2018). Other research has suggested that there is too much emphasis on developing counting strategies in the curriculum and not enough on developing decomposition strategies (Cheng, 2012; Gaidoschik, 2019), and that this may inhibit the development of retrieval. In the current study, however, accurate-min-counters used decomposition strategies as frequently as children in the almost-proficient group, suggesting that emphasizing decomposition strategies is unlikely to be a panacea for moving this group of students toward retrieval.

We propose that current approaches for teaching basic arithmetic are, in fact, inadvertently encouraging children’s continued use of counting-based strategies by not providing a non-phonological route for strengthening problem-answer associations in memory. In particular, we believe there is value in simultaneously leveraging a student’s mental number line (a powerful conceptual structure for organizing numerical knowledge, Siegler & Ramani, 2009) with their ability to subitize (enumerate small sets of four to five objects rapidly using visual-spatial perception, Starkey & Cooper, 1995). We are in the initial stages of testing this hypothesis.

In closing, these findings highlight that the mathematics learning of a substantial percentage of 8- and 9-year-olds appears to be hindered by overreliance on min-counting for single-digit addition. These students are accurate but are slower when it comes to solving simple addition problems relative to most of their peers. Children who display inaccurate-min-counting and inefficient-counting strategies are also disadvantaged, but the difficulties they exhibit have long been recognized in the learning disabilities literature. Difficulties displayed by accurate-min-counters are only now coming to the fore, yet they appear to affect around one-third of third to seventh graders. If changes to teaching practice can help these students develop the faster strategies of retrieval and decomposition before they fall behind their peers, we may see a reduction in the long tail of underachievement in mathematics that concerns educators in many countries.

Additional information

Notes on contributors

Sarah Hopkins

Sarah Hopkins is a senior lecturer in the Faculty of Education at Monash University. Her current research is focused on understanding and addressing students' difficulties learning mathematics and preparing teachers for inclusive classrooms.

James Russo

James Russo is a lecturer in the Faculty of Education at Monash University. His current research interests are in task design, mental computation and estimation in the elementary years, and on examining the teaching and learning of mathematics through an affective lens.

Robert Siegler

Robert S. Siegler is Schiff Foundations Professor of Psychology and Education at Columbia University. He is a recipient of the American Psychological Association's Distinguished Scientific Contribution Award, as well as having been chosen to be a member of the National Academy of Education and of the Society of Experimental Psychologists. His current research focuses on the development of mathematical thinking, particularly children's understanding of rational numbers; ways of improving children’s mathematical thinking; and educational applications of cognitive-developmental theory.

Notes

1. Thevenot et al. (2016) challenged the common assumption that children’s strategies generally evolve from counting to retrieval. They argued that reaction times (generally under 1.7 seconds) recorded for single-digit addition problems with small sums (involving operands from 2 to 4) do not necessarily reflect direct retrieval, even when children report just knowing the answer, but instead represent very fast, compacted counting strategies.

2. As well as the Arithmetic Scratch-Paper Test, Blöte et al. (2001) administered an assessment that required children to solve a set of problems using two different strategies for each problem; however, this test was considered an assessment of conceptual understanding and not strategy flexibility. As noted by Star and Rittle-Johnson (2008), students’ ability to generate multiple strategies is not a good assessment of flexibility since children tend to come up with strategies that are novel but inefficient.

Appendix 1

Items on the MCF-A

Table

Item	Strategy type	Correct response
4 + 7 = 10 + 1	Nonstandard partitioning	4 + 6 or 3 + 7
5 + 8 + 5 = 10 + 8	Noticing	5 + 5
8 + 3 + 2 = 10 + 3	Noticing	8 + 2
10 + 11 = 20 + 1	Standard partitioning	10 + 10
28 + 13 = 38 + 3	Standard partitioning (jump)	28 + 10
11 + 3 + 9 = 20 + 3	Noticing	11 + 9
6 + 18 + 34 = 40 + 18	Noticing	6 + 34
48 + 45 = 90 + 3	Nonstandard partitioning	45 + 45
36 + 37 = 72 + 1	Nonstandard partitioning	36 + 36
44 + 49 = 94–1	Compensating	44 + 50
56 + 33 = 80 + 9	Standard partitioning (split)	50 + 30
22 + 49 = 21 + 50	Compensating	22–1
23 + 44 = 64 + 3	Standard partitioning (jump)	20 + 44
45 + 67 + 82 = 180 + 14	Standard partitioning (split)	40 + 60 + 80
456 + 356 = 800 + 12	Standard partitioning (split)	450 + 350
955 + 445 = 1000 + 400	Standard partitioning (jump)	955 + 45

Appendix 2

Self-reports of strategy use and corresponding RTs (s) for correct trials in choice condition

Table

Strategy	M	SD	No. of trials	% trials
Retrieval	2.4	1.5	2767	48.8
decomposition	5.1	4.4	1817	32.0
min-counting combined	6.4	5.0	933	16.5
min-addend 2	3.9	2.6	188
min-addend 3	4.9	3.0	215
min-addend 4	6.6	5.7	160
min-addend 5	7.7	5.8	130
min-addend 6	7.6	4.3	110
min-addend 7	8.8	4.9	77
min-addend 8	10.8	6.1	38
min-addend 9	13.2	10.1	15
count from first	9.4	4.8	58	1.0
count all	18.4	15.6	51	0.9
don’t know	8.3	6.2	45	0.7

Note. No. of correct trials = 5671 (94.9%). Min-addend 2 are trials that were reportedly solved using a min-counting strategy and problems contained an operand of 2 (2 + 2, 2 + 3, 2 + 4, …), min-added 3 signifies min-counting trials where problems contained an operand of 3 (3 + 3, 3 + 4 …) etc.