Innovation and wages constrained with budgetary deficit and unemployment in the European Union countries

Abstract

This paper aims to research the driving forces of wages across the countries of the European Union (EU-28) during the period 2006-2018. We apply structural equation modelling to analyse relationships between observed variables and latent variables, focusing on factors explaining wages. Based on the literature review, we hypothesized that innovation, budgetary deficit and the rate of unemployment predict wages across EU-28 countries. Our results suggest that innovation is a significant factor in explaining wages. The budgetary deficit has a significant negative impact on wages, while the effect of rate of unemployment is insignificant. The findings of our research underline the importance of policies that accelerate the growth in labour productivity, particularly those which boost innovation and ensure macroeconomic stability, efficient markets, and an adaptable and skilled workforce.

Keywords:

• innovation
• wages
• labour market
• macroeconomic environment
• structural equation modelling
• European Union

Subject classification codes:

• C52
• J21
• J24
• J31
• O31

1. Introduction

Wages in the European Union (EU-28) countries picked up at the end of 2017 and continued to rise during 2018, which was consistent with the decline in unemployment. According to the European Commission (2019), wages are linked to inflation expectations, while nominal wages can slowly rise as inflation moves closer to the reference value of 2% and unemployment stays below its structural rate. Common wage factors, like slack and inflation, give a strong economic integration among EU-28 countries, and direct spillovers from wage setting in one country to the others, which is the outcome of the product, labour, and financial markets, and they all explain a significant portion of the wage dynamics in EU-28 countries in recent years.

Ehrenberg and Smith (2012) classify the drivers of wages into economic and non-market factors. On the employee’s side of the market, an employee invests in new skills if desires to change jobs or uphold the costs of moving. On the employer’s side of the market, hiring and firing workers influences wages with consequences on labour productivity (Yildirim, 2015). Hiring new workers can involve investment in searching and training, while firing workers can be perceived as unfair. Along with the economic factors which intercorrelate with the business cycle, there are non-market driven factors such as laws, customs, and institutions, which can constrain individuals and companies from making choices. Labour laws and employment regulations can influence company flexibility in hiring and firing workers, wage setting and terms of employment.

In addition to labour market dynamics with the rate of unemployment, and the general macroeconomic conditions and (in)stability (Cristea et al., 2020; Meixnerová & Krajňák, 2020), the key factors that drive wages can also be innovation and technological changes pertaining to capital intensity that influence labour productivity (Hong et al., 2018; Mai et al., 2019). IMF (2018) argues that there is a lack of analyses linked with innovation as the driver of wages, and more research should give more in-depth results which could be transformed into actions, leading to the overall effect among EU-28 countries.

The EU-28 countries that have a specific policy which supports innovation can contribute to fostering inclusive growth by reducing labour productivity–wage gaps between small and medium enterprises (SMEs) and large companies, since, according to the OECD (2018), these are the outcomes of boosting innovation in established SMEs. Defining different types of innovation as a key factor for growth in SMEs can improve entrepreneurial performances, but it can also improve the entrepreneurial environment for its stakeholders (Hunt, 2018). Employees can especially benefit from it, because more innovative SMEs are those that are more productive, which is reflected in higher wages and better working conditions. Governments research and development (R&D) and innovation policies can be important in boosting innovation and innovation performances in firms, which could lead to new business models focusing on innovation.

The aim of this paper is to develop a conceptual and testable empirical model for the driving forces of wage formation in EU-28 countries in relation to innovation with the mediating effects of budgetary deficit and unemployment. Nikulin (2015) highlights that majority of analyses of driving forces of wages are based on the Phillips curve and wage curve. Holmlund and Zetterberg (1991) provide evidence on scepticism about competitive model as an accurate representation of wage determination under decentralization. Phillips curve is prevailingly estimated on time-series macroeconomic data while wage curve is estimated on pooled cross sections of microeconomic data (Blanchflower & Oswald, 1995). In this paper we propose modified research approach using aggregate macro-level panel data. Comprehensive and modern structural equation modelling enables observation of relationships between variables and simultaneous investigation of several equations for EU-28 countries in a more effective manner (Coveri & Pianta, 2019). Developed conceptual and empirically testable models summarize evidence on various driving forces of wages and offer insights of possible integration of driving forces of wages derived from the literature into empirical models. Accordingly, the main novelty of this research and its original scientific contributions are in the following four main directions. First, the paper investigates and determines significant driving forces of wages across the EU-28 countries. The structural equation modelling approach based on panel data is applied as an analytical tool for testing the cause-effect relationships between observed variables and latent variables. Based on the literature review and theory, we hypothesized that innovation, the budgetary deficit as one of possible sources of (in)stability of the macroeconomic environment and the rate of unemployment predict wages across EU-28 countries. Second, the structural equation modelling based on panel data has been rarely used in a similar research which allows a simultaneous investigation of several equations and variables at the same time, which is not possible in the case of a partial regression analysis. The research develops both conceptual and empirically testable models. Third, the added value of the research is contribution to study our main hypothesis that innovation is the predominant factor in explaining wage dynamics across EU-28 countries. This main empirical and testable association is mitigated by the direct and indirect effects of budgetary deficit from macro-economic environment and the rate of unemployment. Finally, the findings of our research underline the importance of government and managerial policies that accelerate labour productivity growth, in particularly those which boost innovation and ensure stability, efficient markets, and an adaptable and skilled workforce.

The rest of the paper is structured as follows. In the next section we present the literature review. The third section presents the methodology. In the fourth section the results are presented and explained, while the fifth section discusses their importance and implications. The final section derives a conclusion.

2. Literature review

From a set of different theoretical and empirical models on wage formation the focus is on development of the hypotheses based on the effects of budgetary deficit, the rate of unemployment, and innovation on wages. Our conceptual and empirical approach is based on macroeconomic evidence.

2.1. Budgetary deficit and wages

Roubini and Sachs (1989) argue that the effect of the budget deficit on wages can be explained by the economy stage in the business cycle. In the light of the Keynesian perspective, the budget deficit policy is suggested to be adopted in times of a recession because a certain combination between the increased budget deficit and the change in taxes would contribute to lower unemployment and consequently affect wages. In a situation below full employment, the effect of increased government spending on gross domestic product (GDP) is greater than the effect of lowered taxes. On the other hand, in the situation of full employment, the increased budget deficit would contribute to the increase in the price level. To meet the higher demand, firms compete for labour in the saturated labour market. Firms can only hire additional workers if they offer higher wages. Competition for labour leads to an increase in wages, and higher wages induce higher business costs, which leads to an increase in the price level.

Depending on the macroeconomic circumstances in the business cycles, the adjustments in fiscal policies over time are in a response to changing economic conditions. Budget deficit affects factor prices, wages and profit. According to the standard theory of budget deficit and factor markets (Ball & Mankiw, 1995) the marginal product of labour determines the real wages while marginal product of capital determines the rate of profit. Marginal product of labour decreases when budget deficit reduces the capital stock since each worker has less capital to work with it. Marginal product of capital increases since scarcity of capital makes the marginal unit of capital worth more. In such cases budget deficit leads to lower real wages and higher profit rates.

Roubini and Sachs (1989) provide evidence of supply shocks experienced by industrial economies in the 1970s. Economies faced a substantial decline in the growth rate, a rise in unemployment, and inflation. Such a stagflation situation evoked multiple adjustment problems. Real wages did not adjust to maintain the equilibrium between labour costs and marginal productivity of labour at full employment in the wage bargaining process.

Ekanayake (2013) provides evidence that budget deficit causes inflation when this relationship becomes stronger and public sector wage expenditures increase. The latter therefore present influential factor in budget deficit-inflation relationship highlighting that borrowed money spent on higher public wages causes inflationary pressures. Public debt has adverse effect on investments which consequently affects productivity and tends to lower the wages (Akram, 2016; Mhlaba & Phiri, 2019). Ko (2019) applied the Kaleckian model of growth and distributions to test the effects of increases in budget deficit and wage income tax rate in the short and long-run. Results indicate that government borrowing influence wage-led growth in the short as well as in the long-run.

According to Baqaee (2020), households’ inflation expectations are more responsive to inflationary news than to disinflationary ones. This asymmetry in expectations may lead to downward wage rigidity. In addition, asymmetric expectations suggest that monetary policies can have asymmetric effects on employment and on wages (Grundmann et al., 2020).

Following these literature review, we set the following hypothesis (H):

H1: The effect of budgetary deficit on wages depends on stages in the business cycles.

2.2. The rate of unemployment and wages

Labour market conditions such as the unemployment rate and long-term unemployment rate correspond to lost output and diminishing labour productivity that influences wages. Nikulin (2015) argues that most macro-level studies explain wages by unemployment. Seminal paper by Blanchflower and Oswald (1989) provides evidence of causality from unemployment rates to wages. Namely, higher unemployment rate causes lower wages and vice versa (e.g. Ozturk et al., 2019). Card (1995) argues there are several forerunners behind the idea that unemployment rates affect wages. Different locations of industries determine differentials in the long run probability of unemployment. Compensating differentials theory points that any predictable component of the perseverance of employment requires a compensating differential.

Traditional theory explains labour productivity as result of capital intensity, technical progress with innovation, and skills or educational level of labour as well as the economy structure. There can be also missing link between wages and labour productivity as suggested by Gričar et al. (2021) for the Croatian and Slovenian tourism economy. Such conditions also have limited influence on wage bargaining. In a wage bargaining model high unemployment might reduce ability of workers to claim higher wages. Labour market with high unemployment presents less opportunities for workers to find job. There is an explicit assumption of a trade union that is anxious about its employed and unemployed members. If there is high unemployment more trade union's members are likely to be out of job and those who loose job might have difficulties with finding new job. In such a case trade union's preference might be focused towards greater consideration with the number of jobs. Wage bargaining model taking into account relative costs of bargaining rather payoffs for parties involved makes wages less responsive to unemployment (Hall & Milgrom, 2008).

On the other hand, the efficiency wage theory is based on the characteristic that firms determine wage in a context where wage impacts productivity. Firms are eager to maximize profits and workers adopt their effort to work. Unemployment rate is of central importance as it governs the possibilities of finding another job. In a highly pessimistic labour market workers are afraid of losing their job, so they work harder even if the wage is relatively low (marginal increase in unemployment links to marginal decrease in wages). Firms can lower wages and still sustain motivated workers. Therefore, when unemployment is high the wages can be set low.

Moreover, labour market fluctuations (like wage mark-up, and labour disutility) explain minor share in unemployment cycles while demand shocks and supply factors explain about 2/5 of these cycles, and 1/5 of these cycles is explained by relative price changes (Charalampidis, 2020). Wages of newly hired workers show no more cyclicality than wages of existing workers implying that the latter is better indication of cycles in marginal cost of labour (Gertler et al., 2020). Additionally, on a sample of EU-15 countries external factors in determining wages show significant cross-country variations depended on bargaining structures (Galuščák et al., 2009).

Effects of unemployment on wages can be biased to stages in the business cycles and from downward wage rigidities. Very low unemployment can stimulate wage growth, but negative effects of higher unemployment can be heterogenous between countries depending on the natural rate of unemployment. The reasons for unemployment can be different such as faster wage growth than labour productivity growth, output decline with limited demand during economic cycles, external shocks, and economic policies. Long-term unemployment can be results of structural problems in the economy and mismatches in the labour market.

Long-term unemployment affects older people in a sense of their reservation wage and expectations about willingness to reduce wages over time (Addison et al., 2013). Similar view holds true for young unemployed willing to work for lower wages (Axelrad et al., 2016). On the other hand, Plum (2019) analysed British low-wage sector and employment prospects of unemployed showing that low wages reduce the risk of future unemployment and especially in the case of long-term unemployment low wages increase the prospects of earning higher wages.

We set the following hypothesis:

H2: The rate of unemployment causes downward pressures on wages depending on stages in the business cycles and wage rigidity.

2.3. Innovation and wages

In analysing the relationship between innovation and economic growth Avila-Lopez et al. (2019) based on a study of Maradana et al. (2017) describe innovation with different variables such as patent applications, R&D expenditures, researchers in R&D activities, high-technology exports, scientific and technical journal articles. Scientific and technological knowledge and the ability to innovate are seen as important factors that contribute to increase the labour productivity which consequently influence on wages (Pradhan et al., 2016).

Proxied with the above variables, innovation via labour productivity is a key driver of wages. Coveri and Pianta (2019) confirm that labour productivity is a key driver of wage increases. Labour productivity describes the combination of demand and supply factors and contributes to higher output. Their structural equation model based on panel data confirms that wages grow faster in industries with greater innovation activity.

Innovation can determine the introduction of new products and services with impacts on wages. Coveri and Pianta (2019) distinguish between different technological strategies, namely the technological competitiveness strategy based on product innovation and the cost competitiveness strategy based on processes. Technological competitiveness strategy aims at higher quality of products, entering new markets and pursuing the development of effective demand. As such a strategy, it can lead to higher wages. In addition, such a strategy at the firm level benefits from the knowledge and skills of employees, and their cooperation with distribution of returns from innovation to higher wages. The cost competitiveness strategy, on the other hand, could lower workers' bargaining power and wages (Cirillo, 2014).

Dunne and Schmitz (1995) found that the factories that use the most advanced technology pay the highest wages and employ the greatest fraction of non-production workers, who are generally regarded as more skilled than production workers. Lopez-Sintas and Martinez-Ros (1999) for the Spanish firms found a premium in the paid wages in innovative firms, with the greater impact in small business. Sanders and ter Weel (2000) and Acemoglu (2002) concluded that wages tend to be higher and grow faster in industries with higher technological opportunities, but that is also the case with more educated workers who use computers at work (Awang et al., 2019) and with possessing computer skills earn higher wages (Danyal et al., 2011). For the Canadian manufacturing sector Cozzarin (2016) confirmed that process innovation positively impacts labour productivity and wages, whereas product innovation seems to have only moderate positive effect on wages. Aghion et al. (2017) found that more R&D intensive firms have higher wages and better performance (Arendt & Grabowski, 2019; Chen et al., 2019). Cirillo (2014) analysed the relationship between the type of innovation and wages for professional categories. He found a positive impact of product innovations on wages for all professional groups, except for unskilled manual workers. Pianta and Tancioni (2008) concluded that wages grow faster in sectors with higher innovation expenditure. Moreover, the authors distinguished between high and low-innovation sectors because they are affected by different factors. They found that innovation has positive effects on income dynamics, in addition to the role of innovation on labour productivity gains. Considering possible causes of declining wage inequality, Laporšek et al. (2021) find diminishing returns to education and experience for each successive birth cohort in Slovenia because their skills with the supply shock of the Bologna higher education depreciated. Many young graduates are forced to take low-skilled jobs with lower productivity. Other social variables have been analysed by Taresh et al. (2021).

Not only innovation, but also invention can have some benefits for a firm and its employees, starting with the inventor. An invention can increase the inventor’s annual wage rate over a prolonged period after the invention. Innovation can also affect co-workers in the same firm (Aghion et al., 2017). Following the literature, we set the following hypothesis:

H3: Innovation drives positively real wages.

There are not many studies regarding causal relations between innovation and wages in the literature. Due to possible endogeneity between the studied variables such as between wages and innovation, we employ structural equation model able to deals with direct and indirect causal relations between the variables. For example, Kleinknecht (1998) concluded that low wages and high labour market flexibility eliminate a major incentive for introducing innovation in companies. This is closely connected with the topic of motivational management; effects of wages on innovation. Wage inequality can affect corporative innovation (Miao et al., 2020). Kong et al. (2020) concluded that paying higher relative wages to rank-and-file employees promotes better innovation outcomes in terms of patent quantity and quality. To sum up, we expect positive association between innovation and wages, while the mitigating effects of budgetary deficit and the rate of unemployment on wages can be mixed and heterogenous across the EU-28 countries and over time depending on country-specific macroeconomic and labour market factors and stages in the business cycles.

3. Methodology

We present data of variables, the developed theoretical conceptual model and empirically tested structural equation model.

3.1. Data

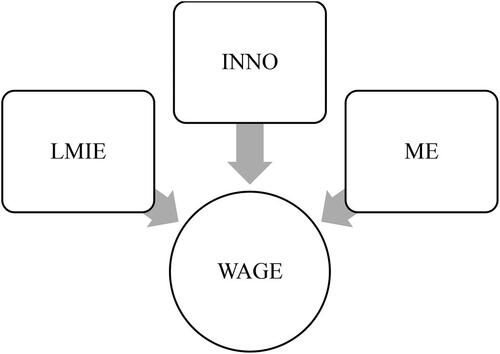
Based on the literature review and available information, the theoretical conceptual model was developed, and it was empirically tested. Theoretical and statistical criteria were used to decide which variables to include in the model and how these variables are related. Considering the theoretical perspective, we specify the observed variables that determine latent (construct) variables. Since we are interested in examining the driving forces of wages across EU-28 countries, we hypothesized a model which has four latent variables, out of which three are exogenous latent variables that affect the endogenous latent variable. The hypothesized theoretical conceptual model is presented in Figure 1.

Figure 1. Hypothesized theoretical conceptual model.

Source: Authors’.

The definition of each latent variable with the observed variables followed the theoretical conceptual model with data availability. Our latent variables are named innovation (INNO), the budgetary deficit as one of reasons for possible (in)stability of the macroeconomic environment (ME), the rate of unemployment (LMIE), and wages (WAGE), and they are defined by using two observed variables (ME, LMI, WAGE), where one latent variable (INNO) is defined by three observed variables. The latent variable named innovation is defined by the following observed variables: human resources in science and technology, patent applications to the European Patent Office, and R&D expenditures. The latent variable named the budgetary deficit as (in)stability of the macroeconomic environment is defined by the following observed variables: general government deficit/surplus and general government gross saving. The latent variable of rate of unemployment is defined by the following observed variables: the unemployment rate and the long-term unemployment rate. The latent variable of wage is defined by the following observed variables: compensation of employees, and wages and salaries. Both observed variables within the latent variable of wage were deflated by the harmonised index of consumer prices (HICP_t). The data for the HICP_t were obtained from Eurostat database source [prc_hicp_aind]. More detail explanation of observed variables included in each latent variable can be reached at Eurostat (2019b).

The data used are for the period 2006-2018 for EU-28 Member States reflecting availability of data. The data were obtained from Eurostat database (Eurostat, 2019a). The indication of data sources is presented in Table 1.

Table 1. Indication of data sources.

Variable name	Observed variable	Data source	Latent variable
Human resources in science and technology	inno1	[hrst_st_ncat]	INNO
Patent applications to the EPO	inno2	[pat_ep_ntot]
R&D expenditures	inno3	[rd_e_gerdtot]
General government deficit/surplus	me1	[tec00127]	ME
General government gross saving	me2	[gov_10a_main]
Unemployment rate	lmie1	[une_rt_a]	LMIE
Long-term unemployment rate	lmie2	[une_ltu_a]
Compensation of employees	wage1	[nama_10_gdp]	WAGE
Wages and salaries	wage2	[nama_10_gdp]

Source: Authors’.

3.2. Structural equation modelling

Structural equation modelling technique has become widely used and applied in understanding latent variables such as innovation climate, innovation performance, open innovation, R&D collaboration, technology infrastructure and their influence on organizational performance measures.

Structural equation modelling is a method used to simultaneously estimate a set of regression equations. The approach enables measuring latent variables and to study the relationship between them, therefore more in depth and more accurate analysis among the investigated constructs is advantageous in comparison to partial regression analysis (Bojnec & Tomšič, 2020; Kline, 2016). Two specific fields of application include confirmatory factor analysis, which involves testing a measurement model, and path analysis, which involves estimating structural relationships between latent variables. The general idea of structural equation modelling is to estimate the model in a way that a sample covariance matrix corresponds as closely as possible to the model covariance matrix (Schumacker & Lomax, 2010). Structural equation models help to establish the relationships between latent variables, given the theoretical conceptual perspective and the researchers’ decisions. Structural equation modelling involves developing a measurement model to define latent variables and then a structural model to establish relationships between latent variable. Structural equation modelling uses two major types of variables. The first are observed variables, which are directly observable or measured. The second type of variables are latent (constructs) variables, which are not directly observable or measured, but they are rather observed or measured indirectly. They are inferred constructs based on which we select observable variables to define the latent variable.

Structural equation modelling was carried out as a two-step modelling approach analysing two conceptually distinct latent variable models: the measurement model and the structural model, as proposed also by Anderson and Gerbing (1988). The measurement model represents an assessment of convergent and discriminant validity, whereas the structural model represents an assessment of predictive validity. The estimations were carried out by using the maximum likelihood method.

4. Results

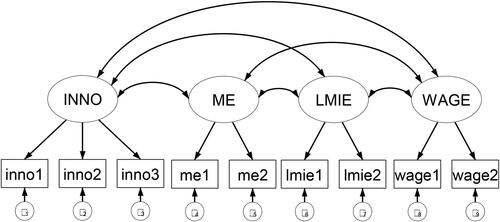
Based on previous research and available information we first confirm and present the measurement model. The analysis of the measurement model is based on the confirmatory factor analysis, which makes a priori statements about the underlying dimensions and their nature. Based on the theoretical conceptual model and the availability of data, we a priori identified observed variables that define the latent variables of innovation (INNO), the budgetary deficit as one of factors of (in)stability of the macroeconomic environment (ME), the rate of unemployment (LMIE), and wages (WAGE). Three of the latent variables are defined by using two observed variables, and one latent variable is defined by three observed variables. The measurement model is presented in Figure 2.

Figure 2. Measurement model.

Source: Authors’.

With the selected observed variables (inno1, inno2, inno3, me1, me2, lmie1, lmie2, wage1, wage2) we tested how well the data fit the model. Testing to what extent the theoretical conceptual model is supported by the obtained sample data can be done using various criteria. For a researcher wanting to determine model fit, this is not an easy task, since several model fit criteria have been developed to assist in interpreting the structural equation model under different assumptions. On top of that, determining model fit in structural equation modelling is not as straightforward as it is in other statistical approaches (Schumacker & Lomax, 2010). Bollen and Long (1993) conclude that there is no such model that would fit all the criteria. Therefore, it is suggested that a researcher includes different criteria, since there is no single solution regarding which model fit criteria is the most appropriate. For model testing in our research we selected those model fit criteria which are most frequently reported in literature in similar studies. The estimation of selected model fit criteria for our measurement model and their critical value is presented in Table 2.

Table 2. Estimation of model fit criteria for measurement model.

Model fit criteria	Critical value	Estimated value of model fit criteria
Chi-squared (χ^2)	>0.05	χ2 = 116.104, df = 46, p = 0.000
Root mean squared error of approximation (RMSEA)	<0.08	0.070
Comparative fit index (CFI)	>0.95	0.981
Tucker-Lewis index (TLI)	>0.95	0.985
Standardized root mean squared residual (SRMR)	<0.08	0.040

Source: Authors’ calculations.

Chi-squared (χ2) criteria compares our model to a saturated model that has no degrees of freedom. Structural equation modelling is trying to reproduce a covariance matrix; it picks the combination of parameter estimates that do the best job in reproducing the covariance matrix. Another model fit criterion is root mean squared error of approximation (RMSEA), which considers how much error there is for each degree of freedom and penalizes the model for unnecessary added complexity. A frequently used structural equation model fit criteria is also the comparative fit index (CFI), which compares our model with the baseline model that assumes there is no relationship among our observed variables. On the one hand, Tucker-Lewis index (TLI) is computed by using baseline comparisons and has the same critical value as CFI. On the other hand, standardized root mean squared residual (SRMR) measures how close we come to reproducing each correlation on average (Acock, 2013). The estimation of model fit criteria for measurement model specifies that four out of five selected model fit criteria indicate good model fit of the measurement model and confirm that the measurement model is appropriate. Therefore, we conclude that our measurement model is appropriate for measuring latent variables and that our measurement model with nine observed and four latent variables as a whole is supported by the obtained sample data.

The reliability of each observed variable can be estimated by applied squared multiple correlation coefficients (R²), a measure of the strength of linear relationships for each observed variable. The R² represents share of with latent variable explained variance in observed variable, while the rest is measurement error. High values of R² indicate high indicator reliability.

R² for indicator variables are presented in Table 3. The most reliable indicator variables are within the latent variables of wages and the rate of unemployment. The lowest R² among the indicator variables is inno1 (0.491), whereas the values of the rest of R² are above 0.790. Based on the values of R², the reliability of observed variables is high or very high, except for inno1.

Table 3. Squared multiple correlation coefficient.

	Squared multiple correlation coefficient
inno1	0.491
inno2	0.946
inno3	0.827
me1	0.790
me2	0.941
lmie1	0.999
lmie2	0.843
wage1	0.996
wage2	0.999

Source: Authors’ calculations.

The reliability of latent (construct) variables can, however, be determined based on construct reliability. Janssens et al. (2008) suggest the following formula to calculate construct reliability: $$\mathit{Construct}\mathrm{}\mathit{reliability}=\mathrm{}\frac{(\sum {\mathit{standardized}\mathrm{}\mathit{coefficients})}^2}{(\sum {\mathit{standardized}\mathrm{}\mathit{coefficients})}^2+\sum \mathit{measurement}\mathrm{}\mathit{errors}}$$

The measurement error is equal to one minus R². The critical value for construct reliability is to be higher than 0.70. The calculated construct reliability is presented in Table 4.

Table 4. Construct reliability.

		Standardized coefficient	Squared multiple correlation coefficient (R^2)	1-squared multiple correlation coefficient	Construct reliability
INNO	inno1	0.700	0.491	0.509	0.900
	inno2	0.972	0.946	0.054
	inno3	0.909	0.827	0.173
	sum	2.581		0.736
	sum^2	6.661
ME	me1	0.888	0.790	0.210	0.928
	me2	0.970	0.941	0.059
	sum	1.858		0.269
	sum^2	3.452
LMIE	lmie1	0.999	0.999	0.001	0.959
	lmie2	0.918	0.843	0.157
	sum	1.917		0.158
	sum^2	3.675
WAGE	wage1	0.998	0.996	0.004	0.999
	wage2	0.999	0.999	0.001
	sum	1.997		0.005
	sum^2	3.988

Source: Authors’ calculations.

Another way to measure the reliability of a latent variable is the variance extracted criterion. This criterion shows which part of the collective variance of the observed variables may be found in the latent variable. In terms of calculations, the formula used here does not differ much from the one used for construct reliability, except that, instead of the square of the sum of the standardized coefficients, it uses the sum of the squares of the standardized coefficients (Janssens et al., 2008): $$\mathit{Variance}\mathrm{}\mathit{extracted}\mathrm{}=\mathrm{}\frac{\sum ({\mathit{standardized}\mathrm{}\mathit{coefficients})}^2}{\sum ({\mathit{standardized}\mathrm{}\mathit{coefficients})}^2+\sum \mathit{measurement}\mathrm{}\mathit{errors}}$$

The critical value for the variance extracted criteria is to be higher than 0.50. The calculated variance extracted criteria are presented in Table 5.

Table 5. Variance extracted.

		Standardized coefficient	Squared multiple correlation coefficient	1-squared multiple correlation coefficient	Variance extracted
INNO	inno1	0.700	0.491	0.509	0.755
	inno2	0.972	0.946	0.054
	inno3	0.909	0.827	0.173
	sum		2.264	0.736
ME	me1	0.888	0.790	0.210	0.866
	me2	0.970	0.941	0.059
	sum		1.731	0.269
LMIE	lmie1	0.999	0.999	0.001	0.921
	lmie2	0.918	0.843	0.157
	sum		1.842	0.158
WAGE	wage1	0.998	0.996	0.004	0.998
	wage2	0.999	0.999	0.001
	sum		1.995	0.005

Source: Authors’ calculations.

Because construct reliability (Table 4) is greater than 0.7 for all latent variables and the variance extracted criteria (Table 5) are greater than 0.5, we conclude that all the observed variables have been measured consistently.

Structural equation modelling also enables a researcher to check convergent and discriminant validity. Convergent validity indicates the degree to which two different observed variables of a latent variable confirm one another. The first condition is that each of the loadings is significant, whereas the second condition is that the correlation between each observed variable and the corresponding latent variable is greater than 0.5 (Table 6).

Table 6. Standardized solution of measurement model.

	Standardized coefficient	p-value
inno1	0.700	0.000
inno2	0.972	0.000
inno3	0.909	0.000
me1	0.888	0.000
me2	0.970	0.000
lmie1	0.999	0.000
lmie2	0.918	0.000
wage1	0.998	0.000
wage2	0.999	0.000

Source: Authors’ calculations.

Based on the standardized solution of measurement model (Table 6), we can conclude that each observed variable loading is significant and greater than 0.50. Since all observed variables in the standardized solution of measurement model are significantly correlated with latent variables, we can confirm convergent validity.

Discriminant validity is achieved when the correlation between latent variables differs significantly from one. To check for discriminant validity, we follow the procedure developed by Fornell and Larcker (1981). Their procedure suggests that for each pair of latent variables, the square of the correlation between these two latent variables should be smaller than their corresponding average variance extracted.

Table 7 presents the mutual variances between the latent variables and can be used to check for discriminant validity. For the element on the diagonal (Table 7), this corresponds to the average variance extracted (Table 5) from the latent variables. The non-diagonal elements are calculated as the square of the correlations between the latent variables. Taking into consideration the values in Table 7, none of the variances is shared by the two latent variables (squared correlation) that is higher than the average variance extracted from these latent variables. The findings indicate discriminant validity for the formed latent variables.

Table 7. Discriminant validity.

	INNO	ME	LMIE	WAGE
INNO	0.755
ME	0.118	0.866
LMIE	0.151	0.269	0.921
WAGE	0.155	0.005	0.016	0.998

Source: Authors’ calculations.

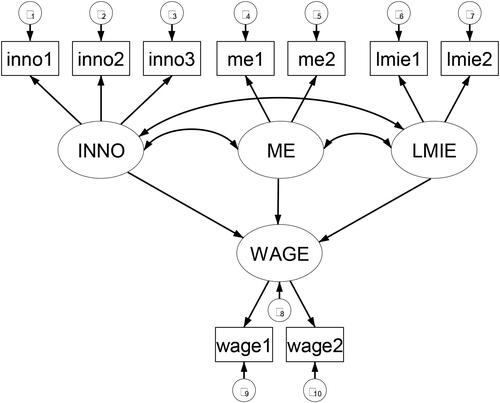
The obtained standardized solution of the measurement model proves to be unidimensional and reliable, and indicates convergent and discriminant validity. Taking into consideration the conclusions made, we continue with the analysis of the structural equation model. In the structural equation model, we allow for different relationships among latent variables. Since we are interested in examining what the driving forces of wages across EU-28 countries are, we hypothesized that innovation, the budgetary deficit as (in)stability of the macroeconomic environment and rate of unemployment predict wages across the EU. We checked the estimated standardized solution for standardized coefficients and their degree of linear relationship, direction and significance. R² of the structural equations model refers to the share of the variance in the endogenous latent variable, which is explained by independent latent variables. The structural equation model estimate was carried out by the maximum likelihood method. We selected different model fit criteria to estimate model fit. Among five selected model fit criteria, four indicate good model fit (χ²=115.743, df = 46, p = 0.000; RMSEA = 0.070; CFI = 0.981; TLI = 0.985; SRMR = 0.042). With a reasonably good model fit, we confirm the structural equation model as a whole. The suggested structural equation model (Figure 3) consists of the exogenous latent variables of innovation (inno), the budgetary deficit and the rate of unemployment (lmie), and the endogenous latent variable of wages (wage), which is predicted by the three exogenous latent variables (inno, me, lmie). The suggested structural equation model is a recursive model.

Figure 3. Structural equation model.

Source: Authors’ calculations.

The standardized solution of the structural equation model is presented in Table 8. Based on the theoretical conceptual model, the relationships between the latent variables presented the foundations for the implied theoretical conceptual model. With structural equation modelling we checked the significance of those relationships. As expected, the strongest significant relationship is the one which depicts the influence of innovation on wages (0.486), which is positive, whereas the influence of the budgetary deficit as a measure of (in)stability of the macroeconomic environment (-0.264) and the rate of unemployment (-0.043) is negative, respectively, and for the latter latent variable the influence is not significant. Statistically significant relationships indicate that the higher the innovation, the higher the wages, and the higher the budgetary deficit and thus possible instability of the macroeconomic environment, the lower the wages. From the obtained results the relationship also indicates that the higher the rate of unemployment, the lower the wages, although this relationship is not significant. Based on the results obtained, we can conclude that innovation is the predominant factor in explaining wages across EU-28 countries and we can therefore confirm the set hypothesis H3.

Table 8. Standardized solution of structural equation model.

	Standardized coefficient	p-value
INNO -> WAGE	0.486	0.000
ME -> WAGE	−0.264	0.000
LMIE -> WAGE	−0.043	0.535
inno1	0.701	0.000
inno2	0.974	0.000
inno3	0.910	0.000
me1	0.889	0.000
me2	0.971	0.000
lmie1	0.999	0.000
lmie2	0.918	0.000
wage1	0.998	0.000
wage2	0.999	0.000

Source: Authors’ calculations.

5. Discussion and implications

Our research has especially addressed simultaneous causality between innovation and wages constrained by budgetary deficit with possible macroeconomic instability and the rates of unemployment in EU-28 countries. It has developed the theoretical conceptual and the tested empirical structural equation model important for business research in more effective manner and for gaining knowledge about the drivers of wages across EU-28 countries, which can improve decision making. The results obtained indicate innovation as the most important driver of wages across EU-28 countries supporting the set H3, while the budgetary deficit with instability of the macroeconomic environment creates downward pressures on wages consistent with the set H1. The negative impact of the rate of unemployment on wages across EU-28 countries was not proven to be significant rejecting the set H2.

European Commission (2019) links the rates of unemployment and other labour market conditions with wage dynamics, while this research did not find significant connection between them. The literature recognizes the motion of labour market connection with the economic and non-economic drivers of wages as the reason why the rate of unemployment variable was included in the structural equation model. Research that looked on the labour market from different perspectives and included rate of unemployment conditions, gained findings that explains the wage changes. In this research the included rate of unemployment variable is not proven to be significant.

Significance between the rise in budgetary deficit as with instability of macroeconomic environment and fall in wages is derivate from the findings in literature discussing the macroeconomic environment and macroeconomic policy tending to affect the economy and wages. The significant negative impact of budgetary deficit on wages was confirmed by our study.

IMF (2018) underlined the lack of analyses that presents innovation as the driver of wages, which could lead to forming more specific policy and managerial solutions and their practical implementation. In this paper it was clearly showed the significant positive link between innovation and wages. The increase in innovation effects the rise in wages through labour productivity and makes it the most significant wage driver.

This striking finding is important for policies and managerial practices with their focus on innovation as a key driver of wages that increase labour productivity that in turn positively effects wages. On the other hand, more satisfied and motivated workers can open windows of opportunities and the possibility for intrapreneurship as an important part of rising the firm’s innovation capacity.

Gaining knowledge about the drivers of wages across EU-28 countries could help policy makers pursue policy measures that accelerate labour productivity growth, in particular those that boost innovation and ensure macroeconomic stability, efficient markets, and a flexible and skilled workforce during increasing global competition. In such a competitive environment, managers are faced with increasingly complex business decisions that determine whether the company will prosper or even survive. In the light of the maximization of firm profit and survival, managerial practices could be linked to the findings and implications which suggest a causal relation between wages and innovation. These practices can increase labour productivity in which wages correspond to the marginal productivity of labour. Adopting such management practices would mean to incentivize employees for efficient and productive work remunerated by wage increases.

6. Conclusion

The developed theoretical conceptual model about the driving forces of wages in EU-28 countries was empirically tested using structural equation modelling during the period 2006-2018. The studied period covers the recession and particularly the post-recession period when there was a modest increase in wages. Among the main driving forces of wages, we hypothesized innovation, the budgetary deficit as possible factor of (in)stability of the macroeconomic environment and the rate of unemployment. The empirical results confirmed that the group of variables concerning innovation was a significant driving factor explaining wage increases. This finding is consistent with IMF (2018) recommendations for better recognition of the link between mentioned variables and on the presence of innovation activities in every economy sector. Innovation driven recovery with strong connection between innovation, labour productivity, and wages could lead to overcoming solution during the economic depression when different types of innovation are needed in different fields of economic and free-time activities.

On the other hand, the group of variables capturing the budgetary deficit with instability of the macroeconomic environment, including the recession period, had a significant negative impact on wages. Both these results are consistent with our theoretical expectations. Global competition creates pressures on prices and revenues, and consequently on wages. A higher value added to markets and wages can be achieved with more innovative products and services and their new varieties. Macroeconomic instabilities with budgetary deficit, particularly during economic recessions, can lead to labour shedding in firms, an increase in unemployment and wage decreases. However, the effect of the group of factors regarding the rate of unemployment was found to be insignificant.

Unlike previous studies that used merely the Phillips and wage curves to determine the drivers of wages, this study adopts a modified research approach based on aggregate macro-level panel data using structural equation modelling. Such an approach allows not only for the observation of bivariate relationships between variables, but also for a more effective simultaneous investigation of multiple equations. Given the paucity of research measuring the impact of the business cycle on wages with different observed variables, these results broaden the field of research and provide insights into the possible integration of the driving forces of wages into empirical models.

The key findings of our research support the policies that are in favour of creating a strong link between wages, innovation and labour productivity. Labour productivity growth can be accelerated by policies that boost innovation and ensure macroeconomic stability, efficient markets, and a flexible and skilled workforce. However, implications are not relevant only for public policy, but also for the managerial practice providing incentives to employees so that more efficient and more productive work is remunerated by wage increases, since there is a mutual causal relation between wages and the driving forces of labour productivity, particularly through innovation.

While the study is limited to EU-28 countries, it can also be relevant to other non-EU-28 OECD countries and emerging market economies. Therefore, the issues for research in the future, along with including some additional groups of macro-economic indicators such as institutional and governance variables, are to extend the data sample on other (groups) of countries and to provide additional comparative analysis. Finally, the recovery from the economic depression situation such as the Corona-19 pandemic learning path enabling environment has induced challenges with new obstacles, but also new opportunities for research focus on its effects on the rate of unemployment and labour market conditions, budgetary deficit and macroeconomic (in)stability, and the role of innovation causing labour productivity and wages.

Disclosure statement

No potential conflict of interest was reported by the authors.