Agency and fidelity in primary teachers’ efforts to develop mathematical resilience

ABSTRACT

Teaching using the principles of mathematical resilience can lead to a broad range of implementations with different emphases, all intended to mitigate the development of mathematical anxiety in learners and its attendant problems. This article considers 12 primary teachers’ responses to the challenge of developing mathematical resilience within their practice. In pairs, these teachers conducted a small-scale study in their classrooms on a chosen aspect of mathematical resilience, supported by termly meetings. The reports made by the participant teachers form the main part of the data. The teachers were inspired to change how they worked with their learners and reported many positive outcomes. The agency which some teachers exercised influenced not only their outworking of the ideas, but also the fidelity with which they adopted the principles underpinning mathematical resilience. The connections and tensions shown here between agency and fidelity have wider implications for successful implementation of similar change efforts.

KEYWORDS:

• Mathematical resilience
• primary teachers
• teachers studying practice
• agency
• fidelity

1. Introduction

There is growing explicit recognition within UK schools of the value of resilience in learning (for example, Claxton 2006; Wosnitza et al. 2018). Resilience can be seen as the capacity of an individual to harness personal and contextual resources to navigate their way through challenges. It is not a stable pre-existing quality of a learner’s personality, but instead something which can be developed to facilitate learning (Knight 2007; McAllister and McKinnon 2009). The growth of resilience is then a dynamic process where personal capacities and learning environments interact over time (Ungar 2012), to enable an individual to experience engagement, commitment, enthusiasm, satisfaction and well-being. The concept of mathematical resilience builds on these understandings as they are especially relevant to learning mathematics (Lee and Johnston-Wilder 2017).

The term ‘mathematical resilience’ is defined as that quality by which some students approach mathematics with confidence in a successful outcome to their effortful work, perseverance in the face of difficulty and a willingness to discuss, reflect and research. The most common experience of young people in mathematics classrooms is a focus on acquisition of skills, solution of routine exercises, preparation for tests and examinations, and a need for speed in calculations (see for example Ofsted 2008, 2012). A wide body of research (for instance Ashcraft and Moore 2009; MA 1999) has further shown that avoidance, anxiety and fear are potent and prevalent features of mathematics learning across many contexts, giving rise to an impedance which can discourage young people from opting to study mathematically rich courses (Johnston-Wilder, Brindley, and Dent 2014) and result in other negative outcomes. Mathematical resilience as a named construct was developed in response to these concerns, although, unlike mathematical anxiety, mathematical resilience is envisioned as ‘a socio-cultural construct which communities can address, not an individual psychological construct’ (Lee and Johnston-Wilder 2017, 278).

Research (see for example Kooken et al. 2016; Lee and Johnston-Wilder 2013; Williams 2014) has established four aspects on which mathematical resilience is based. These are: personal value of mathematics; knowing how to work at mathematics and in particular how to struggle; holding a growth mindset; and being part of a supportive learning community. Further research (for example Johnston-Wilder and Lee 2019) has demonstrated that teaching in ways that encourage the development of these aspects can allow learners to engage with mathematical ideas, even those whose previous mathematical experiences have left them with fear and anxiety. However, despite the growth of interest in this area over the last decade, there is a paucity of research recording and reflecting upon how the relatively broad principle of resilience is ultimately affecting practice across school and classroom contexts.

Here we report on a research study where the principles of mathematical resilience were introduced to a group of teachers by means of a continuing professional development (CPD) course. The study was an exploration of teachers’ views and reported practices as a result of taking part. As such, it considers how those teachers reacted to ideas concerning how to develop mathematical resilience within their learners. The design of the CPD was resonant with the growing base of evidence describing how such programmes can be more potent and effective (summarised in Cordingley et al. 2015). For instance, research indicates the effectiveness of CPD that involves extended interventions (4) and courses which integrate opportunities for ‘peer learning and support’ (5). The method of the course also recognised the argument that CPD should integrate opportunity for action and observation; writers such as Guskey (2002) consider that implementation often precedes change in teachers’ beliefs and professional practice: ‘change is primarily an experientially based learning process for teachers. Practices that are found to work … are retained and repeated. Those that do not work or yield no tangible evidence of success are generally abandoned’ (Guskey 2002, 384).

The CPD took place over one school year with the first author taking the dual role of course facilitator and researcher. The cohort consisted of pairs of teachers from primary and secondary schools who volunteered to take part in four late afternoon sessions of about three hours each, spread throughout the academic year. Here only the data from primary school participants is considered.

In session one, the first author shared some ideas about mathematical resilience with the group, which are outlined in section three of this article. She then supported each pair of teachers as they planned a small-scale action research project which they committed to undertake during the rest of the academic year. The teachers were free to design their own project, cognisant of their own context and limitations. Sessions two and three were managed to facilitate the review of, reflection on and re-planning of aspects of these projects, supporting clear action research cycles (McNiff 2017). In these sessions the teachers had time to report back on what they had done, reflect on what they had found as they worked with the ideas of mathematical resilience, and to ask questions or raise issues. These were responded to mainly by the rest of the cohort, with the first author adding to their answers or questioning ideas further only if she were questioned directly or felt it appropriate or necessary. The teacher pairs were also encouraged to think about what they intended to do next in order to continue to develop mathematical resilience in their schools. The last session allowed the teachers time to write a report on their project.

The accounts and thematic analysis herein together relate how the primary teachers reported their responses to the ideas incorporated in the programme, how they made efforts to change their practice, and the factors within their diverse school environments which supported or frustrated their efforts.

2. Agency and fidelity in teacher practices and change efforts

In some of the following accounts, the teachers communicate that they were able to exercise substantial agency within their professional practice, but in a number of schools certain factors seem to inhibit teachers’ ability, or possibly their desire, to exercise agency. Analysis of the data also reveals some tension between agency, the extent to which the teachers are able in their own contexts to select, develop and deploy ideas as part of their change effort, and the enacted fidelity, the extent to which the teachers implement ideas as promoted on the course.

We consider that teacher agency emerges from a complex interplay of teacher capacity and school conditions, rooted in teachers’ past experiences, their ability to envisage multiple future possibilities and their willingness to take action in the here and now (Priestly, Biesta, and Robinson 2015). Teachers whose past has conditioned them to see a future encompassing the ideas promoted by a CPD offering and who are willing to take action also need school conditions which allow the exercise of that agency. Fidelity is likewise understood (see for example McCuaig and Hay 2014) to refer to the degree to which a programme is implemented as envisioned by the promoters of the ideas.

Teachers have a complex and reciprocal relationship between their beliefs and practices, which develop together and influence each other (Beswick 2005). The meanings teachers attach to an innovation form the basis of their reactions to the innovation; for instance, Handal and Herrington (2003) make the case that curriculum reform in mathematics is heavily steered by the beliefs that teachers hold about both mathematics and the worth of the innovation itself. Further, ‘[i]t is important to recognize that no new program or innovation will be implemented uniformly. Teaching and learning are influenced by a multitude of situational and contextual variables’ (Guskey 2002, 387).

Such an interplay of beliefs, practice and context clearly influenced how the teachers implemented the ideas; those that believed that the ideas promoted by the CPD would be beneficial to their students rapidly implemented the ideas in their practice. Other teachers saw the practices implemented by other participants, and through implementing the ideas themselves came to believe the ideas worked. However, these interactions were predicated on the participants having sufficient agency.

An explanatory framework of this experience is offered by Valsiner (1997). Valsiner’s zone theory, when applied to teacher development, construes a teachers’ zone of proximal development (ZPD) (after Vygotsky 1978) as a set of possibilities for development of new knowledge, beliefs, goals and practices. This ZPD is created by the teacher’s interaction with the environment, the people in it and the resources it offers. Inside the ZPD the teacher has a zone of free movement (ZFM) within their professional context, which Goos (2013) considers to encompass the students, their background and prior learning; the resources that can be accessed; the curriculum and assessment system within which they work; organisational structures, such as grouping of students; and importantly organisational cultures, influencing what is accepted as ‘good’ teaching. Thus the ZFM indicates which teaching actions are permitted.

Valsiner (1997) suggests a third zone, the zone of promoted action (ZPA), which in this case would contain the offered activities designed to promote teaching for mathematical resilience. The interaction of the ZFM and ZPA, or at least each participant’s beliefs regarding their intersection, can be used to frame the tensions that exist between teachers’ fidelity to the promoted action and their agency to enact those practices in their teaching.

3. The construct of mathematical resilience

The CPD programme presented the idea of mathematical resilience, as articulated by Lee and Johnston-Wilder (2017). Approaches to teaching for mathematical resilience include, but are not limited to, encouraging learners to adopt a growth mindset (Boaler 2016; Dweck 2000), extending their appreciation of the personal value of mathematics and of their value within the community of learners, inculcating in learners a knowledge of how to work successfully at learning mathematics, and explicitly modelling how they can find support in order to stay in the ‘growth zone’ (Johnston-Wilder et al. 2013). These four aspects are envisioned as principles that can be adopted by teachers and learners to address negative emotional states which are known to exist in response to some common approaches to teaching mathematics (for example, Hernandez-Martinez and Williams 2013) and thus challenge the associated deleterious cognitive consequences. Each aspect will now be outlined briefly in turn, in a similar way to which they were presented within the CPD programme.

Growth mindset

The principle of adopting a growth mindset requires a consideration of what a learning environment conveys to the students within it. In order to develop mathematical resilience, learners must work within an environment that expects and supports everyone to succeed and within which learning efforts when made result in progress and success. Such an environment is likely to engender an incremental or growth mindset (Yeager and Dweck 2012).

The value of mathematics

Mathematical thinking is used extensively within society (see for example Hoyles, Noss, and Pozzi 1998; Roberts 2002), but these ways are not always visible to school-age learners; for example, cash tills tell the shop assistant what change to give, hiding the calculation involved. Mathematics can be likened to a chameleon (Lee and Johnston-Wilder 2013) hiding in plain sight, and thus it is imperative that the teacher makes clear where and how mathematics is of value to the student. This further involves inviting the student to feel included in those who understand and use mathematics, and it is in that sense that demonstrating value develops mathematical resilience.

How to work at learning mathematics

Improving the students’ knowledge of how to work successfully at learning mathematics requires making plain that learning mathematics requires effort, perseverance and struggle. Path smoothing has often been teachers’ default position (Stigler and Hiebert 2009; Wigley 1992), resulting in students who feel they ‘can’t do it’ when faced with a mathematical situation that cannot be immediately answered. Encouraging children to understand that getting stuck (Mason 1999) and struggling towards a solution are intrinsic parts of learning and using mathematics are therefore important mechanisms for embedding this principle. Part of becoming a resilient mathematical learner is knowing what to do and when and how to seek support when stuck or when the struggle seems too great.

Finding the right support

Offering the optimal degree of challenge is therefore also part of developing mathematical resilience. However, struggle without appropriate support leads to counter-productive anxiety. Teaching for resilience requires ensuring learners know that everyone needs appropriate support in order to learn effectively, but also that what is appropriate differs with the individual and the situation. Lee and Johnston-Wilder (2013) reported that students often did not know how to access support; when ‘stuck’ in mathematics, they felt they had to wait for the teacher. Teaching for mathematical resilience means teachers should aim to be explicit about everyone’s need for support and how and where students can access the support that is appropriate for them.

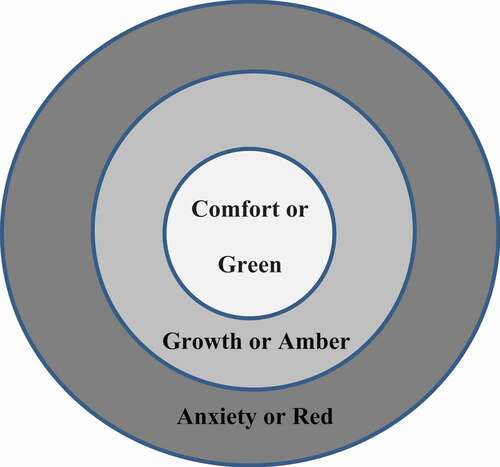
The ‘Growth Zone Model’ (Johnston-Wilder et al. 2013) (Figure 1) was shared with the cohort as a mechanism to stimulate articulation of both the need for the optimal amount of challenge and for appropriate support. In the comfort zone, ideas may be consolidated and confidence built, but no major learning takes place. For effective learning students move into the growth zone, which can feel risky as they move from comfort to uncertainty, but learning requires these somewhat uncomfortable feelings. When the student receives or recruits support sufficient to manage these feelings, they can stay in the growth zone. However, if the challenge is too much or the support insufficient, they may go into the anxiety zone. In the anxiety zone, thinking becomes impossible as the freeze, fight or flight instinct is activated. It may be entering the anxiety zone too often or for too long which causes avoidance and anxiety when faced with mathematics, as reported by Ashcraft and Moore (2009).

Figure 1. The Growth Zone Model.

The mathematical resilience concept was operationalised for CPD purposes as a set of guiding principles which could be exemplified through offered approaches and examples of good practice but was not dependent on or limited to any specific method or resource.

4. Research questions and methodology

The design of the programme has been outlined above. Here the focus will be on the research questions, the nature of the data and how that data was analysed. There will also be a review of ethical considerations and potential sources of bias.

The content and setting of the CPD programme allowed for two central research questions:

• a. How do the ideas of mathematical resilience inform the practice of teachers?

• b. Is mathematical resilience as a construct viewed as effective/useful by teachers of mathematics? Are there barriers to fidelity in the implementation of the principles of mathematical resilience?

Both research questions were predicated on the understanding that teachers are central actors in driving, establishing and resisting change in the classroom.

Considering this, it was determined that the analysis of this data should recognise three main aspects of the teachers’ change efforts, specifically: how the teachers were using the ideas generated through the programme; the teachers’ own reactions and responses to change; and the fidelity of their implementation to the principles of mathematical resilience.

Six primary schools chose to participate in the CPD programme. (The schools were given pseudonyms prior to any analysis, and these are given in Table 1 along with the short forms adopted in the following sections.) Each school sent two teachers, resulting in an initial group of 12 teachers. Of these schools, four completed their final report, Ancastle (An) did not attend the final session due to personnel changes in the school, and the sixth, Riverbank (Ri), only attended the first two sessions. Consequently, we have only limited data for Ri, and they are not included in the analysis shown in Table 1. Ancastle submitted a PowerPoint at the third session giving a more extensive data base for analysis.

Table 1. Themes applying to RQ1 ‘How do the ideas of mathematical resilience inform the practice of teachers?’

	Ancastle (An)	Footacres (Fo)	St Agatha (StA)	Twistmile (Tw)	Viaduct (Vi)
Prominent use of visual metaphor (growth zone/learning pit)		✓	✓	✓	✓
Use of specific phrase or mnemonic	✓			✓	✓
Developing agency of students as learners	✓		✓	✓	✓
Increased emphasis on growth mindset	✓		✓	✓	✓
Recognition of the potential value of mistakes	✓			✓
Changes in types of activity			✓
Changes to routine practice in grouping					✓
Changes to routine practice in differentiation			✓	✓	✓
Changes in resources used during mathematics lessons	✓	✓	✓

This article draws on several data sources. The principal source is the unmodified versions of the reports, averaging just less than 2000 words, submitted by the teachers after they had reflected on what they had written at the fourth meeting. The teachers wrote their own reports, but they were supported by a template agreed between them during the meeting and were also able to request help from the first author or others in the cohort if they felt it was needed. After this final session, the teachers were asked to consider and edit what they had written and to submit their reports to the first author within two weeks.

This data set is supplemented by the plans made by the teachers in the first session and the field notes taken by the researcher during the second and third sessions when the teachers were reporting on their projects and discussing the issues which had arisen. These plans, notes and a PowerPoint presentation submitted by participants from a school (An) who did not attend the final session offer data on the two schools who did not submit a final report. All of this data was used during the analysis process.

Coding and analysis

After the final meeting in June 2016, the report, plans and field note data were collated and analysed using thematic analysis (Braun and Clarke 2006). The authors deployed a dual and complementary approach to coding. The first author analysed the data inductively, dividing the data into short units of meaning and coding without trying to fit them into a pre-existing frame of reference, and then identifying themes and patterns primarily from the data. Conversely, the second author performed a theoretical thematic analysis (Braun and Clarke 2006), working deductively by looking for evidence of themes in the data which mapped more explicitly onto the mathematical resilience framework and then coding appropriately. The researchers compared their findings and agreed upon and named categories which were mutually supported by both analyses. It was intended that this parallel approach would allow for a rich description of the teachers’ responses that was data driven. It was also considered that a dual coding of the data by the two researchers, approaching the data in different ways, would support the reliability of the analysis.

The themes resulting from the analysis considering the first research question ‘How do the ideas of mathematical resilience inform the practice of teachers?’ are given in Table 1, which also shows the schools whose data fell into these themes.

Reliability and sources of bias

The form of the data demands a clear acknowledgement of the multiple sources of potential bias contained therein. The participants were all self-selecting; they attended the course voluntarily because they saw it as something that matched with either their own or their school’s trajectory in development of practice. The teachers were also self-reporting, and as they had invested practical and emotional resources in the innovation, it was to be expected that the participants would report positive accounts of their efforts. Each report was compiled by a different pair of teachers, and despite the provision of a template, each elected to submit their report in the form they considered appropriate. Finally, the combined data set does not equally capture the efforts of teachers who did not submit a final report, and so might underrepresent the elements which prevent teachers from implementing the innovation. Although these concerns cannot be fully discharged, the research questions are not about the efficacy of the innovation as that cannot be ascertained from this data set, but concern how the teachers reported that they used the ideas to inform their practice. The reporting and discussion in this article recognise the problem of positive bias in both the selection and reporting of the data, and the analysis was conducted in a way that sought commonalities in meaning despite differences in structure and emphasis.

The researchers also acknowledge their own potential prejudice towards positive outcomes. The first author had previously argued that working for mathematical resilience would have affirmative outcomes for students (for instance, Lee and Johnston-Wilder 2014, 2017) and was expecting positive reactions. Notwithstanding, the second author does provide some counterbalance, having had less direct history with the ideas and no contact with the participants.

Ethical measures

The teachers were made aware at the first meeting that the author was collecting research data and were asked to give informed consent for their data to be used. It was also made clear, both in the first instance and at subsequent meetings, that if any teachers did not wish their data to be used then it would simply be deleted from the record, but that they would remain part of the course and would continue to be treated in the same way as everyone else. All data reported here was promptly anonymised so that the schools were not immediately identifiable.

Researcher as participant observer

The first author took on the dual roles of course facilitator and researcher. There was some tension between the two roles as the participants knew that the ideas they were exploring had been developed by that author. It was emphasised that the research was about exploring teachers’ reactions to the ideas in the complex realities of school life. There were two methodological aspects that attempted to ensure that the data emanated from the teachers. The first was the author adopting a more passive role following the first meeting, taking notes but letting the teachers steer the conversation and advise one another, unless the participants asked a direct question (Merriam 1998). The second was that any data analysis was only started once the course was complete and the reports submitted, limiting any unconscious steering in discussions.

5. The findings

The analysis of the four accounts, the initial plans made, the PowerPoint submitted by An and supporting field notes are summarised below in two sections, following the research questions.

How do the ideas of mathematical resilience inform the practice of teachers?

Prominent use of visual metaphor

Four schools reported explicitly making use of a visual metaphor in the ways that they chose to implement the principles of mathematical resilience. The teachers at Tw had previously come across the idea of a ‘learning pit’ (Nottingham 2007), which they felt expressed the mathematical resilience idea of needing to ‘struggle’ when learning mathematics in a student-friendly manner. At StA they adopted the image of the growth zone model, thoughtfully combining it with the 6 ‘R’s of Claxton’s learning power model (Claxton 2006), which they had already been using. Vi used a clock stamp that they already had to stamp a visual image in each learner’s book. Their learners were asked to colour in their clock face intermittently during each lesson in order to indicate whether they felt comfortable or were in the growth zone or felt anxious at that time. This gave the teachers the opportunity to discuss with those they saw using a red crayon whether extra help was needed and how that might be accessed or provided. They could also talk to any learners using a green crayon about whether extra challenge might be needed, or whether they needed time in the comfort zone to consolidate their work.

After the third meeting, the teachers at Fo also introduced the growth zone model to their classes, almost certainly as a result of the positive reports from Tw and StA. The teachers remarked in their account on the positive effects of the growth zone model, saying: ‘The Learning Zones also help children to understand the importance of setting high expectations for their own learning ensuring they are sufficiently challenged in every lesson, i.e. not working within the “comfort zone” for long periods.’

At the third meeting An showed a ‘power to learn board’, which provided ideas for the students about how to access help if they needed it. The children used the board as a first strategy when stuck.

Use of a specific phrase or mnemonic

Teachers at three schools made use of a phrase or mnemonic to frame the ideas of mathematical resilience. For example, Vi teachers allowed students to choose their level of challenge, and these choices were labelled using the metaphor of chilli peppers: ‘mild, spicy or extreme’, and Tw teachers exemplified their commitment to ‘learning involving challenge’ by labelling their three levels of challenge ‘tough, tougher and toughest’. These phrases became a routine pattern and a student-focused outworking of the innovation.

Developing the agency of students as learners

One of the ideas from mathematical resilience that each school took up was encouraging their students to become more proactive in their learning, to challenge themselves and to seek appropriate help when they needed it. Many of the schools invited their learners to choose the level of challenge they felt comfortable with rather than imposing challenge on them. The learners were also offered a choice of ways to receive support, so that they were able to choose what was appropriate for them. The teachers at Tw invited their students to become partners in changing the way they worked at mathematics:

The children were actively encouraged to not just challenge themselves, but us, as their teachers. If they felt the work was too easy and they were flying over the pit in their ‘hot air balloon’ then they needed to prove to us that it was not challenging enough and demand a harder task. This was quite an eye opener for children and adults alike. At first, the children would say that it was too easy when in fact, they hadn’t quite understood the task and their work was too hard! However, once the concept had been embedded into the classroom, the children felt quite at ease to come to us and inform us that they had understood the task and they wanted something harder. A year ago, this would not have happened. (Tw)

Increased emphasis on growth mindset

Each participating school emphasised the idea of growth mindset. For example, the teachers at StA felt they had to talk to all the adults in the school and remind them that the school believed in a growth mindset, that everyone could learn with the right support and determination. Talk about mathematics ‘not being for me’ was banned. There were growth zone model posters displayed at An, and at Tw there was talk of finding the way out of the pit, which everyone could do with the right support.

Recognition of the potential value of mistakes

The idea of learning mathematics needing a willingness to struggle was emphasised by all the reporting schools in terms of the need for learners to challenge themselves and not be content to stay in their comfort zone. However, only two reported emphasising the value of making mistakes. At An, they decided to help their learners to see mistakes as part of learning and to learn from them. Any mistakes were marked in pink so that the learners could look back and try to learn from, but not repeat, their mistakes.

Tw used ‘mistake of the day’. At the end of each lesson, the learners were asked to talk about any mistakes that they had made so that other learners could learn from these mistakes. One error was then awarded ‘mistake of the day’.

Changes in types of activity

The teachers at An reported at the second meeting that they had decided to give their learners a set of problems and ask them to ‘play’ with equipment that the teachers provided in order to ‘prove’ their answers. This was consequent from their interpretation of how to enable their students to know how to work at or struggle with mathematics. However, they did not continue as ‘they felt they were causing upset – the children could not figure out what they were supposed to do’.

StA changed the activities they offered to their learners, incorporating problem-solving tasks so that their learners could challenge themselves. This also meant they needed to ensure their learners could access appropriate support. They had already introduced ‘talk partners’ in mathematics. However, as a result of the project prompting their thinking about helping their students know how to work at mathematics, they realised that their students considered ‘getting the right answer’ as paramount, and therefore, when help was sought, the learners thought giving the answer was most helpful. One of the teachers devised a series of scenarios to help students discuss how to give the help and support that would result in others experiencing feelings of successfully overcoming a challenge. The children used the ideas of the growth zone to articulate that ‘giving the answer’ prevented the other going into their ‘growth zone’. The teachers concluded that they continually needed to include the students in a quest to find a good question to ask or words to say to support thinking, so that they had ways to offer support to someone else and enable the other to stay in their growth zone.

Changes to routine practice in grouping

The teachers at Vi reported that they now planned and taught the same content to the whole class, offering differentiation through varying levels of support and a range of activities, and focusing less on distinct levels. The teachers stated they are now less likely to put a ceiling on the students’ learning. Their students no longer sit in groups decided by their attainment and choose instead the way that they want to continue to learn: alone, with a partner, in a group or on the table where the teacher is available to help. If a student wants to join the teacher’s table, they are required to explain exactly why. The teachers require more than ‘I don’t get it’, because they often find that asking the learners to explain exactly ‘what they don’t understand’ enables the learner to understand. The teachers reported their assessment of the impact of the innovation:

We very quickly noticed a change in the atmosphere of our maths lessons. Because the children are now sitting in mixed attainment groups, there seems to be more animated discussion all around the room, rather than it being focused on one or two tables … we have found that children who wouldn’t historically be involved are now putting their hands up and joining in. One hypothesis for this is that they feel more confident now because other children on their table are answering questions, which didn’t happen before. (Vi)

Changes to routine practice in differentiation

Differentiation practices changed in each of the reporting schools. By increasing the agency of their learners, teachers increased the learners’ ability to differentiate the work they completed, so that they were challenged and learning but not made to feel ‘out of their depth’ or anxious. The established learning environment at Tw meant that the changes instigated by the participating teachers would mean changes in customary practice.

Our school is a three-form entry school and has, over the years, had a culture of differentiating not just by classes but also by table. The new concept of Growth Mindset eradicated the need to differentiate by table to encourage challenge for all. This shift in culture was probably the biggest issue for our teachers … During a staff training session to roll the concept out to the whole school, this became the sticking point amongst many colleagues. (Tw)

Changes in resources used during mathematics lessons

The teachers at Fo construed the ideas of mathematical resilience in a very specific way. They established ‘focus groups’ of children from two different age bands, and worked at encouraging students to use concrete resources to support their problem solving in mathematics:

The use of concrete resources doesn’t always guarantee that children will persevere when solving a problem but their resilience can be improved through the use of positive verbal encouragement … [Older primary age] children were often reluctant to use concrete resources as they had a fixed mindset which focused on concrete resources being used by children who are ‘struggling’. (Fo)

Is mathematical resilience as a construct viewed as effective/useful by teachers of mathematics? Are there barriers to fidelity in the implementation of the principles of mathematical resilience?

The ideas of mathematical resilience informed practice selectively at schools where their reports suggest that the teachers were situated to exercise high degrees of agency. The teachers reported that they found the principles of mathematical resilience both useful and effective in making positive changes in their practice. Although there were marked differences in implementation in these schools, each reported that they exhibited a good level of fidelity to the principles of mathematical resilience and viewed it as an effective and useful construct.

Learner perseverance improved

The ideas of mathematical resilience were reported to positively address pre-existing specific student-focused concerns by most of the schools. Schools said, for example, that mathematical resilience positively addressed their concerns that ‘many of our cohort were struggling in the application of certain areas of maths’ (Tw) or that ‘the children seemed to find it all too easy to give up, despite us giving them strategies to cope with being stuck’ (Vi). These schools reported that the pupils’ perseverance improved following the use of the principles of mathematical resilience.

Inclusive practices introduced

Mathematical resilience principles promote inclusion, which was considered important by, for example, the teachers at Vi, who reported:

On our planning, we also highlight key questions and think of ways to phrase them openly to encourage discussion. We use phrases such as ‘What might happen if … ?’ and ‘How can we find out?’ We feel it is important to use ‘we’ rather than ‘you’ to engender a more collaborative classroom where we, as teachers, are part of that collaboration; to give the children the belief that we are finding out with them, that we are in this together.

Speedy dissemination

A further positive commonality in the way the teachers reacted to the ideas of mathematical resilience was the speed with which the rest of each school became interested in the ideas and the teachers’ interventions. Although the teachers at Tw had expected to pilot their ideas for some time, they found that successful innovation can spread organically:

it became apparent that many other members of our teams were interested in this project as they were beginning to see the impact this had on the classes who had started this new approach to learning. Many teachers started to allow their children to self-differentiate and were surprised and thrilled with the results of their children.

A similar comment was offered by StA:

There has been significant interest from other teachers in the school who have enjoyed hearing about the success of this project, and we plan to roll out the Growth Zone Model to all classes throughout next year … We feel that the project has had a significant positive impact on the resilience of our older children and look forward to reaping the benefits in other year groups in the future.

A positive ethos

The ethos in the classroom was said to be improved by using the principles of mathematical resilience. For example, the teachers at Vi stated:

we have found that the children’s relationship with their maths learning has changed. On the whole, the children are more positive, the atmosphere in the classrooms is more positive, more vibrant. During maths lessons, the conversations being had in the classes are supportive. The children are making conjectures and proving their theories. They refer to previous learning and use a myriad of strategies to support each other from resources, to previous learning, to other peers, to adults.

Barriers to implementation

However, some schools were less successful in deploying the ideas of mathematical resilience effectively. The data contained some examples of teacher innovations which came up against barriers specific to that school context. For example, the teachers at An started an attempt to improve their children’s knowledge of how to work at mathematics by challenging them to prove mathematical ideas using manipulables. Offering challenge so that their pupils might appreciate the role that struggle can play in developing mathematical understanding was faithful to the principles of mathematical resilience. However, it seems they did not balance the challenge with helping their children know how to obtain appropriate support and found that their children became upset. Following discussions in the second meeting, they moved onto the idea of offering the children a choice of work or ‘challenge’, and this proved more successful. They had the agency to implement discrete ideas informed by the meetings but showed no consistency in the use of mathematical resilience principles in the classroom.

One enthusiastic pair of teachers at Vi were concerned that they would not be able to implement the principles of mathematical resilience across their school due to the attitudes of some other members of staff. They reported: ‘there are still members of staff who set for maths. This is something that I would like to discourage as I believe that it encourages a ceiling on the learning and is detrimental.’

The account of a further school, Ri, demonstrates the need for teacher agency if the principles of mathematical resilience are to make a difference to the way that learners experience mathematics. The senior leadership at Ri were committed to the integration of an idea they called Orchestrated Learning. The teachers at Ri stated that they tried and failed to amalgamate the principles of mathematical resilience with the change effort mandated in their school: ‘there are issues about working in ways that develop resilience within a very structured school system’.

It seems that they wanted to use the principles with fidelity but felt that they were not given sufficient agency to do so; there was limited intersection between the ZFM and ZPA. Where the individuals reported themselves as having agency, such as at Vi or StA, they reflected on how the mathematical resilience complemented or otherwise other ideas being used in their school and maintained a flexibility in how the innovations were implemented.

6. Discussion

In almost all of the primary schools who took part in the project, mathematical resilience ideas informed a re-thinking of the way that the teachers established the learning environment for mathematics. The context of each school determined which element(s) teachers were attracted to, how they embedded them in practice and what the reported effects were. Nonetheless, there were similarities between schools in the choice of ideas to be implemented, which was an anticipated outcome of the design of the CPD.

In several cases, the success of the project led to an organic outgrowth which had the potential to lead on to further development. Most of the schools who displayed significant fidelity in implementation discussed how, as soon as they started to apply the ideas and get results, other teachers in their school became interested or willing to hear about and adopt the same ideas. Teachers from Tw, Vi and StA saw a growth of resilience markers such as a willingness to continue with problem solving despite setbacks in their own students and quickly began to talk about the ideas with others in their school. Although the teachers’ accounts do not present this process as unproblematic, for example Vi reported having to deal with colleagues with reservations, many of the schools seemed open to innovation.

Valsiner’s (1997) concept of a teacher’s ZFM can be used to frame both the successes and difficulties experienced by the teachers when sharing ideas with colleagues. What a teacher feels permitted to do in their classroom will naturally be influenced by what they see their colleagues doing,and how successful those practices are considered by others; this was seen in StA and Tw where word of mouth influenced the synchronisation of teachers’ ZFM and the steering practices of the school, in line with the sociocultural nature of the zone constructs. Conversely, yet possibly at the same time, a ‘sticking point’ such as that experienced by Tw may have arisen because of differences amongst teachers’ ZFM. Through participation in the project, the teachers developed a perception of what was permitted that was different to that of their colleagues; by appealing to either the evidence of their own success or the authority implicit in the CPD they felt more able to question and challenge established classroom culture. In this way, teachers’ understandings of their professional agency might not only serve to influence their own actions but could also determine the potential for disseminating good practice and innovation throughout their school. It can be conjectured from analysis of the reports offered that a necessary condition for the success of such innovations is that the school context allows teachers the agency to make meaningful changes to at least some elements of routine practice. Such a conclusion would further be supported by Ri, where the change efforts were not successful.

The accounts and summary above might also be taken to imply that there is some association between the success of the change efforts and the degree of fidelity evidenced to the concept of mathematical resilience. In cases where there was a greater degree of fidelity in implementation, the actions of the teachers seemed to lead to successful changes in the environment and discourse of the school. Examples of changes that seemed to exemplify the ideas of mathematical resilience with fidelity were:

• the move away from setting according to attainment in Tw, Vi and StA, producing an inclusive learning environment where much was expected from everyone;

• the work done by StA to ensure that when support was given by peers it was given appropriately and with thought; and

• the change in the way that mathematics discourse was engendered in Tw.

There were schools who evidenced barriers to implementation such as:

• a piecemeal implementation without seeing the principles of mathematical resilience as a whole;

• a determination to continue to use established ideas such as setting;

• a lack of agency allowed to the teachers.

The change effort within this project was designed to challenge teachers’ beliefs and shape their pedagogical knowledge so that they could effectively implement teaching practices designed to allow mathematical resilience to develop within their pupils. Despite many of the teachers gaining knowledge and reconsidering their beliefs, the new teaching practices promoted were in some cases deemed not feasible to implement within their school environments. The analysis here supports Goos’s (2013)assertion that the design of educational change projects should take into account person–environment relationships and how these might constrain (but not fully determine) teachers’ pathways of development.

Successful implementation of change efforts in these accounts therefore appears to hinge on the presence of two key features being present in context. First, individual teachers who are reflective practitioners, willing to consider how the ideas fit in with their school practice and keen to deploy the innovation, and second a school environment which awards agency, or a sufficiently broad ZFM, to those making the change efforts and enough flexibility to allow for a more extensive or considered application of the ideas.

7. Conclusion

Although the biases and limitations inherent in this data limit generalisation, the commonalities and resonances do suggest factors which might support teachers’ change efforts and strengthen future CPD delivery in mathematics education.

The data supports the conclusions of the extant literature by suggesting many ways in which the organisation of the course supported teachers in changing their practice in aspects that showed significant fidelity to the principles of mathematical resilience. For instance, the structure of the course allowed teachers to think through the ideas of mathematical resilience in order to be able to apply them in context. Asking the teachers to work in pairs, and to explore the ideas using a small-scale study, encouraged this process in a way that a pre-determined package of the innovation would not have. This resonates with the finding of Cordingley et al. (2015) that successful programmes ‘helped teachers translate the new practice into their own classroom contexts’ (12).

The course was also set up so that the teachers could both support and influence one another. As the meetings progressed, the teachers asked questions of one another and looked with interest at any artefacts that their co-participants brought to meetings, such as photos of their display boards or their learners’ responses. That many teachers used similar ways to explain resilient working to their learners appears to confirm this pooling of ideas. The form of the course allowed for and supported this extended discussion of issues, trying out ideas and reflection which is again consonant with the conclusions of Cordingley et al. (2015) and Guskey (2002), recognising and supporting teachers as they worked within the intricacies of their situational variables.

Fidelity and agency are both constructive characteristics which may be associated with successful change efforts in education, but there can be a tension between them. In extremis, if a course facilitator presents the outworking of a concept as a set of unassailable, immutable practices, they ensure fidelity but deny agency. This is unlikely to lead to successful innovation, as teachers are unable to respond to the particular needs of their context, especially in cases where there is little intersection between what is being espoused by a CPD facilitator (ZPA) and what is practicable in a specific school context (ZFM). It could likewise be argued that an unquestioning expectation of fidelity is both naïve and limiting. Intersubjectivity is at the heart of teaching as an activity, and it might further be argued that there is a tradition of adaptation within British teaching (Swan 2014). Looking purely at fidelity as a measure of the success of an innovation fails to recognise the complexity of schools and thus the conditions under which teachers must act. The realisation of ideas should encompass a number of pedagogical modifications as teachers act as agentic participants.

Conversely, as agency overtakes fidelity an innovation risks becoming divorced from its intended goals and the associated evidence base. Pertinent questions for future research would therefore be how best to model this tension between fidelity and agency, how it might be best navigated by course facilitators, and finally how, when and by whom an innovative concept should be operationalised. Such research might involve or inform the use of other contemporary educational innovations, such as assessment for learning or mathematics mastery.

The accounts of these teachers are encouraging inasmuch as they repeatedly present invested teachers, striving to improve their own practice and affect student outcomes. The construct of mathematical resilience was seen as valuable by these teachers, and they have shown how it can be operationalised with positive effect on learners in primary classrooms.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Notes on contributors

Clare Lee

Clare Lee is a Senior Lecturer for The Open University teaching on the Masters in Education and Postgraduate Certificate of Education. She also creates open learn courses on education, research, and teaching and assessing mathematics. Her research focuses on how teachers act in the classroom, with a particular focus on teachers of mathematics and the development of mathematical resilience in all learners from young people in school to adult learners.

Robert Ward-Penny

Robert Ward-Penny received his PhD in Education from the University of Warwick in 2013 and is currently working as a mathematics teacher at an international school in the USA. His interests include cross-curricular teaching and learning, and the relationship between philosophy and practice in mathematics education.