A new angle: a teacher’s transformation of mathematics teaching practice and engagement in quantitative reasoning

ABSTRACT

We present a case study of an elementary teacher, Jen, who transformed her mathematics teaching practice and deepened her conception of angle measure. Employing Teacher Development Experiment methodology, rooted in a constructivist perspective of learning, we analysed sets of pre/post interviews and classroom observations, for two lessons on angle measure, occurring one year apart. In between, Jen participated in a year-long, school-wide professional development intervention, to support teachers’ enactment of conceptual mathematics instruction and foster students’ multiplicative and fractional reasoning. Jen transformed her vision and rationale for teaching mathematics, her interpretations of students’ mathematical knowing, and her view of what constitutes evidence of mathematical learning. In conjunction, she deepened her knowledge of angle measure, engaging in quantitative reasoning and conceptualising angles as quantities. We discuss implications for supporting teachers to transform their mathematics teaching practice via fostering shifts in their goals for instruction and growth in their mathematical understanding.

KEYWORDS:

• Teaching and learning
• quantitative reasoning
• geometry

Teachers’ goals for instruction, whether tacit or explicit, impact students’ opportunities to learn. One broad goal that teachers can have is to promote students’ conceptual learning, so students may conceptualise mathematics beyond just explaining their thinking when executing a procedure to find an answer. Employing Teacher Development Experiment methodology (Simon, 2000), a specialised form of case study rooted in constructivist theory, we report a case of an early-career elementary teacher, Jen, who transformed her elementary mathematics teaching practice to promote students’ conceptual learning of angle measure. We illustrate how changes in a teacher’s practice intertwined with shifts in her instructional goals and deepening of her mathematical knowledge.

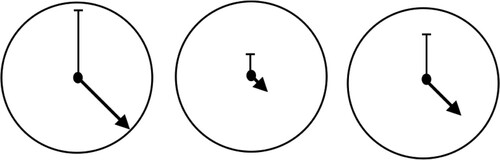
Consider a lesson to introduce students to angle measure. One teacher’s goal can be for students to find amounts of degrees for given angles. Another teacher’s goal can be for students to conceive of an angle as a measure of a rotation, or “turn” (Clements & Burns, 2000; Clements, Battista, Sarama, & Swaminathan, 1996; Tzur & Clark, 2006). A teacher with the former goal may have students determine measures of unknown angles, then explain how they found those measures (e.g. “I subtracted 22 from 90 to find 68 degrees”). A teacher with the latter goal may have students engage in activity, through which they can come to understand angle via reflecting on the results of their activity (e.g. Simon & Tzur, 2004). For instance, a teacher may engage students in turning spinners of different sizes (i.e. begin at the 12:00 position, and rotate clockwise less than one full spin, see Figure 1) to represent the same amount of “turn.” In the first example, the answer is central; students are to find some amount of degrees, then explain how they got it. In the second example, the concept is central. Here, students are to investigate an attribute, a “turn,” and conceive of that attribute as something they possibly could measure. Thereby they can engage in quantitative reasoning (Thompson, 1994, 2011).

Figure 1. Three spinners: different sizes, same amount of “turn.”

To promote students’ conceptual mathematics learning places demands on teachers’ practice. One demand is teachers’ noticing of their students’ thinking, which can be thought of as comprising three aspects: identifying strategies children use, interpreting children’s thinking, and determining next steps based on that interpretation (Jacobs, Lamb, & Philipp, 2010). To interpret children’s thinking requires teachers to “decenter,” to acknowledge that children can operate in ways different from the teacher and endeavour to understand those ways of operating (Confrey, 1990; Hackenberg, 2010; Teuscher, Moore, & Carlson, 2016). For example, a child may turn a spinner counterclockwise, or begin in a different position. A teacher who rushes to correct or fix the child’s actions may miss opportunities to interpret their thinking.

Ball and Forzani (2009) state that a teacher’s “primary responsibility is to see the content from others’ perspectives” (p. 499), which entails decentring. We view this responsibility to encompass a teacher’s perspective on their students as doers and learners of mathematics. For instance, teachers’ notions of their students’ capabilities can influence their goals for instruction, which in turn can impact the kind of tasks students encounter. The notion of “seeing from another’s perspective” also extends to research. With Teacher Development Experiment methodology, researchers articulate their perspective of a teacher’s perspective on mathematics knowing and learning, to account for the teacher’s practice as a sensible, coherent system (Simon, 2000; Simon & Tzur, 1999). Hence, an anti-deficit stance (e.g. Adiredja, 2019) is crucial both for teachers’ engagement in instruction to promote conceptual learning and for researchers’ investigation of teachers’ practice.

We investigate the following research question: How do aspects of an early-career teacher’s mathematics teaching practice intertwine as they work to promote students’ conceptual mathematics learning? In this case study, we focus on how a teacher deepened her mathematical knowledge, as she cultivated her vision and rationale for teaching mathematics, her interpretations of her students’ thinking, and her view of what constitutes evidence of mathematical learning.

Theoretical and conceptual background

We appeal to constructivist theory to guide our approach (Confrey, 1990; Steffe & Kieren, 1994; Thompson, 2000). From a constructivist lens, individuals make meaning and construct knowledge via reflection on their actions (Simon, Tzur, Heinz, & Kinzel, 2004). Likewise, we assume that teachers engage in sensible, goal-directed actions, even if those actions are different from what researchers would do (Simon & Tzur, 1999). To situate this study, we appeal to three related areas: teachers’ purposeful instruction to foster students’ learning of new mathematical ideas, their own knowledge of those ideas, and their perspectives of their students’ thinking. Drawing on Simon’s (1995) hypothetical learning trajectory, Tzur (2010) put forward three interrelated elements of conception-based teaching, which he termed a “teaching triad.” The elements include a teacher’s selection of tasks to promote learning, their interpretations of their students’ thinking, and their decisions regarding what to teach next. We conceive of a teacher’s practice to encompass all elements of the teaching triad. To organise this section, first we explain what we mean by teacher practice to promote conceptual mathematics learning (Simon & Tzur, 1999). Second, we discuss how teachers can engage in decentring (Confrey, 1990; Hackenberg, 2010; Teuscher et al., 2016), to enact “pedagogical empathy” to focus instruction on students’ conceptions. Third, we draw on Thompson’s (2011) theory of quantitative reasoning to explain how students and teachers can conceptualise attributes of mathematical objects (e.g. an angle’s amount of turn) as being possible to measure.

Teacher practice to promote students’ conceptual mathematics learning

By practice, we mean teachers’ engagement in instructional actions (e.g. planning, instructing, assessing), including their goal-directed intentions guiding their instruction, which may be tacit or explicit (Simon & Tzur, 1999). A teacher’s goals impact their vision of what mathematics teaching and learning is, their rationale for their teaching plans and moves, their interactions with their students, and their notions of what constitutes learning. To engage students in conceptual mathematics learning, a teacher can provide opportunities for them to develop new conceptions of mathematical ideas to extend beyond what they currently know. These conceptions are more than just learning a textbook definition of some mathematical idea, such as angle. They involve particular ways of thinking. For example, a conceptual learning goal can be for students to conceive of an attribute of an angle (e.g. an amount of turn) as something possible to measure (Clements et al., 1996; Clements & Burns, 2000). Teachers have many instructional goals; we distinguish between conceptual goals for students’ learning and other goals, such as having students complete a task or assessment item.

Tasks play a central role in instruction for conceptual mathematics learning (Simon & Tzur, 2004). By tasks, we mean more than artefacts; tasks encompass designers, teachers, and students’ intentions for and engagement with those artefacts (Johnson, Coles, & Clarke, 2017). While tasks are central, evidence of students’ progress toward a conceptual learning goal is more than task completion. For example, a teacher may notice (Jacobs et al., 2010) how a student moves their hands in a sweeping motion when talking about an angle, or that two students drew angles that appear differently sized, but have the same amount of “turn” (see Figure 1). As teachers develop their practice, their noticing can extend to interpretation of how students’ actions, utterances, and inscriptions indicate progress towards the intended learning goal. For example, a teacher may interpret a student’s hand motions as evidence of conceptualising angles as something more than just static shapes, or ask students if two angles can appear differently sized and still have the same measure. Noticing is crucial for interpreting, because to interpret, teachers need to pay attention to each and every student’s language and actions.

The use of tasks to promote conceptual learning is not a neutral endeavour (Adiredja, 2019). Conceptual instruction necessitates teachers’ views of students as capable doers and thinkers of mathematics. Hence, instructional practices that promote students’ safety and well-being are central to nurture conceptual learning. Sharing one’s mathematical thinking is personal, and potentially risky, and when students feel valued and validated, they can feel more open to offering their ideas. Therefore, it is important for teachers to recognise the sensibilities in students’ responses, even if those responses are unexpected.

Decentring: a form of pedagogical empathy

Decentring refers to one’s “ability to see a situation as perceived by another human being” (Confrey, 1990, p. 108). Accordingly, we consider decentring to be a form of “pedagogical empathy.” A few researchers have addressed the construct of pedagogical empathy, in teacher education and university mathematics instructional contexts (Crichton & Carter, 2017; Uhing, 2020). Crichton and Carter (2017) situate the construct between educators, characterising pedagogical empathy as being receptive to professional decisions of other educators, even if those decisions are different from one’s own. Uhing (2020) situates the construct between teachers and students, characterising pedagogical empathy in terms of instructor perceptions of student feelings during classroom instruction. Both characterisations assume that pedagogical empathy can influence teachers’ practice. When we state that decentring is a form of pedagogical empathy, we locate the construct within teacher-student interactions. That is, we combine teachers’ perceptions of students’ feelings as well as their noticing and interpretation of students’ thinking.

Building from Thompson (2000), Teuscher et al. (2016) argued that a central aspect of decentring was reflective interaction, in which teachers made efforts to understand students’ thinking. Engaging in reflective interactions, a teacher could interpret “in-the-moment” situations, to consider how a student could be perceiving the situation. Particularly, a teacher could observe students engaging in work with angles, and notice students are doing different things from what the teacher expected (e.g. focusing on arc length instead of the amount of turn). By decentring, teachers can avoid perceiving difference as error and rushing to fix students’ mistakes.

With decentring, we mean more than just acknowledging that students think in ways different from a teacher. Hackenberg (2010) uses the term “cognitive decentering” to refer to this crucial distinction, in which a teacher can background their own perspective, to attempt to make sense of a situation from a student’s perspective. For example, a teacher may interpret a student’s hand motions as evidence of their progress towards conceiving of rotation as a measurable attribute of angle. We relate the notion of reflective interaction to Schön’s (1983) construct of “reflection-in-action,” a process by which professionals think on their practice, in the midst of or following that practice. Like a person who acts based on their empathy for another human being, teachers who decentre can foster their students’ learning via actions that enact pedagogical empathy.

Thompson’s theory of quantitative reasoning and angle measure

Engaging in instruction to promote students’ conceptual learning intertwines with a teacher’s own mathematical conceptions (Ball & Forzani, 2009; Simon et al., 2004). We use intertwining to communicate a reflexive, rather than a causal relationship, as we view each to inform the other. To theorise teachers’ mathematical conceptions (e.g. of angle), we draw on Thompson’s theory of quantitative reasoning (Thompson, 1994, 2011). Thompson has explained how people may conceive of attributes of mathematical objects as being possible to measure, calling this kind of conception a “quantity.” This means that quantities are not something “out there” for people to see, rather they are human creations.

We focus on the concept of angle measure, an important idea for elementary students to learn (Clements et al., 1996; Clements & Burns, 2000). When a child conceives of an angle as a quantity, they can think of an attribute of an angle (e.g. an amount of rotation) as being possible to measure. While children may conceive of many attributes of angles, they benefit from opportunities to conceive of angles as something other than a static image (Clements et al., 1996; Clements & Burns, 2000; Tzur & Clark, 2006). Thompson has stressed that people’s conceptions of measurability can occur without engaging in an actual act of measurement. That is, students can conceive of an angle as a quantity without determining particular amounts of degree measures. In contrast, students may determine angle measures without conceiving of angles as quantities. We assert that teachers’ conceptual instruction for angle measure intertwines with their own notions of angles.

Method

Background: an intervention to promote conceptual mathematics instruction

This case study took place within a larger, U.S. National Science Foundation funded research project, a professional development (PD) intervention to promote elementary teachers’ engagement in conceptual mathematics instruction to foster students’ multiplicative and fractional reasoning. Through the project, we aimed to support teachers to diagnose their students’ mathematical reasoning (not just judge students’ answers as correct or incorrect), set conceptual goals for mathematics learning, select tasks that can adapt to students’ different ways of reasoning, and implement those tasks in ways that are responsive to students’ reasoning (see Tzur et al., 2020). Anchor tasks, designed to promote students’ conceptual learning via playful activities, were a key part of the project (see Reinke, 2020). We intended to provide teachers and students with classroom-ready situations that could become “taken-as-shared” (Yackel & Cobb, 1996), such as building towers from cubes (Tzur et al., 2020) or equally sharing paper strips considered as French fries (Tzur & Hunt, 2015). The project included grades 3–5 teachers in four elementary schools; two schools participated for two years and two schools (Jen’s included) participated for one year. The PD intervention included two week-long summer PD institutes, one year apart, with classroom support from the research team during the intervening school year. In schools participating for two years, teachers received one more year of team support.

Jen was in her first year of teaching when this study began. She taught in a neighbourhood school in a large midwestern U.S. city; the school served a population of 93% students of colour (73% Hispanic), with 85% of students receiving free or reduced-cost lunch (an indicator of low socioeconomic status). Over 55% of the students were learning English as an additional language, with Spanish being their most common home language. Jen, a White teacher, was fluent in English and Spanish. She had completed graduate coursework in Culturally Responsive Instruction (Au, 2007), where she learned to draw on students’ linguistic resources to promote their learning.

Teacher development experiment methodology

We employ Teacher Development Experiment methodology (Simon, 2000), a specialised form of case study in which researchers engage in generating and testing hypotheses about mathematics teachers’ goal directed activity. Two key assumptions underlie this methodology. First, researchers assume that actions in which a teacher engages are sensible and coherent to the teacher. Second, researchers assume that teachers’ perspectives on knowing and learning drive their work of teaching. An overarching goal for researchers is to better understand why teachers do what they do when teaching children mathematics. To this end, Simon and Tzur (1999) have devised a particular research method, called “Account of Practice,” as part of the methodology.

Account of Practice data sets consist of cycles of teacher interviews and classroom observations. Each Account of Practice set consists of at least one pre- and one post-lesson interview, with a classroom observation in between. The interviews are to be conducted within at least 24 h of the classroom lesson, ideally just before or after the lesson. Researchers “strive to create a coherent account of each teacher’s practice by explaining the teacher's perspective from the researchers’ perspectives” (Simon & Tzur, 1999, p. 254). This means researchers have work to do, to acknowledge and interrogate their own implicit biases, which may impact their interpretations.

Researcher positionality

Our author team is composed of four White women and two White men. We bring life experiences from different social classes, encompassing different parts of the U.S. and the world. Each of us has classroom teaching experience, together spanning students ages 4 through adult, in public and private school settings. Fostering and studying conceptual learning necessitates researchers’ views of teachers as capable, knowledgeable, and sensible. We recognise that teachers can experience a research situation differently from researchers, and through our methods we aim to value and validate the complex work of teaching. To this end, Jen has contributed her perspective to our analysis, to calibrate our interpretations with her reflections.

Account of practice sets: dimensions and guidelines

In preparation for conducting and analysing the Account of Practice sets, we identified six interrelated dimensions (Table 1). These dimensions intertwined the broader project aims with assumptions underlying Teacher Development Experiment methodology, to make explicit what we meant by accounting for a teacher’s practice in our setting. We organised the sets around these dimensions, acknowledging that our choices foregrounded some aspects of teachers’ practice, and backgrounded others.

Table 1. Six dimensions guiding account of practice sets.

1	Teachers’ vision of mathematics teaching
2	Teachers’ conceptual knowledge of the mathematical content they teach
3	Teachers’ assumptions of their students’ mathematical knowing
4	Teachers’ differentiation for cognitively and linguistically diverse students
5	Teachers’ rationale for their teaching moves
6	Teachers’ views of what constitutes evidence of mathematical learning

Table 2 provides guiding interview questions linked to the six dimensions and three focus areas for observation, to inform researchers’ interviews and field notes. We view the questions to be guidelines, not a script, to promote interviewers’ flexibility when responding in real time, while keeping broader aims in mind. While for us the guiding questions connect to the six dimensions, we do not assume teachers to be aware of those dimensions, or to respond to a particular dimension because that is what we intended. By design, our analysis methods address this sensitivity. Viewing a situation through another’s perspective is at the heart of Teacher Development Experiment methodology, and we see our design move as one way that we strive to explain a researcher’s perspective of a teacher’s perspective.

Table 2. Guiding questions and focus areas.

Pre-Interview	Guiding Questions: Tell me about the lesson you will teach. Show me the tasks/activities that students will do. o How did you decide on them? o How did you decide to sequence them? o Why did you include particular numbers/diagrams? (For the task that seems most central to the lesson) Can you give me an example of how you think three different students might make sense of this task? How does this lesson fit with what students have already learned? What math do you intend for students to learn in this lesson? o How will you help students to move from not knowing to knowing what you intend for them to learn? o How will you know that students learned what you intended for them to learn? How will you differentiate for students with different language needs?
Classroom Observation	Focus areas: Specific student responses to tasks/activities. Teacher questions/moves that relate to different students’ thinking Instances when the teacher deviates from the stated plan and/or makes real-time adjustments for students’ thinking.
Post-Interview	Guiding Questions: How did the lesson go? Was it how you expected? (For the task that seems most central to the lesson) How did different students work on the task? (Use examples from field notes) (For a question/move recorded in field notes, preferably related to the above task) Why did you ask that question/make that move? Why did you change your plan and/or make adjustments? Do you think students learned what you intended for them to learn today? How do you know?

Data sources and analysis

Our case study of Jen draws on two Account of Practice sets, occurring one year apart, each consisting of a pre-interview, a classroom observation, and a post-interview. These sets were part of a larger body of interviews and observations, conducted as part of the broader researcher project. In each set, Jen taught a lesson focused on angle measure. Johnson served as the interviewer, and Gardner video recorded; both wrote field notes during lesson observations for ongoing analysis. Between the sets, Gardner spent at least one day per week in Jen’s school, to promote trust and comfort with the research team. Jen’s practice and reflection during these two sets were consistent with the larger corpus of data of her instruction.

Retrospective analysis comprised four phases. First, while watching each interview, Johnson created a rough transcription, typing while listening. Then Johnson refined the transcription, including annotations via still images and/or notes. Next, Johnson separated the transcript into timestamped chunks, based on conversation topics.

Second, Johnson coded the interviews, starting with the pre-interview from Account of Practice Set 1. While the six dimensions (Table 1) comprised the initial codes, new codes emerged via our analysis methods. Continuing into the post-interview from the first set, Johnson refined the initial codes to account for Jen’s reflection on her students’ mathematical knowing and her own instructional moves. By the pre-interview for Account of Practice Set 2, the codes became stable.

Third, Johnson created reflective memos from the coded interview transcripts, one memo per interview, working in chronological order by interview. Each reflective memo began with a description of the classroom lesson, to calibrate Jen’s description of the lesson with video evidence. Guided by the six dimensions (Table 1), the memos included instances when the researcher intended to gather evidence of a particular dimension and Jen responded with evidence of some other dimension. Through this phase, we intended to make explicit our recognition that even though an interviewer can ask a question with a goal in mind, the interviewee may not share that goal. We view this as an instance of our efforts to guard against our implicit biases in data analysis.

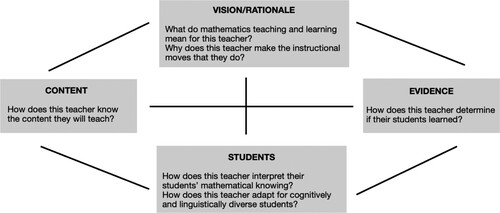
Fourth, working from the reflective memos, Johnson developed two written accounts of Jen’s practice, one for each year. Johnson organised the accounts into four key areas: Vision and Rationale, Students, Evidence, and Content. Linked to the six dimensions, these areas arose from our analysis of Jen’s case. Figure 2 illustrates the areas, including guiding questions for each. We included lines between each area to communicate that these areas inform and relate to each other. We chose to make the “vision/rationale” and “student” areas larger, because they incorporated the teacher’s perspective, and the teacher’s perspective of their students’ perspective. Next, we looked across the two data sets with two questions in mind: What remained stable? What changed? To address these questions, we turned to theory.

Figure 2. Four key areas of each written account of practice.

Throughout the analysis process, we engaged in triangulation across the author team, vetting each phase of analysis and weighing claims against the corpus of data. As a member check, Jen reviewed and contributed to our reflective memos, written accounts of practice, and draft manuscript. We asked Jen if our writing and analysis made sense from her perspective, encouraging her to share her thoughts, questions, and disagreements. In an email correspondence with Johnson, Jen wrote: “I particularly like the title for the article! The details are as I remember them, and I of course feel valued as an educator.”

Results

We organise the results into five sections, interweaving transcript data and researcher analysis, rather than separating the two. The first section contains descriptions of each lesson, to invite readers into Jen’s mathematics teaching practice. The remaining sections address the four key areas shown in Figure 2: Content, Vision and Rationale, Students, and Evidence. We organise each section by the Account of Practice sets, to distinguish Jen’s practice from one year to the next. In our interpretations, we draw connections to the construct of decentring and to Thompson’s theory of quantitative reasoning.

Descriptions of Jen’s lessons on angle measure

As a U.S. public school teacher, Jen was required to teach to state mathematics standards, with her district evaluation tied to her students’ performance on standardised tests. Both lessons were students’ introduction to angle measure. In Account of Practice Set 1, her lesson focused on the state standard in which students were to find unknown angles in diagrams via addition and subtraction. A year later, in Account of Practice Set 2, her lesson focused on a different standard, the concept of angle and measurement. Both lessons followed a “launch, explore, summarize” format (Stein, Engle, Smith, & Hughes, 2008), with Jen fostering a welcoming classroom environment inviting her students to participate.

We begin each lesson description with researcher and teacher perspectives – the research team’s intentions for the lesson observation, along with Jen’s stated goals for the lesson, which she shared in the pre-interview of each Account of Practice set. Then we describe each lesson, based on video recordings.

Account of Practice Set 1: angle measure lesson Year 1

To set the stage, the research team asked to observe a lesson in which Jen would teach students new content. Jen chose a lesson on angle measure, because standardised testing cut short her time for teaching geometry topics. In the pre-interview, Jen identified this learning goal: “How can they use known angles to determine the measures of unknown angles?” When Johnson asked Jen what she thought students would learn as a result of the lesson, she clarified her goal, saying “I’m hoping they might see that angles can be split apart, angles can be combined to form new angles.”

During the “launch,” Jen implemented a “Find Your Match” activity, in which students could draw on their prior knowledge of angles. Each student received a card containing a diagram, term, or measure; then they were to find another student with a matching card. For example, one card had a drawing of a right angle and its match had the term “right angle.” Next, Jen instructed students to sit on the carpet, near the smart board, for a whole group discussion. Jen did an angle demonstration, with polygon manipulatives; tracing the edges of the manipulatives, she showed students how two angles could combine to make a new angle (Figure 3). During the “explore,” students moved to their table groups of four, and worked on a worksheet on adjacent angles. Given two missing angle measures (e.g. 90° and 22°), students were to find a missing measure, either a part or a whole. If students finished early, they received a bonus worksheet where they could make generalisations about what they noticed. Here, Jen wanted students to characterise angles, for example “all of these angles are right angles and they’re all 90 degrees.” During the “summarize,” Jen asked students to share their generalisations.

Figure 3. Jen’s angle demonstration.

Account of Practice Set 2: angle measure lesson Year 2

To set the stage, Johnson asked to observe a lesson in which Jen’s content focus was outside the scope of the PD intervention (multiplicative and fractional reasoning). Jen decided on angle measure, because it was the same topic as the previous year’s observation. In an informal conversation with Gardner, Jen asked if there were resources she might consult. Gardner went to Tzur, the lead researcher on the project, who shared an article describing a Mathematical Merry-Go-Round task for learning angles (Tzur & Clark, 2006). In the pre-interview, Jen said she was “still learning how to decide, well what task will promote that intended learning,” and that reading and reflecting on articles helped her to understand the purpose for tasks. Jen identified the following learning goal: “we’re going to just construct together, a definition of angle.” As a result of the lesson, she intended students “to construct that an angle is a quantity, it’s a measure, based on a starting point and an endpoint.”

During the “launch,” students were seated on the carpet in front of the smart board. Jen displayed pictures of Merry-Go-Rounds, one from an amusement park and another from a playground. She then told students that they would play a “Mathematical Merry-Go-Round game,” which she demonstrated with the help of a student. During the “explore,” students worked in pairs (Partners A and B) to create “matching rides” via a tactile activity with pins, circle transparencies, and markers. Figure 4 (left) shows an image of the circle transparency; a drawing pin (“pushpin”) held the centre to the table. Jen described students’ work as follows:

They’re [Partner A] supposed to rotate while the center is still pushed in, till Partner B says stop. Then they’ll make a mark. And the rule is they can’t make a complete circle. They’ll [then] remove the pushpins [and] the transparency, and use a ruler and a marker to trace these line segments.

Next, students switched roles and Partner B tried to produce a “matching” ride, placing the pushpin at a different location on the radius (See marks on the circle transparency in Figure 4, left). During the “summarize,” Jen shared images of one pair’s work (Figure 4, right), then asked students to discuss whether either of Partner B’s attempts could match Partner A’s ride.

Figure 4. Mathematical Merry-Go-Round: circle transparency (left), student work (right).

Content: Jen’s knowledge of angle measure

Jen deepened her knowledge of angle measure, through her own self-directed efforts. The broader PD intervention invited teachers to deepen their own conceptions and engage students in conceptual mathematics instruction, with a focus on multiplicative and fractional reasoning. Jen extended this to angle measure, a topic outside the scope of the project’s PD.

Account of Practice Set 1: finding missing angle measures

In the pre-interview, Jen said that she wanted to make mathematics relevant for her students, to show them a way that they could “actually use the measure of angles.” With the polygon demonstration (Figure 3), she intended to connect to students’ prior knowledge: “They do know that a triangle is one half of a square. Then they should very easily be able to understand half of 90 would be 45.” She viewed angles as things with amounts of degrees that students could “find,” even without a tool, such as a protractor: With the worksheet, students could find missing angle measures using addition or subtraction.

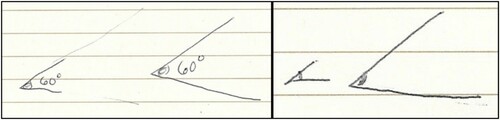
In the post-interview, Johnson sketched angles (Figure 5, left), then asked Jen what she might say to a student who thought: “those can’t be the same, because this angle is really small and this angle is really big.” Jen responded:

That hasn’t come up yet, as we have studied angles. But I think they’ve done a good job of seeing and visualising the angle as this piece (the small arcs in Figure 5, right). They are not necessarily thinking about the lines of the angle, per se.

Jen’s response suggested that she expected her students to focus on the space in the interior of the angle, where the degree measure and/or arc symbol were typically written. We viewed this interpretation to be consistent with a conception of an angle as being a static image that one can “see” in an object, such as a polygon manipulative. Such an interpretation is different from a conception of angle as having an attribute, such as a rotation, which is possible to measure (Clements et al., 1996; Clements & Burns, 2000; Tzur & Clark, 2006). Hence, prior to the PD intervention, Jen demonstrated a pre-quantity notion of angle, per Thompson’s theory.

Figure 5. How might students “see” angles?

Account of Practice Set 2: creating “angles” as measures of amounts of rotation

In the pre-interview, Jen shared her written lesson notes, which included sketches of angles that appeared different, yet had the same measure (Figure 6). Jen intended to illustrate a challenge she anticipated her students might have: “sometimes they confuse the length of those rays, or line segments, with the measure of the angle.” Johnson asked Jen what she thought an angle measured, to learn more about what Jen meant when she described an angle as “a quantity.” Jen replied: “Distance between the starting point and the endpoint. Distance between these boundaries.” While talking, Jen moved a pencil along one ray of the angle (Figure 6, right), then extended the pencil in a sweeping, arc-like motion through the interior of the angle to the other ray. We inferred Jen conceived of an attribute of an angle, the “distance” (rotation amount) as something that could be measured, and therefore conceived of an angle as a quantity. Jen’s motions, along with her engagement of students in a task that involved angles as measuring rotations, suggested that she conceived of the “distance” as something other than a linear distance between the two rays (Clements et al., 1996).

Figure 6. Two different looking angles.

To further support our inference above, we note that in the post-interview, Jen began to use the terms “rotation” and “turn” to describe angles and interpret student work. Furthermore, when she monitored students’ work in pairs, she asked questions to learn how students were focusing on the “lines” (the rays) and the “rotation.” One way she did this was by asking students “Do the lines matter?” Jen intended students to realise that the “lines” did not matter, the rotation is what matters.

In Account of Practice Set 2, Jen identified an attribute of an angle, its rotation, and intended to help her students do that as well. Jen’s discussion in the post-interview added evidence to what she meant by the “distance” in the pre-interview. For Jen, the “distance” was a rotation that one could measure even if the rays of the angle were drawn such that the lengths appeared different (Figure 6). Hence, Jen’s conception of angle deepened from one year to the next. Angles became more than unknown amounts to “find;” they were objects with an attribute (an amount of rotation) that was possible to measure, or a quantity, per Thompson’s theory.

Vision and rationale: what Jen means by learning goals

Jen transformed her vision and rationale for teaching mathematics, enhancing her notions of learning goals. In Account of Practice Set 1, Jen distinguished students’ strategies from the learning goal for the lesson, communicating that the lesson objective guided her instruction. In Account of Practice Set 2, Jen expanded this notion, to distinguish what students would do to complete a task (a task goal) from a conceptual learning goal that she had set for the lesson.

Account of Practice Set 1: distinguishing students’ strategies from the learning goal

Jen welcomed students’ uses of different strategies to find missing degree measures. Furthermore, she valued students’ explanations of how they arrived at different answers. In the pre-interview, Jen and Johnson discussed an example, with two complementary angles, one of which had a known measure (22°). Johnson asked Jen how she wanted students to explain their answers. Jen responded: “I don’t think explaining the subtraction step by step is really meeting the objective of the lesson … the subtraction strategy isn’t necessarily the focus or the goal. [Rather] It’s, do they recognise the known and unknown.” Jen distinguished her learning goal from calculation steps. We viewed her distinction between students’ strategies and the learning goal to be a productive notion on which she could expand.

Notably, Jen recognised that students have mathematical knowledge, even if they may not be able to produce language to demonstrate that knowledge. She also made consistent efforts to support students’ language production. Prior to her angle demonstration with polygon manipulatives (Figure 3), Jen displayed a drawing of three different types of angles (Figure 7). She frontloaded mathematical terms for the students, so they would know the lesson topic. In the post-interview, Johnson asked Jen about the meanings that she wanted students to have for the terms she introduced: “Like that right angle, that 90. What’s the 90? Or what’s less than 90? What do you want them to look at?” Jen responded

I just want them to understand what those measures mean. Like if it is 90 degrees, it is a straight, right angle … With an acute angle, I mean I want them to look at the measure and understand it is a smaller angle.

Figure 7. Angles: right (90°), acute (less than 90°), and obtuse (greater than 90°).

For Jen, the angle measure seemed to mean the number of degrees and apparent size, and she wanted to provide students with vocabulary to support their work.

Account of Practice Set 2: distinguishing task goals from conceptual learning goals

Jen distinguished students’ task goals from her conceptual goal for their learning (see Simon & Tzur, 1999). In the Mathematical Merry-Go-Round task, a task goal for students was to create a matching “ride,” like the ones shown in Figure 4. In the post-interview, she explained “Trying to match the ride seems more like a goal of the task, [whereas] trying to see the angle is the conception that we want them to reach.” We inferred that she viewed students’ work on the task as a means to help them develop the understanding she intended – a distinction intertwined with her conception of angle as a quantity.

Jen continued to foster students’ language production, but she refined her approach. This time, she introduced formal terms after students engaged with tasks, such as the Mathematical Merry Go Round. She based this move on her participation in the PD intervention: “I have learned that you don’t explicitly frontload the term.” In fact, at the end of the lesson’s “launch,” one student asked “Is this even math?” In the post-interview, Johnson brought up the student’s question. Jen connected back to a task, the French fry (Tzur & Hunt, 2015), that she implemented earlier in the year:

I think that speaks to how they’re used to math being presented to them. It’s ‘name a concept.’ Just like in the article, I didn’t say angle. Just like with French fry, we didn’t say this is to learn fractions. So then they wonder, is this math?

Jen’s response demonstrated how she could decentre, empathising with her students as learners and viewing their perspectives as sensible. Notably, she seemed to understand that students could develop meaning for mathematical concepts through their goal-directed work on tasks, which they then could link to a term. Drawing on her expertise with language instruction, Jen moved from vocabulary acquisition to meaning making, as recommended by Moschkovich (2015).

Students: Jen’s interpretation of her students’ mathematical knowing

Jen transformed her interpretation of her students’ mathematical knowing. Before the PD intervention, Jen invited students to share their ideas, and welcomed them, even if they were different from her own. In Account of Practice Set 1, Jen expected her students would “see” mathematics in the way that she did. In Account of Practice Set 2, Jen refined this notion, using her students’ actions, utterances, and inscriptions to interpret conceptions underlying what they were “seeing.”

Account of Practice Set 1: expecting students’ “seeing of math” to match hers

Jen fostered students’ active participation and invited them to share their thinking. In the pre-interview, she stated: “I want them to try and explore on their own, and I know that they can.” When Jen monitored her students’ work, she noticed the arithmetic operations they were using, looking for either addition or subtraction. Her focus was evidenced in her differentiation for a student who received out-of-class intervention: “He’ll still have the same objective, use these known angles to find an unknown, but he has smaller acute angles, and he’ll be using addition only.” Jen stated that he had been working on addition, and she wanted to support that.

In the post-interview, Jen shared her thinking related to a surprising comment from a student. After her polygon demonstration (Figure 3), one student said “I think finding angles is like finding area.” Even though the comment surprised Jen, she treated his response as sensible, demonstrating an anti-deficit perspective of the student’s knowing: “I could see his connection because we are looking at the inside of the polygon, or the angles.” Jen weighed the challenge of encouraging students’ responses, while trying to keep a focus on the learning goal, saying: “I wanted to value that, but I also didn’t want the kids thinking that this was an area, that our objective was to find area.” Jen appealed to arithmetic operations to explain her thinking:

Because the operation that you use for area is very clear, they know that very well. It’s multiplication. I didn't want them thinking we could use multiplication to solve for the unknowns. Cause that was not how we solved today. It was addition, subtraction.

Jen’s own mathematical concepts (angle measure, area) included a distinction based on the operations used to find each (addition/subtraction, multiplication). Her response, as well as her seeing of sensibility in the student’s response (“I could see his connection”), indicated how her own mathematical knowing served in her interpretation of students’ responses. She valued students’ different ways of thinking, and she wanted to be sure students were not confused about the task at hand, as she interpreted (“saw”) the mathematics.

Account of Practice Set 2: wanting to know what her students “see”

Through their work on the Mathematical Merry-Go-Round task, Jen expected that students could develop an understanding of angle as a quantity: “They’re going to be learning and conceptualising this, understanding that, changing the [rider’s] seat (see Figure 4, left) isn’t going to change the angle, the measure of that quantity.” Jen’s conceptual goal intertwined with a shift in both her own understanding of angle as a quantity and ways that she interpreted her students’ responses. Jen planned to pay attention to different aspects of students’ physical actions and language production: “I’m going to look for how kids are tracing the line segments;” “I’m going to look for also, are they using their previous estimate to adjust;” and “I’m going to look for kids that are using specific language. So are they using ray? I don’t know if they have this language.” Not only did Jen continue to demonstrate an anti-deficit perspective, her plans positioned her to learn even more about her students’ thinking, to move further in her decentring. For example, she expected that students could have different ways of going about the task and could bring in terms, even if she did not frontload formal terms at the start of the lesson.

In the post-interview, Johnson asked Jen what she noticed in her students’ work. In addition to detailing what her students said and did, Jen interpreted those actions and utterances in light of the conceptual learning goal. She recounted over one dozen student responses, and interpreted those responses in ways that positioned students as capable thinkers and doers of mathematics. She knew that students might produce the same language (e.g. angle), yet have different ways of “seeing” angle. Reflecting on a student interaction, Jen said “I asked, what does that mean, what’s an angle? And he said, ‘oh, I’m going to make it more straight.’ He meant, when he showed me, make the line more straight (Jen held her fingers out to approximate a distance.)” We inferred Jen’s interpretation to mean that the student was still thinking about an angle’s measure as “being connected to the lines,” and still working towards conceiving of a rotation as an attribute of an angle that was possible to measure. Jen demonstrated that she was going beyond just recognising that her students had different perspectives own, to actively seeking to learn more about her students’ thinking. Put another way, Jen was engaging in what Hackenberg (2010) termed “cognitive decentering.”

Evidence: Jen’s notions of what constitutes evidence of students’ learning

Jen’s shift in her interpretation of her students’ mathematical knowing intertwined with changes in her notions of what constituted evidence of students’ learning. Prior to our PD intervention, Jen seemed to equate students’ learning with their successful task completion. In Account of Practice Set 1, Jen focused on whether students were using the arithmetic operations she expected. In Account of Practice Set 2, Jen interpreted her students’ actions, utterances, and inscriptions as evidence of their progress toward conceptualising an angle as a quantity.

Account of Practice Set 1: monitoring students’ task completion

In the pre-interview, Johnson asked Jen what she would use as evidence of students’ learning. Jen responded: “I want to see how they’re determining this unknown angle. Are they using the right operation? Are they talking about that with others if they are struggling?” Consistent with Jen’s interest in knowing her students’ strategies, she wanted to know the arithmetic operations they used to arrive at their answers.

In the post-interview, Johnson asked Jen how she thought a specific student had progressed towards the learning goal: “Right off the bat, [that student] seemed a little bit challenged, but then by the end she was on the bonus sheet … I was happy with how she moved in that short amount of time in terms of the objective.” Jen’s response demonstrated her sensitivity to and empathy for her students. Just because a student started off struggling, it did not define them. Notably, Jen interpreted the student’s progress towards the learning goal in terms of task completion. For Jen, a learning goal was something students either accomplished or had yet to accomplish. If students successfully completed one worksheet, then they were ready for the next one.

Account of Practice Set 2: interpreting students’ physical actions and language productions

As Jen transformed her instruction to promote students’ conceptual learning, she moved beyond gauging students’ task completion to gathering evidence of changes in student thinking, via interpreting their actions, utterances, and inscriptions. In the pre-interview, Jen spontaneously contrasted the two lessons: “Last year I taught angles to the kids. This year they’re going to learn for themselves what angles are.” To inquire into this distinction between teaching and learning, Johnson asked Jen what she would take as evidence of student learning. Jen connected this to students’ actions as evidence of how they might conceive of angle: “When they’re tracing the line segments, if they have that understanding that the distance doesn’t matter.” Appealing to our earlier analysis, by “distance doesn’t matter” we interpret that Jen was referring to the lengths of the segments that students drew when they created angles as a measure of rotation to represent Merry-Go-Round “rides.”

In the post-interview, Jen described how she interpreted her students’ actions and utterances in light of the conceptual learning goal. She noticed students’ actions and listened to their responses to diagnose how they were thinking of a rotation, when comparing “rides” with segments of different lengths (See Figure 4, right). As Jen moved toward promoting students’ conceptual learning, she expanded the ways in which she could interpret their progress. For Jen, a learning goal had become a conceptual (thinking) continuum, along which students could make progress via their work on related tasks.

Discussion

We presented a case of a teacher who developed her practice across four key areas (see Figure 2). Jen transformed her vision/rationale for teaching, her interpretation of her students’ mathematical knowing, and her knowledge of what constitutes evidence of learning. In conjunction, she deepened her content knowledge of angle measure, engaging in quantitative reasoning (Thompson, 1994, 2011) and conceptualising angles as quantities.

We discuss three main findings from Jen’s case. First, a teacher’s shift in goals for students’ learning, from finding answers to engaging in reasoning, intertwines with a shift in what constitutes evidence of students’ learning. Second, decentring can engender practice to promote students’ quantitative reasoning, because it involves interpreting what and how students “see” (think) when engaging with mathematical tasks. Third, teachers’ and researchers’ perspectives on learners’ capabilities contribute to the Teacher Development Experiment methodology, by foregrounding the learners as agents of their mathematical knowing.

When teachers overemphasise answer finding, mathematical concepts can be reduced to “window dressing” in service of arithmetic operations and end results. For example, if a teacher’s goal is for students to find unknown amounts (e.g. degree measures), answers can matter more than the ideas those amounts represent. In contrast, if a teacher’s goal is for students to conceive of an attribute of an angle (e.g. a rotation), as something possible to measure, the mathematical ideas are central. Furthermore, Jen’s case manifests how a teacher’s goals can impact their enactment of lesson structures. She demonstrates how one can leverage the “launch, explore, summarize” lesson structure to make room for students to investigate a mathematical concept and for her to interpret their thinking. In future studies, researchers can investigate how teachers’ engagement in instruction to promote conceptual learning may impact their implementation of various lesson structures.

By decentring, teachers can empathise with their students’ learning of new-to-them mathematics, even if that mathematics is familiar to the teacher, such as the way that Jen responded to the student’s query of whether the lesson was “math.” With the construct of “mathematical caring relations,” connecting cognition and affect, Hackenberg (2010) alludes to a role of empathy in promoting students’ mathematics conceptual learning. We view decentring, a form of “pedagogical empathy,” to be crucial to a teacher's work to promote students’ quantitative reasoning. Likewise, researchers can empathise with the challenge of the work of teaching, and thereby employ an anti-deficit lens on the teachers whose practice they study.

Through Teacher Development Experiment methodology, researchers provide their perspective on teacher’s practice, via a lens of mathematics knowing and learning (Simon, 2000; Simon & Tzur, 1999). We have expanded this lens to include teachers’ views of their students’ capabilities as learners. For instance, we illustrated Jen’s anti-deficit view of her students in her instruction across both Account of Practice sets. With this expansion, we work to hold ourselves accountable to make explicit what we include as evidence to inform a researcher’s perspective of a teacher’s perspective.

Implications and concluding remarks

Clarke and Hollingsworth (2002, p. 965) assert: “We must accord the same dignity and status to teachers’ developing practices that we exhort them to accord to developing student practices.” Broadly, our study has implications for promoting teachers’ development. In their model of teachers’ professional growth, Clarke and Hollingsworth (2002) connect a teacher’s participation in a professional development intervention to a teacher’s locus of practice, which encompasses what a teacher does in practice, how a teacher interprets results of their actions, and a teacher’s ways of knowing that underlie their actions and interpretations. The four key areas shown in Figure 2 elaborate on a teacher’s locus of practice, bringing a teacher’s perspective of their students’ perspective into focus.

We have provided evidence of a transformation in a teacher’s mathematics teaching practice, in conjunction with a deepening of mathematical understanding, in a content area outside the scope of a PD intervention. This evidence highlights two key implications from Jen’s case. First, a teacher’s engagement in quantitative reasoning can intertwine with changes in their mathematics teaching practice to promote students’ conceptual learning. That is, a teacher’s mathematical knowledge and practice can develop concurrently, rather than in a lock-step fashion. Second, a teacher’s decentring, a form of pedagogical empathy, can engender anti-deficit views of their students’ mathematical capabilities, because students’ different ways of working can become something to value and nurture, rather than redirect and fix.

Acknowledgement

Opinions and conclusions are those of the authors. This study was supported in part by a grant from the Office of Research Services at the University of Colorado Denver.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This research was funded by the U.S. National Science Foundation under Grant DRL-1503206; Division of Research on Learning in Formal and Informal Settings.