Numerical study on acoustic matching between driver and resonator of loudspeaker-driven thermoacoustic refrigerator

ABSTRACT

This paper thoroughly investigates achieving acoustic matching in loudspeaker-driven thermoacoustic refrigerators (LSDTARs), elucidating the coupling mechanism between the acoustic source and the resonator. A comprehensive model of the LSDTAR is developed to analyze the resonator’s acoustic characteristics and the loudspeaker’s electrical-mechanical-acoustic response. Two critical indices are identified for effective acoustic matching: utilizable acoustic power in the thermoacoustic core and electroacoustic efficiency. The results reveal that the system’s radial size and the loudspeaker’s electrical-mechanical parameters are crucial in determining acoustic matching. LSDTARs with smaller diameters show a higher potential for acoustic matching, whereas larger systems require balancing acoustic power and electroacoustic efficiency. Enhancing the loudspeaker’s force factor is critical to enhancing electroacoustic efficiency, particularly at acoustic resonance. Joint optimization of the loudspeaker’s stiffness and moving mass enhances acoustic power and electroacoustic efficiency, thereby facilitating acoustic matching. This study deepens the understanding of the coupling dynamics in LSDTARs and presents essential guidelines for their design.

KEYWORDS:

• Thermoacoustic refrigerator
• acoustic matching
• acoustic characteristic
• electroacoustic efficiency
• loudspeaker

1. Introduction

Refrigeration, an essential aspect of energy utilization, is integral to various industries such as food preservation, cold chain logistics, electronics, and aerospace. Traditional and typical refrigeration systems, consisting of compressors, evaporators, condensers, and expansion valves, employ compressed vapor cycles of refrigerant for heat transfer, achieving cooling effects (Miller and Miller 2011). Despite their widespread application, these systems are costly and spatially demanding and pose environmental risks in the case of refrigerant leakage, including ozone depletion and global warming. Thermoacoustic refrigeration (Chen et al. 2021; Jin et al. 2015; Swift 1988, 2017), in contrast, offers an economical and environmentally friendly alternative, drawing attention from the acoustics and thermodynamics community.

Thermoacoustic refrigeration utilizes the thermoacoustic effect, replacing mechanical compression with thermoacoustic resonance for cooling. The working fluid oscillates under the drive of acoustic waves, thermally and viscously interacting with solid boundaries within a specified distance in the thermoacoustic (TA) core, producing a directional time-averaged heat flow. Thermoacoustic refrigerators (TARs) are broadly categorized into electric-driven types (Alamir 2020) and heat-driven types (Alcock, Tartibu, and Jen 2018; Xiao et al. 2023) based on the nature of the driving source. Compared to the latter, electric-driven TAR generally employs loudspeakers, linear alternators, and piezoelectric actuators, eliminating the need for a large temperature gradient during operation. Commercial loudspeakers, known for low manufacturing cost, ease of procurement, and simple structure, are widely applied in acoustic drivers. Since Hofler created the first standing-wave loudspeaker-driven thermoacoustic refrigerator (LSDTAR) in 1986 (Hofler 1986), which achieved a cooling temperature as low as $200\mathrm{K}$ and a maximum relative Carnot coefficient of performance of 12%, a series of LSDTARs with more significant cooling efficiency and capacity have been manufactured, including the space thermoacoustic refrigerator (STAR) (Garrett, Adeff, and Hofler 1993), the shipboard electronics thermoacoustic chiller (SETAC) (Ballaster and McKelvey 1995) and Frankenfridge (Poese and Garrett 2000). Due to the reliance on acoustic wave driving, enhancing the cooling capacity of LSDTARs necessitates focused interests in designing advanced acoustic drivers (El-Rahman et al. 2020; Hail et al. 2015; Steiner et al. 2021) and employing dual acoustic drivers (Chen, Tang, and Yu 2022; Poignand et al. 2011, 2013; Ramadan et al. 2021) to increase the acoustic radiation power. Parallel developments in resonator system optimization, including geometry and structural design adjustments (Alamir 2019; Feng et al. 2018; Luo, Huang, and Nguyen 2007; Ning and Li 2013), along with the adjustment and selection of the working frequencies (Chen 2015; Lihoreau et al. 2002; Tu et al. 2005), are also crucial.

Although many studies have focused on cooling capacity and the temperature difference across the TA core of LSDTARs (Alamir 2020; Pan, Wang, and Shen 2012; Poese and Garrett 2000; Poignand et al. 2011; Ramadan et al. 2021; Tijani 2001), effective control of acoustic characteristics is more significant in improving the performance of the system as the heat transfer is determined by the acoustic field distribution in the TA core (Chen and Xu 2021; Sun et al. 2023; Wheatley et al. 1983). Effective acoustic control encompasses both the acoustic source and the load. Matching the loudspeaker to the resonator system in LSDTARs and optimizing acoustic load for impedance matching have been shown to enhance maximum acoustic power and electroacoustic efficiency (Wakeland 2000). Taking into account the structural characteristics inside the resonator, detailed electrical-mechanical-acoustic coupling models have been developed for LSDTAR systems to optimize the design of loudspeakers coupled with resonators (Bailliet, Pierrick Lotton, and Gusev 2000; Tijani 2001), offering valuable guidance to enhance the system’s electro-acoustic efficiency. Furthermore, the coupling behavior between the loudspeaker and the resonator induces nonlinear effects within the system (David, Mao, and Jaworski 2006), and some of them have been found to play a positive role in improving both the acoustic pressure of the fundamental wave and the electroacoustic efficiency of the system (Fan et al. 2015). These studies highlight the importance of investigating the acoustic matching between the loudspeaker and the resonator.

Despite these advancements, research focusing on maximizing usable acoustic power in the TA core while minimizing electroacoustic efficiency losses remains limited. Distinct from prior research that concentrated predominantly on either enhancing the maximum values of acoustic power or electroacoustic efficiency alone through individual resonator parameters (Wakeland 2000) or on the distribution of the acoustic field (Bailliet, Pierrick Lotton, and Gusev 2000), this study aims to deepen the understanding of the design methodologies for electric-driven TARs by investigating the coupling mechanism between the acoustic driver and the resonator system. The critical factors that affect acoustic matching between them are identified as they directly determine the amount of acoustic energy converted to thermal energy in the TA core, as well as the overall energy efficiency of the system, which is pivotal for enhancing the performance of LSDTAR. By analyzing the frequency response of the coupled system, this study guides the selection of driving frequency and structural parameters of the coupling system that maximize the usable acoustic power for the TA core while maintaining high electroacoustic efficiency of the driver, thereby achieving acoustic matching in the design and operation of LSDTAR. The following sections are organized as follows: Section 2 details the physical model of the baseline LSDTAR. Section 3 develops the system-level refrigerator model and provides indices for acoustic matching. Section 4 presents and discusses the coupling mechanisms and methods to achieve acoustic matching in the system. Finally, conclusions are drawn in Section 5.

2. Physical model description

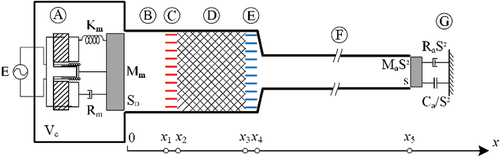
Figure 1 presents the baseline LSDTAR investigated in this study with alphabetically labeled components from A to G. It incorporates an acoustic driver and a resonator system. The acoustic source employs a closed-box loudspeaker system, which comprises an electrodynamic loudspeaker housed within an enclosure. The resonator system comprises a thermoacoustic (TA) core, a pair of heat exchangers, two tubes of varying diameters, and a large cavity. In particular, tube F employs a reduced diameter to minimize the loss of acoustic power (Hofler 1986; Swift 1997). The axial positions at the junctions of each component are labeled from $0$ to $x_5$, respectively. Table A1 lists the detailed parameters of the baseline LSDTAR.

Figure 1. (a) Schematic diagram and (b) experimental rig of the LSDTAR system. Labeled in the figure are the A-loudspeaker system, B-large diameter tube, C-ambient heat exchanger, D-TA core, E-cold heat exchanger, F-small diameter tube, and G-cavity.

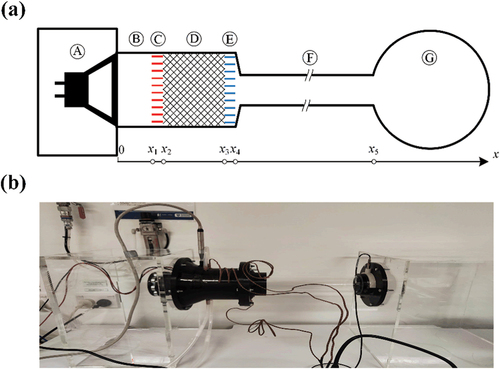
The TA core D, made of stacked ceramic plates, is tightly sandwiched between copper heat exchange materials, configured in parallel, acting as the ambient heat exchanger (AHE) C on one side and the cold heat exchanger (CHE) E on the other. Air is used as the working fluid, pressurized to a standard atmosphere, and the working environment is kept at a room temperature of $25{}^{\circ }\mathrm{C}$. Once the system operates at the appropriate acoustic frequency, acoustic power is consumed within the TA core. This generates a time-averaged heat flow from the cold end (in contact with CHE) to the ambient temperature end (in contact with AHE), thereby establishing a temperature gradient in the TA core along the direction of sound propagation.

3. Methodologies

Considering only the plane acoustic wave propagating along the axis in the resonator, the driving frequency of the LSDTAR must conform to the constraint (Kinsler et al. 2000)

(1) $\mathit{f}<1.84\frac{a}{2\mathit{\pi r}},$(1)

where $\mathit{a}$ denotes the velocity of sound, and $\mathit{r}$ is the radius of the tube.

3.1. System-level model for refrigerator

3.1.1. Acoustic analysis of resonant tube

As the basis of LSDTAR lies in acoustics, we first set up an acoustic model to calculate the acoustic field distribution within the resonator from component B to F (Figure 1). The starting point is the momentum and continuity equations of linear thermoacoustics, as deduced by Rott (Rott 1980)

(2) $\frac{d{p}_1}{\mathit{dx}}=-\frac{i\omega {\rho }_m}{A_f\left(1-f_v\right)}{U}_1,$(2)

(3) $\frac{d{U}_1}{\mathit{dx}}=-\left[1+(\mathit{\gamma }-1)f_k\right]\frac{i\omega A_f}{\mathit{\gamma }{p}_{\mathrm{m}}}{p}_1+\frac{f_k-f_v}{\left(1-f_v\right)\left(1-{\mathrm{P}}_{\mathrm{r}}\right)}\frac{1}{{\mathit{T}}_{\mathrm{m}}}\frac{\mathit{d}{\mathit{T}}_{\mathrm{m}}}{\mathit{dx}}{U}_1,$(3)

where $\mathit{p}$, $\mathit{U}$ and $\mathit{T}$ represent acoustic pressure, volume flow rate, and temperature, respectively, $A_f$ stands for the cross-section area of the fluid flow channel, $\mathit{\gamma }$ signifies specific heat ratio, $\mathit{\sigma }$ is Prandtl number, the subscripts “1” and “m” denote the first-order and mean values, and $f_v$ and $f_k$ are the thermal-viscous functions.

This paper focuses on the acoustic characteristics of LSDTAR, therefore setting $\mathit{d}{T}_m/\mathit{dx}=0$ as a necessary condition. To still treat $p_1$ and $U_1$ as lumped parameters, the resonator system is discretized into infinitesimal segments of length $\mathrm{\Delta x}$ (Ueda and Kato 2008). For any two adjacent segments (i.e., points $\mathit{j}$ and $\mathit{j}+1$) with $\mathrm{\Delta x}=x_{\mathit{j}+1}-x_j$, $\mathit{d}{p}_1\to \mathrm{\Delta p}=p_{\mathit{j}+1}-p_j$, $p_1\to p_j$, $U_1\to U_j$, $\mathit{d}{U}_1\to \mathrm{\Delta U}=U_{\mathit{j}+1}-U_j$, the conservation of mass and momentum equations in the form of a transfer matrix are written as

(4) $\left[\begin{array}{c}{p}_{1,\mathit{i}+1}\\ U_{1,\mathit{i}+1}\end{array}\right]=\left[\begin{array}{cc}cos(\mathit{k}\Delta \mathit{x})& -\frac{j\omega {\rho }_m}{A_f\mathit{k}(1-f_v)}sin(\mathit{k}\Delta \mathit{x})\\ \frac{A_f\mathit{k}(1-f_v)}{\mathit{j\omega }{\rho }_m}sin(\mathit{k}\Delta \mathit{x})& cos(\mathit{k}\Delta \mathit{x})\end{array}\right]\left[\begin{array}{c}{p}_{1,\mathit{i}}\\ U_{1,\mathit{i}}\end{array}\right]={\mathbf{T}}_i\left[\begin{array}{c}{p}_{1,\mathit{i}}\\ U_{1,\mathit{i}}\end{array}\right],$(4)

where the complex wave number $\mathit{k}$ is given by

(5) $\mathit{k}=\sqrt{\frac{{\omega }^2}{a^2}\frac{1+(\gamma -1)f_k}{1-f_v}}.$(5)

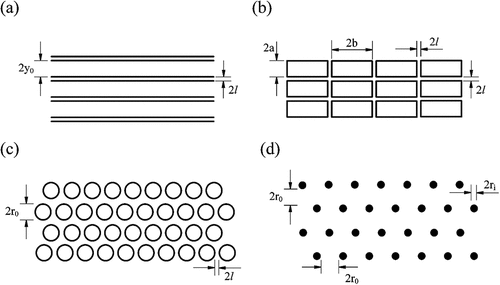
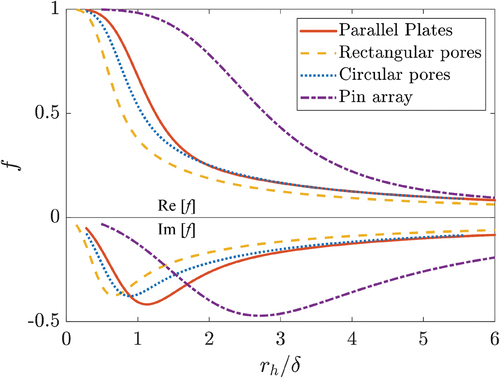
$A_f$ and $f_{\mathit{v},\mathit{k}}$ are two critical structural parameters that influence the acoustic characteristics of the resonator system. These two parameters correlate directly with the diameter of the tube, the HXs, and the TA core, along with the structural geometry of the TA core. The typical geometries of the TA core flow channels (Swift 2017) include parallel plates, rectangular pores, circular pores, and pin array, as illustrated in Figure 2. This study focuses exclusively on comparing the differences between these geometrical configurations, necessitating a consistent $A_f$ value across all comparisons. The distinct characteristics of each geometry are identifiable through the spatial-average function (see Appendix B), indicating that the primary effect of different geometries is on thermal viscous loss $f_{\mathit{v},\mathit{k}}$ within the TA core.

Figure 2. Typical geometries of TA core flow channels.

In particular, at $\mathit{x}=x_4$ where the diameter of the tube changes, the boundary conditions are determined by the continuity of $p_1$ and $U_1$—or equivalently, the continuity of acoustic impedance, following the law of mass conservation. Let ${\mathbf{T}}_{\mathbf{i}}$ denote the transfer matrix linking $p_1$ and $U_1$ at two $\mathit{x}$-axial positions, then $p_1$ and $U_1$ from $\mathit{x}=0$ to $\mathit{x}=x_5$ satisfy

(6) $\left[\begin{array}{c}{p}_{1,5}\\ U_{1,5}\end{array}\right]={\mathbf{T}}_{\mathbf{T}}\left[\begin{array}{c}{p}_{1,0}\\ U_{1,0}\end{array}\right]={\mathbf{T}}_{\mathbf{F}}{\mathbf{T}}_{\mathbf{E}}{\mathbf{T}}_{\mathbf{D}}{\mathbf{T}}_{\mathbf{C}}{\mathbf{T}}_{\mathbf{B}}\left[\begin{array}{c}{p}_{1,0}\\ U_{1,0}\end{array}\right],$(6)

where subscripts “B,” “C,” “D,” “E,” and “F” refer to the components of the LSDTAR (Figure 1). Correspondingly, ${\mathbf{T}}_B$ to ${\mathbf{T}}_F$ are $2\times 2$ matrices linking $p_1$ and $U_1$ at both ends of each component. At $\mathit{x}=0$ and $\mathit{x}=x_5$, we have

(7a) $p_{1,5}={\mathrm{T}}_{\mathrm{T},11}{p}_{1,0}+{\mathrm{T}}_{\mathrm{T},12}{U}_{1,0},$(7a)

(7b) $U_{1,5}={\mathrm{T}}_{\mathrm{T},21}{p}_{1,0}+{\mathrm{T}}_{\mathrm{T},22}{U}_{1,0},$(7b)

where ${\mathrm{T}}_{\mathrm{T},11}$, ${\mathrm{T}}_{\mathrm{T},12}$, ${\mathrm{T}}_{\mathrm{T},21}$, ${\mathrm{T}}_{\mathrm{T},22}$ are the four elements of the matrix ${\mathbf{T}}_{\mathbf{T}}$. Here, we utilize acoustic impedance to characterize the acoustic properties of the working fluid.

(8a) $\frac{{\mathit{p}}_{1,0}}{U_{1,0}}=Z_{\mathit{a},0},$(8a)

(8b) $\frac{{\mathit{p}}_{1,5}}{U_{1,5}}=Z_{\mathit{a},5}.$(8b)

Solving the Eqs. (7)-(8) yields

(9) $Z_{\mathit{a},0}=\frac{{\mathrm{T}}_{\mathrm{T},12}-Z_{\mathit{a},5}\cdot {\mathrm{T}}_{\mathrm{T},22}}{Z_{\mathit{a},5}\cdot {\mathrm{T}}_{\mathrm{T},21}-{\mathrm{T}}_{\mathrm{T},11}}.$(9)

This indicates that $Z_{\mathit{a},0}$ is influenced by variations in ${\mathbf{T}}_{\mathbf{T}}$, primarily induced by changes in diameter $\mathit{D}$, along with $Z_{\mathit{a},5}$, which is mainly influenced by external loads. Finally, when ${\mathbf{T}}_{\mathbf{T}}$ and $Z_{\mathit{a},5}$ is determined, $p_1$ and $U_1$ at any position can be calculated using Eq.(4)(4) $\left[\begin{array}{c}{p}_{1,\mathit{i}+1}\\ U_{1,\mathit{i}+1}\end{array}\right]=\left[\begin{array}{cc}cos(\mathit{k}\Delta \mathit{x})& -\frac{j\omega {\rho }_m}{A_f\mathit{k}(1-f_v)}sin(\mathit{k}\Delta \mathit{x})\\ \frac{A_f\mathit{k}(1-f_v)}{\mathit{j\omega }{\rho }_m}sin(\mathit{k}\Delta \mathit{x})& cos(\mathit{k}\Delta \mathit{x})\end{array}\right]\left[\begin{array}{c}{p}_{1,\mathit{i}}\\ U_{1,\mathit{i}}\end{array}\right]={\mathbf{T}}_i\left[\begin{array}{c}{p}_{1,\mathit{i}}\\ U_{1,\mathit{i}}\end{array}\right],$(4) . For more on the acoustic boundary conditions at $\mathit{x}=x_5$, see Appendix C.

Given that this study is based on linear thermoacoustic theory, it is crucial to confirm that the calculated acoustic pressure amplitude adheres to the conditions of linear acoustics, thereby avoiding turbulence in the gas flow. The verification metrics are the acoustic Mach number $M_a$ and the acoustic Reynolds number $R_y^{{\delta }_v}$ (Swift 2017).

(10) $M_a=\frac{p_1}{{\rho }_m{a}^2}<0.1,$(10)

(11) $R_y^{{\delta }_v}=\frac{⟨u_1⟩{\delta }_v{\rho }_m}{\mathit{\mu }}<500,$(11)

where $⟨u_1⟩$ is the average velocity and $\mathit{\mu }$ represents the dynamic viscosity of the fluid.

3.1.2. Frequency response analysis of loudspeaker

We proceed to analyze the electro-mechano-acoustic behavior of the loudspeaker coupled with the resonator system. The vibratory system of the loudspeaker can be equivalently modeled as a damped spring-piston system when the perimeter of the diaphragm is significantly smaller than the acoustic wavelength. By using equivalent mechanical symbols to represent the acoustic boundary condition at $\mathit{x}=x_5$, the equivalent model of the LSDTAR is obtained, as illustrated in Figure 3. Additionally, by representing the resonator system’s characteristics using the acoustic impedance at $\mathit{x}=x_0$, $Z_{\mathit{a},0}$, the equivalent circuit diagram of the LSDTAR is derived, as depicted in Figure 4. It consists of three parts from left to right: the electrical, mechanical, and acoustic domains (Borwick 2012).

Figure 3. Schematic diagram of the system with acoustic boundary conditions.

Figure 4. The equivalent circuit diagram for the loudspeaker system (a) incorporates electrical, mechanical, and acoustic domains. Simplified diagram in equivalent (b) electrical and (c) mechanical impedance domains.

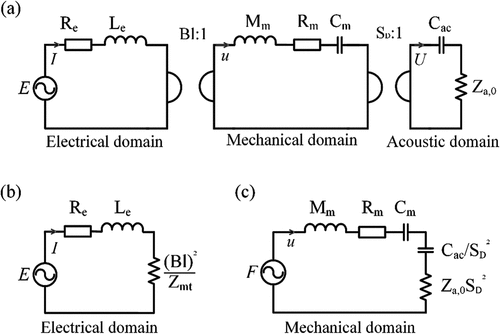
For the electrical domain, $\mathit{E}$, $R_e$, $L_e$, and $\mathit{Bl}$ denote the driving voltage, the direct current resistance, the inductance of the voice coil, and the force-electric coupling factor of the loudspeaker, respectively. Within the mechanical domain, $M_m$ is the equivalent mass of the loudspeaker vibratory system, while $R_m$ and $C_m$ (=$1/K_m$) are the equivalent mechanical resistance and compliance (the reciprocal of stiffness) of the loudspeaker’s suspension system, respectively. Regarding the acoustic domain, $S_D$ denotes the diaphragm’s effective acoustic radiation area, and $C_{\mathit{ac}}$ represents the acoustic compliance contributed by the air elasticity within the closed box. $Z_{\mathit{a},0}$ signifies the acoustic impedance of the resonator at $\mathit{x}=0$, incorporating the impedance contributions from the components B to G. For a more straightforward calculation of the system’s frequency response, the electrical gyrator is removed. This leads to the equivalent mechanical and electrical analog circuit diagrams of the system, represented in Figure 4(b,c), respectively. $\mathit{F}$ stands for the ampere force acting on the voice coil. $Z_{\mathit{mt}}$ represents the total equivalent mechanical impedance of the whole system, comprising the series combination of the mechanical impedance inherent to the loudspeaker and the equivalent one of the resonator system, as expressed:

(12a) $Z_{\mathit{mt}}=R_m+\mathit{j}\left(\mathit{\omega }{M}_m-\frac{K_m}{\mathit{\omega }}\right)+\frac{1}{\mathit{j\omega }{\mathit{C}}_{\mathit{ac}}}{S_D}^2+Z_{\mathit{a},0}{S_D}^2,$(12a)

(12b) $C_{\mathit{ac}}=\frac{V_1}{\mathit{\rho }{a}^2},$(12b)

where $V_1$ refers to the volume of air in the closed box. Consequently, the current $\mathit{I}$ that the voice coil carries and the vibration speed of the diaphragm, $\mathit{u}$, can be expressed as (Borwick 2012)

(13) $\mathit{I}=\frac{E}{R_e+\mathit{j\omega }{L}_e+{(\mathit{Bl})}^2/Z_{\mathit{mt}}}\equiv \frac{E}{{\mathit{Z}}_{\mathit{et}}},$(13)

where $Z_{\mathit{et}}$ is employed to represent the total equivalent electrical impedance of the TAR system and

(14) $\mathit{u}=\frac{F}{{\mathit{Z}}_{\mathit{mt}}}=\frac{\mathit{BlI}}{{\mathit{Z}}_{\mathit{mt}}}.$(14)

At $\mathit{x}=0$, the air’s volume flow rate $U_{1,0}$ can be represented by the volume of the gas column displaced $\mathit{dx}$ by the diaphragm over the cross-section, within the time duration $\mathit{dt}$

(15) $U_{1,0}=\frac{\mathit{dV}}{\mathit{dt}}=\frac{S_D\mathit{dx}}{\mathit{dt}}=S_D\mathit{u}.$(15)

Acoustic pressure $\mathit{p}$ at $\mathit{x}=0$ can be calculated by

(16) $p_{1,0}=U_{1,0}{Z}_{\mathit{a},0}.$(16)

The dynamic response of the LSDTAR is influenced by its driving frequency, which requires the calculation of the resonance frequency. Resonance occurs when the reactance part of the system’s equivalent mechanical impedance equals zero, as indicated by

(17) $\mathrm{\Im }[Z_{\mathit{mt}}]=\mathrm{\Im }[Z_{\mathit{md}}+Z_{\mathit{ma}}],$(17)

where $\mathrm{\Im }[]$ signifies the imaginary part of a complex quantity. Note that the natural frequencies of both the loudspeaker and the resonator system determine the system’s resonance frequency. The natural frequency of the loudspeaker vibratory system is calculated by

(18) ${\omega }_s=\sqrt{\frac{1}{M_m}(K_m+\frac{{S_D}^2}{C_{\mathit{ac}}})}.$(18)

For the resonator system, resonance is attained when the reactance of acoustic impedance at $\mathit{x}=0$ equals zero, denoted by

(19) $\mathrm{\Im }[Z_{\mathit{a},0}]=0.$(19)

3.2. Power and electroacoustic efficiency

The available acoustic power in the TA core is crucial for electric-driven TAR systems as it determines whether sufficient acoustic energy can be converted into thermal energy. The time-averaged acoustic power flowing along the $\mathit{x}$-axis is written as

(20) ${\dot{W}}_2=\frac{1}{2}\mathrm{\Re }\left[p_1\widetilde{U_1}\right]=\frac{1}{2}|p_1||U_1|cos{\theta }_{p_1,U_1},$(20)

where ${\theta }_{p_1,U_1}$ denotes the phase difference between $p_1$ and $U_1$, and the subscript “2” represents the product of two first-order quantities. Therefore, the acoustic power that can be utilized in the TA core is represented as $\mathrm{\Delta }{\dot{W}}_2$ = ${\dot{W}}_2$ at $x_2$ - ${\dot{W}}_2$ at $x_3$.

Electroacoustic efficiency is also a significant metric in assessing system performance. The time-averaged electrical power consumed by the system, ${\dot{W}}_{\mathit{e}}$, can be represented as

(21) ${\dot{W}}_{\mathit{e}}=\frac{1}{2}\mathrm{\Re }\left[\mathit{E}\tilde{I}\right],$(21)

where $\mathit{E}$ and $\mathit{I}$ are the input voltage and current amplitude. Electroacoustic efficiency is calculated by

(22) ${\eta }_{\mathit{ea}}=\frac{\mathrm{\Delta }{\dot{W}}_2}{{\dot{W}}_{\mathit{e}}}.$(22)

Both $\mathrm{\Delta }{\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$ are used as indices to evaluate the effectiveness of acoustic matching in LSDTAR. The former determines the maximum power used for acoustic-to-heat energy conversion in the TA core, whereas the latter indicates the efficiency for electric-to-acoustic energy conversion in the loudspeaker. A LSDTAR system is considered to have achieved acoustic matching when $\mathrm{\Delta }{\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$ reach a significantly high value, for example, exceeding $70\mathrm{\%}$ of their respective peak values.

4. Results and discussions

4.1. Baseline LSDTAR

First, the electrical and acoustic characteristics of the baseline LSDTAR are analyzed. Boundary condition at $\mathit{x}=x_5$ is obtained by Eq. (C3). The loudspeaker employs a 5MR450-NDY series driver manufactured by PRV Audio. Its natural frequency (with a closed box), calculated using Eq. (18)(18) ${\omega }_s=\sqrt{\frac{1}{M_m}(K_m+\frac{{S_D}^2}{C_{\mathit{ac}}})}.$(18) , is $f_{\mathit{sd}}=155\mathrm{Hz}$. The fundamental natural frequency of the resonator system, determined by Eq. (19)(19) $\mathrm{\Im }[Z_{\mathit{a},0}]=0.$(19) , is also equal to $f_{\mathit{sr}}=155\mathrm{Hz}$. Moreover, the operating frequency, as calculated by Eq. (1)(1) $\mathit{f}<1.84\frac{a}{2\mathit{\pi r}},$(1) , should not exceed $2032\mathrm{Hz}$ and therefore is set within the range of $0-700\mathrm{Hz}$.

Following the analysis in Section 3.1, the frequency response for the following parameters is calculated. Electrical characteristics involve the system’s total equivalent electrical impedance $Z_{\mathit{et}}$, the current in the voice coil $\mathit{I}$, the electrical power consumed ${\dot{W}}_{\mathit{e}}$, and the electroacoustic efficiency ${\eta }_{\mathit{ea}}$. 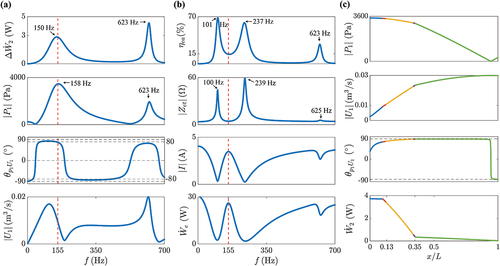Acoustic characteristics include the acoustic pressure amplitude $|p_1|$ and the volume flow rate amplitude $|U_1|$ at $\mathit{x}=x_2$, the phase difference ${\theta }_{p_1,U_1}$ between $p_1$ and $U_1$, and the available acoustic power $\mathrm{\Delta }{\dot{W}}_2$ in the TA core, as shown in Figure 5(a,b).

Figure 5. Dependence of electrical and acoustic parameters of LSDTAR on $\mathit{f}$.

Focusing initially on the acoustic characteristics within the acoustic matching index, it is observed that both $\mathrm{\Delta }{\dot{W}}_2$ and $|p_1|$ reach their peak values singularly near $\mathit{f}=f_0=155\mathrm{Hz}$ and at $\mathit{f}=623\mathrm{Hz}$, indicative of an acoustic resonance condition. ${\theta }_{p_1,U_1}$ typically ranges from ${80}^{\circ }$ to ${90}^{\circ }$, signifying that the acoustic field inside the TA core is dominated by standing waves. Figure 5(c) illustrates the acoustic field distribution in the resonant tube at $f_0$, with the orange area representing the location of the TA core. At $\mathit{x}=0$, $|p_1|$ reaches the only antinode, while $|U_1|$ reaches the only node. Near the end of the resonant tube, $|p_1|$ reaches the only node, and $|U_1|$ reaches the only antinode. This visualization confirms that the baseline LSDTAR essentially functions as a quarter-wavelength standing-wave acoustic system. Acoustic power is consumed in the TA core, and the variation in $|p_1|$ and ${\theta }_{p_1,U_1}$ at $\mathit{x}=\mathit{L}$ is attributed to the acoustic impedance of the resonant cavity.

Turning to the other index, the electroacoustic efficiency ${\eta }_{\mathit{ea}}$, Figure 5(b) demonstrates that ${\eta }_{\mathit{ea}}$ achieves minimal values within $f_0\pm 5\mathrm{Hz}$, with peaks emerging on either side of $f_0$. This “inverse relationship” between ${\eta }_{\mathit{ea}}$ and ${\dot{W}}_2$ suggests that acoustic matching between the source and resonator has not been achieved, implying a lower energy utilization efficiency of the system at $\mathit{f}=f_0$. This result arises from the coupling effect between the driver and the resonator system, which share the same natural frequency. According to vibration theory, the LSDTAR system can be conceptualized as a two-degree-of-freedom (2DOF) system. Its frequency response characteristics are determined by the properties of individual components and their interactions and mutual coupling. Compared to an isolated loudspeaker, a resonator’s presence influences the vibration system’s dynamic state, altering its impedance (reflected in the “dual-peak” feature of $Z_{\mathit{et}}$). Combined with the induced electromotive force in the voice coil, it correspondingly leads to variations in $\mathit{I}$ and ${\dot{W}}_{\mathit{e}}$. Considering the frequency response of $\mathrm{\Delta }{\dot{W}}_2$, ${\eta }_{\mathit{ea}}$ is found to be minimal near $f_0$ and exhibits a “dual peak” characteristic on both sides of $f_0$. For an alternative calculation method for mechanical behaviors of the LSDTAR and a comparable damped 2DOF spring-mass model, see Appendix C.

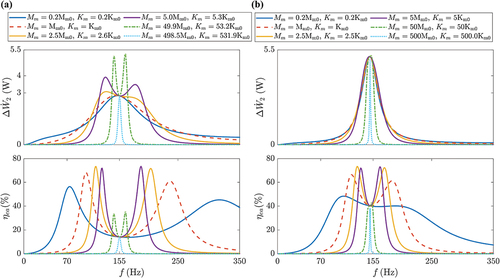
Based on the results obtained and in conjunction with the mathematical model of the refrigerator, a parametric analysis has been conducted to thoroughly investigate the effect of variations in key parameters, including the system size and loudspeaker parameters, on ${\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$. This investigation is pivotal for exploring methods to achieve acoustic matching in the LSDTAR. Note that the following analysis is conducted primarily around the first acoustic resonance frequency, which is of more excellent practical utility for operating the LSDTAR.

4.2. Effect of diameter of resonator system

We initially focus on examining the influence of the radial dimension, specifically the cross-sectional area controlled by $S_D$ that encompasses the resonator tube (including the HXs and the TA core) and the sound radiation area of the loudspeaker, on the acoustic matching in the LSDTAR. Typically, the demand for a large cooling capacity implies the employment of a larger diameter for the TA core (Tijani 2001). Here, $S_D=\mathit{\pi }{D}^2/4$. Maintaining the natural frequency of the loudspeaker and the resonator system consistent (ranging between $150-155\mathrm{Hz}$, which can be achieved by slightly adjusting the length of tube F) and using $D_0$ under baseline conditions as the reference, Figure 6 illustrates the frequency response of $\mathrm{\Delta }{\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$ within the $0-400\mathrm{Hz}$ range, as $\mathit{D}$ varies.

Figure 6. Frequency response of $\mathrm{\Delta }{\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$ with different $S_D$.

As observed, a decrease in $\mathit{D}$ results in a sharper and higher resonance peak in the frequency response curve of $\mathrm{\Delta }{\dot{W}}_2$, but an excessively small $\mathit{D}$ decreases the peak value. This phenomenon can be explained by two factors: acoustic impedance and thermal-viscous losses. When $\mathit{D}$ is reduced, the cross-sectional area $\mathit{A}$ decreases, leading to an increase in acoustic impedance (given by $Z_a={\rho }_m\mathit{a}/\mathit{A}$). This increase restricts and reflects sound waves more effectively, enhancing the resonance effect. At specific frequencies $\mathit{f}$, a smaller $\mathit{D}$ in the resonant tube system reduces thermal-viscous losses within the tube. The consequent reduction in damping enhances the quality factor $\mathit{Q}$, resulting in sharper resonance peaks. An excessively small $\mathit{D}$ leads to a significantly reduced $U_1$, which subsequently causes a rapid decrease in $\mathrm{\Delta }{\dot{W}}_2$. ${\eta }_{\mathit{ea}}$ maintains its “dual-peak” characteristic, with both peak frequencies converging toward $f_0=155\mathrm{Hz}$ as $\mathit{D}$ decreases and the minimal value at this frequency notably increases. This is mainly because $S_D$ determines the coupling strength between the loudspeaker and the resonator system. When $S_D$ is sufficiently small, the resonator dominates the acoustic characteristics, while the loudspeaker governs the electrical parts. Since their natural frequencies are aligned, LSDTAR operates optimally at the acoustic resonance frequency $f_0$. This elucidates the fundamental reason behind the frequency selection for smaller diameter LSDTARs (Bailliet, Pierrick Lotton, and Gusev 2000; Tijani 2001). However, for devices requiring large refrigeration capacities, the operating frequency should not be set to $f_0$, but rather a balance between $\mathrm{\Delta }{\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$ must be considered, and the achievement of acoustic matching may require exploration of other approaches. Overall, reducing the diameter of the tube to a certain extent can facilitate acoustic matching in LSDTAR, thereby achieving a higher $\mathrm{\Delta }{\dot{W}}_2$ while maintaining a reasonably large ${\eta }_{\mathit{ea}}$.

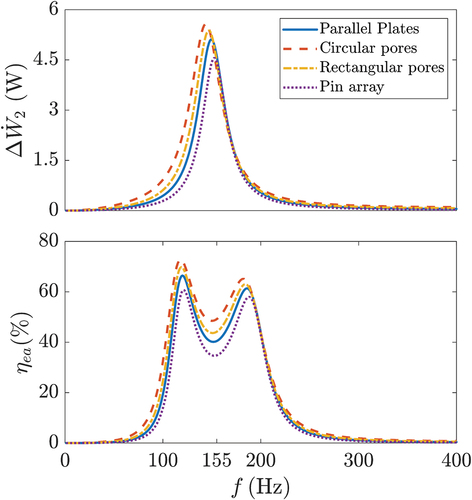
4.3. Effect of TA core geometry

TA core is a key component in thermoacoustic devices, significantly influencing the system’s heat transfer. This section analyzes the impact of the TA core’s structural geometry on the acoustic matching in LSDTAR. To exclusively compare the differences between various geometries, the porosity is set to a constant value, ensuring a consistent $A_f$. The different geometries of the TA core mainly influence its internal thermal viscous losses. Figure 7 illustrates the frequency response of $\mathrm{\Delta }{\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$ within the $0-400\mathrm{Hz}$ range as the geometry of the TA core varies. For the TAR with $\mathit{D}=0.5D_0$, the impact of different TA core geometries on acoustic matching is not significant. Compared to other geometric structures, the system’s $\mathrm{\Delta }{\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$ are highest when the circular pores are employed, especially under acoustic resonance conditions where the minimum value of ${\eta }_{\mathit{ea}}$ is also the largest. In contrast, the pin array, which is the most challenging to manufacture, yields the lowest values for these parameters. Overall, the use of circular pores in the TA core is beneficial for achieving higher $\mathrm{\Delta }{\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$ at the resonance frequency, thus fulfilling acoustic matching requirements.

Figure 7. Frequency response of $\mathrm{\Delta }{\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$ with different TA core geometry.

4.4. Effect of loudspeaker

In this subsection, we examine the effect of the loudspeaker, including the $\mathit{Bl}$ product, the stiffness $K_m$, and the moving mass $M_m$, on the acoustic matching in the LSDTAR.

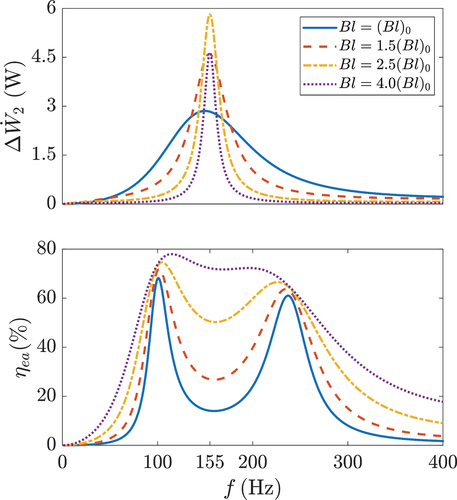
4.4.1. factor

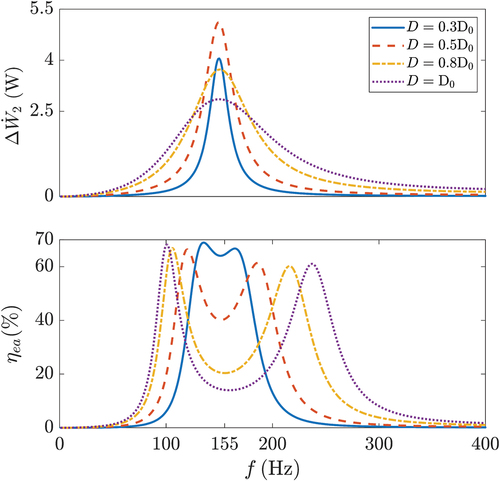
The effect of the $\mathit{Bl}$ product, which influences the driving force of the speaker’s vibrational system, is first studied. Using $(\mathit{Bl}{)}_0$ as a reference under baseline conditions, Figure 8 depicts the frequency response of $\mathrm{\Delta }{\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$ within the $0-400\mathrm{Hz}$ range as $\mathit{Bl}$ varies. Note that the variation of $\mathit{Bl}$ product does not affect the natural frequency of the loudspeaker vibration system.

Figure 8. Frequency response of $\mathrm{\Delta }{\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$ with different $\mathit{Bl}$.

As $\mathit{Bl}$ increases, the frequency response curve of $\mathrm{\Delta }{\dot{W}}_2$ gradually sharpens, achieving a higher resonance peak at $f_0=155\mathrm{Hz}$. The $\mathit{\eta ea}$ increases throughout the frequency range, particularly at $f_0$, where the minimum value obtained is significantly enhanced, leading to a smoother transition between the two peak values. This is mainly due to the increasing dominance of $\mathit{Bl}$ in altering the system’s total equivalent electrical impedance $\mathit{Zet}$. An excessively large $\mathit{Bl}$ increases the size and manufacturing cost of the loudspeaker (Borwick 2012) but does not effectively contribute to the increase of $\mathrm{\Delta }{\dot{W}}_2$. Overall, increasing $\mathit{Bl}$ not only favors the enhancement of acoustic power available to the TA core but also significantly improves the electroacoustic efficiency of the system at the acoustic resonance frequency, thereby facilitating acoustic matching in LSDTAR.

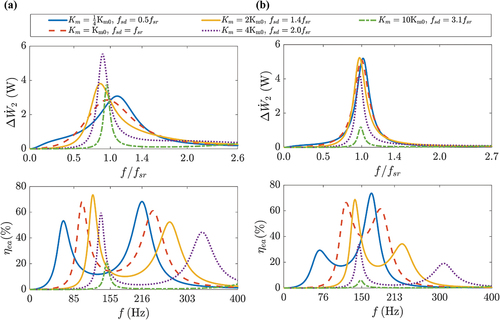
4.4.2. Stiffness $K_m$

Subsequently, the impact of variations in $K_m$ is investigated. With the resonator’s natural frequency $f_{\mathit{sr}}$ held constant, and using $K_{\mathit{m}0}$ in the baseline conditions as a reference, Figure 9 demonstrates the frequency response of $\mathrm{\Delta }{\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$ for two typical diameters ($\mathit{D}=D_0$ and $\mathit{D}=0.5D_0$) within the $0-400\mathrm{Hz}$ range, as $K_m$ varies.

Figure 9. Frequency response of $\mathrm{\Delta }{\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$ with different $K_m$ for:(a) $\mathit{D}=D_0$ (b) $\mathit{D}=0.5D_0$.

For the TAR with $\mathit{D}=D_0$ (Figure 9(a)), as $K_m$ increases, the curve of $\mathrm{\Delta }{\dot{W}}_2$ becomes progressively higher and sharper, accompanied by a slight decrease in its peak frequency. In contrast, the peak frequency of ${\eta }_{\mathit{ea}}$ increases steadily, with the first peak frequency increasingly approaching that of $\mathrm{\Delta }{\dot{W}}_2$, showing a trend of initial increase followed by a subsequent decrease in its peak. In the case of the $\mathit{D}=0.5D_0$ TAR setup (Figure 9(b)), a reasonable increase in $K_m$ ($2K_{\mathit{m}0}$) has an insignificant impact on the peak of $\mathrm{\Delta }{\dot{W}}_2$, but it aids in enhancing ${\eta }_{\mathit{ea}}$ of the system operating at the acoustic resonance frequency. Overall, a reasonable increase in $K_m$ is advantageous for achieving higher values of both $\mathrm{\Delta }{\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$ at the resonant frequency, thereby fulfilling the requirements of acoustic matching.

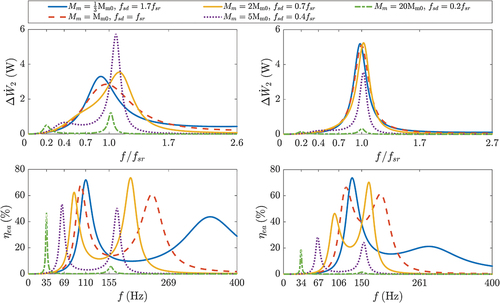
4.4.3. Moving mass $M_m$

Next, the impact of variations in $M_m$ is analyzed. By maintaining $f_{\mathit{sr}}=155\mathrm{Hz}$ and referencing the baseline condition $M_{\mathit{m}0}$, Figure 10 displays the frequency response of $\mathrm{\Delta }{\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$ within the range of $0-400\mathrm{Hz}$ for two diameters, as $M_m$ varies.

Figure 10. Frequency response of $\mathrm{\Delta }{\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$ with different $M_m$ for:(a) $\mathit{D}=D_0$ (b) $\mathit{D}=0.5D_0$.

For the system with $\mathit{D}=D_0$ (Figure 10(a)), an increase in $M_m$ results in a sharper and higher peak in $\mathrm{\Delta }{\dot{W}}_2$ curve, while the peak and corresponding frequency of $\mathit{\eta ea}$ progressively decrease. For the TAR with $\mathit{D}=0.5D_0$ (Figure 10(b)), a slight increase in $M_m$ has a negligible impact on $\mathrm{\Delta }{\dot{W}}_2$ but contributes to a particular enhancement in $\mathit{\eta ea}$ at the same frequency. Additionally, when $M_{m}5M_{\mathit{m}0}$, both $\mathrm{\Delta }{\dot{W}}_2$ and $\mathit{\eta ea}$ achieve an additional, smaller peak, with the frequency corresponding to the natural frequency of the loudspeaker. This is primarily because, at higher values of $M_m$, the loudspeaker’s behavior dominates that of the coupled system. In general, an increase in $M_m$ causes one of the peak frequencies of $\mathit{\eta ea}$ to gradually converge with that of $\mathrm{\Delta }{\dot{W}}_2$, thus facilitating the acoustic matching in the system.

4.4.4. Stiffness $K_m$ and Moving mass $M_m$

Based on the results presented in Sections 4.4.2 and 4.4.3, especially for refrigerators with larger diameters, acoustic matching is primarily achieved by adjusting the natural frequency of the loudspeaker to be different from that of the resonator. The implications of concurrent modifications in $K_m$ and $M_m$ are discussed. According to Eq. (18)(18) ${\omega }_s=\sqrt{\frac{1}{M_m}(K_m+\frac{{S_D}^2}{C_{\mathit{ac}}})}.$(18) , maintaining a near-equivalent ratio of variation in $K_m$ and $M_m$ ensures that $f_{\mathit{sd}}=f_{\mathit{sr}}$.

Figure 11 illustrates the frequency response of $\mathrm{\Delta }{\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$ within the range of $0-400\mathrm{Hz}$ for two diameters under simultaneous variation in $K_m$ and $M_m$. It is evident that all frequency response curves attain an extremum at $f_0$; the trend of ${\eta }_{\mathit{ea}}$ for TARs of both sizes is consistent, with both peaks gradually increasing and their frequencies approaching $f_0$. In particular, TAR with a smaller diameter exhibits a higher value at $f_0$, approximately twice that of the larger diameter. The most significant difference is manifested in $\mathrm{\Delta }{\dot{W}}_2$. For TAR devices with $\mathit{D}=D_0$ (Figure 11(a)), as $K_m$ and $M_m$ increase concurrently, a “dual-peak” characteristic gradually emerges around $f_0$ in $\mathrm{\Delta }{\dot{W}}_2$, with the peaks enlarging and the curve transitioning from a maximum at $f_0$ to a minimum, and eventually back to a maximum. This occurs because the acoustic characteristics of the system evolve with the concurrent increase in $K_m$ and $M_m$. Initially, the system’s acoustics are dominated by the characteristics of the resonator. As $K_m$ and $M_m$ increase, there is a transition to a state where the resonator and loudspeaker equally influence the acoustic behavior. Eventually, the system shifts to a state predominantly governed by the loudspeaker. In the case of the TAR device with a diameter of $\mathit{D}=0.5D_0$ (Figure 11(b)), $\mathrm{\Delta }{\dot{W}}_2$ remains essentially unchanged. This is because when the system dimension $S_D$ is smaller, the resonator primarily dictates the acoustic characteristics. Compared to independently adjusting $K_m$ or $M_m$, modifying both parameters concurrently is advantageous for simultaneously enhancing both $\mathrm{\Delta }{\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$. Moreover, this joint adjustment results in a greater alignment of their peak frequencies, thereby achieving acoustic matching in the LSDTAR.

Figure 11. Frequency response of $\mathrm{\Delta }{\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$ with different $K_m$ and $M_m$ for:(a) $\mathit{D}=D_0$ (b) $\mathit{D}=0.5D_0$.

5. Conclusions

This paper investigates the determinants and strategies for achieving acoustic matching between the acoustic source and resonator in a loudspeaker-driven thermoacoustic refrigerator (LSDTAR). Initially, a detailed model of the refrigerator is established to calculate the acoustic field characteristics in the resonator and the frequency response of the loudspeaker’s electrical-mechanical-acoustic parameters. Following this, two critical indices for acoustic matching in LSDTAR are proposed: the utilizable acoustic power in the thermoacoustic (TA) core $\mathrm{\Delta }{\dot{W}}_2$ and the electroacoustic efficiency of the loudspeaker, ${\eta }_{\mathit{ea}}$. Finally, a comprehensive analysis is conducted on the effects of variations in system size and the electrical-mechanical parameters of the loudspeaker. The main findings of this study are summarized as follows:

1. The coupling behavior between the loudspeaker and the resonator significantly reduces the ${\eta }_{\mathit{ea}}$ when LSDTAR operates at the acoustic resonance frequency. The frequency response of the loudspeaker’s electrical-mechanical parameters is influenced not only by the resonator’s acoustic behavior but also by their mutual coupling, thereby affecting the realization of acoustic matching between them.

2. The system’s radial size $S_D$ determines the coupling strength between the loudspeaker and the resonator. LSDTARs with smaller diameters are more likely to achieve acoustic matching, whereas larger diameter devices require a consideration of trade-offs between achieving a higher ${\eta }_{\mathit{ea}}$ and a larger $\mathrm{\Delta }{\dot{W}}_2$.

3. Enhancing the loudspeaker’s force factor $\mathit{Bl}$ is beneficial for achieving acoustic matching and notably assists in boosting ${\eta }_{\mathit{ea}}$ at acoustic resonance. A reasonable equivalent increase in $K_m$ and $M_m$ favors a concurrent enhancement of $\mathrm{\Delta }{\dot{W}}_2$ and ${\eta }_{\mathit{ea}}$, aligning their peak frequencies more closely, thereby facilitating acoustic matching.

The analytical results of this study elucidate the coupling mechanism between the acoustic source and the resonator and provide guidelines for acoustic matching in the LSDTAR. Future work will focus on matching the acoustic and refrigeration performance in electric-driven TARs.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work is financially supported by the Ph.D. scholarship from China Scholarship Council [No. 202106430004] and the Natural Science Foundation of Jiangsu Province [Contract No. BK20230848].

Appendix A

Key parameters of the baseline LSDTAR

Table A1. Key parameters of the baseline LSDTAR.

Components	Labels	Parameters	Values and units
Loudspeaker system	A	Driving voltage (peak) $\mathit{E}$	15 $\mathrm{V}$
		$\mathit{Bl}$ factor	7.94 $\mathrm{T}\cdot \mathrm{m}$
		Dc resistance $R_e$	3.7 $\mathrm{\Omega }$
		Inductance $L_e$	$0.02\mathrm{mH}$ at $1\mathrm{kHz}$
		Stiffness $K_m$	8.13$\times {10}^3$ $\mathrm{N}/\mathrm{m}$
		Mechanical mass $M_m$	9.14$\times {10}^{-3}$ $\mathrm{kg}$
		Mechanical resistance $R_m$	0.4 $\mathrm{N}\cdot \mathrm{s}/\mathrm{m}$
		Acoustic radiation area $S_D$	0.0079 ${\mathrm{m}}^2$
		Air volume in closed-box $V_1$	0.016 ${\mathrm{m}}^3$
Large diameter tube	B	Diameter $D_1$	0.1 $\mathrm{m}$
		Length $L_1$	0.04 $\mathrm{m}$
Heat exchangers	C and E	Diameter $D_1$	0.1 $\mathrm{m}$
		Lengths $L_2$ and $L_4$	0.01 $\mathrm{m}$ and 0.005 $\mathrm{m}$
		Porosity $\mathit{\psi }$	0.71
		Gap between fin plates $\mathit{d}$	0.0025 $\mathrm{m}$
Thermoacoustic core	D	Diameter $D_1$	0.1 $\mathrm{m}$
		Length $L_3$	0.086 $\mathrm{m}$
		Porosity ${\psi }_1$	0.73
		Hydraulic radius $r_h$	4.05$\times {10}^{-4}$ $\mathrm{m}$
Small diameter tube	F	Diameter $D_2$	0.0565 $\mathrm{m}$
		Length $L_5$	0.26 $\mathrm{m}$
Cavity	G	Volume $V_{\mathit{rc}}$	0.332 ${\mathrm{m}}^3$
Air (at 101,325 Pa,300K)		Density ${\rho }_m$	1.1768 $\mathrm{kg}/{\mathrm{m}}^3$
		Speed of sound $\mathit{a}$	347 $\mathrm{m}/\mathrm{s}$
		Thermal conductivity $\mathit{\kappa }$	0.0263 $\mathrm{W}/(\mathrm{m}\cdot \mathrm{K})$
		Viscosity $\mathit{\mu }$	1.847$\times {10}^{-5}$ $\mathrm{kg}/(\mathrm{m}\cdot \mathrm{s})$
		Specific heat ratio $\mathit{\gamma }$	1.4
		Isobaric specific heat $c_p$	1006 $\mathrm{J}/(\mathrm{kg}\cdot \mathrm{K})$

Appendix B

Thermal-viscous functions

The thermal-viscous function $f_v$ and $f_k$ is written as Swift (2017)

(B1) $f_{\mathit{v},\mathit{k}}=\left\{\begin{array}{cc}\frac{(1-\mathit{j}){\mathit{\delta }}_{\mathit{v},\mathit{k}}}{2r_h},& \mathrm{resonance}\mathrm{tubes},\\ \frac{tanh\left((1+j)r_h/{\delta }_{\mathit{v},\mathit{k}}\right)}{(1+\mathit{j})r_h/{\delta }_{\mathit{v},\mathit{k}}},& \mathrm{parallel}\mathrm{plates},\\ \frac{2J_1\left[(\mathit{i}-1)\mathcal{R}/\mathit{\delta }\right]}{J_0\left[(\mathit{i}-1)\mathcal{R}/\mathit{\delta }\right]\cdot \left(\mathit{i}-1\right)\mathcal{R}/\mathit{\delta }},& \mathrm{circular}\mathrm{pores},\\ 1-\frac{64}{{\pi }^4}\sum _{\begin{array}{c}\mathit{m},\mathit{n}\mathrm{odd}\end{array}}\frac{1}{m^2{n}^2{C}_{\mathit{mn}}},& \mathrm{rectangular}\mathrm{pores},\\ -\frac{2{\alpha }_i}{{\alpha }_o^2-{\alpha }_i^2}\frac{Y_1\left({\alpha }_o\right)J_1\left({\alpha }_i\right)-J_1\left({\alpha }_o\right)Y_1\left({\alpha }_i\right)}{Y_1\left({\alpha }_o\right)J_0\left({\alpha }_i\right)-J_1\left({\alpha }_o\right)Y_0\left({\alpha }_i\right)},& \mathrm{pin}\mathrm{array}\end{array}\right.$(B1)

where $r_h$ is the hydraulic radius, ${\delta }_v=\sqrt{2\mathit{\mu }/{\rho }_m\mathit{\omega }}$ and ${\delta }_k=\sqrt{2\mathit{\kappa }/{\rho }_m{c}_p\mathit{\omega }}$ represent the viscous and thermal penetration depth with $\mathit{\mu }$, $\mathit{\kappa }$ denoting the dynamic viscosity and thermal conductivity of the air, $\mathit{\alpha }=(\mathit{i}-1)\mathit{r}/{\delta }_{\mathit{v},\mathit{k}}$, and $C_{\mathit{mn}}=1-\mathit{i}\frac{{\pi }^2{\delta }^2}{8y_0^2{z}_0^2}\left(m^2{z}_0^2+n^2{y}_0^2\right)$. The real and imaginary components of $f_{\mathit{v},\mathit{k}}$ as functions of $r_h/\mathit{\delta }$ are illustrated in Figure B1.

Figure B1. Thermal-viscous functions for different geometries of TA core.

Appendix C

Varying boundary conditions

Since the resonator is connected at $\mathit{x}=0$ to the loudspeaker system A and $\mathit{x}=x_5$ to the cavity G, constraints are imposed on the boundary conditions for the tube. When an external acoustic load is connected at the end of the resonator, $\mathit{x}=x_5$, the acoustic field distribution within the TAR system undergoes alterations. If the linear dimensions of the load are substantially smaller than the acoustic wavelength (Chen et al. 2022), it can be modeled as a lumped parameter system. Here, we employ the acoustic impedance at $\mathit{x}=x_5$ to serve as a clear and simplified representation of the characteristics of the acoustic load:

(C1) $Z_a=R_a+\mathit{j}\left(\mathit{\omega }{M}_a-\frac{1}{\omega C_a}\right),$(C1)

where $\mathit{\omega }=2\mathit{\pi f}$ signifies the angular frequency, $\mathit{f}$ is the frequency, and $R_a$, $M_a$ and $C_a$ denote acoustic resistance, acoustic inertance, and acoustic compliance, respectively. Acoustic loads present various real-world analogies depending on their parameters. Generally, a load with high $M_a$ and low $R_a$ and $C_a$ is equivalent to a long and narrow tube or a rigid wall with a small hole or gap. Therefore, in a tube with a length $\mathit{l}$ and a cross-sectional area $\mathit{S}$, $M_a$, $C_a$ and viscous resistance $R_v$ can be calculated by Swift (2017)

(C2a) $M_a\approx \mathit{\rho l}/\mathit{S},$(C2a)

a

(C2b) $C_a=\mathit{Sl}/\mathit{\gamma }{p}_m,$(C2b)

(C2c) $R_v\approx \mathit{\mu }\Pi \mathit{l}/S^2{\delta }_v.$(C2c)

One with significantly higher $C_a$ and negligible $R_a$ and $M_a$ is likened to a large cavity filled with gas or comparable to a deformable membrane. Therefore, the cavity’s equivalent $C_a$ due to the”air spring” contributes to the acoustic impedance, expressed as

(C3a) $Z_a^{\prime }=-\mathit{j}\left(\frac{1}{\omega C_a^{\prime }}\right),$(C3a)

(C3b) $C_a^{\prime }=\frac{{\mathit{V}}_{\mathit{rc}}}{a^2\mathit{\rho }},$(C3b)

where $\mathit{\rho }$ and $\mathit{a}$ are the density and the speed of sound of the air, and $V_{\mathit{rc}}$ is the volume of the cavity. Furthermore, when the resonator terminates in an unflanged open end, it becomes necessary to incorporate the acoustic radiation impedance, $Z_r$, into consideration (Kinsler et al. 2000)

(C4) $Z_r=\frac{\mathit{\rho a}}{S_F}\left[\frac{1}{4}{(\frac{\omega }{a}\mathit{r})}^2+\mathit{j}0.6\frac{\omega }{a}\mathit{r}\right],$(C4)

where $S_F$ and $\mathit{r}$ are the cross-section area and radius of the tube, and $\mathit{j}=\sqrt{-1}$.

Appendix D

D.2. D.1. Alternative calculation method for mechanical behaviors of the LSDTAR

The acoustic source utilized in this study is a commercial moving-coil loudspeaker. The loudspeaker vibration system, comprising the voice coil, diaphragm, and suspension system, features mechanical resistance $R_m$, moving mass $M_m$, and stiffness $K_m$, with the vibrator acting as a piston with an effective area $S_D$. The vibration system is driven by the Ampere force produced by the voice coil, given by $\mathit{F}(\mathit{t})=F_0{e}^{\mathit{j\omega t}}$. According to Newton’s second law, the equation of motion for the moving mass is represented as follows

(D1) $M_m\frac{d^2\mathit{x}}{\mathit{d}{t}^2}=-R_m\frac{\mathit{dx}}{\mathit{dt}}-\left(K_m+\frac{{S_D}^2}{C_{\mathit{ac}}}\right)\mathit{x}-S_D\mathit{p}(0,\mathit{t})+\mathit{F}(\mathit{t}),$(D1)

where $\mathit{x}$ is the displacement. Using $\mathit{x}=x_0{e}^{\mathit{j\omega t}}$ and $\mathit{u}(0,\mathit{t})=\mathit{dx}/\mathit{dt}$, the input impedance of the loudspeaker can be derived as

(D2) $Z_{\mathit{md}}=R_m+\mathit{j}\left(\mathit{\omega }{M}_m-\frac{K_m}{\mathit{\omega }}\right)+\frac{1}{\mathit{j\omega }{\mathit{C}}_{\mathit{ac}}}{S_D}^2.$(D2)

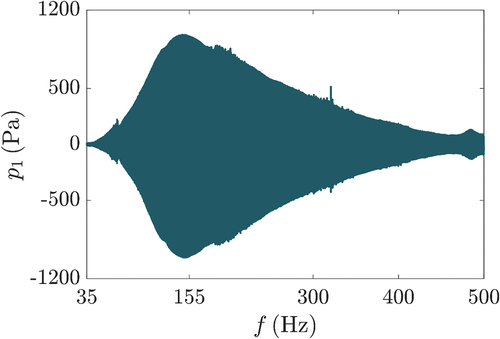
To verify the accuracy of this model, we conducted a frequency sweep experiment on the acoustic pressure amplitude $p_1$ at $\mathit{x}=x_1$, covering a frequency range of $35-500\mathrm{Hz}$ with a speaker drive voltage peak-to-peak value of $15\mathrm{V}$. The results indicate a sound pressure peak of approximately $980\mathrm{Pa}$, with a peak frequency of $149\mathrm{Hz}$, which deviates slightly from the $158\mathrm{Hz}$ observed in Figure 5. This deviation is primarily due to the buffer section at the diameter change in the actual resonant tube system, resulting in a slightly longer tube length than the theoretical calculation, thus increasing the resonance frequency. The lower $|p_1|$ is attributed to the relatively low drive voltage in the preliminary test and the nonlinear effects within the tube causing changes in acoustic impedance, which also limits the radiated acoustic pressure. Overall, the accuracy of the loudspeaker’s lumped element model in this study can be verified.

Figure D1. The frequency sweep profile of $p_1$ at $\mathit{x}=x_1$.

The volume flow rate of the air column it drives at $\mathit{x}=0$ is written as

(D3) $M_{\mathit{a},0}\frac{\mathit{dU}}{\mathit{dt}}+R_{\mathit{a},0}\mathit{U}+\frac{1}{{\mathit{C}}_{\mathit{a},0}}\int \mathit{Udt}=\mathit{p}(0,\mathit{t}).$(D3)

By Using $\mathit{U}=\mathit{j\omega }{x}_0{S}_D{e}^{\mathit{j\omega t}}=\mathit{j\omega }{U}_{1,0}{e}^{\mathit{j\omega t}}$, and subsequently eliminating the time factor $e^{\mathit{j\omega t}}$ from both sides, the following is derived

(D4a) $\left(-M_m{\omega }^2+R_m\mathit{\omega j}+K_m+\frac{{S_D}^2}{C_{\mathit{ac}}}\right)\frac{{\mathit{U}}_{1,0}}{\mathit{\omega }{S}_D}=F_0-S_D{p}_{1,0},$(D4a)

(D4b) $\left(\mathit{j\omega }{M}_{\mathit{a},0}+R_{\mathit{a},0}+\frac{1}{\mathit{j\omega }{\mathit{C}}_{\mathit{a},0}}\right)U_{1,0}=p_{1,0}.$(D4b)

When air resonates, $p_{1,0}$ reaches its maximum, and the net external force exerted on the loudspeaker vibration system reaches a minimum, resulting in a minimal value for $U_{1,0}$. This suggests that at $\mathit{f}=f_0$, most of the acoustic energy radiated by the loudspeaker is absorbed by the resonator system, and the vibration of the loudspeaker diaphragm is partially suppressed.

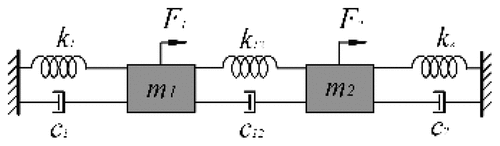
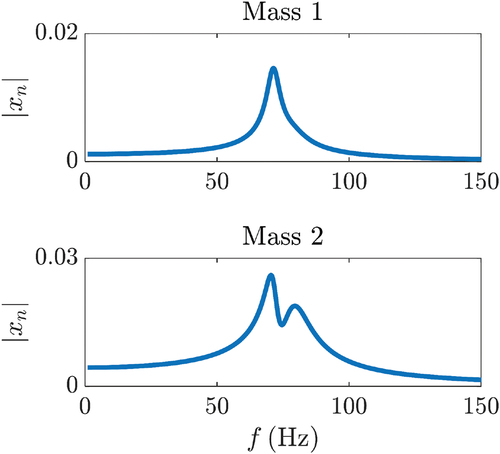
D.2. Weakly coupled 2DOF model

Similarly, consider a two-degree-of-freedom (2DOF) spring-mass system with viscous damping, as illustrated in Figure D2. Key parameters are listed in Table D1. Note that the natural frequencies of the two oscillators are identical. The governing differential equation for the system’s motion is

(D5a) $m_1{\dot{x}}_1+(c_1+c_2){\dot{x}}_1-c_2{\dot{x}}_2+(k_1+k_2)x_1-k_2{x}_2=F_1,$(D5a)

(D5b) $m_2{\dot{x}}_2-c_2{\dot{x}}_1+(c_2+c_3){\dot{x}}_2-k_2{x}_1+(k_2+k_3)x_2=F_2.$(D5b)

The steady-state frequency response of $m_2$ under the action of an excitation force is shown in Figure D3. It can be observed that the dimensionless amplitude, $|x_n|$, of $m_2$ exhibits two peaks, corresponding to resonances, as a function of frequency.

Figure D2. Schematic of the weakly coupled 2DOF model.

Figure D3. Normalized displacement-frequency response of $m_1$ and $m_2$.

Table D1. Key parameters of the 2DOF system.

Parameters		Values and units
Stiffness	$k_1$	$4000\mathrm{N}/\mathrm{m}$
	$k_2$	$2000\mathrm{N}/\mathrm{m}$
	$k_{12}$	$300\mathrm{N}/\mathrm{m}$
Mass	$m_1$	$0.02\mathrm{kg}$
	$m_2$	$0.01\mathrm{kg}$
Damping	$c_1$	$0.4\mathrm{N}\cdot \mathrm{s}/\mathrm{m}$
	$c_2$	$0.6\mathrm{N}\cdot \mathrm{s}/\mathrm{m}$
	$c_{12}$	$0.2\mathrm{N}\cdot \mathrm{s}/\mathrm{m}$