A total error-based multiquadric method for surface modeling of digital elevation models

Abstract

Digital elevation model (DEM) source data are subject to both horizontal and vertical errors owing to improper instrument operation, physical limitations of sensors, and bad weather conditions. These factors may bring a negative effect on some DEM-based applications requiring low levels of positional errors. Although classical smoothing interpolation methods have the ability to handle vertical errors, they are prone to omit horizontal errors. Based on the statistical concept of the total least squares method, a total error-based multiquadric (MQ-T) method is proposed in this paper to reduce the effects of both horizontal and vertical errors in the context of DEM construction. In nature, the classical multiquadric (MQ) method is a vertical error regression procedure, whereas MQ-T is an orthogonal error regression model. Two examples, including a numerical test and a real-world example, are employed in a comparative performance analysis of MQ-T for surface modeling of DEMs. The numerical test indicates that MQ-T performs better than the classical MQ in terms of root mean square error. The real-world example of DEM construction with sample points derived from a total station instrument demonstrates that regardless of the sample interval and DEM resolution, MQ-T is more accurate than classical interpolation methods including inverse distance weighting, ordinary kriging, and Australian National University DEM. Therefore, MQ-T can be considered as an alternative interpolator for surface modeling with sample points subject to both horizontal and vertical errors.

Keywords:

• interpolation
• accuracy
• positional error
• least squares method

1 Introduction

Land surface plays a significant role in modulating atmospheric, geomorphic, hydrologic, and ecological processes operating on or near the Earth’s surface (Wilson 2012). This linkage is often so strong that an accurate understanding of the nature and magnitude of the aforementioned processes is significantly determined by the quality of digital elevation models (DEMs). It is therefore natural to pay more attention to DEM construction in the flow chart of digital terrain analysis (Hutchinson and Gallant 2000; Chu et al. 2014; Blanchard, Rogan, and Woodcock 2010). Various techniques used recently to collect elevation points have been generally grouped into the following three categories: ground survey, topographic map, and remote sensing (Fisher and Tate 2006; Noh and Howat 2015; Rastogi, Agrawal, and Ajai 2015). Remote-sensing-based techniques such as photogrammetry (Noh and Howat 2015; Baltsavias 1999), interferometry (Farr et al. 2007; Gómez et al. 2012; Kellndorfer et al. 2004), and light detection and ranging (LiDAR) (Chu et al. 2014; Ackermann 1999; DeWitt, Warner, and Conley 2015) have been widely employed during the past three decades to derive DEMs. However, improper instrument operation, physical limitations of sensors, and bad weather conditions have caused errors during the data acquisition process (Gil et al. 2014; Chirico, Malpeli, and Trimble 2012; Gómez et al. 2012; Zandbergen 2010). Errors are intrinsic attributes of spatial data sets (Yue et al. 2007), and positional errors of sample points have both planimetric and vertical components (DeWitt, Warner, and Conley 2015; Höhle 2013).

Following the rapid development of data acquisition systems, point density of remote-sensing-derived information has become increasingly significant (Tarolli 2014; Müller et al. 2014; Næsset 2015). Moreover, high-density data have been widely used in new fields of application regarding the extraction of three-dimensional (3D) information of features such as buildings, dikes, and breaklines (Vosselman 2012). All of these applications require high positional accuracy in both vertical and horizontal directions.

Because source errors in DEMs can be propagated and magnified through interpolation, which affects the accuracy of DEMs, smoothing interpolation methods rather than exact methods are preferable in the context of DEM construction. Thus far, many classical smoothing methods have been developed for surface modeling, such as nugget variance-based kriging and thin plate spline (TPS). Theoretically, the two methods adopt an essential framework of dividing observations into two components including signal and noise to simultaneously recover the spatially coherent signal and to remove discontinuous noise. Many numerical and real-world examples indicate that smoothing interpolation methods yield satisfactory results in dealing with noisy sample points. For example, Hutchinson and Gessler (1994) proved the smoothness of TPS and recommended this method for analyzing spatial data. Billings, Newsam, and Beatson (2002) achieved a smooth fitting of geographical data by using continuous global surfaces. Grohmann and Steiner (2008) proposed the use of kriging interpolation to resample the Shuttle Radar Topography Mission (SRTM) DEM with a higher resolution, where the nugget effect was used to obliterate SRTM noise. The Australian National University DEM (ANUDEM) was modified to smooth the noise of SRTM in low-relief regions with extensive distributary streamline networks (Hutchinson 2009).

The aforementioned least squares-based smoothing methods focused only on the removing vertical errors of source data without considering horizontal error. This may be reasonable for DEM construction because horizontal errors lead to vertical errors, particularly in steep-slope areas (Fan et al. 2014). However, if no rule is adopted to consider horizontal error, horizontal displacement of a DEM could occur. This result can further influence the positional accuracy of model derivatives such as ridge and valley features (Reinoso 2010). Moreover, this may impose a negative effect on some DEM-based applications such as single-ray intersection (Rodarmel et al. 2006), routine surveying (Lee, Yu, and Pyeon 2003), image registration (Van Niel et al. 2008), and automatic extraction of 3D information (Maas 2003). Thus, horizontal errors of sample points should be addressed in addition to vertical errors during DEM construction.

In statistics, the total least squares method (TLS), introduced by Golub and Van Loan (1980), has been widely used to solve an over-determined system of linear equations in which both dependent and independent variables are subject to errors. TLS is a natural generalization of the least squares approximation method (Schaffrin et al. 2006). In geometry, the least squares and TLS assess the fitting accuracy in different ways: The least squares method minimizes the sum of the squared vertical distances from data points to the fitting surface (line), whereas the TLS method minimizes the sum of the squared orthogonal distances from data points to the fitting surface (line). Hence, TLS is more suitable than the least squares method for addressing both horizontal and vertical errors (Markovsky and Van Huffel 2007). However, TLS cannot be directly applied to DEM construction. Several interpolators have been recently proposed to generate DEMs, such as inverse distance weighting (IDW), ordinary kriging (OK), and multiquadric (MQ) (Lu and Wong 2008; Goovaerts 1997; Franke 1982). Studies have demonstrated that MQ is a satisfactory interpolation method in terms of timing, storage, accuracy, surface visual aesthetics, and ease of implementation (Franke 1982; Aguilar et al. 2005; Chen and Li 2013; Chen et al. 2015). Therefore, the objectives of this paper are (1) to develop a total error-based MQ (MQ-T) to reduce the effects of both horizontal and vertical errors, (2) to test the robustness of MQ-T to both horizontal and vertical errors during surface modeling, and (3) to compare the performance of MQ-T with those of classical interpolations including OK, IDW, and ANUDEM for DEM construction.

The remainder of this paper is organized as follows. Section 2 describes the principle of MQ-T. In Section 3, a numerical test for surface modeling with five groups of synthetic data sets subject to errors with different distributions is employed to compare the robustness of MQ-T with that of the classical MQ. Then, a real-world example of DEM construction with sample points derived from a total station instrument is used to compare the accuracies of MQ-T and MQ with those of classical interpolation methods. A discussion and conclusions are provided in Section 4.

2 Principle of MQ-T

2.1 MQ

If a surface model is formulated as , based on the MQ method, the function value of at the point can be analytically expressed as (Chen et al. 2015)

(1)

where m is the polynomial degree, n is the number of sample points, p_j(x, y) and b_j are the jth basis and coefficient of the polynomial, respectively, r_ij is the distance from the interpolated point (x_i, y_i) to the jth data point, and and w represent a mapping function and its weighting coefficient, respectively.

In order to perform interpolations with MQ, the parameters w and b must be known. Given the training data set , the number of sample points (n) is smaller than that of unknown parameters (n + m). Thus, the ridge regression technique (Hoerl and Kennard 1970) was presently adopted in the estimation of w and b. On the basis of ridge regression, the objective function of MQ can be formulated as

(2)

where , , , e is the error inherent to sample points,, , and c is a smoothing parameter controlling the tradeoff between data fitness and the smoothness of the fitted function.

We constructed the Lagrangian function as follows:

(3)

where is the Lagrange multiplier. The conditions for optimality are given by

(4)

After eliminating w and e, the following equation is obtained:

(5)

where , , , , and is the basis function, which is obtained with a kernel step as . Thus, the matrix formulated in Equation (1) can be transformed into

(6)

for MQ

(7)

where s is a shape parameter. Its optimal value depends on the number and distribution of data points, the data vector, and computation precision (Kansa and Carlson 1992).

After obtaining and b by solving Equation (5), the function value at any point can be computed with Equation (6) without considering w and b. However, only vertical errors inherent to the response variable are considered during MQ computation. In the following section, MQ-T is developed to consider both vertical and horizontal errors, hence building model robustness.

2.2 MQ-T

Equation (1) can be considered as a hyperplane with the normal vector . In geometry, the vertical error of a sample point corresponds to the vertical distance between such a point and the hyperplane, whereas error in both horizontal and vertical directions, or total error, is the orthogonal distance. Thus, we can express the total error as

(8)

where is the total error of the ith sample point.

Similarly, the objective function of MQ-T is derived as

(9)

Compared with MQ, MQ-T is more robust to errors. This is because MQ-T considers errors associated to both response and input variables, whereas MQ computes error related only to the response variable. We constructed the Lagrangian of MQ-T as

(10)

Here, we adopted an iterative scheme to obtain the minimization of . We first fixed the term and computed the variables w and b. Then, based on the newly determined w, the term was updated. The process was repeated until both w and b stabilized.

On the basis of such an iterative scheme, the conditions for MQ-T optimality were determined as

(11)

According to Equation (11),

(12)

Considering , the iterative form of Equation (12) could be expressed as

(13)

where i is the number of iterations.

Equation (5) is a special case of Equation (13) with a null . In practice, the initial value of was computed by solving Equation (5). Then, Equation (13) was iteratively solved until and b converged.

In summary, the procedure of MQ-T for surface modeling involved the following steps:

1. Determine the optimal smoothing parameter c based on k-fold cross-validation in the context of MQ simulation (e.g., k = 10). In k-fold cross-validation, the original sample is randomly partitioned into k equal-sized subsamples. A single individual of the k subsamples is retained as validation data for testing the model, and the remaining k – 1 subsamples are used as training data. The cross-validation process is then repeated k times, where each of the k subsamples is used once as validation data. The k results from the folds can then be combined to produce a single estimation.

2. Solve Equation (5) to obtain the initial values of and b.

3. Iteratively solve Equation (13) until and b stabilize.

4. Perform surface modeling based on Equation (6).

3 Comparative accuracy analyses

In our accuracy analyses, a numerical test and a real-world example were, respectively, employed to assess the interpolation accuracy of MQ-T. In the numerical test, the simulation results of MQ-T were compared with those of MQ for surface modeling with sample points subject to errors drawn from different distributions. In the real-world example, both MQ and MQ-T were used to construct DEMs with sample points derived from a total station instrument. The results were then compared with those of three classical interpolation methods including OK, IDW, and ANUDEM.

3.1 Numerical test

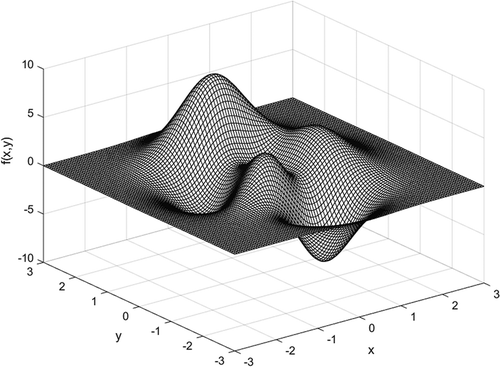
A Gaussian synthetic surface (Figure 1) was employed in the comparative analysis of simulation accuracies associated with MQ and MQ-T, so that the true value could be predetermined to avoid uncertainty arising from uncontrollable data errors. The formulation of the test surface was

(14)

Figure 1. Gaussian synthetic surface.

The computational domain of the test surface was and . The total number of grid cells was 101 × 101, and the grid resolution was 0.06 in both x and y directions. 31 × 31 grid cells were randomly selected as sample points to construct the surface. The sample points were subject to the following errors:

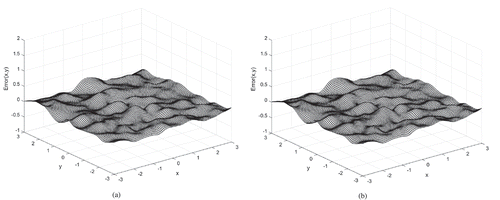
• Case 1: Only vertical (z) errors, drawn from the normal distribution N(0,0.02), with a mean of 0 and a variance of 0.02.

• Case 2: Only horizontal errors; both x and y coordinates are subject to errors. These errors are drawn from the normal distribution N(0,0.01) with a mean of 0 and a variance of 0.01. Thus, the total error variance in the horizontal was 0.02, which is equal to the vertical in Case 1.

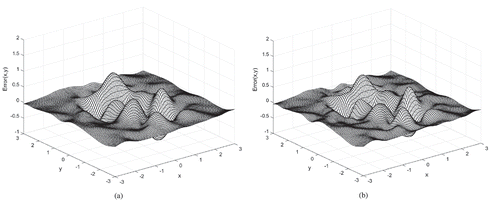
• Case 3: Horizontal and vertical errors both drawn from the normal distribution N(0,0.01). The variance of horizontal errors was larger than that of vertical errors.

• Case 4: Horizontal and vertical errors drawn from the normal distribution N(0,0.01) and N(0,0.02), respectively. The variance of horizontal errors was equal to that of vertical errors.

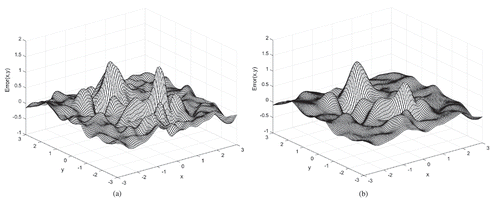
• Case 5: Horizontal and vertical errors drawn from the normal distributions N(0,0.01) and N(0,0.03), respectively. The variance of horizontal errors was smaller than that of vertical errors.

Root mean square error (RMSE), mean error (ME), and error range (ER; maximum error minus minimum error) were adopted as accuracy measures. RMSE and ME are, respectively, expressed as

(15)

(16)

where z_i and s_i represent the ith true and simulated values, respectively; and n represents the number of checkpoints.

Quantitative statistics (Table 1) indicate that MQ and MQ-T are more sensitive to horizontal errors than vertical errors under the same variance (i.e., 0.02) in terms of RMSE and ER. For example, from Case 1 to Case 2, the RMSEs of MQ decrease from 0.0627 to 0.1478, whereas those of MQ-T decrease from 0.0621 to 0.1393. This is reasonable when considering that the least squares method is statistically optimal under a normal distribution of vertical errors. In Case 3, when the sample points are subject to both horizontal and vertical errors, the accuracies of the two interpolators are lower than those in Cases 1 and 2 in terms of RMSE and ME. With the increase in vertical error variance from 0.01 in Case 3 to 0.03 in Case 5, MQ and MQ-T return their best and worst results in Cases 4 and 5, respectively. For example, the ERs of MQ and MQ-T in Case 4 are 1.1085 and 1.1804, whereas those in Case 5 are 2.2270 and 1.6714, respectively. This indicates that the increase ratio of ER is 100% for MQ and only 41% for MQ-T. Hence, MQ-T has a high robustness to sampling errors. Irrespective of error distributions in the five cases, MQ-T is more accurate than MQ in terms of RMSE.

Table 1. Accuracy comparison between MQ and MQ-T under different error distributions.

Case	Error distribution		Method	Smoothing parameter	RMSE	ME	ER
	x and y	z
Case 1	–	N(0,0.02)	MQ	16.01	0.0627	0.0066	0.4733
			MQ-T	4568.0	0.0621	0.0066	0.4502
Case 2	N(0,0.01)	–	MQ	21.43	0.1478	−0.0030	1.6228
			MQ-T	2454.2	0.1393	−0.0021	1.4379
Case 3	N(0,0.01)	N(0,0.01)	MQ	3.64	0.1749	−0.0227	1.5247
			MQ-T	3349.5	0.1637	−0.0235	1.4133
Case 4	N(0,0.01)	N(0,0.02)	MQ	25.47	0.1587	−0.0141	1.1085
			MQ-T	1497.5	0.1427	−0.0158	1.1804
Case 5	N(0,0.01)	N(0,0.03)	MQ	31.11	0.2083	0.0263	2.2270
			MQ-T	867.8	0.1791	0.0261	1.6714

The error surfaces of MQ and MQ-T for Cases 1, 3, and 5 are shown in Figures 2–4, respectively. Regardless of the interpolation method, all surfaces become rougher with increasing error standard deviation. MQ and MQ-T yield similar results for all cases. Comparatively, MQ-T reveals a slightly flatter surface than MQ for Case 5.

Figure 2. Error surfaces of (a) MQ and (b) MQ-T for Case 1.

Figure 3. Error surfaces of (a) MQ and (b) MQ-T for Case 3.

Figure 4. Error surfaces of (a) MQ and (b) MQ-T for Case 5.

3.2 Real-world example

3.2.1 Study site and data collection

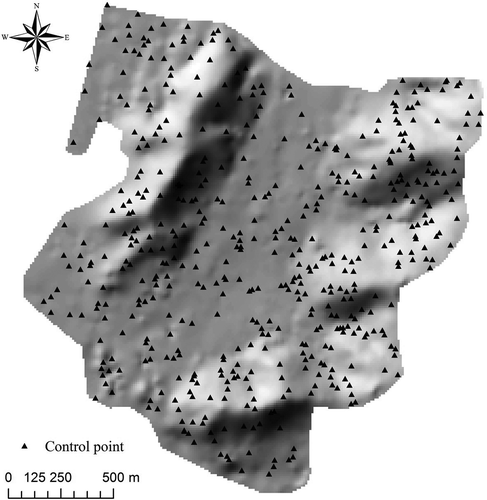
The study area, located in Jinan city, Shandong province, China (36°40′N, 117°00′E), covers an area of 3.36 km² limited by Mount Taishan to the south and the Yellow River to the north. The elevations range from 109.6 to 364.5 m with a mean elevation of 181.0 m and standard deviation of 51.1 m. To improve the sampling accuracy, 500 control points were first measured (Figure 5) in the study area by using global navigation satellite system real-time kinematic with vertical and horizontal accuracies of 2 and 1 cm, respectively. Then, based on these control points, 5394 points with vertical and horizontal accuracies of 3 and 2 cm, respectively, were collected by a total station instrument with three surveyors. The sampling density was 0.0016 point/m², and the corresponding sampling interval (SI) was 25 m.

Figure 5. Distribution of the 500 control points in the study site.

3.2.2 Classical interpolation methods

In addition to MQ and MQ-T, classical interpolation methods such as OK, IDW, and ANUDEM were used for DEM construction. OK and IDW belong to smoothing and exact interpolation categories, respectively, and are widely employed in DEM construction (Goovaerts 1997; Hutton and Brazier 2012). ANUDEM is an interpolation method specifically designed for the creation of hydrologically correct DEMs (Hutchinson 1989). For OK, a semivariogram must be manually fitted before performing interpolations. In the present work, OK was conducted by using GS+ geostatistical software. This computer code provides all geostatistical components, including semivariance analysis through kriging and mapping, in a single integrated software program that is well known for its flexibility and user-friendly interface. The interpolation result of IDW depends on the power parameter and the number of neighboring points. The optimal parameters of IDW were selected by using the 10-fold cross-validation technique. For ANUDEM, the value of the vertical standard error parameter is equal to the nugget variance square root of the semivariogram. Both IDW and ANUDEM were performed by using the Spatial Analyst Tools Module of ArcGIS 10.2.

3.2.3 Results

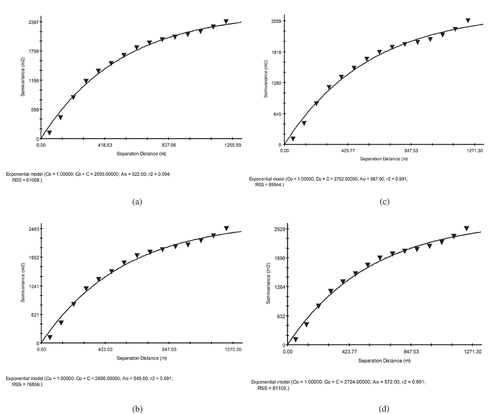
First, four groups of data sets with different SIs were drawn from the original sample points to construct 10-m-resolution DEMs. The relationship between the SI and the number of sample points is depicted in Table 2. Table 3 provides the optimal parameters of IDW, ANUDEM, MQ, and MQ-T under different SIs, and Figure 6 displays the kriging semivariograms.

Table 2. Relationship between the number of sample points and sample interval (SI).

Number of sample points	SI (m)
2100	40
2742	35
3721	30
5394	25

Table 3. Optimal parameters of IDW, ANUDEM, MQ, and MQ-T under different SIs.

Methods	Parameter	SI (m)
		40	35	30	25
IDW	Number of neighbors	5	10	5	15
	Power	2	3	2	3
ANUDEM	Vertical standard error	1	1	1	1
MQ	Smoothing parameter	0.50	1.76 × 10^−^4	4.03 × 10^−^3	1.28 × 10^−^4
MQ-T	Smoothing parameter	1.48	7.87 × 10^−^3	4.67 × 10^−^4	4.87 × 10^−^3

Figure 6. Kriging semivariograms fitted with different sample point groups. (a) Semivariogram fitted with 2100 points (i.e., SI = 40 m), (b) semivariogram fitted with 2742 points (i.e., SI = 35 m), (c) semivariogram fitted with 3721 points (i.e., SI = 30 m), and (d) semivariogram fitted with 5394 points (i.e., SI = 25 m).

The 500 control points were used to assess the accuracies of the DEMs. The results, shown in Table 4, indicate that irrespective of the interpolation method, the involved accuracy becomes lower in terms of RMSE with an increase in SI. For example, when the SI increases from 25 to 40 m, the RMSEs of IDW, OK, and ANUDEM change from 2.48 to 3.65 m, 1.84 to 2.43 m, and 2.28 to 2.68 m, respectively, whereas the changes in MQ and MQ-T are from 1.73 to 2.38 m and 1.73 to 2.26 m, respectively. Comparatively, MQ and MQ-T have better performances than the classical interpolators for all SIs. Moreover, MQ-T is slightly more accurate than MQ concerning all SIs, except when SI = 25 m. On average, MQ-T has the best performance, closely followed by MQ and OK. Specifically, the RMSEs of IDW, OK, ANUDEM, and MQ are 3.05, 2.22, 2.49, and 2.11 m, respectively, while that of MQ-T is 2.04 m. Namely, the accuracy of MQ-T is about 33.1%, 8.1%, and 18.1% higher than those of IDW, OK, and ANUDEM, respectively.

Table 4. RMSEs of all interpolation methods for 10-m-resolution DEM construction under different SIs in the real-world example (unit: m).

SI	IDW	OK	ANUDEM	MQ	MQ-T
40	3.65	2.43	2.68	2.38	2.26
35	3.11	2.37	2.55	2.24	2.11
30	2.97	2.22	2.43	2.09	2.06
25	2.48	1.84	2.28	1.73	1.73
Average	3.05	2.22	2.49	2.11	2.04

We then investigated the effect of spatial resolution, that is, 40, 30, 20, and 10 m, on the accuracies of the DEMs under SI = 30 m. The results, shown in Table 5, indicate that the accuracies of all interpolation methods increase with increasing DEM resolution. Furthermore, MQ-T is more accurate than the classical interpolators. On average, MQ-T produces the best results. Specifically, the RMSEs of IDW, OK, ANUDEM, and MQ are 3.69, 3.28, 3.77, and 3.20 m, respectively, while that of MQ-T is 3.06 m. MQ-T is about 1.21, 1.07, 1.23, and 1.05 times as accurate as IDW, OK, ANUDEM, and MQ, respectively.

Table 5. RMSEs of all interpolation methods for different resolution DEM construction under 30-m SI in the real-world example (unit: m).

Resolution	IDW	OK	ANUDEM	MQ	MQ-T
40	4.55	4.63	5.17	4.49	4.27
30	3.98	3.50	4.32	3.57	3.45
20	3.27	2.77	3.14	2.65	2.44
10	2.97	2.22	2.43	2.09	2.06
Average	3.69	3.28	3.77	3.20	3.06

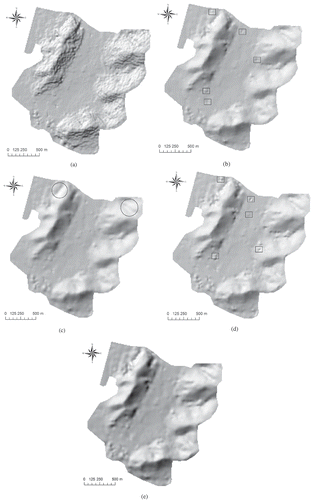
The hillshades of 10-m-resolution DEMs constructed with SI = 35 m are shown in Figure 7. The results indicate that IDW generates the roughest surface, particularly in the left and right boundary areas. The surfaces of OK and MQ are significantly smoother than that of IDW. However, many isolated pits and artificial mounds are present, as flagged by the rectangles in Figures 7(b) and (d). The map of ANUDEM is so smooth that many subtle terrain features disappeared, such as those marked by the circles in Figure 7(c). Comparatively, MQ-T produces a better result in which the subtle terrain features are maintained and the artificial pits and mounds are removed.

Figure 7. Hillshades of (a) IDW, (b) OK, (c) ANUDEM, (d) MQ, and (e) MQ-T for 10-m-resolution DEMs constructed with 35-m SI. Isolated pits and artificial mounds are flagged by the rectangles in the maps of OK and MQ. Omitted subtle terrain features are marked by the circles in the map of ANUDEM.

To assess computational cost, we list the computing time of all interpolation methods spent in the construction of 10-m-resolution DEMs with 2100 sample points. A desktop computer with a 64-bit Windows 7 operating system, a quad-core Intel (R) Core™ i7-4790 CPU, 3.6 GHz, and 8 GB memory was used in the experiment. The gathered observations (Table 6) demonstrate that IDW is the fastest method. This result is expected because IDW is a point-to-point interpolation procedure with no solution of linear systems. ANUDEM is significantly faster than OK, MQ, and MQ-T owing to the very sparse system of linear equations involved in ANUDEM, which can be efficiently solved (Hutchinson 1989). MQ-T has the lowest speed because it employs an iterative procedure to smooth both horizontal and vertical errors. OK and MQ solve their systems only once; thus, they are more efficient than MQ-T.

Table 6. Computational costs of all methods for constructing 10-m-resolution DEMs with 2100 sample points (i.e., SI = 40 m).

Methods	Computing time (s)
IDW	0.38
OK	8.61
ANUDEM	2.60
MQ	8.63
MQ-T	12.25

To reflect the relationship established between DEM error and terrain slope, correlation coefficients between the terrain slopes and interpolation errors for DEMs under SI = 30 m at 500 control points were determined (Table 7). In comparison, the interpolation errors of OK have the strongest and weakest correlations with terrain slopes for 40-m- and 10-m-resolution DEMs, respectively. The associated correlation coefficients are 0.588 and 0.310, respectively. On average, IDW and MQ have the weakest and strongest correlations with the values of 0.382 and 0.505, respectively.

Table 7. Correlation coefficients between interpolation errors and terrain slopes for DEMs under 30-m SI.

Resolution	IDW	OK	ANUDEM	MQ	MQ-T
40	0.320	0.588	0.552	0.535	0.537
30	0.343	0.540	0.529	0.566	0.487
20	0.481	0.478	0.468	0.580	0.519
10	0.382	0.310	0.341	0.340	0.333
Average	0.382	0.479	0.473	0.505	0.469

4 Discussion and conclusions

4.1 Discussion

Thus far, many studies have been conducted to investigate the effect of various factors on the accuracy of DEMs, such as topographic variability, sampling density, interpolation method, and spatial resolution (Anderson, Thompson, and Austin 2005; Anderson et al. 2006; Guo et al. 2010; Liu and Zhang 2011; Aguilar et al. 2005). All relevant studies agree that morphology has the most significant influence on DEM quality, followed by sampling density and the interpolation method used. Moreover, few differences exist between interpolation methods if the sampling density is high. However, for areas with low sample density, it is very important to select a proper interpolator (Erdogan 2009; Chaplot et al. 2006; Weber and Englund 1992; Lu and Wong 2008; Guo et al. 2010). In the present investigation, we found that irrespective of sample density, MQ-T is more accurate than IDW, OK, ANUDEM, and MQ for producing DEMs with different resolutions. The high accuracy of MQ-T is related to its ability to smooth both horizontal and vertical errors inherent to sample points. In our study, only one hilly area was employed to validate the efficiency of MQ-T. Considering the significant effect of terrain morphology on DEM accuracy, future research will concentrate on validating the robustness of MQ-T under different landforms.

In our test, the implementation codes of MQ and MQ-T were programed with MATLAB software, which offers ease in solving linear equation systems. We found that MQ-T is significantly slower than the other methods (Table 6), because it requires iteratively solving a system of linear equations. Theoretically, the solution of linear equation systems makes MQ-T computationally impossible for large data sets typical of LiDAR-derived files. In practice, we demonstrated that when the number of sample points was 100,000, the MQ-T program could not work with our computer, issuing an out-of-memory warning. This problem can be overcome by performing the function locally. In the process of local interpolation, only those points located in the neighborhood of a given point to be estimated are used to conduct interpolations (Cleveland and Devlin 1988); however, the local interpolation scheme may lead to minor discontinuities in the resulting surface. Alternatively, it is possible to conduct a segmentation procedure with a flexible overlapping neighborhood (Mitasova and Hofierka 1993). In this method, the interpolation function is performed within a segment using the points located within it and additional points from its neighborhood. This guarantees a smooth connection of segments and is thus an efficient solution of the system of linear equations.

4.2 Conclusions

Stemming from TLS methods for addressing dependent and independent variable errors in linear equation systems, an MQ-T method has been developed in the present work to reduce the effect of both horizontal and vertical errors of sample points on the accuracy of DEMs. Two examples, including a numerical test and a real-world example, were employed to assess the interpolation accuracy of MQ-T. In the numerical test, the performances of MQ-T and MQ for surface modeling were compared under five groups of simulated data sets subject to errors with different distributions. The results showed that irrespective of error distribution, MQ-T is more accurate than MQ in terms of RMSE. The real-world example of DEM construction demonstrated that MQ-T produces better results than both MQ and classical interpolation methods including IDW, OK, and ANUDEM in terms of RMSE regardless of the sample interval and DEM resolution. Therefore, MQ-T can be considered as an alternative method for interpolating sample points subject to both horizontal and vertical errors.

Acknowledgments

This work is supported by National Natural Science Foundation of China [grant number 41371367], [grant number 41101433]; Qingdao Science and Technology Program of Basic Research Project [grant number 13-1-4-239-jch]; SDUST Research Fund; Joint Innovative Center for Safe And Effective Mining Technology and Equipment of Coal Resources, Shandong Province; and Special Project Fund of Taishan Scholars of Shandong Province.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work is supported by National Natural Science Foundation of China [grant number 41371367], [grant number 41101433]; Qingdao Science and Technology Program of Basic Research Project [grant number 13-1-4-239-jch]; SDUST Research Fund; Joint Innovative Center for Safe And Effective Mining Technology and Equipment of Coal Resources, Shandong Province; and Special Project Fund of Taishan Scholars of Shandong Province.