Recovery of parameters of cancellous bone by acoustic interrogation

Abstract

The parameter recovery problem for cancellous bone by acoustic interrogation is investigated numerically. Biot’s equations coupled with boundary integral equations are used to model ultrasound propagation through a bone sample immersed in a water tank. The mathematical formulation for two-dimensional orthotropic bone is presented, but numerical results are only discussed in the isotropic case. The inversion procedure consists in minimizing some error on the pressure at measurement points located outside the bone sample. For this purpose, two different minimization algorithms are considered. A number of numerical tests are performed for a range of frequencies, which demonstrate the model’s ability to recover some bone parameters with satisfactory accuracy.

Keywords:

• Biot model
• boundary integral equation
• cancellous bone
• minimization procedure
• ultrasound

AMS Subject Classifications:

• 31A25
• 35R30
• 49N45
• 74A65
• 74G75
• 76Q05

1. Introduction

Since 70% of the variance of bone strength is accounted for by bone density, quantitative ultrasound techniques could provide an important new diagnostic tool.[1–26] Moreover, in contrast to X-ray densitometry, ultrasound which also measures bone density does not ionize the tissue, and its implementation is relatively inexpensive. Since the loss of bone density and the destruction of bone microstructure is most evident in osteoporotic cancellous bone, which consists of trabeculae and marrow, it is natural to consider the possibility of developing accurate ultrasound models for the insonification of cancellous bone. It would be of enormous clinical advantages if accurate methods could be developed using ultrasound interrogation to diagnose osteoporosis and bone fractures.

Cancellous bone is a two-component material consisting of a calcified bone matrix with interstitial fatty marrow. Hence, mathematical models such as Biot’s model for poroplastic media are applicable.[18, 27–32] One particular ultrasonic technique for assessing bone mineral density is by measuring the calcaneal broadband ultrasonic attenuation (BUA) and speed of sound, which are highly correlated with calcaneal bone mineral density.[25, 33] This method uses the travel time of sound between two transducers with a bone sample between them and the travel time in the absence of the specimen to determine the compressional wave velocity in the bone.

Another experiment involves measuring the spectra of the phase velocity $c(\mathit{\omega })$ and of the attenuation rate $\mathit{\alpha }(\mathit{\omega })$, where $\mathit{\omega }$ is the frequency of the sound wave. Many investigations reported that the attenuation is linear from 200 to 600 kHz and also from 600 kHz to 1 MHz,[16, 17, 19] i.e. $\mathit{\alpha }(\mathit{\omega })$ is assumed to be a linear function as $\mathit{\alpha }(\mathit{\omega })=\mathrm{BUA}\mathit{\omega }+K$ with $K$ being a constant. The BUA coefficient is the gradient in dB/MHz evaluated by linear regression and is thought relevant to the evaluation of osteoporosis.[7] Hoffmeister et al. [34] found that, in the range 0.5–1 MHz, BUA exhibits a significant correlation with the anterior–posterior and medial–lateral directions but not in the superior–inferior orientation. A break point in the slopes was observed at about 1 MHz, whereas other researchers observed one at about 400 kHz. Others observed measurable nonlinear attenuation at frequencies below 400 kHz for unfatted bone from human cadavers.[23] Langton et al. [17] found that the BUA value of the ultrasonic spectrum measured on the calcaneus is significantly lower in older women with osteoporotic fracture compared to younger women without these fractures. However, Chaffai et al. [4] found that attenuation varies in terms of frequency roughly as ${\mathit{\omega }}^{1.1\pm 0.3}$.

Hodgskinson et al. [35] found that density is a good predictor of stiffness of cancellous bone and as there is also a good correlation between strength and stiffness, it is also a good predictor of strength. In that paper, the authors investigated the ability of ultrasound to predict the mechanical properties of cancellous bone. They found that the speed of sound in cubes of cancellous bone can give structure-specific information and that indeed knowledge of both density and velocity allows for a better prediction of stiffness than either density or velocity alone. Ashman et al. [1], Ashman and Rho [2] used ultrasound to measure the elastic properties of cancellous bone, whereas Fry and Barger [9] used ultrasound to characterize both cortical and cancellous bone.

Moreover, bone rigidity depends to a large extent not only on bone density but also on the trabecular microstructure. This microstructure determines the Biot bone parameters, i.e. they may be determined using homogenization theory.[36–38] Use of Biot’s model requires determination of the parameters upon which it depends. This can be an expensive process if done experimentally. In the present paper, we investigate whether these parameters can be ascertained by acoustic interrogation. We revisit the parameter identification problem for two-dimensional bone samples, which we have previously investigated in simplified cases,[27–30, 39] the understanding being that this is a predecessor to the full three-dimensional problem.

In Buchanan and Gilbert [27], Buchanan et al. [28], the bone sample was situated in a water tank and we used a boundary element method to model the direct problem and the inversion procedure. The direct problem was solved using a finer mesh size than in the inversion procedure. Some noise was also added to the solution of the direct problem. In these works, simulations were performed for bone specimens of relatively high porosities, and five Biot parameters (porosity $\mathit{\beta }$, permeability $k$, pore size $a$ and real parts of the bulk and shear moduli, Re $K_b$ and Re $\mathit{\mu }$) were determined. The algorithm was uniformly successful in finding the porosity to within 3%. Errors for the remaining parameters were often higher, but the target values of these parameters varied over at least one order of magnitude. The procedure took much CPU time because of the eigenvalues introduced by a finite water tank. The papers [29, 30] were an attempt to do away with the water tank and we modelled the problem by replacing the bone sample by an infinite slab. In this case, we were able to numerically compute, to great accuracy, the Green’s function for the source in the water using residue calculus. The results were for the most part reasonable; however, inversion times were long, ranging from six to nine hours. Table 1 summarizes the results of the various inversion schemes used in Buchanan and Gilbert [30]. More recently, Buchanan et al. [40] investigated an indirect inversion approach based on the numerical solution for a set of effective velocities and transmission coefficients in order to ameliorate the difficulties posed by a direct minimization.

Table 1. Summary of the average and worst errors made by five variants of the inversion algorithm for Problems 71w, ..., 91w in Buchanan and Gilbert [30]: Two-phase algorithm with univariate Phase 1; Two-phase algorithm with alternative Phase 1; Three-phase algorithm using the result with the lowest objective function value; Three-phase algorithm using the midpoint of the lowest and highest values; Three-phase algorithm using the mean. See [30] for more details.

Variant	Error	$\mathit{\beta }$ (%)	$k$ (%)	$a$ (%)	$\mathrm{R}e{K}_b$ (%)	$\mathrm{R}e\mathit{\mu }$ (%)
Phase 2	Avg.	0.36	10.33	12.13	5.41	7.62
	Worst	1.13	25.75	28.94	17.59	28.59
Phase 2 Alt	Avg.	0.58	15.47	17.54	3.50	4.77
	Worst	2.41	26.09	29.46	6.92	12.42
Phase 3 Obj	Avg.	0.53	13.99	15.50	6.11	7.58
	Worst	2.02	30.24	34.10	17.59	28.59
Phase 3 Mid	Avg.	0.30	12.52	15.87	9.57	9.60
	Worst	0.77	23.41	27.44	23.06	21.86
Phase 3 Mean	Avg.	0.30	12.27	13.31	7.60	8.88
	Worst	0.94	23.52	25.94	21.12	34.73

In the present paper, we consider an improved Biot model for orthotropic bone, accounting for dissipation due to tortuosity (i.e. due to the presence of pores of arbitrary size). The bone sample is taken to be a square, and an efficient numerical scheme is devised by adopting a boundary integral formulation for the water tank, so that we need not solve for the entire domain. Only the region occupied by the bone sample is discretized as in Buchanan and Gilbert [27], Buchanan et al. [28], Gilbert et al. [39]. Section 2 presents Biot’s model for cancellous bone in the orthotropic and isotropic cases. Section 3 describes the boundary integral formulation for a two-dimensional bone sample immersed in a water tank. Section 4 outlines the numerical scheme to solve the governing equations. Section 5 discusses the inversion results, including convergence and sensitivity tests. Three Biot parameters are examined (porosity, and real parts of the bulk and shear moduli). Finally, concluding remarks are given in Section 6.

2. Biot model for cancellous bone

2.1. Orthotropic case

The Biot–Stoll model treats a poroplastic medium as an elastic frame with interspinal pore fluid.[41–43] Cancellous bone is anisotropic; however, as pointed out by Williams [32], if the acoustic waves passing through it travel in the trabecular direction, then an isotropic model may be acceptable. We will simulate a two-dimensional version of the experiments described in McKelvie and Palmer [18] and Hosokawa and Otani [31]. The motions of the frame and fluid within the bone are tracked by position vectors $\mathbf{u}=(u_1,u_2)$ and $\mathbf{U}=(U_1,U_2)$, respectively. In Cartesian coordinates $(x_1,x_2)$, the two-dimensional constitutive equations relating strain to stress, for an orthotropic material,[44] read$$\begin{array}{cc}\hfill {\mathit{\sigma }}_{11}& =\frac{E_1{e}_{11}+{\mathit{\nu }}_1{E}_2{e}_{22}}{(1-{\mathit{\nu }}_1{\mathit{\nu }}_2)}+Q\mathit{ϵ},\hfill \\ \hfill {\mathit{\sigma }}_{22}& =\frac{{\mathit{\nu }}_2{E}_1{e}_{11}+E_2{e}_{22}}{(1-{\mathit{\nu }}_1{\mathit{\nu }}_2)}+Q\mathit{ϵ},\hfill \\ \hfill {\mathit{\sigma }}_{12}& =\mathit{\mu }{e}_{12},{\mathit{\sigma }}_{21}=\mathit{\mu }{e}_{21},\hfill \\ \hfill s& =Qe+R\mathit{ϵ},\hfill \end{array}$$

where the solid and fluid dilatations are given by(1) $$\begin{array}{c}\hfill e=\mathrm{\nabla }·\mathbf{u}=\frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_1}+\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_2},\mathit{ϵ}=\mathrm{\nabla }·\mathbf{U}=\frac{\mathit{\partial }{U}_1}{\mathit{\partial }{x}_1}+\frac{\mathit{\partial }{U}_2}{\mathit{\partial }{x}_2},\end{array}$$(1)

and the strains are defined by(2) $$\begin{array}{c}\hfill e_{11}=\frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_1},e_{12}=e_{21}=\frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_2}+\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_1},e_{22}=\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_2}.\end{array}$$(2)

The parameters $E_1$ and $E_2$ denote the Young moduli, and ${\mathit{\nu }}_1$ and ${\mathit{\nu }}_2$ denote the Poisson ratios, in the $x_1$- and $x_2$-directions, respectively. In compliance form, Equations (1(1) $$\begin{array}{c}\hfill e=\mathrm{\nabla }·\mathbf{u}=\frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_1}+\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_2},\mathit{ϵ}=\mathrm{\nabla }·\mathbf{U}=\frac{\mathit{\partial }{U}_1}{\mathit{\partial }{x}_1}+\frac{\mathit{\partial }{U}_2}{\mathit{\partial }{x}_2},\end{array}$$(1) ) and (2(2) $$\begin{array}{c}\hfill e_{11}=\frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_1},e_{12}=e_{21}=\frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_2}+\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_1},e_{22}=\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_2}.\end{array}$$(2) ) become$$\begin{array}{cc}& e_{11}=-\frac{{\mathit{\nu }}_2{Q}^2{\mathit{\sigma }}_{22}{\mathit{\nu }}_1-{\mathit{\nu }}_2{Q}^2{\mathit{\nu }}_1{\mathit{\sigma }}_{11}+{\mathit{\sigma }}_{22}{\mathit{\nu }}_1{E}_{2}R-Q{\mathit{\nu }}_1{E}_{2}s-Q^2{\mathit{\sigma }}_{22}-E_{2}R{\mathit{\sigma }}_{11}+E_{2}sQ+Q^2{\mathit{\sigma }}_{11}}{-Q^2{E}_1+R{E}_2{E}_1+{\mathit{\nu }}_1{E}_{2}s{Q}^2+Q^2{\mathit{\nu }}_2{E}_1{E}_2-E_2{Q}^2},\hfill \\ \hfill & e_{22}=\frac{-{\mathit{\nu }}_2{Q}^2{\mathit{\nu }}_1{\mathit{\sigma }}_{11}+{\mathit{\nu }}_2{Q}^2{\mathit{\sigma }}_{22}{\mathit{\nu }}_1{E}_1+Q^2{\mathit{\sigma }}_{11}-Q^2{\mathit{\sigma }}_{22}+s{\mathit{\nu }}_2{E}_{1}Q-s{E}_{1}Q-R{\mathit{\nu }}_2{\mathit{\nu }}_1{E}_1{\mathit{\sigma }}_{11}+R{E}_1{\mathit{\sigma }}_{22}{\mathit{\nu }}_2}{-Q^2{E}_1+R{E}_2{E}_1+{\mathit{\nu }}_1{E}_2{Q}^2+Q^2{\mathit{\nu }}_2{E}_1-E_2{Q}^2},\hfill \\ \hfill & e_{12}=\frac{{\mathit{\sigma }}_{12}}{\mathit{\mu }},\hfill \\ \hfill & \mathit{ϵ}=\frac{-E_{2}Q{\mathit{\sigma }}_{11}+{\mathit{\nu }}_2{E}_{1}Q{\mathit{\sigma }}_{11}{\mathit{\sigma }}_{12}+{\mathit{\nu }}_1{E}_{2}Q{\mathit{\sigma }}_{22}+E_1{E}_{2}s-E_{1}Q{\mathit{\sigma }}_{22}}{-Q^2{E}_1+R{E}_2{E}_1+{\mathit{\nu }}_1{E}_2{Q}^2+Q^2{\mathit{\nu }}_2{E}_1-E_2{e}_{11}{Q}^2}.\hfill \end{array}$$

Assuming no body forces, an argument based upon Lagrangian dynamics [41, 45] leads to the following equations of motion for the displacements and dilatations,(3) $$\begin{array}{cc}\hfill \left(\mathit{\mu }{\mathbb{H}}^{\top }+\frac{1}{1-{\mathit{\nu }}_1{\mathit{\nu }}_2}\mathbb{E}\mathbb{H}\right)\mathbf{u}+Q\mathbb{H}\mathbf{U}& =\frac{{\mathit{\partial }}^2}{\mathit{\partial }{t}^2}({\mathit{\rho }}_{11}\mathbf{u}+{\mathit{\rho }}_{12}\mathbf{U})+b\frac{\mathit{\partial }}{\mathit{\partial }t}(\mathbf{u}-\mathbf{U}),\hfill \\ \hfill \mathrm{\nabla }(Qe+R\mathit{ϵ})& =\frac{{\mathit{\partial }}^2}{\mathit{\partial }{t}^2}({\mathit{\rho }}_{12}\mathbf{u}+{\mathit{\rho }}_{22}\mathbf{U})-b\frac{\mathit{\partial }}{\mathit{\partial }t}(\mathbf{u}-\mathbf{U}),\hfill \end{array}$$(3)

where$$\mathbb{H}:=\left(\begin{array}{cc}\frac{{\mathit{\partial }}^2}{\mathit{\partial }{x}_1^2}& \frac{{\mathit{\partial }}^2}{\mathit{\partial }{x}_1\mathit{\partial }{x}_2}\\ \frac{{\mathit{\partial }}^2}{\mathit{\partial }{x}_1\mathit{\partial }{x}_2}& \frac{{\mathit{\partial }}^2}{\mathit{\partial }{x}_2^2}\end{array}\right),$$

is the Hessian matrix operator, ${\mathbb{H}}^{\top }$ is its transpose and$$\mathbb{E}:=\left(\begin{array}{cc}{E}_1& {\mathit{\nu }}_2{E}_1\\ {\mathit{\nu }}_1{E}_2& E_2\end{array}\right).$$

Here, ${\mathit{\rho }}_{11}$ and ${\mathit{\rho }}_{22}$ are density parameters for the solid and fluid, respectively, ${\mathit{\rho }}_{12}$ is a density coupling parameter, and $b$ is a dissipation parameter. These are calculated from the inputs of Table 2 using the formulas$$\begin{array}{cc}\hfill {\mathit{\rho }}_{11}& =(1-\mathit{\beta }){\mathit{\rho }}_r-\mathit{\beta }({\mathit{\rho }}_f-T\mathit{\beta }),\hfill \\ \hfill {\mathit{\rho }}_{12}& =\mathit{\beta }({\mathit{\rho }}_f-T\mathit{\beta }),\hfill \\ \hfill {\mathit{\rho }}_{22}& =T{\mathit{\beta }}^2,\hfill \end{array}$$

where $T$ is the tortuosity.

Table 2. Parameters in Biot’s model for cancellous bone.

Symbol	Parameter
${\mathit{\rho }}_f$	Density of the pore fluid
${\mathit{\rho }}_r$	Density of frame material
$K_b$	Complex frame bulk modulus
$\mathit{\mu }$	Complex frame shear modulus
$K_f$	Fluid bulk modulus
$K_r$	Frame material bulk modulus
$\mathit{\beta }$	Porosity
$\mathit{\eta }$	Viscosity of pore fluid
$\mathrm{\Lambda }$	Viscous characteristic length
${\mathit{\alpha }}_{\infty }$	Asymptotic tortuosity
$k$	Permeability

In the time-harmonic case,$$\mathbf{u}(x_1,x_2,t)=\widehat{\mathbf{u}}(x_1,x_2)e^{i\mathit{\omega }t},\mathbf{U}(x_1,x_2,t)=\widehat{\mathbf{U}}(x_1,x_2)e^{i\mathit{\omega }t}.$$

Substituting these representations into (3(3) $$\begin{array}{cc}\hfill \left(\mathit{\mu }{\mathbb{H}}^{\top }+\frac{1}{1-{\mathit{\nu }}_1{\mathit{\nu }}_2}\mathbb{E}\mathbb{H}\right)\mathbf{u}+Q\mathbb{H}\mathbf{U}& =\frac{{\mathit{\partial }}^2}{\mathit{\partial }{t}^2}({\mathit{\rho }}_{11}\mathbf{u}+{\mathit{\rho }}_{12}\mathbf{U})+b\frac{\mathit{\partial }}{\mathit{\partial }t}(\mathbf{u}-\mathbf{U}),\hfill \\ \hfill \mathrm{\nabla }(Qe+R\mathit{ϵ})& =\frac{{\mathit{\partial }}^2}{\mathit{\partial }{t}^2}({\mathit{\rho }}_{12}\mathbf{u}+{\mathit{\rho }}_{22}\mathbf{U})-b\frac{\mathit{\partial }}{\mathit{\partial }t}(\mathbf{u}-\mathbf{U}),\hfill \end{array}$$(3) ) and dropping, the hats give$$\begin{array}{cc}\hfill \left(\mathit{\mu }{\mathbb{H}}^{\top }+\frac{1}{1-{\mathit{\nu }}_1{\mathit{\nu }}_2}\mathbb{E}\mathbb{H}\right)\mathbf{u}+Q\mathbb{H}\mathbf{U}+{\tilde{p}}_{11}\mathbf{u}+{\tilde{p}}_{12}\mathbf{U}& =\mathbf{0},\hfill \\ \hfill \mathrm{\nabla }(Qe+R\mathit{ϵ})+{\tilde{p}}_{12}\mathbf{u}+{\tilde{p}}_{22}\mathbf{U}& =\mathbf{0},\hfill \end{array}$$

where$${\tilde{p}}_{11}:={\mathit{\omega }}^2{\mathit{\rho }}_{11}-i\mathit{\omega }b,{\tilde{p}}_{12}:={\mathit{\omega }}^2{\mathit{\rho }}_{12}+i\mathit{\omega }b,{\tilde{p}}_{22}:={\mathit{\omega }}^2{\mathit{\rho }}_{22}-i\mathit{\omega }b.$$

Following Fellah et al. [7, 8], an improvement over the standard Biot–Stoll model is obtained by replacing the assumption of cylindrical pores in the dissipation term by a more realistic configuration.[46] This yields$$\begin{array}{cc}\hfill \left(\mathit{\mu }{\mathbb{H}}^{\top }+\frac{1}{1-{\mathit{\nu }}_1{\mathit{\nu }}_2}\mathbb{E}\mathbb{H}\right)\mathbf{u}+Q\mathbb{H}\mathbf{U}+p_{11}\mathbf{u}+p_{12}\mathbf{U}& =\mathbf{0},\hfill \\ \hfill \mathrm{\nabla }(Qe+R\mathit{ϵ})+p_{12}\mathbf{u}+p_{22}\mathbf{U}& =\mathbf{0},\hfill \end{array}$$

where$$p_{11}:={\mathit{\omega }}^2[(1-\mathit{\beta }){\mathit{\rho }}_r+\mathit{\beta }{\mathit{\rho }}_f(\mathit{\alpha }(\mathit{\omega })-1)],p_{12}:=-{\mathit{\omega }}^2\mathit{\beta }{\mathit{\rho }}_f(\mathit{\alpha }(\mathit{\omega })-1),p_{22}:={\mathit{\omega }}^2\mathit{\beta }{\mathit{\rho }}_f\mathit{\alpha }(\mathit{\omega }),$$

and$$\mathit{\alpha }(\mathit{\omega })={\mathit{\alpha }}_{\infty }\left(1+\frac{i\mathit{\eta }\mathit{\beta }}{\mathit{\omega }{\mathit{\alpha }}_{\infty }{\mathit{\rho }}_{f}k}\sqrt{1+\frac{4{\mathit{\alpha }}_{\infty }^2{k}^2{\mathit{\rho }}_f\mathit{\omega }}{i\mathit{\eta }{\mathrm{\Lambda }}^2{\mathit{\beta }}^2}}\right).$$

It is inconvenient to use both the solid displacement $\mathbf{u}$ and the fluid displacement $\mathbf{U}$ as unknowns. A more convenient set of unknowns are the solid displacement and the pressure $s=Qe+R\mathit{ϵ}$. To this end, we make the substitutions(4) $$\begin{array}{c}\hfill \mathbf{U}=-\frac{1}{p_{22}}\left(\mathrm{\nabla }s+p_{12}\mathbf{u}\right),\mathit{ϵ}=\frac{1}{R}\left(s-Qe\right),\end{array}$$(4)

to obtain$$\left(\mathit{\mu }{\mathbb{H}}^{\top }+\frac{1}{1-{\mathit{\nu }}_1{\mathit{\nu }}_2}\mathbb{E}\mathbb{H}-\frac{p_{12}}{p_{22}}Q\mathbb{H}\right)\mathbf{u}+\left(p_{11}-\frac{p_{12}^2}{p_{22}}\right)\mathbf{u}-\left(\frac{p_{12}+Q\mathbb{H}}{p_{22}}\right)\mathrm{\nabla }s=\mathbf{0},$$

and$${\mathrm{\nabla }}^{2}s+\frac{p_{22}}{R}s+\left(p_{12}-\frac{p_{22}Q}{R}\right)e=0.$$

This system is well posed under traction boundary conditions. For further details, see the Appendices 1–3.

2.2. Isotropic case

Bone is orthotropic; hence, our eventual goal is to investigate parameter retrieval in this case. However, as the problem increases in difficulty with the number of parameters, we first test our procedure on isotropic bone. By assuming isotropy, the constitutive equations simplify to(5) $$\begin{array}{cc}\hfill {\mathit{\sigma }}_{11}& =2\mathit{\mu }{e}_{11}+\mathit{\lambda }e+Q\mathit{ϵ},\hfill \\ \hfill {\mathit{\sigma }}_{22}& =2\mathit{\mu }{e}_{22}+\mathit{\lambda }e+Q\mathit{ϵ},\hfill \\ \hfill {\mathit{\sigma }}_{12}& =\mathit{\mu }{e}_{12},{\mathit{\sigma }}_{21}=\mathit{\mu }{e}_{21}.\hfill \end{array}$$(5)

It is this case we shall investigate the undetermined coefficient problem for and leave the orthotropic inverse problem for a subsequent publication. The parameter $\mathit{\mu }$, the complex frame shear modulus, is a measured quantity. The other parameters $\mathit{\lambda }$, $R$ and $Q$ occurring in the constitutive equations are calculated from the measured or estimated values of the parameters given in Table 2, using the formulas$$\begin{array}{cc}\hfill \mathit{\lambda }& =K_b-\frac{2}{3}\mathit{\mu }+\frac{{\left(K_r-K_b\right)}^2-2\mathit{\beta }{K}_r(K_r-K_b)+{\mathit{\beta }}^2{K}_r^2}{D-K_b},\hfill \\ \hfill R& =\frac{{\mathit{\beta }}^2{K}_r^2}{D-K_b},\hfill \\ \hfill Q& =\frac{\mathit{\beta }{K}_r[\left(1-\mathit{\beta }\right)K_r-K_b]}{D-K_b},\hfill \end{array}$$

where$$D=K_r[1+\mathit{\beta }(K_r/K_f-1)].$$

The bulk and shear moduli $K_b$ and $\mathit{\mu }$ are often given imaginary parts to account for frame viscoelasticity. Assuming that the bone system oscillates harmonically, Equations (3(3) $$\begin{array}{cc}\hfill \left(\mathit{\mu }{\mathbb{H}}^{\top }+\frac{1}{1-{\mathit{\nu }}_1{\mathit{\nu }}_2}\mathbb{E}\mathbb{H}\right)\mathbf{u}+Q\mathbb{H}\mathbf{U}& =\frac{{\mathit{\partial }}^2}{\mathit{\partial }{t}^2}({\mathit{\rho }}_{11}\mathbf{u}+{\mathit{\rho }}_{12}\mathbf{U})+b\frac{\mathit{\partial }}{\mathit{\partial }t}(\mathbf{u}-\mathbf{U}),\hfill \\ \hfill \mathrm{\nabla }(Qe+R\mathit{ϵ})& =\frac{{\mathit{\partial }}^2}{\mathit{\partial }{t}^2}({\mathit{\rho }}_{12}\mathbf{u}+{\mathit{\rho }}_{22}\mathbf{U})-b\frac{\mathit{\partial }}{\mathit{\partial }t}(\mathbf{u}-\mathbf{U}),\hfill \end{array}$$(3) ) become(6) $$\begin{array}{cc}\hfill \mathit{\mu }{\mathrm{\nabla }}^2\mathbf{u}+\mathrm{\nabla }[(\mathit{\lambda }+\mathit{\mu })e+Q\mathit{ϵ}]+(p_{11}\mathbf{u}+p_{12}\mathbf{U})& =\mathbf{0},\hfill \\ \hfill \mathrm{\nabla }(Qe+R\mathit{ϵ})+(p_{12}\mathbf{u}+p_{22}\mathbf{U})& =\mathbf{0}.\hfill \end{array}$$(6)

3. Boundary value problem

In a typical in vitro experiment, a bone specimen is placed in a water tank. The regions occupied by the bone specimen and the water are denoted by ${\mathrm{\Omega }}^b$ and ${\mathrm{\Omega }}^w$, respectively. In ${\mathrm{\Omega }}^w$, the two-dimensional equations for fluid pressure $P$ and fluid displacement ${\mathbf{U}}^w=(U_1^w,U_2^w)$ read(7) $$\begin{array}{cc}\hfill -{\mathrm{\nabla }}^{2}P-k_0^{2}P& =-q\mathit{\delta }(\mathbf{x};{\mathbf{x}}_0;k_0),\hfill \end{array}$$(7) (8) $$\begin{array}{cc}\hfill \mathrm{\nabla }P-{\mathit{\rho }}^w{\mathit{\omega }}^2{\mathbf{U}}^w& =\mathbf{0},\hfill \end{array}$$(8)

where ${\mathit{\rho }}^w$ is the water density, ${\mathbf{x}}_0$ is the location of the point source, $q$ and $k_0$ are the amplitude and wavenumber of the emitted signal, respectively. As stated above, in order to formulate a well-posed boundary value problem, one must modify the present form of Biot’s Equation (6(6) $$\begin{array}{cc}\hfill \mathit{\mu }{\mathrm{\nabla }}^2\mathbf{u}+\mathrm{\nabla }[(\mathit{\lambda }+\mathit{\mu })e+Q\mathit{ϵ}]+(p_{11}\mathbf{u}+p_{12}\mathbf{U})& =\mathbf{0},\hfill \\ \hfill \mathrm{\nabla }(Qe+R\mathit{ϵ})+(p_{12}\mathbf{u}+p_{22}\mathbf{U})& =\mathbf{0}.\hfill \end{array}$$(6) ), since there are not enough transmission conditions for the components of displacements fields $\mathbf{u}$ and $\mathbf{U}$. Using $s$ as defined in (4(4) $$\begin{array}{c}\hfill \mathbf{U}=-\frac{1}{p_{22}}\left(\mathrm{\nabla }s+p_{12}\mathbf{u}\right),\mathit{ϵ}=\frac{1}{R}\left(s-Qe\right),\end{array}$$(4) ), we obtain(9) $$\begin{array}{c}\hfill {\mathrm{\nabla }}^{2}s+\frac{p_{22}}{R}s+\left(p_{12}-\frac{p_{22}Q}{R}\right)e=0,\end{array}$$(9)

together with(10) $$\begin{array}{c}\hfill \mathit{\mu }{\mathrm{\nabla }}^2\mathbf{u}+\mathrm{\nabla }[(\mathit{\lambda }+\mathit{\mu }-\frac{Q^2}{R})e+(\frac{Q}{R}-\frac{p_{12}}{p_{22}})s]+(p_{11}-\frac{p_{12}^2}{p_{22}})\mathbf{u}=\mathbf{0}.\end{array}$$(10)

Equations (9(9) $$\begin{array}{c}\hfill {\mathrm{\nabla }}^{2}s+\frac{p_{22}}{R}s+\left(p_{12}-\frac{p_{22}Q}{R}\right)e=0,\end{array}$$(9) ) and (10(10) $$\begin{array}{c}\hfill \mathit{\mu }{\mathrm{\nabla }}^2\mathbf{u}+\mathrm{\nabla }[(\mathit{\lambda }+\mathit{\mu }-\frac{Q^2}{R})e+(\frac{Q}{R}-\frac{p_{12}}{p_{22}})s]+(p_{11}-\frac{p_{12}^2}{p_{22}})\mathbf{u}=\mathbf{0}.\end{array}$$(10) ) then form the modified Biot equations for $\mathbf{u}$ and $s$ in the bone specimen ${\mathrm{\Omega }}^b$. These equations should be satisfied by $\mathbf{u}$ and $s$ together with boundary conditions on the interface between bone and water. These are:

• Continuity of the flux: from (8(8) $$\begin{array}{cc}\hfill \mathrm{\nabla }P-{\mathit{\rho }}^w{\mathit{\omega }}^2{\mathbf{U}}^w& =\mathbf{0},\hfill \end{array}$$(8) ), we have$${\mathit{\rho }}^w{\mathit{\omega }}^2[\mathit{\beta }\mathbf{n}·\mathbf{U}+(1-\mathit{\beta })\mathbf{n}·\mathbf{u}]={\mathit{\rho }}^w{\mathit{\omega }}^2\mathbf{n}·{\mathbf{U}}^w\equiv 0,$$ and thus(11) $$\begin{array}{c}\hfill {\mathit{\rho }}^w{\mathit{\omega }}^2\left([1-\mathit{\beta }(1+\frac{p_{12}}{p_{22}})]\mathbf{n}·\mathbf{u}-\frac{\mathit{\beta }}{p_{22}}\frac{\mathit{\partial }s}{\mathit{\partial }n}\right)=0,\end{array}$$(11) where $\mathbf{n}$ is the exterior unit normal to ${\mathrm{\Omega }}^b$, pointing into the water.

• Continuity of the aggregate pressure:(12) $$\begin{array}{c}\hfill {\mathit{\sigma }}_{\ell j}{n}_j+s{n}_{\ell }=-P{n}_{\ell },\end{array}$$(12) since an expansion of the bone induces a compression in the water.

• Continuity of the pore pressure:(13) $$\begin{array}{c}\hfill s=-\mathit{\beta }P.\end{array}$$(13)

• Vanishing of the tangential frame stress: ${\mathit{\sigma }}_{12}\equiv {\mathit{\sigma }}_{21}=0$ which is equivalent to(14) $$\begin{array}{c}\hfill \frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_2}+\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_1}=0.\end{array}$$(14)

In addition, it is understood that the pressure $P$ is also required to satisfy the two-dimensional Sommerfeld radiation condition at infinity. We have so far given the precise formulation of the exterior transmission problem (ETP) consisting of Equations (9(9) $$\begin{array}{c}\hfill {\mathrm{\nabla }}^{2}s+\frac{p_{22}}{R}s+\left(p_{12}-\frac{p_{22}Q}{R}\right)e=0,\end{array}$$(9) ), (10(10) $$\begin{array}{c}\hfill \mathit{\mu }{\mathrm{\nabla }}^2\mathbf{u}+\mathrm{\nabla }[(\mathit{\lambda }+\mathit{\mu }-\frac{Q^2}{R})e+(\frac{Q}{R}-\frac{p_{12}}{p_{22}})s]+(p_{11}-\frac{p_{12}^2}{p_{22}})\mathbf{u}=\mathbf{0}.\end{array}$$(10) ) for the unknowns $\mathbf{u}$, $s$ in ${\mathrm{\Omega }}^b$ and Equation (7(7) $$\begin{array}{cc}\hfill -{\mathrm{\nabla }}^{2}P-k_0^{2}P& =-q\mathit{\delta }(\mathbf{x};{\mathbf{x}}_0;k_0),\hfill \end{array}$$(7) ) for the unknown $P$ in ${\mathrm{\Omega }}^w$, together with transmission conditions (11(11) $$\begin{array}{c}\hfill {\mathit{\rho }}^w{\mathit{\omega }}^2\left([1-\mathit{\beta }(1+\frac{p_{12}}{p_{22}})]\mathbf{n}·\mathbf{u}-\frac{\mathit{\beta }}{p_{22}}\frac{\mathit{\partial }s}{\mathit{\partial }n}\right)=0,\end{array}$$(11) )–(14(14) $$\begin{array}{c}\hfill \frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_2}+\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_1}=0.\end{array}$$(14) ) and the radiation condition at infinity.

From the computational point of view, it is more convenient to reduce the ETP to a nonlocal problem in a finite computational domain such as ${\mathrm{\Omega }}^b$.[39] For this purpose, we now reduce the Helmholtz Equation (7(7) $$\begin{array}{cc}\hfill -{\mathrm{\nabla }}^{2}P-k_0^{2}P& =-q\mathit{\delta }(\mathbf{x};{\mathbf{x}}_0;k_0),\hfill \end{array}$$(7) ) to a boundary integral equation using the Green representation of $P$ in ${\mathrm{\Omega }}^w$. More precisely, we seek a solution of (7(7) $$\begin{array}{cc}\hfill -{\mathrm{\nabla }}^{2}P-k_0^{2}P& =-q\mathit{\delta }(\mathbf{x};{\mathbf{x}}_0;k_0),\hfill \end{array}$$(7) ) in the form of a single-layer potential in terms of the unknown density function $\mathit{\phi }$,$$P(\mathbf{x},{\mathbf{x}}_0)=-qG(\mathbf{x},{\mathbf{x}}_0;k_0)-{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{x},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })d{S}_{\mathit{\zeta }},\mathbf{x}\in {\mathrm{\Omega }}^w,$$

where $G(\mathbf{x},{\mathbf{x}}_0,k_0)$ is free-space Helmholtz Green’s function given by$$G(\mathbf{x},{\mathbf{x}}_0,k_0):=\frac{i}{4}{H}_0^{(1)}(k_0||\mathbf{x}-{\mathbf{x}}_0||),$$

and $H_0^{(1)}$ is a Hankel function of the first kind. Clearly, the density function $\mathit{\phi }$ is related to the unknowns $\mathbf{u}$ and $\mathbf{U}$ via the transmission conditions (11(11) $$\begin{array}{c}\hfill {\mathit{\rho }}^w{\mathit{\omega }}^2\left([1-\mathit{\beta }(1+\frac{p_{12}}{p_{22}})]\mathbf{n}·\mathbf{u}-\frac{\mathit{\beta }}{p_{22}}\frac{\mathit{\partial }s}{\mathit{\partial }n}\right)=0,\end{array}$$(11) )–(14(14) $$\begin{array}{c}\hfill \frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_2}+\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_1}=0.\end{array}$$(14) ).

If the boundary $\mathit{\partial }{\mathrm{\Omega }}^b$ of the bone sample has positive orientation, then letting $\mathbf{x}\to \mathbf{X}\in \mathit{\partial }{\mathrm{\Omega }}^b$, we obtain from condition (12(12) $$\begin{array}{c}\hfill {\mathit{\sigma }}_{\ell j}{n}_j+s{n}_{\ell }=-P{n}_{\ell },\end{array}$$(12) ) that(15) $$\begin{array}{c}\hfill \mathit{\lambda }\mathrm{\nabla }·\mathbf{u}+2\mathit{\mu }\frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_1}+Q\mathit{ϵ}+s=qG(\mathbf{X},{\mathbf{x}}_0;k_0)+{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }},\end{array}$$(15)

and(16) $$\begin{array}{c}\hfill \mathit{\lambda }\mathrm{\nabla }·\mathbf{u}+2\mathit{\mu }\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_2}+Q\mathit{ϵ}+s=qG(\mathbf{X},{\mathbf{x}}_0;k_0)+{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }}.\end{array}$$(16)

Note that in deriving these equations, we have tacitly employed condition (14(14) $$\begin{array}{c}\hfill \frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_2}+\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_1}=0.\end{array}$$(14) ). In view of the similarity between (15(15) $$\begin{array}{c}\hfill \mathit{\lambda }\mathrm{\nabla }·\mathbf{u}+2\mathit{\mu }\frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_1}+Q\mathit{ϵ}+s=qG(\mathbf{X},{\mathbf{x}}_0;k_0)+{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }},\end{array}$$(15) ) and (16(16) $$\begin{array}{c}\hfill \mathit{\lambda }\mathrm{\nabla }·\mathbf{u}+2\mathit{\mu }\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_2}+Q\mathit{ϵ}+s=qG(\mathbf{X},{\mathbf{x}}_0;k_0)+{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }}.\end{array}$$(16) ), a subtraction of these two equations leads to the simple relation(17) $$\begin{array}{c}\hfill \frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_1}-\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_2}=0.\end{array}$$(17)

Hence in computation, we may use (17(17) $$\begin{array}{c}\hfill \frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_1}-\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_2}=0.\end{array}$$(17) ) and either (15(15) $$\begin{array}{c}\hfill \mathit{\lambda }\mathrm{\nabla }·\mathbf{u}+2\mathit{\mu }\frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_1}+Q\mathit{ϵ}+s=qG(\mathbf{X},{\mathbf{x}}_0;k_0)+{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }},\end{array}$$(15) ) or (16(16) $$\begin{array}{c}\hfill \mathit{\lambda }\mathrm{\nabla }·\mathbf{u}+2\mathit{\mu }\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_2}+Q\mathit{ϵ}+s=qG(\mathbf{X},{\mathbf{x}}_0;k_0)+{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }}.\end{array}$$(16) ), but not both. Here, the term $\mathit{ϵ}$ should be replaced by $\mathit{ϵ}=(s-Qe)/R$ from (4(4) $$\begin{array}{c}\hfill \mathbf{U}=-\frac{1}{p_{22}}\left(\mathrm{\nabla }s+p_{12}\mathbf{u}\right),\mathit{ϵ}=\frac{1}{R}\left(s-Qe\right),\end{array}$$(4) ).

Figure 1. Profiles of $u_1$, $u_2$, $s$, $\mathit{\phi }$ and $-P$ for $N=90$, $\mathit{\omega }=250$ kHz and $\mathit{\beta }=0.7$.

Figure 2. Profiles of $u_1$, $u_2$, $s$, $\mathit{\phi }$ and $-P$ for $N=90$, $\mathit{\omega }=250$ kHz and $\mathit{\beta }=0.83$.

Figure 3. Profiles of $u_1$, $u_2$, $s$, $\mathit{\phi }$ and $-P$ for $N=90$, $\mathit{\omega }=250$ kHz and $\mathit{\beta }=0.9$.

Figure 4. Profiles of $u_1$, $u_2$, $s$, $\mathit{\phi }$ and $-P$ for $N=90$, $\mathit{\omega }=500$ kHz and $\mathit{\beta }=0.7$.

Figure 5. Profiles of $u_1$, $u_2$, $s$, $\mathit{\phi }$ and $-P$ for $N=90$, $\mathit{\omega }=500$ kHz and $\mathit{\beta }=0.83$.

Figure 6. Profiles of $u_1$, $u_2$, $s$, $\mathit{\phi }$ and $-P$ for $N=90$, $\mathit{\omega }=500$ kHz and $\mathit{\beta }=0.9$.

Next, the flux continuity condition (11(11) $$\begin{array}{c}\hfill {\mathit{\rho }}^w{\mathit{\omega }}^2\left([1-\mathit{\beta }(1+\frac{p_{12}}{p_{22}})]\mathbf{n}·\mathbf{u}-\frac{\mathit{\beta }}{p_{22}}\frac{\mathit{\partial }s}{\mathit{\partial }n}\right)=0,\end{array}$$(11) ) leads to the natural boundary condition for $s$,(18) $$\begin{array}{cc}& {\mathit{\rho }}^w{\mathit{\omega }}^2\left([1-\mathit{\beta }(1+\frac{p_{12}}{p_{22}})]\mathbf{n}·\mathbf{u}-\frac{\mathit{\beta }}{p_{22}}\frac{\mathit{\partial }s}{\mathit{\partial }n}\right)+q\frac{\mathit{\partial }G}{\mathit{\partial }n}(\mathbf{X},{\mathbf{x}}_0;k_0)\hfill \\ \hfill & =\frac{1}{2}\mathit{\phi }({\mathbf{x}}_0,\mathbf{X})-{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\frac{\mathit{\partial }G}{\mathit{\partial }n}(\mathbf{X},\mathit{\zeta };k_0)\mathrm{d}{s}_{\mathit{\zeta }}.\hfill \end{array}$$(18)

Note that the normal derivatives of $G$ in (18(18) $$\begin{array}{cc}& {\mathit{\rho }}^w{\mathit{\omega }}^2\left([1-\mathit{\beta }(1+\frac{p_{12}}{p_{22}})]\mathbf{n}·\mathbf{u}-\frac{\mathit{\beta }}{p_{22}}\frac{\mathit{\partial }s}{\mathit{\partial }n}\right)+q\frac{\mathit{\partial }G}{\mathit{\partial }n}(\mathbf{X},{\mathbf{x}}_0;k_0)\hfill \\ \hfill & =\frac{1}{2}\mathit{\phi }({\mathbf{x}}_0,\mathbf{X})-{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\frac{\mathit{\partial }G}{\mathit{\partial }n}(\mathbf{X},\mathit{\zeta };k_0)\mathrm{d}{s}_{\mathit{\zeta }}.\hfill \end{array}$$(18) ) are taken with respect to $\mathbf{X}$. Finally, from the representation formula for $P$, condition (13(13) $$\begin{array}{c}\hfill s=-\mathit{\beta }P.\end{array}$$(13) ) leads to a boundary integral equation for $\mathit{\phi }$,(19) $$\begin{array}{c}\hfill \mathit{\beta }{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }}-s+\mathit{\beta }qG(\mathbf{X},{\mathbf{x}}_0;k_0)=0.\end{array}$$(19)

It is worth mentioning that the right-hand sides of (15(15) $$\begin{array}{c}\hfill \mathit{\lambda }\mathrm{\nabla }·\mathbf{u}+2\mathit{\mu }\frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_1}+Q\mathit{ϵ}+s=qG(\mathbf{X},{\mathbf{x}}_0;k_0)+{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }},\end{array}$$(15) ), (16(16) $$\begin{array}{c}\hfill \mathit{\lambda }\mathrm{\nabla }·\mathbf{u}+2\mathit{\mu }\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_2}+Q\mathit{ϵ}+s=qG(\mathbf{X},{\mathbf{x}}_0;k_0)+{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }}.\end{array}$$(16) ), (18(18) $$\begin{array}{cc}& {\mathit{\rho }}^w{\mathit{\omega }}^2\left([1-\mathit{\beta }(1+\frac{p_{12}}{p_{22}})]\mathbf{n}·\mathbf{u}-\frac{\mathit{\beta }}{p_{22}}\frac{\mathit{\partial }s}{\mathit{\partial }n}\right)+q\frac{\mathit{\partial }G}{\mathit{\partial }n}(\mathbf{X},{\mathbf{x}}_0;k_0)\hfill \\ \hfill & =\frac{1}{2}\mathit{\phi }({\mathbf{x}}_0,\mathbf{X})-{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\frac{\mathit{\partial }G}{\mathit{\partial }n}(\mathbf{X},\mathit{\zeta };k_0)\mathrm{d}{s}_{\mathit{\zeta }}.\hfill \end{array}$$(18) ) and (19(19) $$\begin{array}{c}\hfill \mathit{\beta }{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }}-s+\mathit{\beta }qG(\mathbf{X},{\mathbf{x}}_0;k_0)=0.\end{array}$$(19) ) contain no singularities since, for the first three equations, the source point ${\mathbf{x}}_0$ is in ${\mathrm{\Omega }}^b$ whereas, for (18(18) $$\begin{array}{cc}& {\mathit{\rho }}^w{\mathit{\omega }}^2\left([1-\mathit{\beta }(1+\frac{p_{12}}{p_{22}})]\mathbf{n}·\mathbf{u}-\frac{\mathit{\beta }}{p_{22}}\frac{\mathit{\partial }s}{\mathit{\partial }n}\right)+q\frac{\mathit{\partial }G}{\mathit{\partial }n}(\mathbf{X},{\mathbf{x}}_0;k_0)\hfill \\ \hfill & =\frac{1}{2}\mathit{\phi }({\mathbf{x}}_0,\mathbf{X})-{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\frac{\mathit{\partial }G}{\mathit{\partial }n}(\mathbf{X},\mathit{\zeta };k_0)\mathrm{d}{s}_{\mathit{\zeta }}.\hfill \end{array}$$(18) ), the singularity is cancelled because of the last term on the right-hand side.

Before we formulate what is called the nonlocal problem for the ETP, some observations are in order. We observe that the transmission conditions (15(15) $$\begin{array}{c}\hfill \mathit{\lambda }\mathrm{\nabla }·\mathbf{u}+2\mathit{\mu }\frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_1}+Q\mathit{ϵ}+s=qG(\mathbf{X},{\mathbf{x}}_0;k_0)+{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }},\end{array}$$(15) ) and (16(16) $$\begin{array}{c}\hfill \mathit{\lambda }\mathrm{\nabla }·\mathbf{u}+2\mathit{\mu }\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_2}+Q\mathit{ϵ}+s=qG(\mathbf{X},{\mathbf{x}}_0;k_0)+{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }}.\end{array}$$(16) ) can be considered as natural boundary conditions for the displacement field $\mathbf{u}$ for given $s$ and $\mathit{\phi }$, whereas condition (18(18) $$\begin{array}{cc}& {\mathit{\rho }}^w{\mathit{\omega }}^2\left([1-\mathit{\beta }(1+\frac{p_{12}}{p_{22}})]\mathbf{n}·\mathbf{u}-\frac{\mathit{\beta }}{p_{22}}\frac{\mathit{\partial }s}{\mathit{\partial }n}\right)+q\frac{\mathit{\partial }G}{\mathit{\partial }n}(\mathbf{X},{\mathbf{x}}_0;k_0)\hfill \\ \hfill & =\frac{1}{2}\mathit{\phi }({\mathbf{x}}_0,\mathbf{X})-{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\frac{\mathit{\partial }G}{\mathit{\partial }n}(\mathbf{X},\mathit{\zeta };k_0)\mathrm{d}{s}_{\mathit{\zeta }}.\hfill \end{array}$$(18) ) is a natural condition for the stress $s$ if $\mathbf{u}$ and $\mathit{\phi }$ are known. From the variational point of view, both equations define the relevant Dirichlet–Neumann maps. On the other hand, condition (19(19) $$\begin{array}{c}\hfill \mathit{\beta }{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }}-s+\mathit{\beta }qG(\mathbf{X},{\mathbf{x}}_0;k_0)=0.\end{array}$$(19) ) only relates the trace of the stress $s$ and the density function $\mathit{\phi }$, which may be considered as a boundary integral equation for $\mathit{\phi }$ given the stress $s$. With these observations, we are now in a position to state the nonlocal problem for the ETP:

Table 3. Convergence test on $\mathit{\beta }$ with the NM algorithm for varying resolutions and $\mathit{\eta }={\mathit{\eta }}_1$.

$\mathit{\omega }$	low/high	$\mathit{\beta }$	$f_{min}$	% error
Guess/Target		0.7
250 kHz	25/90	0.6945	0.3671	0.7857
	45/90	0.6940	0.1654	0.8571
	65/90	0.6971	0.0697	0.4142
Guess/Target		0.7
500 kHz	25/90	0.7345	0.2366	4.929
	45/90	0.7172	0.1171	2.443
	65/90	0.7081	0.0486	1.157
Guess/Target		0.83
250 kHz	25/90	0.8350	0.3014	0.6024
	45/90	0.8304	0.1178	0.0602
	65/90	0.8298	0.0439	0.0241
Guess/Target		0.83
500 kHz	25/90	0.8581	0.4467	3.389
	45/90	0.8406	0.2174	1.277
	65/90	0.8343	0.0865	0.5181
Guess/Target		0.9
250 kHz	25/90	0.8844	0.7037	1.733
	45/90	0.8993	0.3412	0.0778
	65/90	0.9015	0.1162	0.1667
Guess/Target		0.9
500 kHz	25/90	0.9437	0.2791	4.855
	45/90	0.9040	0.0992	0.4444
	65/90	0.9020	0.0799	0.2222

Table 4. Convergence test on $\mathit{\beta }$ with the NM algorithm for varying resolutions and $\mathit{\eta }={\mathit{\eta }}_2$.

$\mathit{\omega }$	low/high	$\mathit{\beta }$	$f_{min}$	% error
Guess/Target		0.7
250 kHz	25/90	0.6944	0.1879	0.800
	45/90	0.6944	0.0871	0.800
	65/90	0.6973	0.0374	0.3857
Guess/Target		0.7
500 kHz	25/90	0.7711	0.2949	10.157
	45/90	0.7405	0.1284	5.786
	65/90	0.7201	0.0485	2.871
Guess/Target		0.83
250 kHz	25/90	0.9019	0.9753	8.663
	45/90	0.9054	0.9556	9.084
	65/90	0.8276	0.2619	0.2891
Guess/Target		0.83
500 kHz	25/90	0.8476	0.4707	2.120
	45/90	0.8389	0.2729	1.072
	65/90	0.8338	0.1327	0.4578
Guess/Target		0.9
250 kHz	25/90	0.9030	0.3626	0.333
	45/90	0.9031	0.1363	0.3444
	65/90	0.9020	0.0514	0.2222
Guess/Target		0.9
500 kHz	25/90	0.8990	0.2912	0.1111
	45/90	0.8998	0.1329	0.0222
	65/90	0.8999	0.0567	0.0111

Table 5. Comparison test on $\mathit{\beta }$ between $RN=11$ and $RN=100$ for $\mathit{\eta }={\mathit{\eta }}_1$. Here $N=50$ for the high resolution and $N=25$ for the low resolution.

$\mathit{\omega }$	$\mathit{\beta }$	$f_{min}$	% error
Guess/Target	0.7
250 kHz
11 Receiving nodes	0.7032	0.2692	0.4571
100 Receiving nodes	0.7035	0.2690	0.5000
Guess/Target	0.7
500 kHz
11 Receiving nodes	0.7252	0.1318	3.600
100 Receiving nodes	0.7252	0.1290	3.600
Guess/Target	0.83
250 kHz
11 Receiving nodes	0.8345	0.2124	0.5422
100 Receiving nodes	0.8345	0.2164	0.5422
Guess/Target	0.83
500 kHz
11 Receiving nodes	0.8504	0.3870	2.458
100 Receiving nodes	0.8504	0.3865	2.458
Guess/Target	0.9
250 kHz
11 Receiving nodes	0.8898	0.5700	1.133
100 Receiving nodes	0.8897	0.5645	1.144
Guess/Target	0.9
500 kHz
11 Receiving nodes	0.9033	0.1118	0.3667
100 Receiving nodes	0.9034	0.1142	0.3777

Table 6. Comparison test on $\mathit{\beta }$ between $RN=11$ and $RN=100$ for $\mathit{\eta }={\mathit{\eta }}_2$. Here, $N=50$ for the high resolution and $N=25$ for the low resolution.

$\mathit{\omega }$	$\mathit{\beta }$	$f_{min}$	% error
Guess/Target	0.7
250 kHz
11 Receiving nodes	0.6983	0.1096	0.2429
100 Receiving nodes	0.6989	0.1118	0.1571
Guess/Target	0.7
500 kHz
11 Receiving nodes	0.7513	0.1542	7.329
100 Receiving nodes	0.7514	0.1555	7.343
Guess/Target	0.83
250 kHz
11 Receiving nodes	0.9044	0.985	8.964
100 Receiving nodes	0.9043	0.9845	8.952
Guess/Target	0.83
500 kHz
11 Receiving nodes	0.8407	0.3091	1.289
100 Receiving nodes	0.8407	0.3098	1.289
Guess/Target	0.9
250 kHz
11 Receiving nodes	0.9029	0.2592	0.3222
100 Receiving nodes	0.9029	0.2551	0.3222
Guess/Target	0.9
500 kHz
11 Receiving nodes	0.8998	0.1911	0.0222
100 Receiving nodes	0.8999	0.1980	0.0111

Table 7. Comparison test on $\mathit{\beta }$ between $RN=11$ and $RN=100$ for $\mathit{\eta }={\mathit{\eta }}_1$. Here, $N=50$ for the high resolution and $N=25$ for the low resolution. Receiving nodes are placed near the top, bottom and to the right of the bone sample.

$\mathit{\omega }$	$\mathit{\beta }$	$f_{min}$	% error
Guess/Target	0.7
250 kHz
11 Receiving nodes	0.6998	0.2555	0.0286
100 Receiving nodes	0.6999	0.2554	0.0143
Guess/Target	0.7
500 kHz
11 Receiving nodes	0.7269	0.1739	3.840
100 Receiving nodes	0.7269	0.1735	3.840
Guess/Target	0.83
250 kHz
11 Receiving nodes	0.8342	0.1323	0.5060
100 Receiving nodes	0.8342	0.1323	0.5060
Guess/Target	0.83
500 kHz
11 Receiving nodes	0.8500	0.3708	2.4096
100 Receiving nodes	0.8499	0.3698	2.4000
Guess/Target	0.9
250 kHz
11 Receiving nodes	0.8928	0.5111	0.8000
100 Receiving nodes	0.8929	0.5077	0.7889
Guess/Target	0.9
500 kHz
11 Receiving nodes	0.9040	0.0912	0.4444
100 Receiving nodes	0.9041	0.0903	0.4560

Table 8. Comparison test on $\mathit{\beta }$ between $RN=11$ and $RN=100$ for $\mathit{\eta }={\mathit{\eta }}_2$. Here, $N=50$ for the high resolution and $N=25$ for the low resolution. Receiving nodes are placed near the top, bottom and to the right of the bone sample.

$\mathit{\omega }$	$\mathit{\beta }$	$f_{min}$	% error
Guess/Target	0.7
250 kHz
11 Receiving nodes	0.6884	0.0618	1.657
100 Receiving nodes	0.6885	0.0620	1.643
Guess/Target	0.7
500 kHz
11 Receiving nodes	0.7465	0.1699	6.643
100 Receiving nodes	0.7464	0.1716	6.629
Guess/Target	0.83
250 kHz
11 Receiving nodes	0.9076	0.9937	9.350
100 Receiving nodes	0.9076	0.9937	9.350
Guess/Target	0.83
500 kHz
11 Receiving nodes	0.8396	0.2685	1.157
100 Receiving nodes	0.8396	0.2679	1.157
Guess/Target	0.9
250 kHz
11 Receiving nodes	0.9046	0.2252	0.5111
100 Receiving nodes	0.9046	0.2234	0.5111
Guess/Target	0.9
500 kHz
11 Receiving nodes	0.8979	0.0842	0.2333
100 Receiving nodes	0.8980	0.0854	0.2222

Find the four unknowns $u_1$, $u_2$, $s$, $\mathit{\phi }$. The first three unknowns are required to satisfy the Biot Equations (9(9) $$\begin{array}{c}\hfill {\mathrm{\nabla }}^{2}s+\frac{p_{22}}{R}s+\left(p_{12}-\frac{p_{22}Q}{R}\right)e=0,\end{array}$$(9) ) and (10(10) $$\begin{array}{c}\hfill \mathit{\mu }{\mathrm{\nabla }}^2\mathbf{u}+\mathrm{\nabla }[(\mathit{\lambda }+\mathit{\mu }-\frac{Q^2}{R})e+(\frac{Q}{R}-\frac{p_{12}}{p_{22}})s]+(p_{11}-\frac{p_{12}^2}{p_{22}})\mathbf{u}=\mathbf{0}.\end{array}$$(10) ) and the boundary conditions (or rather the transmission conditions) either (15(15) $$\begin{array}{c}\hfill \mathit{\lambda }\mathrm{\nabla }·\mathbf{u}+2\mathit{\mu }\frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_1}+Q\mathit{ϵ}+s=qG(\mathbf{X},{\mathbf{x}}_0;k_0)+{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }},\end{array}$$(15) )or (16(16) $$\begin{array}{c}\hfill \mathit{\lambda }\mathrm{\nabla }·\mathbf{u}+2\mathit{\mu }\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_2}+Q\mathit{ϵ}+s=qG(\mathbf{X},{\mathbf{x}}_0;k_0)+{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }}.\end{array}$$(16) ), (17(17) $$\begin{array}{c}\hfill \frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_1}-\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_2}=0.\end{array}$$(17) ) and (18(18) $$\begin{array}{cc}& {\mathit{\rho }}^w{\mathit{\omega }}^2\left([1-\mathit{\beta }(1+\frac{p_{12}}{p_{22}})]\mathbf{n}·\mathbf{u}-\frac{\mathit{\beta }}{p_{22}}\frac{\mathit{\partial }s}{\mathit{\partial }n}\right)+q\frac{\mathit{\partial }G}{\mathit{\partial }n}(\mathbf{X},{\mathbf{x}}_0;k_0)\hfill \\ \hfill & =\frac{1}{2}\mathit{\phi }({\mathbf{x}}_0,\mathbf{X})-{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\frac{\mathit{\partial }G}{\mathit{\partial }n}(\mathbf{X},\mathit{\zeta };k_0)\mathrm{d}{s}_{\mathit{\zeta }}.\hfill \end{array}$$(18) ), where the density function $\mathit{\phi }$ may be considered as an unknown parameter subject to the constraint (19(19) $$\begin{array}{c}\hfill \mathit{\beta }{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }}-s+\mathit{\beta }qG(\mathbf{X},{\mathbf{x}}_0;k_0)=0.\end{array}$$(19) ).

We note that if $\mathit{\phi }$ is given, then we have an uncoupled system for the displacement components $u_1$, $u_2$ and stress $s$. On the other hand, if $u_1$, $u_2$ and $s$ are given, then the unknown density function $\mathit{\phi }$ is required to satisfy the standard Fredholm boundary integral equation of the first kind (19(19) $$\begin{array}{c}\hfill \mathit{\beta }{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }}-s+\mathit{\beta }qG(\mathbf{X},{\mathbf{x}}_0;k_0)=0.\end{array}$$(19) ). In general, this is a coupled system for the four unknowns, and can only be treated by numerical methods, which is the content of the next section.

4. Numerical approximation

In this section, we will assume that the bone specimen is a square of dimension $L\times L$. We discretize the domain into a uniform mesh consisting of $N\times N$ points. In order to solve the coupled system of Equations (9(9) $$\begin{array}{c}\hfill {\mathrm{\nabla }}^{2}s+\frac{p_{22}}{R}s+\left(p_{12}-\frac{p_{22}Q}{R}\right)e=0,\end{array}$$(9) ), (10(10) $$\begin{array}{c}\hfill \mathit{\mu }{\mathrm{\nabla }}^2\mathbf{u}+\mathrm{\nabla }[(\mathit{\lambda }+\mathit{\mu }-\frac{Q^2}{R})e+(\frac{Q}{R}-\frac{p_{12}}{p_{22}})s]+(p_{11}-\frac{p_{12}^2}{p_{22}})\mathbf{u}=\mathbf{0}.\end{array}$$(10) ), (15(15) $$\begin{array}{c}\hfill \mathit{\lambda }\mathrm{\nabla }·\mathbf{u}+2\mathit{\mu }\frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_1}+Q\mathit{ϵ}+s=qG(\mathbf{X},{\mathbf{x}}_0;k_0)+{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }},\end{array}$$(15) ) or (16(16) $$\begin{array}{c}\hfill \mathit{\lambda }\mathrm{\nabla }·\mathbf{u}+2\mathit{\mu }\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_2}+Q\mathit{ϵ}+s=qG(\mathbf{X},{\mathbf{x}}_0;k_0)+{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }}.\end{array}$$(16) )–(19(19) $$\begin{array}{c}\hfill \mathit{\beta }{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }}-s+\mathit{\beta }qG(\mathbf{X},{\mathbf{x}}_0;k_0)=0.\end{array}$$(19) ), we use a finite-difference method.

The discretization of derivatives is carried out in the following way: second-order central difference schemes are used for the bulk equations, and either backward or forward second-order schemes are used for the boundary conditions depending on the node location. Tangential derivatives along the boundary are discretized using only first-order backward schemes. The reason for this is to avoid special treatment of boundary nodes in order to keep implementation of the finite-difference method relatively simple. Finally, the quadrature of the boundary integrals in (15(15) $$\begin{array}{c}\hfill \mathit{\lambda }\mathrm{\nabla }·\mathbf{u}+2\mathit{\mu }\frac{\mathit{\partial }{u}_1}{\mathit{\partial }{x}_1}+Q\mathit{ϵ}+s=qG(\mathbf{X},{\mathbf{x}}_0;k_0)+{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }},\end{array}$$(15) ) or (16(16) $$\begin{array}{c}\hfill \mathit{\lambda }\mathrm{\nabla }·\mathbf{u}+2\mathit{\mu }\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_2}+Q\mathit{ϵ}+s=qG(\mathbf{X},{\mathbf{x}}_0;k_0)+{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }}.\end{array}$$(16) ), (18(18) $$\begin{array}{cc}& {\mathit{\rho }}^w{\mathit{\omega }}^2\left([1-\mathit{\beta }(1+\frac{p_{12}}{p_{22}})]\mathbf{n}·\mathbf{u}-\frac{\mathit{\beta }}{p_{22}}\frac{\mathit{\partial }s}{\mathit{\partial }n}\right)+q\frac{\mathit{\partial }G}{\mathit{\partial }n}(\mathbf{X},{\mathbf{x}}_0;k_0)\hfill \\ \hfill & =\frac{1}{2}\mathit{\phi }({\mathbf{x}}_0,\mathbf{X})-{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\frac{\mathit{\partial }G}{\mathit{\partial }n}(\mathbf{X},\mathit{\zeta };k_0)\mathrm{d}{s}_{\mathit{\zeta }}.\hfill \end{array}$$(18) ) and (19(19) $$\begin{array}{c}\hfill \mathit{\beta }{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }}-s+\mathit{\beta }qG(\mathbf{X},{\mathbf{x}}_0;k_0)=0.\end{array}$$(19) ) is based on constant interpolation of the solution between grid points. The resulting system is then solved by Gaussian elimination. For instance, following this scheme and using the appropriate standard finite-difference formulas$$\begin{array}{cc}& \frac{\mathit{\partial }f}{\mathit{\partial }x}(x_i,y_j)\approx \frac{-3f_{i,j}+4f_{i+1,j}-f_{i+2,j}}{2h},(\mathrm{forward})\hfill \\ \hfill & \frac{\mathit{\partial }f}{\mathit{\partial }x}(x_i,y_j)\approx \frac{f_{i-2,j}-4f_{i-1,j}+3f_{i,j}}{2h},(\mathrm{backward})\hfill \\ \hfill & \frac{{\mathit{\partial }}^{2}f}{\mathit{\partial }{x}^2}(x_i,y_j)\approx \frac{f_{i-1,j}-2f_{i,j}+f_{i+1,j}}{h^2},\hfill \\ \hfill & \frac{{\mathit{\partial }}^{2}f}{\mathit{\partial }x\mathit{\partial }y}(x_i,y_j)\approx \frac{f_{i+1,j+1}-f_{i+1,j-1}+f_{i-1,j-1}-f_{i-1,j+1}}{4h^2},\hfill \end{array}$$

Equation (16(16) $$\begin{array}{c}\hfill \mathit{\lambda }\mathrm{\nabla }·\mathbf{u}+2\mathit{\mu }\frac{\mathit{\partial }{u}_2}{\mathit{\partial }{x}_2}+Q\mathit{ϵ}+s=qG(\mathbf{X},{\mathbf{x}}_0;k_0)+{\int }_{\mathit{\partial }{\mathrm{\Omega }}^b}G(\mathbf{X},\mathit{\zeta };k_0)\mathit{\phi }({\mathbf{x}}_0,\mathit{\zeta })\mathrm{d}{s}_{\mathit{\zeta }}.\end{array}$$(16) ) on the left side of the square away from the corners becomes$$\begin{array}{cc}& (\mathit{\lambda }+2\mathit{\mu }-\frac{Q^2}{R})(-3u_{1_{(i,j)}}+4u_{1_{(i+1,j)}}-u_{1_{(i+2,j)}})+2(\mathit{\lambda }-\frac{Q^2}{R})(u_{2_{(i,j)}}-u_{2_{(i,j-1)}})\hfill \\ \hfill & +2h(1+\frac{Q}{R})s_{(i,j)}-2h^2\sum _{{\mathit{\zeta }}_{(m,n)}\in \mathit{\partial }{\mathrm{\Omega }}^b}G({\mathbf{X}}_{(i,j)},{\mathit{\zeta }}_{(m,n)};k_0)\mathit{\phi }({\mathbf{x}}_0,{\mathit{\zeta }}_{(m,n)})=2hqG({\mathbf{X}}_{(i,j)},{\mathbf{x}}_0;k_0).\hfill \end{array}$$

Here,$$G(\mathbf{X},\mathit{\zeta };k_0)=\left\{\begin{array}{cc}{\displaystyle \frac{i}{4}{H}_0^{(1)}(k_0||\mathbf{X}-\mathit{\zeta }||),}\hfill & \mathbf{X}\ne \mathit{\zeta },\hfill \\ {\displaystyle \frac{i}{8\mathit{\pi }}h\left[log\left(\frac{2}{h}\right)+1\right],}\hfill & \mathbf{X}=\mathit{\zeta },\hfill \end{array}\right.$$

and $h$ is the mesh spacing.

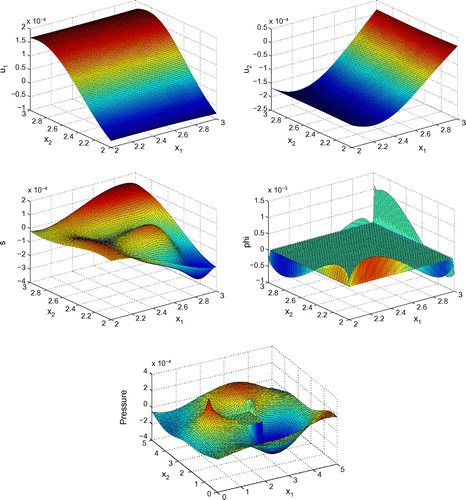
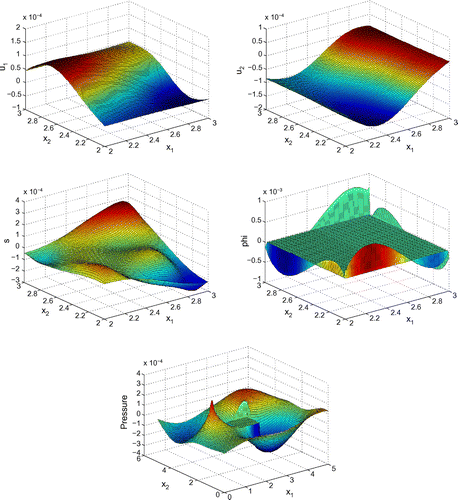
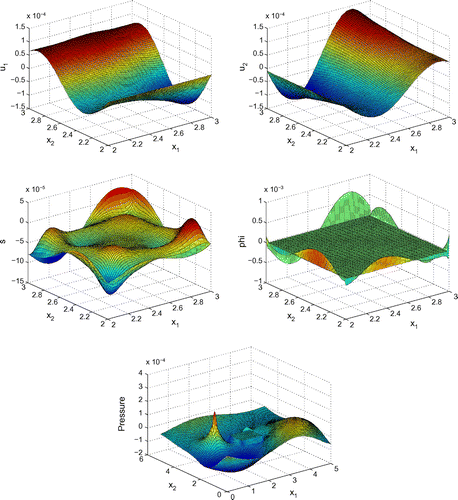
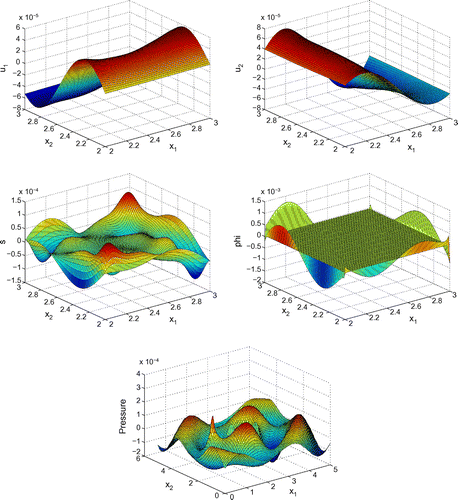
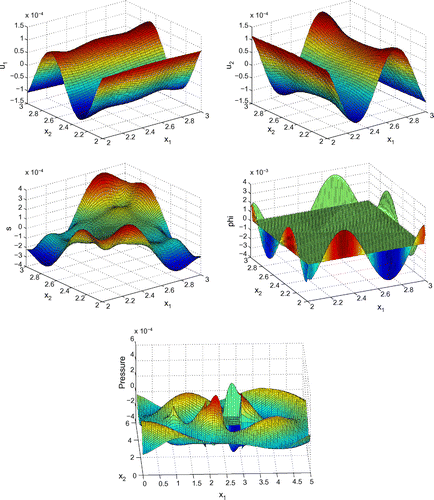
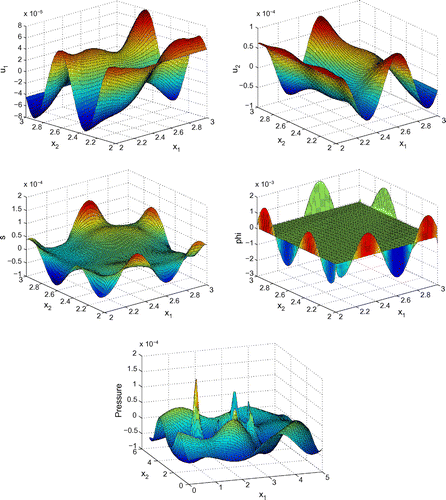
Before proceeding with numerical tests for this model, as an illustration, Figures 1–6 show dimensionless profiles of $u_1$, $u_2$, $s$ (in ${\mathrm{\Omega }}^b$), $\mathit{\phi }$ (on $\mathit{\partial }{\mathrm{\Omega }}^b$) and $-P$ (in ${\mathrm{\Omega }}^w$), using $L=1$ and $N=90$, for various frequencies $\mathit{\omega }$ and porosities $\mathit{\beta }$. Values of physical parameters used in these numerical simulations are given in the next section. We restrict ourselves to relatively low ultrasonic frequencies, 250 and 500 kHz, where Biot’s model is supposed to be applicable. Moreover, in view of applications to quantitative ultrasound techniques for the diagnosis of osteoporosis, we pay particular attention to relatively high bone porosities.

5. Numerical experiments

5.1. Convergence/accuracy tests

To validate our model, we perform several tests using different optimization procedures. These are the Nelder–Mead (NM) simplex algorithm and the Differential Evolution (DE) scheme. As in Buchanan and Gilbert [30], to implement the NM algorithm, we use the MATLAB command fminsearch. A MATLAB code for the DE scheme can be found at http://www1.icsi.berkeley.edu/~storn/code.html. To our knowledge, this is the first time that DE is applied to the present context.

Before we discuss our numerical experiments, let us briefly describe these two derivative-free optimization methods. The fact that there is no derivative data needed to use these algorithms makes them applicable to a wide variety of problems. However, this type of optimization methods also has significant drawbacks. The DE scheme is an example of a population-based stochastic search method that is used for global optimization. One very appealing feature of this scheme is that very little user input is required. For instance, unlike the NM algorithm, no initial guess is needed to start the search with DE. This is a particularly salient feature since it has the effect of being able to stimulate some level of uncertainty in determining the parameters of cancellous bone. More specifically, to find an accurate minimum using the NM algorithm, one must have an accurate guess in the first place, otherwise it may converge to a local minimum. The DE scheme eliminates any bias in this regard. The main drawback of evolutionary algorithms is that, depending on the cost function, convergence may be slow.[47] For more information regarding the DE scheme, see [48]. The NM algorithm is another example of a direct search method, which can be applied to a wide variety of cost functions, just as with DE. Since a starting guess must be supplied to initiate the algorithm, convergence to a global minimum may not occur, especially if the cost function has many minima. It is for this reason that we compare the NM and DE results, since the latter may be more successful at finding the global minimum. Moreover, the NM algorithm may not be desirable to use for problems with many variables to be determined (as shown in Nelder and Mead [49]) and, in higher dimensions, there is a large number of function evaluations needed for convergence. This can be very time intensive especially when the cost function is complicated. For further details on the NM algorithm and its convergence properties, we refer the reader to [49, 50].

We now discuss our numerical experiments. For a given value of $\mathit{\beta }$, we may calculate the pressure at a certain number $RN$ of receiving nodes outside of the bone specimen. We do this for two different resolutions to compare the results. For our tests, we assume that the centre of the square is located at $(5L/2,5L/2)$, and that the source is positioned at ${\mathbf{x}}_0=(L,5L/2)$ outside of the square. The physical parameters we specify are (in dimensional SI units): $L=0.01$, ${\mathit{\rho }}_f=950$, ${\mathit{\rho }}_r=1960$, $K_f=2\times {10}^9$, $K_r=2\times {10}^{10}$, $a_{\infty }=1.13$ and $\mathrm{\Lambda }=5\times {10}^{-6}$. In order to see if the model can handle changes in physical parameters, we use two different values for $\mathit{\eta }$, ${\mathit{\eta }}_1=1.5$ (blood marrow) and ${\mathit{\eta }}_2=0.001$ (water), thus each set of numerical tests is performed twice.

To begin our numerical testing, let $P_{\ell }^{\ast }$ represent the pressure at point ${\mathbf{x}}_{\ell }=(x_i,y_j)$. Trial values $P_{\ell }$ produced by a set of Biot parameters are compared to the values $P_{\ell }^{\ast }$ using the objective function(20) $$\begin{array}{c}\hfill f(P_{\ell },P_{\ell }^{\ast })=\frac{{\displaystyle {\left[\sum _{\ell =1}^{RN}{(P_{\ell }^{\ast }-P_{\ell })}^2\right]}^{1/2}}}{{\displaystyle {\left[\sum _{\ell =1}^{RN}{(P_{\ell }^{\ast })}^2\right]}^{1/2}}}.\end{array}$$(20)

For our first test, we compare varying sets of resolutions. We are interested in determining the value of $\mathit{\beta }$ that minimizes the objective function (20(20) $$\begin{array}{c}\hfill f(P_{\ell },P_{\ell }^{\ast })=\frac{{\displaystyle {\left[\sum _{\ell =1}^{RN}{(P_{\ell }^{\ast }-P_{\ell })}^2\right]}^{1/2}}}{{\displaystyle {\left[\sum _{\ell =1}^{RN}{(P_{\ell }^{\ast })}^2\right]}^{1/2}}}.\end{array}$$(20) ), with $f_{min}$ denoting this minimum. The minimization procedure is done using the NM simplex algorithm. We use the lower resolutions $N=(25,45,65)$ to produce the trial values, and compare these to the higher resolution $N=90$. Due to limitations in computing resources, simulations with resolutions higher than $N=90$ were prohibitive. For this test, the pressure is calculated at $RN=11$ receiving points outside the square, opposite to the source. These points are evenly spaced in the interval $x_1=4L$ and $L\le x_2\le 4L$. The stopping criterion that we imposed in the minimization depends on the scheme. For the NM algorithm, we typically used the default criterion in fminsearch. For the stopping criterion in the DE scheme as discussed later, we specified a maximum of 150 iterations. Our choice of 150 iterations was based on experimental observations. We can see from the results in Tables 3 and 4 that the numerical scheme does appear to converge and that, in most cases, our guess for $\mathit{\beta }$ is quite accurate. We also mention that there does appear to be good frequencies and bad frequencies to use for the purpose of obtaining numerical data.

For our next test, we determine if increasing the number of measurement points $RN$ will make our results more accurate. We compare the results for $RN=11$ to those for $RN=100$ (distributed over the same interval $x_1=4L$, $L\le x_2\le 4L$). Due to the larger number of constraints for $RN=100$, computations were found to be more demanding in CPU time. Therefore, to carry out this test, we use $N=50$ for the high resolution and $N=25$ for the low resolution. From Tables 5 to 6, we can see that there is no significant change in results when we take more receiving nodes. However, placement of nodes may have an effect on numerical data. As an additional test, we place evenly spaced receiving nodes at $5L/2\le x_1\le 4L$, $x_2=4L$ near the top of the square, at $5L/2\le x_1\le 4L$, $x_2=L$ near the bottom of the square and nodes to the right of the square at $x_1=4L$, $2L\le x_2\le 3L$. Both cases $RN=11$ and $RN=100$ are examined. Again, from Tables 7 to 8, we see that there is no much difference when we alter the placement of the measurement points. Therefore, for convenience in the following tests, we will use $RN=11$ receiving nodes evenly placed to the right of the bone sample, at $x_1=4L$ and $L\le x_2\le 4L$.

Next, we minimize the objective function (20(20) $$\begin{array}{c}\hfill f(P_{\ell },P_{\ell }^{\ast })=\frac{{\displaystyle {\left[\sum _{\ell =1}^{RN}{(P_{\ell }^{\ast }-P_{\ell })}^2\right]}^{1/2}}}{{\displaystyle {\left[\sum _{\ell =1}^{RN}{(P_{\ell }^{\ast })}^2\right]}^{1/2}}}.\end{array}$$(20) ) using the DE scheme and compare these results to the values obtained by minimizing with the NM algorithm. Here again, we take $N=25$ for the low resolution and $N=50$ for the high resolution. Tables 9 and 10 indicate that the NM minimum agrees with the DE one in most cases, which suggests that our model is robust in particular with respect to the minimization procedure.

Table 9. Comparison between the NM and DE minima for $\mathit{\eta }={\mathit{\eta }}_1$. Here, $N=50$ for the high resolution and $N=25$ for the low resolution.

$\mathit{\omega }$	$\mathit{\beta }$	$f_{min}$	% error
Guess/Target	0.7
250 kHz
NM	0.7032	0.2692	0.4571
DE	0.7032	0.2692	0.4571
Guess/Target	0.7
500 kHz
NM	0.7252	0.1318	3.600
DE	0.7252	0.1318	3.600
Guess/Target	0.83
250 kHz
NM	0.8345	0.2124	0.5422
DE	0.8345	0.2124	0.5422
Guess/Target	0.83
500 kHz
NM	0.8504	0.3870	2.458
DE	0.8504	0.3870	2.458
Guess/Target	0.9
250 kHz
NM	0.8898	0.5700	1.133
DE	0.8898	0.5700	1.133
Guess/Target	0.9
500 kHz
NM	0.9033	0.1118	0.3667
DE	0.9033	0.1118	0.3667

Figure 7. Sensitivity test on $\mathit{\beta }$ for $\mathit{\eta }={\mathit{\eta }}_1$. Here, $N=90$ for the high resolution and $N=65$ for the low resolution. The vertical dashed line corresponds to the target value of $\mathit{\beta }$ specified in the high-resolution simulation. Both frequencies 250 and 500 kHz are considered.

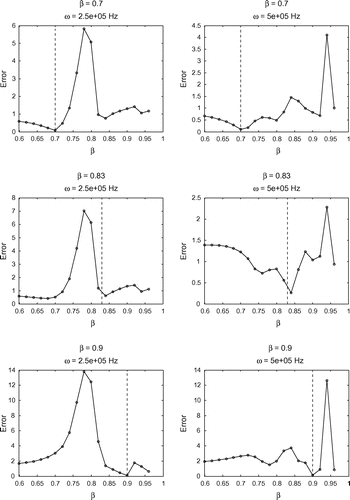
Table 10. Comparison between the NM and DE minima for $\mathit{\eta }={\mathit{\eta }}_2$. Here, $N=50$ for the high resolution and $N=25$ for the low resolution.

$\mathit{\omega }$	$\mathit{\beta }$	$f_{min}$	% error
Guess/Target	0.7
250 kHz
NM	0.6983	0.1096	0.2429
DE	0.6983	0.1096	0.2429
Guess/Target	0.7
500 kHz
NM	0.7513	0.1542	7.329
DE	0.7513	0.1542	7.329
Guess/Target	0.83
250 kHz
NM	0.9044	0.9850	8.964
DE	0.9044	0.9850	8.964
Guess/Target	0.83
500 kHz
NM	0.8407	0.3091	1.289
DE	0.8407	0.3091	1.289
Guess/Target	0.9
250 kHz
NM	0.9029	0.2582	0.3222
DE	0.9029	0.2582	0.3222
Guess/Target	0.9
500 kHz
NM	0.8998	0.1911	0.0222
DE	0.9571	0.4379	6.344

Finally, we perform a sensitivity test on the determination of $\mathit{\beta }$. In this case, a target high-resolution $(N=90$) simulation is performed for a given value of $\mathit{\beta }$ and compared with trial low-resolution ($N=65$) simulations for a range of values of $\mathit{\beta }$. The comparison is based on a direct evaluation of the objective function (20(20) $$\begin{array}{c}\hfill f(P_{\ell },P_{\ell }^{\ast })=\frac{{\displaystyle {\left[\sum _{\ell =1}^{RN}{(P_{\ell }^{\ast }-P_{\ell })}^2\right]}^{1/2}}}{{\displaystyle {\left[\sum _{\ell =1}^{RN}{(P_{\ell }^{\ast })}^2\right]}^{1/2}}}.\end{array}$$(20) ) without minimization. 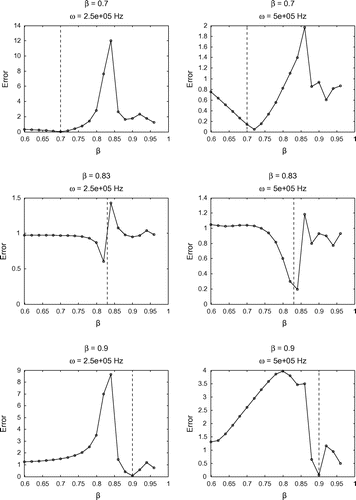These results are presented in Figures 7 and 8 and show that the minimum of the objective function occurs near the target value of $\mathit{\beta }$ in all cases. This is consistent with the findings from our previous tests, and further supports the robustness of our model.

Figure 8. Sensitivity test on $\mathit{\beta }$ for $\mathit{\eta }={\mathit{\eta }}_2$. Here, $N=90$ for the high resolution and $N=65$ for the low resolution. The vertical dashed line corresponds to the target value of $\mathit{\beta }$ specified in the high-resolution simulation. Both frequencies 250 and 500 kHz are considered.

These preliminary results are encouraging in regards to trying to recover other parameters by this approach, and suggest that we may have some success at recovering additional parameters. After the minimization procedure is carried out, we can use our guess for $\mathit{\beta }$ to determine guesses for other parameters. In particular, this value allows us to calculate guess values for the following parameters: Re $K_b$, and Re $\mathit{\mu }$. We can obtain these guesses using the following formulas in terms of $\mathit{\beta }$:

• The real parts of $K_b$ and $\mathit{\mu }$ are calculated by the formulas of Williams [32],(21) $$\begin{array}{cc}\hfill \mathrm{R}e{K}_b& =\frac{E}{3(1-2\mathit{\nu })}{V}_f^n,\hfill \\ \hfill \mathrm{R}e\mathit{\mu }& =\frac{E}{2(1+\mathit{\nu })}{V}_f^n,\hfill \end{array}$$(21) where $V_f=1-\mathit{\beta }$ is the bone volume fraction. Following Hosokawa and Otani [31], we use $n=1.46$, $E=2.2\times {10}^{10}$ and $\mathit{\nu }=0.32$ for the exponent, Young modulus and Poisson ratio of solid (cortical) bone, respectively.

• The imaginary parts of $K_b$ and $\mathit{\mu }$ are calculated assuming a log decrement $\ell$, i.e. $\mathrm{I}m{K}_b^{\ast }=\ell \mathrm{R}e{K}_b^{\ast }/\mathit{\pi }$ and $\mathrm{I}m\mathit{\mu }=\ell \mathrm{R}e{\mathit{\mu }}^{\ast }/\mathit{\pi }$ with $\ell =0.1$, as typically used in underwater acoustics.[45]

These guesses have errors that are compounded mainly by two things: the error in our guess on $\mathit{\beta }$ and the fact that these formulas are approximations to begin with. This leads us to question whether an alternative method to obtain guesses for Re $K_b$ and Re $\mathit{\mu }$ may be more suitable. In the following section, we would like to obtain guesses for Re $K_b$ and Re $\mathit{\mu }$ without considering them to be explicit functions of $\mathit{\beta }$.

5.2. Multivariate minimization

Having found guesses for the parameter $\mathit{\beta }$ alone, we would like to determine if accurate guesses for Re $K_b$ and Re $\mathit{\mu }$ can also be obtained. To produce these guesses, we use the DE algorithm. The reason for this choice is that it does not require a starting value. We use the same objective function (20(20) $$\begin{array}{c}\hfill f(P_{\ell },P_{\ell }^{\ast })=\frac{{\displaystyle {\left[\sum _{\ell =1}^{RN}{(P_{\ell }^{\ast }-P_{\ell })}^2\right]}^{1/2}}}{{\displaystyle {\left[\sum _{\ell =1}^{RN}{(P_{\ell }^{\ast })}^2\right]}^{1/2}}}.\end{array}$$(20) ) as previously. Bone porosity is fixed using the average of the guess values for $\mathit{\beta }$ as given by the NM and DE schemes in Tables 9 and 10. By doing so, we try to avoid some bias in the selection of $\mathit{\beta }$, although the average is not different from the guess values in most cases.

Table 11. Guesses for Biot parameters produced by the DE scheme in the case $\mathit{\eta }={\mathit{\eta }}_1$.

$\mathit{\omega }$	$f_{min}$	$\mathit{\beta }$	Re $K_b$	Re $\mathit{\mu }$
Guess/Target		0.7	$3.5123\mathrm{e}+9$	$1.4369\mathrm{e}+9$
250 kHz	0.2681	0.7032	$4.5593\mathrm{e}+9$	$1.4151\mathrm{e}+9$
500 kHz	0.1099	0.7251	$9.5275\mathrm{e}+8$	$1.2933\mathrm{e}+9$
Guess/Target		0.83	$1.5327\mathrm{e}+9$	$6.2701\mathrm{e}+8$
250 kHz	0.1988	0.8345	$2.5792\mathrm{e}+9$	$5.9996\mathrm{e}+8$
500 kHz	0.3866	0.8504	$9.8725\mathrm{e}+8$	$5.1853\mathrm{e}+8$
Guess/Target		0.9	$7.0631\mathrm{e}+8$	$2.8895\mathrm{e}+8$
250 kHz	0.5696	0.8898	$5.7437\mathrm{e}+8$	$3.3229\mathrm{e}+8$
500 kHz	0.1109	0.9033	$7.6595\mathrm{e}+8$	$2.7407\mathrm{e}+8$

Table 12. Guesses for Biot parameters produced by the DE scheme in the case $\mathit{\eta }={\mathit{\eta }}_2$.

$\mathit{\omega }$	$f_{min}$	$\mathit{\beta }$	Re $K_b$	Re $\mathit{\mu }$
Guess/Target		0.7	$3.5123\mathrm{e}+9$	$1.4369\mathrm{e}+9$
250 kHz	0.0903	0.6983	$8.8536\mathrm{e}+8$	$1.4431\mathrm{e}+9$
500 kHz	0.1309	0.7513	$1.1369\mathrm{e}+9$	$1.0909\mathrm{e}+9$
Guess/Target		0.83	$1.5327\mathrm{e}+9$	$6.2701\mathrm{e}+8$
250 kHz	0.9850	0.9044	$1.6535\mathrm{e}+8$	$2.7056\mathrm{e}+8$
500 kHz	0.3073	0.8407	$1.0459\mathrm{e}+9$	$5.6728\mathrm{e}+8$
Guess/Target		0.9	$7.0631\mathrm{e}+8$	$2.8895\mathrm{e}+8$
250 kHz	0.2537	0.9029	$2.2512\mathrm{e}+8$	$2.7667\mathrm{e}+8$
500 kHz	0.1655	0.9285	$6.5012\mathrm{e}+8$	$2.7932\mathrm{e}+8$

Table 13. Errors on the guesses obtained by the DE scheme for $\mathit{\eta }={\mathit{\eta }}_1$.

$\mathit{\omega }$	$f_{min}$	$\mathit{\beta }$	Re $K_b$	Re $\mathit{\mu }$
Guess/Target		0.7	$3.5123\mathrm{e}+9$	$1.4369\mathrm{e}+9$
250 kHz	0.2681	0.4571%	29.81%	1.52%
500 kHz	0.1099	3.600%	72.87%	9.99%
Guess/Target		0.83	$1.5327\mathrm{e}+9$	$6.2701\mathrm{e}+8$
250 kHz	0.1988	0.5422%	68.28%	4.31%
500 kHz	0.3866	2.4578%	35.39%	17.30%
Guess/Target		0.9	$7.0631\mathrm{e}+8$	$2.8895\mathrm{e}+8$
250 kHz	0.5696	1.1333%	18.68%	15.00%
500 kHz	0.1109	0.3667%	8.44%	5.15%

Table 14. Errors on the guesses obtained by the DE scheme for $\mathit{\eta }={\mathit{\eta }}_2$.

$\mathit{\omega }$	$f_{min}$	$\mathit{\beta }$	Re $K_b$	Re $\mathit{\mu }$
Guess/Target		0.7	$3.5123\mathrm{e}+9$	$1.4369\mathrm{e}+9$
250 kHz	0.0903	0.2429%	74.793%	0.4315%
500 kHz	0.1309	7.329%	67.631%	24.079%
Guess/Target		0.83	$1.5327\mathrm{e}+9$	$6.2701\mathrm{e}+8$
250 kHz	0.9844	8.964%	76.59%	6.364%
500 kHz	0.3073	1.289%	31.758%	9.526%
Guess/Target		0.9	$7.0631\mathrm{e}+8$	$2.8895\mathrm{e}+8$
250 kHz	0.2537	0.3222%	85.312%	55.874%
500 kHz	0.1654	6.344%	7.956%	3.331%

It can be seen from Tables 11 to 14 that we have varying degrees of success depending on the value of $\mathit{\beta }$, and we are able to recover the real part of $\mathit{\mu }$ with better accuracy. Importantly, the orders of magnitude are well recovered in all cases. Based on this numerical evidence, it seems reasonable to use this model and scheme for producing guesses for the parameters of cancellous bone in the range of frequencies $250$–$500$ kHz.

6. Conclusions

Upon comparison with Phase 1 tests in Buchanan and Gilbert [30], our numerical results in the present paper may be viewed as being successful. Except in one case, errors made on the guess for $\mathit{\beta }$ were well under 10%. Recovery of Re $K_b$ still proves troublesome; however, guesses here are more stable. Another success is the recovery of the parameter Re $\mathit{\mu }$. Except in the extreme case where $\mathit{\beta }=0.9$, we observe errors well below $34$% on this guess, which is the lowest error obtained in Buchanan and Gilbert [30]. We would like to point out again that Buchanan and Gilbert [30] considered a simplified situation where the bone sample is an infinite slab, and they did not include effects of tortuosity in their model. The nicest feature of the present method of parameter recovery is that it does not require large sets of trial data, since the DE scheme requires no starting value.

If we compare with Table 1, our guesses for $\mathit{\beta }$ and Re $\mathit{\mu }$ may be viewed again as successful. While errors may be slightly higher, we must note that our method of determining these guesses is significantly simpler, and does not require multiple initial guesses. Finally, we note that the change in viscosity does not significantly alter the error ranges on our results. With the experience gained from the present study, we plan to tackle the parameter recovery problem for the orthotropic case in the near future.

Additional information

Funding

This research was partially supported by the NSF through [grant number DMS-0920850] and the Simons Foundation through [grant number 246170]. P. Guyenne thanks Prof. Masahiro Yamamoto and the Graduate School of Mathematical Sciences at the University of Tokyo for their hospitality during a visit in the summer 2013.

Appendix 1

Well posedness of the formulation

In the isotropic case,[51] it was shown using a variational approach that the Biot transmission problem is well posed. A variation of the same arguments may be used in the orthotropic case. We outline the procedure below on how this may be done by listing a sequence of theorems by which one may establish this result. The theorems are straightforward to establish by emulating the arguments of [51] (see also [52, 53]). We begin by introducing several useful definitions.

Definition A.1

(Nonhomogeneous transmission problem (${\mathrm{TP}}_f$)) The problem consists of finding the triplet $(\mathbf{u},s,P)$ such that$$\left(\mathit{\mu }{\mathbb{H}}^{\top }+\frac{1}{1-{\mathit{\nu }}_1{\mathit{\nu }}_2}\mathbb{E}\mathbb{H}-\frac{p_{12}}{p_{22}}Q\mathbb{H}+p_{11}-\frac{p_{12}^2}{p_{22}}\right)\mathbf{u}-\left(\frac{p_{12}+Q\mathbb{H}}{p_{22}}\right)\mathrm{\nabla }s=\mathbf{0}\mathrm{in}{\mathrm{\Omega }}^b,$$

and(A1) $$\begin{array}{cc}& {\mathrm{\nabla }}^{2}s+\frac{p_{22}}{R}s+\left(p_{12}-\frac{p_{22}Q}{R}\right)e=0\text{in}{\mathrm{\Omega }}^b,\hfill \end{array}$$(A1) (A2) $$\begin{array}{cc}& -\left({\mathrm{\nabla }}^{2}P+k_0^{2}P\right)=f\mathrm{in}{\mathrm{\Omega }}^w,\hfill \end{array}$$(A2)

where $f:=-\mathrm{\nabla }·\mathbf{f}$, having compact support in ${\mathrm{\Omega }}^w$, together with the transmission conditions(A3) $$\begin{array}{cc}& {\displaystyle \left[\underline{\underline{\mathit{\sigma }}}(\mathbf{u})+Q\mathrm{\nabla }·\mathbf{U}+s\right]\mathbf{n}=-P\mathbf{n}\mathrm{on}\mathrm{\Gamma }=\mathit{\partial }{\mathrm{\Omega }}^b,}\hfill \end{array}$$(A3) (A4) $$\begin{array}{cc}& {\displaystyle {\mathit{\rho }}^w{\mathit{\omega }}^2\left[1-\mathit{\beta }\left(1+\frac{p_{12}}{p_{22}}\right)\right]\mathbf{u}·\mathbf{n}-\frac{\mathit{\beta }{\mathit{\rho }}^w{\mathit{\omega }}^2}{p_{22}}\frac{\mathit{\partial }s}{\mathit{\partial }n}=\frac{\mathit{\partial }P}{\mathit{\partial }n}-\mathbf{n}·\mathbf{f}\mathrm{on}\mathrm{\Gamma },}\hfill \end{array}$$(A4) (A5) $$\begin{array}{cc}& {\displaystyle s=-\mathit{\beta }P\mathrm{on}\mathrm{\Gamma },}\hfill \end{array}$$(A5)

where $\underline{\underline{\mathit{\sigma }}}(\mathbf{u})$ and $\underline{\underline{\mathit{\epsilon }}}(\mathbf{u})$ denote the stress and strain tensors,$$\begin{array}{cc}& {\displaystyle \underline{\underline{\mathit{\sigma }}}(\mathbf{u})=\left(\begin{array}{cc}\frac{E_1{e}_{11}+{\mathit{\nu }}_1{E}_2{e}_{22}}{1-{\mathit{\nu }}_1{\mathit{\nu }}_2}& \mathit{\mu }{e}_{12}\\ \mathit{\mu }{e}_{12}& \frac{E_2{e}_{22}+{\mathit{\nu }}_2{E}_1{e}_{11}}{1-{\mathit{\nu }}_1{\mathit{\nu }}_2}\end{array}\right),}\hfill \\ \hfill & {\displaystyle \underline{\underline{\mathit{\epsilon }}}(\mathbf{u})=\frac{1}{2}\left(\mathrm{\nabla }\mathbf{u}+\mathrm{\nabla }{\mathbf{u}}^{\top }\right),}\hfill \end{array}$$

and the fluid dilatation is given by$$\mathrm{\nabla }·\mathbf{U}=\frac{1}{R}\left(s-Qe\right).$$

In addition, we impose vanishing of the tangential frame stress ${\mathit{\sigma }}_{12}={\mathit{\sigma }}_{21}=0$ on $\mathrm{\Gamma }$ and assume that the Sommerfeld radiation condition holds for $P$. In this formulation, transmission conditions (A3(A3) $$\begin{array}{cc}& {\displaystyle \left[\underline{\underline{\mathit{\sigma }}}(\mathbf{u})+Q\mathrm{\nabla }·\mathbf{U}+s\right]\mathbf{n}=-P\mathbf{n}\mathrm{on}\mathrm{\Gamma }=\mathit{\partial }{\mathrm{\Omega }}^b,}\hfill \end{array}$$(A3) ) and (A4(A4) $$\begin{array}{cc}& {\displaystyle {\mathit{\rho }}^w{\mathit{\omega }}^2\left[1-\mathit{\beta }\left(1+\frac{p_{12}}{p_{22}}\right)\right]\mathbf{u}·\mathbf{n}-\frac{\mathit{\beta }{\mathit{\rho }}^w{\mathit{\omega }}^2}{p_{22}}\frac{\mathit{\partial }s}{\mathit{\partial }n}=\frac{\mathit{\partial }P}{\mathit{\partial }n}-\mathbf{n}·\mathbf{f}\mathrm{on}\mathrm{\Gamma },}\hfill \end{array}$$(A4) ) represent, respectively, the continuity of the flux and continuity of the aggregate pressure, while condition (A5(A5) $$\begin{array}{cc}& {\displaystyle s=-\mathit{\beta }P\mathrm{on}\mathrm{\Gamma },}\hfill \end{array}$$(A5) ) expresses the continuity of pore pressure.

For the uniqueness proof, we now introduce the traction-free solution for the bone as in fluid–structure interaction problems.[52]

Definition A.2

(Traction-free problem) The problem for $(\mathbf{u},s)$ in ${\mathrm{\Omega }}^b$ consists of the partial differential Equations (A1(A1) $$\begin{array}{cc}& {\mathrm{\nabla }}^{2}s+\frac{p_{22}}{R}s+\left(p_{12}-\frac{p_{22}Q}{R}\right)e=0\text{in}{\mathrm{\Omega }}^b,\hfill \end{array}$$(A1) ) and (A2(A2) $$\begin{array}{cc}& -\left({\mathrm{\nabla }}^{2}P+k_0^{2}P\right)=f\mathrm{in}{\mathrm{\Omega }}^w,\hfill \end{array}$$(A2) ) together with the homogeneous boundary conditions$$\begin{array}{cc}& {\displaystyle \left[\underline{\underline{\mathit{\sigma }}}(\mathbf{u})+Q\mathrm{\nabla }·\mathbf{U}+s\right]\mathbf{n}=\mathbf{0}\mathrm{on}\mathrm{\Gamma },}\hfill \\ \hfill & {\displaystyle {\mathit{\rho }}^w{\mathit{\omega }}^2\left[1-\mathit{\beta }\left(1+\frac{p_{12}}{p_{22}}\right)\right]\mathbf{u}·\mathbf{n}-\frac{\mathit{\beta }{\mathit{\rho }}^w{\mathit{\omega }}^2}{p_{22}}\frac{\mathit{\partial }s}{\mathit{\partial }n}=\frac{\mathit{\partial }P}{\mathit{\partial }n}\mathrm{on}\mathrm{\Gamma },}\hfill \\ \hfill & {\displaystyle s=0\mathrm{on}\mathrm{\Gamma },}\hfill \end{array}$$

which is called the traction-free problem for $(\mathbf{u},s)$, and the corresponding nontrivial solutions are referred to as the traction-free solutions.

For the variational formulation, we now reduce the partial differential Equation (A2(A2) $$\begin{array}{cc}& -\left({\mathrm{\nabla }}^{2}P+k_0^{2}P\right)=f\mathrm{in}{\mathrm{\Omega }}^w,\hfill \end{array}$$(A2) ) for $P$ to a boundary integral equation on $\mathrm{\Gamma }$. We use the indirect approach for the reduction of partial differential equations by seeking a solution $P$ in the form of a single-layer potential(A6) $$\begin{array}{c}\hfill P=-\mathbf{S}\mathit{\varphi }+P_f\text{in}{\mathrm{\Omega }}^w,\end{array}$$(A6)

where $\mathit{\varphi }$ is an unknown density function and $\mathbf{S}\mathit{\varphi }$ is the single-layer potential$$\mathbf{S}\mathit{\varphi }(\mathbf{x}):=\frac{i}{4}{\int }_{\mathrm{\Gamma }}{H}_0^{(1)}(k_0||\mathbf{x}-\mathbf{y}||)\mathit{\varphi }(\mathbf{y})\mathrm{d}{s}_y,\mathbf{x}\in {\mathrm{\Omega }}^w,$$

where $-i{H}_0^{(1)}/4$ denotes the fundamental solution of the Helmholtz operator ${\mathrm{\nabla }}^2+k_0^2$, and$$P_f(\mathbf{x}):=\frac{i}{4}{\int }_{\mathrm{supp}(f)}{H}_0^{(1)}(k_0||\mathbf{x}-\mathbf{y}||)f(\mathbf{y})d\mathbf{y},\mathbf{x}\in {\mathrm{\Omega }}^w,$$

is a particular solution of (A2(A2) $$\begin{array}{cc}& -\left({\mathrm{\nabla }}^{2}P+k_0^{2}P\right)=f\mathrm{in}{\mathrm{\Omega }}^w,\hfill \end{array}$$(A2) ), which is known. Hence, if ${P|}_{\mathrm{\Gamma }}$ is given, by applying the trace operator ${\mathit{\gamma }}_0$ to (A6(A6) $$\begin{array}{c}\hfill P=-\mathbf{S}\mathit{\varphi }+P_f\text{in}{\mathrm{\Omega }}^w,\end{array}$$(A6) ), we obtain a boundary integral equation for the known density $\mathit{\varphi }$,(A7) $$\begin{array}{c}\hfill {P|}_{\mathrm{\Gamma }}=-\mathbf{V}\mathit{\varphi }+{\mathit{\gamma }}_0{P}_f,\end{array}$$(A7)

where $\mathbf{V}={\mathit{\gamma }}_0\mathbf{S}$ is the single-layer boundary integral operator. Then from the transmission condition ($B_3$), we arrive at the boundary integral equation(A8) $$\begin{array}{c}\hfill \mathbf{V}\mathit{\varphi }-\frac{1}{\mathit{\beta }}s={\mathit{\gamma }}_0{P}_f.\end{array}$$(A8)

Definition A.3

(Nonlocal boundary value problem)The ${\mathrm{TP}}_f$ is termed a nonlocal boundary value problem for the triplet $(\mathbf{u},s,\mathit{\varphi })$ if the latter satisfies (A1(A1) $$\begin{array}{cc}& {\mathrm{\nabla }}^{2}s+\frac{p_{22}}{R}s+\left(p_{12}-\frac{p_{22}Q}{R}\right)e=0\text{in}{\mathrm{\Omega }}^b,\hfill \end{array}$$(A1) ), (A2(A2) $$\begin{array}{cc}& -\left({\mathrm{\nabla }}^{2}P+k_0^{2}P\right)=f\mathrm{in}{\mathrm{\Omega }}^w,\hfill \end{array}$$(A2) ) and the boundary integral Equation (A8(A8) $$\begin{array}{c}\hfill \mathbf{V}\mathit{\varphi }-\frac{1}{\mathit{\beta }}s={\mathit{\gamma }}_0{P}_f.\end{array}$$(A8) ), together with the transmission conditions (A3(A3) $$\begin{array}{cc}& {\displaystyle \left[\underline{\underline{\mathit{\sigma }}}(\mathbf{u})+Q\mathrm{\nabla }·\mathbf{U}+s\right]\mathbf{n}=-P\mathbf{n}\mathrm{on}\mathrm{\Gamma }=\mathit{\partial }{\mathrm{\Omega }}^b,}\hfill \end{array}$$(A3) ), (A7(A7) $$\begin{array}{c}\hfill {P|}_{\mathrm{\Gamma }}=-\mathbf{V}\mathit{\varphi }+{\mathit{\gamma }}_0{P}_f,\end{array}$$(A7) ) and (A4(A4) $$\begin{array}{cc}& {\displaystyle {\mathit{\rho }}^w{\mathit{\omega }}^2\left[1-\mathit{\beta }\left(1+\frac{p_{12}}{p_{22}}\right)\right]\mathbf{u}·\mathbf{n}-\frac{\mathit{\beta }{\mathit{\rho }}^w{\mathit{\omega }}^2}{p_{22}}\frac{\mathit{\partial }s}{\mathit{\partial }n}=\frac{\mathit{\partial }P}{\mathit{\partial }n}-\mathbf{n}·\mathbf{f}\mathrm{on}\mathrm{\Gamma },}\hfill \end{array}$$(A4) ) where$$\frac{\mathit{\partial }P}{\mathit{\partial }n}=\frac{1}{2}\mathit{\varphi }-\mathbf{K}\mathit{\varphi }+\frac{\mathit{\partial }{P}_f}{\mathit{\partial }n}.$$

The boundary integral operator $\mathbf{K}$ is defined by$$\mathbf{K}\mathit{\varphi }(\mathbf{x}):=\frac{i}{4}{\int }_{\mathrm{\Gamma }}\frac{\mathit{\partial }{H}_0^{(1)}}{\mathit{\partial }n}(k_0||\mathbf{x}-\mathbf{y}||)\mathit{\varphi }(\mathbf{y})\mathrm{d}{s}_y,\mathbf{x}\in \mathrm{\Gamma },$$

where the normal derivative is taken with respect to $\mathbf{x}$. We note that condition (A4(A4) $$\begin{array}{cc}& {\displaystyle {\mathit{\rho }}^w{\mathit{\omega }}^2\left[1-\mathit{\beta }\left(1+\frac{p_{12}}{p_{22}}\right)\right]\mathbf{u}·\mathbf{n}-\frac{\mathit{\beta }{\mathit{\rho }}^w{\mathit{\omega }}^2}{p_{22}}\frac{\mathit{\partial }s}{\mathit{\partial }n}=\frac{\mathit{\partial }P}{\mathit{\partial }n}-\mathbf{n}·\mathbf{f}\mathrm{on}\mathrm{\Gamma },}\hfill \end{array}$$(A4) ) can be explicitly written in terms of $\mathit{\varphi }$ as$$\frac{\mathit{\partial }s}{\mathit{\partial }n}=\frac{p_{22}}{\mathit{\beta }}\left\{\left[1-\mathit{\beta }\left(1+\frac{p_{12}}{p_{22}}\right)\right]\mathbf{u}·\mathbf{n}-\frac{1}{{\mathit{\rho }}^w{\mathit{\omega }}^2}\left(\frac{1}{2}\mathit{\varphi }-\mathbf{K}\mathit{\varphi }\right)\right\}+\frac{p_{22}}{\mathit{\beta }{\mathit{\rho }}^w{\mathit{\omega }}^2}\left(\mathbf{n}·\mathbf{f}-\frac{\mathit{\partial }{P}_f}{\mathit{\partial }n}\right),$$

which will be needed for the variational formulation in the next section.

Appendix 2

Variational formulation

We consider the variational formulation of the nonlocal boundary value problem using the ideas of [51]. As usual, by multiplying (A8(A8) $$\begin{array}{c}\hfill \mathbf{V}\mathit{\varphi }-\frac{1}{\mathit{\beta }}s={\mathit{\gamma }}_0{P}_f.\end{array}$$(A8) ) with the conjugate of a test vector $\mathbf{v}$ and integrating by parts, we obtain(B1) $$\begin{array}{cc}& {\int }_{{\mathrm{\Omega }}^b}\left[\frac{1}{1-{\mathit{\nu }}_1{\mathit{\nu }}_2}\left(\begin{array}{cc}{E}_1{e}_{11}+{\mathit{\nu }}_1{E}_2{e}_{22}& 0\\ 0& {\mathit{\nu }}_2{E}_1{e}_{11}+E_2{e}_{22}\end{array}\right):\overline{\underline{\underline{e}}(\mathbf{v})}+2\mathit{\mu }\underline{\underline{\mathit{\epsilon }}}(\mathbf{u}):\overline{\underline{\underline{\mathit{\epsilon }}}(\mathbf{v})}\right.\hfill \\ \hfill & -\left.\frac{Q^2}{R}(\mathrm{\nabla }·\mathbf{u})(\mathrm{\nabla }·\overline{\mathbf{v}})+\left(\frac{Q}{R}-\frac{p_{12}}{p_{22}}\right)s\mathrm{\nabla }·\overline{\mathbf{v}}-\left(p_{11}-\frac{p_{12}^2}{p_{22}}\right)\mathbf{u}·\overline{\mathbf{v}}\right]d\mathbf{x}\hfill \\ \hfill & -{\int }_{\mathrm{\Gamma }}\left[\left(\begin{array}{cc}{E}_1{e}_{11}+{\mathit{\nu }}_1{E}_2{e}_{22}& 0\\ 0& {\mathit{\nu }}_2{E}_1{e}_{11}+E_2{e}_{22}\end{array}\right):2\mathit{\mu }\underline{\underline{\mathit{\epsilon }}}(\mathbf{u})-\frac{Q^2}{R}\mathrm{\nabla }·\mathbf{u}+\left(\frac{Q}{R}-\frac{p_{12}}{p_{22}}\right)s\right]\hfill \\ \hfill & \times \mathbf{n}·\overline{\mathbf{v}}\mathrm{d}s=0.\hfill \end{array}$$(B1)

We define the sesquilinear bilinear form$$a(\mathbf{u},\mathbf{v}):={\int }_{{\mathrm{\Omega }}^b}\left[\frac{1}{1-{\mathit{\nu }}_1{\mathit{\nu }}_2}\left(\begin{array}{cc}{E}_1{e}_{11}+{\mathit{\nu }}_1{E}_2{e}_{22}& 0\\ 0& {\mathit{\nu }}_2{E}_1{e}_{11}+E_2{e}_{22}\end{array}\right):\overline{\underline{\underline{e}}(\mathbf{v})}+2\mathit{\mu }\underline{\underline{\mathit{\epsilon }}}(\mathbf{u}):\overline{\underline{\underline{\mathit{\epsilon }}}(\mathbf{v})}\right]d\mathbf{x},$$

and by rewriting the boundary term in (B1(B1) $$\begin{array}{cc}& {\int }_{{\mathrm{\Omega }}^b}\left[\frac{1}{1-{\mathit{\nu }}_1{\mathit{\nu }}_2}\left(\begin{array}{cc}{E}_1{e}_{11}+{\mathit{\nu }}_1{E}_2{e}_{22}& 0\\ 0& {\mathit{\nu }}_2{E}_1{e}_{11}+E_2{e}_{22}\end{array}\right):\overline{\underline{\underline{e}}(\mathbf{v})}+2\mathit{\mu }\underline{\underline{\mathit{\epsilon }}}(\mathbf{u}):\overline{\underline{\underline{\mathit{\epsilon }}}(\mathbf{v})}\right.\hfill \\ \hfill & -\left.\frac{Q^2}{R}(\mathrm{\nabla }·\mathbf{u})(\mathrm{\nabla }·\overline{\mathbf{v}})+\left(\frac{Q}{R}-\frac{p_{12}}{p_{22}}\right)s\mathrm{\nabla }·\overline{\mathbf{v}}-\left(p_{11}-\frac{p_{12}^2}{p_{22}}\right)\mathbf{u}·\overline{\mathbf{v}}\right]d\mathbf{x}\hfill \\ \hfill & -{\int }_{\mathrm{\Gamma }}\left[\left(\begin{array}{cc}{E}_1{e}_{11}+{\mathit{\nu }}_1{E}_2{e}_{22}& 0\\ 0& {\mathit{\nu }}_2{E}_1{e}_{11}+E_2{e}_{22}\end{array}\right):2\mathit{\mu }\underline{\underline{\mathit{\epsilon }}}(\mathbf{u})-\frac{Q^2}{R}\mathrm{\nabla }·\mathbf{u}+\left(\frac{Q}{R}-\frac{p_{12}}{p_{22}}\right)s\right]\hfill \\ \hfill & \times \mathbf{n}·\overline{\mathbf{v}}\mathrm{d}s=0.\hfill \end{array}$$(B1) ), we see that$$\begin{array}{cc}\hfill a(\mathbf{u},\mathbf{v})+{\int }_{{\mathrm{\Omega }}^b}\left(\frac{Q}{R}-\frac{p_{12}}{p_{22}}\right)s\mathrm{\nabla }·\overline{\mathbf{v}}d\mathbf{x}-{\int }_{{\mathrm{\Omega }}^b}\left(p_{11}-\frac{p_{12}^2}{p_{22}}\right)\mathbf{u}·\overline{\mathbf{v}}d\mathbf{x}& \\ \hfill +{\int }_{\mathrm{\Gamma }}\left(1+\frac{p_{12}}{p_{22}}\right)s\mathbf{n}·\overline{\mathbf{v}}\mathrm{d}s-{\int }_{\mathrm{\Gamma }}\left[\mathit{\lambda }\mathrm{\nabla }·\mathbf{u}+2\mathit{\mu }\underline{\underline{\mathit{\epsilon }}}(\mathbf{u})+\frac{Q}{R}(s-Q\mathrm{\nabla }·\mathbf{u})+s\right]\mathbf{n}·\overline{\mathbf{v}}\mathrm{d}s& =0.\hfill \end{array}$$

Hence, the above equation with the transmission condition (A8(A8) $$\begin{array}{c}\hfill \mathbf{V}\mathit{\varphi }-\frac{1}{\mathit{\beta }}s={\mathit{\gamma }}_0{P}_f.\end{array}$$(A8) ) leads to the variational equation(B2) $$\begin{array}{cc}\hfill a(\mathbf{u},\mathbf{v})+{\int }_{{\mathrm{\Omega }}^b}\left(\frac{Q}{R}-\frac{p_{12}}{p_{22}}\right)s\mathrm{\nabla }·\overline{\mathbf{v}}d\mathbf{x}-{\int }_{{\mathrm{\Omega }}^b}\left(p_{11}-\frac{p_{12}^2}{p_{22}}\right)\mathbf{u}·\overline{\mathbf{v}}d\mathbf{x}& \\ \hfill -\left[1-\mathit{\beta }\left(1+\frac{p_{12}}{p_{22}}\right)\right]{〈\mathbf{V}\mathit{\varphi }\mathbf{n},\overline{\mathbf{v}}〉}_{\mathrm{\Gamma }}=-\left[1-\mathit{\beta }\left(1+\frac{p_{12}}{p_{22}}\right)\right]{〈{\mathit{\gamma }}_0{P}_f,\overline{\mathbf{v}}〉}_{\mathrm{\Gamma }},& \forall \mathbf{v}\in {\left(H^1({\mathrm{\Omega }}^b)\right)}^2.\hfill \end{array}$$(B2)

Repeating this process for the $s$-equation by multiplying (A1(A1) $$\begin{array}{cc}& {\mathrm{\nabla }}^{2}s+\frac{p_{22}}{R}s+\left(p_{12}-\frac{p_{22}Q}{R}\right)e=0\text{in}{\mathrm{\Omega }}^b,\hfill \end{array}$$(A1) ) with the conjugate of a test function $\mathit{\tau }$ and integrating by parts leads to the variational equation(B3) $$\begin{array}{cc}& b(s,\mathit{\tau })+p_{22}{\int }_{{\mathrm{\Omega }}^b}\left(\frac{Q}{R}-\frac{p_{12}}{p_{22}}\right)(\mathrm{\nabla }·\mathbf{u})\overline{\mathit{\tau }}d\mathbf{x}-{\int }_{{\mathrm{\Omega }}^b}\frac{p_{22}}{R}s\overline{\mathit{\tau }}d\mathbf{x}\hfill \\ \hfill & -\frac{p_{22}}{\mathit{\beta }}\left[1-\mathit{\beta }\left(1+\frac{p_{12}}{p_{22}}\right)\right]{〈\mathbf{u}·\mathbf{n},\overline{\mathit{\tau }}〉}_{\mathrm{\Gamma }}+\frac{p_{22}}{\mathit{\beta }{\mathit{\rho }}^w{\mathit{\omega }}^2}{〈\frac{1}{2}\mathit{\varphi }-\mathbf{K}\mathit{\varphi },\overline{\mathit{\tau }}〉}_{\mathrm{\Gamma }}\hfill \\ \hfill & =\frac{p_{22}}{\mathit{\beta }{\mathit{\rho }}^w{\mathit{\omega }}^2}{〈\mathbf{n}·\mathbf{f}-\frac{\mathit{\partial }{P}_f}{\mathit{\partial }n},\overline{\mathit{\tau }}〉}_{\mathrm{\Gamma }},\forall \mathit{\tau }\in H^1({\mathrm{\Omega }}^b),\hfill \end{array}$$(B3)

where $b(s,\mathit{\tau })$ is the sesquilinear form$$b(s,\mathit{\tau })={\int }_{{\mathrm{\Omega }}^b}\mathrm{\nabla }s·\mathrm{\nabla }\overline{\mathit{\tau }}d\mathbf{x}.$$

Following [51], the boundary integral Equation (A8(A8) $$\begin{array}{c}\hfill \mathbf{V}\mathit{\varphi }-\frac{1}{\mathit{\beta }}s={\mathit{\gamma }}_0{P}_f.\end{array}$$(A8) ) may be put into variational form as(B4) $$\begin{array}{c}\hfill \frac{p_{22}}{2{\mathit{\rho }}^w{\mathit{\omega }}^2}{〈\mathbf{V}\mathit{\varphi },\overline{\mathit{\psi }}〉}_{\mathrm{\Gamma }}-\frac{p_{22}}{2{\mathit{\rho }}^w{\mathit{\omega }}^2\mathit{\beta }}{〈s,\overline{\mathit{\psi }}〉}_{\mathrm{\Gamma }}=\frac{p_{22}}{2{\mathit{\rho }}^w{\mathit{\omega }}^2}{〈{\mathit{\gamma }}_0{P}_f,\overline{\mathit{\psi }}〉}_{\mathrm{\Gamma }},\forall \mathit{\psi }\in H^{-1/2}(\mathrm{\Gamma }).\end{array}$$(B4)

Collecting (B2(B2) $$\begin{array}{cc}\hfill a(\mathbf{u},\mathbf{v})+{\int }_{{\mathrm{\Omega }}^b}\left(\frac{Q}{R}-\frac{p_{12}}{p_{22}}\right)s\mathrm{\nabla }·\overline{\mathbf{v}}d\mathbf{x}-{\int }_{{\mathrm{\Omega }}^b}\left(p_{11}-\frac{p_{12}^2}{p_{22}}\right)\mathbf{u}·\overline{\mathbf{v}}d\mathbf{x}& \\ \hfill -\left[1-\mathit{\beta }\left(1+\frac{p_{12}}{p_{22}}\right)\right]{〈\mathbf{V}\mathit{\varphi }\mathbf{n},\overline{\mathbf{v}}〉}_{\mathrm{\Gamma }}=-\left[1-\mathit{\beta }\left(1+\frac{p_{12}}{p_{22}}\right)\right]{〈{\mathit{\gamma }}_0{P}_f,\overline{\mathbf{v}}〉}_{\mathrm{\Gamma }},& \forall \mathbf{v}\in {\left(H^1({\mathrm{\Omega }}^b)\right)}^2.\hfill \end{array}$$(B2) )–(B4(B4) $$\begin{array}{c}\hfill \frac{p_{22}}{2{\mathit{\rho }}^w{\mathit{\omega }}^2}{〈\mathbf{V}\mathit{\varphi },\overline{\mathit{\psi }}〉}_{\mathrm{\Gamma }}-\frac{p_{22}}{2{\mathit{\rho }}^w{\mathit{\omega }}^2\mathit{\beta }}{〈s,\overline{\mathit{\psi }}〉}_{\mathrm{\Gamma }}=\frac{p_{22}}{2{\mathit{\rho }}^w{\mathit{\omega }}^2}{〈{\mathit{\gamma }}_0{P}_f,\overline{\mathit{\psi }}〉}_{\mathrm{\Gamma }},\forall \mathit{\psi }\in H^{-1/2}(\mathrm{\Gamma }).\end{array}$$(B4) ), we have the variational formulation for the nonlocal boundary value problem.

Definition B.1

(Variational formulation) Given f, find the triplet $(\mathbf{u},s,\mathit{\varphi })\in {\left(H^1({\mathrm{\Omega }}^b)\right)}^2\times H^1({\mathrm{\Omega }}^b)\times H^{-1/2}(\mathrm{\Gamma })$ such that(B5) $$\begin{array}{c}\hfill \mathcal{A}\{(\mathbf{u},s,\mathit{\varphi }),(\mathbf{v},\mathit{\tau },\mathit{\psi })\}={\mathcal{L}}_f(\mathbf{v},\mathit{\tau },\mathit{\psi }),\end{array}$$(B5)

for all $(\mathbf{v},\mathit{\tau },\mathit{\psi })\in {\left(H^1({\mathrm{\Omega }}^b)\right)}^2\times H^1({\mathrm{\Omega }}^b)\times H^{-1/2}(\mathrm{\Gamma }),$ where $\mathcal{A}$ and ${\mathcal{L}}_f$ are, respectively, the sesquilinear form and linear functional defined by(B6) $$\begin{array}{cc}\hfill \mathcal{A}\{(\mathbf{u},s,\mathit{\varphi }),(\mathbf{v},\mathit{\tau },\mathit{\psi })\}& :=a(\mathbf{u},\mathbf{v})+b(s,\mathit{\tau })+\frac{p_{22}}{2{\mathit{\rho }}^w{\mathit{\omega }}^2}{〈\mathbf{V}\mathit{\varphi },\overline{\mathit{\psi }}〉}_{\mathrm{\Gamma }}\hfill \\ \hfill & +\left(\frac{Q}{R}-\frac{p_{12}}{p_{22}}\right)\left({\int }_{{\mathrm{\Omega }}^b}s\mathrm{\nabla }·\overline{\mathbf{v}}d\mathbf{x}+p_{22}{\int }_{{\mathrm{\Omega }}^b}(\mathrm{\nabla }·\mathbf{u})\overline{\mathit{\tau }}d\mathbf{x}\right)\hfill \\ \hfill & -\left(p_{11}-\frac{p_{12}^2}{p_{22}}\right){\int }_{{\mathrm{\Omega }}^b}\mathbf{u}·\overline{\mathbf{v}}d\mathbf{x}-\frac{p_{22}}{R}{\int }_{{\mathrm{\Omega }}^b}s\overline{\mathit{\tau }}d\mathbf{x}\hfill \\ \hfill & -\left[1-\mathit{\beta }\left(1+\frac{p_{12}}{p_{22}}\right)\right]\left({〈\mathbf{V}\mathit{\varphi }\mathbf{n},\overline{\mathbf{v}}〉}_{\mathrm{\Gamma }}+\frac{p_{22}}{\mathit{\beta }}{〈\mathbf{u}·\mathbf{n},\overline{\mathit{\tau }}〉}_{\mathrm{\Gamma }}\right)\hfill \\ \hfill & +\frac{p_{22}}{\mathit{\beta }{\mathit{\rho }}^w{\mathit{\omega }}^2}\left({〈\frac{1}{2}\mathit{\varphi }-\mathbf{K}\mathit{\varphi },\overline{\mathit{\tau }}〉}_{\mathrm{\Gamma }}-\frac{1}{2}{〈s,\overline{\mathit{\psi }}〉}_{\mathrm{\Gamma }}\right),\hfill \\ \hfill {\mathcal{L}}_f(\mathbf{v},\mathit{\tau },\mathit{\psi })& :=-\left[1-\mathit{\beta }\left(1+\frac{p_{12}}{p_{22}}\right)\right]{〈{\mathit{\gamma }}_0{P}_f,\overline{\mathbf{v}}〉}_{\mathrm{\Gamma }}+\frac{p_{22}}{\mathit{\beta }{\mathit{\rho }}^w{\mathit{\omega }}^2}{〈\mathbf{n}·\mathbf{f}-\frac{\mathit{\partial }{P}_f}{\mathit{\partial }n},\overline{\mathit{\tau }}〉}_{\mathrm{\Gamma }}\hfill \\ \hfill & +\frac{p_{22}}{2{\mathit{\rho }}^w{\mathit{\omega }}^2}{〈{\mathit{\gamma }}_0{P}_f,\overline{\mathit{\psi }}〉}_{\mathrm{\Gamma }}.\hfill \end{array}$$(B6)

Appendix 3

Existence and uniqueness

From the definition of the sesquilinear form $\mathcal{A}(·,·)$ in (B6(B6) $$\begin{array}{cc}\hfill \mathcal{A}\{(\mathbf{u},s,\mathit{\varphi }),(\mathbf{v},\mathit{\tau },\mathit{\psi })\}& :=a(\mathbf{u},\mathbf{v})+b(s,\mathit{\tau })+\frac{p_{22}}{2{\mathit{\rho }}^w{\mathit{\omega }}^2}{〈\mathbf{V}\mathit{\varphi },\overline{\mathit{\psi }}〉}_{\mathrm{\Gamma }}\hfill \\ \hfill & +\left(\frac{Q}{R}-\frac{p_{12}}{p_{22}}\right)\left({\int }_{{\mathrm{\Omega }}^b}s\mathrm{\nabla }·\overline{\mathbf{v}}d\mathbf{x}+p_{22}{\int }_{{\mathrm{\Omega }}^b}(\mathrm{\nabla }·\mathbf{u})\overline{\mathit{\tau }}d\mathbf{x}\right)\hfill \\ \hfill & -\left(p_{11}-\frac{p_{12}^2}{p_{22}}\right){\int }_{{\mathrm{\Omega }}^b}\mathbf{u}·\overline{\mathbf{v}}d\mathbf{x}-\frac{p_{22}}{R}{\int }_{{\mathrm{\Omega }}^b}s\overline{\mathit{\tau }}d\mathbf{x}\hfill \\ \hfill & -\left[1-\mathit{\beta }\left(1+\frac{p_{12}}{p_{22}}\right)\right]\left({〈\mathbf{V}\mathit{\varphi }\mathbf{n},\overline{\mathbf{v}}〉}_{\mathrm{\Gamma }}+\frac{p_{22}}{\mathit{\beta }}{〈\mathbf{u}·\mathbf{n},\overline{\mathit{\tau }}〉}_{\mathrm{\Gamma }}\right)\hfill \\ \hfill & +\frac{p_{22}}{\mathit{\beta }{\mathit{\rho }}^w{\mathit{\omega }}^2}\left({〈\frac{1}{2}\mathit{\varphi }-\mathbf{K}\mathit{\varphi },\overline{\mathit{\tau }}〉}_{\mathrm{\Gamma }}-\frac{1}{2}{〈s,\overline{\mathit{\psi }}〉}_{\mathrm{\Gamma }}\right),\hfill \\ \hfill {\mathcal{L}}_f(\mathbf{v},\mathit{\tau },\mathit{\psi })& :=-\left[1-\mathit{\beta }\left(1+\frac{p_{12}}{p_{22}}\right)\right]{〈{\mathit{\gamma }}_0{P}_f,\overline{\mathbf{v}}〉}_{\mathrm{\Gamma }}+\frac{p_{22}}{\mathit{\beta }{\mathit{\rho }}^w{\mathit{\omega }}^2}{〈\mathbf{n}·\mathbf{f}-\frac{\mathit{\partial }{P}_f}{\mathit{\partial }n},\overline{\mathit{\tau }}〉}_{\mathrm{\Gamma }}\hfill \\ \hfill & +\frac{p_{22}}{2{\mathit{\rho }}^w{\mathit{\omega }}^2}{〈{\mathit{\gamma }}_0{P}_f,\overline{\mathit{\psi }}〉}_{\mathrm{\Gamma }}.\hfill \end{array}$$(B6) ), it is not difficult to see that $\mathcal{A}(·,·)$ satisfies a Gårding’s inequality. Setting $(\mathbf{v},\mathit{\tau },\mathit{\psi })=(\mathbf{u},s,\mathit{\varphi })$, we obtain(C1) $$\begin{array}{cc}\hfill \mathcal{A}\{(\mathbf{u},s,\mathit{\varphi }),(\mathbf{u},s,\mathit{\varphi })\}& :=a(\mathbf{u},\mathbf{u})+b(s,s)+\frac{p_{22}}{2{\mathit{\rho }}^w{\mathit{\omega }}^2}{〈\mathbf{V}\mathit{\varphi },\overline{\mathit{\varphi }}〉}_{\mathrm{\Gamma }}\hfill \\ \hfill & +\left(\frac{Q}{R}-\frac{p_{12}}{p_{22}}\right)\left({\int }_{{\mathrm{\Omega }}^b}s\mathrm{\nabla }·\overline{\mathbf{u}}d\mathbf{x}+p_{22}{\int }_{{\mathrm{\Omega }}^b}(\mathrm{\nabla }·\mathbf{u})\overline{s}d\mathbf{x}\right)\hfill \\ \hfill & -\left(p_{11}-\frac{p_{12}^2}{p_{22}}\right){\int }_{{\mathrm{\Omega }}^b}{\Vert \mathbf{u}||}^{2}d\mathbf{x}-\frac{p_{22}}{R}{\int }_{{\mathrm{\Omega }}^b}{|s|}^{2}d\mathbf{x}\hfill \\ \hfill & -\left[1-\mathit{\beta }\left(1+\frac{p_{12}}{p_{22}}\right)\right]\left({〈\mathbf{V}\mathit{\varphi }\mathbf{n},\overline{\mathbf{u}}〉}_{\mathrm{\Gamma }}+\frac{p_{22}}{\mathit{\beta }}{〈\mathbf{u}·\mathbf{n},\overline{s}〉}_{\mathrm{\Gamma }}\right)\hfill \\ \hfill & +\frac{p_{22}}{\mathit{\beta }{\mathit{\rho }}^w{\mathit{\omega }}^2}\left({〈\frac{1}{2}\mathit{\varphi }-\mathbf{K}\mathit{\varphi },\overline{s}〉}_{\mathrm{\Gamma }}-\frac{1}{2}{〈s,\overline{\mathit{\varphi }}〉}_{\mathrm{\Gamma }}\right).\hfill \end{array}$$(C1)

We can show that$$\mathrm{Re}\mathcal{A}\{(\mathbf{u},s,\mathit{\varphi }),(\mathbf{u},s,\mathit{\varphi })\}=a(\mathbf{u},\mathbf{u})+b(s,s)+\frac{p_{22}}{2{\mathit{\rho }}^w{\mathit{\omega }}^2}{〈\mathbf{V}\mathit{\varphi },\overline{\mathit{\varphi }}〉}_{\mathrm{\Gamma }}+\mathcal{C}\{(\mathbf{u},s,\mathit{\varphi }),(\mathbf{u},s,\mathit{\varphi })\},$$

where $\mathcal{C}$ is compact on ${\left(H^1({\mathrm{\Omega }}^b)\right)}^2\times H^1({\mathrm{\Omega }}^b)\times H^{-1/2}(\mathrm{\Gamma })$. In fact, we have:

Theorem C.1

The sesquilinear form in (C1(C1) $$\begin{array}{cc}\hfill \mathcal{A}\{(\mathbf{u},s,\mathit{\varphi }),(\mathbf{u},s,\mathit{\varphi })\}& :=a(\mathbf{u},\mathbf{u})+b(s,s)+\frac{p_{22}}{2{\mathit{\rho }}^w{\mathit{\omega }}^2}{〈\mathbf{V}\mathit{\varphi },\overline{\mathit{\varphi }}〉}_{\mathrm{\Gamma }}\hfill \\ \hfill & +\left(\frac{Q}{R}-\frac{p_{12}}{p_{22}}\right)\left({\int }_{{\mathrm{\Omega }}^b}s\mathrm{\nabla }·\overline{\mathbf{u}}d\mathbf{x}+p_{22}{\int }_{{\mathrm{\Omega }}^b}(\mathrm{\nabla }·\mathbf{u})\overline{s}d\mathbf{x}\right)\hfill \\ \hfill & -\left(p_{11}-\frac{p_{12}^2}{p_{22}}\right){\int }_{{\mathrm{\Omega }}^b}{\Vert \mathbf{u}||}^{2}d\mathbf{x}-\frac{p_{22}}{R}{\int }_{{\mathrm{\Omega }}^b}{|s|}^{2}d\mathbf{x}\hfill \\ \hfill & -\left[1-\mathit{\beta }\left(1+\frac{p_{12}}{p_{22}}\right)\right]\left({〈\mathbf{V}\mathit{\varphi }\mathbf{n},\overline{\mathbf{u}}〉}_{\mathrm{\Gamma }}+\frac{p_{22}}{\mathit{\beta }}{〈\mathbf{u}·\mathbf{n},\overline{s}〉}_{\mathrm{\Gamma }}\right)\hfill \\ \hfill & +\frac{p_{22}}{\mathit{\beta }{\mathit{\rho }}^w{\mathit{\omega }}^2}\left({〈\frac{1}{2}\mathit{\varphi }-\mathbf{K}\mathit{\varphi },\overline{s}〉}_{\mathrm{\Gamma }}-\frac{1}{2}{〈s,\overline{\mathit{\varphi }}〉}_{\mathrm{\Gamma }}\right).\hfill \end{array}$$(C1) ) satisfies the Gårding’s inequality in the form$$\begin{array}{ccc}\hfill \mathrm{Re}\mathcal{A}\{(\mathbf{u},s,\mathit{\varphi }),(\mathbf{u},s,\mathit{\varphi })\}& \ge \hfill & \hfill \mathit{\alpha }\left({\Vert \mathbf{u}\Vert }_{{\left(H^1({\mathrm{\Omega }}^b)\right)}^2}^2+{\Vert s\Vert }_{H^1({\mathrm{\Omega }}^b)}^2+{\Vert \mathit{\varphi }\Vert }_{H^{-1/2}(\mathrm{\Gamma })}^2\right)\\ \hfill & -\mathit{\delta }\left({\Vert \mathbf{u}\Vert }_{{\left(H^{1-\mathit{ϵ}}({\mathrm{\Omega }}^b)\right)}^2}^2+{\Vert s\Vert }_{H^{1-\mathit{ϵ}}({\mathrm{\Omega }}^b)}^2+{\Vert \mathit{\varphi }\Vert }_{H^{-1/2-\mathit{ϵ}}(\mathrm{\Gamma })}^2\right),\hfill \end{array}$$

where $\mathit{\alpha }>0$ and $\mathit{\delta }\ge 0$ are constants, and $\mathit{ϵ}>0$ is a small parameter.

As is well known, Gårding’s inequality implies the validity of the Fredholm alternative. Hence, uniqueness implies existence. For this purpose, we now consider the homogeneous ${\mathrm{TP}}_f$ with $f=0$, since the uniqueness of the solution to the variational Equation (B5(B5) $$\begin{array}{c}\hfill \mathcal{A}\{(\mathbf{u},s,\mathit{\varphi }),(\mathbf{v},\mathit{\tau },\mathit{\psi })\}={\mathcal{L}}_f(\mathbf{v},\mathit{\tau },\mathit{\psi }),\end{array}$$(B5) ) will be depending upon that of the ${\mathrm{TP}}_f$.

Theorem C.2

If the triplet $(\mathbf{u},s,P)$ is a classical solution of the homogeneous ${\mathrm{TP}}_0$ with Im $k_0=0$, then $P=0$.

The proof follows [51] and the reader can supply the details. We remark that this theorem does imply that the components $(\mathbf{u},s)$ of the triplet $(\mathbf{u},s,P)$ considered in the TP${}_0$ are trivial solutions, since they may be solutions of the traction-free problem. Hence, in order to ensure the existence of a solution to the variational Equation (B5(B5) $$\begin{array}{c}\hfill \mathcal{A}\{(\mathbf{u},s,\mathit{\varphi }),(\mathbf{v},\mathit{\tau },\mathit{\psi })\}={\mathcal{L}}_f(\mathbf{v},\mathit{\tau },\mathit{\psi }),\end{array}$$(B5) ), we make the following assumptions:

1. There is no traction-free solution.

2. The square of the wavenumber, $k_0^2$, is not an eigenvalue of the Dirichlet problem for the negative Laplacian in ${\mathrm{\Omega }}^b$.

We remark that Assumption (2) is a guarantee for the invertibility of the single-layer operator $\mathbf{V}$ (see [53, p.30]). We finally summarize our results in the following theorem.

Theorem C.3

Under Assumptions (1) and (2), there exists a unique solution of the ${\mathrm{TP}}_f$ in ${\left(H^1({\mathrm{\Omega }}^b)\right)}^2\times H^1({\mathrm{\Omega }}^b)\times H^{-1/2}(\mathrm{\Gamma })$.