Material characterization and interfacial boundary identification by solving an inverse elasto statics boundary elements problem

Abstract

An inverse geometry problem of identifying simultaneously two irregular interfacial boundaries along with the mechanical properties of the interface domain located between the components of multiple (three) connected regions is investigated. A discrete number of displacement measurements obtained from a uniaxial tension test are used as extra information to solve this inverse problem. A unique combination of global and local optimization method is used, that is, the imperialist competitive algorithm (ICA) to find the best initial guesses of the unknown parameters to be used by the local optimization methods, that is, the conjugate gradient method (CGM) and the simplex method (SM). The CGM and SM are used in series. The performance of these local optimization methods is dependents on the initial guesses of the unknown boundaries and the mechanical properties, that is, Poisson’s ratio and Young’s modulus, so ICA provides the best initial guesses. The boundary elements method is employed to solve the direct two-dimensional (2D) elastostatics problem. A fitness function, which is the summation of squared differences between measured and computed displacements at identical locations on the exterior boundary, is minimized. Several example problems are solved and the accuracy of the obtained results is discussed. The influence of the value of the material properties of the subregions and the effect of measurement errors on the estimation process are also addressed.

Keywords:

• Inverse problem
• material characterization
• boundary elements method (BEM)
• interfacial boundary configurations
• imperialist competitive algorithm
• conjugate gradient method
• simplex method

Introduction

Inverse application of the boundary elements method (BEM) to identify internal flaws, cavities, cracks and inclusions inside solid bodies dates back to late 1980s.[1–7] Similar methodology has also been used in the case of shape estimation problems, to identify the shape of cavities and inclusions inside solid bodies.[8–16] Unknown parameters in inverse heat transfer problems include the estimation of the boundary condition,[17,18] thermal properties,[19–21] energy production [22] and so on.

The first paper addressing the problem of Identifying irregular interfacial boundary configuration between two homogenous, isotropic bodies was published by Huang and Chao [23]. In this study, the inverse steady-state heat conduction problem along with the conjugate gradient method (CGM) and the Levenberg–Marquardt algorithm were implemented to identify a single-interface boundary using boundary temperature measurements. This study is continued in order to identify simultaneously two interfacial boundaries in a multiple region domain using boundary temperature measurements.[24]

An inverse 2D elastostatics problem along with the genetic algorithm (GA) and the CGM are used to identify a single irregular interfacial boundary.[25]

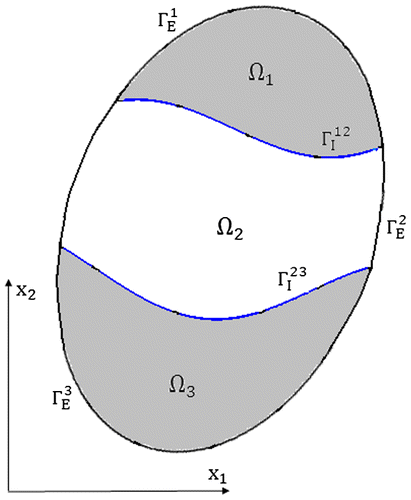
In this study, inverse application of the 2D elasto statics boundary elements problem is implemented to identify simultaneously two irregular interfacial boundaries along with the mechanical properties of the interface domain region (Ω₂) as shown in Figure 1. Due to the success of this study, extension to the identification of multiirregular interfacial boundaries could be proposed as future investigation. Correlation of the two unknown boundaries, that is, ${\mathrm{\Gamma }}_I^{1,2}$ and ${\mathrm{\Gamma }}_I^{2,3}$, makes this highly ill-posed inverse problem difficult to converge.

Figure 1. Three connected homogeneous bodies.

ICA in combination with CGM and SM was found to be just as effective as other global optimization methods such as the GA [12–14] or particle swarm optimization (PSO).[26] Since the GA and PSO have been investigated previously, the imperialist competitive algorithm (ICA), which is more recent and very user-friendly, is used in this study.

Another advantage of this proposed inverse process is that there is no need to use any regularization method. With good initial guesses obtained by ICA, the CGM and the simplex method (SM) converge smoothly.

In this work, first, the governing differential equations for solving the direct 2D elastostatics problem by the BEM is considered, and then, the global and local optimization methods used in this study are introduced. Several example problems are solved, and the accuracy of the obtained results is discussed.

Direct problem

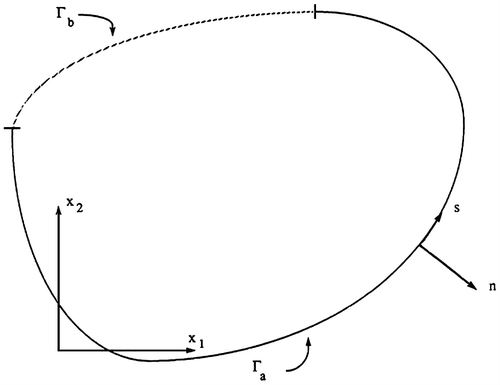
A linear elastic solid of uniform thickness h, loaded in some manner, is considered.

The equations of equilibrium in terms of displacements for an elastic solid body are as follows:(1) $$\begin{array}{c}\frac{\mathit{\partial }}{\mathit{\partial }x{}_1}\left(c{}_{11}\frac{\mathit{\partial }u{}_1}{\mathit{\partial }x{}_1}+c{}_{12}\frac{\mathit{\partial }u{}_2}{\mathit{\partial }x{}_2}\right)+\frac{\mathit{\partial }}{\mathit{\partial }x{}_2}(c{}_{33}\frac{\mathit{\partial }u{}_2}{\mathit{\partial }x{}_1}+c{}_{33}\frac{\mathit{\partial }u{}_2}{\mathit{\partial }x{}_2})=0\hfill \\ \frac{\mathit{\partial }}{\mathit{\partial }x{}_1}\left(c{}_{33}\frac{\mathit{\partial }u{}_2}{\mathit{\partial }x{}_1}+c{}_{33}\frac{\mathit{\partial }u{}_1}{\mathit{\partial }x{}_2}\right)+\frac{\mathit{\partial }}{\mathit{\partial }x{}_2}(c{}_{12}\frac{\mathit{\partial }u{}_1}{\mathit{\partial }x{}_1}+c{}_{22}\frac{\mathit{\partial }u{}_2}{\mathit{\partial }x{}_2})=0\hfill \end{array}$$(1)

where c₁₁, c₁₂, c₂₂ and c₃₃ are material constants. The boundary conditions are as follows:(2) $$\begin{array}{cc}u{}_i=f{}_i(s)\hfill & \text{on}{\mathrm{\Gamma }}_a\hfill \\ t{}_i=\mathit{\sigma }{}_{ij}n{}_{j}h=g{}_i(s)\hfill & \text{on}{\mathrm{\Gamma }}_b\hfill \end{array}$$(2)

For $i=1,2$ and $j=1,2$ where u_i is the component of displacement in the i direction, t_i is the component of traction in the i direction, n₁ and n₂ are components of the outward-directed unit normal to the boundary Γ, s is a coordinate along the boundary, as shown in Figure 2, and f_i(s) and g_i(s) are prescribed functions.

Figure 2. Plane homogeneous body.

The BEM used to determine the displacement at any point xⁱ in Ω as shown in Figure 2 can be determined from [26] as follows:(3) $$u{}_j(x^i)=-{\int }_{\mathrm{\Gamma }}{T}_{kj}(x,x^i)u_k(x)\text{d}s(x)+{\int }_{\mathrm{\Gamma }}{U}_{kj}(x,x^i)t_k(x)\text{d}s(x)$$(3)

where, $j=1,2$ and $k=1,2$ with summation on k. This equation is called the ‘filed equation’. U₁₁ and U₂₁ are the displacements and T₁₁, and T₂₁ are the tractions at point x in the infinite plane caused by an unit force in the x₁ direction applied at point x. Similarly, $U_{12},U_{22}$ and $T_{12},T_{22}$ are the displacements and tractions at point x due to a unit force in the x₂ direction, that is, the fundamental singular solution. u_k, and $t_k,k=1,2$ are the known displacements and tractions everywhere on Γ.

The boundary integral equation [27] is used to find unknown boundary displacements, that is(4) $${\mathit{\alpha }}_{kJ}^i{u}_k^i+{\int }_{\mathrm{\Gamma }}{T}_{kJ}u{}_K\text{d}s={\int }_{\mathrm{\Gamma }}{U}_{kJ}t{}_K\text{d}s{x}^i\text{on}\mathrm{\Gamma }$$(4)

where $u_k^i=u_k(x^i)$ and ${\mathit{\alpha }}_{kj}^i=(1/2){\mathit{\delta }}_{kj}$ if the boundary is smooth at xⁱ, and ${\mathit{\delta }}_{kj}^{}$ is the kronecker delta.

After the boundary discretization into linear elements, then Equation (4(4) $${\mathit{\alpha }}_{kJ}^i{u}_k^i+{\int }_{\mathrm{\Gamma }}{T}_{kJ}u{}_K\text{d}s={\int }_{\mathrm{\Gamma }}{U}_{kJ}t{}_K\text{d}s{x}^i\text{on}\mathrm{\Gamma }$$(4) ) could be written in matrix form as follows:(5) $$\left[H\right]\left\{u\right\}=\left[G\right]\left\{t\right\}$$(5)

The matrix $\left[H\right]$ is 2 N × 2 N and $\left[G\right]$ is 2 N × 4 N where, N is the number of nodes on the discretized boundary.

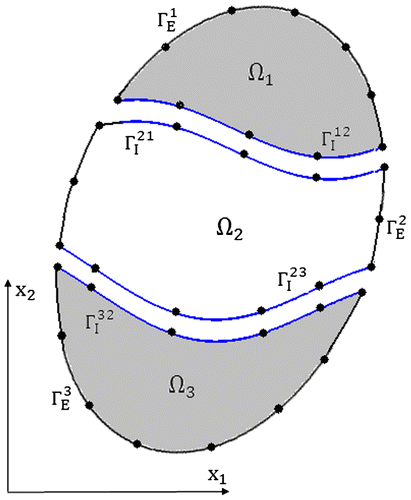
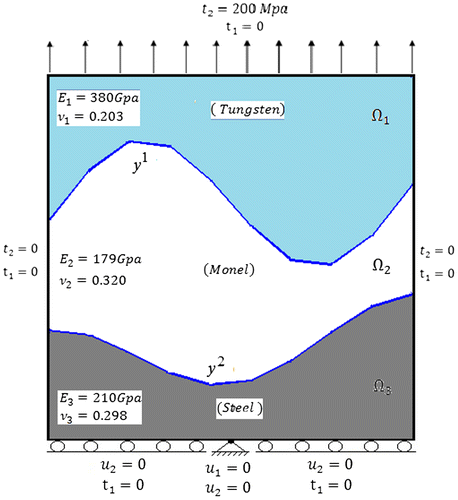
For the inhomogeneous body shown in Figure 3, the domain Ω is divided into three subdomains Ω₁, Ω₂ and Ω₃, each having its own Poisson’s ratio and Young’s modulus. If Equation (5(5) $$\left[H\right]\left\{u\right\}=\left[G\right]\left\{t\right\}$$(5) ) is applied to each subdomain, then for three subdomains:$$\begin{array}{c}\left[H_E^1{H}_I^{12}\right]\left\{\begin{array}{c}{u}_E^1\hfill \\ u_I^{12}\hfill \end{array}\right\}=\left[G_E^1{G}_I^1\right]\left\{\begin{array}{c}{t}_E^1\hfill \\ t_I^{12}\hfill \end{array}\right\}\hfill \\ \left[H_E^2{H}_I^{21}{H}_I^{23}\right]\left\{\begin{array}{c}{u}_E^2\hfill \\ u_I^{21}\hfill \\ u_I^{23}\hfill \end{array}\right\}=\left[G_E^2{G}_I^2\right]\left\{\begin{array}{c}{t}_E^2\hfill \\ t_I^{21}\hfill \\ t_I^{23}\hfill \end{array}\right\}\hfill \\ \left[H_E^3{H}_I^{32}\right]\left\{\begin{array}{c}{u}_E^3\hfill \\ u_I^{32}\hfill \end{array}\right\}=\left[G_E^3{G}_I^3\right]\left\{\begin{array}{c}{t}_E^3\hfill \\ t_I^{32}\hfill \end{array}\right\}\hfill \end{array}(6)$$

Figure 3. Three connected homogeneous bodies.

where $t_E^1,u_E^1$ are tractions and displacements on ${\mathrm{\Gamma }}_E^1$; …, $t_I^{12},u_I^{12}$ are tractions and displacements on ${\mathrm{\Gamma }}_I^{1,2}$ which is the boundary between material Ω₁ and material Ω₂; $t_E^2,u_E^2$ are tractions and displacements on ${\mathrm{\Gamma }}_E^2$; $t_I^{21},u_I^{21}$ are tractions and displacements on ${\mathrm{\Gamma }}_I^{2,1}$; $t_I^{23},u_I^{23}$ are tractions and displacements on ${\mathrm{\Gamma }}_I^{2,3}$; $t_E^3,u_E^3$ are tractions and displacements on ${\mathrm{\Gamma }}_E^3$ and $t_I^{32},u_I^{32}$ are tractions and displacements on ${\mathrm{\Gamma }}_I^{3,2}$, in x₁ and x₂ direction.

For each point i on ${\mathrm{\Gamma }}_I^{1,2}$ and ${\mathrm{\Gamma }}_I^{2,3}$ the interface displacement conditions are:(7) $$\begin{array}{c}{u}_I^{12}=u_I^{21}\Rightarrow \left\{\begin{array}{c}{u}_{x_1}^i\left|{}_{{\mathrm{\Gamma }}_I^{1,2}}=\right.u_{x_1}^i\left|{}_{{\mathrm{\Gamma }}_I^{2,1}}\right.\hfill \\ u_{x_2}^i\left|{}_{{\mathrm{\Gamma }}_I^{1,2}}=\right.u_{x_2}^i\left|{}_{{\mathrm{\Gamma }}_I^{2,1}}\right.\hfill \end{array}\right.\hfill \\ u_I^{32}=u_I^{23}\Rightarrow \left\{\begin{array}{c}{u}_{x_1}^i\left|{}_{{\mathrm{\Gamma }}_I^{3,2}}=\right.u_{x_1}^i\left|{}_{{\mathrm{\Gamma }}_I^{2,3}}\right.\hfill \\ u_{x_2}^i\left|{}_{{\mathrm{\Gamma }}_I^{3,2}}=\right.u_{x_2}^i\left|{}_{{\mathrm{\Gamma }}_I^{2,3}}\right.\hfill \end{array}\right.\hfill \end{array}$$(7)

And for tractions:(8) $$\begin{array}{c}{t}_I^{12}=-t_I^{21}\Rightarrow \left\{\begin{array}{c}t{}_{x_1}^{(2i-1)}\left|{}_{{\mathrm{\Gamma }}_I^{1,2}}=\right.t{}_{x_1}^{(2i)}\left|{}_{{\mathrm{\Gamma }}_I^{1,2}}=\right.-t{}_{x_1}^{(2i-1)}\left|{}_{{\mathrm{\Gamma }}_I^{2,1}}=\right.-t{}_{x_1}^{(2i)}\left|{}_{{\mathrm{\Gamma }}_I^{2,1}}\right.\hfill \\ t{}_{x_2}^{(2i-1)}\left|{}_{{\mathrm{\Gamma }}_I^{1,2}}=\right.t{}_{x_2}^{(2i)}\left|{}_{{\mathrm{\Gamma }}_I^{2,1}}=\right.-t{}_{x_2}^{(2i-1)}\left|{}_{{\mathrm{\Gamma }}_I^{21}}=\right.-t{}_{x_2}^{(2i)}\left|{}_{{\mathrm{\Gamma }}_I^{2,1}}\right.\hfill \end{array}\right.\hfill \\ t_I^{32}=-t_I^{23}\Rightarrow \left\{\begin{array}{c}t{}_{x_1}^{(2i-1)}\left|{}_{{\mathrm{\Gamma }}_I^{3,2}}=\right.t{}_{x_1}^{(2i)}\left|{}_{{\mathrm{\Gamma }}_I^{3,2}}=\right.-t{}_{x_1}^{(2i-1)}\left|{}_{{\mathrm{\Gamma }}_I^{2,3}}=\right.-t{}_{x_1}^{(2i)}\left|{}_{{\mathrm{\Gamma }}_I^{2,3}}\right.\hfill \\ t{}_{x_2}^{(2i-1)}\left|{}_{{\mathrm{\Gamma }}_I^{3,2}}=\right.t{}_{x_2}^{(2i)}\left|{}_{{\mathrm{\Gamma }}_I^{3,2}}=\right.-t{}_{x_2}^{(2i-1)}\left|{}_{{\mathrm{\Gamma }}_I^{2,3}}=\right.-t{}_{x_2}^{(2i)}\left|{}_{{\mathrm{\Gamma }}_I^{2,3}}\right.\hfill \end{array}\right.\hfill \end{array}$$(8)

Imposing the interface conditions on Equation (6$$\begin{array}{c}\left[H_E^1{H}_I^{12}\right]\left\{\begin{array}{c}{u}_E^1\hfill \\ u_I^{12}\hfill \end{array}\right\}=\left[G_E^1{G}_I^1\right]\left\{\begin{array}{c}{t}_E^1\hfill \\ t_I^{12}\hfill \end{array}\right\}\hfill \\ \left[H_E^2{H}_I^{21}{H}_I^{23}\right]\left\{\begin{array}{c}{u}_E^2\hfill \\ u_I^{21}\hfill \\ u_I^{23}\hfill \end{array}\right\}=\left[G_E^2{G}_I^2\right]\left\{\begin{array}{c}{t}_E^2\hfill \\ t_I^{21}\hfill \\ t_I^{23}\hfill \end{array}\right\}\hfill \\ \left[H_E^3{H}_I^{32}\right]\left\{\begin{array}{c}{u}_E^3\hfill \\ u_I^{32}\hfill \end{array}\right\}=\left[G_E^3{G}_I^3\right]\left\{\begin{array}{c}{t}_E^3\hfill \\ t_I^{32}\hfill \end{array}\right\}\hfill \end{array}(6)$$) gives:(9) $$\left[\begin{array}{ccccc}{H}_E^1\hfill & H_I^{12}\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & H_I^{21}\hfill & H_E^2\hfill & H_I^{23}\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & H_I^{32}\hfill & H_E^3\hfill \end{array}\right]\left\{\begin{array}{c}{u}_E^1\hfill \\ u_I^{12}\hfill \\ u_E^2\hfill \\ u_I^{23}\hfill \\ u_E^3\hfill \end{array}\right\}=\left[\begin{array}{ccccc}{G}_E^1\hfill & G_I^{12}\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & -G_I^{21}\hfill & G_E^2\hfill & G_I^{23}\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & -G_I^{32}\hfill & G_E^3\hfill \end{array}\right]\left\{\begin{array}{c}{t}_E^1\hfill \\ t_I^{12}\hfill \\ t_E^2\hfill \\ t_I^{23}\hfill \\ t_E^3\hfill \end{array}\right\}$$(9)

In summary,(10) $$\left[H\ast \right]\left\{\begin{array}{c}{u}_E^1\hfill \\ u_I^{12}\hfill \\ u_E^2\hfill \\ u_I^{23}\hfill \\ u_E^3\hfill \end{array}\right\}=\left[G\ast \right]\left\{\begin{array}{c}{t}_E^1\hfill \\ t_I^{12}\hfill \\ t_E^2\hfill \\ t_I^{23}\hfill \\ t_E^3\hfill \end{array}\right\}$$(10)

the matrix $\left[H\ast \right]$ is $2(N_1+N{}_2+N_3+N{}_4+N_5)\times 2(N_1+N{}_2+N_3+N{}_4+N_5)$ and $\left[G\ast \right]$ is $2(N_1+N{}_2+N_3+N{}_4+N_5)\times 4(N_1+N{}_2+N_3+N{}_4+N_5)$ where N₁ is the number of nodes on exterior boundary of Ω₁, N₂ is the number of nodes on exterior boundary of Ω₂, N₃ is the number of nodes on exterior boundary of Ω₃, N₄ is the number of nodes on interface boundary ${\mathrm{\Gamma }}_I^{1,2}$, and N₅ is the number of nodes on the interface boundary ${\mathrm{\Gamma }}_I^{2,3}$.

Equation (10(10) $$\left[H\ast \right]\left\{\begin{array}{c}{u}_E^1\hfill \\ u_I^{12}\hfill \\ u_E^2\hfill \\ u_I^{23}\hfill \\ u_E^3\hfill \end{array}\right\}=\left[G\ast \right]\left\{\begin{array}{c}{t}_E^1\hfill \\ t_I^{12}\hfill \\ t_E^2\hfill \\ t_I^{23}\hfill \\ t_E^3\hfill \end{array}\right\}$$(10) ) is reordered based on known outer boundary conditions and then solved for the values of unknown displacements and tractions at the outer boundary nodes as well as all displacements and tractions at the interface boundary nodes ${\mathrm{\Gamma }}_I^{1,2}$and ${\mathrm{\Gamma }}_I^{2,3}$.

The inverse problem

In the previous section, the use of BEM to solve the direct 2D elastostatics problem for a multiply connected domain containing regions Ω₁, Ω₂and Ω₃ was presented. In the direct problem, the governing differential equations, geometry, material properties and the boundary conditions are given and the unknown boundary data are calculated. In the inverse problem, some of the geometric features, such as the shape of the interfacial boundaries and/or material properties, are unknown, but some of the boundary data, that is, displacements or tractions can be measured and used as additional information to identify unknown parameters.

In this section, as shown in Figure 4, the shape and location of the interfacial boundaries ${\mathrm{\Gamma }}_I^{1,2}$ and ${\mathrm{\Gamma }}_I^{2,3}$, and mechanical properties, that is, Young’s modulus and Poisson’s ratio of the interface domain (Ω₂) are unknown, but displacements measured on the left and right sides of the body under uniaxial tension are used as additional information.

Figure 4. Geometric parameters of interfacial configuration and problem modelling.

The following column vectors are introduced:

$\left[u_e\right]$: A column vector containing M measured boundary displacements, reflecting the true value of the unknown parameters.

$\left[u_c\right]$: A column vector containing the same M boundary displacements computed by the BEM corresponding to the estimated value of the unknown parameters.

[Γ¹]: A column vector containing n unknown parameters corresponding to the interfacial boundary${\mathrm{\Gamma }}_I^{1,2}$.

[Γ²]: A column vector containing n unknown parameters corresponding to the interfacial boundary${\mathrm{\Gamma }}_I^{2,3}$.

[Γ³]: A column vector containing 2 unknown parameters corresponding to the mechanical properties of the interface domain (Ω₂).(11) $$\begin{array}{c}\left[{\mathrm{\Gamma }}^1\right]={\left[y_1^1,y_2^1,...,y_n^1\right]}^T\hfill \\ \left[{\mathrm{\Gamma }}^2\right]={\left[y_1^2,y_2^2,...,y_n^2\right]}^T\hfill \\ \left[{\mathrm{\Gamma }}^3\right]={\left[E_2,{\mathit{\nu }}_2\right]}^T\hfill \end{array}$$(11)

To keep the continuity of the interfacial boundary, only the y-component of the nodal locations on two interfacial boundaries are assumed unknown, and the distance in the x-direction between the two adjacent nodes are kept constant, as shown in Figure 4. Therefore, the unknown column vector [Γ] is defined as follows:(12) $$\left[{\mathrm{\Gamma }}^{}\right]=\left[{\mathrm{\Gamma }}^1{\mathrm{\Gamma }}^2{\mathrm{\Gamma }}^3\right]={\left[y_1^1,y_2^1,\dots ,y_n^1,y_1^2,y_2^2,\dots ,y_n^2,E_2,{\mathit{\nu }}_2\right]}^T$$(12)

This consists of 2n + 2 unknown parameters. The fitness function, which is the summation of squared differences between the measured displacements and calculated displacements at the same locations on the exterior left and right boundaries, is defined as follow:(13) $$F(\tilde{\mathrm{\Gamma }})=\sum _{m=1}^M{\left[u_c^m-u_e^m\right]}_{}^2$$(13)

where ‘~’ denotes the estimated values of the unknown parameters.

Since convergence of local optimization methods, such as CGM, highly depends on very good initial guesses of the unknown parameters, ICA is first used to find the best suited possible values. The CGM uses the best initial guesses found, in order to start its process until convergence is reached. Finally, SM uses the results obtained from CGM as its best initial guesses to accurately identify the interfacial boundaries and mechanical properties of the interface domain. It will be shown in the example problems that the use of two local optimization methods in series reduces the error in converged results by about four percent.

Optimization methods

The global optimization method used in this study is the ICA. ICA is a novel global search heuristic inspired by sociopolitical competition. Like other evolutionary methods, ICA starts with an initial population. Population individuals called countries are divided into two types, namely colonies and imperialists, that together form empire. Some of the best countries in the population are selected to be the imperialists and the rest form the colonies of these imperialists. Imperialistic competition among these empires forms the basis of ICA. During this competition, weak empires collapse and powerful ones take possession of their colonies. Ideally, imperialistic competition converges to a state in which there is only one empire, and its colonies are in the same position and have the same cost as the imperialist. After dividing all colonies among imperialists and creating the initial empires, these colonies start moving toward their relevant imperialist country. The colony moves toward the imperialist by x units. In this movement, θ and x are random numbers with uniform distribution. Further information about ICA could be found in [28].

The first local optimization method used in this study is the CGM. CGM is based on minimizing the fitness function, that is, Equation (13(13) $$F(\tilde{\mathrm{\Gamma }})=\sum _{m=1}^M{\left[u_c^m-u_e^m\right]}_{}^2$$(13) ). To minimize this function, the direction of descent p^k(Γ) and the search step size β^k in the following equation is needed [29]:(14) $${\widehat{\mathrm{\Gamma }}}^{k+1}(y_i)={\widehat{\mathrm{\Gamma }}}^k(y_i)+{\mathit{\beta }}^k{p}^k(y_i)$$(14)

where k = 1, … , iTer_CGM and iTer_CGM is the maximum number of iteration in the CGM. The direction of descent is given by(15) $$p^k(y_i)=-g^k(y_i)+{\mathit{\gamma }}^k{p}^{k-1}(y_i)$$(15)

where $g^k(\widehat{\mathrm{\Gamma }})$ are gradient directions at iteration k. According to Polack-Ribiere,[30] the conjugate coefficients γ^k are(16) $${\mathit{\gamma }}^k=\frac{{(g^{k+1}-g^k)}^T{g}^{k+1}}{{(g^k)}^T{g}^k}$$(16)

where ${\mathit{\gamma }}^0=0$. In cases where algorithm does not converge after N step, γ gets the value of zero.

The gradient function $g^k(\widehat{\mathrm{\Gamma }})$ is computed using the finite difference method.(17) $$\begin{array}{cc}{g}_{ij}(\widehat{\mathrm{\Gamma }})\hfill & =\frac{\mathit{\partial }{F}_i(\widehat{\mathrm{\Gamma }})}{\mathit{\partial }{\widehat{y}}_j}=\frac{F_i\left[\widehat{\mathrm{\Gamma }}(y_1,\dots ,y_j+\mathit{\delta }{y}_j,\dots ,y_N)\right]-F_i\left[\widehat{\mathrm{\Gamma }}(y_1,\dots ,y_j,\dots ,y_N)\right]}{\mathit{\delta }{y}_j}\hfill \\ \mathit{\delta }{y}_j\hfill & ={10}^{-4}\times y_j\hfill \end{array}$$(17)

To compute the search step size β^k, using Equation (14(14) $${\widehat{\mathrm{\Gamma }}}^{k+1}(y_i)={\widehat{\mathrm{\Gamma }}}^k(y_i)+{\mathit{\beta }}^k{p}^k(y_i)$$(14) ), the function $F(\widehat{\mathrm{\Gamma }})$ in step k + 1could be written as follows:(18) $$F\left[{\widehat{\mathrm{\Gamma }}}^{k+1}\right]=\sum _{m=1}^M{\left[u_c^m({\widehat{\mathrm{\Gamma }}}^k+{\mathit{\beta }}^k{p}^k)-u_e^m\right]}^2$$(18)

Using Taylor series, it is written in the form:(19) $$F\left[{\widehat{\mathrm{\Gamma }}}^{k+1}\right]=\sum _{m=1}^M{\left[u_c^m({\widehat{\mathrm{\Gamma }}}^k)-{\mathit{\beta }}^k\mathrm{\Delta }{u}_c^m(p^k)-u_e^m\right]}^2$$(19)

where $u_c^m({\widehat{\mathrm{\Gamma }}}^k)$ is computed by solving the direct problem using BEM. The search step size β^k is determined by minimizing the function given by Equation (14(14) $${\widehat{\mathrm{\Gamma }}}^{k+1}(y_i)={\widehat{\mathrm{\Gamma }}}^k(y_i)+{\mathit{\beta }}^k{p}^k(y_i)$$(14) ) with respect to β^k. The following expression results:(20) $${\mathit{\beta }}^k=\frac{{\sum }_{m=1}^M\left[u_c^m({\widehat{\mathrm{\Gamma }}}^k)-u_e^m\right]\mathrm{\Delta }{u}_c^m({\widehat{\mathrm{\Gamma }}}^k)}{{\sum }_{m=1}^M{\left[\mathrm{\Delta }{u}_c^m({\widehat{\mathrm{\Gamma }}}^k)\right]}^2}$$(20)

where $\mathrm{\Delta }{u}_c^m$ needed to compute β^k, is computed by solving direct problem with $\mathrm{\Delta }{\widehat{\mathrm{\Gamma }}}^k=p^k$.

The other local optimization method used is the SM. SM is an algorithm for solving the classical linear programming problem, developed by George B. Dantzig in 1947. Simplex is a simple nongradient optimization algorithm seeking the vector of parameters corresponding to the global extreme (maximum or minimum) of any n-dimensional function F(x₁, x₂, … , x_n), searching through the parameter space.

The two-dimensional simplex starts with three observations of the system response obtained with three different (x₁, x₂) parameter settings. These three observations correspond to the vertices of a triangle constituting the 1st simplex. In 3D space, four initial observations are required to define a tetrahedral body, and so on for the impossible to visualized spaces of higher dimensions.

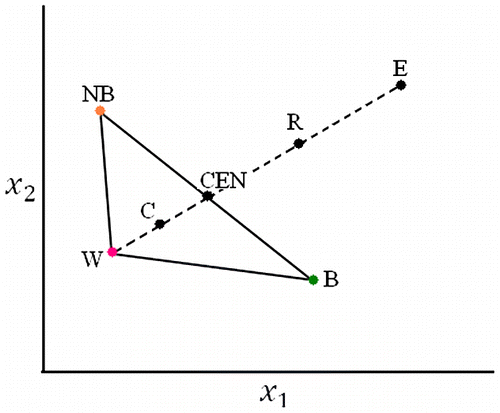
From the evaluation of the response of each observation (RB: the response of the best point B, RNB: response of next best point NB, RW: response of worst point W), the position of the next point to be evaluated is indicated by reflection, expansion, or contraction operations as shown in Figure 5.

Figure 5. Simplex method.

The iterations are terminated when no more significant improvement of the response is observed on moving from one simplex to another. It should be emphasized that when there are local extremes, it is highly probable that the algorithm to fail.[31]

Problem set-up to obtain displacement measurements

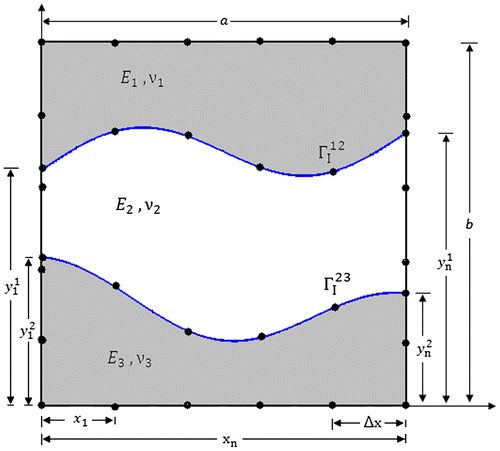
To simulate the experimental measurements of displacement, a rectangular multiply connected domain of dimensions (1 m × 1 m) made up of Tungsten ${\mathrm{\Omega }}_1(E_{Tu}=380\text{GPa},\mathit{\nu }=0.203)$, Monel \ ${\mathrm{\Omega }}_2(E_{Mo}=179\text{GPa}\mathit{\nu }=0.320)$ and Steel ${\mathrm{\Omega }}_3(E_{St}=210\text{GPa},\mathit{\nu }=0.298)$ \ with known boundary shape, under uniaxial tension as shown in Figure 6 is solved by direct BEM for boundary displacements. The outer boundaries are divided into 64 linear elements and each interface boundary is divided into 14 elements.

Figure 6. Plane inhomogeneous body with boundary conditions.

The boundary displacement on the left and right sides of this model are computed and used as experimental results. Since the values of the fitness function or displacements at each iteration are not good indicators of convergence with knowledge of the actual shape of each interface boundary, in order to investigate the convergence process, an error coefficient is defined as follows:(21) $$\%\text{error}=\frac{{\sum }_{i=1}^N\left|(y_i^{\text{est}}-y_i^{\text{act}})/y_i^{act}\right|}{N}\times 100$$(21)

In this error coefficient, $y_i^{act}$ is the actual nodal location on each interface boundary, and $y_i^{est}$ is the estimated location, and N is the number of locations. In this study, first, we solve the direct problem with known interfacial boundaries and known mechanical properties to compute the displacements on the exterior boundaries and then these computed displacements are used as the experimental measurements needed to solve the inverse problem.

Identification of the location and geometry of multi interfacial boundaries and mechanical properties of the interface domain

In order to solve the inverse problem and successfully estimate two interface boundaries simultaneously, some constraints need to be imposed:(22) $$\begin{array}{c}{y}_i^1>y_i^{2}i=1,2,\dots N\hfill \\ 0<y_i^1,y_i^2<1\hfill \\ 0<{\mathit{\nu }}_2<\frac{1}{2}\hfill \end{array}$$(22)

where N is the number of nodes on each interfacial boundary. These constraints are necessary since, at some stage of the estimation process, the two interface boundaries would interfere with one another or they might be found outside of the problem domain or interfere with the exterior boundaries.

The first task is to find the best initial guesses of the two interface boundaries and the mechanical properties of the interface domain. This information is needed for the local optimization methods, CGM and SM.

The initial guesses of interface boundaries are found by the ICA as straight lines drawn through the first and the last nodal locations located at some unknown vertical distance from the bottom. CGM uses these initial guesses in order to converge to the estimated shape of interface boundaries and mechanical properties of the interface domain. Iterations stop after the following criterion is satisfied.(23) $$\text{stoping criteria}=\frac{F_n-F_{n-1}}{F_{n-1}}<\mathit{\epsilon }$$(23)

where F_n is the value of fitness function at iteration n and ɛ is taken to be a small number as 0.001.

Finally, the SM is employed in order to use the converged results found from CGM as its initial guesses to get a more accurate shape of the interface boundaries and mechanical properties of the interface domain.

Example problems

Three different examples are selected to show the ability of the proposed procedure to identify any shape of the interfacial configuration located anywhere in the domain. In all examples, the shape of the interfacial configuration is defined by a function. This allows us to investigate different locations and geometries and present the accuracy of the obtained results by computing the error coefficient, %error presented in Equation (21(21) $$\%\text{error}=\frac{{\sum }_{i=1}^N\left|(y_i^{\text{est}}-y_i^{\text{act}})/y_i^{act}\right|}{N}\times 100$$(21) ).

In the first example, two different and continuous interfacial boundaries are selected as follows:(24) $$\begin{array}{cc}{y}^1(x)\hfill & =(0.1x+0.6)+0.2sin(2\mathit{\pi }x)0<x<1\hfill \\ y^2(x)\hfill & =(0.1x+0.2)+0.1cos(2\mathit{\pi }x)0<x<1\hfill \end{array}$$(24)

The interface domain Ω₂ is made up of Monel $(E_2=179GPa,{\mathit{\nu }}_2=0.320)$.

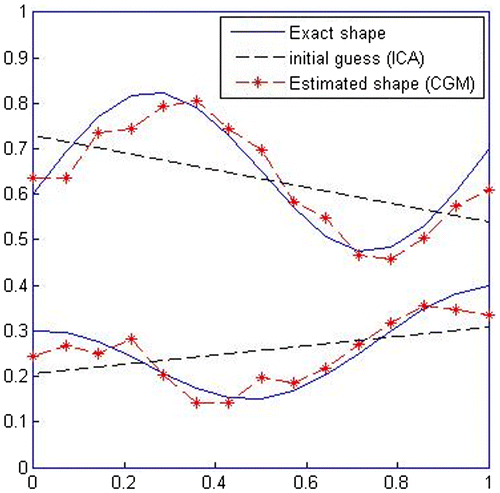
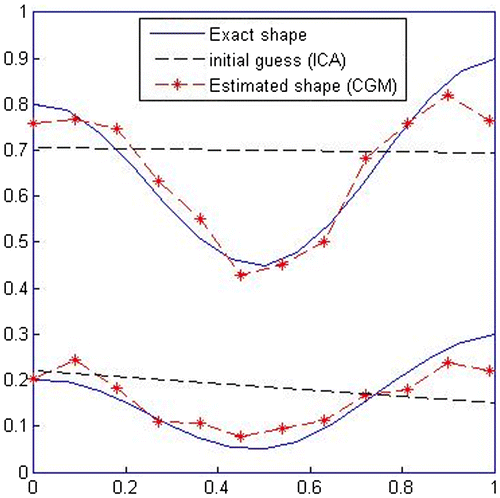
As shown in Figure 7, the initial guesses of interface boundaries are obtained by the ICA as two straight lines and the initial guesses of mechanical properties of interface domain are found as $E_2=283GPa,{\mathit{\nu }}_2=0.20$. Then, CGM uses these initial guesses to reach convergence. In this stage, the obtained results for mechanical properties of interface domain are $E_2=185GPa,{\mathit{\nu }}_2=0.30$ and the converged results have 8.97% error.

Figure 7. Estimation of the shape of interfacial boundaries with ICA and CGM.

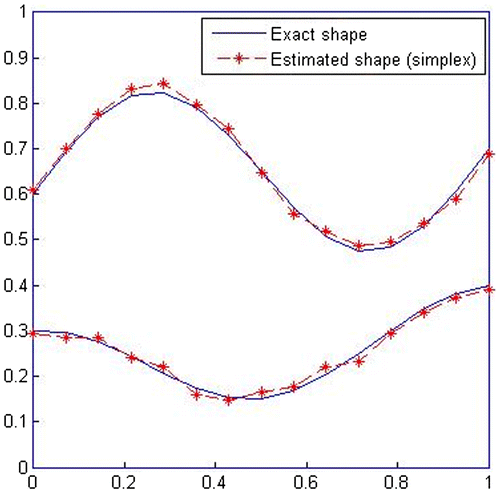
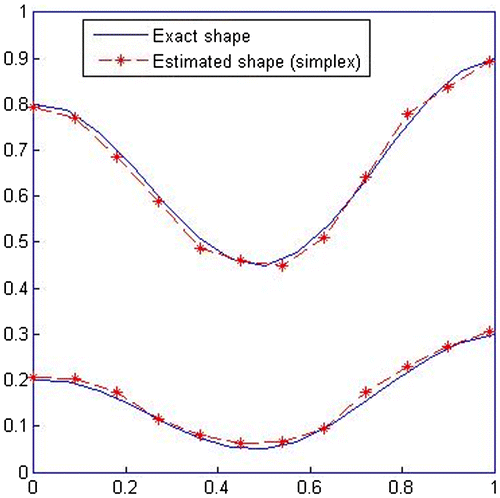
Finally, the SM is employed, which uses the interface boundaries and mechanical properties of the interface domain obtained by CGM, as its first guesses to identify a more accurate shape of the interface boundaries as shown by Figure 8, and the obtained results for the mechanical properties of interface domain are found as $E_2=180GPa,{\mathit{\nu }}_2=0.318$.

Figure 8. Estimation of the shape of interfacial boundaries with SM using CGM answers.

The result of this additional step in the estimation process is that, error is reduced to 2.2%, which indicates 6.77% improvement in final converged results. The accuracy of the identified interfacial boundaries is about 97.8%.

In the second example, the actual interfacial boundaries are defined as follows:(25) $$\begin{array}{cc}{y}^1(x)\hfill & =(0.1x+0.6)+0.2cos(2\mathit{\pi }x)0<x<1\hfill \\ y^2(x)\hfill & =(0.1x+0.1)+0.1cos(2\mathit{\pi }x)0<x<1\hfill \end{array}$$(25)

In this example, one of the boundaries is assumed to be located close to the lower exterior boundary. The interface domain Ω₂ is made up of Molybdenum $(E_2=331GPa,{\mathit{\nu }}_2=0.307)$.

The initial guesses along with the identified shape of the interface boundaries from CGM are shown in Figure 9 with the converged values of the mechanical properties as $E_2=310GPa,{\mathit{\nu }}_2=0.289$.

Figure 9. Estimation of the shape of interfacial boundaries with ICA and CGM.

In this stage, the converged results have 9.9% error. As before, SM is employed to further estimate the interface boundaries and mechanical properties of the interface domain.

As shown in Figure 10, the two interface boundaries are identified with 95.75% accuracy with the converged values of the mechanical properties as $E_2=329GPa,{\mathit{\nu }}_2=0.310$. The improvement in accuracy is 4.65% as the result of using SM.

Figure 10. Estimation of the shape of interfacial boundaries with SM using CGM answers.

In the third example, the actual interface boundaries are defined as follows:(26) $$\begin{array}{cc}{y}^1(x)\hfill & =\left\{\begin{array}{cc}0.8x+0.1\hfill & 0<x<0.625\hfill \\ (0.04x+0.8)+0.25sin(2\mathit{\pi }x)\hfill & 0.625<x<1\hfill \end{array}\right.\hfill \\ y^2(x)\hfill & =\left\{\begin{array}{cc}(0.5x+0.1)+0.25cos(2\mathit{\pi }x)\hfill & 0<x<0.5\hfill \\ 0.5x+1\hfill & 0.5<x<1\hfill \end{array}\right.\hfill \end{array}$$(26)

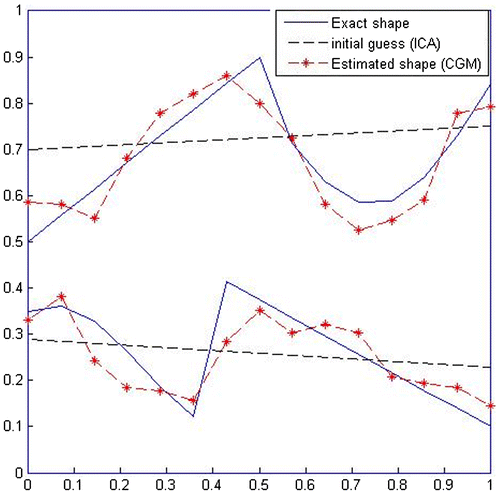
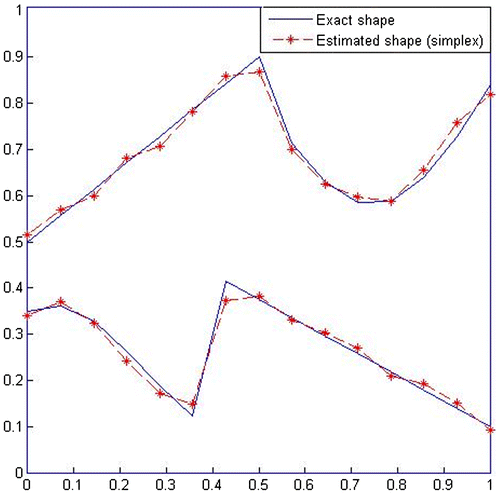
The interface domain Ω₂ is made up of Molybdenum $(E_2=331GPa,{\mathit{\nu }}_2=0.307)$.

As shown in Figures 11 and 12, the two interface boundaries are identified with 94.55% accuracy with the converged values of the mechanical properties as $E_2=327GPa,{\mathit{\nu }}_2=0.305$. The improvement in accuracy is 5.045% as the result of using SM.

Figure 11. Estimation of the shape of interfacial boundaries with ICA and CGM.

Figure 12. Estimation of the shape of interfacial boundaries with SM using CGM answers.

Investigating the effect of material properties at the three regions Ω₁, Ω₂and Ω₃ on the identifying problem

To investigate the effect of material properties on the convergence of this inverse problem, three different combinations of materials introduced in Table 1 are examined. It is observed that as the difference in material properties of the subdomains forming the multiply (three) connected domain decreases, even though convergence is achieved, the errors in converged results increase.

Table 1. The influences of material properties on estimation of the irregular boundary configurations.

Case number	Material		$E(GPa)$	$\mathit{\nu }$	Percent error
	Tungsten	Ω1	380	0.203
1	Mone	Ω2	179	0.320	2.205
	Stee	Ω3	210	0.298
	Mone	Ω1	179	0.320
2	Nickel	Ω2	127	0.322	4.863
	Molybdenum	Ω3	331	0.307
	Gary cast iron	Ω1	100	0.211
3	Yellow brass	Ω2	106	0.324	6.942
	Phosphor bronze	Ω3	111	0.349

The effect of experimental measurement errors on the estimation process

The next question investigated is the effect of inevitable experimental errors on the identification problem.

The erroneous experimental measurements are obtained by simulating the ‘experiment’ as follows.

The body is first analysed by the BEM using the actual shape of the interfacial boundaries and material properties.

Then, random errors are added to the computed boundary displacements, and these are taken to be the measured data. These errors are generated according to the following:(27) $${[u_e^m]}_{\text{error}}={[u_e^m]}_{\text{ideal}}(1\pm {\mathit{\eta }}^m)$$(27)

Where η is the percent random number.

The unknown parameters are estimated using simulated experimental measurements with 1%, 2% and 3% errors. The results are shown in Figure 13. For errors up to 2%, even with an increase in error coefficient, the estimation process leads to acceptable shape of the interface boundaries, but after 2%, the estimation process lead to the wrong shape of interface boundaries.

Figure 13. Estimation of the interfacial boundaries using erroneous experimental measurements of displacement.

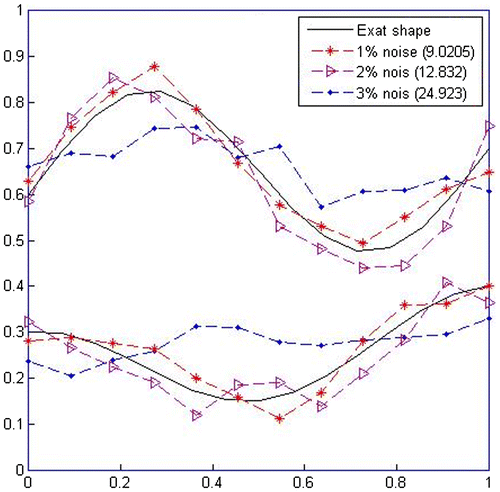
As shown in Figure 13 for the case of 3% a random error in experimental measurements, the estimated shape of the interfacial boundaries is not acceptable and the inverse problem has converged to unrealistic results.

Conclusion

The inverse application of BEM to indentify simultaneously two unknown irregular interfacial boundaries and mechanical properties of the interface domain of an inhomogeneous body by utilizing surface displacement measurements and a unique combination of global (ICA), and local (CGM and SM) methods proves to be an effective optimizing procedure. Several cases involving different functional forms of interfacial boundary shape, different material properties and different measurement errors were considered, and from the examples presented, it is concluded that this combination of global and local optimization methods is very effective and reliable to identify any shape of interfacial configurations located anywhere within the problem domain.

Based on the results of this investigation, the following conclusions are drawn:

•	The best initial guesses of the unknown interfacial boundaries could effectively be obtained by the ICA.
•	Using CGM and SM in series proved to be highly effective in reducing the %error in converged results.
•	SM converges reasonably fast to the accurate results when good initial guesses obtained by CGM are used.
•	Convergence is achieved even with inevitable measurement errors up to 2%, but when experimental errors exceed 2%, the estimation procedure leads to an unrealistic shape of the interfacial boundaries.
•	As the difference in material properties of the sub regions (Ω1, Ω2 and Ω3), decreases the %error coefficient in converged results also increases.

Disclosure statement

No potential conflict of interest was reported by the authors.