Structural parameters identification of uncertain multi-storey shear buildings using fuzzy neural network modelling

Abstract

Present paper proposes a fuzzy neural network (FNN)-based modelling for the identification of structural parameters of uncertain multi-storey shear buildings. Here, the method is developed to identify uncertain structural mass, stiffness and damping matrices from the dynamic responses of the structure without any optimization processes that are generally used to solve inverse vibration problems. Uncertainty has been taken in term of fuzzy numbers. The governing equations of motion are first solved by the classical method to get responses of the consecutive stories. Further the governing equations of motion are modified based on relative responses of consecutive stories in such a way that the new set of equations can be implemented in a cluster of FNNs. As such the model starts solving the nth floor by FNN modelling to estimate the structural parameters. Subsequently, series of FNN models are used to estimate the parameters for (n − 1)th storey to the first storey. One may note that single layer FNNs have been used for training for each cluster of the FNN such that the converged weights give the uncertain structural parameters. The initial weights in the FNN architecture are taken as the design parameters in uncertain (fuzzy) form. In order to validate the present model, various example problems of different multi-storey shear structures have been considered. Related results are incorporated in term of tables and graphs. Comparisons between theoretical and identified results are carried out and are found to be in good agreement.

Keywords:

• System identification
• mass
• stiffness
• damping
• fuzzy neural network
• shear buildings

1. Introduction

In system identification problems, a set of inputs and resulting outputs for a system is known and we develop a mathematical description or model of the system. Structural dynamic problems are generally of two types, direct and indirect problems. In direct problems, the equations governing the system and the parameters of the system are known. These parameters are used to find the response of the system for a specific input. In inverse problems, the output response for a given input is known, but either the governing equation or some of the parameters of the physical process are unknown. In system identification for structural problems, we identify or estimate structural parameters such as stiffness, vibration signatures such as frequencies, mode shapes, damping ratios and structural response. System identification techniques play an important role in investigating and reducing gap between the structural systems and their structural design models and have become an increasingly interesting research topic for the purpose of structural health monitoring, damage assessment and safety evaluation of existing engineering structures.

Dynamic behaviour of structures can be studied analytically, numerically and/or experimentally. Though different methods are used to study the dynamic behaviour, each method has its own advantages and limitations. In order to reconciliate these limitations or shortcomings and to determine the dynamic properties of a structure, model correlation and model updating procedure/method should be performed. Model updating refers to the methodology that determines the most plausible structural model for an instrumented structural system. In this regard, we may mention few papers on model updating of structural systems.[1–4] A state-space-oriented system identification theory and a judicious use of wavelet transformation techniques for extracting impulse response functions are presented in Friswell and Mottershead [1]. Alvin et al. [2] introduced certain new methods and presented the principles and techniques of time-series methods for fault detection, identification and estimation in vibrating structures. Two novel methods for simultaneous identification of mass, stiffness and damping matrices for modal updating of multistory shear buildings have been developed by Khanmirza et al. [3]. Modal updating is studied on various structures but most widely studied structural systems are the shear buildings. Previous works state that model updating of shear buildings depend mostly on the use of modal parameter identification and physical or structural parameter identification to drive the corresponding update procedures. Since eigen mode data are obtainable from the established modal testing techniques and eigen modes contain a large amount of information about the structure in compact form, modal parameter data such as mode shapes, damping ratios and frequencies have been frequently used in modal updating of the structural systems.[5–7] A method was developed by Mahmoudabadi et al. [5] for parametric system identification for a classically damped linear system using frequency domain and extended their work for non-classically damped linear systems subjected to six components of earthquake ground motions. Hegde and Sinha [6] proposed an efficient procedure to determine the natural frequencies, modal damping ratios and mode shapes for torsionally coupled shear buildings using earthquake response records. The procedure applies eigenrealization algorithm to generate the state-space model of the structure using the cross-correlations among the measured responses. A methodology for identification of state-space models of a building structure using time histories of the earthquake-induced ground motion and of the corresponding structural responses is presented by Hong et al. [7]. The identification methodology is based on the Eigensystem Realization Algorithm with Data Correlation complemented by the Observer Kalman Filter Identification algorithm for the identification of the Markov’s parameters of the system. Studies related to structural damage detection using artificial neural network (ANN) have been done by various researchers. A non-parametric structural damage detection methodology based on non-linear system identification approaches has been given by Masri et al. [8] for health monitoring of structure-unknown systems. Kao and Hung [9] gave two steps for structural damage detection. The first step involves system identification using neural system identification networks (NSINs) to identify the undamaged and damaged states of a structural system and the second step involves structural damage detection using the aforementioned trained NSINs to generate free vibration responses with the same initial condition or impulsive force. Pillai and Krishnapillai [10] presented a multistage identification scheme for structural damage detection with the use of modal data using a hybrid neural network strategy. An approach to detect structural damage using ANN method with progressive substructure zooming has been presented by Bakhary et al. [11]. This method also uses the substructure technique together with a multi-stage ANN models to detect the location and extent of the damage. Zhang et al. [12] studied the application of neural networks to damage detection in structures. To avoid the false positives of damages in the deterministic identification method induced by uncertainties in measurement noise, Zhang et al. [13] proposed a probabilistic method to identify damages of the structures with uncertainties under unknown input. The proposed probabilistic method is developed from a deterministic simultaneous identification method of structural physical parameters and input based on dynamic response sensitivity. The application of ANNs and wavelet analysis to develop an intelligent and adaptive structural damage detection system has been investigated by Shi and Yu [14]. A probabilistic approach for damage identification considering measurement noise uncertainties has been given by Lei et al. [15]. The probability of identified structural damage is further derived based on the reliability theory.

As regards [16–20] gave various methodologies for different type of problems in system identification. A procedure which systematically modifies and identifies the structural parameters using the prior known estimates of the parameters with the corresponding vibration characteristics and the known dynamic data is given by Chakraverty [16]. Nicoud et al. [17] presented a system identification methodology that explicitly treats factors which affect the success of identification. The methodology also involves identification of model characteristics including boundary conditions rather than simply determining parametric values. A structural parameter identification and damage detection approach using displacement measurement time series is proposed by Xu et al. [18]. The performance of this approach is validated experimentally with a frame structure model in a healthy condition and with joint connection damages. Nandakumar and Shankar [19] presented a novel inverse scheme based on consistent mass transfer matrix to identify the stiffness parameters of structural members. They used a non-classical heuristic particle swarm optimization algorithm (PSO). Billmaier and Bucher [20] discussed selective sensitivity analysis and used this method to solve system identification problems. Some of the related publications may be mentioned as those of [21–23]. Brownjohn [21] used modal analysis procedure, Natural Excitation Technique with Eigensystem Realization Algorithm and frequency domain decomposition (or IPP) to study ambient vibration in tall buildings. Identification of physical parameters such as mass, damping and stiffness matrices of linear structures have been studied by Yang et al. [22] based on Hilbert–Huang spectral analysis. Chakraverty [23] used Holzer criteria along with some other numerical methods to estimate the global mass and stiffness matrices of the structure from modal test data. Physical parameter system identification methods to determine the stiffness and damping matrices of shear-storey buildings have been proposed by Yoshitomi and Takewaki [24]. Beskhyroun et al. [25] investigated the dynamic behaviour of a full scale 13-storey-reinforced concrete building under forced vibration, ambient vibration and distal earthquake excitation. A number of studies [26–29] have used ANN for solving structural identification problems. Wu et al. [26] developed a concept of decentralized parametric evaluation neural networks for parametric identification of substructures. Based on the trained decentralized parametric evaluation neural networks and the RRMS error of substructures, the structural parameter of stiffness of each subsystem can be forecasted with high accuracy. In particular, Huang et al. [27] identified the dynamic characteristics of a steel frame using the back-propagation neural network. A procedure for identification of structural parameters of two-storey shear buildings by an iterative training of neural networks was proposed by Chakraverty [28]. System identification of an actively controlled structure using frequency response functions with the help of ANNs has also been studied by Pizano [29] for single-input, single-output and multiple-input single-output system. Yun and Bahng [30] proposed a neural network-based substructural identification for the estimation of the stiffness parameters of a complex structural system, particularly for the case with noisy and incomplete measurement of the modal data. Neural network-based strategy was also developed by Xu et al. [31] for direct identification of structural parameters from the time domain dynamic responses of a structure without any eigenvalue analysis. A neural network-based method to determine the modal parameters of structures from field measurement data was given by Chen [32]. The author trained the neural network using the observed dynamic responses and then directly identified the modal parameters of the structures using the weight matrices of the neural network. It may be seen from above that ANNs provide a fundamentally different approach to system identification problems. They have been successfully applied for identification and control of dynamic systems in various field of engineering because of its excellent learning capacity and high tolerance to partially inaccurate data. Rather than system identification problems, ANNs are also used in different fields of engineering problems such as [33–35]. A novel constructive and destructive parsimonious extreme learning machine was proposed by Wang et al. [33]. Wang et al. [34] introduced a constructive multi-output extreme learning machine to deal with large tanker motion dynamics identification. Wang et al. [35] extended traditional single-hidden layer feed-forward to generalized single-hidden layer feed-forward network by employing the polynomial functions of inputs as output weights and applied this concept for solving regression problems.

The above literature review shows that various types of ANN are developed to deal with data in exact or crisp form. But in actual practice the experimental data obtained from equipment are with errors that may be due to human or equipment errors thereby giving uncertain form of the data along with uncertain structural parameters. Although one may also use probabilistic methods to handle such problems. But the probabilistic method requires huge quantity of data which may not be easy or feasible in particular for structural parameters. In view of the above, various research works are being done by using fuzzy neural networks (FNNs) in different fields. Ishibuchi et al. [36] developed architecture for neural networks where the input vectors are in terms of fuzzy numbers. A methodology for FNNs where the weights and biases are taken as fuzzy numbers and the input vectors as real numbers has been proposed Ishibuchi et al. [37]. A FNN with trapezoidal fuzzy weights was also presented by Ishibuchi et al. [38]. They have developed the methodology in such a way that it can handle fuzzy inputs as well as real inputs. In this respect, Ishibuchi et al. [39] derived a general algorithm for training a fuzzified feed-forward neural network that has fuzzy inputs, fuzzy targets and fuzzy connection weights. The derived algorithms are also applicable to the learning of fuzzy connection weights with various shapes such as triangular and trapezoidal. Another new algorithm for learning fuzzified neural networks has also been developed by Ishibuchi et al. [40]. Lu [41] proposed a FNN-based technique to construct an adaptive car-following indicator. A new learning law for Mamdani and Takagi-Sugeno-Kang type FNNs based on input-to-state stability approach was suggested by Yu and Li [42]. The new learning schemes employ a time-varying learning rate that is determined from input–output data and model structure. Stable learning algorithms for the premise and the consequence parts of fuzzy rules are also proposed. A self-constructing FNN employing extended Kalman filter was designed and developed by Er et al. [43]. Wang [44] presented a generalized ellipsoidal basis function-based online self-constructing FNN which implements a Takagi-Sugeno-Kang (TSK) fuzzy inference system. The states of the art for the application of FNN in diagnosis, recognition, image processing and intelligence robot control of medicine are reviewed by Zhang [45]. They also proposed the application of FNN in medicine. Three new algorithms for Takagi-Sugeno-Kang fuzzy system based on training error and genetic algorithm are proposed by Malek et al. [46]. Recent work on robust FNN sliding mode control scheme for IPMSM drives were also developed by Leu et al. [47].

In this paper, identification of structural parameters such as mass, stiffness and damping matrices of shear buildings using single layer neural network is presented in fuzzified form. To identify the physical parameters in fuzzified form the governing equations of motion are used systematically in a series (cluster) of FNNs. The governing equations of motion is first solved by the classical method to get responses of the consecutive stories and then the governing equations of motion are modified based on relative responses of consecutive stories in such a way that the new set of equations can be implemented in a cluster of FNNs. Here, single-layer FNNs have been used for training for each cluster of the FNN such that the converged weights give the uncertain structural parameters.

2. Fuzzy set theory and preliminaries

The following Fuzzy arithmetic operations are used in this paper for defining fuzzified neural network in Ref. [48].

(A)	Let X be an universal set. Then the fuzzy subset A of X is defined by its membership function

$${\mathit{\mu }}_A:X\to \left[0,1\right]$$

	which assign a real number ${\mathit{\mu }}_A\left(x\right)$ in the interval $\left[0,1\right]$, to each element x ∈ X, where the value of ${\mathit{\mu }}_A\left(x\right)$ at x shows the grade of membership of x in A.
(B)	Given a fuzzy set A in X and any real number $\mathit{\beta }\in \left[0,1\right]$, then the β– cut or β– level or cut worthy set of A, denoted by Aβ is the crisp set

$$A_{\mathit{\beta }}=\left\{x\in X\left|{\mathit{\mu }}_A\left(x\right)\ge \mathit{\beta }\right.\right\}$$

(C)	A triangular fuzzy number (TFN) A can be defined as a triplet $\left[a_1,a_2,a_3\right]$. Its membership function is defined as

$${\mathit{\mu }}_A\left(x\right)=\left\{\begin{array}{cc}0,\hfill & x<a_1\hfill \\ \frac{x-a_1}{a_2-a_1},\hfill & a_1\le x\le a_2\hfill \\ \frac{a_3-x}{a_3-a_2},\hfill & a_2\le x\le a_3\hfill \\ 0,\hfill & x>a_3\hfill \end{array}\right.$$

Above TFN may be transformed to an interval form A_β by β– cut as$$A_{\mathit{\beta }}=\left[{\underline{a}}^{\left(\mathit{\beta }\right)},{\overline{a}}^{\left(\mathit{\beta }\right)}\right]=\left[\left(a_2-a_1\right)\mathit{\beta }+a_1,-\left(a_3-a_2\right)\mathit{\beta }+a_3\right]$$

where ${\underline{a}}^{\left(\mathit{\beta }\right)}$ and ${\overline{a}}^{\left(\mathit{\beta }\right)}$ are the lower and upper limits of the β– level set A_β.

2.1. Operation of fuzzy numbers

We introduce arithmetic operations on fuzzy numbers and the results are expressed in terms of membership functions $\forall x,y,z\in R$ as below

(1)	Addition: ${\mathit{\mu }}_{A\left(+\right)B}\left(z\right)=\text{max}\left\{{\mathit{\mu }}_A\left(x\right)\wedge {\mathit{\mu }}_B\left(y\right)\left|z=x+y\right.\right\}$
(2)	Multiplication: ${\mathit{\mu }}_{A\left(·\right)B}\left(z\right)=\text{max}\left\{{\mathit{\mu }}_A\left(x\right)\wedge {\mathit{\mu }}_B\left(y\right)\left|z=x·y\right.\right\}$
(3)	Non-linear mapping: ${\mathit{\mu }}_{f\left(\text{Net}\right)}\left(z\right)=\text{max}\left\{{\mathit{\mu }}_{\text{Net}}\left(x\right)\left|z=f(x)\right.\right\}$

3. Learning algorithm for single layer FNN

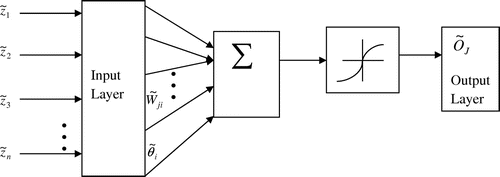
A neural network is said to be a FNN if at least one of its input, output and weight sets have values in fuzzified form. In FNNs, neurons are connected as they are connected in traditional neural networks and a typical single-layer FNN is shown in Figure 1. Following are the steps in FNN using the fuzzy computation defined above.

Step 1:	Initialize input weights $\left({\tilde{W}}_{ji}\right)$ and bias weights ${\tilde{\mathit{\theta }}}_i$ in fuzzified form.
Step 2:	Present the training pairs in the form $\left\{{\tilde{Z}}_1,{\tilde{d}}_1;{\tilde{Z}}_2,{\tilde{d}}_2;\dots {\tilde{Z}}_I,{\tilde{d}}_J\right\}$ where ${\tilde{Z}}_I=\left(\left[{\underline{z}}_1,z_{1}c,{\overline{z}}_1\right],\left[{\underline{z}}_2,z_{2}c,{\overline{z}}_2\right],\dots ,\left[{\underline{z}}_n,z_{n}c,{\overline{z}}_n\right]\right)$ are inputs and ${\tilde{d}}_J=\left(\left[{\underline{d}}_1,d_{1}c,{\overline{d}}_1\right],\left[{\underline{d}}_2,d_{2}c,{\overline{d}}_2\right],\dots ,\left[{\underline{d}}_n,d_{n}c,{\overline{d}}_n\right]\right)$ are desired values for the given inputs in fuzzified form. The inputs and desired values can be written in β– cut form as ${\tilde{Z}}_I=\left(\left[{\underline{z}}_1^{\mathit{\beta }},{\overline{z}}_{{}_1}^{\mathit{\beta }}\right],\left[{\underline{z}}_{{}_2}^{\mathit{\beta }},{\overline{z}}_{{}_2}^{\mathit{\beta }}\right],\dots ,\left[{\underline{z}}_{{}_n}^{\mathit{\beta }},{\overline{z}}_{{}_n}^{\mathit{\beta }}\right]\right)$, ${\tilde{d}}_J=\left(\left[{\underline{d}}_{{}_1}^{\mathit{\beta }},{\overline{d}}_{{}_1}^{\mathit{\beta }}\right],\left[{\underline{d}}_{{}_2}^{\mathit{\beta }},{\overline{d}}_{{}_2}^{\mathit{\beta }}\right],\dots ,\left[{\underline{d}}_{{}_n}^{\mathit{\beta }},{\overline{d}}_{{}_n}^{\mathit{\beta }}\right]\right).$
Step 3:	Calculate the output of the network for the input ${\tilde{Z}}_I$ in β– cut form

Figure 1. Single-layer FNN.

$${\tilde{O}}_J=\tilde{f}\left({\text{Net}}_J\right)$$

1. where $\left({\text{Net}}_J\right)=\sum _{j=1}^J{\tilde{W}}_{ji}{\tilde{O}}_I+{\tilde{\mathit{\theta }}}_{i}i=1,2,\dots ,I\text{and}j=1,2,\dots ,J$ and $\tilde{f}$ is the fuzzy unipolar activation function defined by

$$\tilde{f}({\text{Net}}_J)=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\left[1+exp(-\mathit{\gamma }{\text{Net}}_J)\right]$}\right.$$

Step 4:

The error value is then computed as

$$\tilde{E}=\frac{\mathit{\beta }}{2}\left[{\left({\underline{d}}_J^{\mathit{\beta }}-{\underline{O}}_J^{\mathit{\beta }}\right)}^2+{\left({\overline{d}}_J^{\mathit{\beta }}-{\overline{O}}_J^{\mathit{\beta }}\right)}^2\right]$$

Step 5:

The weight is modified as

$${\tilde{W}}_{ji}^{\mathit{\beta }}\left(\text{New}\right)=\left[{\underline{W}}_{ji}^{\mathit{\beta }}\left(\text{New}\right),{\overline{W}}_{ji}^{\mathit{\beta }}\left(\text{New}\right)\right]=\left[{\underline{W}}_{ji}^{\mathit{\beta }}\left(\text{Old}\right),{\overline{W}}_{ji}^{\mathit{\beta }}\left(\text{Old}\right)\right]+\left[\mathrm{\Delta }{\underline{W}}_{ji}^{\mathit{\beta }},\mathrm{\Delta }{\overline{W}}_{ji}^{\mathit{\beta }}\right]j=1,2,\dots ,J\text{and}i=1,2,\dots ,I$$

where change in weights are calculated as

$$\mathrm{\Delta }{\tilde{W}}_{{}_{ji}}^{\mathit{\beta }}=\left[\mathrm{\Delta }{\underline{W}}_{ji}^{\mathit{\beta }},\mathrm{\Delta }{\overline{W}}_{ji}^{\mathit{\beta }}\right]=\left[-\mathit{\eta }\frac{\mathit{\partial }\tilde{E}}{\mathit{\partial }{\underline{W}}_{ji}^{\mathit{\beta }}},-\mathit{\eta }\frac{\mathit{\partial }\tilde{E}}{\mathit{\partial }{\overline{W}}_{ji}^{\mathit{\beta }}}\right]j=1,2,\dots ,J\text{and}i=1,2,\dots ,I$$

In the similar fashion the bias weights are also updated.

4. System identification of structural parameters in fuzzified form

Let us consider a shear building with n-storey structural system governed by the following set of linear differential equations in fuzzified form as(1) $$[\tilde{M}]{\{\ddot{\tilde{X}}\}}_t+[\tilde{C}]{\{\dot{\tilde{X}}\}}_t+[\tilde{K}]{\{\tilde{X}\}}_t={\{\tilde{F}\}}_t$$(1)

where ${\left\{\tilde{X}\right\}}_t={\left\{{\tilde{x}}_1,{\tilde{x}}_2,{\tilde{x}}_3,\dots ,{\tilde{x}}_n\right\}}_t^T$, ${\left\{\ddot{\tilde{X}}\right\}}_t={\left\{{\ddot{\tilde{x}}}_1,{\ddot{\tilde{x}}}_2,{\ddot{\tilde{x}}}_3,\dots ,{\ddot{\tilde{x}}}_n\right\}}_{{}_t}^T$ and ${\left\{\dot{\tilde{X}}\right\}}_t={\left\{{\dot{\tilde{x}}}_1,{\dot{\tilde{x}}}_2,{\dot{\tilde{x}}}_3,\dots ,{\dot{\tilde{x}}}_n\right\}}_{{}_t}^T$ indicates displacement, acceleration and velocity vectors of the consecutive n^th-storey in fuzzified form respectively. Moreover, $\left\{\tilde{M}\right\}=$ $\left[\underline{M},Mc,\overline{M}\right]$ is n × n mass matrix of the structure in fuzzified form and is given by$$\left\{\tilde{M}\right\}=\left[\begin{array}{ccccc}\left[{\underline{m}}_1,m_{1}c,{\overline{m}}_{{}_1}\right]& 0& \dots & \dots & 0\\ 0& \left[{\underline{m}}_2,m_{2}c,{\overline{m}}_2\right]& 0& \dots & 0\\ \dots & \dots & \dots & \dots & \dots \\ \dots & \dots & 0& \left[{\underline{m}}_{n-1},m_{n-1}c,{\overline{m}}_{n-1}\right]& 0\\ 0& \dots & \dots & 0& \left[{\underline{m}}_n,m_{n}c,{\overline{m}}_n\right]\end{array}\right],$$

$\left\{\tilde{C}\right\}=$ $\left[\underline{C},Cc,\overline{C}\right]\text{represents}n\times n$ damping matrix of the structure in fuzzified form and is written as$$\left\{\tilde{C}\right\}=\left[\begin{array}{ccccc}\left[{\underline{c}}_1,c_1,{\overline{c}}_1\right]+\left[{\underline{c}}_2,c_{2}c,{\overline{c}}_2\right]& -\left[c_2,c_{2}c,{\overline{c}}_2\right]& 0& \dots & 0\\ -\left[{\underline{c}}_2,c_{2}c,{\overline{c}}_2\right]& \left[{\underline{c}}_2,c_{2}c,{\overline{c}}_2\right]+\left[{\underline{c}}_3,c_{3}c,{\overline{c}}_3\right]& -\left[{\underline{c}}_3,c_{3}c,{\overline{c}}_3\right]& \dots & 0\\ \dots & \dots & \dots \\ 0& \dots & -\left[{\underline{c}}_{n-1},c_{n-1}c,{\overline{c}}_{n-1}\right]& \left[{\underline{c}}_{n-1},c_{n-1}c,{\overline{c}}_{n-1}\right]+\left[{\underline{c}}_n,c_{n}c,{\overline{c}}_n\right]& -\left[{\underline{c}}_n,c_{n}c,{\overline{c}}_n\right]\\ 0& \dots & -\left[{\underline{c}}_n,c_{n}c,{\overline{c}}_n\right]& \left[{\underline{c}}_n,c_{n}c,{\overline{c}}_n\right]\end{array}\right],$$

$\text{and}\left\{\tilde{K}\right\}$ = $\left[\underline{K},Kc,\overline{K}\right]\text{is}n\times n$ stiffness matrix of the structure in fuzzified form which may be obtained as$$\left\{\tilde{K}\right\}=\left[\begin{array}{ccccc}\left[{\underline{k}}_1,k_{1}c,{\overline{k}}_1\right]+\left[{\underline{k}}_2,k_{2}c,{\overline{k}}_2\right]& -\left[{\underline{k}}_2,k_{2}c,{\overline{k}}_2\right]& 0& \dots & 0\\ -\left[{\underline{k}}_2,k_{2}c,{\overline{k}}_2\right]& \left[{\underline{k}}_2,k_{2}c,{\overline{k}}_2\right]+\left[{\underline{k}}_3,k_{3}c,{\overline{k}}_3\right]& -\left[{\underline{k}}_3,k_{3}c,{\overline{k}}_3\right]& \dots & 0\\ \dots & \dots & & \dots & \\ 0& \dots & -\left[{\underline{k}}_{n-1},k_{n-1}c,{\overline{k}}_{n-1}\right]& \left[{\underline{k}}_{n-1},k_{n-1}c,{\overline{k}}_{n-1}\right]+\left[{\underline{k}}_n,k_{n}c,{\overline{k}}_n\right]& -\left[{\underline{k}}_n,k_{n}c,{\overline{k}}_n\right]\\ 0& & \dots & -\left[{\underline{k}}_n,k_{n}c,{\overline{k}}_n\right]& \left[{\underline{k}}_n,k_{n}c,{\overline{k}}_n\right]\end{array}\right].$$

Solution for Equation (1(1) $$[\tilde{M}]{\{\ddot{\tilde{X}}\}}_t+[\tilde{C}]{\{\dot{\tilde{X}}\}}_t+[\tilde{K}]{\{\tilde{X}\}}_t={\{\tilde{F}\}}_t$$(1) ) for free vibration with given mass and stiffness values in fuzzified form gives the corresponding fuzzy eigenvalues and eigenvectors. These are denoted, respectively, by ${\tilde{\mathit{\lambda }}}_i$ and ${\left\{\tilde{A}\right\}}_i={\left\{\underline{A},Ac,\overline{A}\right\}}_i$, $i=1\dots ,n$ where ${\tilde{\mathit{\omega }}}_i^2\left(={\tilde{\mathit{\lambda }}}_i\right)$ are the system’s natural frequency in fuzzified form. It may be noted that the free vibration equation will be a fuzzy eigenvalue problem. The fuzzy eigenvalue and vector are obtained then by considering different sets of lower, centre and upper stiffness and mass values. Here, the above procedure has been used so that we may handle the inverse of the matrices in crisp form separately as lower, centre and upper values. And that is why now we will replace the ‘~’ from all notations and will consider the case for lower form first and similarly for centre and upper form. Hence, the modal matrix Ref. [49] for lower form $\left\{\underline{A}\right\}$ may be written as$$\left[\underline{A}\right]=\left[{\left\{\underline{A}\right\}}_1{\left\{\underline{A}\right\}}_2\cdots {\left\{\underline{A}\right\}}_n\right]$$

Denoting the diagonal matrix made up of the eigenvalues in lower form as ${\underline{\mathit{\lambda }}}_i$, as ${\left[\underline{\mathit{\lambda }}\right]}_{n\times n}$, a new set of coordinates in lower form $\left\{\underline{y}\right\}$ related to the coordinates $\left\{\underline{X}\right\}$ is introduced by the well-known transformation$$\left\{\underline{X}\right\}=\left[\underline{A}\right]\left\{\underline{y}\right\}.$$

Proceeding by transforming into normal coordinates $\left(\left\{\underline{X}\right\}=\left[\underline{A}\right]\left\{\underline{y}\right\}\right)$ and premultiplying Equation (1(1) $$[\tilde{M}]{\{\ddot{\tilde{X}}\}}_t+[\tilde{C}]{\{\dot{\tilde{X}}\}}_t+[\tilde{K}]{\{\tilde{X}\}}_t={\{\tilde{F}\}}_t$$(1) ) with ${\left[\underline{A}\right]}^T$ we get(2) $${\left[\underline{A}\right]}^T\left[\underline{M}\right]\left[\underline{A}\right]\left\{\underline{\ddot{y}}\right\}+{\left[\underline{A}\right]}^T\left[\underline{C}\right]\left[\underline{A}\right]\left\{\underline{\dot{y}}\right\}+{\left[\underline{A}\right]}^T\left[\underline{K}\right]\left[\underline{A}\right]\left\{\underline{y}\right\}={\left[\underline{A}\right]}^T\left\{\underline{F}\right\}$$(2)

Rewriting Equation (2(2) $${\left[\underline{A}\right]}^T\left[\underline{M}\right]\left[\underline{A}\right]\left\{\underline{\ddot{y}}\right\}+{\left[\underline{A}\right]}^T\left[\underline{C}\right]\left[\underline{A}\right]\left\{\underline{\dot{y}}\right\}+{\left[\underline{A}\right]}^T\left[\underline{K}\right]\left[\underline{A}\right]\left\{\underline{y}\right\}={\left[\underline{A}\right]}^T\left\{\underline{F}\right\}$$(2) ) in terms of generalized mass and spectral matrices, we obtain(3) $$\left[\underline{P}\right]\left\{\underline{\ddot{y}}\right\}+{\left[\underline{A}\right]}^T\left[\underline{C}\right]\left[\underline{A}\right]\left\{\underline{\dot{y}}\right\}+\left[\underline{S}\right]\left\{\underline{y}\right\}={\left[\underline{A}\right]}^T\left\{\underline{F}\right\}$$(3)

where $\left[\underline{P}\right]={\left[\underline{A}\right]}^T\left[\underline{M}\right]\left[\underline{A}\right]$ and $\left[\underline{S}\right]={\left[\underline{A}\right]}^T\left[\underline{K}\right]\left[\underline{A}\right]$

Thus, we get the uncoupled equation as(4) $${\underline{P}}_i{\underline{\ddot{y}}}_i+{\underline{\overline{C}}}_i{\underline{\dot{y}}}_i+{\underline{S}}_i{\underline{y}}_i={\underline{\overline{F}}}_{i}fori=1,2,\dots ,n$$(4)

where ${\left[\underline{A}\right]}^T\left[\underline{C}\right]\left[\underline{A}\right]=\left[\underline{\overline{C}}\right]$ and ${\left[\underline{A}\right]}^T\left\{\underline{F}\right\}=\left\{\underline{\overline{F}}\right\}$

The above differential equations can be solved and the final solution may be written by$$\left(\left\{\underline{X}\right\}=\left[\underline{A}\right]\left\{\underline{y}\right\}\right)$$

In the similar manner we can proceed for centre and upper form too. After finding out the solution, Equation (1(1) $$[\tilde{M}]{\{\ddot{\tilde{X}}\}}_t+[\tilde{C}]{\{\dot{\tilde{X}}\}}_t+[\tilde{K}]{\{\tilde{X}\}}_t={\{\tilde{F}\}}_t$$(1) ) is rewritten to get the following set of equations in fuzzified form(5) $${\tilde{m}}_1{\ddot{\tilde{x}}}_1+\left({\tilde{c}}_1+{\tilde{c}}_2\right){\dot{\tilde{x}}}_1-{\tilde{c}}_2{\dot{\tilde{x}}}_2+\left({\tilde{k}}_1+{\tilde{k}}_2\right){\tilde{x}}_1-{\tilde{k}}_2{x}_2={\tilde{f}}_1$$(5) (6) $${\tilde{m}}_2{\ddot{\tilde{x}}}_2-{\tilde{c}}_2{\dot{\tilde{x}}}_1+\left({\tilde{c}}_2+{\tilde{c}}_3\right){\dot{\tilde{x}}}_2-{\tilde{c}}_3{\dot{\tilde{x}}}_3-{\tilde{k}}_2{\tilde{x}}_1+\left({\tilde{k}}_2+{\tilde{k}}_3\right){\tilde{x}}_2-{\overleftrightarrow{k}}_3{\tilde{x}}_3={\tilde{f}}_2$$(6) $$⋮$$(7) $${\tilde{m}}_{n-1}{\ddot{\tilde{x}}}_{n-1}-{\tilde{c}}_{n-1}{\dot{\tilde{x}}}_{n-2}+\left({\tilde{c}}_{n-1}+{\tilde{c}}_n\right){\dot{\tilde{x}}}_{n-1}-{\tilde{c}}_n{\dot{\tilde{x}}}_n-{\tilde{k}}_{n-1}{\tilde{x}}_{n-2}+\left({\tilde{k}}_{n-1}+{\tilde{k}}_n\right){\tilde{x}}_{n-1}-{\overleftrightarrow{k}}_n{\tilde{x}}_n={\tilde{f}}_{n-1}$$(7) (8) $${\tilde{m}}_n{\ddot{\tilde{x}}}_n-{\tilde{c}}_n{\dot{\tilde{x}}}_{n-1}+{\tilde{c}}_n{\dot{\tilde{x}}}_n-k_n{x}_{n-1}+{\tilde{k}}_n{\tilde{x}}_n={\tilde{f}}_n$$(8)

Equation (8(8) $${\tilde{m}}_n{\ddot{\tilde{x}}}_n-{\tilde{c}}_n{\dot{\tilde{x}}}_{n-1}+{\tilde{c}}_n{\dot{\tilde{x}}}_n-k_n{x}_{n-1}+{\tilde{k}}_n{\tilde{x}}_n={\tilde{f}}_n$$(8) ) is then written as(9) $${\tilde{m}}_n{\ddot{\tilde{x}}}_n+{\tilde{c}}_n\left[{\dot{\tilde{x}}}_n-{\dot{\tilde{x}}}_{n-1}\right]+{\tilde{k}}_n\left[{\tilde{x}}_n-{\tilde{x}}_{n-1}\right]={\tilde{f}}_n$$(9)

The above equation may now be presented as(10) $${\tilde{m}}_n{\ddot{\tilde{x}}}_n+{\tilde{c}}_n{\dot{\tilde{d}}}_n+{\tilde{k}}_n{\tilde{d}}_n={\tilde{f}}_n$$(10)

where ${\dot{\tilde{d}}}_n=\left[{\dot{\tilde{x}}}_n-{\dot{\tilde{x}}}_{n-1}\right]\text{and}{\tilde{d}}_n=\left[{\tilde{x}}_n-{\tilde{x}}_{n-1}\right]$

Here, ${\dot{\tilde{d}}}_n$ and ${\tilde{d}}_n$ indicate the known relative velocity and displacement in fuzzified form for $n\text{th}$ storey. Using the single layer FNN, Equation (10(10) $${\tilde{m}}_n{\ddot{\tilde{x}}}_n+{\tilde{c}}_n{\dot{\tilde{d}}}_n+{\tilde{k}}_n{\tilde{d}}_n={\tilde{f}}_n$$(10) ) is solved. Inputs for this FNN are taken as structural acceleration, relative velocity and relative displacement for the $n\text{th}$storey. Output of the network is taken as the applied force at time t. To solve Equation (10(10) $${\tilde{m}}_n{\ddot{\tilde{x}}}_n+{\tilde{c}}_n{\dot{\tilde{d}}}_n+{\tilde{k}}_n{\tilde{d}}_n={\tilde{f}}_n$$(10) ) a continuous training process with n training patterns are done using FNN and the converged weight matrix of the neural network is thus obtained. From this weight matrix the corresponding physical parameters such as ${\tilde{m}}_n,{\tilde{c}}_n$ and ${\tilde{k}}_n$ in fuzzified form are obtained. 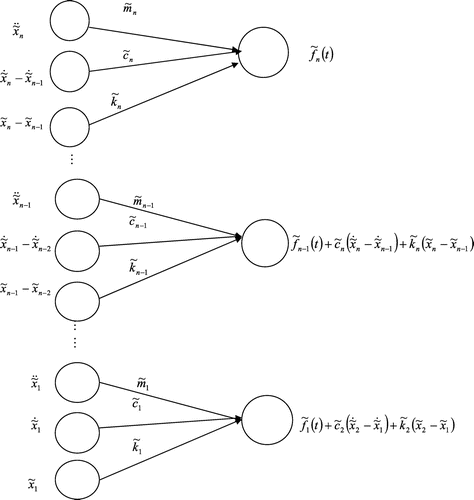Identified parameters of $n\text{th}$ storey are then used to identify the parameters of $(n-1)\text{th}$ storey using Equation (7). Proceeding in the same manner the parameters of $(n-2)\text{th}$ storey are determined and the process goes on till the unknown parameters of the first storey are obtained. The cluster of FNN diagram for n-storey structure is shown in Figure 2.

Figure 2. Proposed cluster FNN model for n-storey shear structure.

5. Results and discussion

The developed method has been used for different storey shear structures with damping and without damping cases. FNN training is done till a desired accuracy is achieved. The methodology has been discussed by giving the results for following two cases.

Case (i) Without Damping: In this case three problems are considered which are

(a)	Two storey
(b)	Four storey
(c)	Eight storey

Case (ii) With Damping: In this case only one problem of three-storey shear structure has been considered

(a)	Three storey

Case (i) (a) Two-storey shear building:

Structural parameter of shear building has been identified using the direct method where the data are considered to be in fuzzified form. To generate the data initially the theoretical values of the structural parameters are taken. These generated data are used first to train the neural network for n training patterns thus by establishing the converged weight matrix of the neural network. Corresponding component of the converged weight matrix gives the unknown or present structural parameters. Then the trained and theoretical data has been compared to show the efficiency of the proposed method. These ideas have been applied in all the cases. The initial structural parameter matrices in fuzzified form are taken as: storey masses ${\tilde{m}}_1=\left[1.5,2,2.5\right]$, ${\tilde{m}}_2=\left[1,1.5,2\right]$ kNs² m⁻¹, and the storey stiffnesses ${\tilde{k}}_1=\left[390,400,410\right]$, ${\tilde{k}}_2=\left[290,300,310\right]$ kNm⁻¹. The harmonic force exerted in the shear building are assumed in fuzzified form viz. ${\tilde{f}}_1\left(t\right)=\left[90sin(1.6\mathit{\pi }t)+\mathit{\pi },100sin(1.6\mathit{\pi }t)+\mathit{\pi },110sin(1.6\mathit{\pi }t)+\mathit{\pi }\right]$ and ${\tilde{f}}_2\left(t\right)=\left[90sin(1.6\mathit{\pi }t),100sin(1.6\mathit{\pi }t),110sin(1.6\mathit{\pi }t)\right]$ kN. Table 1 includes the comparison of identified structural parameters with the theoretical parameters.

Table 1. Identified mass and stiffness parameters of two-storey shear building in fuzzified form under the forced-vibration test (without damping).

Parameter	Storey	Theoretical	Identified
Mass (kN s^2 m^−1)	M1	[1.5, 2, 2.5]	[1.4650, 1.9866, 2.4939]
	M2	[1,1.5, 2]	[1.0457, 1.6859, 2.3077]
Stiffness (kN m^−1)	K1	[390, 400, 410]	[389.9991, 399.9994, 409.9997]
	K2	[290, 300, 310]	[290.4673, 299.1889, 308.5296]

(b) Four-storey shear building:

In this problem, the structural parameters in fuzzified form are: the storey masses ${\tilde{m}}_1=\left[3,3.5,4\right]$, ${\tilde{m}}_2=\left[3,3.5,4\right]$, ${\tilde{m}}_3=\left[2.5,3,3.5\right]$, ${\tilde{m}}_4=\left[2,2.5,3\right]$ kNs² m⁻¹, and the storey stiffnesses ${\tilde{k}}_1=\left[1190,1200,1210\right]$, ${\tilde{k}}_2=\left[1190,1200,1210\right]$, ${\tilde{k}}_3=\left[790,800,810\right]$ ${\tilde{k}}_4=\left[590,600,610\right]$ kNm⁻¹. The harmonic forces exerted in the shear building are taken as ${\tilde{f}}_1\left(t\right)=\left[90sin(1.6\mathit{\pi }t)+\mathit{\pi },100sin(1.6\mathit{\pi }t)+\mathit{\pi },110sin(1.6\mathit{\pi }t)+\mathit{\pi }\right]$, ${\tilde{f}}_2\left(t\right)=\left[90sin(1.6\mathit{\pi }t),100sin(1.6\mathit{\pi }t),110sin(1.6\mathit{\pi }t)\right]$, ${\tilde{f}}_3\left(t\right)=\left[0.5sin\left(3.2\mathit{\pi }t\right),1.0sin\left(3.2\mathit{\pi }t\right),1.5sin\left(3.2\mathit{\pi }t\right)\right]$ and ${\tilde{f}}_4\left(t\right)=\left[1.0sin\left(3.2\mathit{\pi }t\right),2.0sin\left(3.2\mathit{\pi }t\right),3.0sin\left(3.2\mathit{\pi }t\right)\right]$ kN. Dynamic displacements of four DOFs with duration of 1s are stored and are used to train the FNN for identification procedure. Comparisons between the identified and theoretical parameters of the structures in fuzzified form are incorporated in Table 2.

Table 2. Identified mass and stiffness parameters of four-storey shear building in fuzzified form under the forced-vibration test (without damping).

Parameter	Storey	Theoretical	Identified
Mass (kN s^2 m^−1)	M1	[3, 3.5, 4]	[2.859, 3.549, 4.001]
	M2	[3, 3.5, 4]	[2.900, 3.501, 3.898]
	M3	[2.5, 3.0, 3.5]	[2.2771, 3.0825, 3.2257]
	M4	[2, 2.5, 3]	[1.7690, 2.4627, 2.9828]
Stiffness (kN m^−1)	K1	[1190, 1200, 1210]	[1190.00, 1199.0988, 1210.00]
	K2	[1190, 1200, 1210]	[1190.00, 1199.008, 1210.051]
	K3	[790, 800, 810]	[789.9977, 799.9974, 810.001]
	K4	[590, 600, 610]	[589.9983, 599.991, 610.000]

(c) Eight-storey shear building:

In this case, the structural parameters viz., the storey masses and stiffnesses of the structure in fuzzified form are given in Table 3. The harmonic force in fuzzified form exerted in the eight storey of the building is ${\tilde{f}}_8\left(t\right)=\left[1.0sin\left(3.2\mathit{\pi }t\right),2.0sin\left(3.2\mathit{\pi }t\right),3.0sin\left(3.2\mathit{\pi }t\right)\right]$ kN. The dynamic displacements of eight DOFs with duration of 1 s are stored and are used to train the FNN for identification procedure. The identified structural parameters are compared with the theoretical structural parameters of this structural system. Corresponding result are shown in Table 3.

Table 3. Identified mass and stiffness parameters of eight-storey shear building in fuzzified form under the forced-vibration test (without damping).

Parameter	Storey	Theoretical	Identified
Mass (kN s^2 m^−1)	M1	[3, 3.5, 4]	[2.899, 3.500, 3.999]
	M2	[2.5, 3, 3.5]	[2.500, 3.00, 3.500]
	M3	[2.5, 3, 3.5]	[2.3425, 2.9435, 3.500]
	M4	[2.5, 3, 3.5]	[2.4504, 2.8900, 3.500]
	M5	[2, 2.5, 3]	[1.6672, 2.4378, 3.00]
	M6	[2, 2.5, 3]	[1.6916, 2.4998, 3.00]
	M7	[2, 2.5, 3]	[1.9706, 2.3492, 3.00]
	M8	[1.5, 2, 2.5]	[1.2336, 1.9928, 2.500]
Stiffness (kN m^−1)	K1	[1190, 1200, 1210]	[1190.00, 1199.9879, 1210.00]
	K2	[1190, 1200, 1210]	[1190.00, 1200.001, 1210.00]
	K3	[790, 800, 810]	[789.998, 799.9985, 810.000]
	K4	[790, 800, 810]	[789.999, 799.9997, 810.000]
	K5	[790, 800, 810]	[789.9998, 799.9992, 810.000]
	K6	[590, 600, 610]	[589.9994, 599.9955, 610.000]
	K7	[590, 600, 610]	[589.9997, 599.8989, 610.00]
	K8	[590, 600, 610]	[589.9988, 599.8999, 610.00]

Case (ii) (a) Three-storey shear building:

Structural parameters in fuzzified form are taken as: the storey masses ${\tilde{m}}_1=\left[2.5,3,3.5\right]$, ${\tilde{m}}_2=\left[2.5,3,3.5\right],$ ${\tilde{m}}_3=\left[1.5,2,2.5\right]$ kNs² m⁻¹ and the storey stiffnesses ${\tilde{k}}_1=\left[1190,1200,1210\right]$, ${\tilde{k}}_2=\left[790,800,810\right]$, ${\tilde{k}}_3=\left[590,600,610\right]$ kNm⁻¹; the damping values ${\tilde{c}}_1=\left[7,8,9\right]$, ${\tilde{c}}_2=\left[4,5,6\right],$ ${\tilde{c}}_3=\left[3,4,5\right]$ kNsm⁻¹. The harmonic forces exerted in the shear building in fuzzified form are considered as ${\tilde{f}}_1\left(t\right)=\left[90sin(1.6\mathit{\pi }t)+\mathit{\pi },100sin(1.6\mathit{\pi }t)+\mathit{\pi },110sin(1.6\mathit{\pi }t)+\mathit{\pi }\right]$, ${\tilde{f}}_2\left(t\right)=\left[90sin(1.6\mathit{\pi }t),100sin(1.6\mathit{\pi }t),110sin(1.6\mathit{\pi }t)\right]$ and ${\tilde{f}}_3\left(t\right)=\left[0.5sin\left(3.2\mathit{\pi }t\right),1.0sin\left(3.2\mathit{\pi }t\right),1.5sin\left(3.2\mathit{\pi }t\right)\right]$ kN. Comparisons between the identified and theoretical structural parameters are incorporated in Table 4. The epoch versus mass, stiffness and damping for three storey are plotted in Figures 3–11 to show that how the structural parameters converge.

Table 4. Identified mass and stiffness parameters of three-storey shear building in fuzzified form under the forced-vibration test (with damping).

Parameter	Storey	Theoretical	Identified
Mass (kN s^2 m^−1)	M1	[2.5, 3, 3.5]	[2.5101, 3.001,3.498]
	M2	[2.5, 3, 3.5]	[2.596, 2.8881, 3.373]
	M3	[1.5, 2, 2.5]	[1.5737, 1.6837, 2.139]
Stiffness (kN m^−1)	K1	[1190, 1200, 1210]	[1190.95, 1199.001, 1210.95]
	K2	[790, 800, 810]	[789.991, 799.957, 809.992]
	K3	[590, 600, 610]	[589.993, 599.990, 609. 995]
Damping (kN s m^−1)	C1	[7–9]	[6.599, 7.895, 8.999]
	C2	[4–6]	[3.999, 4.999, 5.999]
	C3	[3–5]	[2.9980, 3.9835, 4.9867]

Figure 3. Convergence of fuzzified mass parameter (M₁) with respect to number of epoch for three-storey shear structure (with damping).

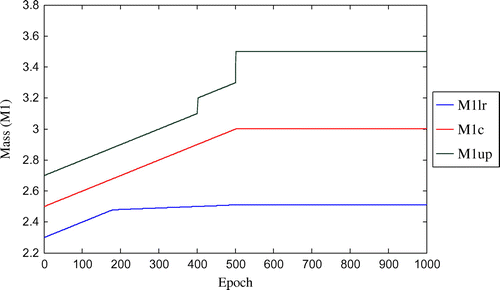
Figure 4. Convergence of fuzzified mass parameter (M₂) with respect to number of epoch for three-storey shear structure (with damping).

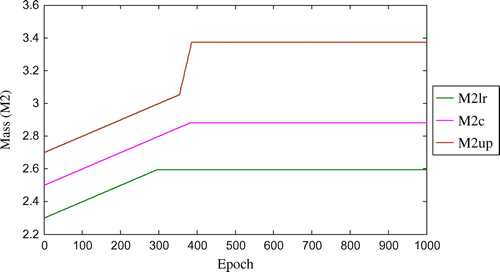
Figure 5. Convergence of fuzzified mass parameter (M₃) with respect to number of epoch for three-storey shear structure (with damping).

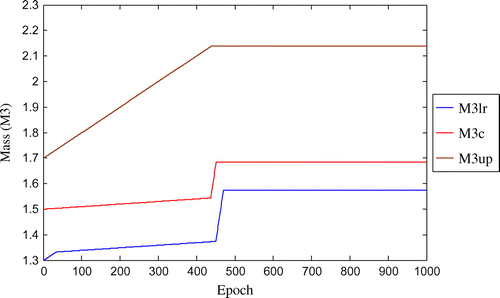
Figure 6. Convergence of fuzzified damping parameter (C₁) with respect to number of epoch for three-storey shear structure (with damping).

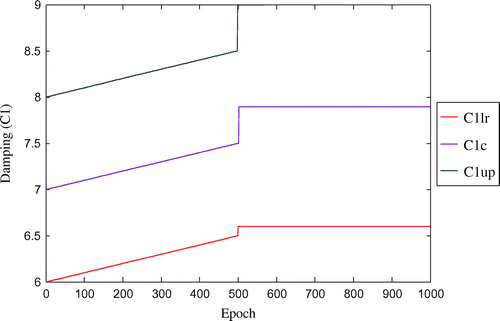
Figure 7. Convergence of fuzzified damping parameter (C₂) with respect to number of epoch for three-storey shear structure (with damping).

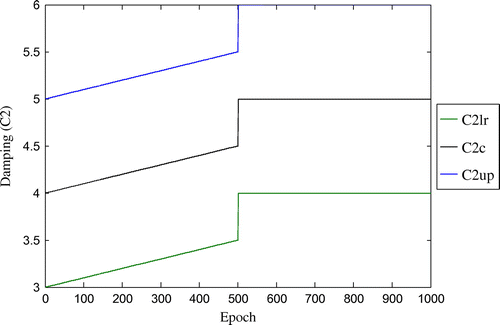
Figure 8. Convergence of fuzzified stiffness parameter (C₃) with respect to number of epoch for three-storey shear structure (with damping).

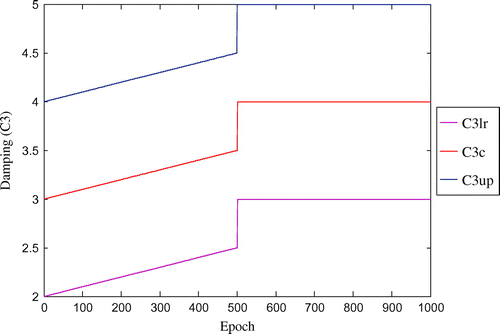
Figure 9. Convergence of fuzzified stiffness parameter (K₁) with respect to number of epoch for three-storey shear structure (with damping).

Figure 10. Convergence of fuzzified stiffness parameter (K₂) with respect to number of epoch for three-storey shear structure (with damping).

Figure 11. Convergence of fuzzified stiffness parameter (K₃) with respect to number of epoch for three-storey shear structure (with damping).

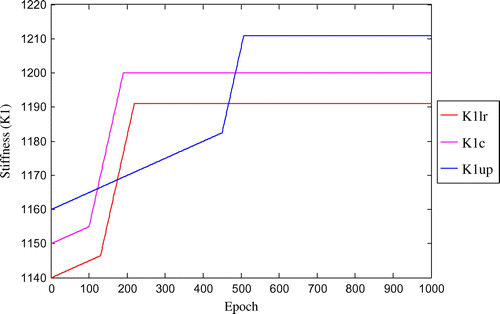
6. Concluding remarks

This paper uses the powerful soft computing technique viz. single layer FNN for identification of uncertain structural parameters. If the available information and/or data are uncertain or non-probabilistic in nature, then the mathematical model needs to be developed accordingly. As such, FNN has been developed which can handle uncertain or fuzzified data. Here, direct method for system identification of uncertain multistory shear structures from their dynamic responses has been proposed in fuzzified form. Governing equations of motion are modified based on relative responses of consecutive stories and are implemented in a series/cluster of FNN models. Various example problems have been solved and related results are reported to show the reliability and powerfulness of the method. It is worth mentioning that the cluster of FNN may directly estimate the structural parameters in fuzzified form. The fuzzy estimates are certainly useful for design engineers by knowing the lower, centre and upper bounds of the structural parameters.

Disclosure statement

No potential conflict of interest was reported by the authors.

Funding

This work was supported by the Ministry of Earth Sciences (MoES), New Delhi to carry out this investigation.

Acknowledgement

The author would like to acknowledge funding from Ministry of Earth Sciences (MoES), New Delhi to carry out this investigation. The authors also thank the anonymous reviewers for their suggestions which have helped in improving the contents of this paper.