The bi-Helmholtz equation with Cauchy conditions: ill-posedness and regularization methods

Abstract

In this paper, the bi-Helmholtz equation with Cauchy conditions is nominated in a n-dimensional strip domain. It is shown that this Cauchy problem may be ill-posed in the sense of Hadamard. In order to overcome the ill-posedness, a suitable regularization method has to be applied to the Cauchy problem. Hence, two well-known wavelet and Fourier regularization methods are used for solving this ill-posed problem. Regarding our experiences, wavelet and Fourier regularization methods act similarly, since these methods remove high frequencies in the frequency space which are the reason for ill-posedness. To explore abilities of the wavelet regularization method, stability of the solution with the Meyer wavelet regularization is investigated by obtaining some error bounds. It is demonstrated numerically that Shannon wavelet is an alternative to the Meyer wavelet in the regularization method. It is explored that the Fourier regularization method for solving the bi-Helmholtz equation with the Cauchy conditions is also applicable. Numerical algorithms of the desired regularization methods are proposed in detail based on the fast Fourier transform (FFT). Various numerical examples in two-dimensional strip domain are shown for the validation and verification of the regularization techniques.

Keywords:

• Cauchy conditions
• bi-Helmholtz equation
• wavelet regularization method
• Fourier regularization method
• fast Fourier transform(FFT)

2010 Mathematics Subject Classifications:

• 65N20
• 65N21
• 65N12
• 65T60

1. Introduction

The Helmholtz-type equation with Cauchy conditions has many applications in engineering and applied sciences; for example, the vibration of structures [1], acoustics [2], electromagnetism [3], wave propagation [4], and scattering [5]. Recently, the ill-posed Cauchy problem for the Helmholtz equation was investigated in a strip domain and some mollification regularization methods have been proposed [6,7]. The Helmholtz equation is also employed in the study of the nonlocal differential beam models of micro- and nano-electromechanical systems, carbon nanotubes, and nanomaterials [8]. In this reference, it has been shown that the bi-Helmholtz type operator is more effective than the Helmholtz type for describing wave dispersion of atomic models. Based on development of the bi-Helmholtz in nonlocal strain-gradient elasticity theory, analysis of wave propagation in a porous double-nanobeam system with graded material properties has been performed in some studies [9,10]. An innovative stress-driven nonlocal integral elastic model of the bi-Helmholtz type has been presented for inflected Bernoulli-Euler nanobeams [11]. From the past to today, the bi-Helmholtz equation on a bounded domain has also several applications in engineering and sciences such as in the boundary element method [12] and streamfunction formulations of the Navier-Stokes equations [13].

This paper is concerned with the study of the ill-posedness of the bi-Helmholtz equation with Cauchy conditions. In fact, it can be proven that this problem has a unique solution which does not depend continuously on the given noisy data. The general approach to overcome the ill-posedness of the Helmholtz and bi-Helmholtz equations with Cauchy conditions is to apply a regularization method. Tikhonov and Fourier regularization methods are some proposed standard and classical techniques to regularize such ill-posed problems [14–16]. However, there are some other techniques such as local discontinuous Galerkin, reproducing kernel, meshless, and Robin-Dirichlet algorithms to tackle some ill-posed problems, see e.g. [17–22].

A technical method for regularizing such problems is the wavelet method. It is worth pointing out that many researchers are interested in exploiting some wavelet bases for solving linear/non-linear partial differential equations with boundary/initial-boundary conditions. One improvement of the wavelet method for solving such problems is the adaptive wavelet method, see e.g. [23–27]. Recently, the wavelet regularization method has come to be exploited as a powerful tool to regularize Cauchy type problems [16,28]. The main goal of this paper is to apply wavelet and Fourier regularization techniques to solve the bi-Helmholtz equation with the Cauchy conditions and study the advantages and drawbacks of these techniques in regularizing the considered problem. One of the most important subjects in the regularization methods is to find an appropriate regularization parameter which depends on both the problem and the method. In ill-posed problems, a regularization parameter can be obtained by an a-periori and/or a-posteriori regularization parameter choice rules [29,30]. Due to the complexity of the Meyer wavelet method and the nature of the bi-Helmholtz equation, we proceed to an a-priori choice rule and leave the a-posteriori choice rule to the future works.

The rest of the paper is organized as follows. Section 2 is devoted to representing the bi-Helmholtz equation with the Cauchy conditions and it is shown that this problem may be ill-posed. In Section 3, a wavelet regularization method is applied for solving the ill-posed problem. To establish analytic results, we choose the Meyer wavelet. Also, we apply the Fourier regularization method in this section. In Section 4, numerical algorithms for the wavelet and Fourier regularization methods based on the FFT are proposed. In Section 5, the regularization methods are illustrated. Finally, Section 6 is devoted to a brief conclusion.

2. Solution and ill-posedness of the bi-Helmholtz Cauchy problem

We consider the following homogeneous bi-Helmholtz equation with Cauchy conditions (1) $\begin{array}{rl}& {\gamma }^4{\mathrm{\Delta }}^{2}u(x,\mathbf{y})-{\eta }^2\mathrm{\Delta }u(x,\mathbf{y})+u(x,\mathbf{y})=0,(x,\mathbf{y})\in (0,1)\times {\mathbb{R}}^n,\\ & \frac{{\mathrm{\partial }}^{j}u(0,\mathbf{y})}{\mathrm{\partial }{x}^j}={\phi }_j\left(\mathbf{y}\right),j=1,2,3,4,\mathbf{y}\in {\mathbb{R}}^n,\end{array}$(1) where $\mathrm{\Delta }=\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}+\sum _{j=1}^n\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{y}_j^2}$ and ${\mathrm{\Delta }}^2=\mathrm{\Delta }\left(\mathrm{\Delta }\right)$ denote Laplace and bi-Laplace operators, respectively, γ and η are positive real numbers, and ${\phi }_j\left(\mathbf{y}\right)\in L^2\left({\mathbb{R}}^n\right)$ for j = 1, 2, 3, 4 are given functions. Applying multi-dimensional Fourier transform to problem (1(1) $\begin{array}{rl}& {\gamma }^4{\mathrm{\Delta }}^{2}u(x,\mathbf{y})-{\eta }^2\mathrm{\Delta }u(x,\mathbf{y})+u(x,\mathbf{y})=0,(x,\mathbf{y})\in (0,1)\times {\mathbb{R}}^n,\\ & \frac{{\mathrm{\partial }}^{j}u(0,\mathbf{y})}{\mathrm{\partial }{x}^j}={\phi }_j\left(\mathbf{y}\right),j=1,2,3,4,\mathbf{y}\in {\mathbb{R}}^n,\end{array}$(1) ) with respect to $\mathbf{y}=(y_1,y_2,\dots ,y_n)$, namely, $\hat{f}(x,\mathit{\omega })=\frac{1}{\sqrt{2\pi }}{\int }_{{\mathbb{R}}^n}f(x,\mathbf{y})e^{-i\mathit{\omega }\cdot \mathbf{y}}\mathrm{d}\mathbf{y},\mathit{\omega }=({\omega }_1,{\omega }_2,\dots ,{\omega }_n)\in {\mathbb{R}}^n,$ we have (2) $\begin{array}{rl}& {\gamma }^4\frac{{\mathrm{\partial }}^4\hat{u}(x,\mathit{\omega })}{\mathrm{\partial }{x}^4}-({\eta }^2+2{\gamma }^4|\mathit{\omega }{|}^2)\frac{{\mathrm{\partial }}^2\hat{u}(x,\mathit{\omega })}{\mathrm{\partial }{x}^2}\\ & +({\eta }^2|\mathit{\omega }{|}^2+|\mathit{\omega }{|}^4+1)\hat{u}(x,\mathit{\omega })=0,(x,\mathit{\omega })\in (0,1)\times {\mathbb{R}}^n,\\ & \frac{{\mathrm{\partial }}^j\hat{u}(0,\mathit{\omega })}{\mathrm{\partial }{x}^j}={\hat{\phi }}_j\left(\mathit{\omega }\right),j=1,2,3,4,\mathit{\omega }\in {\mathbb{R}}^n.\end{array}$(2) By setting $\alpha =\frac{\mathrm{R}\mathrm{e}\left(z\right)}{\sqrt{2}{\gamma }^2},\text{β}=\frac{\mathrm{I}\mathrm{m}\left(z\right)}{\sqrt{2}{\gamma }^2},z=\sqrt{{\eta }^2+2{\gamma }^4|\mathit{\omega }{|}^2-\sqrt{4{\gamma }^8|\mathit{\omega }{|}^4-4{\gamma }^4|\mathit{\omega }{|}^4-4{\gamma }^4+{\eta }^4}},$ the solution of problem (2(2) $\begin{array}{rl}& {\gamma }^4\frac{{\mathrm{\partial }}^4\hat{u}(x,\mathit{\omega })}{\mathrm{\partial }{x}^4}-({\eta }^2+2{\gamma }^4|\mathit{\omega }{|}^2)\frac{{\mathrm{\partial }}^2\hat{u}(x,\mathit{\omega })}{\mathrm{\partial }{x}^2}\\ & +({\eta }^2|\mathit{\omega }{|}^2+|\mathit{\omega }{|}^4+1)\hat{u}(x,\mathit{\omega })=0,(x,\mathit{\omega })\in (0,1)\times {\mathbb{R}}^n,\\ & \frac{{\mathrm{\partial }}^j\hat{u}(0,\mathit{\omega })}{\mathrm{\partial }{x}^j}={\hat{\phi }}_j\left(\mathit{\omega }\right),j=1,2,3,4,\mathit{\omega }\in {\mathbb{R}}^n.\end{array}$(2) ) can be written as $\hat{u}(x,\mathit{\omega })=c_1\cosh \alpha x\cos \text{β}x+c_2\cosh \alpha x\sin \text{β}x+c_3\sinh \alpha x\cos \text{β}x+c_4\sinh \alpha x\sin \text{β}x,$ where $c_j$ for $j=1,2,3,4,$ depend on $\eta ,\gamma ,{\hat{\phi }}_1,{\hat{\phi }}_2,{\hat{\phi }}_3,$ and ${\hat{\phi }}_4$.

Remark 2.1

The study of ill-posedness of problem (1(1) $\begin{array}{rl}& {\gamma }^4{\mathrm{\Delta }}^{2}u(x,\mathbf{y})-{\eta }^2\mathrm{\Delta }u(x,\mathbf{y})+u(x,\mathbf{y})=0,(x,\mathbf{y})\in (0,1)\times {\mathbb{R}}^n,\\ & \frac{{\mathrm{\partial }}^{j}u(0,\mathbf{y})}{\mathrm{\partial }{x}^j}={\phi }_j\left(\mathbf{y}\right),j=1,2,3,4,\mathbf{y}\in {\mathbb{R}}^n,\end{array}$(1) ) for arbitrary $\eta ,\gamma >0$ is very complicated. By setting $\eta =\sqrt{2}$ and $\gamma =1$, we verify that (1(1) $\begin{array}{rl}& {\gamma }^4{\mathrm{\Delta }}^{2}u(x,\mathbf{y})-{\eta }^2\mathrm{\Delta }u(x,\mathbf{y})+u(x,\mathbf{y})=0,(x,\mathbf{y})\in (0,1)\times {\mathbb{R}}^n,\\ & \frac{{\mathrm{\partial }}^{j}u(0,\mathbf{y})}{\mathrm{\partial }{x}^j}={\phi }_j\left(\mathbf{y}\right),j=1,2,3,4,\mathbf{y}\in {\mathbb{R}}^n,\end{array}$(1) ) is an ill-posed problem.

The bi-Helmholtz equation with Cauchy conditions in the two-dimensional domain $(0,1)\times \mathbb{R}$, for $\eta =\sqrt{2},\gamma =1$, reads as (3) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^4}+2\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^2\mathrm{\partial }{y}^2}+\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{y}^4}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}+u=0,(x,y)\in (0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}={\phi }_j\left(y\right),j=1,2,3,4,y\in \mathbb{R}.\end{array}$(3) Applying the Fourier transform regarding variable $y$ to problem (3(3) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^4}+2\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^2\mathrm{\partial }{y}^2}+\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{y}^4}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}+u=0,(x,y)\in (0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}={\phi }_j\left(y\right),j=1,2,3,4,y\in \mathbb{R}.\end{array}$(3) ), we have (4) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^4\hat{u}}{\mathrm{\partial }{x}^4}-2(|\omega {|}^2+1)\frac{{\mathrm{\partial }}^2\hat{u}}{\mathrm{\partial }{x}^2}+(|\omega {|}^2+1{)}^2\hat{u}(x,\omega )=0,(x,\omega )\in (0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^j\hat{u}(0,\omega )}{\mathrm{\partial }{x}^j}={\hat{\phi }}_j\left(\omega \right),j=1,2,3,4,\omega \in \mathbb{R}.\end{array}$(4) The solution of problem (4(4) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^4\hat{u}}{\mathrm{\partial }{x}^4}-2(|\omega {|}^2+1)\frac{{\mathrm{\partial }}^2\hat{u}}{\mathrm{\partial }{x}^2}+(|\omega {|}^2+1{)}^2\hat{u}(x,\omega )=0,(x,\omega )\in (0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^j\hat{u}(0,\omega )}{\mathrm{\partial }{x}^j}={\hat{\phi }}_j\left(\omega \right),j=1,2,3,4,\omega \in \mathbb{R}.\end{array}$(4) ) is (5) $\begin{array}{rl}\hat{u}(x,\omega )& =c_1\cosh x\sqrt{|\omega {|}^2+1}+c_2\sinh x\sqrt{|\omega {|}^2+1}\\ & +c_{3}x\cosh x\sqrt{|\omega {|}^2+1}+c_{4}x\sinh x\sqrt{|\omega {|}^2+1}\\ c_1& ={\hat{\phi }}_1\left(\omega \right),\\ c_2& =\frac{3}{2\sqrt{|\omega {|}^2+1}}{\hat{\phi }}_2\left(\omega \right)-\frac{1}{2(|\omega {|}^2+1{)}^{\frac{3}{2}}}{\hat{\phi }}_4\left(\omega \right),\\ c_3& =-\frac{1}{2}{\hat{\phi }}_2\left(\omega \right)+\frac{1}{2(|\omega {|}^2+1)}{\hat{\phi }}_4\left(\omega \right),\\ c_4& =-\frac{1}{2}\sqrt{|\omega {|}^2+1}{\hat{\phi }}_1\left(\omega \right)+\frac{1}{2\sqrt{|\omega {|}^2+1}}{\hat{\phi }}_3\left(\omega \right),\end{array}$(5) and consequently problem (3(3) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^4}+2\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^2\mathrm{\partial }{y}^2}+\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{y}^4}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}+u=0,(x,y)\in (0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}={\phi }_j\left(y\right),j=1,2,3,4,y\in \mathbb{R}.\end{array}$(3) ) has the following solution $u(x,y)=\frac{1}{\sqrt{2\pi }}{\int }_{\mathbb{R}}\hat{u}(x,\omega )e^{i\omega y}\mathrm{d}\omega .$

Remark 2.2

According to (5(5) $\begin{array}{rl}\hat{u}(x,\omega )& =c_1\cosh x\sqrt{|\omega {|}^2+1}+c_2\sinh x\sqrt{|\omega {|}^2+1}\\ & +c_{3}x\cosh x\sqrt{|\omega {|}^2+1}+c_{4}x\sinh x\sqrt{|\omega {|}^2+1}\\ c_1& ={\hat{\phi }}_1\left(\omega \right),\\ c_2& =\frac{3}{2\sqrt{|\omega {|}^2+1}}{\hat{\phi }}_2\left(\omega \right)-\frac{1}{2(|\omega {|}^2+1{)}^{\frac{3}{2}}}{\hat{\phi }}_4\left(\omega \right),\\ c_3& =-\frac{1}{2}{\hat{\phi }}_2\left(\omega \right)+\frac{1}{2(|\omega {|}^2+1)}{\hat{\phi }}_4\left(\omega \right),\\ c_4& =-\frac{1}{2}\sqrt{|\omega {|}^2+1}{\hat{\phi }}_1\left(\omega \right)+\frac{1}{2\sqrt{|\omega {|}^2+1}}{\hat{\phi }}_3\left(\omega \right),\end{array}$(5) ), ill-posedness of the problem is obvious since small perturbations on ${\phi }_i,i=1,2,3,4,$ can make dramatic change in output results due to multiplying by terms such as $\cosh x\sqrt{|\omega {|}^2+1}$ and $\sinh x\sqrt{|\omega {|}^2+1}$, specially for large $|\omega |$.

To show the ill-posedness of problem (3(3) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^4}+2\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^2\mathrm{\partial }{y}^2}+\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{y}^4}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}+u=0,(x,y)\in (0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}={\phi }_j\left(y\right),j=1,2,3,4,y\in \mathbb{R}.\end{array}$(3) ), we consider this problem with ${\phi }_1\ne 0,{\phi }_i=0,i=2,3,4$. We impose the following particular perturbation on the measured data (6) ${\phi }_1(y;ϵ)={\phi }_1\left(y\right)+ϵ\sin \left(\frac{y}{ϵ}\right),0<ϵ\ll 1.$(6) The corresponding solution arisen from the perturbed data is (7) $\begin{array}{rl}u(x,y;ϵ)& =u(x,y)+\frac{1}{2}ϵ\sin \left(\frac{y}{ϵ}\right)\\ & \times \left(2\cosh \left(x\sqrt{\frac{1}{{ϵ}^2}+1}\right)-x\sqrt{\frac{1}{{ϵ}^2}+1}\sinh \left(x\sqrt{\frac{1}{{ϵ}^2}+1}\right)\right).\end{array}$(7) For a fixed 0<$x$<1, one can verify that (8) $\parallel u(x,\cdot ;ϵ)-u(x,\cdot ){\parallel }_{\mathrm{\infty }}\ge c{e}^{x/ϵ},$(8) where 0<$c$<1 is a constant. When $ϵ$ tends to zero, we have $\underset{ϵ\to 0}{lim}\parallel {\phi }_1(\cdot ;ϵ)-{\phi }_1(\cdot ){\parallel }_{\mathrm{\infty }}=0$ from (6(6) ${\phi }_1(y;ϵ)={\phi }_1\left(y\right)+ϵ\sin \left(\frac{y}{ϵ}\right),0<ϵ\ll 1.$(6) ), while for 0<$x$<1, we have $\underset{ϵ\to 0}{lim}\parallel u(x,\cdot ;ϵ)-u(x,\cdot ){\parallel }_{\mathrm{\infty }}=\mathrm{\infty }$ from (8(8) $\parallel u(x,\cdot ;ϵ)-u(x,\cdot ){\parallel }_{\mathrm{\infty }}\ge c{e}^{x/ϵ},$(8) ). This leads to conclude that problem (3(3) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^4}+2\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^2\mathrm{\partial }{y}^2}+\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{y}^4}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}+u=0,(x,y)\in (0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}={\phi }_j\left(y\right),j=1,2,3,4,y\in \mathbb{R}.\end{array}$(3) ) is ill-posed for the particular case. Similarly, it can be shown that problem (3(3) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^4}+2\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^2\mathrm{\partial }{y}^2}+\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{y}^4}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}+u=0,(x,y)\in (0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}={\phi }_j\left(y\right),j=1,2,3,4,y\in \mathbb{R}.\end{array}$(3) ) is also ill-posed for other cases. For instance, we consider problem (3(3) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^4}+2\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^2\mathrm{\partial }{y}^2}+\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{y}^4}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}+u=0,(x,y)\in (0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}={\phi }_j\left(y\right),j=1,2,3,4,y\in \mathbb{R}.\end{array}$(3) ) for $i$ = 1 with ${\phi }_1\left(y\right)=e^{-y^2}$ together with the noisy solution stated by (6(6) ${\phi }_1(y;ϵ)={\phi }_1\left(y\right)+ϵ\sin \left(\frac{y}{ϵ}\right),0<ϵ\ll 1.$(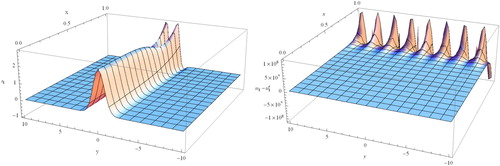6) ). The exact solution u and corresponding error $u(x,y)-u(x,y;\frac{1}{10})$ are shown in Figure 1. The infinity norm of the exact solution on the domain is about 2.8 but the corresponding norm of the noisy solution is more than ${10}^8$ while $\parallel {\phi }_1^{ϵ}-{\phi }_1{\parallel }_{\mathrm{\infty }}\le \frac{1}{10}$.

Figure 1. Left: Exact solution of problem (3(3) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^4}+2\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^2\mathrm{\partial }{y}^2}+\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{y}^4}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}+u=0,(x,y)\in (0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}={\phi }_j\left(y\right),j=1,2,3,4,y\in \mathbb{R}.\end{array}$(3) ) for ${\phi }_1\left(y\right)=e^{-y^2},{\phi }_i\left(y\right)=0,i=2,3,4.$ Right: The corresponding error of unregularized solution (7(7) $\begin{array}{rl}u(x,y;ϵ)& =u(x,y)+\frac{1}{2}ϵ\sin \left(\frac{y}{ϵ}\right)\\ & \times \left(2\cosh \left(x\sqrt{\frac{1}{{ϵ}^2}+1}\right)-x\sqrt{\frac{1}{{ϵ}^2}+1}\sinh \left(x\sqrt{\frac{1}{{ϵ}^2}+1}\right)\right).\end{array}$(7) ), with $ϵ=\frac{1}{10}$.

3. Error analysis of wavelet and Fourier regularization methods

The bi-Helmholtz equation with Cauchy conditions has been converted to the frequency space. Since high frequencies cause the ill-posedness, the problem needs to be regularized on the frequency domain. Meyer, Shannon, and Daubechies scaling functions have compact supports in the frequency space. So these scaling functions and their corresponding wavelets can act as low-pass filters to remove high frequencies of the perturbed problem. Regarding to the numerical experiences, we infer that the Meyer and Shannon wavelets can overcome ill-posedness of the problem more effective than Daubechies wavelets. Since the Meyer wavelet and scaling functions are defined in the Fourier domain, therefore we choose the Meyer wavelet in order to find a bound of error and prove the stability of the method. Another reason for selecting the Meyer wavelet is that the Fourier transform of the Meyer wavelet is an analytic function on the frequency domain.

To regularize ill-posed problem (3(3) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^4}+2\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^2\mathrm{\partial }{y}^2}+\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{y}^4}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}+u=0,(x,y)\in (0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}={\phi }_j\left(y\right),j=1,2,3,4,y\in \mathbb{R}.\end{array}$(3) ), we decompose its solution to $u=\sum _{i=1}^4{u}_i$ such that for $i=1,2,3,4,u_i$ is the solution of the following simpler problem (9) $\begin{array}{rl}& {\mathrm{\Delta }}^2{u}_i(x,y)-2\mathrm{\Delta }{u}_i(x,y)+u_i(x,y)=0,(x,y)\in (0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^j{u}_i(0,y)}{\mathrm{\partial }{x}^j}={\delta }_{i,j+1}{\phi }_{j+1}\left(y\right),j=0,1,2,3y\in \mathbb{R},\end{array}$(9) where ${\delta }_{i,j+1}$ is the Kronecker symbol.

3.1. Meyer wavelet: definitions and properties

According to [31], the Fourier transform of Meyer original scaling and corresponding wavelet functions are given by $\begin{array}{rl}\hat{\mathrm{\Phi }}\left(\omega \right)& =\frac{1}{\sqrt{2\pi }}\left\{\begin{array}{ll}1,& |\omega |\le \frac{2\pi }{3},\\ \cos \left(\frac{\pi }{2}\nu \left(\frac{3}{4\pi }|\omega |-1\right)\right),& \frac{2\pi }{3}\le |\omega |\le \frac{4\pi }{3},\\ 0,& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e},\end{array}\right.\\ \hat{\mathrm{\Psi }}\left(\omega \right)& =\frac{1}{\sqrt{2\pi }}\left\{\begin{array}{ll}{e}^{\frac{iw}{2}}\sin \left(\frac{\pi }{2}\nu \left(\frac{3}{2\pi }|\omega |-1\right)\right),& \frac{2\pi }{3}\le |\omega |\le \frac{4\pi }{3},\\ e^{\frac{iw}{2}}\cos \left(\frac{\pi }{2}\nu \left(\frac{3}{4\pi }|\omega |-1\right)\right),& \frac{4\pi }{3}\le |\omega |\le \frac{8\pi }{3},\\ 0,& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e},\end{array}\right.\end{array}$ where $\nu$ can be chosen as a $C^k\left(\mathbb{R}\right)$ or $C^{\mathrm{\infty }}\left(\mathbb{R}\right)$ function with the property $\nu \left(x\right)+\nu (1-x)=1$ for all $x$ in $\mathbb{R}$. As an example, $\nu \left(x\right)=\left\{\begin{array}{ll}0,& x\le 0,\\ x^4(35-84x+70x^2-20x^3),& 0\le x\le 1,\\ 1,& x\ge 1.\end{array}\right.$ The multiresolution analysis of the Meyer wavelet can be generated by the following nested subspaces $V_j=\mathrm{S}\mathrm{p}\mathrm{a}\mathrm{n}\left\{{\mathrm{\Phi }}_{j,k}\right(\cdot ):=2^{\frac{j}{2}}\mathrm{\Phi }(2^j\cdot -k)|k\in \mathbb{Z}\},j\in \mathbb{Z}.$ The collection $\{{\mathrm{\Phi }}_{j,k}|j,k\in \mathbb{Z}\}$ forms an orthonormal basis for $L^2\left(\mathbb{R}\right)$. In addition, the Fourier transform of wavelet and scaling functions in level $j$ read as (10) ${\hat{\mathrm{\Psi }}}_{j,k}\left(\omega \right)=2^{-\frac{j}{2}}{e}^{-ik{2}^{-j}\omega }\hat{\mathrm{\Psi }}\left(2^{-j}\omega \right),{\hat{\mathrm{\Phi }}}_{j,k}\left(\omega \right)=2^{-\frac{j}{2}}{e}^{-ik{2}^{-j}\omega }\hat{\mathrm{\Phi }}\left(2^{-j}\omega \right).$(10) For all $k\in \mathbb{Z}$, the functions in (10(10) ${\hat{\mathrm{\Psi }}}_{j,k}\left(\omega \right)=2^{-\frac{j}{2}}{e}^{-ik{2}^{-j}\omega }\hat{\mathrm{\Psi }}\left(2^{-j}\omega \right),{\hat{\mathrm{\Phi }}}_{j,k}\left(\omega \right)=2^{-\frac{j}{2}}{e}^{-ik{2}^{-j}\omega }\hat{\mathrm{\Phi }}\left(2^{-j}\omega \right).$(10) ) are compactly supported, since $\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}{\hat{\mathrm{\Psi }}}_{j,k}=\left[-\frac{8\pi }{3}{2}^j,-\frac{2\pi }{3}{2}^j\right]\cup \left[\frac{2\pi }{3}{2}^j,\frac{8\pi }{3}{2}^j\right],\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}{\hat{\mathrm{\Phi }}}_{j,k}=\left[-\frac{4\pi }{3}{2}^j,\frac{4\pi }{3}{2}^j\right].$ We consider the following projectors $P_{J}f=\sum _{k\in \mathbb{Z}}⟨f,{\mathrm{\Phi }}_{J,k}⟩{\mathrm{\Phi }}_{J,k},Q_{J}f=\sum _{k\in \mathbb{Z}}⟨f,{\mathrm{\Psi }}_{J,k}⟩{\mathrm{\Psi }}_{J,k},$ where $f\in L^2\left(\mathbb{R}\right)$ and $⟨\cdot ,\cdot ⟩$ denotes the inner product in $L^2\left(\mathbb{R}\right)$. Some useful properties of these operators are given as $\begin{array}{rl}& \widehat{P_{J}f}\left(\omega \right)=0,\mathrm{f}\mathrm{o}\mathrm{r}|\omega |\ge \frac{4}{3}\pi 2^J,\\ & \widehat{Q_{J}f}\left(\omega \right)=0,\left(\widehat{(I-P_J)f}\right)\left(\omega \right)=\widehat{Q_{J}f}\left(\omega \right),\mathrm{f}\mathrm{o}\mathrm{r}|\omega |<\frac{4}{3}\pi 2^J.\end{array}$ Bernstein's inequality has a key role in the stability analysis. This inequality is represented in the following lemma [32].

Lemma 3.1

Let $\{V_j{\}}_{j\in \mathbb{Z}}$ be a Meyer multiresolution analysis. For all $\phi \in V_J,$ it is concluded that ${∥\frac{{\mathrm{d}}^k}{\mathrm{d}{t}^k}\phi ∥}_{H^r\left(\mathbb{R}\right)}\le C{2}^{(J-1)k}\parallel \phi {\parallel }_{H^r\left(\mathbb{R}\right)},J,k\in \mathbb{N},r\in \mathbb{R},$ where $C$ is a positive constant and $\parallel \cdot {\parallel }_{H^r\left(\mathbb{R}\right)}$ denotes norm of Sobolev space $H^r\left(\mathbb{R}\right)$ defined by $\parallel \phi {\parallel }_{H^r\left(\mathbb{R}\right)}={\left({\int }_{\mathbb{R}}|\hat{\phi }\left(\omega \right){|}^2(1+|\omega {|}^2{)}^r\mathrm{d}\omega \right)}^{\frac{1}{2}}.$

Now, we define the following operators ${\mathcal{G}}_x^i:L^2\left(\mathbb{R}\right)\to L^2\left(\mathbb{R}\right),\left({\mathcal{G}}_x^i\phi \right)\left(y\right)=u_i(x,y),i=1,2,3,4.$

Proposition 3.2

Let $\{V_j{\}}_{j\in \mathbb{Z}}$ be Meyer multiresolution analysis. For $J\in \mathbb{N}$ and any $\phi \in V_J,$ the following inequalities hold $\begin{array}{rl}& \parallel {\mathcal{G}}_x^1\phi {\parallel }_{H^r\left(\mathbb{R}\right)}\le \left(C{2}^J{e}^{2^{J}x}+6\right)\parallel \phi {\parallel }_{H^r\left(\mathbb{R}\right)},\parallel {\mathcal{G}}_x^2\phi {\parallel }_{H^r\left(\mathbb{R}\right)}\le \left(\frac{7}{8}C{e}^{2^{J}x}+7\right)\parallel \phi {\parallel }_{H^r\left(\mathbb{R}\right)},\\ & \parallel {\mathcal{G}}_x^3\phi {\parallel }_{H^r\left(\mathbb{R}\right)}\le \left(\frac{1}{8}C{e}^{2^{J}x}+2\right)\parallel \phi {\parallel }_{H^r\left(\mathbb{R}\right)},\parallel {\mathcal{G}}_x^4\phi {\parallel }_{H^r\left(\mathbb{R}\right)}\le \left(\frac{5}{16}C{e}^{2^{J}x}+5\right)\parallel \phi {\parallel }_{H^r\left(\mathbb{R}\right)},\end{array}$ where $r\in \mathbb{R},0<x\le 1,$ and $C$ is the positive constant in Lemma 3.1.

Proof.

We prove the inequality for the operator ${\mathcal{G}}_x^1$. Other cases are similar. According to the definition of the norm $H^r\left(\mathbb{R}\right)$ and the solution (5(5) $\begin{array}{rl}\hat{u}(x,\omega )& =c_1\cosh x\sqrt{|\omega {|}^2+1}+c_2\sinh x\sqrt{|\omega {|}^2+1}\\ & +c_{3}x\cosh x\sqrt{|\omega {|}^2+1}+c_{4}x\sinh x\sqrt{|\omega {|}^2+1}\\ c_1& ={\hat{\phi }}_1\left(\omega \right),\\ c_2& =\frac{3}{2\sqrt{|\omega {|}^2+1}}{\hat{\phi }}_2\left(\omega \right)-\frac{1}{2(|\omega {|}^2+1{)}^{\frac{3}{2}}}{\hat{\phi }}_4\left(\omega \right),\\ c_3& =-\frac{1}{2}{\hat{\phi }}_2\left(\omega \right)+\frac{1}{2(|\omega {|}^2+1)}{\hat{\phi }}_4\left(\omega \right),\\ c_4& =-\frac{1}{2}\sqrt{|\omega {|}^2+1}{\hat{\phi }}_1\left(\omega \right)+\frac{1}{2\sqrt{|\omega {|}^2+1}}{\hat{\phi }}_3\left(\omega \right),\end{array}$(5) ) for $i$ = 1, it is concluded that $\begin{array}{rl}\parallel {\mathcal{G}}_x^1\phi {\parallel }_{H^r\left(\mathbb{R}\right)}& ={\left({\int }_{\mathbb{R}}|\widehat{{\mathcal{G}}_x^1\phi }\left(\omega \right){|}^2(1+|\omega {|}^2{)}^r\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & =\left({\int }_{\mathbb{R}}{\left|\hat{\phi }\left(\omega \right)\cosh x\sqrt{|\omega {|}^2+1}-\frac{1}{2}\hat{\phi }\left(\omega \right)\sqrt{|\omega {|}^2+1}x\sinh x\sqrt{|\omega {|}^2+1}\right|}^2\right.\\ & \times {\left.(1+|\omega {|}^2{)}^r\mathrm{d}\omega \phantom{{\int }_{\mathbb{R}}{\left|\hat{\phi }\left(\omega \right)\cosh x\sqrt{|\omega {|}^2+1}-\frac{1}{2}\hat{\phi }\left(\omega \right)\sqrt{|\omega {|}^2+1}x\sinh x\sqrt{|\omega {|}^2+1}\right|}^2}\right)}^{\frac{1}{2}}\\ & \le {\left({\int }_{\mathbb{R}}{\left|\hat{\phi }\left(\omega \right)\cosh x\sqrt{|\omega {|}^2+1}\right|}^2(1+|\omega {|}^2{)}^r\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & +\frac{1}{2}{\left({\int }_{\mathbb{R}}{\left|\hat{\phi }\left(\omega \right)\sqrt{|\omega {|}^2+1}x\sinh x\sqrt{|\omega {|}^2+1}\right|}^2(1+|\omega {|}^2{)}^r\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & =:{\mathfrak{I}}_1+\frac{1}{2}{\mathfrak{I}}_2.\end{array}$ Using the Taylor series and Lemma 1 for ${\mathfrak{I}}_1$, we get $\begin{array}{rl}{\mathfrak{I}}_1& \le {\left({\int }_{|\omega |<1}{\left|\hat{\phi }\left(\omega \right)\cosh \sqrt{2}x\right|}^2(1+|\omega {|}^2{)}^r\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & +{\left({\int }_{|\omega |\ge 1}{\left|\hat{\phi }\left(\omega \right)\cosh \sqrt{2}|\omega |x\right|}^2(1+|\omega {|}^2{)}^r\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & \le e^{\sqrt{2}}{\left({\int }_{|\omega |<1}{\left|\hat{\phi }\left(\omega \right)\right|}^2(1+|\omega {|}^2{)}^r\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & +{\left({\int }_{|\omega |\ge 1}{\left|\hat{\phi }\left(\omega \right)\sum _{n=0}^{\mathrm{\infty }}\frac{2^n{x}^{2n}}{\left(2n\right)!}{\omega }^{2n}\right|}^2(1+|\omega {|}^2{)}^r\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & \le e^{\sqrt{2}}\parallel \phi {\parallel }_{H^r\left(\mathbb{R}\right)}+\sum _{n=0}^{\mathrm{\infty }}\frac{2^n{2}^n{x}^{2n}}{\left(2n\right)!}{\left({\int }_{|\omega |\ge 1}{\left|\hat{\phi }\left(\omega \right)(i\omega {)}^{2n}\right|}^2(1+|\omega {|}^2{)}^r\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & =e^{\sqrt{2}}\parallel \phi {\parallel }_{H^r\left(\mathbb{R}\right)}+\sum _{n=0}^{\mathrm{\infty }}\frac{2^{2n}{x}^{2n}}{\left(2n\right)!}\parallel \frac{{\mathrm{d}}^{2n}}{\mathrm{d}{t}^{2n}}\phi {\parallel }_{H^r\left(\mathbb{R}\right)}\\ & \le e^{\sqrt{2}}\parallel \phi {\parallel }_{H^r\left(\mathbb{R}\right)}+\sum _{n=0}^{\mathrm{\infty }}\frac{2^{2n}{x}^{2n}}{\left(2n\right)!}C{2}^{(J-1)2n}\parallel \phi {\parallel }_{H^r\left(\mathbb{R}\right)}\\ & \le \left(C{e}^{2^{J}x}+e^{\sqrt{2}}\right)\parallel \phi {\parallel }_{H^r\left(\mathbb{R}\right)}.\end{array}$ Also, it can be concluded that ${\mathfrak{I}}_2\le \left(\frac{e^{\sqrt{2}}}{\sqrt{2}}+C{2}^{J-1}{e}^{2^{J}x}\right)\parallel \phi {\parallel }_{H^r\left(\mathbb{R}\right)}.$ Finally, the following result holds $\begin{array}{rl}\parallel {\mathcal{G}}_x^1\phi {\parallel }_{H^r\left(\mathbb{R}\right)}& \le \left(C{e}^{2^{J-\frac{1}{2}}x}+e^{\sqrt{2}}+\frac{1}{4}{e}^{\sqrt{2}}+C{2}^{J-2}{e}^{2^{J}x}\right)\parallel \phi {\parallel }_{H^r\left(\mathbb{R}\right)}\\ & \le \left(C{2}^J{e}^{2^{J}x}+6\right)\parallel \phi {\parallel }_{H^r\left(\mathbb{R}\right)}.\end{array}$

3.2. Regularization method by Meyer wavelet

We focus on the wavelet regularization for problem (9(9) $\begin{array}{rl}& {\mathrm{\Delta }}^2{u}_i(x,y)-2\mathrm{\Delta }{u}_i(x,y)+u_i(x,y)=0,(x,y)\in (0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^j{u}_i(0,y)}{\mathrm{\partial }{x}^j}={\delta }_{i,j+1}{\phi }_{j+1}\left(y\right),j=0,1,2,3y\in \mathbb{R},\end{array}$(9) ) for the case when $i$ = 1. All assumptions, subjects, and proofs in this part are useful and applicable for the remaining cases, i.e. i = 2, 3, 4. Let $u_1$ be the solution of problem (9(9) $\begin{array}{rl}& {\mathrm{\Delta }}^2{u}_i(x,y)-2\mathrm{\Delta }{u}_i(x,y)+u_i(x,y)=0,(x,y)\in (0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^j{u}_i(0,y)}{\mathrm{\partial }{x}^j}={\delta }_{i,j+1}{\phi }_{j+1}\left(y\right),j=0,1,2,3y\in \mathbb{R},\end{array}$(9) ) such that the measured data ${\phi }_1^{ϵ}\in L^2\left(\mathbb{R}\right)$ of ${\phi }_1$ satisfies $\parallel {\phi }_1-{\phi }_1^{ϵ}{\parallel }_{H^r\left(\mathbb{R}\right)}\le \delta$ for some positive $\delta$ and non-positive $r$. This restriction is considered on $r$, since $L^2\left(\mathbb{R}\right)\subseteq H^r\left(\mathbb{R}\right)$ for $r\le 0$. We assume that for any $s\ge r$, $\parallel u_1(1,\cdot ){\parallel }_{H^s\left(\mathbb{R}\right)}\le M$, where $M$ is a positive constant.

Proposition 3.3

For a fixed $J\in \mathbb{N}$ and $\phi$ in $V_J,$ we have $\parallel Q_J\phi {\parallel }_{H^r\left(\mathbb{R}\right)}\le 4e^{-2^J}{2}^{-J(s-r)}M.$

Proof.

Setting $I_J=[-\frac{4}{3}\pi 2^J,\frac{4}{3}\pi 2^J]$, we define operator ${\mathcal{M}}_J$ such that $\widehat{{\mathcal{M}}_J\phi }=(1-{\chi }_{I_J})\hat{\phi }$. Thanks to the Parseval formula, one can verify that $\begin{array}{rl}{Q}_J\phi & =\sum _{k\in \mathbb{Z}}⟨\phi ,{\mathrm{\Psi }}_{J,k}⟩{\mathrm{\Psi }}_{J,k}=\sum _{k\in \mathbb{Z}}⟨\hat{\phi },{\hat{\mathrm{\Psi }}}_{J,k}⟩{\mathrm{\Psi }}_{J,k}=\sum _{k\in \mathbb{Z}}⟨(1-{\chi }_{I_J})\hat{\phi },{\hat{\mathrm{\Psi }}}_{J,k}⟩{\mathrm{\Psi }}_{J,k}\\ & =\sum _{k\in \mathbb{Z}}⟨\widehat{{\mathcal{M}}_J\phi },{\hat{\mathrm{\Psi }}}_{J,k}⟩{\mathrm{\Psi }}_{J,k}=Q_J{\mathcal{M}}_J\phi .\end{array}$ Therefore, $\begin{array}{rl}\parallel Q_J\phi {\parallel }_{H^r\left(\mathbb{R}\right)}& =\parallel Q_J{\mathcal{M}}_J\phi {\parallel }_{H^r\left(\mathbb{R}\right)}\le \parallel {\mathcal{M}}_J\phi {\parallel }_{H^r\left(\mathbb{R}\right)}\\ & \le {\left({\int }_{|\omega |\ge \frac{2}{3}\pi 2^J}|\hat{\phi }\left(\omega \right){|}^2(1+|\omega {|}^2{)}^r\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & =\left({\int }_{|\omega |\ge \frac{2}{3}\pi 2^J}{\left|\frac{1}{\cosh \sqrt{|\omega {|}^2+1}-\frac{1}{2}\sqrt{|\omega {|}^2+1}\sinh \sqrt{|\omega {|}^2+1}}{\hat{u}}_1(1,\omega )\right|}^2\right.\\ & \times {\left.(1+|\omega {|}^2{)}^r\mathrm{d}\omega \phantom{{\int }_{|\omega |\ge \frac{2}{3}\pi 2^J}{\left|\frac{1}{\cosh \sqrt{|\omega {|}^2+1}-\frac{1}{2}\sqrt{|\omega {|}^2+1}\sinh \sqrt{|\omega {|}^2+1}}{\hat{u}}_1(1,\omega )\right|}^2}\right)}^{\frac{1}{2}}\\ & \le {\left({\int }_{|\omega |\ge \frac{2}{3}\pi 2^J}|4e^{-\sqrt{|\omega {|}^2+1}}\frac{1}{(1+|\omega {|}^2{)}^{\frac{s-r}{2}}}{|}^2|{\hat{u}}_1(1,\omega ){|}^2(1+|\omega {|}^2{)}^s\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & \le 4\underset{|\omega |\ge \frac{2}{3}\pi 2^J}{sup}{e}^{-\sqrt{|\omega {|}^2+1}}\frac{1}{(1+|\omega {|}^2{)}^{\frac{s-r}{2}}}{\left({\int }_{|\omega |\ge \frac{2}{3}\pi 2^J}|{\hat{u}}_1(1,\omega ){|}^2(1+|\omega {|}^2{)}^s\right)}^{\frac{1}{2}}\\ & \le 4\underset{|\omega |\ge \frac{2}{3}\pi 2^J}{sup}{e}^{-|\omega |}|\omega {|}^{-(s-r)}\parallel g_1{\parallel }_{H^s\left(\mathbb{R}\right)}\\ & \le 4e^{-2^J}{2}^{-J(s-r)}M.\end{array}$

Proposition 3.4

For any fixed $J\in \mathbb{N}$ and ${\phi }_i\in V_J,i=1,2,3,4,$ suppose $\parallel {\phi }_i-{\phi }_i^{ϵ}{\parallel }_{H^r\left(\mathbb{R}\right)}\le \delta$. For $r\le min\{0,s\}$ and $\parallel u_i(1,\cdot ){\parallel }_{H^s\left(\mathbb{R}\right)}\le M,i=1,2,3,4,$ the following inequalities are hold (11) $\begin{array}{rl}\parallel {\mathcal{G}}_x^1({\phi }_1-P_J{\phi }_1^{ϵ}){\parallel }_{H^r\left(\mathbb{R}\right)}& \le 2C{e}^{2^{J}x}\delta +4(2^{J}C+1)e^{-(1-x)2^J}{2}^{-J(s-r)}M\\ & +24e^{-2^J}{2}^{-J(s-r)}M+6\delta ,\\ \parallel {\mathcal{G}}_x^2({\phi }_2-P_J{\phi }_2^{ϵ}){\parallel }_{H^r\left(\mathbb{R}\right)}& \le C{e}^{2^{J}x}\delta +C{e}^{-(1-x)2^J}{2}^{-J(s-r)}M+28e^{-2^J}{2}^{-J(s-r)}M\\ & +D{2}^{-J(s-r)}M+7\delta ,\\ \parallel {\mathcal{G}}_x^3({\phi }_3-P_J{\phi }_3^{ϵ}){\parallel }_{H^r\left(\mathbb{R}\right)}& \le \frac{1}{8}C{e}^{2^{J}x}\delta +\frac{1}{2}C{e}^{-(1-x)2^J}{2}^{-J(s-r)}\\ & +8e^{-2^J}{2}^{-J(s-r)}M+E{e}^{-J(s-r)}M+2\delta ,\\ \parallel {\mathcal{G}}_x^4({\phi }_4-P_J{\phi }_4^{ϵ}){\parallel }_{H^r\left(\mathbb{R}\right)}& \le \frac{5}{16}C{e}^{2^{J}x}\delta +\frac{5}{4}C{e}^{-(1-x)2^J}{2}^{-J(s-r)}M\\ & +20e^{-2^J}{2}^{-J(s-r)}M+F{2}^{-J(s-r)}M+5\delta ,\end{array}$(11) where $C,D,E,$ and $F$ are positive constants.

Proof.

We prove only the first inequality of (11(11) $\begin{array}{rl}\parallel {\mathcal{G}}_x^1({\phi }_1-P_J{\phi }_1^{ϵ}){\parallel }_{H^r\left(\mathbb{R}\right)}& \le 2C{e}^{2^{J}x}\delta +4(2^{J}C+1)e^{-(1-x)2^J}{2}^{-J(s-r)}M\\ & +24e^{-2^J}{2}^{-J(s-r)}M+6\delta ,\\ \parallel {\mathcal{G}}_x^2({\phi }_2-P_J{\phi }_2^{ϵ}){\parallel }_{H^r\left(\mathbb{R}\right)}& \le C{e}^{2^{J}x}\delta +C{e}^{-(1-x)2^J}{2}^{-J(s-r)}M+28e^{-2^J}{2}^{-J(s-r)}M\\ & +D{2}^{-J(s-r)}M+7\delta ,\\ \parallel {\mathcal{G}}_x^3({\phi }_3-P_J{\phi }_3^{ϵ}){\parallel }_{H^r\left(\mathbb{R}\right)}& \le \frac{1}{8}C{e}^{2^{J}x}\delta +\frac{1}{2}C{e}^{-(1-x)2^J}{2}^{-J(s-r)}\\ & +8e^{-2^J}{2}^{-J(s-r)}M+E{e}^{-J(s-r)}M+2\delta ,\\ \parallel {\mathcal{G}}_x^4({\phi }_4-P_J{\phi }_4^{ϵ}){\parallel }_{H^r\left(\mathbb{R}\right)}& \le \frac{5}{16}C{e}^{2^{J}x}\delta +\frac{5}{4}C{e}^{-(1-x)2^J}{2}^{-J(s-r)}M\\ & +20e^{-2^J}{2}^{-J(s-r)}M+F{2}^{-J(s-r)}M+5\delta ,\end{array}$(11) ). Other inequalities are proved similarly. With considering $\parallel {\mathcal{G}}_x^1{\phi }_1-{\mathcal{G}}_x^1{P}_J{\phi }_1^{ϵ}{\parallel }_{H^r\left(\mathbb{R}\right)}\le \parallel {\mathcal{G}}_x^1{\phi }_1-{\mathcal{G}}_x^1{P}_J{\phi }_1{\parallel }_{H^r\left(\mathbb{R}\right)}+\parallel {\mathcal{G}}_x^1{P}_J{\phi }_1-{\mathcal{G}}_x^1{P}_J{\phi }_1^{ϵ}{\parallel }_{H^r\left(\mathbb{R}\right)},$ and using the result of Proposition 3.2, we show that $\begin{array}{rl}\parallel {\mathcal{G}}_x^1{P}_J{\phi }_1-{\mathcal{G}}_x^1{P}_J{\phi }_1^{ϵ}{\parallel }_{H^r\left(\mathbb{R}\right)}& =\parallel {\mathcal{G}}_x^1{P}_J({\phi }_1-{\phi }_1^{ϵ}){\parallel }_{H^r\left(\mathbb{R}\right)}\le (C{2}^J{e}^{2^{J}x}+6)\parallel P_J({\phi }_1-{\phi }_1^{ϵ}){\parallel }_{H^r\left(\mathbb{R}\right)}\\ & \le (C{2}^J{e}^{2^{J}x}+6)\delta .\end{array}$ To compute the upper bound of $\parallel {\mathcal{G}}_x^1{\phi }_1-{\mathcal{G}}_x^1{P}_J{\phi }_1{\parallel }_{H^r\left(\mathbb{R}\right)}$, we define $\begin{array}{rl}\mathcal{K}(x,\omega )& :={\left|\left(\cosh x\sqrt{|\omega {|}^2+1}-\frac{1}{2}x\sqrt{|\omega {|}^2+1}\sinh x\sqrt{|\omega {|}^2+1}\right)\left(\widehat{(I-P_J){\phi }_1}\right)\left(\omega \right)\right|}^2\\ & \times (1+|\omega {|}^2{)}^r.\end{array}$ Then $\begin{array}{rl}\parallel {\mathcal{G}}_x^1{\phi }_1-{\mathcal{G}}_x^1{P}_J{\phi }_1{\parallel }_{H^r\left(\mathbb{R}\right)}& ={\left({\int }_{\mathbb{R}}\mathcal{K}(x,\omega )\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & \le {\left({\int }_{|\omega |\ge \frac{4}{3}\pi 2^J}\mathcal{K}(x,\omega )\mathrm{d}\omega \right)}^{\frac{1}{2}}+{\left({\int }_{|\omega |<\frac{4}{3}\pi 2^J}\mathcal{K}(x,\omega )\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & =:{\mathfrak{I}}_3+{\mathfrak{I}}_4.\end{array}$ By setting $\mathcal{T}(x,\omega ):=\left(\cosh x\sqrt{|\omega {|}^2+1}-\frac{1}{2}x\sqrt{|\omega {|}^2+1}\sinh x\sqrt{|\omega {|}^2+1}\right),$ the upper-bounds for ${\mathfrak{I}}_3$ is obtained as follows $\begin{array}{rl}{\mathfrak{I}}_3& ={\left({\int }_{|\omega |\ge \frac{4}{3}\pi 2^J}{\left|\mathcal{T}(x,\omega )\widehat{{\phi }_1}\left(\omega \right)\right|}^2(1+|\omega {|}^2{)}^r\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & ={\left({\int }_{|\omega |\ge \frac{4}{3}\pi 2^J}{\left|\frac{\mathcal{T}(x,\omega )}{\mathcal{T}(1,\omega )}{\hat{u}}_1(1,\omega )\right|}^2(1+|\omega {|}^2{)}^r\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & \le {\left({\int }_{|\omega |\ge \frac{4}{3}\pi 2^J}{\left|\frac{e^{x\sqrt{|\omega {|}^2+1}}}{\frac{1}{4}{e}^{\sqrt{|\omega {|}^2+1}}}\right|}^2{\left|{\hat{u}}_1(1,\omega )\right|}^2(1+|\omega {|}^2{)}^r\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & ={\left({\int }_{|\omega |\ge \frac{4}{3}\pi 2^J}{\left|4e^{(x-1)\sqrt{|\omega {|}^2+1}}\right|}^2{\left|{\hat{u}}_1(1,\omega )\right|}^2(1+|\omega {|}^2{)}^r\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & \le 4\underset{|\omega |\ge \frac{4}{3}\pi 2^J}{sup}\left(e^{(x-1)\sqrt{|\omega {|}^2+1}}\frac{1}{(1+|\omega {|}^2{)}^{\frac{s-r}{2}}}\right){\left({\int }_{|\omega |\ge \frac{4}{3}\pi 2^J}|{\hat{u}}_1(1,\omega ){|}^2(1+|\omega {|}^2{)}^s\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & \le 4\underset{|\omega |\ge \frac{4}{3}\pi 2^J}{sup}{e}^{(x-1)|\omega |}|\omega {|}^{-(s-r)}\parallel g_1{\parallel }_{H^r\left(\mathbb{R}\right)}\\ & \le 4e^{-(1-x)2^J}{2}^{-J(s-r)}M.\end{array}$ In the following, we derive upper-bound of ${\mathfrak{I}}_4$ as $\begin{array}{rl}{\mathfrak{I}}_4& \le (C{2}^J{e}^{2^{J}x}+6)\parallel Q_J{\phi }_1{\parallel }_{H^r\left(\mathbb{R}\right)}\\ & \le 4C{e}^{-(1-x)2^J}{2}^{-J(s-r)}M+24e^{-2^J}{2}^{-J(s-r)}M.\end{array}$ So it is concluded that $\begin{array}{rl}\parallel {\mathcal{G}}_x^1{\phi }_1-{\mathcal{G}}_x^1{P}_J{\phi }_1{\parallel }_{H^r\left(\mathbb{R}\right)}& \le 4e^{-(1-x)2^J}{2}^{-J(s-r)}M+4C{e}^{-(1-x)2^J}{2}^{-J(s-r)}M\\ & +24e^{-2^J}{2}^{-J(s-r)}M.\end{array}$ The first assertion of this proposition appears as follows $\begin{array}{rl}\parallel {\mathcal{G}}_x^1{\phi }_1-{\mathcal{G}}_x^1{P}_J{\phi }_1^{ϵ}{\parallel }_{H^r\left(\mathbb{R}\right)}& \le 4e^{-(1-x)2^J}{2}^{-J(s-r)}M+4C{2}^J{e}^{-(1-x)2^J}{2}^{-J(s-r)}M\\ & +24e^{-2^J}{2}^{-J(s-r)}M+(2C{e}^{2^{J}x}+6)\delta =2C{e}^{2^{J}x}\delta \\ & +4(2^{J}C+1)e^{-(1-x)2^J}{2}^{-J(s-r)}M+24e^{-2^J}{2}^{-J(s-r)}M+6\delta .\end{array}$

Stability of the method is guaranteed by using the following Theorem.

Theorem 3.5

Taking $J=\tilde{J}:=[{\log }_2(\ln \left(\frac{M}{\delta }\right(\ln \frac{M}{\delta }{)}^{-(s-r)}\left)\right)]$ in Proposition 3.4, all of the right hand sides of (11(11) $\begin{array}{rl}\parallel {\mathcal{G}}_x^1({\phi }_1-P_J{\phi }_1^{ϵ}){\parallel }_{H^r\left(\mathbb{R}\right)}& \le 2C{e}^{2^{J}x}\delta +4(2^{J}C+1)e^{-(1-x)2^J}{2}^{-J(s-r)}M\\ & +24e^{-2^J}{2}^{-J(s-r)}M+6\delta ,\\ \parallel {\mathcal{G}}_x^2({\phi }_2-P_J{\phi }_2^{ϵ}){\parallel }_{H^r\left(\mathbb{R}\right)}& \le C{e}^{2^{J}x}\delta +C{e}^{-(1-x)2^J}{2}^{-J(s-r)}M+28e^{-2^J}{2}^{-J(s-r)}M\\ & +D{2}^{-J(s-r)}M+7\delta ,\\ \parallel {\mathcal{G}}_x^3({\phi }_3-P_J{\phi }_3^{ϵ}){\parallel }_{H^r\left(\mathbb{R}\right)}& \le \frac{1}{8}C{e}^{2^{J}x}\delta +\frac{1}{2}C{e}^{-(1-x)2^J}{2}^{-J(s-r)}\\ & +8e^{-2^J}{2}^{-J(s-r)}M+E{e}^{-J(s-r)}M+2\delta ,\\ \parallel {\mathcal{G}}_x^4({\phi }_4-P_J{\phi }_4^{ϵ}){\parallel }_{H^r\left(\mathbb{R}\right)}& \le \frac{5}{16}C{e}^{2^{J}x}\delta +\frac{5}{4}C{e}^{-(1-x)2^J}{2}^{-J(s-r)}M\\ & +20e^{-2^J}{2}^{-J(s-r)}M+F{2}^{-J(s-r)}M+5\delta ,\end{array}$(11) ) tend to zero as $\delta \to 0$ since (12) $\parallel {\mathcal{G}}_x^1{\phi }_1-{\mathcal{G}}_x^1{P}_{\tilde{J}}{\phi }_1^{ϵ}{\parallel }_{H^r\left(\mathbb{R}\right)}\le {\delta }^{\frac{1}{4}(1-x)}{M}^x{\left(\ln \frac{M}{\delta }\right)}^{-x(s-r)},$(12) and for $i=2,3,4,$ (13) $\parallel {\mathcal{G}}_x^i{\phi }_i-{\mathcal{G}}_x^i{P}_{\tilde{J}}{\phi }_i^{ϵ}{\parallel }_{H^r\left(\mathbb{R}\right)}\le C_i{2}^{s-r}{\left(\ln \frac{M}{\delta }{\left(\ln \frac{M}{\delta }\right)}^{-(s-r)}\right)}^{-(s-r)}M,$(13) where $C_i$ for i = 2, 3, 4 are positive constants.

Proof.

Similarly, it is enough to prove the inequality (12(12) $\parallel {\mathcal{G}}_x^1{\phi }_1-{\mathcal{G}}_x^1{P}_{\tilde{J}}{\phi }_1^{ϵ}{\parallel }_{H^r\left(\mathbb{R}\right)}\le {\delta }^{\frac{1}{4}(1-x)}{M}^x{\left(\ln \frac{M}{\delta }\right)}^{-x(s-r)},$(12) ). According to $\tilde{J}$, one gets ${\log }_2\left(\ln \left(\frac{M}{\delta }{\left(\ln \frac{M}{\delta }\right)}^{-(s-r)}\right)\right)-1<\tilde{J}\le {\log }_2\left(\ln \left(\frac{M}{\delta }{\left(\ln \frac{M}{\delta }\right)}^{-(s-r)}\right)\right).$ We have $\begin{array}{rl}& 2^{\tilde{J}}\le \ln \left(\frac{M}{\delta }{\left(\ln \frac{M}{\delta }\right)}^{-(s-r)}\right),\\ & e^{2^{\tilde{J}}x}\le {\delta }^{-x}{M}^x{\left(\ln \frac{M}{\delta }\right)}^{-x(s-r)},\\ & 2^{-\tilde{J}}\le 2{\left(\ln \left(\frac{M}{\delta }{\left(\ln \frac{M}{\delta }\right)}^{-(s-r)}\right)\right)}^{-1},\\ & e^{-2^{\tilde{J}}}\le {\delta }^{\frac{1}{2}}{M}^{-\frac{1}{2}}{\left(\ln \frac{M}{\delta }\right)}^{\frac{(s-r)}{2}},\\ & e^{-(1-x)2^{\tilde{J}}}={\delta }^{\frac{1}{2}(1-x)}{M}^{-\frac{1}{2}(1-x)}{\left(\ln \frac{M}{\delta }\right)}^{\frac{(1-x)(s-r)}{2}}.\end{array}$ Substituting these results in the first inequality of (11(11) $\begin{array}{rl}\parallel {\mathcal{G}}_x^1({\phi }_1-P_J{\phi }_1^{ϵ}){\parallel }_{H^r\left(\mathbb{R}\right)}& \le 2C{e}^{2^{J}x}\delta +4(2^{J}C+1)e^{-(1-x)2^J}{2}^{-J(s-r)}M\\ & +24e^{-2^J}{2}^{-J(s-r)}M+6\delta ,\\ \parallel {\mathcal{G}}_x^2({\phi }_2-P_J{\phi }_2^{ϵ}){\parallel }_{H^r\left(\mathbb{R}\right)}& \le C{e}^{2^{J}x}\delta +C{e}^{-(1-x)2^J}{2}^{-J(s-r)}M+28e^{-2^J}{2}^{-J(s-r)}M\\ & +D{2}^{-J(s-r)}M+7\delta ,\\ \parallel {\mathcal{G}}_x^3({\phi }_3-P_J{\phi }_3^{ϵ}){\parallel }_{H^r\left(\mathbb{R}\right)}& \le \frac{1}{8}C{e}^{2^{J}x}\delta +\frac{1}{2}C{e}^{-(1-x)2^J}{2}^{-J(s-r)}\\ & +8e^{-2^J}{2}^{-J(s-r)}M+E{e}^{-J(s-r)}M+2\delta ,\\ \parallel {\mathcal{G}}_x^4({\phi }_4-P_J{\phi }_4^{ϵ}){\parallel }_{H^r\left(\mathbb{R}\right)}& \le \frac{5}{16}C{e}^{2^{J}x}\delta +\frac{5}{4}C{e}^{-(1-x)2^J}{2}^{-J(s-r)}M\\ & +20e^{-2^J}{2}^{-J(s-r)}M+F{2}^{-J(s-r)}M+5\delta ,\end{array}$(11) ), we get $\begin{array}{rl}\parallel {\mathcal{G}}_x^1({\phi }_1-P_{\tilde{J}}{\phi }_1^{ϵ}){\parallel }_{H^r\left(\mathbb{R}\right)}& \le 2C{\delta }^{1-x}{M}^x{\left(\ln \frac{M}{\delta }\right)}^{-x(s-r)}\\ & +4\left(C\ln \left(\frac{M}{\delta }{\left(\ln \frac{M}{\delta }\right)}^{-(s-r)}\right)+1\right){\delta }^{\frac{1}{2}(1-x)}{M}^{-\frac{1}{2}(1-x)}\\ & \times {\left(\ln \frac{M}{\delta }\right)}^{\frac{(1-x)(s-r)}{2}}\times 2^{(s-r)}{\left(\ln \left(\frac{M}{\delta }{\left(\ln \frac{M}{\delta }\right)}^{-(s-r)}\right)\right)}^{-(s-r)}\\ & +24{\delta }^{\frac{1}{2}}{M}^{-\frac{1}{2}}{\left(\ln \frac{M}{\delta }\right)}^{\frac{(s-r)}{2}}\\ & \times 2^{(s-r)}{\left(\ln \left(\frac{M}{\delta }{\left(\ln \frac{M}{\delta }\right)}^{-(s-r)}\right)\right)}^{-(s-r)}M+6\delta \\ & \le {\delta }^{\frac{1}{4}(1-x)}{M}^x{\left(\ln \frac{M}{\delta }\right)}^{-x(s-r)}.\end{array}$

3.3. Fourier regularization method

As shown in Section 2, small perturbation on high frequency components is the main reason of ill-posedness. So the idea of the Fourier regularization method is to cut off the high frequencies in the Fourier space. Therefore, the Fourier regularized solution of problem (5(5) $\begin{array}{rl}\hat{u}(x,\omega )& =c_1\cosh x\sqrt{|\omega {|}^2+1}+c_2\sinh x\sqrt{|\omega {|}^2+1}\\ & +c_{3}x\cosh x\sqrt{|\omega {|}^2+1}+c_{4}x\sinh x\sqrt{|\omega {|}^2+1}\\ c_1& ={\hat{\phi }}_1\left(\omega \right),\\ c_2& =\frac{3}{2\sqrt{|\omega {|}^2+1}}{\hat{\phi }}_2\left(\omega \right)-\frac{1}{2(|\omega {|}^2+1{)}^{\frac{3}{2}}}{\hat{\phi }}_4\left(\omega \right),\\ c_3& =-\frac{1}{2}{\hat{\phi }}_2\left(\omega \right)+\frac{1}{2(|\omega {|}^2+1)}{\hat{\phi }}_4\left(\omega \right),\\ c_4& =-\frac{1}{2}\sqrt{|\omega {|}^2+1}{\hat{\phi }}_1\left(\omega \right)+\frac{1}{2\sqrt{|\omega {|}^2+1}}{\hat{\phi }}_3\left(\omega \right),\end{array}$(5) ) is defined as (14) $u^{ϵ,\tau }(x,y):=\frac{1}{\sqrt{2\pi }}{\int }_{\mathbb{R}}{\hat{u}}^{ϵ}(x,\omega ){\chi }_{\tau }{\mathrm{e}}^{i\omega x}\mathrm{d}\omega ,$(14) where parameter $\tau$ has to be determined appropriately and ${\chi }_{\tau }$ is the characteristic function of interval $[-\tau ,\tau ]$. The following theorem proposes a suitable choice of $\tau$ and presents the corresponding error bounds of the Fourier regularized approximate solution which guarantees the convergence of the method.

Theorem 3.6

For $i=1,2,3,4,$ and some $s\ge 0,$ suppose $\parallel {\phi }_i-{\phi }_i^{ϵ}\parallel \le \delta$ and $\parallel u_i(1,\cdot ){\parallel }_{H^s\left(\mathbb{R}\right)}\le M,$ where $M$ is a positive constant. Choosing $\tau :=\left(\right(\ln \frac{M}{\delta }(\ln \frac{M}{\delta }{)}^{-s/2}{)}^2-1{)}^{\frac{1}{2}},$ the following error estimates hold (15) $\parallel u_i(x,\cdot )-u_i^{ϵ,\tau }(x,\cdot )\parallel \le C{M}^x{\delta }^{1-x}{\left(\ln \frac{M}{\delta }\right)}^{\frac{s(1-x)}{2}},i=1,2,3,4,$(15) where $C$ is a positive constant.

Proof.

Due to the similarity between the proofs for different $i$, we prove the theorem for $i=1$. Using (5(5) $\begin{array}{rl}\hat{u}(x,\omega )& =c_1\cosh x\sqrt{|\omega {|}^2+1}+c_2\sinh x\sqrt{|\omega {|}^2+1}\\ & +c_{3}x\cosh x\sqrt{|\omega {|}^2+1}+c_{4}x\sinh x\sqrt{|\omega {|}^2+1}\\ c_1& ={\hat{\phi }}_1\left(\omega \right),\\ c_2& =\frac{3}{2\sqrt{|\omega {|}^2+1}}{\hat{\phi }}_2\left(\omega \right)-\frac{1}{2(|\omega {|}^2+1{)}^{\frac{3}{2}}}{\hat{\phi }}_4\left(\omega \right),\\ c_3& =-\frac{1}{2}{\hat{\phi }}_2\left(\omega \right)+\frac{1}{2(|\omega {|}^2+1)}{\hat{\phi }}_4\left(\omega \right),\\ c_4& =-\frac{1}{2}\sqrt{|\omega {|}^2+1}{\hat{\phi }}_1\left(\omega \right)+\frac{1}{2\sqrt{|\omega {|}^2+1}}{\hat{\phi }}_3\left(\omega \right),\end{array}$(5) ) and (14(14) $u^{ϵ,\tau }(x,y):=\frac{1}{\sqrt{2\pi }}{\int }_{\mathbb{R}}{\hat{u}}^{ϵ}(x,\omega ){\chi }_{\tau }{\mathrm{e}}^{i\omega x}\mathrm{d}\omega ,$(14) ), we have $u_1^{ϵ,\tau }(x,y):=\frac{1}{\sqrt{2\pi }}{\int }_{\mathbb{R}}\mathcal{T}(x,\omega ){\hat{\phi }}_1^{ϵ}(x,\omega ){\chi }_{\tau }{\mathrm{e}}^{i\omega x}\mathrm{d}\omega .$ Exploiting the Parseval relation, we get $\begin{array}{rl}\parallel u_1(x,\cdot )-u_1^{ϵ,\tau }(x,\cdot )\parallel & =\parallel \mathcal{T}(x,\cdot ){\hat{\phi }}_1(\cdot )-\mathcal{T}(x,\cdot ){\hat{\phi }}_1^{ϵ}(\cdot ){\chi }_{\tau }(\cdot )\parallel \\ & \le \parallel \mathcal{T}(x,\cdot ){\hat{\phi }}_1(\cdot )-\mathcal{T}(x,\cdot ){\hat{\phi }}_1(\cdot ){\chi }_{\tau }(\cdot )\parallel \\ & +\parallel \mathcal{T}(x,\cdot ){\hat{\phi }}_1(\cdot ){\chi }_{\tau }(\cdot )-\mathcal{T}(x,\cdot ){\hat{\phi }}_1^{ϵ}(\cdot ){\chi }_{\tau }(\cdot )\parallel \\ & ={\left({\int }_{|\omega |>\tau }|\mathcal{T}(x,\omega ){\hat{\phi }}_1\left(\omega \right){|}^2\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & +{\left({\int }_{|\omega |\le \tau }|\mathcal{T}(x,\omega )\left({\hat{\phi }}_1\right(\omega )-{\hat{\phi }}_1^{ϵ}(\omega \left)\right){|}^2\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & ={\left({\int }_{|\omega |>\tau }{\left|\frac{\mathcal{T}(x,\omega )}{\mathcal{T}(1,\omega )(1+|\omega {|}^2{)}^s}{\hat{u}}_1(1,\omega )(1+|\omega {|}^2{)}^s\right|}^2\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & +{\left({\int }_{|\omega |\le \tau }|\mathcal{T}(x,\omega )\left({\hat{\phi }}_1\right(\omega )-{\hat{\phi }}_1^{ϵ}(\omega \left)\right){|}^2\mathrm{d}\omega \right)}^{\frac{1}{2}}\\ & \le \underset{|\omega |>\tau }{sup}\left|\frac{\mathcal{T}(x,\omega )}{\mathcal{T}(1,\omega )(1+|\omega {|}^2{)}^s}\right|\parallel {\hat{u}}_1(1,\omega ){\parallel }_{H^s\left(\mathbb{R}\right)}\\ & +\underset{|\omega |\le \tau }{sup}|\mathcal{T}(x,\omega )|\parallel {\hat{\phi }}_1-{\hat{\phi }}_1^{ϵ}\parallel \\ & \le \underset{|\omega |>\tau }{sup}4{\mathrm{e}}^{-(1-x)\sqrt{|\omega {|}^2+1}}M+\underset{|\omega |\le \tau }{sup}2x\sqrt{|\omega {|}^2+1}{\mathrm{e}}^{x\sqrt{|\omega {|}^2+1}}\delta \\ & =4M^x{\delta }^{1-x}{\left(\ln \frac{M}{\delta }\right)}^{\frac{s(1-x)}{2}}\\ & +2x\ln \left(\frac{M}{\delta }{\left(\ln \frac{M}{\delta }\right)}^{-\frac{s}{2}}\right){\delta }^{(1-x)}{M}^x{\left(\ln \frac{M}{\delta }\right)}^{-\frac{sx}{2}}\\ & =C{M}^x{\delta }^{1-x}{\left(\ln \frac{M}{\delta }\right)}^{\frac{s(1-x)}{2}}.\end{array}$

4. Numerical algorithms based on FFT

Regarding the effectiveness of the proposed regularization methods in Section 3, the numerical algorithms are given in detail by using the spectral methods based on FFT [33]. Because the solution of problem (3(3) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^4}+2\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^2\mathrm{\partial }{y}^2}+\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{y}^4}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}+u=0,(x,y)\in (0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}={\phi }_j\left(y\right),j=1,2,3,4,y\in \mathbb{R}.\end{array}$(3) ) is a periodic function or tends to zero, we solve the problem in the finite domain $(0,1)\times (a,b)$, for appropriate a and b. With a fixed $x\in (0,1)$, the interval $(a,b)$ is splitted to $N$ subintervals with step length $h=\frac{b-a}{N}$. In problem (3(3) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^4}+2\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{x}^2\mathrm{\partial }{y}^2}+\frac{{\mathrm{\partial }}^{4}u}{\mathrm{\partial }{y}^4}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}-2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}+u=0,(x,y)\in (0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}={\phi }_j\left(y\right),j=1,2,3,4,y\in \mathbb{R}.\end{array}$(3) ), input data ${\phi }_i,i=1,2,3,4$ are measured by ${\phi }_i^{ϵ}$ and the corresponding solutions are denoted by $u_i^{ϵ}$, respectively. We note that the variable $\omega$ in the frequency space has to be considered as a vector in the discrete case.

4.1. Discrete Fourier representations for partial derivatives

Discrete Fourier transform is a suitable approach to compute the approximate solution of problem (5(5) $\begin{array}{rl}\hat{u}(x,\omega )& =c_1\cosh x\sqrt{|\omega {|}^2+1}+c_2\sinh x\sqrt{|\omega {|}^2+1}\\ & +c_{3}x\cosh x\sqrt{|\omega {|}^2+1}+c_{4}x\sinh x\sqrt{|\omega {|}^2+1}\\ c_1& ={\hat{\phi }}_1\left(\omega \right),\\ c_2& =\frac{3}{2\sqrt{|\omega {|}^2+1}}{\hat{\phi }}_2\left(\omega \right)-\frac{1}{2(|\omega {|}^2+1{)}^{\frac{3}{2}}}{\hat{\phi }}_4\left(\omega \right),\\ c_3& =-\frac{1}{2}{\hat{\phi }}_2\left(\omega \right)+\frac{1}{2(|\omega {|}^2+1)}{\hat{\phi }}_4\left(\omega \right),\\ c_4& =-\frac{1}{2}\sqrt{|\omega {|}^2+1}{\hat{\phi }}_1\left(\omega \right)+\frac{1}{2\sqrt{|\omega {|}^2+1}}{\hat{\phi }}_3\left(\omega \right),\end{array}$(5) ) (for more detail, see [33]). Without loss of generality, we consider solution $u$ over the domain $(0,1)\times (0,L)$. Suppose that $u_{m,n}=u(x_m,y_n)$, as $N$ discrete samples of this solution for a fixed $x_m\in (0,1)$, and $y_n=\frac{nL}{N},n=0,\dots ,N-1$, are approximated by the following discrete fourier representation (16) $u_{m,n}:=u(x_m,y_n)\simeq \sum _{k=0}^{N-1}{U}_{m,k}{\mathrm{e}}^{+\frac{2\pi i}{N}nk},$(16) where Fourier coefficients $U_{m,k},k=0,1,\dots ,N-1$ are obtained as follows $U_{m,k}=\frac{1}{N}\sum _{n=0}^{N-1}{u}_{m,n}{\mathrm{e}}^{-\frac{2\pi i}{N}nk}.$ It is worth mentioning that all Fourier coefficients $U_{m,k}$ can be computed from $u_{m,n}$, or vice versa, in $O(N\log N)$ operations by the FFT algorithm. It is easy to observe that each term $U_{m,k}{\mathrm{e}}^{\frac{2\pi i}{N}nk}$ in (16(16) $u_{m,n}:=u(x_m,y_n)\simeq \sum _{k=0}^{N-1}{U}_{m,k}{\mathrm{e}}^{+\frac{2\pi i}{N}nk},$(16) ) can be replaced by $U_{m,k}{\mathrm{e}}^{\frac{2\pi i}{N}n(k+lN)}$ for any integer l. Therefore, formula (16(16) $u_{m,n}:=u(x_m,y_n)\simeq \sum _{k=0}^{N-1}{U}_{m,k}{\mathrm{e}}^{+\frac{2\pi i}{N}nk},$(16) ) can be reformulated as $u_{m,n}\simeq U_{m,0}+\sum _{0<k<N/2}(U_{m,k}{\mathrm{e}}^{+\frac{2\pi i}{L}k{y}_n}+U_{m,N-k}{\mathrm{e}}^{-\frac{2\pi i}{L}k{y}_n})+U_{m,N/2}\cos \left(\frac{\pi }{L}N{y}_n\right).$ The approximate formulae for the first and second derivatives of $u$ with respect to $y$ at $(x_m,y_n)$ are given as follows $\begin{array}{rl}(u_y{)}_{m,n}& \simeq \sum _{k=1}^{\frac{N}{2}-1}\frac{2\pi i}{L}k(U_{m,k}{\mathrm{e}}^{+\frac{2\pi i}{N}nk}+U_{m,N-k}{\mathrm{e}}^{-\frac{2\pi i}{N}nk})=:\sum _{k=0}^{N-1}(U_y{)}_{m,k}{\mathrm{e}}^{\frac{2\pi i}{N}nk},\\ (u_{yy}{)}_{m,n}& \simeq -\sum _{k=1}^{\frac{N}{2}-1}{\left(\frac{2\pi }{L}k\right)}^2(U_{m,k}{\mathrm{e}}^{+\frac{2\pi i}{N}nk}+U_{m,N-k}{\mathrm{e}}^{-\frac{2\pi i}{N}nk})-{\left(\frac{\pi }{L}N\right)}^2{U}_{\frac{N}{2}}(-1{)}^n\\ & =:\sum _{k=0}^{N-1}(U_{yy}{)}_{m,k}{\mathrm{e}}^{\frac{2\pi i}{N}nk}.\end{array}$

4.2. Wavelet regularization algorithm

In this part, we summarize the wavelet regularization method for the bi-Helmholtz equation with Cauchy conditions in Algorithm 4.1. First, we simulate noisy vectors ${\mathrm{\Phi }}_i^{ϵ}$ from given functions ${\phi }_i,i=1,2,3,4,$ with the error bound ε. Getting ${\mathrm{\Phi }}_i^{ϵ}$, we discretize functions ${\phi }_i$ to obtain vector ${\mathrm{\Phi }}_i$ and add a different random real number of interval $[-ϵ,ϵ]$ to each component of ${\mathrm{\Phi }}_i$. The value $\delta$ can be calculated by the following discrete norm (17) $\delta =\parallel {\mathrm{\Phi }}_i-{\mathrm{\Phi }}_i^{ϵ}\parallel :=\frac{1}{N}\sqrt{\sum _{k=0}^{N-1}\left(\right({\mathrm{\Phi }}_i{)}_k-({\mathrm{\Phi }}_i^{ϵ}{)}_k{)}^2}.$(17)

We design the detail of the wavelet regularization algorithm in the following.

4.3. Fourier regularization algorithm

We provide detail of the Fourier regularization method in Algorithm 4.2. In this algorithm, $\mathcal{N}$ is the parameter of the Fourier regularization method in the discrete form. By the choice of small $\mathcal{N}$, some necessary details of the solution will be missed. For large $\mathcal{N}$, the method will not be able to remove the high frequencies. The suitable approach for determining $\mathcal{N}$ is to apply Theorem 3.6.

Remark 4.1

Regarding to $\tau =\left(\right(\ln \frac{M}{\delta }(\ln \frac{M}{\delta }{)}^{-s/2}{)}^2-1{)}^{\frac{1}{2}}$ in Theorem 3.6, it can be shown that (18) $\mathcal{N}:=\left[\frac{L}{2\pi }{\left({\left(\ln \frac{M}{\delta }{\left(\ln \frac{M}{\delta }\right)}^{-s/2}\right)}^2-1\right)}^{\frac{1}{2}}\right],$(18) where $L=b-a$.

5. Numerical experiments

As observed, applying the Fourier transform to problem (1(1) $\begin{array}{rl}& {\gamma }^4{\mathrm{\Delta }}^{2}u(x,\mathbf{y})-{\eta }^2\mathrm{\Delta }u(x,\mathbf{y})+u(x,\mathbf{y})=0,(x,\mathbf{y})\in (0,1)\times {\mathbb{R}}^n,\\ & \frac{{\mathrm{\partial }}^{j}u(0,\mathbf{y})}{\mathrm{\partial }{x}^j}={\phi }_j\left(\mathbf{y}\right),j=1,2,3,4,\mathbf{y}\in {\mathbb{R}}^n,\end{array}$(1) ) with perturbed data leads to the ill-posedness. This ill-posedness causes the standard numerical methods not to be able to approximate the exact solution properly. Therefore, application of an appropriate regularization method that matches to the transformed problem is needed. In this section, Fourier and wavelet regularization methods are exploited to the various ill-posed problems that stemmed from Cauchy conditions. To approximate the perturbed given functions in the original problem, we set $\hat{J}:=max\{\tilde{J},4\}$ such that $\hat{J}\le {\log }_{2}N.$ In numerical examples, we suppose that $s-r=1$ unless we emphasize on some numbers. In Theorem 3.5, we set $C_i=1$, for i = 2, 3, 4. Also, we will consider $n=1$ for all examples.

Example 5.1

We consider the following Cauchy problems (19) $\begin{array}{r}\left\{\begin{array}{ll}{\mathrm{\Delta }}^{2}u-2\mathrm{\Delta }u+u=0,& \mathrm{i}\mathrm{n}(0,1)\times \mathbb{R},\\ u(0,y)={\mathrm{e}}^{-y^2}\cos 3y,& y\in \mathbb{R},\\ \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}=0,j=1,2,3,& y\in \mathbb{R},\end{array}\right.\end{array}$(19) (20) $\begin{array}{r}\left\{\begin{array}{ll}{\mathrm{\Delta }}^{2}u-2\mathrm{\Delta }u+u=0,& \mathrm{i}\mathrm{n}(0,1)\times \mathbb{R},\\ u(0,y)=0,& y\in \mathbb{R},\\ \frac{\mathrm{\partial }u(0,y)}{\mathrm{\partial }x}={\mathrm{e}}^{-y^2}\cos 3y,& y\in \mathbb{R},\\ \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}=0,j=2,3,& y\in \mathbb{R}.\end{array}\right.\end{array}$(20) Algorithm 4.1 is applied to problems (19(19) $\begin{array}{r}\left\{\begin{array}{ll}{\mathrm{\Delta }}^{2}u-2\mathrm{\Delta }u+u=0,& \mathrm{i}\mathrm{n}(0,1)\times \mathbb{R},\\ u(0,y)={\mathrm{e}}^{-y^2}\cos 3y,& y\in \mathbb{R},\\ \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}=0,j=1,2,3,& y\in \mathbb{R},\end{array}\right.\end{array}$(19) ) and (20(20) $\begin{array}{r}\left\{\begin{array}{ll}{\mathrm{\Delta }}^{2}u-2\mathrm{\Delta }u+u=0,& \mathrm{i}\mathrm{n}(0,1)\times \mathbb{R},\\ u(0,y)=0,& y\in \mathbb{R},\\ \frac{\mathrm{\partial }u(0,y)}{\mathrm{\partial }x}={\mathrm{e}}^{-y^2}\cos 3y,& y\in \mathbb{R},\\ \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}=0,j=2,3,& y\in \mathbb{R}.\end{array}\right.\end{array}$(20) ) by setting $a=-2\pi ,b=2\pi ,N=32,$ and $\hat{J}=4,5$. Results of the applied Meyer wavelet regularization algorithm to problems (19(19) $\begin{array}{r}\left\{\begin{array}{ll}{\mathrm{\Delta }}^{2}u-2\mathrm{\Delta }u+u=0,& \mathrm{i}\mathrm{n}(0,1)\times \mathbb{R},\\ u(0,y)={\mathrm{e}}^{-y^2}\cos 3y,& y\in \mathbb{R},\\ \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}=0,j=1,2,3,& y\in \mathbb{R},\end{array}\right.\end{array}$(19) ) and (20(20) $\begin{array}{r}\left\{\begin{array}{ll}{\mathrm{\Delta }}^{2}u-2\mathrm{\Delta }u+u=0,& \mathrm{i}\mathrm{n}(0,1)\times \mathbb{R},\\ u(0,y)=0,& y\in \mathbb{R},\\ \frac{\mathrm{\partial }u(0,y)}{\mathrm{\partial }x}={\mathrm{e}}^{-y^2}\cos 3y,& y\in \mathbb{R},\\ \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}=0,j=2,3,& y\in \mathbb{R}.\end{array}\right.\end{array}$(20) ) for various values of x are reported in Table 1 and Table 2, respectively. The notation $u^{ϵ,W}$ is used for the wavelet regularization solution with noisy data given in these problems. Thanks to the wavelet regularization method, we conclude that the regularized solution is stabilized when $x$ tends to 1.

Table 1. The corresponding errors of wavelet regularized solution $u^{ϵ,W}$ of problem (19(19) $\begin{array}{r}\left\{\begin{array}{ll}{\mathrm{\Delta }}^{2}u-2\mathrm{\Delta }u+u=0,& \mathrm{i}\mathrm{n}(0,1)\times \mathbb{R},\\ u(0,y)={\mathrm{e}}^{-y^2}\cos 3y,& y\in \mathbb{R},\\ \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}=0,j=1,2,3,& y\in \mathbb{R},\end{array}\right.\end{array}$(19) ) for various values of $x$ and $ϵ$.

$x$	$ϵ$	$\delta$	$\hat{J}$	$\parallel u-u^{ϵ,W}{\parallel }_2$
$x$thinsp;= 0.5	1E−1	2.0480E−2	4	2.6495E−2
	1E−5	1.6908E−6	4	1.0492E−2
	1E−15	1.7408E−16	5	5.6018E−4
$x$ = 0.7	1E−1	1.4270E−2	4	3.7860E−2
	1E−5	1.5322E−6	4	3.3792E−2
	1E−15	1.7580E−16	5	6.7418E−3
$x$ = 0.9	1E−1	1.8868E−2	4	3.1046E−1
	1E−5	1.9293E−6	4	2.1362E−1
	1E−15	1.8336E−16	5	4.8179E−2

Table 2. The corresponding errors of wavelet regularized solution $u^{ϵ,W}$ of problem (20(20) $\begin{array}{r}\left\{\begin{array}{ll}{\mathrm{\Delta }}^{2}u-2\mathrm{\Delta }u+u=0,& \mathrm{i}\mathrm{n}(0,1)\times \mathbb{R},\\ u(0,y)=0,& y\in \mathbb{R},\\ \frac{\mathrm{\partial }u(0,y)}{\mathrm{\partial }x}={\mathrm{e}}^{-y^2}\cos 3y,& y\in \mathbb{R},\\ \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}=0,j=2,3,& y\in \mathbb{R}.\end{array}\right.\end{array}$(20) ) for various values of $x$ and $ϵ$.

x	ε	δ	$\hat{J}$	$\parallel u-u^{ϵ,W}{\parallel }_2$
x = 0.5	1E−1	1.6078E−2	4	1.8078E−2
	1E−5	1.9993E−6	4	6.0924E−3
	1E−15	1.4811E−16	5	1.7472E−4
x = 0.7	1E−1	1.57497E−2	4	2.4284E−2
	1E−5	1.7295E−6	4	7.5344E−3
	1E−15	1.6946E−16	5	4.4322E−4
x = 0.9	1E−1	1.3650E−2	4	4.3072E−1
	1E−5	1.9062E−6	4	2.1852E−2
	1E−15	1.5772E−16	5	4.6769E−3

Example 5.2

In this example, we compare the effects of the Meyer, Shannon, and Daubechies wavelets on the following Cauchy problem (21) $\begin{array}{rl}& {10}^3{\mathrm{\Delta }}^{2}u-\mathrm{\Delta }u+u=0,\mathrm{i}\mathrm{n}(0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}={\phi }_j\left(y\right),j=1,2,3,4,y\in \mathbb{R}.\end{array}$(21) By applying the wavelet regularization Algorithm 4.2, we investigate numerically the effectiveness of these wavelets for problem (21(21) $\begin{array}{rl}& {10}^3{\mathrm{\Delta }}^{2}u-\mathrm{\Delta }u+u=0,\mathrm{i}\mathrm{n}(0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}={\phi }_j\left(y\right),j=1,2,3,4,y\in \mathbb{R}.\end{array}$(21) ) with the following cases $\begin{array}{rl}\mathrm{C}\mathrm{a}\mathrm{s}\mathrm{e}1& :{\phi }_1\left(y\right)={\phi }_2\left(y\right)={\mathrm{e}}^{-y^2}\cos \left(3y\right),{\phi }_3\left(y\right)={\phi }_4\left(y\right)=\sin \left(y\right),\\ & a=-\pi ,b=\pi ,N=32,\hat{J}=4,\\ \mathrm{C}\mathrm{a}\mathrm{s}\mathrm{e}2& :{\phi }_1\left(y\right)={\phi }_3\left(y\right)=\sin \left(y\right),{\phi }_2\left(y\right)={\phi }_4\left(y\right)=\cos \left(y\right),\\ & a=-2\pi ,b=2\pi ,N=32,\hat{J}=4.\end{array}$ The results of the Meyer, Shannon, and Daubechies wavelets are reported for Case 1 and Case 2 in Figure 2 and Figure 3 at x = 0.8 and for various values of ε. From Figure 2 and Figure 3, it is found out that the wavelet regularization method with the Meyer and Shannon wavelets produce better results than the wavelet regularization method with Daubechies wavelet. Although Shannon wavelet is not analytic in the whole of the frequency domain, it can overcome the ill-posedness of Cauchy problems given in this example.

Figure 2. Case 1 of Example 5.2. Plots of the wavelet regularized solutions for $ϵ=0.05,0.0005$ at left and middle, respectively. Right: plot of absolute errors versus $1/ϵ$ at $x$ = 0.8.

Figure 3. Case 2 of Example 5.2. Plots of wavelet regularized solutions for $ϵ=0.05,0.0005$ at left and middle, respectively. Right: plot of absolute errors versus $1/ϵ$ at $x$ = 0.8.

Example 5.3

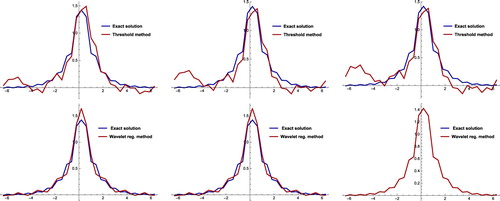
We want to compare the wavelet regularization and wavelet thresholding methods. It is also worth pointing out that the wavelet thresholding method is applied exceedingly to signal denoising and image processing (see e.g. [35–38]) and also the ill-posed problem [34]. In fact, the wavelet regularization method is used without applying any thresholding method. We consider the following problem (22) $\begin{array}{rl}& {\mathrm{\Delta }}^{2}u-2\mathrm{\Delta }u+u=0,\mathrm{i}\mathrm{n}(0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}={\mathrm{e}}^{-|y|},j=0,1,2,3,y\in \mathbb{R}.\end{array}$(22) In Algorithm 4.1, we set $a=-2\pi ,b=2\pi ,N=32,\mathrm{a}\mathrm{n}\mathrm{d}\hat{J}=4$. Figure 4 shows that the solution of problem (22(22) $\begin{array}{rl}& {\mathrm{\Delta }}^{2}u-2\mathrm{\Delta }u+u=0,\mathrm{i}\mathrm{n}(0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}={\mathrm{e}}^{-|y|},j=0,1,2,3,y\in \mathbb{R}.\end{array}$(22) ), obtained by the wavelet regularization method, tends to exact solution as $ϵ$ decreases to zero while the solution of problem (22(22) $\begin{array}{rl}& {\mathrm{\Delta }}^{2}u-2\mathrm{\Delta }u+u=0,\mathrm{i}\mathrm{n}(0,1)\times \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}={\mathrm{e}}^{-|y|},j=0,1,2,3,y\in \mathbb{R}.\end{array}$(22) ), obtained by the thresholding method, does not converge to the exact solution as $ϵ\to 0$.

Figure 4. First row: plots of threshold regularized solutions for Example 5.3 at $x$ = 0.5 for $ϵ={10}^{-5},{10}^{-10},{10}^{-15}$ from left to right, respectively, with $N$ = 32. Second row: plots of the corresponding wavelet regularized solutions of first row by using Shannon wavelet.

Example 5.4

In this example, we use the Fourier regularization method and Algorithm 4.2 for solving the following Cauchy problem (23) $\begin{array}{rl}& {\mathrm{\Delta }}^{2}u-2\mathrm{\Delta }u+u=0,\mathrm{i}\mathrm{n}(0,1)\times \mathbb{R},\\ & u(0,y)={\mathrm{e}}^{-y^2},y\in \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}=0,j=1,2,3,y\in \mathbb{R},\end{array}$(23) In Algorithm 4.2, we set $a=-2\pi ,b=2\pi ,N=128,\mathrm{a}\mathrm{n}\mathrm{d}\mathcal{N}=9,13,18$. The results of the Fourier regularization method for various values of $x$ and $s$ = 1 are reported in Table 3. In this table, the notation $u^{ϵ,F}$ is used for the Fourier regularized solution of the Cauchy problem (23(23) $\begin{array}{rl}& {\mathrm{\Delta }}^{2}u-2\mathrm{\Delta }u+u=0,\mathrm{i}\mathrm{n}(0,1)\times \mathbb{R},\\ & u(0,y)={\mathrm{e}}^{-y^2},y\in \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}=0,j=1,2,3,y\in \mathbb{R},\end{array}$(23) ). Thanks to the Fourier regularization method, we conclude (see second row of Figure 5) that the regularized solution is stabilized when $x$ tends to 1.

Figure 5. First row: plots of exact solutions of problem (23(23) $\begin{array}{rl}& {\mathrm{\Delta }}^{2}u-2\mathrm{\Delta }u+u=0,\mathrm{i}\mathrm{n}(0,1)\times \mathbb{R},\\ & u(0,y)={\mathrm{e}}^{-y^2},y\in \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}=0,j=1,2,3,y\in \mathbb{R},\end{array}$(23) ) in Example 5.4 with / without noisy data at $x$ = 0.8 for $ϵ=0.05,0.005,0.0005,$ from left to right, respectively, where $N$ = 128. Second row: plots of exact and Fourier regularized solutions of problem(23(23) $\begin{array}{rl}& {\mathrm{\Delta }}^{2}u-2\mathrm{\Delta }u+u=0,\mathrm{i}\mathrm{n}(0,1)\times \mathbb{R},\\ & u(0,y)={\mathrm{e}}^{-y^2},y\in \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}=0,j=1,2,3,y\in \mathbb{R},\end{array}$(23) ) in Example 5.4 with $\mathcal{N}=9,13,18$ at $x$ = 0.8 from left to right, respectively.

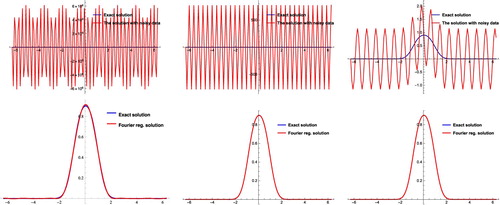
Table 3. The corresponding errors of Fourier regularized solution $u^{ϵ,F}$ of problem (23(23) $\begin{array}{rl}& {\mathrm{\Delta }}^{2}u-2\mathrm{\Delta }u+u=0,\mathrm{i}\mathrm{n}(0,1)\times \mathbb{R},\\ & u(0,y)={\mathrm{e}}^{-y^2},y\in \mathbb{R},\\ & \frac{{\mathrm{\partial }}^{j}u(0,y)}{\mathrm{\partial }{x}^j}=0,j=1,2,3,y\in \mathbb{R},\end{array}$(23) ) in Example 5.4 for s = 1 and various values of x and ε.

x	ε	δ	$M_{max}$	$\parallel u-u^{ϵ,F}{\parallel }_2$
x = 0.5	5E−2	3.1250E−3	9	1.2903E−4
	5E−3	3.1250E−4	13	7.4511E−7
	5E−4	3.1250E−5	18	1.3292E−9
x = 0.7	5E−2	3.1250E−3	9	1.2480E−4
	5E−3	3.1250E−4	13	1.1524E−5
	5E−4	3.1250E−5	18	4.1378E−7
x = 0.9	5E−2	3.1250E−3	9	2.0536E−3
	5E−3	3.1250E−4	13	1.8255E−3
	5E−4	3.1250E−5	18	1.8241E−3

6. Conclusion

In this paper, a Cauchy problem of the bi-Helmholtz equation has been studied. It has been shown that this problem may be ill-posed. This situation means that the solution does not depend continuously on the given data. We have figured out that the usage of the regularization technique is mandatory. Among the various regularization methods, wavelet and Fourier regularization methods have been selected. The bi-Helmholtz equation has been transformed to the Fourier domain and explicit expressions of the Fourier transformations of the Meyer wavelet and scaling functions are defined in this domain. Moreover, these functions are analytic in the Fourier domain. Based on these reasons, the wavelet which fits well to our analysis is the Meyer wavelet. By deriving some essential error estimates, we have shown that applying the Meyer wavelet leads to the stability of solutions. Numerical results indicate that Shannon wavelet regularization method is able to regularize the perturbed problem. The Meyer and Shannon wavelets have compact support in the frequency space as well as the Meyer wavelet. So this property of wavelets acts as a low-pass filter for high frequencies which are the source of ill-posedness. There are some restriction when we use wavelets as frequency filters. For instance at finer level of multiresolution and larger regularization parameter $\tilde{J}$, the support of wavelets in frequency space increase exponentially, therefore in practice they can not filter any frequencies. On the other hand, if we choose a small level of multiresolution, wavelets are not able to approximate measured data as much as possible. We suggest a formula for $\hat{J}$ instead of $\tilde{J}$ to reduce the restrictions. Also, error estimates of the Fourier regularization method show that this method is applicable as well as wavelet regularization methods. In this method, we transform measured data to frequency space and remove high frequencies. The parameter of regularization in Fourier method is the number of components that we choose as high frequencies. From the illustrated examples, wavelet and Fourier regularization methods are two valuable tools to reduce the effect of the ill-posedness as much as possible for solving the bi-Helmholtz equation with Cauchy conditions. We predict that wavelet and Fourier regularization methods can exploit to overcome the ill-posedness of the backward heat conduction problem with time-fractional derivative and a class of non-linear time-dependent partial differential equations. Due to the complexity of the Meyer wavelet method and the nature of the bi-Helmholtz equation, we have obtained the regularization parameter using an a-priori choice rule and we leave an a-posteriori choice rule to the future works.

Acknowledgments

The authors appreciate the reviewers for all valuable comments and suggestions, which helped us to improve the quality of the article.

Disclosure statement

No potential conflict of interest was reported by the author(s).