https://orcid.org/0000-0002-6685-9956
Abstract
In this article, we present the development of a workshop on mosaic constructions through isometric transformations in a STEAM perspective focusing on the integration of Mathematics and Art and the utilization of GeoGebra. As objectives, we seek to develop mathematical skills through the execution of artistic techniques and reflections on products and actions through GeoGebra commands. We wish to develop understanding of mathematics licensing isometry in proposals for remote activities in the Microsoft Teams platform, considering constructivist theory, in a way compatible with the perspective of learning of the Hypothetical Learning Trajectory (THA) developed in four phases: learning, planning, implementation and reflection. The generalization processes using the GeoGebra spreadsheet produced important information about its conceptualization, emerging application, and validation schemes. The results show that there was a positive attitude on the part of the participants for the development of new proposals in GeoGebra in the context of isometry.
1. Introduction
Geometry has many different approaches and is related to the development of Mathematics, in addition to involving numerous aspects of the cultural life of a people through visual and aesthetic senses. Learning and teaching geometry can allow teachers and students to engage with other areas of mathematics and find encouragement and motivation to improve.
Jones (Citation2002, p. 122) argues that: ‘Teaching geometry well involves knowing how to recognize interesting geometrical problems and theorems, appreciating the history and cultural context of geometry, and understanding the many and varied uses to which geometry is put’.
The author points out that:
The study of geometry contributes to helping students develop the skills of visualization, critical thinking, intuition, perspective, problem-solving, conjecturing, deductive reasoning, logical argument, and proof. Geometric representations can be used to help students make sense of other areas of mathematics: fractions and multiplication in arithmetic, the relationships between the graphs of functions (of both two and three variables), and graphical representations of data in statistics. Spatial reasoning is important in other curriculum areas as well as mathematics: science, geography, art, design, and technology. Working with practical equipment can also help develop fine motor skills. (Jones, Citation2002, p. 123)
The proposal, guidance and examples presented herein served as a starting point in the transition from formal to non-formal education and in adapting the teacher’s role as mediator and inspiration. In a non-formal environment, the participants, undergraduates in Mathematics, were co-responsible for the quality of the educational process, as learning could take place through interactions and collaborations.
Using digital technologies in the educational context allows the teachers greater flexibility to adapt their teaching strategies in favour of learning. However, the teachers will need to find the educator within themselves and become a mediator, recognizing these new resources as instruments of communication and representation of knowledge, which should serve to facilitate learning.
In a learning environment, the initial situation is what the student knows, what they are capable of, what they can do and what they want to learn. The educator’s challenge is to create an environment in which students can discover their potential, acquire autonomy, responsibility, discipline, respect for others and self-confidence. Good equipment and technological resources are not an effective learning environment – it is up to the teacher to use the educational technology that uses these resources, with the intention of favouring learning.
An environment that favours the learning of Mathematics content must also provide a collaborative context, encourage investigation and critical thinking, offer activities to stimulate a higher-level cognitive area, requiring reflection, analysis, synthesis and evaluation, in addition to increasing the student’s social skills and self-esteem.
It is important that the teachers, when identifying themselves as learning mediators, challenge the student to reflect on the meaning and understanding of the learning process, have theoretical assumptions that support their pedagogical techniques, because much of what is done in the classroom class can be explained by learning and psychology theories.
For each educational objective, there must be a good didactic choice in relation to the type of learning desired. It is reasonable to have some knowledge of the theories that underlie these choices.
The theoretical support that each teacher brings can be explicit, reflecting their conception of learning theories, or implicit, personal, non-formalized, the result of their vision of learning, but which directs their decisions and the design of their course.
2. Theoretical considerations
This study was developed considering the constructivist theory, compatible with the Hypothetical Learning Trajectory (HLT) learning perspective developed in four phases: learning, planning, implementation, and reflection.
2.1. Constructivism
Constructivism is a theory that explains how human intelligence develops and is based on the principle that knowledge is constructed by the individual as a result of his interactions with the environment, i.e. it is the result of reflections that the individual makes about their actions.
For constructivism, learning is a process by which the individual constructs knowledge. This means that they are active agents of their learning, which results in their own transformation; they do not transfer external knowledge to their memory but create interpretations of the world based on their previous experience and on their interrelationships with people based on new stimuli/information (Ferraz, Citation2008, p. 61).
Learning activities based on constructivism aim to build knowledge. The constructivist approach implies carrying out activities that stimulate cognitive activities that give meaning to the learning object and result from interaction and reflection.
A didactic situation in which the student is involved and can reflect on their experience favours the construction of their knowledge and understanding of the world. Each one builds their rules and mental models, according to their interaction with the elements of the didactic situation.
Creating a constructivist learning environment implies creating situations in which the student feels the need to know, can experience an experience and is encouraged to reflect on it. Knowledge results from action on the object.
Vygotsky studied the construction of knowledge as a social process, which involves negotiations between individuals, sharing meanings, in a socio-interactionist approach.
For Vygotsky, the subject is not only active, but interactive; it is in the exchange with other subjects and with themselves that knowledge, roles and social functions are internalized, which allows the formation of knowledge and consciousness itself. It is a process that moves from the social level – interpersonal relationships – to the internal individual level – intrapersonal relationships (Ferraz, Citation2008, p. 64).
According to Vygotsky, knowledge is constructed through the interaction between people and, mainly, the communication between them. Language (the linguistic system used for communication) is the main tool for organizing mental processes, first in collective activities and then in individual ones. Learning activities are effective when they can be used to activate development processes that become functional by internationalizing knowledge.
Seymour Papert (1928–2016) introduced the term constructionist to characterize constructivist environments in which the learner actually builds some product of interest, adding that the construction of knowledge structures occurs especially and properly in a context in which the learner is consciously engaged in building a meaningful product.
It consists in proposing situations to the participants that can be destabilizing and, with this, provoke an affective involvement and a feeling of empowerment, which results in achievement, self-confidence and motivation to learn more.
We consider that the teacher who engages in a constructivist environment must have mastered the content of their expertise, knowledge of learning theories, practical experience and, above all, be continuously in a state of learning.
2.2. Hypothetical learning trajectory
The design of a teaching-learning activity is a task that requires clarity from the teacher regarding the educational objectives and knowledge about the teaching-learning process.
In this aspect, we find in the Hypothetical Learning Trajectory a theoretical contribution to the construction of the proposed activity, prepared considering a learning goal present in the proposed tasks and a hypothetical processing of how learning will be achieved in the construction of knowledge in a constructivist perspective according to Vygotsky.
The authors in Simon and Tzur (Citation2004) consider that the selection of learning tasks and the hypotheses about the learning process are interdependent, i.e. they are based on each other and, underlying this construct, the following characteristics can be considered in an HLT:
The construction of an HLT is based on understanding the participants’ current knowledge.
An HLT is a vehicle for planning learning of particular mathematical concepts.
Mathematics Tasks provide tools to promote the learning of specific mathematical concepts and, therefore, are a fundamental part of the teaching process.
Because of the hypothetical and inherently uncertain nature of this process, the teacher will be required to systematically modify every aspect of the HLT. (Simon & Tzur, Citation2004, p. 93)
The teacher, by assuming what participants will do in the development of the activity, is intrinsically considering a learning hypothesis, which will be verified in the analysis of the results obtained, becoming an investigation subject matter (Simon et al., Citation2018).
The developed HLT intends to achieve some learning objectives for the topic, such as using different GeoGebra commands to obtain different geometric transformations in the plane and make use of them.
We are guided by the question: what characteristics can be identified in the participants’ performance during the development of the proposed HLT for the use of GeoGebra in the construction of a mosaic?
Participants’ knowledge is expected to expand through favourable situations mediated by the teacher, both in relation to the isometric concepts involved and the commands revealed in GeoGebra.
Participants’ performance should be verified in a proposal to build a mosaic or planning part of a plan using GeoGebra, in a constructivist perspective of learning present in the Hypothetical Learning Trajectory, elaborated in a STEAM context. Accordingly, the Mathematics activity role is explored in the learning of concepts of geometric transformations in the application of an HLT.
This research was developed in three phases, considering, in each one, the HLT components. The participants are two Mathematics undergraduates, with some knowledge and use of GeoGebra, and the interactions took place in two online meetings through Microsoft Teams and were recorded with the authorization of both participants.
2.3. Isometric transformations
Isometric Transformations are processes by which when moving all the points of a geometric figure, according to certain rules, an image of the original figure is created. The term ‘transformation’ designates a category of functions, with an algebraic character, thus establishing a link between Geometry and Algebra. Exploring it is an important topic in Mathematics because it allows connections to be established between Mathematics and other areas of knowledge, particularly the Arts. The use of GeoGebra in this context should serve Education as a mechanism and means for effective learning.
The study of isometric or geometric transformations is a subject that is related to everyday life, because when observing the objects present in our daily life, one can perceive the symmetry in various human constructions, such as buildings, furniture, cars; company logos; in flowers; the image of an object in the mirror and in the human body.
Mosaics are the paving formed with figures that can cover the plane or a part thereof and are present in Eastern, Islamic, Celtic, Japanese, Western art. They were built to cover ceilings, walls, floors in temples, decorative objects in palaces or modern homes.
Activity proposals may aim to enable students to identify geometric transformations and verify, using Dynamic Geometry software such as GeoGebra, some properties thereof and of the transformed figures. It allows, for example, identifying some types of paving or tessellation with patterns of repeated figures that cover the plane without ‘holes’ or ‘overlays’ as present in mosaics.
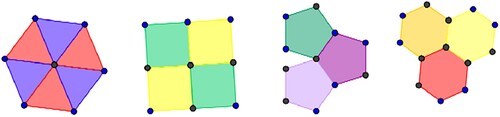
For geometric figures to cover a plane without ‘holes’ or ‘overlays’, their angles, when positioned with their respective vertices at the same point, have the sum of their measures equal to 360°. Triangles, squares, and hexagons verify this rule, which does not happen with the pentagon, as can be seen in Figure of possible polygons to pave a plane.
Figure 1. Possible polygons to pave a plane.
A geometric transformation can be considered as a bijective application between two geometric figures, because, from an original geometric figure, another geometrically congruent figure is formed: same shape and size or similar and same shape and regardless of size.
Isometries are examples of transformations. They are transformations of the plane that do not distort shapes and sizes. Therefore, they are also known as rigid movements; they take a figure over another that is congruent to it.
Until the nineteenth century, geometric transformations had an intuitive character and, from the Erlanger Program by Felix Klein (1849–1925), a German mathematician who researched the interconnections between Group Theory and Geometry, geometric transformations were formalized when considering homotheties and similarities as the main group of Euclidean geometry and isometries as a subgroup of the similarity group.
The author in Fernandes (Citation2007) argues that:
From a strictly artistic point of view, the paving is an ancestral artistic manifestation. Examples can be seen in the Alhambra monastery (13th–14th century), located in the city of Granada, in Spain. Its attraction is its interiors, which are decorated with Islamic art paving and show a remarkable knowledge of the combinatorial possibilities of this technique. (Fernandes, Citation2007, p. 32)
It should be noted that geometric transformations are not limited to isometries and similarities. Bastos (Citation2007) states that:
The world of geometric transformations is vast. In addition to the transformations that we know best — isometries and similarities — we have countless examples of geometric transformations, with which our students could come into contact, not to know their names or list their properties, but to realize the richness of this area of geometry and that, as in other mathematical subjects, there is a common structure behind so much diversity. (Bastos, Citation2007, p. 24)
The author in Fernandes (Citation2007) argues that:
With the increasing use of computers, mathematics has gained space as a means of artistic production. This, even without taking into account the fact that the generality of the algorithms presents in the artistic production software use, intensely, mathematical tools that cover fields ranging from differential geometry and linear algebra to complex numbers to quaternions, to mention only a few.
From the outset, in many cases, the visual representations of many mathematical objects have in themselves an intrinsic aesthetic value, which allows to serve Mathematics as Art, only with minor modifications. (Fernandes, Citation2007, p. 30)
In Sourin (Citation2021) the author argues that:
Information visualization involves various mathematical models, and it has become important in modern science and technology especially in cases where simple plots and diagrams are insufficient. It has applications across many disciplines including visual analytics where analytic reasoning is supported by various methods of interactive visualization. (Sourin, Citation2021, p. 9)
As we can see, geometric transformations are configured as a significant topic and, if explored with creativity, they can develop important skills in the student regarding the understanding of Mathematics.
3. Materials and methods
We present in this study the development of a synchronous workshop on the Microsoft Teams platform, whose objective was to analyze how two Mathematics undergraduates mobilize skills and develop didactic-mathematical knowledge during the implementation of a didactic proposal that addresses geometric transformations for the construction of a mosaic, involving GeoGebra commands and tools.
To achieve the objective of building a mosaic, preliminary activities that will support the construction need to be developed, accompanied by questions involving other Mathematical constructions and topics such as angles, quadrilaterals, triangles, etc. Thus, when studying the proposed construction of a mosaic, the teacher is expected to identify the Mathematical topics that need to be known in advance, such as some transformations with the use of GeoGebra. In this study, participants had a certain mastery of the use of GeoGebra.
We point out that symmetry is the preservation of shape and configuration through a point, a line or a plane. With symmetry, one shape is obtained from another while preserving its characteristics such as angles, side lengths, distance, types and sizes.
The techniques used for this process are called isometric transformations and each one produces a different type of symmetry. Isometric transformations include: Translation – Reflection – Rotation – Glide Reflection.
We can use different procedures for the construction of a mosaic and we will present, as an example, the development of the construction of the base of a mosaic by means of rotation in a triangle using GeoGebra. We then use translation to obtain a paving.
To start the HLT, we present and share, in the Microsoft Teams window, the video available to students and represented in (Figure ), as an example in the development of the construction of the base of a mosaic through the rotation of a triangle to obtain a hexagon using GeoGebra. We then use translation to obtain a paving using the GeoGebra Spreadsheet.
Figure 2. Rotation of a Triangle. Source –- All M.C Escher works © Cordon Art – Baarn – Holland All rights reserved. Used by permission.
The information offered by the video, about the steps performed in an isometric transformation, allowed the participants to know the possible ways that could be obtained in the activities that would be developed in GeoGebra.
Both participants, in a synchronous context, had GeoGebra open, the entire time, on their respective computers for the simultaneous construction of the mosaic. When in doubt, they shared the respective image of the construction on their computer for clarification.
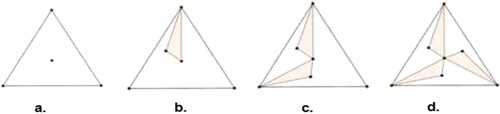
A Hypothetical Learning Trajectory is considered to consist of three components: an objective that, in this proposal, is the construction of a mosaic; the mathematical tasks that will be used to promote the participants’ learning, which were divided into three steps; and an assumption of how the participants will understand each step. In step 1, the objective is to obtain a part of the mosaic base, considering the interior of an equilateral triangle; in step 2, and after completing step 1, the objective is to obtain the base of the mosaic and, lastly, in step three, the objective is to pave a part of the plane with the base obtained.
Some challenges that arose in the context of the activities were directed to the types of isometry that would be used, but did not hinder the work performed.
3.1. Steps to obtain a part of the mosaic base
According to the HLT components, the objective of section 3.1 is to introduce the rotation transformation to obtain the 1st part of the base of a mosaic using some geometry concepts such as equilateral triangle, centroid and rotational motion. When interacting with these concepts, GeoGebra commands will be introduced to obtain, for example, the centroid of the triangle, rotate objects and change their properties, etc.
Our assumption, in conducting step 1, is that some difficulties may be observed in the construction of this base, such as obtaining the centroid and, also, when choosing the direction of the rotation movement. With the use of the Microsoft Teams platform, synchronously, it is possible to share the computer screen and the participant can interact with the researcher to clarify any difficulty in performing the steps of the activities.
The oral guidance for the construction is as follows: starting with the configuration of the objects that will be obtained in the view window, i.e. for the labels of the created objects not to compromise the visualization, has been indicate the following: in menu, select Options > Label > Less for new objects indicated in Figure .
Figure 3. GeoGebra Label Options.
The initial steps will allow building the 1st part of the mosaic base. Follow each construction item by the respective constructions as in Figure below. Note that auxiliary constructs were hidden using GeoGebra’s ‘hide objects’ tool. The instructions for the development of the construction of the mosaic base are as follows.
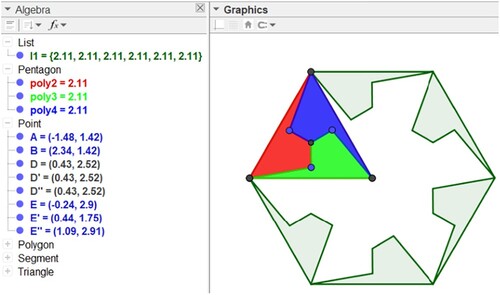
construct an equilateral triangle (indicated by pol1, Figure a) of vertices A, B, C and obtain the centroid, the meeting point of the medians, with the command:
Centroid(<Polygon>) i.e. Centroid(poly1)
build a polygon, inside the initial triangle (Figure b), using the centroid and one of its vertices.
rotate this polygon 120° (Figure c) using the Rotation tool or type in Rotate(<Object>, <Angle>, <Point>), counterclockwise, where the point is the centroid of the initial triangle. Click, in this order: on the polygon, on the centroid and write 120° in the window that pops-up, i.e. Rotate(t1, 120°, D)
repeat the previous procedure for the new interior polygon created in item c (Figure d).
build a new interior polygon by uniting the six interior points and hide the smaller interior polygon.
repeat the procedure above twice and colour the three polygons of your choice. Right click each polygon and click on properties. Click on the ‘style’ tab and increase the ‘fill’ to 75.
colour (Figures and ) each pentagon inside the initial triangle forming the 1st part of the base for the mosaic.
Figure 4. Steps to obtain the mosaic base.
Figure 5. Colouring the first part of the mosaic base.
Figure 6. First part of the mosaic base.
In this step, we obtain an equilateral triangle (pol1) with three pentagons in its interior: pol2, pol3 and pol4.
In conducting Step 1, the participants had some difficulty in constructing the three pentagons inside the equilateral triangle during the choice of the respective vertices.
3.2. Steps to get the paving base
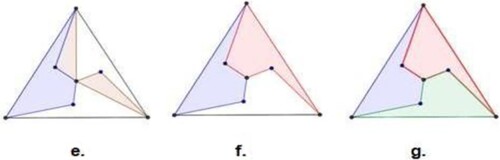
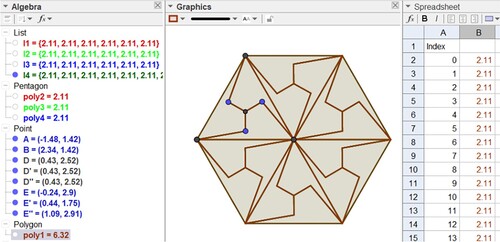
This step will allow you to build the 2nd part of the mosaic base. We have to replicate the figure of the 1st part, mosaic base, to form a hexagon.
We can build all the polygons needed for the mosaic base with the command:
IterationList(<Expression>, <Variables>, <Start Values>, <Count>)
In the above command, to rotate, we use, in <Expression>, the command:
Rotate(<Object>, <Angle>, <Point>)
With these commands, we can obtain the polygons that make up the hexagon as follows:
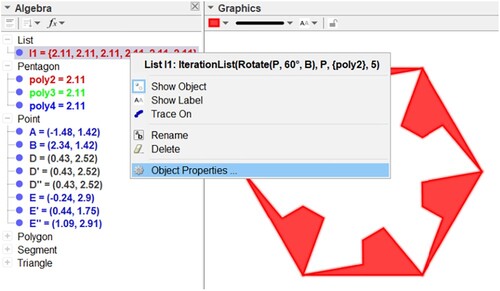
IterationList(Rotate(P, 60°, B), P, {poly2}, 5)
As it is an iteration list, the second element of this list will be the poly2 pentagon obtained in the previous iteration.
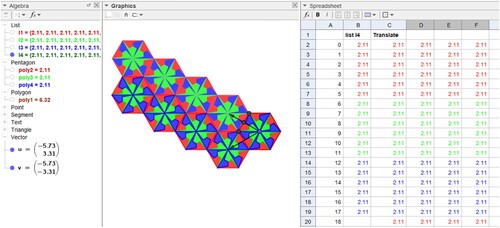
By pressing ‘Enter’, the command will create a list, in the algebra window, which is the first set of pentagons that will comprise the mosaic (Figure ).
Figure 7. Constructing the mosaic base.
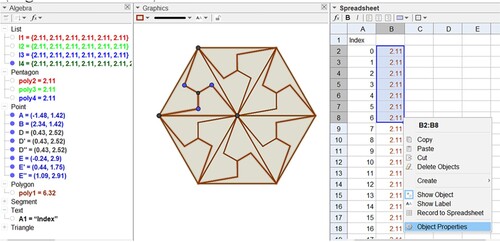
As they have the same colour, we may change the colour of the list by right clicking the list (Figure ), and, in ‘Properties’, we select the ‘Colour’ tab.
Figure 8. Constructing the mosaic base.
In the list, there is a repeated element, which is the first polygon that we used for its construction and which we call poly2. Just hide that polygon. We recommend leaving the list with all polygons, because, at other times, we can use it to do some isometries (rotation, translation, and reflections).
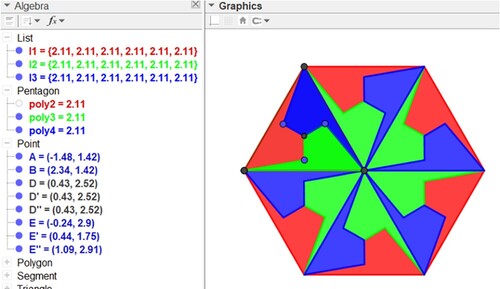
Repeat the same process for the other two pentagons that make up the mosaic base element (Figure ) that is:
IterationList(Rotate(P, 60°, B), P, {poly3}, 5) and IterationList(Rotate(P, 60°, B), P, {poly4}, 5)
Figure 9. Constructing the mosaic base.
Figure 10. Mosaic base.
Our assumption, expressed by the participants, is that they did not know some commands used and would indicate rotations of the pentagons one by one. We explained that, for a construction with better results, it is important to use generic commands that allow you to quickly obtain the desired figure. Accordingly, the commands described above were suggested, which were not known to either undergraduate.
In this 2nd part, the participants concluded the meeting activity by obtaining the mosaic base, and a new meeting was scheduled to complete the activity proposal.
3.2. Steps to start paving
In this step, according to the HLT, we conjectured that the participants were not aware of the commands used, such as transferring a drop-down list to the spreadsheet; using advanced commands to programme dynamic colours and others. Considering Vygotsky, knowledge was constructed through the interaction between the participants and the researcher and, mainly, commands were assimilated through the communication between them.
The GeoGebra commands described below enabled the construction of a part of the mosaic and allowed the participants to analyze other possibilities of using them in other Mathematics content. The commands used are below.
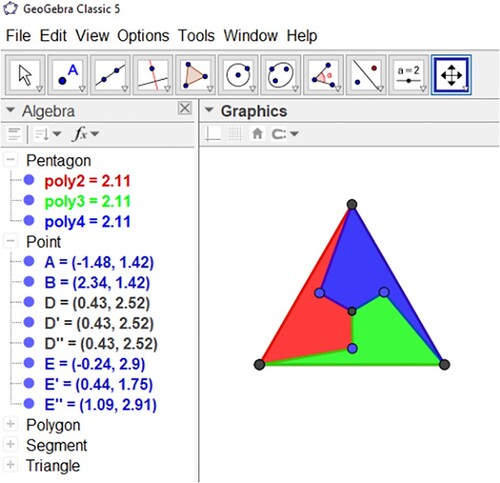
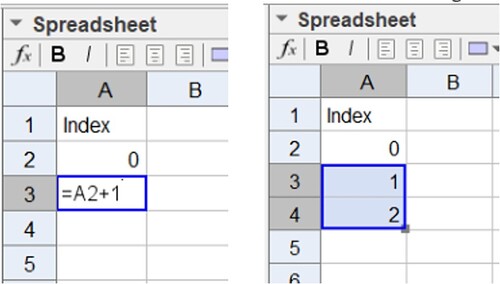
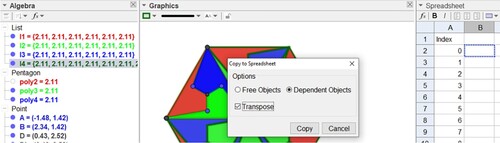
Open the spreadsheet and, in column A, cell A1, type the word ‘index’. In cell A2, type 0; in cell A3, type = A2 + 1, so that the cell adds 1 to the value of cell A2. Position the mouse pointer in the lower right corner of cell A3 and then drag it to cell A4 and it will add 1 to the value that is stored in cell A3, as seen in Figure .
Figure 11. Creating the index column in the Spreadsheet Window.
Position the mouse in the lower right corner of cell A4 and drag it to line 39, because through these values we establish a condition to change the fill colour of the elements that make up the mosaic.
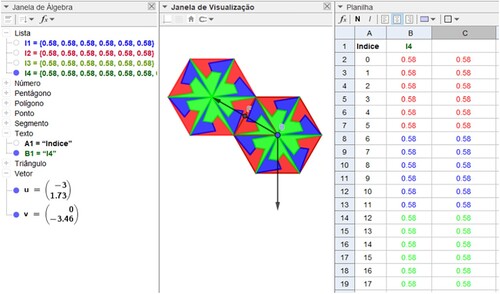
Create a list l4 with the command Union(l1), Union(l2, l3) to store all mosaic elements in a column of a spreadsheet.
Keep Ctrl (or Shift) pressed, and drag list l4 from the Algebra window to row 2 and column B of the Sheet. Select the objects (Figure ) as Dependents (so that when you modify the objects in the spreadsheet, the corresponding item in the Preview Window and Algebra Window will be updated) and Transpose to obtain it in column.
Figure 12. Copying list l4 to Spreadsheet.
These commands will allow the construction of the mosaic to be manipulated by commands applied to the columns of the spreadsheet as shown below.
Hide the pentagons and lists in the algebra window, leaving only list l4 visible as shown in Figure .
Figure 13. Mosaic base obtained from the spreadsheet.
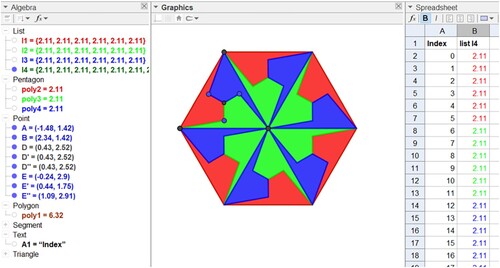
Right-click the first 6 rows of the Sheet and change the colour of the objects using the Colours tab of the Properties dialog window and increase transparency to 75. Repeat this procedure twice for the next 6 rows, changing the respective colours, and get the mosaic base, now dependent on the spreadsheet. We thus obtain a part of the paving of the plane (Figures and ).
Figure 14. Changing the object colours in the spreadsheet.
Figure 15. Obtaining the mosaic base using the spreadsheet.
As of this moment, it is necessary to start the paving of the plane by means of translation commands. Therefore, appropriate vectors must be defined in different directions as exemplified below.
Different vectors were created, as shown below, and, as the participants had some difficulty in defining them, the researcher asked them to share the respective construction in Microsoft Teams to verify the path used. Once the problem has been identified (incorrect vector direction and modulus) the construction can be continued as follows.
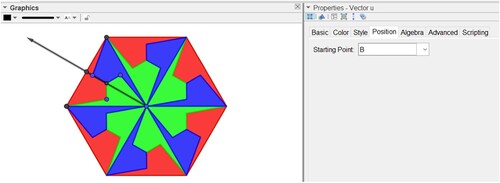
Define translation vectors to translate the mosaic base to pave the plane. Vector u can be obtained with the command u = 2*Vector(B, F), where F is the midpoint of the AC side of poly1 obtained with the command F = Midpoint(A, C) (polygon constructed in item 3.1). In properties, position, move the vector origin to point B as indicated in Figure .
Figure 16. Move the vector origin to point B.
Then, using the command: Rotate(<Object>, <Angle>, <Point>) we obtain another translation vector v = Rotate(u, 60°, B). These two vectors allow us to translate the mosaic base to start the paving according to the following commands.
In Cell C2, use command: = Translate(B2,u)
Red: If($A2 ≤ 5, 1, 0); Green: If(6 ≤ $A2 ≤ 11, 1, 0); Blue: If(12 ≤ $A2 ≤ 17, 1, 0) and transparency 0.75.
To use the translation of the mosaic base in another direction, we use vector v and, in cell C20, use the command = Translate(B2,v) and, again, in this cell, programme the dynamic colours by clicking in properties, advanced as follows (Figure ):
Red: If(Mod($A20, 18) ≤ 5, 1, 0); Green: If(6 ≤ Mod($A20, 18) ≤ 11, 1, 0);
Blue: If(12 ≤ Mod($A20, 18) ≤ 17, 1, 0)
Figure 17. Paving Sketch with Translation and u vector.
Figure 18. Paving Sketch with Translation and v vector.
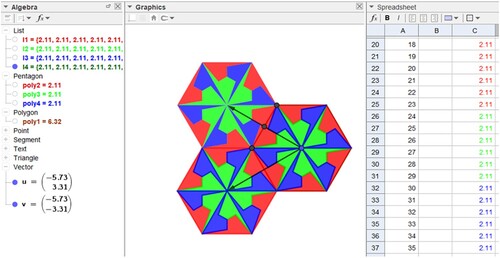
Selecting column C, from cell C2 to cell C37, and dragging to the right for the subsequent columns, we obtain a paving covering part of the plane (Figures and ) through the translation command by a vector.
Figure 19. Paving Sketch with Translation and u and v vectors.
Figure 20. Paving Sketch with Translation and u and v vectors.
By creating other vectors in different directions, with different measures, using translation commands and programming dynamic colours, the objects obtained in the spreadsheet will cover other regions of the plane, and a mosaic is obtained.
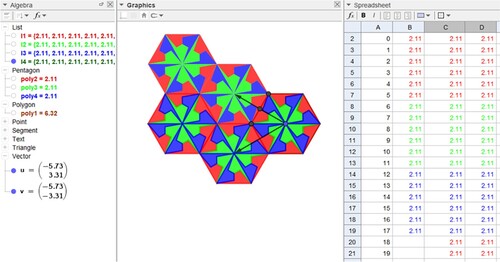
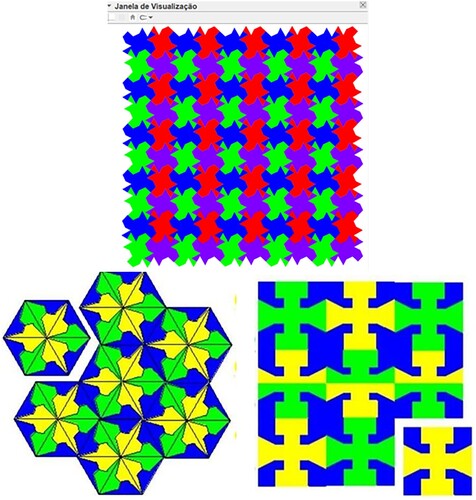
It is possible to use other construction techniques to obtain mosaics using GeoGebra, as shown in Figure .
Figure 21. Other mosaics constructed in GeoGebra.
In each of the techniques to obtain the mosaics in Figure , other isometric transformations will be necessary for the construction, which can be obtained with the aid of GeoGebra. Some applets on isometry can be searched, for example, in https://www.geogebra.org/m/q2mshbgh.
4. Discussions and conclusions
In this paper, we presented proposals with theoretical contribution to constructivism and HLT that allowed, with the appropriate methodology, to explore isometric or geometric transformations and their relations with art in the STEAM context.
The use of GeoGebra evidenced its possibilities in the development of activities and revealed the importance of inserting technology in the practice of the teacher and the student.
Both participants sent their respective mosaics revealing mastery of the indications of the proposal.
The understanding of what isometry is, which polygons can fill a plane, what a mosaic is and, in the technological aspect, the discovery of GeoGebra commands that can evidence new discoveries were manifested by the participants. They also recorded that they were not aware of the possibility of obtaining mosaics using commands and spreadsheets.
With the theoretical and practical knowledge presented, the teacher is expected to have clarity in their objectives, be able to properly choose the learning strategy, and implement their teaching plan more effectively.
Works of this nature can contribute, in some way, to the teaching practice and the area of Mathematics Education, either by using this activity in the classroom, or to inspire teachers with interdisciplinary ideas and in the creation of activity proposals using GeoGebra.
The generalization processes using the GeoGebra spreadsheet allowed important information about its conceptualization, emerging application, and validation schemes. The results show that there was a positive attitude on the part of the participants for the development of new proposals in GeoGebra in the context of isometry.
The use of GeoGebra in this context served as a mechanism and means for consistent learning, contributing to create an affective involvement or curiosity that resulted in the engagement of the participants, creating an internal need to learn.
When inserting an educational technology such as GeoGebra into your planning, you need to feel safe and confident in the face of the challenge. This does not mean radically changing all your planning, and with the use of GeoGebra, some content can be approached and treated through inspiring and creative activities.
Disclosure statement
No potential conflict of interest was reported by the author(s).
References
- Abas, S. J., & Salman, A. S. (1995). Symmetries of Islamic geometrical patterns. Singapore: World Scientific Publishing Co.
- Bastos, R. (2007). Notas sobre o Ensino da Geometria: Transformações Geométricas. Grupo de Trabalho de Geometria. Revista Educação e Matemática. No. 94, APM.
- Bilac, C. U. (2008). Possibilidades da aprendizagem de transformações geométricas com o uso do Cabri-Géomètre [Master’s Degree Dissertation]. PUC-SP, São Paulo. http://www.pucsp.br/pos/edmat/mp/dissertacao/cristina_ulian_bilac.pdf.
- Fernandes, A. M. (2007). Arte, Matemática e “Arte e Matemática”. Revista Educação e Matemática. No. 94, APM. https://em.apm.pt/index.php/em/article/view/1621/1660.
- Ferraz, A. P. d. C. M. (2008). Instrumento para facilitar o processo de planejamento e desenvolvimento de materiais instrucionais para a modalidade a distância [Doctorate thesis]. Escola de Engenharia de São Carlos da Universidade de São Paulo. https://www.teses.usp.br/teses/disponiveis/18/18140/tde-14012009-225604/publico/0820059_DirMatIns_DR.pdf.
- Jones, K. (2002). Issues in the teaching and learning of geometry. In L. Haggarty (Ed.), Aspects of teaching secondary mathematics: Perspectives on practice (Chap. 8, pp. 121–139). Routledge Falmer. ISBN: 0-415-26641-6
- Simon, M. A., Kara, M., Placa, N., & Avitzur, A. (2018). Towards an integrated theory of mathematics conceptual learning and instructional design: The learning through activity theoretical framework. The Journal of Mathematical Behavior, 52, 95–112. https://doi.org/10.1016/j.jmathb.2018.04.002
- Simon, M. A., & Tzur, R. (2004). Explicating the role of mathematical tasks in conceptual learning: An elaboration of the hypothetical learning trajectory. Mathematical Thinking and Learning, 6(2), 91–104. https://doi.org/10.1207/s15327833mtl0602_2
- Sourin, A. (2021). Undergraduate topics in computer science. Ian Mackie (Ed.). Springer Nature Switzerland AG.