Abstract
Infectious diseases are responsible for the extinction of a number of species. In conventional epidemic models, the transition from endemic population persistence to extirpation takes place gradually. However, if host demographics exhibits a strong Allee effect (AE) (population decline at low densities), extinction can occur abruptly in a catastrophic population crash. This might explain why species suddenly disappear even when they used to persist at high endemic population levels. Mathematically, the tipping point towards population collapse is associated with a saddle-node bifurcation. The underlying mechanism is the simultaneous population size depression and the increase of the extinction threshold due to parasite pathogenicity and Allee effect. Since highly pathogenic parasites cause their own extinction but not that of their host, there can be another saddle-node bifurcation with the re-emergence of two endemic equilibria. The implications for control interventions are discussed, suggesting that effective management may be possible for ℛ0≫1.
AMS Subject Classification :
1. Introduction
Parasites and pathogens are now recognized as integral parts of virtually all ecosystems Citation18 Citation38 Citation41. There is a large body of evidence showing that disease agents can substantially affect their host population Citation4 Citation28 Citation37. Besides causing a depression in population size, infectious diseases have also been attributed to playing a role in the extinction of species Citation13 Citation14 Citation30 Citation50 Citation54 Citation60.
Transmission of disease is influenced by aggregation patterns in the host population as well as its social organization and behavioural traits Citation19 Citation23. Two different types of incidence (new infections per unit time) are usually distinguished Citation7 Citation31 Citation43. Density-dependent (mass action) transmission assumes that the effective contact rate between susceptible and infective individuals increases linearly with population size. In contrast, the number of contacts is independent of population size if transmission is frequency-dependent (also called standard incidence or proportionate mixing).
Populations subject to density-dependent transmission have been regarded as relatively safe from disease-induced extinction, as infection vanishes with declining population size – but see Citation15 Citation36 Citation57 for other forces causing extinction at low density. Frequency-dependent incidences are well known to have the capability of driving populations to extinction, see the review in Citation14. This is because disease transmission goes on even in small populations due to the constant contact rate.
Since the influential paper by Anderson and May Citation3 highlighting the role of parasites in regulating natural populations, numerous mathematical models have been developed, which also take the host population as a dynamic variable Citation5 Citation8 Citation10 Citation27 Citation39 Citation48 rather than fixing it at a constant level (as has been traditionally assumed for human disease models in developed countries). Epidemic models with frequency-dependent incidence typically predict host population extinction in appropriate parameter regimes Citation11 Citation24 Citation25 Citation61. The extinction is preceded by a continuous population decline when the control parameters approach the eradication regime. The transition to extinction, therefore, takes place gradually, and small population sizes are typical correlates of imminent species loss.
This paper highlights that extinction can occur directly and abruptly in a catastrophic collapse from high population levels if the host population exhibits a strong Allee effect (AE) (also called critical depensation) Citation12 Citation55. The AE describes the phenomenon that populations benefit from large population sizes (e.g. due to higher success rates in finding mating partners, predator dilution or reductions in inbreeding). At low densities, populations experience positive density dependence as they have difficulties in maintaining social functioning, for instance. If the AE is strong (weak), the population growth rate is negative (reduced) at low densities. AEs have been demonstrated in, or proposed for, an increasing number of species, e.g. saiga antelopes Citation45, polar bears Citation47 and Atlantic cod Citation51.
Only recently, the impacts of an AE have been considered in epidemiological models. (Although this paper is mainly motivated by animal diseases and therefore epizootiological problems, it uses epidemiological notation throughout). Deredec and Courchamp Citation15 as well as Hilker et al. Citation34 Citation35 conclude that the combination of parasitism and AE generally increases the likelihood of extinction. Thieme et al. Citation57 and Hilker et al. Citation36 consider density-dependent transmission and show that host extinction is possible therein as well. Moreover, these models exhibit a rich dynamical behaviour including super- and sub-critical Hopf bifurcations, homoclinic bifurcations and tristability.
This article reconsiders a simple epidemiological model of SI type with frequency-dependent incidence and a strong AE in the host demographics Citation35. While the original publication is primarily concerned with spatio-temporal dynamics (additionally taking into account spatial diffusion), the current focus is on the bifurcation behaviour of the spatially homogeneous model without diffusion. A typical phenomenon in epidemic models with strong AE is bistability, i.e. the outcome (extinction or survival of the population) depends on the initial condition. A super-critical number of infectives can eradicate the host even if its initial state is beyond the minimum viable size defined in the disease-free system. This paper reports that a spontaneous population crash to extinction is possible for all initial conditions. This takes place via a saddle-node bifurcation, in which two endemic equilibria disappear. The loss of the endemic attractor renders the system monostable with extinction as inevitable outcome.
The remainder of this paper is organized as follows. Section 2 briefly introduces the model and derives basic reproduction numbers. They are used in Section 3 to summarize the equilibria and their stability in biologically insightful terms. Section 4 presents a numerical continuation and bifurcation study. The main emphasis is on how varying control parameters impacts the persistence of the host population and the establishment of the disease. Section 5 highlights the relevance for management actions and illustrates the differences to host populations without the AE. Section 6 compares the bifurcation behaviour with a backward bifurcation (BB), pointing out that the two scenarios are fundamentally different, even though both of them involve multiple non-trivial stationary states and saddle-node bifurcations. Finally, Section 7 presents the main conclusions and discusses their implications for the understanding of extinction dynamics.
2. Model description
This section describes the epidemic compartment model with frequency-dependent disease transmission and a strong AE in the host demographics Citation35. It also introduces basic reproduction numbers that will be used to express the existence and stability of stationary states in the following section.
2.1. Model assumptions and equations
The model structure can be illustrated by the following transfer diagram
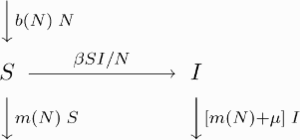 Note that all quantities are dimensionless. The total host population size N=N(t) at time t>0 is assumed to consist of a susceptible (S) and an infective (I) part, N=S+I. That is, there is no recovery from the disease. Disease transmission is frequency-dependent with coefficient β describing the effective contact rate, henceforth referred to as transmissibility. The disease is pathogenic and induces an additional per capita mortality rate μ in the infectives, henceforth referred to as pathogenicity (sometimes also called virulence). The background mortality is described by the density-dependent per capita death rate m(N). There is no vertical transmission, i.e. the offspring of infectives is susceptible. The per capita birth rate b(N) is density-dependent as well. The difference between birth and natural death rate is the net growth rate
Note that all quantities are dimensionless. The total host population size N=N(t) at time t>0 is assumed to consist of a susceptible (S) and an infective (I) part, N=S+I. That is, there is no recovery from the disease. Disease transmission is frequency-dependent with coefficient β describing the effective contact rate, henceforth referred to as transmissibility. The disease is pathogenic and induces an additional per capita mortality rate μ in the infectives, henceforth referred to as pathogenicity (sometimes also called virulence). The background mortality is described by the density-dependent per capita death rate m(N). There is no vertical transmission, i.e. the offspring of infectives is susceptible. The per capita birth rate b(N) is density-dependent as well. The difference between birth and natural death rate is the net growth rate of the population. In the absence of disease, the population dynamics is described by
. In the presence of disease, it is convenient to formulate the model in (N, i) state variables, where i=I/N is the prevalence of the disease (fraction of population being infective). The model equations then read
2.2. Reproduction numbers
The basic reproduction number of the disease is the number of secondary cases produced by a single infective during its entire lifetime when it is introduced into a completely susceptible population (i.e. N≡ S). For models (1) and (2), this yields
If the host population is at carrying capacity, the disease can invade if
If the host population goes extinct (N→0), the fraction of infectives within the vanishing population can be strictly positive or zero, depending on whether the infectives decay more slowly or more quickly than the total population, respectively. The total population approximately decays at rate r u if N is assumed to be small, whereas the infectives decay at an approximate rate if I is small compared with N. The difference between these two growth rates at zero population density can be expressed in the quantity
3. Equilibria and their stability
The existence and stability of stationary states of system (1) have been studied in Citation35 for gen-eralized demographic functions yielding a strong AE, that is for b(N) being concave and m(N) being non-decreasing and convex. This section briefly recalls these results, applied to the demographic functions (2), and reformulates them in terms of reproduction numbers. This allows for a novel, biologically more insightful interpretation, which forms the basis for understanding the bifurcation behaviour investigated in Section 4.
Model (1) and (2) has the following four (semi-)trivial equilibria .
| • |
| ||||
| • |
| ||||
| • |
| ||||
| • |
| ||||
A necessary condition for non-trivial equilibria is β>μ; otherwise, i→0 as t→∞, cf. Equations Equation(1b). Endemic equilibria can be found as the intersections of the two quadratic nullclines
Introducing the auxiliary function
First, consider Φ(1)>0. If Φ(u)>0, there is no root of Φ(N) in the interval of interest. Endemic equilibria, therefore, do not exist. If, conversely, Φ(u)<0, there is a single root , with
.
Second, consider Φ(1)<0, which implies Φ(u)<0. Then the number of roots depends on the location of the parabola's top : (i) if
, there are two roots
and
with
; (ii) if
, the previous two roots collide in a unique root
; (iii) if
, there is no root. The critical relation
for two endemic equilibria to exist can be solved explicitly in terms of model parameters (see Appendix). Reformulating in terms of the basic reproduction number by substituting one of the epidemiological parameters, one obtains that
The above results can be summarized as follows in terms of the basic reproduction number, using the relationships and
. shows a corresponding sequence of phase plane illustrations.
Figure 1. Phase plane illustrations with nullclines and stationary states of model (1) and (2). Solid (dashed) lines are the nullclines of infectives (total populations). Black (grey) points mark stable (unstable) equilibria. If the system is bistable (all panels except [e]), the stable manifolds of the saddle point separating the basins of attraction are shown in dotted lines. Parameter values: (a) μ=3.9, (b) μ=3.65, (c) μ=3, (d) μ=2.4, (e) μ=2, (f) μ=0.5 and β=4, u=0.1, r=2, d=0.2.
![Figure 1. Phase plane illustrations with nullclines and stationary states of model (1) and (2). Solid (dashed) lines are the nullclines of infectives (total populations). Black (grey) points mark stable (unstable) equilibria. If the system is bistable (all panels except [e]), the stable manifolds of the saddle point separating the basins of attraction are shown in dotted lines. Parameter values: (a) μ=3.9, (b) μ=3.65, (c) μ=3, (d) μ=2.4, (e) μ=2, (f) μ=0.5 and β=4, u=0.1, r=2, d=0.2.](/cms/asset/b398794c-62ca-42cd-9b0c-a411118aebdf/tjbd_a_402815_o_f0001g.gif)
First, if
Second, there is a unique endemic equilibrium if
.
is always an unstable saddle point. It organizes the effective extinction threshold in the presence of disease. That is, depending on the initial condition the population either goes extinct or survives at carrying capacity. The basins of attraction are separated by the stable manifolds plotted in dotted line in . Host eradication is even possible if the initial population size is larger than the Allee threshold. The disease, therefore, increases the extinction basin beyond u.
Third, consider . If
or
, provided that these critical values exist, there are two non-trivial stationary states (, 1f). The additional equilibrium is
is always locally stable and has a larger population size
,
. The system remains bistable with either endemicity or host extinction as the eventual outcome. Conversely, if
, there is no non-trivial stationary state at all (. This occurs after the two endemic equilibria
and
coalesce and disappear at one of the critical values. It corresponds to too strong a disease, reducing population size
and at the same time increasing the effective extinction threshold. As a consequence, neither the disease nor the host can persist, and the system is rendered monostable.
4. Bifurcation behaviour
The bifurcation diagrams in show how the total population and prevalence change with varying basic reproduction number ℛ0. It is assumed that ℛ0 is varied by altering transmissibility β. If , the infection cannot invade the population at carrying capacity. However, if
, the disease-free equilibrium
loses stability, and the locally stable endemic equilibrium
emerges in a transcritical bifurcation. It coexists with the unstable endemic equilibrium
, which already arises if
. The two non-trivial states collide and annihilate each other in a saddle-node bifurcation at
. The endemic solutions are suddenly lost, and the system abruptly undergoes a transition to a qualitatively very different behaviour. Namely, the population always goes extinct, whereas the population size
in endemic equilibrium was bounded well away from zero.
Figure 2. Bifurcation diagrams for varying basic reproduction number (by increasing β). Solid (dashed) lines correspond to stable (unstable) equilibria. The arrow indicates the abrupt population collapse from a level of a large population size N*+ after a saddle-node (SN) bifurcation. The critical values of ℛ0 are explained in the main text. Other parameter values: μ=1, u=0.1, r=2, d=0.2.
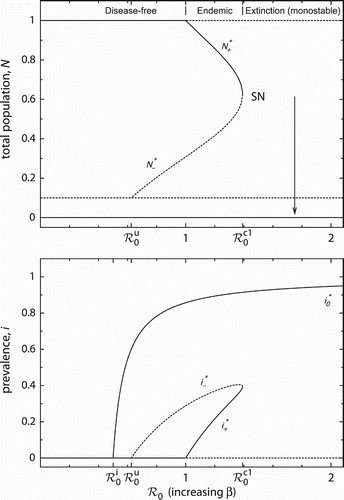
The critical basic reproduction number is a tipping point, marking the unexpected population collapse. For
, the dynamics, therefore, becomes monostable with the extinction state
being globally stable. For
, the system is bistable: one of the attractors always is an extinction state – either
or
depending on
– while the other attractor is either
or
corresponding to a disease-free or endemic scenario (
), respectively.
The basic reproduction number can not only be altered by controlling transmissibility β, but also by varying pathogenicity μ – the other disease-related parameter. Note that an increase in ℛ0 corresponds to a decrease in μ, cf. EquationEquation (3). shows the corresponding bifurcation diagram of the total host population. (The diagram for the prevalence is not shown but is qualitatively similar.) The first part of the bifurcation diagram is analogous to the one in for changing β. In particular, there is a saddle-node bifurcation for
, after which the population goes extinct. However, there is another critical reproduction number
,
, for which a second saddle-node bifurcation occurs. This gives rise to two endemic equilibria again. As abruptly as the endemic attractor disappears at
, it re-emerges after the extinction regime at
. Note that the phase-plane diagrams in correspond to a sequence of decreasing μ.
Figure 3. If the basic reproduction number is varied by changing pathogenicity, the bifurcation diagram reveals a second saddle-node bifurcation (SN2). Parameter values: β=4, u=0.1, r=2, d=0.2.
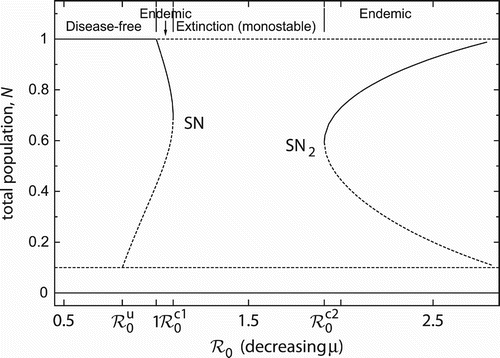
It is well known Citation2
Citation3 that the maximum degree of host population depression (here resulting in extinction) is achieved by parasites with moderate to low pathogenicity, i.e. moderate to high ℛ0. If pathogenicity is too low (i.e. too large a ℛ0), the disease cannot cause sufficient case fatalities, enabling the host to persist at endemic equilibrium with large population size (). Conversely, if pathogenicity is too high (i.e. too small a ℛ0), increased mortality of infectives limits their potential to spread the disease (
) or even leads to their eradication (
).
The sequence of ‘endemicity – extinction – endemicity’ can be observed in other models with frequency-dependent transmission as well. The novelty in a model with strong AE, however, is that the transition between the regimes takes place via two saddle-node bifurcations. This results in a much more drastic change of behaviour. The transitions in models without AE are induced by transcritical bifurcations, which correspond to a more continuous and smooth evolution.
summarizes the model behaviour in the two-parameter plane (μ, β). The dynamical outcome can, therefore, be characterized in terms of the disease-related parameters. The saddle-node bifurcation conditions define a nonlinear relationship between β and μ, whereas the other critical values of the basic reproduction number define a linear relationship. Fixing a pathogenicity μ and traversing vertically through by varying β reveals that the saddle-node bifurcation line can be crossed at most once. Note the minimum value of pathogenicity μc for saddle-node bifurcations to occur, cf. EquationEquation (6). Similarly, if transmissibility β is fixed and traversed horizontally by changing μ, there is a minimum value of transmissibility βc as well, cf. EquationEquation (7)
. The saddle-node bifurcation line can be crossed twice. Mathematically, this can be understood by noting that both nullclines depend on μ, whereas only one nullcline depends on β, cf. EquationEquation (4)
.
Figure 4. Domains of model behaviour in the two-parameter plane. Stable equilibria in each domain are indicated. The grey domain is monostable with eventual host extinction. All other domains are bistable. The hatched domain can be endemic, while the remaining white domains can be disease-free. Host extinction is always possible. Bold (thin) lines are saddle-node (transcritical) bifurcation curves. The dotted line marks the emergence of the unstable endemic equilibrium E −. See the main text for more details. Parameter values: u=0.1, r=2, d=0.2.
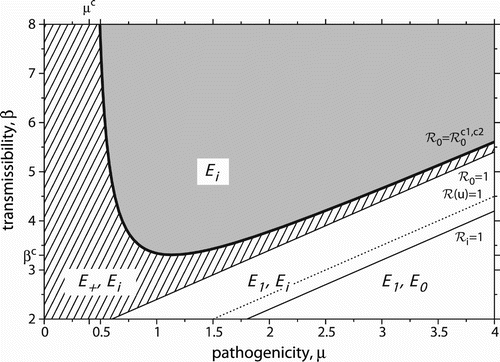
The Allee threshold u (as well as the intrinsic growth rate r) appears in both nullclines, thus also defining two critical tipping points for saddle-node bifurcations. It can be shown that there exists a minimum value of u, for which the ‘double-tipping’ can occur. That is, the AE needs to be sufficiently severe. However, there are also examples, in which a ‘double-tipping’ always exists (i.e. including u→0).
5. Consequences to control interventions and comparison with logistic demographics
The aim of this section is threefold: first, to illustrate the implications of the abrupt host population extinction after a saddle-node bifurcation; second, to show that decreasing ℛ0 can be disadvantageous; and third, to showcase the difference to populations without AE.
System (1) does not exhibit a saddle-node bifurcation if demographics are logistic, e.g.
Figure 5. Time evolutions for varied basic reproduction numbers. (a), gradual transition from population persistence to extinction in the logistic model (8), (b) abrupt population collapse in the Allee effect model (2) when increasing ℛ0 (by increasing β), (c) decreasing ℛ0 (by varying μ) can lead to a population crash as well. Basic reproduction numbers are varied in equidistant steps. Initial conditions are fixed at N(t≡0)=1, i(t≡0)=0.01. Parameter values: μ=1, B=1, M=0.1 in the logistic model, u=0.1, r=2, d=0.2 in the Allee effect models with μ=1 (b) and β=4 (c).

In a population with strong AE, disease-induced extinction occurs abruptly when increasing ℛ0, cf. . Host populations with substantial size (for ) can disappear all of a sudden if the basic reproduction number is increased just a tiny bit (
).
considers the case when control measures aim at reducing ℛ0 by increasing pathogenicity. The time plots look similar to the ones in . However, the order of reproduction numbers is reversed. The starting point is an endemic infection with only moderate population depression (). Decreasing ℛ0 reduces host population size – initially only marginally, but once the tipping point
induced by the second saddle-node bifurcation is passed, the population quickly goes extinct. Interventions aimed at altering the basic reproduction number, therefore, need to be planned carefully. Merely reducing ℛ0 is not always beneficial.
6. Differences to backward bifurcations
In recent years, backward bifurcations (BBs) in epidemic models have received considerable attention in the literature, see e.g. Citation6
Citation17
Citation21
Citation29
Citation40
Citation42
Citation46
Citation52
Citation53
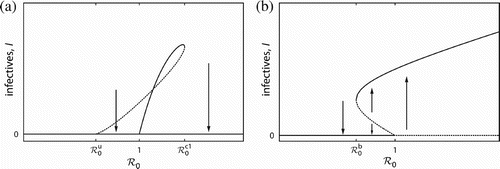
Citation59. It is interesting to contrast the bifurcation behaviour of the AE model presented here with a BB, see and , respectively. The discussion in this section is restricted to the case in which is unfeasible, i.e. there is only a single saddle-node bifurcation in the AE model as it occurs with varying transmissibility. Note that the diagrams show the infectives I on the vertical axis. Both scenarios have multiple endemic equilibria and can be bistable. However, the following differences demonstrate that the bifurcation behaviour is fundamentally different.
| 1. | The disease can be endemic in the AE model only for | ||||
| 2. | The saddle-node bifurcation occurs in the AE model beyond the disease invasion threshold at | ||||
| 3. | The direction of the saddle-node bifurcation is mirror-inverted. That is, increasing ℛ0 leads to the disappearance of the endemic equilibria in the AE model and to their emergence in a BB model. The former is the basis for the abrupt population collapse. The latter can lead to an abrupt explosion in infectives if ℛ0 is increased beyond unity as well as to a sudden eradication of disease if ℛ0 is reduced below | ||||
| 4. | The backward bifurcation induces a critical behaviour primarily for the infectives I, i.e. whether infection quickly establishes or suddenly disappears. The criticality in the AE model, in contrast, relates mainly to the total host population N, cf. the bifurcation diagram in . If | ||||
| 5. | The bistability and the two endemic equilibria in the AE model are due to the strong AE. Interestingly, infection can render the system monostable. The bistability and the endemic equilibria in a BB model are induced by disease characteristics, see [49 for a review. | ||||
7. Discussion and conclusions
Conventional epidemic models (without demographic AE) predict that parasites can eradicate their host if transmission is frequency-dependent. The transition from population persistence to extinction takes place gradually when control parameters vary continuously. There is increasing evidence, however, for positive density dependence leading to strong AEs in host demographics Citation12. The mathematical model considered here suggests that extinction occurs abruptly due to a fold catastrophe (saddle-node bifurcation). Marginal changes in model parameters can thus lead to dramatic consequences, namely the spontaneous collapse of the host to deletion.
Extinction research increasingly focuses on synergistic interactions between different processes. In combination, single extinction drivers such as habitat destruction or overexploitation pose a much larger threat to endangered species than in isolation, as they may reinforce themselves in declining populations due to amplifying feedbacks Citation9. Parasitism and AEs are two such examples that have long been recognized to increase the risk of extirpations. Their joint interplay acts as an extreme accelerator in the transition towards extinction. In particular, they define a tipping point at which the population collapses all of a sudden.
The subtlety of the tipping point is that the host can be extremely abundant just before it. illustrates that the population crashes from a level of over 75 % of the carrying capacity to nil. Establishing predictors of such spontaneous collapse appears to be difficult, if not impossible. This would be important for identifying potential extinction risks and guiding management actions. Close before the tipping point (), the extirpation is accompanied by prolonged transient dynamics Citation32, cf. and . The population seems to be stable over a considerable time horizon even though it is ultimately commited to its deterministic extinction debt. In nature, however, the transients are likely to be superimposed by perturbations and stochastic effects. These factors could speed up or slow down the extirpation. Recognizing the transient approach to deletion is difficult, and even if it can be identified at all, it might be too late for interventions. Moreover, the transients occur only after the tipping point and not beforehand (from the point of view starting with persistence). Therefore, the imminent disaster is almost impossible to anticipate in practice.
Mathematically, the tipping point is associated with a saddle-node bifurcation. When the two non-trivial equilibria and
annihilate each other, there is no endemic attractor left and extinction is inevitable.
emerges from the disease-free carrying capacity state if
. Obviously,
has a larger population size than
, which bifurcates from the Allee threshold state on the disease-free boundary into the interior of the phase plane if
. The emergence of the unstable equilibrium
is essential for the saddle-node bifurcation to occur. As a saddle point,
organizes the extinction basin in the phase plane (cf. ). In host populations without critical depensation, it is clearly not possible that an endemic equilibrium arises from the Allee threshold. Abrupt crashes to extinction thus appear to be characteristic for strong AEs.
Biologically, the spontaneous population collapse is the consequence of two mechanisms. The first one is the regulatory potential of parasites. This leads to a depression of the host population size at endemic equilibrium. The second mechanism is that additional mortality due to the disease increases the likelihood of extinction. That is, the effective extinction threshold becomes larger. The infection, therefore, ‘attacks’ the host from two ends of the population size spectrum, thus narrowing down the range in which endemic persistence is possible. Extinction takes place if the range of viable population sizes ceases to exist. Metaphorically speaking, the endemic population equilibrium is finally absorbed by the expanding extinction basin.
Sudden host population deletion due to fold catastrophes can also be observed in other epidemic models, in which the strong AE is incorporated differently. Numerical experiments show that the frequency-dependent model by Deredec and Courchamp Citation15 exhibits a saddle-node bifurcation as well (the authors did not report the possibility of multiple endemic equilibria). Furthermore, if one changes the density-dependent model by Thieme et al. Citation57 to obey a frequency-dependent incidence, two endemic equilibria and their disappearance in a saddle-node bifurcation too become possible.
The abrupt extinction appears to be rather general for AE populations with frequency-dependent transmission. This incidence pattern is typically suggested for sexually transmitted diseases Citation58 and infections in populations with territorial or social behaviour Citation1. In density-dependent transmission models, abrupt host extinction seems to be less general. In Citation57 multiple equilibria are not possible – this may be due to the assumptions that infectives do not reproduce at all or that mortality is density-independent. The model in Citation36 – the same as in Equations (1) and (2) but with density-dependent incidence – allows for fold catastrophes, but in a more restricted parameter range (e.g. there exists a maximum pathogenicity below which saddle-node bifurcations are possible). Furthermore, the situation appears to be more complex as three non-trivial equilibria and tristability are possible. The difference between frequency-dependent and density-dependent transmission is that the former can maintain infections in smaller population sizes, whereas the latter cannot promote disease spread if population size is too small Citation32. Therefore, the unstable endemic equilibrium emanating from the disease-free Allee threshold state is not generally possible for density-dependent incidences.
The existence of a second saddle-node bifurcation when varying pathogenicity rather than transmissibility is the consequence of the simple fact that highly pathogenic parasites cause their own extinction but not that of their host. The two saddle-node bifurcations, if they exist, are separate from each other (cf. ). They are not related, e.g. by sharing the same saddle point as in scenarios with three endemic equilibria Citation26
Citation36
Citation44. This discontinuity has profound implications for control measures aimed at impacting the reproduction number. Increasing ℛ0 can be beneficial for the host if it is changed beyond , thus facilitating endemic persistence rather extinction. Decreasing ℛ0 can be disadvantageous if it is reduced below
, because it can cause host eradication (as illustrated in .
The separate branches of endemic equilibria also complicate a model analysis that is based on numerical continuation of stationary states and bifurcations. Computer software such as MatCont Citation16, AUTO Citation20 or XPPAUT Citation22 might not detect the second saddle-node bifurcation. The re-emerging non-trivial equilibria can, therefore, remain hidden and be missed if the analysis is restricted to numerical tools.
Emerging and introduced infectious diseases have been implicated in the extinction of a large number of species (cf. references in Section 1). If infected populations are additionally subject to a strong AE, they may be at much higher risk than previously thought. Even if population size is considerably large and close to carrying capacity, tiny parameter variations can trigger an unpredictable and drastic population crash towards eradication. The underlying mechanisms – population depression and critical depensation due to a strong AE – are fairly basic and could occur simultaneously in many animal and plant populations. The insights gained from this study are of particular interest for wildlife management and conservation biology. They also shed new light on the effectiveness of pathogens as potential biological control agents and on the difficulties associated with species reintroductions. Moreover, the dramatic changes occurring for large reproduction numbers call for shifting the focus of disease control away from the threshold . The tipping points
with their catastrophic consequences appear to be much more significant. Small parameter changes around
may preserve the population in its existence, while the aim of reducing ℛ0 below one might be unrealistic and gain relatively little additional benefit.
Acknowledgements
The author is a Ciência 2007 fellow, supported by the Fundação para a Ciência e a Tecnologia, Financiamento Base 2008 – ISFL/1/209.
Additional information
Notes on contributors
Frank M. Hilker
Department of Mathematical Sciences, University of Bath, Bath, BA2 7AY, UKReferences
- Altizer , S. , Nunn , C. L. , Thrall , P. H. , Gittleman , J. L. , Antonovics , J. , Cunningham , A. A. , Dobson , A. P. , Ezenwa , V. , Jones , K. E. , Pedersen , A. B. , Poss , M. and Pulliam , J. R.C. 2003 . Social organization and parasite risk in mammals: Integrating theory and empirical studies . Annu. Rev. Ecol. Evol. Syst. , 34 : 517 – 547 .
- Anderson , R. M. 1979 . Parasite pathogenicity and the depression of host population equilibria . Nature , 279 : 150 – 152 .
- Anderson , R. M. and May , R. M. 1979 . Population biology of infectious diseases: Part I . Nature , 280 : 361 – 367 .
- Anderson , R. M. , Jackson , H. C. , May , R. M. and Smith , A. M. 1981 . Population dynamics of fox rabies in Europe . Nature , 289 : 765 – 770 .
- Anderson , R. M. , May , R. M. and McLean , A. R. 1988 . Possible demographic consequences of AIDS in developing countries . Nature , 332 : 228 – 234 .
- Arino , J. , McCluskey , C. C. and van den Driessche , P. 2003 . Global results for an epidemic model with vaccination that exhibits backward bifurcation . SIAM J. Appl. Math. , 64 : 260 – 276 .
- Begon , M. , Bennett , M. , Bowers , R. G. , French , N. P. , Hazel , S. M. and Turner , J. 2002 . A clarification of transmission terms in host-microparasite models: Numbers, densities and areas . Epidemiol. Infect. , 129 : 147 – 153 .
- Brauer , F. 1990 . Models for the spread of universally fatal diseases . J. Math. Biol. , 28 : 451 – 462 .
- Brook , B. W. , Sodhi , N. S. and Bradshaw , C. J.A. 2008 . Synergies among extinction drivers under global change . Trends Ecol. Evol. , 23 : 453 – 460 .
- Busenberg , S. N. and Hadeler , K. P. 1990 . Demography and epidemics . Math. Biosci. , 101 : 63 – 74 .
- Busenberg , S. and van den Driessche , P. 1990 . Analysis of a disease transmission model in a population with varying size . J. Math. Biol. , 28 : 257 – 270 .
- Courchamp , F. , Berec , L. and Gascoigne , J. 2008 . Allee Effects in Ecology and Conservation , New York : Oxford University Press .
- Daszak , P. , Berger , L. , Cunningham , A. A. , Hyatt , A. D. , Green , D. E. and Speare , R. 1999 . Emerging infectious diseases and amphibian population declines . Emerg. Infect. Dis. , 5 : 735 – 748 .
- de Castro , F. and Bolker , B. 2005 . Mechanisms of disease-induced extinction . Ecol. Lett. , 8 : 117 – 126 .
- Deredec , A. and Courchamp , F. 2006 . Combined impacts of Allee effects and parasitism . Oikos , 112 : 667 – 679 .
- Dhooge , A. , Govaerts , W. and Kuznetsov , Y. A. 2003 . MATCONT: A MATLAB package for numerical bifurcation analysis of ODEs . ACM Trans. Math. Softw. , 29 : 141 – 164 .
- Diekmann , O. and Kretzschmar , M. 1991 . Patterns in the effects of infectious diseases on population growth . J. Math. Biol. , 29 : 539 – 570 .
- Dobson , A. and Hudson , P. J. 1986 . Parasites, disease and the structure of ecological communities . Trends Ecol. Evol. , 1 : 11 – 15 .
- Dobson , A. and Poole , J. 1998 . “ Conspecific aggregation and conservation biology ” . In Behavioral Ecology and Conservation Biology , Edited by: Caro , T. M. 193 – 208 . Oxford : Oxford University Press .
- Doedel , E. 1981 . AUTO: A program for the automatic analysis of autonomous systems . Congr. Numer. , 30 : 265 – 284 .
- Dushoff , J. , Huang , W. and Castillo-Chavez , C. 1998 . Backwards bifurcations and catastrophe in simple models of fatal diseases . J. Math. Biol. , 36 : 227 – 248 .
- Ermentrout , B. 2002 . Simulating, analyzing, and animating dynamical systems: A guide to XPPAUT for researchers and students , Philadelphia : SIAM .
- Fromont , E. , Pontier , D. and Langlais , M. 1998 . Dynamics of a feline retrovirus (FeLV) in host populations with variable spatial structure . Proc. R. Soc. Lond. B , 265 : 1097 – 1104 .
- Gao , L. Q. and Hethcote , H. W. 1992 . Disease transmission models with density-dependent demographics . J. Math. Biol. , 30 : 717 – 731 .
- Getz , W. M. and Pickering , J. 1983 . Epidemic models – thresholds and population regulation . Am. Nat. , 121 : 892 – 898 .
- Gomes , M. G.M. , Rodrigues , P. , Hilker , F. M. , Mantilla-Beniers , N. B. , Muehlen , M. , Paulo , A. C. and Medley , G. F. 2007 . Implications of partial immunity on the prospects for tuberculosis control by post-exposure interventions . J. Theor. Biol. , 248 : 608 – 617 .
- Greenhalgh , D. 1997 . Hopf bifurcation in epidemic models with a latent period and non-permanent immunity . Math. Comput. Modelling , 25 : 85 – 107 .
- Grenfell , B. T. and Dobson , A. P. 1995 . Ecology of Infectious Diseases in Natural Populations , Edited by: Grenfell , B. T. and Dobson , A. P. Cambridge : Cambridge University Press .
- Hadeler , K. P. and Castillo-Chavez , C. 1995 . A core group model for disease transmission . Math. Biosci. , 128 : 41 – 55 .
- Harvell , C. D. , Mitchell , C. E. , Ward , J. R. , Altizer , S. , Dobson , A. P. , Ostfeld , R. S. and Samuel , M. D. 2002 . Climate warming and disease risks for terrestrial and marine biota . Science , 296 : 2158 – 2162 .
- Hethcote , H. W. 2000 . The mathematics of infectious diseases . SIAM Rev. , 42 : 599 – 653 .
- Hilker , F. M. Epidemiological models with demographic Allee effect . BIOMAT 2008 – International Symposium on Mathematical and Computational Biology . Edited by: Mondiani , R. P. World Scientific Co. Pvt. Ltd . submitted for publication
- Hilker , F. M. and Schmitz , K. 2008 . Disease-induced stabilization of predator-prey oscillations . J. Theor. Biol. , 255 : 299 – 306 .
- Hilker , F. M. , Lewis , M. A. , Seno , H. , Langlais , M. and Malchow , H. 2005 . Pathogens can slow down or reverse invasion fronts of their hosts . Biol. Invasions , 7 : 817 – 832 .
- Hilker , F. M. , Langlais , M. , Petrovskii , S. V. and Malchow , H. 2007 . A diffusive SI model with Allee effect and application to FIV . Math. Biosci. , 206 : 61 – 80 .
- Hilker , F. M. , Langlais , M. and Malchow , H. 2009 . The Allee effect and infectious diseases: Extinction, multistability, and the (dis-)appearance of oscillations . Am. Nat. , 173 : 72 – 88 .
- Hudson , P. J. , Rizzoli , A. , Grenfell , B. T. , Heesterbeek , H. and Dobson , A. P. 2001 . The Ecology of Wildlife Diseases , Oxford : Oxford University Press .
- Hudson , P. J. , Dobson , A. P. and Lafferty , K. D. 2006 . Is a healthy ecosystem one that is rich in parasites? . Trends Ecol. Evol. , 21 : 381 – 385 .
- Jacquez , J. A. , Simon , C. P. , Koopman , J. , Sattenspiel , L. and Perry , T. 1989 . Modeling and analyzing HIV transmission: The effect of contact patterns . Math. Biosci. , 92 : 119 – 199 .
- Kribs-Zaleta , C. M. and Velasco-Hernández , J. X. 2000 . A simple vaccination model with multiple endemic states . Math. Biosci. , 164 : 183 – 201 .
- Lafferty , K. D. , Allesina , A. , Arim , M. , Briggs , C. J. , De Leo , G. , Dobson , A. P. , Dunne , J. A. , Johnson , P. T.J. , Kuris , A. M. , Marcogliese , D. J. , Martinez , N. D. , Memmott , J. , Marquet , P. A. , McLaughlin , J. P. , Mordecai , E. A. , Pascual , M. , Poulin , R. and Thieltges , D. W. 2008 . Parasites in food webs: The ultimate missing links . Ecol. Lett. , 11 : 533 – 546 .
- Martcheva , M. and Thieme , H. R. 2003 . Progression age enhanced backward bifurcation in an epidemic model with super-infection . J. Math. Biol. , 46 : 385 – 424 .
- McCallum , H. , Barlow , N. and Hone , J. 2001 . How should pathogen transmission be modelled? . Trends Ecol. Evol. , 16 : 295 – 300 .
- Medley , G. F. , Lindop , N. A. , Edmunds , W. J. and Nokes , D. J. 2001 . Hepatitis-B virus endemicity: Heterogeneity, catastrophic dynamics and control . Nat. Med. , 7 : 619 – 624 .
- Milner-Gulland , E. J. , Bukreeva , O. M. , Coulson , T. , Lushchekina , A. A. , Kholodova , M. V. , Bekenov , A. B. and Grachev , I. A. 2003 . Conservation: Reproductive collapse in saiga antelope harems . Nature , 422 : 135
- Moghadas , S. M. 2004 . Analysis of an epidemic model with bistable equilibria using the Poincaré index . Appl. Math. Comput. , 149 : 689 – 702 .
- Molnár , P. K. , Derocher , A. E. , Lewis , M. A. and Taylor , M. K. 2008 . Modelling the mating system of polar bears: A mechanistic approach to the Allee effect . Proc. R. Soc. Lond. B , 275 : 217 – 226 .
- Pugliese , A. 1990 . Population models for diseases with no recovery . J. Math. Bio. , 28 : 65 – 82 .
- Roberts , M. G. 2007 . The pluses and minuses of R 0 . J. R. Soc. Interface , 4 : 949 – 961 .
- Rothschild , B. M. and Laub , R. 2006 . Hyperdisease in the late Pleistocene: Validation of an early 20th century hypothesis . Naturwissenschaften , 93 : 557 – 564 .
- Rowe , S. , Hutchings , J. A. , Bekkevold , D. and Rakitin , A. 2004 . Depensation, probability of fertilization, and the mating system of Atlantic cod (Gadus morhua L.) . ICES J. Mar. Sci. , 61 : 1144 – 1150 .
- Safan , M. , Heesterbeek , H. and Dietz , K. 2006 . The minimum effort required to eradicate infections in models with backward bifurcation . J. Math. Bio. , 53 : 703 – 718 .
- Singer , B. H. and Kirschner , D. E. 2004 . Influence of backward bifurcation on interpretation of R 0 in a model of epidemic tuberculosis with reinfection . Math. Biosci. Eng. , 1 : 81 – 93 .
- Smith , K. F. , Sax , D. F. and Lafferty , K. D. 2006 . Evidence for the role of infectious disease in species extinction and endangerment . Conserv. Biol. , 20 : 1349 – 1357 .
- Stephens , P. A. , Sutherland , W. J. and Freckleton , R. P. 1999 . What is the Allee effect? . Oikos , 87 : 185 – 190 .
- Thieme , H. R. 1992 . Epidemic and demographic interaction in the spread of potentially fatal diseases in growing populations . Math. Biosci. , 111 : 99 – 130 .
- Thieme , H. R. , Dhirasakdanon , T. , Han , Z. and Trevino , R. 2009 . Species decline and extinction: Synergy of infectious diseases and Allee effect? . J. Bio. Dyn. , 3 : 305 – 323 .
- Thrall , P. H. , Antonovics , J. and Hall , D. W. 1993 . Host and pathogen coexistence in sexually transmitted and vector-borne diseases characterized by frequency-dependent disease transmission . Am. Nat. , 142 : 543 – 552 .
- van den Driessche , P. and Watmough , J. 2000 . A simple SIS model with a backward bifurcation . J. Math. Biol. , 40 : 525 – 540 .
- Wyatt , K. B. , Campos , P. F. , Gilbert , M. T.P. , Kolokotronis , S. O. , Hynes , W. H. , DeSalle , R. , Ball , S. J. , Daszak , P. , MacPhee , R. D.E. and Greenwood , A. D. 2008 . Historical mammal extinction on Christmas Island (Indian Ocean) correlates with introduced infectious disease . PLoS One , 3 : e3602
- Zhou , J. and Hethcote , H. W. 1994 . Population size dependent incidence in models for diseases without immunity . J. Math. Biol. , 32 : 809 – 834 .
Appendix A. Existence conditions for two nontrivial stationary states
There are two endemic equilibria if and
, with
. The latter inequality can be solved explicitly in terms of model parameters. Solving for the transmissibility, one obtains
or
, where
Solving for the pathogenicity, one obtains μ<μ1 or μ>μ2, where