The effect of costs associated with toxin production in a competitive system

Abstract

In this paper, we study a two-species competitive system where both the species produce toxin against each other at some cost to their growth rates. A much wider set of outcomes is possible for our system. These outcomes are important contrasts to competitive exclusion or bistable attractors that are often the outcomes for competitive systems. We show that toxin helps to gain an advantage in competition for toxic species whenever the cost of toxin production remains within some moderate value; otherwise it may result in the extinction of the species itself.

Keywords:

• allelopathy
• cost and benefit of toxin production
• competitive exclusion

1. Introduction

The allelopathic effect on plankton communities has become an important subject from the environmental perspective. DeCandolle 8 was probably the first person to suggest the possibility that many plants may excrete something from their roots which is injurious to other plants. The term allelopathy was proposed by Molisch 25 and defined by Rice 32 as the effect of one plant on the growth of another through the release of chemical compounds into the environment. In 1996, the International Allelopathy Society revised the definition of allelopathy to include any process involving secondary metabolites produced by plants, algae, bacteria and fungi that influence the growth and development of biological and agricultural systems 18. This includes both the positive (stimulatory) and negative (inhibitory) effect. Though, some biologists restrict the use of this term to negative effects only 17. There are several examples of allelopathic interactions among marine algal species both in vitro and in situ 5 10 11 14 23 28 29 33 39 40 42. A review of different aspects of chemical ecology of microalgae, including allelopathy, can be found in Cembella 3.

The first mathematical representation of allelopathic interaction was probably proposed by Maynard-Smith 24. The author considered a two species Lotka-Volterra competitive system by assuming that each species produces an allelopathic substance at a constant rate to the other, but only when the other is present. Concerning allelopathy among phytoplankton, several models have examined and generalized the model proposed by Maynard-Smith 24. An exhaustive analysis of stability of a general two-species competition system including allelopathic interactions was carried out by Chattopadhyay 6. Since the production of the allelopathic substance is not instantaneous, but occurs after some discrete time lag required for the maturity of both species, Mukhopadhyay et al. 26 modified the system by considering the time delays due to maturities of the species. Further developments of this basic model to include effects of environmental fluctuations together with spatial and temporal heterogeneity in plankton populations also have been studied 27 38. Sole et al. 36 modified the allelopathic interaction term and proved that the role of allelopathy appears to be important only for high concentrations of the toxic algae. Recently, using simple models, Jonsson et al. 19 supported the previous observation and confirmed that allelopathic (hereafter called a toxin) effect does not play any role to the initiation of algal blooms.

Though toxin provides a benefit to the toxic species by suppressing the growth of its competitors, a cost is always associated with the production of toxin. Naturally, the study of benefit and cost of toxin production is in an important issue in research. In a laboratory experiment, Pintar and Starmer 30 investigated the effect of cost in producing killer toxin for the yeast species, Pichia kluyveri, which is able to produce and excrete extracellular toxic potents that can kill other specific sensitive yeasts. Wolch-Salamon et al. 44 also presented a study of the combined effect of dispersal and nutrient availability on the cost and benefit of toxin production. Hsu and Waltman 16 considered mathematical model for two competing populations competing for a single resource where one of the competitors can produce a toxic chemical against its opponent at some cost to its reproductive abilities. Braselton and Waltman 2 investigated the role of density-dependent inhibitor production for two competing populations, one of which is toxic and a fraction of its potential growth is devoted to the production of toxin. Frank 13 also developed models for the dynamics of competition between producer and susceptible strains. He assumed that producer strains pay a cost for toxin production or plasmid carriage in terms of a relatively lower intrinsic rate of increase, but gain the benefit of killing a fraction of the susceptible competitors at a specified rate. But the interaction between two toxic species, where a cost is associated with the production of toxin, still has not been explored. Initiation of such theoretical study will encourage experimental ecologists to perform some experimental studies in this direction.

In this paper, we have concentrated upon the model considered by Chattopadhyay 6, where two toxin-producing phytoplankton species interact with each other. We have assumed that both phytoplankton can produce toxic chemicals against each other at some expense to their own growth. We have found that benefits of toxic killing outweigh their costs only when the cost of toxin production remains within some moderate value. We have also shown that the coexistence and extinction of species are regulated by these cost functions.

2. Model construction

The model, studied and analysed by Chattopadhyay 6 is the following

where N ₁(t), N ₂(t) are the population densities (number of cells per litre) of two competing species; K ₁, K ₂ are the rate of cell proliferation per litre; α₁, α₂ are the rate of intra-specific competition of the first and second species, respectively; β₁₂, β₂₁ are the rate of inter-specific competition of the first and second species, respectively; γ₁, γ₂ are the rate of toxic inhibition of the first species by the second and vice versa and are environmental carrying capacities (representing number of cells per litre). Chattopadhyay 6 observed that the ratio of the toxic substances of the two species plays an important role in shaping the dynamics of the system.

It is reasonable to consider the toxic concentration as a separate entity in the model formulation. We would like to mention that the inclusion of this mechanism has already been applied in chemostat models 2 16. In 2008, Chakraborty et al. 4 also investigated the effect of nutrient limitation on the toxin production by considering the toxin as a different variable. It is to be noted here that photoxidation can cause rapid degradation of toxic compounds 10 22 and the toxins are quickly inactivated by visible light in the 400–510 mm range and by ultraviolet light in the 225 mm range 7 35.

The above observations encouraged us to modify system (1). In the present study, we have considered a two species competitive system where each species, N ₁ and N ₂, produces a substance toxic to the other. We have represented the toxins produced by both the species, by separate variables, P ₁ and P ₂, respectively. d ₁ and d ₂ are the degradation of toxic substances produced by the first and second species, respectively. It is known that, for algal populations, there is a trade-off between growth rate and the metabolic costs associated with the changes produced for their own protection 41. In our model, we have made the assumption that a portion of the growth rates, and , respectively, of both the species is devoted to producing toxic chemicals.

Recent studies have revealed that allelopathic interactions among plankton become important only at the high cell concentrations typical for well-developed plankton blooms 12 19 33 36. In 2005, Sole et al., modelled allelopathic effects among marine microalgae and quantified the importance of this interaction using experimental data. They suggested that the allelopathic effect should be a non-linear function of the amount of toxin present in the medium or, in other words, of the amount of toxic cells. They modified the mathematical form of the allelopathic interaction term proposed by Chattopadhyay 6 to for non-toxic alga N ₁ and toxic alga N ₂, which suggests that the non-toxic alga is significantly affected by the allelopathy term only after the toxic alga has reached relatively high concentrations. In our study, we also consider a similar type of allelopathic interaction terms as and , which reveals that allelopathic interactions become important only when the amount of toxin produced by some species reaches high levels.

With these assumptions, system (1) reduces to

Since all the parameters of system (2) are non-negative and the right-hand side of system (2) is continuous variables (N ₁, N ₂, P ₁, P ₂) with the positive vector , it can be easily shown that they are local Lipschitzian as well as positive invariance in R ₄ ⁺. Hence the solutions of Equation (2) with non-negative initial conditions exist for all future time and are unique. It can be easily shown that system (2) is bounded also.

The system (2) possesses the following equilibria: E ₀=(0, 0, 0, 0), , and the interior equilibrium point . The equilibrium points E ₁ and E ₂ always exist for the assumptions k ₁<1 and k ₂<1. Ecologically, this is an appropriate assumption in the sense that plankton species do not devote all efforts to produce toxin only. We now seek the region of parameter space for which the model equation (2) admits feasible interior equilibria. Any feasible equilibria must correspond to a positive root N ₁* of the equation f(N ₁)=0, where

for which additionally, , , , i.e. must be satisfied. The constants A _i , i=0, 1, 2, 3, 4, 5 are given below:

Equation (3) has atleast one positive real root if A ₅<0 which is satisfied when . Therefore the sufficient condition for the existence of interior equilibrium point is as follows:

3. Local stability analysis

Now we observe the stability nature of the system (2) around different biologically feasible equilibria. In the text, we state only the results and all proofs are appended in the appendix.

Theorem 1

The system (2) is unstable around E ₀ for all parametric values.

Proof

The proof is obvious and hence omitted.   ▪

Theorem 2

The system (2) is locally asymptotically stable (LAS) around E ₁ if where and LAS around E ₂ if where .

Proof

The proofs are given in the appendix.   ▪

Theorem 3

The sufficient conditions for the LAS of the system (2) around unique E* are as follows:

Proof

The proof is given in the appendix.   ▪

Now, we are in a position to present a comparative observations between systems (1) and (2). To visualize the comparison, at a glance, we present a table (Table 1). We observe the following key points:

Table 1. Comparison of the analytical results between the systems (1) and (2).

Equilibria	Model (1)	Model (2)
Plankton free	Unstable saddle point	Unstable saddle point
N 2 free	LAS: iff	LAS: iff
N 1 free	LAS: iff	LAS: iff
Interior	LAS: when exists iff	LAS: when exists if
		(i)
		(ii)

The following analytical results are immediate from Table 1.

•	Both and E 0 are unstable saddle points.
•	is LAS if , whereas E 1 is LAS if . It is to be noted that if k 1<k 2 then LAS of implies the LAS of E 1. But if k 1>k 2, then LAS of does not always imply the LAS of E 1. Therefore, it is clear that whenever the cost of toxin production of N 1 becomes very high compared to that of N 2, it affects the growth rate of N 1 and as a result it becomes much harder to outcompete N 2.
•	is LAS if , whereas E 2 is LAS if . It is to be noted that if k 2<k 1, then LAS of implies the LAS of E 2. But if k 2>k 1, then LAS of does not always imply the LAS of E 2. Here also, whenever the cost of toxin production for N 2 becomes much higher than that of N 2, it becomes much difficult for N 2 to outcompete N 1.
•	The necessary and sufficient condition for LAS of the interior equilibrium point,E*(0), of the system (1) is An unique interior equilibrium point E* of system (2) is LAS which exists if

4. Numerical experiment

For our numerical simulation, most of the fixed parameter values are taken from various literature sources and are given in Table 2. First we would show that the selected set of parameter values is numerically compatible with the experimental observations performed by Schmidt and Hansen 33. Schmidt and Hansen 33 investigated the importance of cell concentration, growth phase and pH to the harmful effects of Chrysochromulina polylepis on the dinoflagellate Heterocapsa triquetra. They also studied the effect of the initial concentration of C. polylepis on the growth response of H. triquetra in mixed cultures. They observed a decrease in the H. triquetra population on Day 4 in the culture with the highest initial C. polylepis concentration (Figure 1); but, with the other two cultures which were initiated at lower C. polylepis concentrations, the decrease in H. triquetra numbers appeared some days later (Days 6 and 7). They also found that irrespective of the initial concentration of C. polylepis, the decline in H. triquetra numbers always began when the C. polylepis concentration reached ca 3×10⁴ cells ml⁻¹. In our system also (system (2)), we have observed similar kind of observations for the set of parameter values taken from Table 2 (Figure 2). We have considered three different initial concentrations of N ₁ (3, 5, and 7 cells ml⁻¹) keeping fixed the initial concentrations of the other variables . We observe that, for higher initial concentrations of N ₁ (7 cells ml⁻¹), N ₂ starts to decrease on Day 3, but for the cases in which N ₁ starts with lower initial concentrations (3 and 5 cells ml⁻¹), decrease of N ₂ starts a few days later (Days 4 and 5, respectively). We also observe that the concentration of N ₂ starts to decrease only when the concentration of N ₁ reaches 12 cells ml⁻¹ irrespective of the initial concentrations of N ₁. Therefore, the output of the numerical simulation of our model qualitatively resembles the experimental observations of Schmidt and Hansen 33.

Figure 1. Figure taken from Schmidt and Hansen 33.

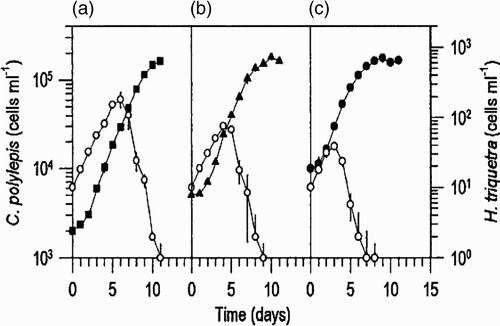
Figure 2. Comparison of the outcome of system (2) for different initial concentrations of N ₁. The dotted curve is due to the initial condition (7, 0.1, 0.1, 0.1), thin line is due to (5, 0.1, 0.1, 0.1) and the bold line is for (3, 0.1, 0.1, 0.1). Parameter values used: k ₁=0.4; k ₂=0.2; d ₁=0.3; d ₂=0.1 and the other parameter values are taken from Table 2.

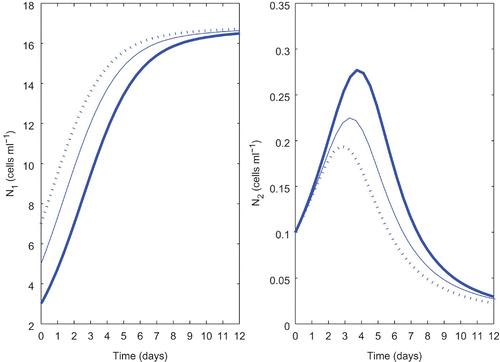
Table 2. The set of fixed parameter values taken from various literature sources.

Parameter	Definition	Values	References
K 1	Rate of cell proliferation	2	Mukhopadhyay et al. 26
K 2	Rate of cell proliferation	1	Mukhopadhyay et al. 26
α1	Rate of intra-specific competition	0.07	Mukhopadhyay et al. 26
	of the first species
α2	Rate of intra-specific competition of the second species	0.08	Mukhopadhyay et al. 26
β12	Rate of inter-specific competition of the first species	0.05	Mukhopadhyay et al. 26
β21	Rate of inter-specific competition of the second species	0.015	Mukhopadhyay et al. 26
γ1	Rate of toxic inhibition of the first species by the second	0.08	Liu and Chen 34
γ2	Rate of toxic inhibition of the second species by the first	0.03	Liu and Chen 34
d 1	Degradation of toxic substances produced by the first species	0.3	–
d 2	Degradation of toxic substances produced by the second species	0.1	–

Since it was quite unclear from the analytical results, we use numerical method to get a clear view regarding the coexistence and extinction of species for different k ₁ and k ₂. Here, mainly we investigate the effect of k ₁ and k ₂ upon the stability of system (2). Specifically, the stability of the system is calculated numerically by testing the Routh–Hurwitz criteria. For this, we plot the stability of different equilibrium points in (k ₁, k ₂) space, where the the other parameter values are fixed as in Table 2 (Figure 3). Then for different parameter set-up, we locate the rest points, determine the eigenvalues of the Jacobian evaluated at the rest points, and solve the ordinary differential equation for different initial conditions.

Figure 3. Domains of stability and instability of system (2). Parameter values are taken from Table 2. The horizontal axis represents the fraction of potential growth devoted to production of toxin for N ₁ (i.e. k ₁). The vertical axis represents the fraction of potential growth devoted to production of toxin for N ₂ (i.e. k ₂).

Figure 3 shows that, the whole parameter space is divided into five non-overlapping regions: R ₁, R ₂, R ₃, R ₄ and R ₅. Note that, each of the regions bears some distinct unique characteristics regarding the stability of the equilibrium points and are listed below.

• (1) R ₁: E* is LAS.

• (2) R ₂: E* and E ₁ are both LAS.

• (3) R ₃: E* and E ₂ are both LAS.

• (4) R ₄: E ₁ is LAS.

• (5) R ₅: E ₂ is LAS.

It is clear from Figure 3 that, whenever k ₁ and k ₂ lie within some moderate values, coexistence occurs. But when the value of k ₁ or k ₂ becomes sufficiently high, it results the extinction of the first or second species, respectively. These findings are in accordance with our analytical observations as well.

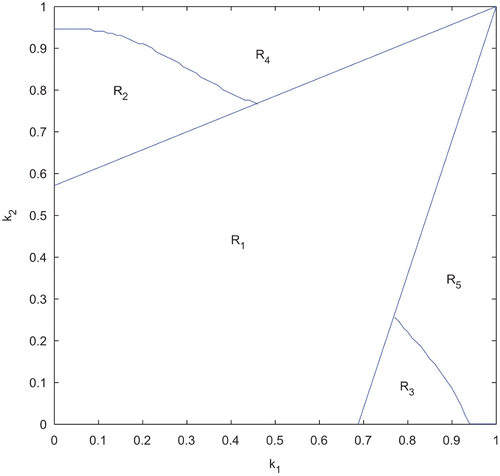
Now, we take points from each of the three regions, R ₁, R ₂, and R ₃ for analysing the existence, stability, and instability behaviour of the equilibrium points. First, we choose k ₁=0.4 and k ₂=0.4 from the region R ₁ and the other parameter values are kept same as in Table 2. For such values, we find three interior equilibrium points among which two are stable and two boundary equilibrium points which are unstable in nature. The eigenvalues of the corresponding equilibrium points are indicated in Table 3. A plot of the trajectories is shown in Figure 4(a). Since two interior equilibria are very close to two boundary equilibria, the enlarged version of these two portions are given in Figure 4(b) and (c). In this case, all the trajectories converge to either of the stable equilibrium points depending on the initial conditions.

Figure 4. Trajectories of the system (2) for k ₁=0.4 and k ₂=0.4 taken from the region R ₁ of Figure 3 and the other parameter values are taken from Table 2. We observe the existence of three interior and two boundary equilibrium points among which two interior equilibrium points are LAS. (b) and (c) Two enlarged portions of (a).

Table 3. Equilibrium points and their stability at k ₁=0.4 and k ₂=0.4.

Equilibrium point	Coordinates	Eigenvalues	Stability
E 1	(17.143, 0, 45.714, 0)	−1.2, 0.3, −0.3, −0.1	Unstable
E 2	(0, 7.5, 0, 30)	0.8, −0.6, −0.3, −0.1	Unstable
E*	(0.011, 7.495, 0.030, 29.981)	−0.8, −0.6, −0.3, −0.1	Stable
	(1.953, 0.638, 5.209, 2.553)	−1.2, −0.5±i 0.4, 0.1	Unstable
	(17.129, 0.005, 45.678, 0.0219)	−1.2, −0.3, −0.3, −0.1	Stable

Now, we move to region R ₂ for the same purpose. We choose k ₁=0.2 and k ₂=0.8 from the region R ₂, and keep the other parameter values same as in Table 2. This gives two biologically feasible interior equilibrium points and two boundary equilibrium points. Interestingly, we observe one positive equilibrium point and one boundary equilibrium point E ₁ are stable. Whereas, the other interior equilibrium point and the boundary equilibrium point E ₂ are unstable saddles. The basic computations are given in Table 4 and a plot of the trajectories is shown in Figure 5. Some trajectories converge to the interior equilibrium point, some of them converge to E ₁ as shown in Figure 5(a). An enlarge version of the portion where one interior and one boundary equilibrium point are close is given in Figure 5(b). It is worthwhile to mention here that the trajectories of attractors are determined by the initial conditions.

Figure 5. Trajectories of the system (2) for k ₁=0.2 and k ₂=0.8 taken from the region R ₂ of Figure 3 and the other parameter values are taken from Table 2. We observe the existence of two interior and two boundary equilibrium points among which one interior and one boundary equilibrium points are LAS. (b) An enlarged portion of (a).

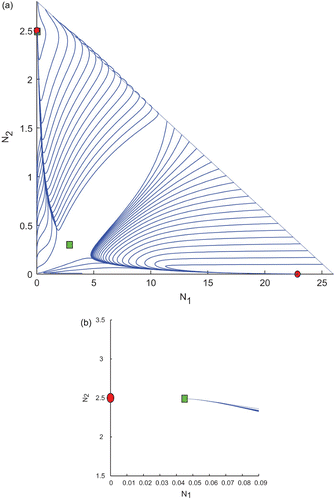
Table 4. Equilibrium points and their stability at k ₁=0.2 and k ₂=0.8.

Equilibrium point	Coordinates	Eigenvalues	Stability
E 1	(22.857, 0, 30.476, 0)	−1.6, −0.3, −0.1, −0.1	Stable
E 2	(0, 2.5, 0, 20.0)	1.5, −0.3, −0.2, −0.1	Unstable
E*	(0.045, 2.488, 0.060, 19.905)	−1.4, −0.3, −0.2, −0.1	Stable
	(2.880, 0.300, 3.840, 2.402)	−1.5, −0.3±i 0.2, 0.1	Unstable

Now, we take k ₁=0.8 and k ₂=0.1, from the region R ₃. Here, the basic computations and the plot of the trajectories are given in Table 5 and Figure 6, respectively. Here, we also find the existence of two interior equilibrium points and two boundary equilibrium points among which one of the interior equilibrium points and the boundary equilibrium point E ₂ are stable and the others are unstable saddles. In this case also, we would like to mention that the trajectories of attractors are determined by the initial conditions.

Figure 6. Trajectories of the system (2) for k ₁=0.8 and k ₂=0.1 taken from the region R ₂ of Figure 3 and the other parameter values are taken from Table 2. We observe the existence of two interior and two boundary equilibrium points among which one interior and one boundary equilibrium points are LAS. (b) An enlarged portion of (a).

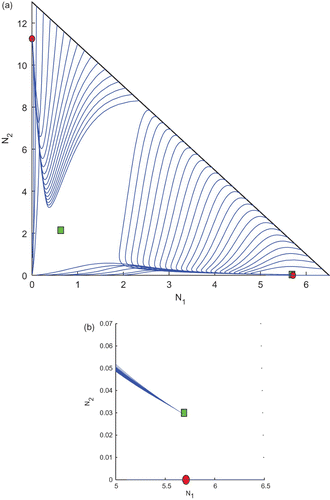
Table 5. Equilibrium points and their stability at k ₁=0.8 and k ₂=0.1.

Equilibrium point	Coordinates	Eigenvalues	Stability
E 1	(5.714, 0, 30.476, 0)	0.8, −0.4, −0.3, −0.1	Unstable
E 2	(0, 11.25, 0, 11.25)	−0.9, −0.3, −0.2, −0.1	Stable
E*	(0.627, 2.142, 3.345, 2.142)	−0.8, −0.4±i 0.2, 0.1	Unstable
	(5.687, 0.029, 30.331, 0.029)	−0.8, −0.4, −0.3, −0.1	Stable

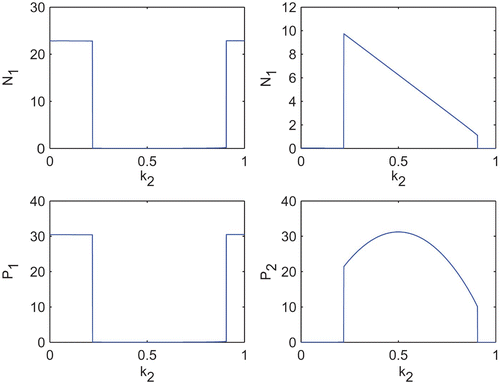
Next, we shall observe the effect of k ₁ and k ₂ upon the equilibrium abundances of both the species. For this, first we fix k ₂=0.2 and vary k ₁ (Figure 7). We observe that, when the toxin production rate (in other words, cost of toxin production) remains very low, abundance of N ₁ as well as its toxin production remains low. Whenever the toxin production rate increases and remains within some moderate values, N ₁ abundance together with its amount of toxin production becomes significantly high and due to such high toxicity, N ₂ abundance remains low. Now, again when the toxin production rate becomes very high, the metabolic cost due to toxin production also becomes very high and affects its growth; competitive advantage due to toxin production cannot compensate for the loss in growth and we observe a drastic fall in N ₁ abundance. Though the toxin production rate remains high, but due to low abundance of N ₁, the toxic effect on N ₂ becomes low which helps to increase N ₂. We also observe the similar behaviour of N ₁ and N ₂ but in an inverse way, when we vary k ₂ and fix k ₁=0.2 (Figure 8).

Figure 7. Equilibrium abundances of the variables of the system (2) for different k ₁. Parameter values are taken from Table 2 and k ₂=0.2.

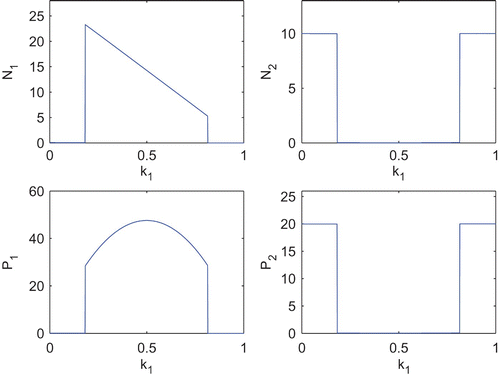
Figure 8. Equilibrium abundances of the variables of the system (2) for different k ₂. Parameter values are taken from Table 2 and k ₁=0.2.

5. Discussion

Phytoplankton species compete with each other for limiting resources, and consequently, they have evolved different strategies to better exploit a resource. Phytoplankton may compete by directly interfering with each other through the release of allelopathic compounds. Allelopathic compounds are secreted into the environment and conferring an advantage to the toxin producing species by killing or inhibiting the growth of other species. One of the main reasons for interest in allelopathy is that it could be one of the main factors that promotes the dominance of marine and freshwater harmful algal bloom (HAB)-forming species over other phytoplankton species 22. Though, the toxin provides a benefit to the toxin-producing species by suppressing the growth of its competitors, a metabolic cost is always associated with the production of toxin. These costs are energetically based. The energy and cellular machinery used to produce toxin cannot be used for reproduction and results in the reduction of population growth rate 30. In order for producers to invade a population of other species, these costs must therefore be compensated by benefits resulting from killing. On the other hand, the costs and benefits of toxin production depend on some environmental conditions 9 13 30 44. Thus, the costs and benefits of toxin production may have some influence on the HAB dynamics. But, it is still not too clear under what conditions do the benefits of toxic killing outweigh the metabolic costs involved. In this study, emphasis has been placed on determining to what extent in toxin production can the toxic species inhibit its competitors.

To demonstrate this, we have considered a two species competitive system considering that each species produces a toxic chemical which is harmful to the other. We have allocated a cost for producing toxic chemicals and toxin concentrations by separate equations. We have assumed that allelopathic effects become significantly important when the amount of toxin present in the system becomes very high (it has been reported by Sole et al. 36; Jonsson 19). For numerical simulations, parameter values are taken from various literature sources. We have investigated the importance of initial cell concentrations on the abundance of other species. It is observed that, when a species starts with higher initial concentrations, it receives an advantage due to toxicity in the early days of the experiment. But, if the initial concentration of the species is low, its toxic effect starts to affect the other a few days later. We have also observed that the concentration of one species starts to decrease only when the concentration of another one exceeds some critical level. These findings are in accordance with the laboratory experiment of Schmidt and Hansen 33.

There are studies where the effect of costs and benefits of toxin production has been discussed. Both the costs and benefits of toxin production are dependent on environmental conditions 9 13 30 44. In nature, plants are constrained to having less than maximum levels of toxin release 1 15 20 31 37 43. In this study, we have also found such types of critical levels of toxin production. We observe that each toxic species gain an advantage in competition over the other by producing toxic chemicals until the metabolic costs associated with toxin production remains within some moderate values. Interestingly, within that range, the competitive advantage due to toxin production may to some extent compensate the loss due to the production of toxic chemicals. But, whenever it crosses the critical value, the metabolic cost due to toxin production also becomes very high and affects its growth. In this case, the metabolic cost outweighs the benefit of toxic killing; as a result abundance of that species decreases and further loss can results species extinction. Therefore, the output of our mathematical model supports the natural evidences. On the other hand, whenever the toxin production rate remains below some critical level, the benefit of toxic killing becomes very low, so that the abundance of the species remains very low in spite of its high growth rate. Thus, finally, we can conclude that, by releasing toxic chemicals, toxin-producing species gain an advantage in competition; but the release of toxic chemicals should remain within some moderate values, otherwise it can result the extinction of species itself. It is observed that cost of toxin production first affects the growth of the population, and then it goes to toxin production. Also, the abundance of the toxic cells has a great impact on allelopathic effect. In this respect, our result resembles the experimental outcomes of Schmidt and Hansen 33.

Acknowledgements

The authors are grateful to the referees for their extremely valuable comments and suggestion on the previous version of the manuscript.

Appendix

First of all, we state a lemma related to the characteristic polynomial of a matrix 21 and then study the stability properties of our system.

Lemma A1

Let A be an n×n matrix which is symmetrically partitioned into upper or lower triangular-block matrices labelled

or

then the characteristic polynomial of the matrix A is equal to the product of the characteristic polynomials of A ₁ and A ₃. Now, we prove Theorems 2–4.

Proof of Theorem 2

The Jacobian matrix for the system (2) about E ₁ is the following

The above Jacobian matrix can be written as

where

and

Note that, the eigen values of the matrix are negative if . Also, the eigen values of the matrix are negative. Therefore the necessary and sufficient condition for LAS of the system (2) around E ₁ is

Similarly, we can show that the necessary and sufficient condition for LAS of the system (2) around E ₂ is

  ▪

Proof of Theorem 3

To determine the local stability character, we compute the Jacobian matrix of the system (2) about E*, which is given below

The characteristic equation for the above is given below

where,

It is obvious that c ₀ and c ₁ are positive. Now c ₂ and c ₃ will be positive if Therefore, all eigen values for the non-zero equilibrium point E* of the system (2) will have negative real part if and c ₄>0 i.e.

  ▪