ABSTRACT
This paper addresses the influence of newly-developed Cattaneo–Christov heat flux model on peristalsis. Analysis has been carried out in a two-dimensional planner channel with wall properties and the Soret effect. An incompressible viscous fluid fills the space inside the channel. The relevant mathematical modeling is developed and a perturbation technique is employed to obtain a series form of solutions about small wave numbers. Expressions of velocity, temperature, concentration and heat transfer are treated graphically, corresponding to elasticity parameters, relaxation time and Prandtl numbers specifically. The graphical results are found distinctive that offers challenging role for further research on the topic. Further, the results of Fourier’s law can be verified when the relaxation time of the Cattaneo–Christov heat flux model is considered absent or concepts of large wavelength and small Reynolds numbers are applied.
1. Introduction
There is growing interest in the study of peristalsis due to its occurrence in extensive environmental, industrial and physiological processes. Some prominent processes, among many others, include the movement of chyme in the digestive tube, the movement of spermatozoa and ova in the cervical canal and fallopian tubes, the carrying of lymph in vessels, the transfer of urine to the bladder, the mixing of food, water transport from the ground to tall trees, and the spontaneous movement of blood vessels. Peristaltic transport is generated through periodic waves travelling beside the walls – thus the peristaltic flow can be developed in tubes or channels. The study of peristaltic activity was initiated by Latham (Citation1966), after which the experimental analysis of Shapiro, Jafferin, and Weinberg (Citation1969) formalized the validity of the theoretical results. Elnaby and Haroun (Citation2008) addressed peristaltic transport with compliant wall effects of viscous fluid, while Vasudev, Rao, Reddy, and Rao (Citation2010) examined the heat transfer phenomenon on peristalsis. In two separate studies, Tripathi and Beg (Citation2014a, Citation2014b) investigated the peristaltic flow of nanofluid and the peristaltic flow of Berger’s fluid through a porous medium. Abd elmaboud and Mekheimer (Citation2011) presented work on second-order non-linear peristaltic flow, while Ali and Hayat (Citation2007) investigated peristaltic motion in an asymmetric channel. The peristaltic flow comprising copper-water nanofluid has been investigated by Abbasi, Hayat, and Ahmad (Citation2015), while Hayat, Tanveer, Yasmin, and Alsaadi (Citation2015) explored the outcomes of Hall currents and thermal deposition on the peristaltically generated flow of Eyring–Powell fluid. Further, the channel walls possess some elastic properties due to their compliant and damping nature. In physical situations such as the movement of blood through vessels and tissues, tension and the damping of walls play an essential role. The instabilities of a plane channel flow induced by a peristaltic wave bounded by compliant walls have been investigated under a large wavelength for small Reynolds numbers by many researchers in recent years (for some representative studies, see Gad, Citation2014; Javed, Hayat, & Alsaedi, Citation2014; Riaz, Nadeem, Ellahi, & Akbar, Citation2014). The compliant wall effects on peristaltic transport have also been reported by Hina, Hayat, Asghar, and Hendi (Citation2012). Some authors have presented their research on the fluid flows followed by peristaltic activity using a numerical approach. Ali, Javid, Sajid, Zaman, and Hayat (Citation2016) addressed the heat transfer phenomenon in a curved channel using numerical analysis, while Abbasi, Hayat, and Alsaedi (Citation2015) conducted a numerical study on the Hall current effects with magnetohydrodynamics (MHD) Carreau–Yasuda fluid in a curved flow configuration. Mustafa, Abbasbandy, Hina, and Hayat (Citation2014) numerically examined the Soret and Dufour effects of peristaltic flow. Moreover, some interesting studies relevant to computational fluid dynamics (CFD) are mentioned in Zhang, Huang, Zhang, Zou, and Tang (Citation2016), Fu, Uddin, and Curley (Citation2016) and Özkan, Wenka, Hansjosten, Pfeifer, and Kraushaar-Czarnetzki (Citation2016).
The transfer of heat is a widespread phenomenon that occurs due to the difference in temperature between a system and its environments. Whenever there is a difference in temperature between two objects, heat starts propagating from the higher temperature field to the lower temperature field. Considerable attention has been devoted to studying the behavior of the heat transport mechanism. Some authors have analyzed the heat transfer mechanism through the empirical law of conduction known as Fourier’s law. In particular, Turkyilmazoglu and Pop (Citation2013) reported heat transfer effects with Jeffery fluid, while Jalil, Asghar, and Imran (Citation2013) found the heat transfer mechanism on the moving surface of a free stream. Hayat, Rafiq, Ahmad, and Yasmin (Citation2015) looked at the impact of melting heat transfer on peristalsis with thermal radiation and Joule heating, and Tripathi (Citation2013) presented a transient heat flow analysis. Further, Ali, Sajid, Javed, and Abbas (Citation2010) examined the heat transfer phenomenon in curved channel, while Sheikholeslami, Hatami, and Ganji (Citation2014) carried out an analysis on nanofluid heat transfer with a magnetic field. However, the above-mentioned studies addressed the heat transfer mechanism using Fourier’s law. This law was considered to be sufficient to describe heat transfer analysis for two centuries. However, the vector field aspect of heat flux requires that the governing equations for heat transfer involve an objective time derivative. Cattaneo on the basis of Cattaneo's law proposed a new model by adding a term of relaxation time in Fourier's law called the modified Fourier heat conduction law. Cattaneo generalizes the modified Fourier heat conduction law by utilizing the Oldroyd’s upper-convected derivative and thus constitutes a single equation for temperature. After the development of the Cattaneo–Christov model, various attempts were made to verify fluid flow according to this law. Christov (Citation2009) investigated the heat equation that describes the frame indifferent expression of the Maxwell–Cattaneo version of heat flux. Straughan (Citation2010) presented the thermal relaxation effects of the Christov heat flux model and found that uniform convection switches to fluctuating convection with narrower channels. Han, Zheng, Li, and Zhang (Citation2014) explored the heat transfer phenomenon of viscoelastic fluid under the Cattaneo–Christov theory, while Haddad (Citation2014) employed the Cattaneo–Christov model to study the thermal instabilities in fluid saturating a porous medium. Mustafa (Citation2015) explored the thermal relaxation aspects of the Cattaneo–Christov model in the flow of a rotating frame, while Khan, Mustafa, Hayat, and Alsaedi (Citation2015) numerically investigated the model with an exponentially stretching surface. Hayat, Imtiaz, Alsaedi, and Almezal (Citation2016) carried out a study for the MHD characteristics of fluid under the Cattaneo–Christov theory with homogeneous–heterogeneous reactions, and Salahuddin, Malik, Hussain, Bilal, and Awais (Citation2016) analyzed the Cattaneo–Christov heat flux model numerically through variable viscosity.
In spite of the considerable importance of the heat transfer mechanism to peristalsis in physical and engineering systems, to date no study has been reported that encountered the heat flux model based on Cattaneo–Christov concepts. The motivation of this work is to predict the behavior of heat flow subject to the Cattaneo–Christov heat flux model under a sinusoidally induced peristaltic wave between compliant walls. An incompressible viscous fluid is employed in a channel to predict the relaxation time effects. Further to exploring the extended heat effects on the concentration field, the Soret effect is employed. Series solutions are obtained for a small wave number and the obtained results are discussed. It is found that convective results (obtained by Fourier’s law) have oscillatory behavior in terms of temperature and concentration. Moreover, in the limiting case, the exact results corresponding to Fourier’s law can be recovered.
2. Mathematical formulation
To begin with, the peristaltically induced flow of an incompressible viscous fluid bounded by horizontal walls with a separating distance of 2d is considered. The flow configuration is such that the fluid flows with speed c in the x-direction along the channel walls whereas the y-direction is transverse to it. Further, the elastic and damping nature of the wall are also taken into account. Through the following expression, the configuration of the wall can be analyzed:
(1)
where
is the wave amplitude,
is the wavelength,
is the distance of the walls from the center of the channel,
is the time, and
and
are the displacements of the upper and lower walls, respectively.
The fundamental equations are based on the conservation of mass, momentum, energy and concentration:
(2)
The momentum equation is
(3)
(4)
(5)
The energy equation q can be obtained from the heat flux model proposed by Christov (Citation2009), whereas the concentration equation encounters the thermo-diffusion or Soret effect. The mathematical expressions are as follows:
(6)
(7)
(8)
The Cattaneo–Christov heat flux model has the form
(9)
where
is the two-dimensional velocity of the viscous fluid,
is the heat flux,
is the temperature of the fluid,
is the thermal conductivity and
is the relaxation time parameter for the heat flux. When
, the simplified expression of Fourier’s law can be deduced. Since we considered an incompressible fluid, the above expression takes the form
(10)
Upon the elimination of q between Equations (4) and (10), the required energy equation reads
(11)
The concentration equation (Equation (5)) is then formulated as:
(12)
where
is the fluid density,
is the dynamic viscosity of the fluid,
is the kinematic viscosity of the fluid,
is the concentration of the fluid,
is the mass diffusivity coefficient,
is the specific heat constant,
is the thermal conductivity,
is the thermal diffusion ratio coefficient and
is the mean temperature of the fluid.
The corresponding conditions at the boundary are given by
(13)
(14)
Here, and
represent the prescribed values of temperature and concentration at the lower channel walls and
and
represent the prescribed values of temperature and concentration at the upper channel walls.
The no-slip condition at the boundary has the form given below:
(15)
(16)
where
is the coefficient of elastic tension,
is the coefficient of the mass per unit area, and
is the coefficient of the viscous damping.
On combining equations (7) and (8) by taking partial derivative of equation (7) with respect to y and partial derivative of equation (8) with respect to x and then subtracting the resultant expression we get
(17)
The stream function and the dimensionless variables are given in the following definitions:
(18)
The dimensionless equations – Equations (11), (12) and (17) – are obtained as follows:
(19)
(20)
(21)
with the conditions
(22)
(23)
(24)
(25)
(26)
In the above equations, the asterisks have been dropped for the simplification of the mathematical expressions. The definitions of the dimensionless amplitude ratio , the Prandtl number
, the wave number
, the Reynolds number
, the relaxation time parameter
, the non-dimensional elasticity parameters
,
and
, the Schmidt number
and the Soret number
are as follows:
(27)
3. Perturbation solutions
The non-linearity of the resulting system suggests the application of the perturbation method about the small wave number . Thus we get the series form of solutions to plot graphs corresponding to the stream function, temperature, concentration and heat transfer coefficient (
) as follows (Hayat, Rafiq, et al., Citation2015):
(28)
3.1. Zero-order system
(29)
(30)
(31)
(32)
(33)
(34)
(35)
The solutions of the above equations subject to the corresponding boundary conditions are
(36)
(37)
(38)
and the heat transfer coefficient by the definition
(39)
It should be noted that Equation (38) is identical to the result in Elnaby and Haroun (Citation2008), which was obtained in the absence of heat and mass transfer.
3.2. First-order system
(40)
(41)
(42)
(43)
(44)
(45)
(46)
and the solution
(47)
(48)
(49)
and the heat transfer coefficient
(50)
where
Here ,
,
,
,
,
,
,
,
,
,
,
,
,
,
and
represent partial derivatives with respect to the corresponding subscripts.
3.3. Second-order system
(51)
(52)
(53)
(54)
(55)
(56)
along with the solutions
(57)
(58)
(59)
(60)
The quantities and
can be determined through algebraic calculations.
4. Results and discussion
To analyze the heat transfer effects on peristalsis we applied the concept of the Cattaneo–Christov heat flux model to the flow of viscous fluid. The stream function equation is comprised of the wall properties, whereas the pair of equations are made for temperature and concentration distribution, and the concentration distribution equation covers the Soret effect. The variations in the fluid velocity , temperature
, concentration
and coefficient of heat transfer
are described in this section.
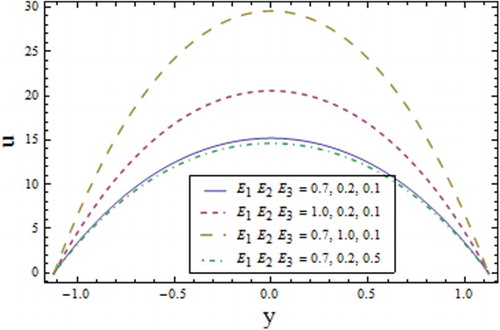
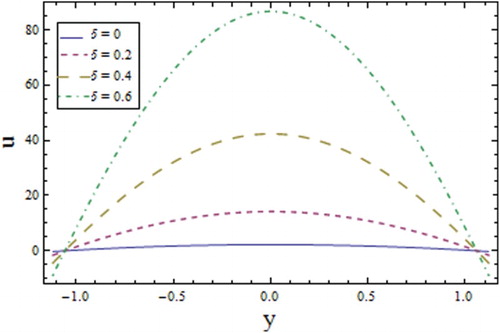
presents the increasing velocity with the wall elastic parameters and
due to their elastic behavior, whereas an increase in the damping parameter
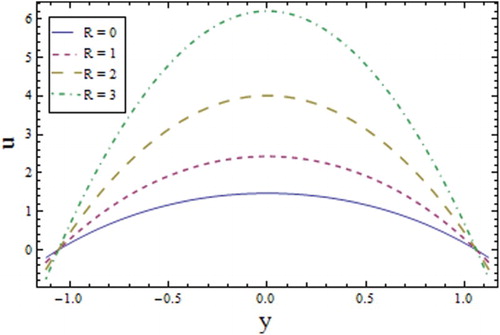
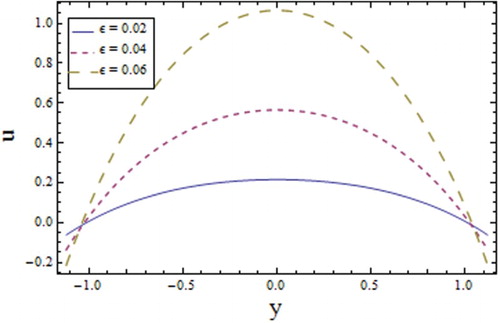
reduces the velocity. Figures – show the increase in velocity with increasing values of the wave number
, Reynolds number
and amplitude ratio parameter
.
Figure 1. Profile of for different values of wall parameters when
,
,
,
and
.
Figure 2. Profile of for different values of wave number when
,
,
,
,
,
and
.
Figure 3. Profile of for different values of Reynolds number when
,
,
,
,
,
, and
.
Figure 4. Profile of for different values of amplitude ratio parameter when
,
,
,
,
,
and
.
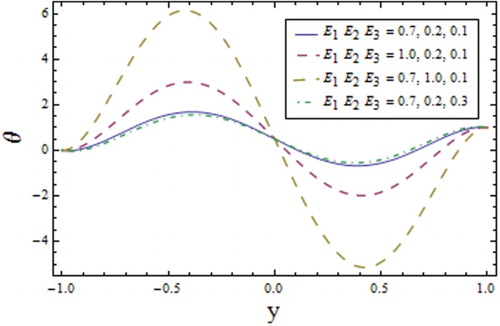
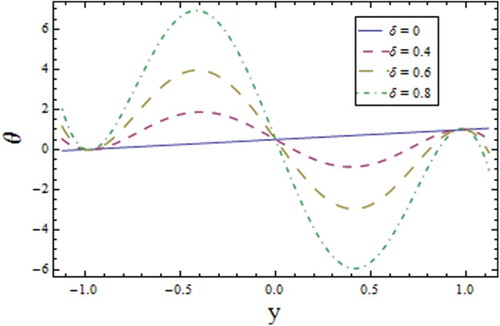
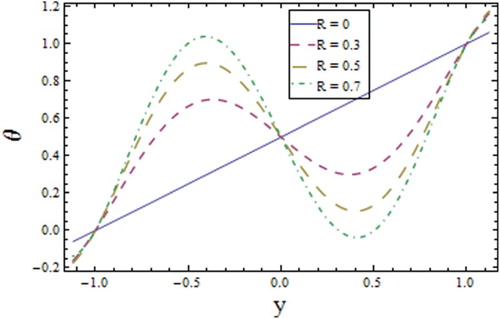
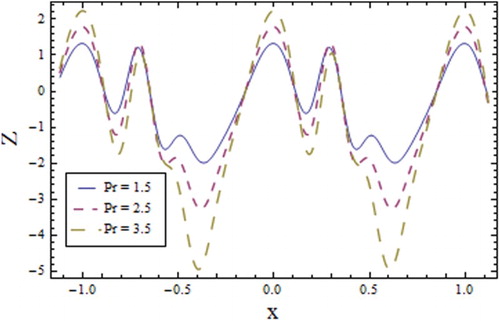
Figures – show the results of oscillatory response of graphs corresponding to temperature, concentration and heat transfer coefficient. It is anticipated that the consideration of the extended heat flux model (Cattaneo–Christov model) is responsible for these results. From it can be seen that the behavior of wall properties towards temperature profile is increasing towards and
, while an increase in
lowers the fluid temperature. represents a decrease in the temperature profile with increasing values of
near the upper wall, as larger values of
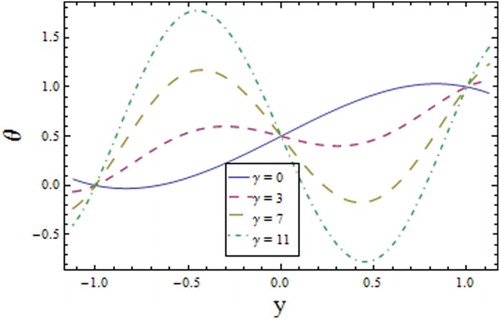
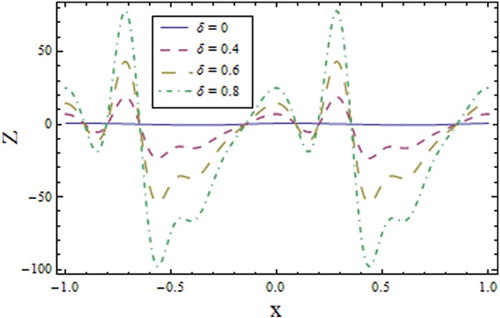
reduce the thermal conductivity of the fluid. The results are found to match well with those obtained by Mustafa (Citation2015) and Hayat et al. (Citation2016) in terms of a single plate placed towards a positive axis in a semi-infinite domain. However, near the negative side of the channel the results are unique. analyzes the impact of the increasing relaxation time of heat flux
on the channel walls. For increasing values of
opposite behavior is noticed, i.e., an increase in
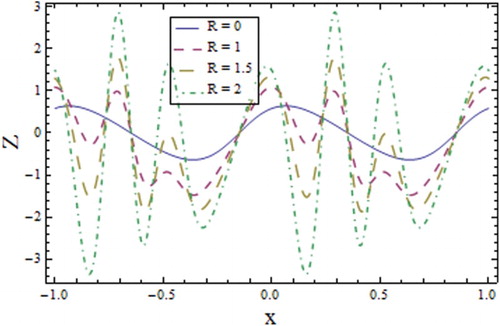
increases the temperature distribution towards the lower wall and decreases the temperature distribution towards the upper wall when the relaxation time increases. These results can be compared qualitatively with Hayat et al. (Citation2016) and Salahuddin et al. (Citation2016) in terms of a half channel. Figures and display a decrease in the temperature profile with increasing values of the wave number
and Reynolds number
at the upper channel wall. Moreover, in absence of
and
we get straight lines corresponding to viscous fluid (see Figures and ). It is noted that by the concepts of a large wavelength and small Reynolds number (Haddad, Citation2014) the results of Fourier’s law can be retrieved, i.e., the Cattaneo–Christov theory becomes identical to Fourier’s law.
Figure 5. Profile of for different values of wall parameters when
,
,
,
,
,
and
.
Figure 6. Profile of for different values of Prandtl number when
,
,
,
,
,
,
,
, and
.
Figure 7. Profile of for different values of relaxation time parameter when
,
,
,
,
,
,
,
, and
.
Figure 8. Profile of for different values of wave number when
,
,
,
,
,
,
,
, and
.
Figure 9. Profile of for different values of Reynolds number when
,
,
,
,
,
,
,
, and
.
Figure 10. Profile of for different values of Reynolds number when
,
,
,
,
,
,
,
,
and
.
Figure 11. Profile of for different values of wave number when
,
,
,
,
,
,
,
,
,
and
.
Figure 12. Profile of for different values of Soret number when
,
,
,
,
,
,
,
,
,
and
.
Figure 13. Profile of for different values of Schmidt number when
,
,
,
,
,
,
,
,
,
and
.
Figure 14. Profile of for different values of Prandtl number when
,
,
,
,
,
,
,
,
,
and
.
Figure 15. Profile of for different values of relaxation time parameter when
,
,
,
,
,
,
,
,
,
and
.
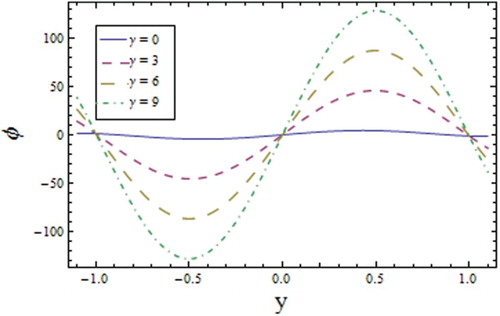
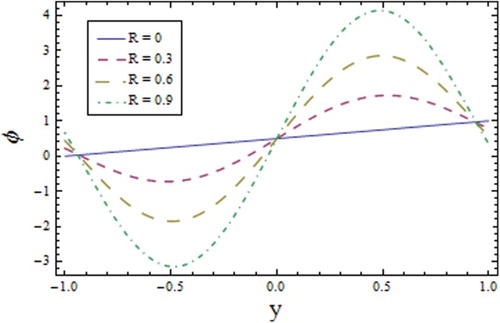
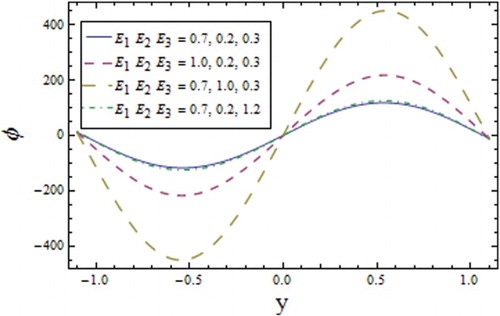
Figures and signify that larger values of and
raise the concentration distribution around the upper wall of the channel. The impact of the Soret number
on the concentration distribution is to cause an increase () since higher values of
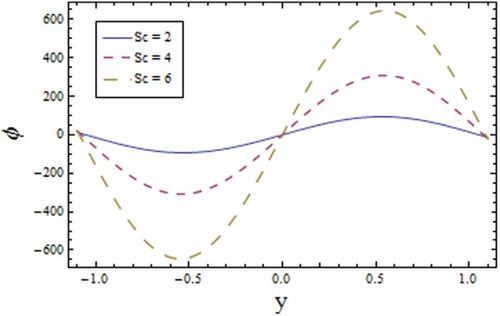
increase the density of the fluid. An increase in the concentration distribution is noticed for the Schmidt number
as greater values of
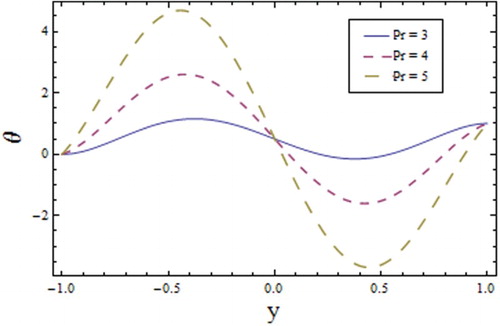
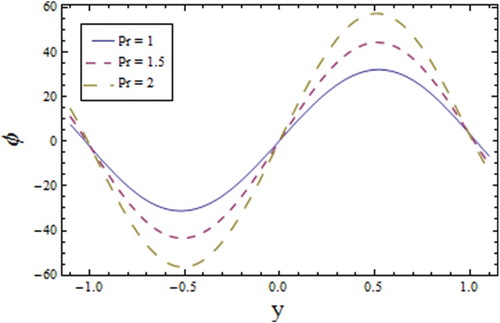
result in a decrease in the molecular diffusion that dominates the intermolecular forces between molecules, hence there is increase in the concentration (see ). The effect of the Prandtl number
on the concentration is to cause an increase because with an increase in
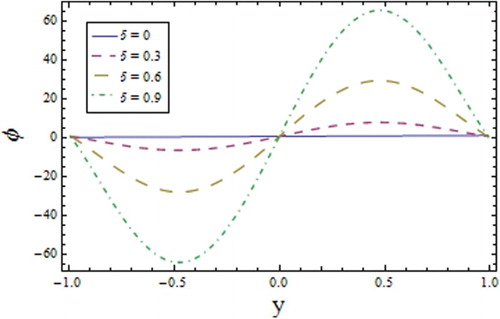
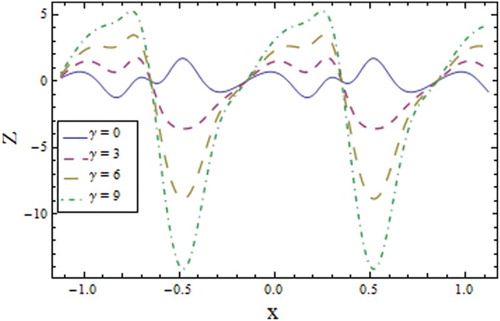
the viscosity increases (see Figure ). Figure exhibits the increasing response of the concentration profile towards the relaxation time
. The wall parameters have an effect on the concentration profile that is opposite to the effect of the temperature (Figure ), i.e.,
and
lessen the concentration of the fluid and
increases it.
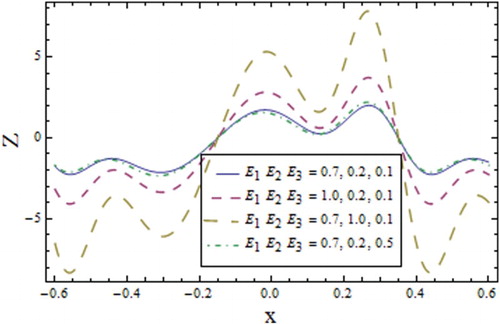
Figures – correspond to the effects of the relaxation time , wall parameters
,
and
, and Prandtl number
on the heat transfer coefficient
. The results shows an increase in the concentration as a result of these parameters, except for the wall damping parameter
which results in a decrease in the concentration (see Figure ). Figures and present the increase in the heat transfer coefficient with growing values of the wave number
and Reynolds number
.
Figure 16. Profile of for different values of wall parameters when
,
,
,
,
,
,
,
and
.
Figure 17. Profile of for different values of relaxation time parameter when
,
,
,
,
,
,
and
.
Figure 18. Profile of for different values of wall parameters when
,
,
,
,
and
.
4.1. Concluding remarks
A study of peristaltic motion with flexible walls occupying a viscous fluid composed of thermal convection effects satisfied by the Cattaneo–Christov heat flux model has been presented. In addition, the thermo-diffusion or Soret effect is also factored into the analysis. The results indicate that the thermal relaxation time plays a key role in the heat transfer process. Thus, an interesting relationship between the temperature and concentration has been found. The graphical results encourage further consideration of the Cattaneo–Christov theory with respect to peristalsis. This work can also be used to compare the results of the Cattaneo–Christov heat flux model to other work on peristaltic theory. The main findings are as follows:
Velocity increases with the wave number and Reynolds number since the speed of the wave as well as its momentum diffusivity increases with increasing values of these parameters.
The decrease on temperature and increase of concentration is noticed for Prandtl number.
In contrast to Fourier’s law, the effect of the relaxation time parameter causes a decrease in temperature, but the concentration increases with γ.
The concentration rises where temperature falls with wave number and Reynolds number.
Due to the generation of fluid viscosity and density, the concentration of the fluid increases as the Schmidt number and Soret number increase.
The absolute heat transfer coefficient increases with an increase in the relaxation time and the Prandtl number.
Figure 19. Profile of for different values of Prandtl number when
,
,
,
,
,
,
and
.
Figure 20. Profile of for different values of Reynolds number when
,
,
,
,
,
,
and
.
Figure 21. Profile of for different values of wave number when
,
,
,
,
,
,
and
.
Disclosure statement
No potential conflict of interest was reported by the authors.
References
- Abbasi, F. M., Hayat, T., & Ahmad, B. (2015). Peristaltic transport of copper-water nanofluid saturating porous medium. Physica E: Low-dimensional Systems and Nanostructures, 67, 47–53. doi:10.1016/j.physe.2014.11.002
- Abbasi, F. M., Hayat, T., & Alsaedi, A. (2015). Numerical analysis for MHD peristaltic transport of Carreau–Yasuda fluid in a curved channel with Hall effects. Journal of Magnetism and Magnetic Materials, 382, 104–110. 10.1016/j.jmmm.2015.01.040 doi: 10.1016/j.jmmm.2015.01.040
- Abd elmaboud, Y., & Mekheimer, K. S. (2011). Non-linear peristaltic transport of a second-order fluid through a porous medium. Applied Mathematical Modelling, 35, 2695–2710. doi:10.1016/j.apm.2010.11.031
- Ali, N., & Hayat, T. (2007). Peristaltic motion of a Carreau fluid in an asymmetric channel. Applied Mathematics and Computation, 193, 535–552. doi:10.1016/j.amc.2007.04.010
- Ali, N., Javid, K., Sajid, M., Zaman, A., & Hayat, T. (2016). Numerical simulations of Oldroyd 8-constant fluid flow and heat transfer in a curved channel. International Journal of Heat and Mass Transfer, 94, 500–508. doi:10.1016/j.ijheatmasstransfer.2015.11.066
- Ali, N., Sajid, M., Javed, T., & Abbas, Z. (2010). Heat transfer analysis of peristaltic flow in a curved channel. International Journal of Heat and Mass Transfer, 53, 3319–3325. doi:10.1016/j.ijheatmasstransfer.2010.02.036
- Christov, C. I. (2009). On frame indifferent formulation of the Maxwell-Cattaneo model of finite-speed heat conduction. Mechanics Research Communications, 36, 481–486. doi:10.1016/j.mechrescom.2008.11.003
- Elnaby, M. A. A., & Haroun, M. H. (2008). A new model for study the effect of wall properties on peristaltic transport of a viscous fluid. Communications in Nonlinear Science and Numerical Simulation, 13, 752–762. 10.1016/j.cnsns.2006.07.007 doi: 10.1016/j.cnsns.2006.07.007
- Fu, C., Uddin, M., & Curley, A. (2016). Insights derived from CFD studies on the evolution of planar wall jets. Engineering Applications of Computational Fluid Mechanics, 10, 44–56. doi:10.1080/19942060.2015.1082505
- Gad, N. S. (2014). Effects of hall currents on peristaltic transport with compliant walls. Applied Mathematics and Computation, 235, 546–554. doi:10.1016/j.amc.2014.02.081
- Haddad, S. A. M. (2014). Thermal instability in Brinkman porous media with Cattaneo–Christov heat flux. International Journal of Heat and Mass Transfer, 68, 659–668. doi:10.1016/j.ijheatmasstransfer.2013.09.039
- Han, S., Zheng, L., Li, C., & Zhang, X. (2014). Coupled flow and heat transfer in viscoelastic fluid with Cattaneo–Christov heat flux model. Applied Mathematics Letters, 38, 87–93. doi:10.1016/j.aml.2014.07.013
- Hayat, T., Imtiaz, M., Alsaedi, A., & Almezal, S. (2016). On Cattaneo–Christov heat flux in MHD flow of Oldroyd-B fluid with homogeneous–heterogeneous reactions. Journal of Magnetism and Magnetic Materials, 401, 296–303. doi:10.1016/j.jmmm.2015.10.039
- Hayat, T., Rafiq, M., Ahmad, B., & Yasmin, H. (2015). Effect of melting heat transfer on peristalsis in the presence of thermal radiation and Joule heating. International Journal of Biomathematics, 8. doi:10.1142/S1793524515500734
- Hayat, T., Tanveer, A., Yasmin, H., & Alsaadi, F. (2015). Simultaneous effects of Hall current and thermal deposition in peristaltic transport of Eyring-Powell fluid. International Journal of Biomathematics, 8(2). doi:10.1142/S1793524515500242
- Hina, S., Hayat, T., Asghar, S., & Hendi, A. A. (2012). Influence of compliant walls on peristaltic motion with heat/mass transfer and chemical reaction. International Journal of Heat and Mass Transfer, 55, 3386–3394. 10.1016/j.ijheatmasstransfer.2012.02.074 doi: 10.1016/j.ijheatmasstransfer.2012.02.074
- Jalil, M., Asghar, S., & Imran, S. M. (2013). Self similar solutions for the flow and heat transfer of Powell-Eyring fluid over a moving surface in a parallel free stream. International Journal of Heat and Mass Transfer, 65, 73–79. doi:10.1016/j.ijheatmasstransfer.2013.05.049
- Javed, M., Hayat, T., & Alsaedi, A. (2014). Peristaltic flow of burgers’ fluid with compliant walls and heat transfer. Applied Mathematics and Computation, 244, 654–671. doi:10.1016/j.amc.2014.07.009
- Khan, J. A., Mustafa, M., Hayat, T., & Alsaedi, A. (2015). Numerical study of Cattaneo-Christov heat flux model for viscoelastic flow due to an exponentially stretching surface. PLOS One. doi:10.1371/journal.pone.0137363
- Latham, T. W. (1966). Fluid motion in peristaltic pump (MS Thesis). Massachusetts Institute of Technology, Cambridge, MA. Retrieved from http://hdl.handle.net/1721.1/17282
- Mustafa, M. (2015). Cattaneo-Christov heat flux model for rotating flow and heat transfer of upper-convected Maxwell fluid. AIP Advances. doi:10.1063/1.4917306
- Mustafa, M., Abbasbandy, S., Hina, S., & Hayat, T. (2014). Numerical investigation on mixed convective peristaltic flow of fourth grade fluid with dufour and soret effects. Journal of the Taiwan Institute of Chemical Engineers, 45, 308–316. doi:10.1016/j.jtice.2013.07.010
- Özkan, F., Wenka, A., Hansjosten, E., Pfeifer, P., & Kraushaar-Czarnetzki, B. (2016). Numerical investigation of interfacial mass transfer in two phase flows using the VOF method. Engineering Applications of Computational Fluid Mechanics, 10, 100–110. doi:10.1080/19942060.2015.1061555
- Riaz, A., Nadeem, S., Ellahi, R., & Akbar, N. S. (2014). The influence of wall flexibility on unsteady peristaltic flow of Prandtl fluid in a three dimensional rectangular duct. Applied Mathematics and Computation, 241, 389–400. doi:10.1016/j.amc.2014.04.046
- Salahuddin, T., Malik, M. Y., Hussain, A., Bilal, S., & Awais, M. (2016). MHD flow of Cattanneo–Christov heat flux model for Williamson fluid over a stretching sheet with variable thickness: Using numerical approach. Journal of Magnetism and Magnetic Materials, 401, 991–997. doi:10.1016/j.jmmm.2015.11.022
- Shapiro, A. H., Jafferin, M. Y., & Weinberg, S. L. (1969). Peristaltic pumping with long wavelengths at low Reynolds number. Journal of Fluid Mechanics, 37, 799–825. doi.org/10.1017/S0022112069000899 doi: 10.1017/S0022112069000899
- Sheikholeslami, M., Hatami, M., & Ganji, D. D. (2014). Nanofluid flow and heat transfer in a rotating system in the presence of a magnetic field. Journal of Molecular Liquids, 190, 112–120. doi:10.1016/j.molliq.2013.11.002
- Straughan, B. (2010). Porous convection with Cattaneo heat flux. International Journal of Heat and Mass Transfer, 53, 2808–2812. doi:10.1016/j.ijheatmasstransfer.2010.02.017
- Tripathi, D. (2013). Study of transient peristaltic heat flow through a finite porous channel. Mathematical and Computer Modelling, 57, 1270–1283. 10.1016/j.mcm.2012.10.030 doi: 10.1016/j.mcm.2012.10.030
- Tripathi, D., & Beg, O. A. (2014a). Peristaltic propulsion of generalized Burgers’ fluids through a non-uniform porous medium: A study of chyme dynamics through the diseased intestine. Mathematical Biosciences, 248, 67–77. doi:10.1016/j.mbs.2013.11.006
- Tripathi, D., & Beg, O. A. (2014b). A study on peristaltic flow of nanofluids: Application in drug delivery systems. International Journal of Heat and Mass Transfer, 70, 61–70. doi:10.1016/j.ijheatmasstransfer.2013.10.044
- Turkyilmazoglu, M., & Pop, I. (2013). Exact analytical solutions for the flow and heat transfer near the stagnation point on a stretching/shrinking sheet in a Jeffrey fluid. International Journal of Heat and Mass Transfer, 57, 82–88. doi:10.1016/j.ijheatmasstransfer.2012.10.006
- Vasudev, C., Rao, U. R., Reddy, M. V., & Rao, G. P. (2010). Effect of heat transfer on peristaltic transport of a Newtonian fluid through a porous medium in an asymmetric vertical channel. European Journal of Scientific Research, 44, 79–92. doi:org/10.1155/2015/163832
- Zhang, Y., Huang, H., Zhang, X., Zou, Y., & Tang, S. (2016). The effect of aspect ratio and axial magnetic field on thermocapillary convection in liquid bridges with a deformable free-surface. Engineering Applications of Computational Fluid Mechanics, 10, 16–28. doi:10.1080/19942060.2015.1101401