Choreographing complexity: investigation of elementary preservice teachers’ quantitative manipulation in large group formations

ABSTRACT

This study accumulated empirical evidence pertaining to preservice teachers’ (n = 62) reasoning processes while choreographing group formations with embedded algebra tasks. The activities were designed to facilitate examination of the potential pedagogical connections between choreographing formation and mathematics, with particular emphasis on creating geometrical formation designs accompanied by corresponding algebraic equations. This study used a reflective thematic analysis to investigate the experiences and sense-making of participants during the choreography activity and related reflection. Analysis of the results revealed that the participants recognised and utilised a multiplicity of connections pertaining to the complexity of the formations and mathematical factors within the equations. This study verified that the participants were able to employ mathematical patterns of increasing levels of complexity to generate original and creative choreography designs for group formations, while completing embedded algebraic tasks. The strategies of developing choreographic positions employed by the participants revealed that mathematical models, especially those using a combination of algebra and geometry, can be useful for designing structural arrangements that are capable of flexibility and change.

KEYWORDS:

• Mathematics education
• early algebra
• dance-themed education
• teacher education

During the past three decades, mathematics education has changed fundamentally in terms of both instructional models and curriculum structures (Bennett, 2022; National Council of Teachers of Mathematics [NCTM], 1989, 2000, 2006; Niss & Højgaard, 2019). Instructional changes include switching from didactic teacher-centred approaches to student-centred pedagogy, particularly by offering students opportunities to explore mathematics through collaborative group activities. However, the challenge of restructuring the sequence for teaching mathematics content within the curriculum remains fundamentally unaddressed in spite of the substantial impact in has on students’ learning (Remillard, Reinke, & Kapoor, 2019). In particular, it is recommended that the traditional “arithmetic-then-algebra” linear-style curriculum should be replaced with a spiral curriculum with algebra employed together with the other five pillars of modern mathematics – numbers, geometry, measurement, data-analysis, and probability (Knuth, Stephens, Blanton, & Gardiner, 2016). This type of spiral curriculum without interruptive content transitions should be introduced as early as kindergarten and continue throughout secondary education and beyond.

Unfortunately, the cross beams necessary for connecting these major curricular pillars (e.g. early algebra) are mostly absent. Instead, different mathematical content areas are routinely taught as independent areas with little or no emphasis placed on highlighting connections (Atiyah, 2001). Especially in early childhood and elementary education, educators tend to teach the different mathematical content areas separately instead of linking them (Hohenwarter & Jones, 2007). Since preparation for algebra is habitually characterised as the essential component of a high-quality elementary mathematics curriculum, students do not get sufficient opportunities to systematically develop the connections among their algebraic thinking and corresponding arithmetic and geometric reasoning (Kilpatrick, Swafford, & Findell, 2001). Research could address this recurring issue by methodically examining curricular structures and teaching methods that are effective for combining vital mathematical topics.

Early algebra in teacher education

Empirical evidences have affirmed that teachers’ effectiveness in design and implementation lessons has a direct impact student academic success (Darling Hammond & Baratz-Snowden 2007). The development knowledge for teaching algebra, as one of the weakest pedagogically prepared contents, is systematically neglected in teacher education programs for early childhood and elementary generalists (Sibgatullin et al., 2022). Encouraging students to develop algebraic thinking skills as early as their first year of formal schooling, during prekindergarten, has been a growing general consensus among educators internationally – based on recognition that early exposure to patterns with sufficient structural complexity can influence a student’s future mathematics learning trajectory during secondary and higher education (Blanton & Kaput, 2005; Blanton et al., 2015; Luken & Sauzet, 2021). However, there is still a lack of agreement on the optimal pedagogical approaches that early childhood educators should acquire during their teacher education programs so that they are properly prepared to implement these teaching methods in their own classrooms (Kieran, 2006). Early algebra, also called pre-algebra, is a distinct topic that is cognitively and pedagogically different from formal algebra. In contrast with formal algebra, during early algebra students are primarily focused on: (A) cultivating mathematical habits of mind, (B) learning processes for demonstrating structured mathematical thinking, and (C) investigating each problem’s larger context (Carraher, Schliemann, & Schwartz, 2008; Papic, Mulligan, & Mitchelmore, 2011). Teacher educators are expected to develop pre-service teachers’ effectiveness at conceptualising these early algebra concepts by demonstrating pedagogical practices with variations to embedding abstract knowledge into real-life sense making scenarios (Wasserman, 2017).

For teachers to effectively support the development of their students’ early algebra capacity, those teachers need to first obtain their own understanding of the key concepts in early algebra (i.e. pattern recognition from simplicity to complexity), while also developing a flexible approach to contextualising that information during their students learning (Hill, Rowan, & Ball, 2005). However, a majority of the elementary classroom teachers responsible for providing early algebra instruction did not receive any substantial early algebra education themselves when they were elementary students (Cai, Ng, & Moyer, 2011). As a key component facilitating the challenging transition from arithmetic to algebra, effective early algebra pedagogy such as developing patterns with simple (e.g. AB pattern) to complex (e.g. Fibonacci sequence) structures from should be designed to purposefully build upon students’ pre-symbolic reasoning abilities towards the development of more abstract mathematical thinking (Hohensee, 2017). In particular, teacher education programs for elementary generalists should strive to provide their future graduates with pedagogical approaches to embedding early algebra topics, such as pattern composition and number relationship exploration, into the context of traditional arithmetic elementary maths education (Charalambous, Hill, Chin, & McGinn, 2020; Lau, 2021).

Choreography-themed mathematics pedagogy

Mathematics teacher educators have developed a variety of choreography -based teaching strategies to deliver instruction on patterns and sequences, measurement of time and distance, and fractional as well as proportional relationships (Belcastro & Schaffer, 2011; Temple et al., 2020). Depending on each individual curriculum developers’ expertise, these learning activities have illustrated the potential for a wide range of dance skills to be used when teaching a variety of mathematical topics. Some previous studies have focused on the positioning of limbs during dance as a method for teaching the concepts of angles and shapes (Kalpana, 2015; Moore & Linder, 2012). Other researchers have focused on dancers’ foot positioning and directional movement as a means for introducing pedagogy that contextualises geometrical transformation concepts (Parsley, & Soriano, 2009; Rosenfeld, 2013).

On the topic of large group formations, mathematics educators have explored cognition process of learning mathematics through collaborative dance formation and mathematic structures in marching band formations. In particular, Vogelstein, Brady, and Hall (2019) investigated geometrical transformations of quadrilaterals and triangles in large-scale dance performance (i.e. 2016 Rio Olympic Games) by asking participants to fold and flip sheets into triangles by replicating the Rio Olympic shows. By remediating school geometry as ensemble learning, Ma and Hall (2018) investigated the mathematical infrastructure of large marching band formations as well as the pedagogical possibilities of implementing walking-scale geometry which may positively impact of band students’ spatial reasoning and social stewardship. More recently, a group of researchers investigated the experience of middle grade students translate dancer-performed choreography into computer-simulated choreography (Steinberg, Gresalfi, Vogelstein, & Brady, 2022). Steinberg’s team found that the dance and choreography themed computer coding tasks facilitated students to stay engaged and solve challenge problem through long-lasting iteration with a variety of reasoning strategies.

Researchers in teacher education have illustrated some of the many different choreography-themed approaches available for contextualising mathematics instruction, but there has not yet been a systematic survey of how dance might be integrated across the mathematics curriculum. In previous research, we (An et al., 2017, 2019; An, Tillman & Hachey, 2021) undertook a series of connected studies that were designed to identify opportunities for instructional connections between choreographing formations and mathematics. In these studies, we identified several pedagogical benefits from choreography-themed mathematics education including: (1) transformation of passive, didactic learning environments into active, kinaesthetic learning environments, (2) encouraging creativity and flexibility during instruction of mathematics, and (3) improving students’ conceptual understanding of mathematics through engaging group collaborations (An et al., 2017).

To further investigate choreography-themed pedagogy as applied to specific mathematics content areas identified as essential by the National Council of Teachers of Mathematics (NCTM, 2000), we previously assessed 109 participants’ teaching strategies for numbers and operations (An et al., 2019). This study identified 20 different approaches for teaching students to understand numbers through embodied activities such as combining small groups of dancers into larger groups and vice versa to physically signify multiplication and division process and creating original choreographing formations in which the number of dancers in specific regions of the stage represents mathematical variables and constants. As a follow-up study designed to focus on geometry education, we evaluated participants’ (n = 48) conceptions for pedagogy that employed stage-performed choreography as a context for learning geometrical concepts (An, Tillman & Hachey, 2021). Such empirical research studies have demonstrated the instructional efficacy of employing choreographed formations to facilitate sociable, engaging, and memorable mathematics instruction.

Research purpose and questions

Because of distinct physical, visual, and spatial features, dance and choreography could play a key role in the development of a robust and holistic mathematics pedagogy that is appropriate for young learners (LaMotte, 2018). One major limitation is the inadequate number of empirical research studies that have examined how formation-themed contextualisation impacts mathematics teaching and learning. Therefore, the current study was undertaken in an attempt to partially address this research gap, specifically by investigating preservice elementary teachers’ pedagogical awareness and conceptual responsiveness to mathematics instruction on the theme of dance formations. The participants in this study were each asked to generate a set of original formations for a team with 48 dancers. The guiding research questions posed in this study focused on further clarifying the role that formation arrangement might play in creating engaging mathematics education. In particular, we investigated the roles of simplicity and complexity of choreographic formations within the preservice elementary teachers’ original formation designs, with the ambition of answering the following research question: How did the participating elementary preservice teachers reason about simplicity and complexity in their choreographed formations and associated equations?

Method

Research setting and participants

The current study builds upon a line of inquiry investigating choreography-themed mathematics curriculum and instruction, which cumulatively has involved over 400 undergraduate students who are enrolled in the teacher education program. While our previous analyses focused on (1) perceptions of choreography-themed mathematics education (An et al., 2017), (2) teaching of quantitative reasoning through choreographing formations (An et al., 2019), and (3) developing geometrical reasoning through dance (An, Tillman & Hachey, 2021), the current study concentrated on examining pedagogical connections between algebraic reasoning and choreographed positions. This study was conducted at a large research university on the southwestern United States border, where senior-level college undergraduate students (n = 62) were invited to participating in the study. The participants were from four sections of a mathematics teaching methods courses. These college students are being trained to be teachers for elementary school, teaching mathematics for prekindergarten to fifth grade with students from four years old to eleven years old. The sample size is determined based on the principle of thematic saturation (Nelson, 2017) to maximise the emergence of different coding categories. All participants had four (12-credit hour) mathematics content courses during their freshmen and sophomore years, while none of them had any college level dance courses before enrolling into the mathematics teaching methods course. The participants in this study were predominantly female (93.5%) and Hispanic (95.2%). The age range of the participants is 21 years old to 34 years old, with a median age of 24 years old.

Description of the learning task

In keeping with some of our previous iterations of mathematics-based dance activities (An et al., 2017, 2019; An, Tillman & Hachey, 2021), the choreographic position design tasks employed colour-coded plastic cubes placed on grid-paper as a medium for designing and developing original formations. A sequence of five preparatory activities (see Table 1) involved locating and moving coloured cubes within a six-by-six matrix, with progressively more challenging mathematics required (see Figure 1). In each preparatory activity, three segments were implemented including (1) formation choreography (20–35 minutes), (2) dance rehearsal (30–50 minutes), and (3) dance performance/debriefing (20 minutes). Each participant had a cumulative over 180 minutes of group dancing experiences took place in regular 3-hour class meetings in three different weeks across the five preparatory activities before they were introduced to the target activity.

Figure 1. Sequence of five preparatory activities with progressively more challenging mathematics.

Table 1. The Description of five preparatory activities.

Choreology Tasks	Learning objectives	Expected student actions
For a pair of dancers	Reflection and rotational symmetry	Execute duet dance based on reversed foot positions between the two dancers
For a group of four dancers	Addition and subtraction	Perform dance in opposite directions to represent the addition and subtraction process
For a group of six dancers	Multiplication and division	Manipulate number of dancers and movements of each dancer to represent multiplications
For a group of eight dancers	Concepts of variables	Perform dance with a number of dancers in specific regions on the stage as a way to represent constants and variables
For a group of 12 dancers	Concepts of functions	Change movement when dancers stand in certain regions on the stage to investigate concepts of function

All five of the pre-activities required choreographing eight distinct formations, but the number of dancers in the formation increased from a pair of dancers (represented by manipulating two cubes), to a group of four dancers (represented by four cubes), then a group of six dancers (i.e. six cubes), a group of eight dancers (i.e. eight cubes), and lastly a group of twelve dancers (i.e. twelve cubes). One of the instructors’ responsibilities during these activities was to facilitate participants’ transition of spatial reasoning from a third-person perspective (i.e. seeing the whole formation from an aerial perspective) during the formation arrangement stage to first-person perspective (i.e. seeing parts of the formation from an individual’s viewpoint) during the dance rehearsal stage. To support this effort, each preparatory task was started with a hands-on activity during which coloured cubes were used to practice the dance rehearsal from the aerial perspective.

The goal of providing the preparatory tasks was to strengthen participants’ conceptual understanding of how choreographers must develop an allocentric (i.e. focused on other persons) understanding of space, rather than the egocentric (i.e. focused on the self) understanding that we each use to navigate the world around us. To accomplish this goal, participants were assigned into different dance teams to implement their chorography. Specifically, seven dance teams were formed from groups of eight participants while one dance team was formed from a group of six participants. Each participant was asked to select a cube with a unique colour to represent themselves on the grid, and then they found their corresponding locations on the open floor based upon their specific cube’s position. Also, while the formations pre-determined each dancer’s position relative to the group, teams had creative freedom to decide each individual dancer’s limb movements and whether they would be synchronised with the other dancers.

After the preparatory tasks were completed, the target choreographic position design task was introduced. While participants were assigned to complete the preparatory tasks in groups, the target choreographic position design task required participants to work independently. The participants were asked to choreograph formations for a large group for 48 dancers (two groups of 24 each). A binary variable was intentionally assigned as a design criteria because it increased the complexity of the choreography patterns, but not so much so that they became unmanageable. For example, when four dancers stand in a row, the unitary unit only can make one formation (i.e. AAAA). Instead, the binary unit (A & B) can make six distinctive internal variations without changing the line structure when four dancers (two from each unit) stand in a row (i.e. ABAB, BABA, AABB, BBAA, ABBA, & BAAB), and eight more distinctive internal variations can be made when the unbalanced conditions are considered (i.e. ABBB, BABB, BBAB, BBBA, AAAB, AABA, ABAA, & BAAA).

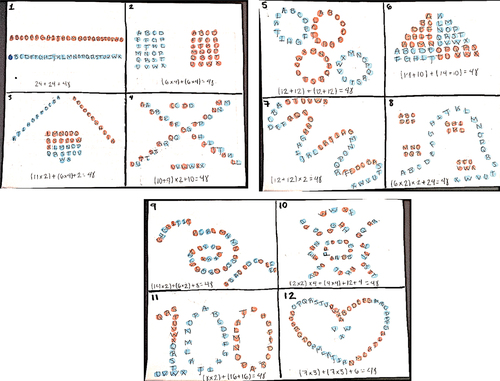
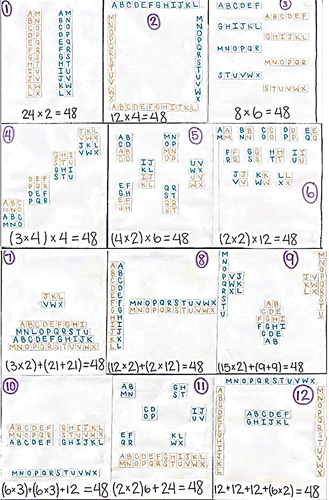
In this task, each participant designed 12 formations (see Figures 2, 3). The guideline for designing the choreographic position was that the formation should be developed from a beginning stage with a simple structure to more advanced stages with increasingly complex structures. Participants were instructed to create formations in which each formation was more complex than the previous one. Thus, the last formation must have the most complex structure. Participants were also asked to use two different colours when evenly distributing the dancers’ choreography, and use letters (i.e. A, B, C, through X) to indicate each specific dancer. Underneath the diagram for each formation, participants were asked to write an equation that mathematically described the formation’s structure.

Figure 2. Example of formation designs from one of the participants

Figure 3. Example of formation designs from another one of the participants.

Data collection and analysis

Both pictorial data and written essays were collected from the participating preservice teachers. For the pictorial data, 62 sets of choreographic position records, including 744 individual formations with corresponding mathematical equations, were collected. Additionally, reflective essays (n = 124) with an average length of 284 words were collected from each participant. The first reflective essay prompted participants to explain the reasoning they employed while developing their formations and to justify what made their later formations (#7–12) more complex than their earlier formations (#1–6). The second reflective essay asked participants to reflect upon the complexity of each choreographed formation and its corresponding mathematical equation. Specifically, participants were asked to analyse whether the simple formations had simple equations while the complex formations had complex equations. A preliminary data analysis based on pictorial data was performed to check the accuracy and consistency between hand-drawing formations and hand-writing mathematics equations with a goal to screening unqualified data. A total of 7 formations with corresponding equations (0.9%) that are spotted with mathematics errors were removed from the second round of analysis.

The collected reflective essays were utilised as the major data resource, while the pictorial data were examined as supportive evidence to triangulate each participant’s testimonies. This study used a reflective thematic analysis [RTA] which we adapted from Braun and Clarke (2006), with our overall goal to investigate the experiences and sense-making of participants during the choreography activity and related reflection. While an inductive analytical process, we note our a priori belief that that data provided information that could be analysed from three viewpoints: (1) from the dancers’ perspective – how blue and orange group dancers were mixed in each formation, (2) from the shape perspective – what each formation looked like from an aerial viewpoint, and (3) from the equation perspective – how the characteristics of the equations corresponded to the formations. The data were analysed from these viewpoints through several steps including (1) review to familiarise researchers with the data; 2) open coding to generate all possible raw code units, (3) categorise similar and related code units into initial themes based on patterns of shared meaning, and (3) generation of themes by refining and naming. To ensure rigour during the data analysis, the collected data were examined by three researchers independently. The developed themes were compared iteratively and cases with discrepancies (3.4% of coding results) of were resolved collectively through group discussion.

Results

The results from this study revealed an observable relationship between the complexity of choreographed formations and their corresponding algebraic-geometrical structures. The analysis of the reflective essays further specified this relationship from the perspectives of (A) the spatial arrangement of dancers, (B) the geometrical shape of formations, and (C) the complexity of corresponding equations (see Table 2). Some of the most prevalent themes employed by the participants when defining the complexity of their dance formations included: (1) the distribution of dancers with the patterns, (2) the number of sides articulated by the overall shape from each formation, and (3) the use of simple addition/subtraction or more complex multiplication/division in the corresponding equations. In one of the simpler formations the dancers were arranged into two large blocks (e.g. all blue team in a row and all red team in another row), as the formations further developed, the dancers were assigned into many smaller clusters of just three dancers. Additionally, the formations that created basic closed shapes with simple reflective symmetry (like rectangles or triangles) were generally identified as simple formations, and the formations that created more open shapes with radial or rotational features (like spirals or clusters) were generally identified as more complex.

Table 2. The definition of complexity in dance formation structures.

Foci	The Definition of Complexity in Dance Formation Structures	Counts (Rate)
On the Dancers	Boys and girls were not equally distributed/paired up	8 (12.9%)
	Boys and girls were mixed (beyond simple AB patterns)	30 (48.4%)
	Dancers spread out over the dance floor (less concentration)	11 (17.7%)
	Consists of more scattered groups/segments in formations	25 (40.3%)
	Dancers move in different directions and/or distances	10 (16.1%)
On the Shape	More diagonals were used	9 (14.5%)
	More curves/loop were used	12 (19.4%)
	Less reflectional symmetry was used	15 (24.2%)
	More rotational symmetry was used	6 (9.7%)
	More complex shapes were used	38 (61.3%)
	Shapes have more sides or overlap	8 (12.9%)
	More radial patterns were used	8 (12.9%)
	Figures with larger perimeters	5 (8.1%)
On the Equation	Smaller numbers were incorporated	12 (19.4%)
	More multiplication/division and less addition/subtraction	41 (61.1%)
	More odd numbers and less even numbers	20 (32.3%)
	Equations with more parenthesis (order of operations)	3 (4.8%)
	Equations with more than three components	14 (22.6%)

A closer analysis of the formations and corresponding algebraic equations (see Table 2) indicated that (1) simple formations were associated with shorter algebraic equations that mostly employed the operations of addition and subtraction among components, whereas (2) complex formations were associated with longer algebraic equations that included multiplication and division operations among components. An emergent relationship was evident between the perceived complexity of the equations and their corresponding formations: The sum or product of two or more compound items (e.g. a×b×c + d×e) was generally associated with more complex formations, while the sum or product of real numbers (e.g. 3a + 4b) was typically associated with simple formations. Among the twelve formations that each participant created, equations based on repeated addition (e.g. “a+b+c”) or repeated multiplication (e.g. “a×b×c”) were often found in participants’ first six choreographed formations, appearing a total of 252 times (approximately two-thirds of all #1–6 formations). In contrast, equations based on mixtures of addition and multiplication (e.g. “n(a+b)+m(c+d)”) were predominantly found in participants’ last six choreographed formations, appearing a total of 231 times (over half of all #7–12 formations). Compound equations such as “n(a×b)+m(c+d)” were only identified within the #7–12 formations (see Table 3).

Table 3. Distribution of equations structures in simple and complex formations.

Equations Identified in Formation
	Simple Formations* (n = 372) Count (Percent)	Complex Formations* (n = 372) Count (Percent)
a+b+c	143 (38.4%)	2 (0.05%)
a×b×c or n(ab)	109 (29.3%)	27 (7.3%)
n(a+b)	75 (20.2%)	79 (21.2%)
n(a+b)+m(c+d)	32 (8.6%)	128 (34.4%)
n(a×b)+m(c×d)	13 (3.5%)	103 (27.7%)
n(a×b)+m(c+d)	0 (0%)	33 (9%)

Note: Simple formations refer to formations #1–6, and complex formations refer to formations #7–12 from each participant’s choreography design.

Five cases were selected to illustrate the different emphases of participants’ explanations of regarding the increasing complexity of the designed choreographic position. These examples were selected based on the diversity of themes represented as well as their high levels of self-insight and honest disclosure. Other cases were excluded to avoid data redundancy due to repetitive themes in their formation development patterns and corresponding rationale (Fusch & Ness, 2015). These exclude cases are not because their formation designs quality and/or their rationale explanations are lower than the selected ones; they were excluded because their formation development patterns and the corresponding rationale either had repetitive themes as the selected five cases. The names of the selected reflection essay authors have been changed to pseudonyms: Catalina, Julieta, Isabella, Amaya, and Norma.

Case #1: Catalina – from regular to asymmetrical shapes

The shape outlined by the formation was frequently mentioned by participants as one of the key variables for distinguishing between complex and simple formations. Formations based on shapes with symmetrical features (e.g. squares, rectangles, and equilateral triangles) were associated with simpler designs whereas those based on irregular or concave polygons (e.g. stars, darts, and bowties) were associated with more complex designs. In particular, Catalina designed her last formation as a mountain with two vertex points inwards and the corresponding equation that she provided for the formation was 2×(3 + 3)+2×(2 + 3)+2×(2 + 3 + 2)+2×(3 + 3) = 48. Catalina specified her perspective on what features made her formations more complex:

In my dance designs, I think that complexity is having different forms that look unique. Symmetry is often being used in dance formations, but I believe complexity comes from how the formations of the dancers are in unsymmetrical formed in sharping irregular figures. I started off with equilateral shapes on first page of designs [for easier designs] and on the second page I had both convex and concave shapes [for more complex designs]. It takes time and effort but once it displays a wonderfully made figure it gives a creative and complex aspect of each shape. From the dancer side, the complexity of the dance design dealt with if I could place them in boy-girl mixed formation or all boys on one side of the stage and girls on the other side of the stage. Also, I needed to figure the different combination of boys and girls being near each other or far away from each other.

Case #2: Julieta – from larger to smaller groups

In order to choreograph for 48 dancers, the participants generally divided their formations into multiple larger segments or smaller clusters. While the beginning formations often had two segments of 24 dancers each (e.g. usually all the blue group in one block and all the orange group in another block), another prevalent methods for dividing up the groupings was based on other factors of 48—including three groups of 16 dancers, four groups of 12 dancers, six groups of 8 dancers, and so forth. For the most part, the participants believed that dividing a larger segment of the group into smaller clusters increased the complexity of the choreographic position. For example, Julietta arranged her last formation in a shape of snowflake with both reflectional and rotational symmetry features and the equation that she provided was 4× [(3 × 2)+(3 + 3)] = 48. Julietta presented her understanding of the transformation between simple and complex arrangements:

My key rationale to guide me to develop more complex designs was to lessen the number of times, or number of students, in a simple form. For example, if I had two large rectangles in one design, my next design would have four smaller rectangles, and so on. My formation structure from simple to complex was also transformed from simple with rows and columns to multiplexed arrangements since they’re more diverse and open and made up of more spread-out groups. I believe the complex formations are formations that you can see the dancers that are taking advantage of the dance space where students aren’t as close together and therefore can’t rely on simply remembering that they are next to one specific classmate. Each student has to remember their placement rather than who they are next to.

Case #3: Isabella – from balanced to irregular formations

One of the frequently mentioned themes on the differences between simple and complex formations was that simple formations are composed with a balanced structure, while complex formations are composed with more asymmetrical and irregular patterns. In terms of the equations employed, the use of odd numbers (as opposed to even numbers) played a dynamic role in the development of more complex formations. By assigning dancers into groups with unequal members (e.g. group A with 3 dancers and group B with 5 dancers, rather than two groups with 4 dancers each), and then manipulating these group clusters into curved or asymmetrical shapes, increasingly complex formations could be created. As an illustration, Isabella recounted her approach for the development of increasingly complex formations within her choreography:

I believe complex formations are the ones that cannot end up grouping evenly. Some common features you can find in my simple equations are addition with larger numbers and [with] factors of 2. In complex equations I used [more] smaller numbers and also tried to stay away from even numbers and incorporated more odd numbers. For example, in my formation #11, which was the star with no visible pattern and there was no way to distribute dancers evenly [within each subgroup] with the design I chose. My formation #12 which I considered the most complex because of the position the students were in. The dancers are expected to create two circular shapes in where they are dancing in. I would classify this as a complex formation because of the equation: (3 + 3 + 3 + 3 + 3 + 3 + 3 + 3)×2 = 48. The students formed a circle by forming a “triangle” where there are two students [two girls or two boys] next to each other and behind them in the middle is one student [one girl or one boy]. These eight small “triangles” come together to form a circle. The “times two” was for making two circles-one circle has 2/3 of boys and another circle has 2/3 of girls.

Case #4: Amaya – from addition to multiplication

One of the requirements during the target task was that participants needed to write a mathematical equation under each formation’s design. Many of the participants recognised that the complexity of each mathematical equation’s format was positively correlated with the complexity of the resulting formations. As the findings showed, most of the simple formations had a corresponding equation that was based primarily on adding or multiplying real numbers. In contrast, most of the complex formations had a corresponding equation that required applying order of operations. In particular, equations that necessitated the use of operator precedence were understood to be of high complexity by the participants. Amaya commented about the complexity within her own choreographic position designs and how they transited from addition to repeated multiplications especially doubles:

In simple formations, I decided to go with ideas that could easily been seen as addition equations rather than multiplication. For example, for the first [the simplest] formation, I used the equation 24 + 24. For the second formation, I used the equation 20 + 20 + 8. For the complex formations, I decided to create dances that would involve using a multi-step equation to get the overall answer. Some common features of my equations are that they require to be multiplied or added together to receive the overall answer. For example, for my more complex formation such as the seventh formation I used the equation 4 × 9 + 12, for the ninth formation I have (2 × 3) + (18 × 2) + (2 × 3), and for the eleventh formation I have [(4 × 3)+(4 × 3)]×2 to get 48. As I was doing the equations, I noticed that the most common thing I did was double some of the positions resulting in repeated operations like a number times two or three. I also noticed how I repeated the same factors throughout the equations like 2,3,4,6, and 12 so the students would be constantly grouped in 2’s 4’s and so on.

Case #5: Norma – from equations to images

While completing the target choreographic position design task, the majority of participants developed their formations first, and then based their mathematical equations on those formations. However, a number of participants chose to propose equations first, and then based their formations on those equations. By utilising their understanding of a selected equation’s structure, some of the participants could draw their mental images on paper to develop their choreographic position. Some of the formations were described by the participants as graphical representations of the equations, as implemented in structures such as rows and columns. Norma described how she developed her mental image as well as the formations based on her equations:

The key rationale to guide my formations development is by seeing how the previous formation was formed and to make the next formation looks different that the audience can see a new pattern being formed. I decided to first create my equations then draw the design on paper. By having the equation first and then creating the formation also helped me determine how many [dancers] in each section, and how the pattern or the way I want to demonstrate the final product. For example, in formation #3 my equation being 6 × 4 × 2 = 48 and it helped me build a mental images there that I can either have six groups of 4 blue [boys] and six groups of 4 orange [girls] each or I can have four groups of 6 blue [boys] and four groups of 6 orange [girls]. My equation for the last formation was (8 × 2)+(6 × 2)+(4 × 2)+(3 × 2)+(2 × 2)+2 = 48. From the equation you can easily predict that it is a tower—[the formation] begins with having eight pairs of girls and boys, then six of such pairs, then four pairs, three pairs, two pairs, and one pair at the end. When I was developing formations, I always think that I need to ensure that audience can to see the students (e.g. parents can find their own children) in the show and I tried to guide audience to guess what figure would it come next.

Discussion

Our goal for implementing this research study was to accumulate empirical evidence pertaining to preservice teachers’ reasoning processes while choreographing group dances with embedded algebra tasks. Analysis of the results revealed that the participants recognised and utilised a multiplicity of connections pertaining to the complexity of the formations and mathematical-spatial factors within the equations. These factors included: (1) even versus odd numbers, (2) linear versus curved contours, (3) regular versus asymmetrical shapes, (4) addition versus multiplication, (5) subtraction versus division, (6) segmented versus scattered elements, and (7) other mathematical variables discussed earlier in this paper. The selected formation development rationales by Catalina, Julieta, Isabella, Amaya, and Norma differed in their methods for decomposing the target number (i.e. 48) into smaller sets with a dozen of computational-structural variations. These variations were emerged as hints to demonstrate participants’ numeral and operational flexibility of pedagogically manipulating mathematical values by applying rules of operations intuitively, which is crucial to their early algebra pedagogy (Blanton et al., 2015, Luken & Sauzet, 2021).

During this study, the choreographic formation development activities required using geometrical and algebraic processes including (1) grouping, dividing, and sorting dancers, (2) determine the location of each dancers, the shape that each formation can be made, and the way of transformation among formations, (3) understanding algebraic concepts such as variables and constants – providing learners with opportunities to better comprehend the essential concepts of early algebra (Carraher, Schliemann, & Schwartz, 2017). By determining the size and number of groups in one formation and then changing those aspects in the next formation, the mechanics of variables were observed. The participants examined the mathematical differences between “three groups of four dancers (3 × 4)” and “four groups of three dancers (4 × 3)”, as well as why these two arrangements are interrelated. Unlike strictly algebraic representations employing symbols and the rules for manipulating them, the diagrams of the formations provided a visual means for comprehending the modified formations (Hohensee, 2017; Van Amerom, 2003).

Findings verified that the participants were able to employ mathematical patterns of increasing levels of complexity to generate original and creative choreographic position designs for group formations, while completing embedded quantitative manipulation tasks. As the results illustrated, most of the participating preservice teachers applied more than one of the identified perspectives while developing choreographed formations from simple to complex. The strategies of developing choreographic positions employed revealed that mathematical models, especially combination of algebra thinking and geometrical reasoning, can be useful for designing structural arrangements that are capable of flexibility and change (Carraher & Schliemann, 2014). The algebraic equations supplemented the geometric illustrations and supported the participating preservice teachers’ development of an understanding about the pedagogical connections between choreographic position and mathematics instruction. The requirement to design increasingly complex formations focused the participants’ attention on the group’s overall visual effect. The strategies employed to address this requirement included a wide range of mathematical concepts from geometry (e.g. how to arrange dancers) to algebra (e.g. how to apply patterns), which were integrated into the process of designing the more advanced formations. Throughout the quantitative decomposing and recomposing processes, mathematical knowledge was applied towards the solution of meaningful problems conducted within a theme designed to be engaging for the participants and their future students (Kilpatrick, Swafford, & Findell, 2001).

One of the main findings from this study was that we identified multiple strategies that preservice teachers employed for using algebraic equations to design formations with increasing levels of complexity. For example, relationships amongst dancers could be adjusted by manipulating the equations’ complexity. Transitioning from formations based on “a+b = 48” to “a+b+c = 48” to “a+b+c+d = 48”, for instance, created formations shifting from two to three to four groups of dancers. Likewise, the multiplication involved in algebraic equations such as “a×b=c” could help choreograph inner structures of each segmentfor instance, into rows and columns. So if one of the segments had 36 dancers, then different iterations of “a×b=c” could generate a variety of combinations such as six rows with six columns, four rows with nine columns, twelve rows with three columns. Furthermore, equations that employed a combination of addition and multiplication such as “n(a×b)+m(c+d)=x” were frequently utilised to develop the designs for the most complex of the choreographed formations. In the same case of choreographing for 36 dancers, this algebraic equation could guide the choreographer to further specify the geometrical features, such as directions, distances, and locations, of their team of dancers.

Although preparation for algebraic thinking has often been cited in the official elementary school curriculum as a focus area (Kaput, Carraher, & Blanton, 2017), the general teaching approach, even as early as with kindergarten students, remains predominantly focused on manipulating equations with unknowns. Engagement strategies for students often rely upon replacing traditional variable names such as “x” and “y” with images of shapes, or animals, or fruits. Unfortunately, such simplistic attempts at making education enjoyable generally have little impact on the learning process. Developmentally appropriate algebra preparation should instead focus on emphasising essential, fundamental conceptual aspects of algebraic thinking such as recognising patterns, uncovering relations, and learning to make appropriate and justifiable generalisations (Presser, Clements, Ginsburg, & Ertle, 2015). The study suggested that methods for teaching early algebra during elementary school could include whole class inquiry-based activities by associating the contents of arithmetic and geometry together to offer students with abundant opportunities to manipulate quantitative values with structural variations.

A number of limitations need to be addressed in this study. First, even though each participant performed over 120 minutes of dances during the preparatory stage, no dance was implemented during the target task in the research stage and only the formation designing was focused. Thus, whether the algebraic thinking can be developed through actual dance practice is unknown. We invite future empirical research to extend the exploration from paper-based formation to stage based dance practice. Second, the formation design task by separation of the 48 dancers into blue-orange group binary is only to facilitate the algebra equation development, and the other variables (e.g. first graders versus second graders; or class A versus class B) are ignored but could have been used to improve the level of complexities. Also, an overwhelming majority of participants in the current study are Hispanic females living in the Mexican-American borderland were, their demonstrated mathematical and chorographical capacities might not be transferable to participants with a different demographic and geographic profile.

During the past two decades, instruction that incorporates dance, music, and other performing arts disciplines has been theoretically discussed by researchers and pedagogically employed by teachers interested in teaching core subjects (the subjects that are regularly assessed through normal-referenced standardised tests such as mathematics and reading) in K-12 schools (Belcastro & Schaffer, 2011; Rosenfeld, 2013). Nevertheless, educators lack the empirical research necessary for validating a replicable approach to developing interdisciplinary mathematics pedagogy appropriate for integration across the K-12 school curriculum. Perhaps mathematics concepts inspected within multimodal forms of representation, such as the formation development activities examined in this paper, could positively impact mathematical reasoning. Conceptually understanding how algebraic equations work is essential to making progress in learning algebra, and thus instruction examining how to manipulate variables and balance an equation are foundational for building up to more advanced algebraic thinking (Ionescu & Vasc, 2014; Lau, 2021). Our study invites future research on how to continue the development, evaluation, and optimisation of a systematic approach to the integration of dance into K-12 mathematical instruction and the impacts on students’ mathematical learning and engagement.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Notes on contributors

Song A. An

Song A. An, Ph.D., is an associate pro-fessor in Mathematics Education at The University of Texas at El Paso. His current research is about generating and evaluat-ing innovative teaching strategies, espe-cially play and game based, that can more effectively engage students in learning mathematics via such pedagogical strategies as problem-solving, simula-tions, discovery, contextualized challenges, and interdis-ciplinary projects. He is the recipient of the University of Texas System Regents’ Outstanding Teaching Award in 2017.

Daniel A. Tillman

Daniel A. Tillman, Ph.D., is an Associ-ate Professor in Educational Technolo-gy at The University of Texas at El Paso (UTEP) as well as the co-director of the College of Education Makerspace. His current research focuses on the diffusion of technology innovations into K-12 education, physical and digital multimedia in elementary school science and mathematics education, and the STEM career pipeline and mainline. He teaches both graduate and undergrad-uate courses about instructional technology and instruc-tional design.

Alyse C. Hachey

Alyse C. Hachey, Ph.D., is the Co-Chair of the Teacher Education Department, Division Director of BELSS (Bilingual Education, Early Childhood Education, Literacy Education and Sociocultural Studies), Associate Professor and lead faculty for Early Childhood Education at The University of Texas at El Paso. Her teaching and research interests focus on early childhood cognition and curriculum devel-opment and post-secondary online learning and reten-tion, particularly for college populations often designated at high-risk of dropout.

Karime Smith

Karime Smith is currently a PhD student of Teaching, Learning and Culture with an emphasis on STEM Education at the University of Texas at El Paso. She is a visual arts instructor with over 10 years of experience. Her current research interests lie in math learning, visual mathematics, creativity, and underrepresented minorities in STEM education.