Approximate optimal iterative approach for a class of oscillatory neuron models

ABSTRACT

Control of oscillatory neuron models becomes a growing interest due to the application of implanted stimulus electrodes in mitigating pathological behaviours. We present an approximate optimal iterative control method for minimum-current control of the FitzHugh–Nagumo model with external disturbance. We first focus on revealing optimality conditions based on the Pontryagin's maximum principle and constructing a related nonlinear two-point boundary value problem. Then, we transform the problem into two iterative sequences of linear differential equations. The control law is finally derived and composed of feedback and compensation terms which can be approximated using approximate iterative approach. Simulations illustrate the results.

KEYWORDS:

• FitzHugh–Nagumo model
• optimal control
• approximate optimal iterative approach
• oscillatory neuron

1. Introduction

Recently, control of neuron systems by external current stimuli/input has drawn considerable attention due to its applications in deep brain simulation and oscillatory neurocomputers (Dasanayake & Li, 2011; Handa & Sharma, 2016; Osipov, Kurths, and Zhou, 2007; Uhlhaas & Singer, 2006). Many results, concerning the neuron energy efficiency (Niven & Laughlin, 2008; Sengupta, Stemmler, Laughlin, & Niven, 2010), have been developed related to optimal electrical stimulation in single neuron for different control performances, such as minimum energy and spike times. In the field of theoretical neuroscience and automatic control, many control theoretic methods have been employed for optimal controls of spiking neurons (Dasanayake & Li, 2015; Lou & Swamy, 2017; Moehlis, Shea-Brown, & Rabitz, 2006; Nabi, Stigen, Moehlis, & Netoff, 2013; Wilson, Holt, Netoff, & Moehlis, 2015). In particular, in the context of phase-reduced neuron models, a constrained magnitude input current as the stimulus was applied to cause a neuron to spike with a maximal firing rate in Moehlis et al. (2006). The maximum principle was used to derive charge-balanced minimum-power controls for a general phase model of neuron oscillators (Dasanayake & Li, 2015). In Wilson et al. (2015), the authors developed an energy optimal control strategy to entrain heterogeneous noisy neurons and apply it to numerical models of noisy phase oscillators and to vitro hippocampal neurons. In spite of these advances, it has not received much attention until now with few results (Danzl, Hespanha, & Moehlis, 2009; Nabi, Mirzadeh, Gibou, & Moehlis, 2013; Yi, Wang, Li, Wei, & Deng, 2016) appearing on control of conductance-based neuron models which are more intricate than phase-reduced models. In particular, Nabi et al. (2013) designed an event-based desynchronizing control stimulus for a network of pathologically synchronized coupled neurons and employed a Hamilton–Jacobi–Bellman (HJB) approach to transform the optimal control problem into solving numerical solution of an HJB partial differential equation by an level set method. By using similar HJB framework, Danzl et al. (2009) proposed an event-based minimum-time optimal control for oscillatory neurons and the results were extended to a network of globally coupled neurons. From the view point of extracellular electric field stimulus, the optimization of stimulus energy for a reduced two-compartment neuron model was addressed in Yi et al. (2016). Particular motivation for the study on optimal control of oscillatory neuron models using approximate iterative-type approach comes from its board application to approximate solution of optimal control problem for nonlinear systems and the rapid development of computer ability.

As an important spiking neuron model, the FitzHugh–Nagumo model was introduced as a simplified model of the cell membrane (FitzHugh, 1961). During recent years, many approaches have been developed for the case of the FitzHugh–Nagumo model with or without the influence of random perturbations, see Barbu, Cordoni, and Di Persio (2016) and Uzunca, Küçükseyhan, Yucel, and Karasözen (2017), where the model is described by partial differential equations with reaction-diffusion terms. In recent years, the study of control in the class of FitzHugh–Nagumo models has attracted some attention, including (Chavarette, Balthazar, Peruzzi, & Rafikov, 2009; Ciszak et al., 2017; Danzl et al., 2009; FitzHugh, 1961; Hilhorst & Rybka, 2010; Liu & Wang, 2017; Sun & Yang, 2016; Uzunca, Küçükseyhan, Yücel, & Karasözen, 2017; Yi et al., 2016; Zheng, 2015, 2016). In particular, an event-based control approach for reduced Hodgkin–Huxley model and FitzHugh–Nagumo model was developed in Danzl et al. (2009) by means of the Hamilton-Jacobi-Bellman approach. The FitzHugh–Nagumo type reaction-diffusion system is also a generic model in physiology, describing complex wave phenomena in excitable or oscillatory media (Uzunca et al., 2017). Optimal control of semi-linear reaction-diffusion equations is an active research field with many applications in controlling pattern formation (Zheng, 2015), boundary control matched disturbance (Liu & Wang, 2017) and physical processes in motion of turbulence (Zheng, 2016), to give a few examples. Although some existing works addressed optimal control or stabilization problems for FitzHugh–Nagumo type reaction-diffusion systems (Hilhorst & Rybka, 2010; Sun & Yang, 2016; Uzunca et al., 2017), in this paper, we shall mainly focus on the FitzHugh–Nagumo model described by a second-order original differential equation as in Chavarette et al. (2009) and Ciszak et al. (2017). By means of Sinha's theory and a linear feedback control strategy, Chavarette et al. (2009) reduced the oscillatory movement of a Fitzhugh–Nagumo system to a stable equilibrium point, but the designed optimal controller depended on a limited matrix G. In Ciszak et al. (2017), Ciszak et al. addressed several dynamical regimes of a FitzHugh–Nagumo model driven by a feedback control composed of a high-pass or an all-pass filter, and explored the relationship between complex dynamical regimes and control parameters (such as the external driving amplitude A, time constant τ and coupling strength coefficient α). We believe that efficient optimal control approaches for FitzHugh–Nagumo systems should play a more prominent role in analysis and control of conductance-based neuron models. Existing approximation iteration approaches for optimal control of nonlinear systems, such as Galerkin approximation (Beard, Saridis, & Wen, 1997; Kim, Kim, & Lim, 2005) and Riccati-equation approximation sequence method (Banks, 1986; Çimen & Banks, 2004), have limitations in the lack of convergence or in high computation complexity.

In this paper, inspired from Çimen and Banks (2004), Sun and Fan (2008) and Gao, Zhang, and Zhang (2008), we aim at developing an approximate iterative approach (AIA) that can be applied to optimal control of a dimensionless FitzHugh–Nagumo model with external disturbance so as to guarantee the minimum-current suboptimal performance. The optimal control law is composed of an exact linear feedback and a nonlinear compensation term and the convergence of the developed approximate iterative algorithm is proved. Since the proposed AIA is related to a pair of vector iterations and the solution of the optimal control is transformed into a limit process of the nonlinear compensated vector sequence, the computational complexity can be greatly reduced. By simulation, we compare the results with those obtained by an orthogonal collocation method and a state-dependent Riccati equation approach, which illustrates that the results using the proposed approach are comparable to those obtained by other methods.

2. FitzHugh–Nagumo model

As is well-known, the Hodgkin–Huxley model is very important in describing the transmission of an action potential through a cell membrane (Reddy & Murthy, 2013). However, due to the large number of variables, the phase space dynamics of the equation is hard to be visualized. The FitzHugh–Nagumo model, as a simplification of the Hodgkin–Huxley model, was introduced in FitzHugh (1961) and experimentally verified by Nagumo, Arimoto, and Yoshizawa (1962) using electrical circuits. Here, we consider the FitzHugh–Nagumo neural model (Danzl et al., 2009; Keener & Sneyd, 2008) described in a dimensionless form (1) where v is the voltage potential of the neuron membrane, ω is the inactivation of the sodium channels, represents the input current, δ acts as the singular perturbation parameter and v evolves on a much faster time scale than ω. The neural system can exhibit periodic spiking dynamics, while neurons consisting of such coupled models may be firing in synchronism and lead to pathological behaviours. An efficient way to desynchronize is to use the phaseless set of system states which is extremely sensitive to background noise (Danzl et al., 2009). For the FitzHugh–Nagumo model (1(1) ), the origin is the phaseless set contained by the basin of attraction of the periodic orbit (Danzl et al., 2009), and thus our objective is to construct a minimum-current optimal control law to reach the origin.

3. Minimum-current optimal control

In this section, we introduce the minimum-current optimal control problem of a stochastic version of the FitzHugh–Nagumo model. The dynamics of the neuron model (1(1) ) with external disturbance can be written as (2) where is the state vector of the system, is the external input injected to the neuron, is an additional disturbance (which may be sinusoidal disturbance, periodic disturbance, persistent disturbance (Gao, 2008), uniform noise or white Gaussian noise) with intensity d, , is a constant vector, In practice, for treatment of pathological behaviours, such as Parkinson's disease (Rubchinsky, Park, & Worth, 2012) and obstructive sleep apnea, electrical stimuli in a deep brain stimulation setting is an efficient way with a requirement of clinically reducing stimulation energy. Motivated by this, the interest of this work is in developing an approximate optimal iterative approach for the neuron model when controlling neurons to achieve certain desired behaviour or driving the neurons to their phaseless sets.

Considering the neuron system (2(2) ), the objective is to find the minimum-current input which would drive the states of the neuron to the phaseless set in some prespecified length of time This is achieved by minimizing an objective function (3) where is the desired terminal state, Q, are positive semi-definite matrices and R>0 is a positive constant. These parameters reflect the relative values of the weights determining the relative importance of minimizing each term; e.g., a high R relative to Q and would emphasize minimization of the input current. In practice, if one extremely needs to achieve certain desired behaviour or drive the neurons to their phaseless sets, one could set high weight coefficients Q and . Extending the optimal control concepts to the neuron systems is motivated by control applications where a high-power stimulus is harmful to the biological tissues and low-power electrical stimulus plays an important role in reducing the power consumption in a neurological implant.

Consider the Hamiltonian for the system (2(2) ) given by (4) where λ is the co-state variable vector.

According to the Pontryagin's maximum principle, the optimality conditions are obtained by the following nonlinear two-point boundary value problem (BVP) (5) where and , and the optimal control law is given by (6) Generally, it is hard to analytically solve the nonlinear two-point BVP (5(5) ) except for a few simple cases. In the next section, we introduce a transformation of the two-point BVP and an approximation iterative approach to overcome this difficulty.

4. Approximation optimal iterative design process

By (5(5) ), let us construct the set of two-point BVPs (7) and the corresponding optimal control sequence (8) where denotes the initial states during before the first iteration, which is used to calculate and when

Note that remains unchanged during each iteration as it is an additional disturbance. The following theorem shows the relationship between the kth optimal solution and the optimal state trajectory and optimal control law .

Theorem 4.1

Convergence

Let and denote solution sequences of (7(7) ) and (8(8) ), respectively. Then, and uniformly converge to the optimal state trajectory and the optimal control law respectively, for the system (2(2) ) with the quadratic objective function (3(3) ).

Proof.

When k=1, it follows from (7(7) ) that for all (9a) (9b) (9c) For , let us define (10) Then, (9(9a) ) can be written as (11a) (11b) (11c) Since (9(9a) ) is a nonlinear two-point BVP, let us denote (12) where is an adjoint vector introduced to compensate the nonlinearity of system and is the unique positive semi-definite solution to a Riccati matrix differential equation that will specified later.

Then, substituting (12(12) ) into (11a(11a) ) gives (13)

Calculating the derivative of both sides of (12(12) ) and using (13(13) ) yields (14) On the other hand, substituting (12(12) ) into (11b(11b) ) gives (15) Using the equivalence between (14(14) ) and (15(15) ), we obtain the Riccati matrix differential equation (16) and the adjoint vector differential equation (17) Since for all , Equations (16(16) ) and (17(17) ) can be solved with known and . Then, substituting (12(12) ) into (8(8) ), we obtain the optimal control law for k=1 (18) Meanwhile, with the solutions of Equations (16(16) ) and (17(17) ), one can derive from (13(13) ). Similarly, using such an iteration strategy, we can obtain , for . In particular, after k−1 iterations, we have known. At the kth iteration, it follows from (7(7) ) (19a) (19b) (19c) Denote (20) Calculating the derivative of both sides of (20(20) ) and using (19a(19a) ) yields (21) On the other hand, substituting (20(20) ) into (19b(19b) ) gives (22) Using the equivalence between (14(14) ) and (15(15) ), we obtain the Riccati matrix differential equation (23) and the adjoint vector differential equation (24) Substituting (20(20) ) into (8(8) ), we obtain the kth optimal control law (25) In addition, substituting (20(20) ) into (19a(19a) ), we can get the kth optimal closed-loop system (26) Using the Cauchy sequence theorem and transfer matrix method, one can readily obtain that solutions to the sequence of (24(24) ) uniformly converge to the solution of the following equation (27) and solutions to the sequence of (26(26) ) uniformly converge to the solution of the following equation (28) That is, (29) In addition, using the fact , since the control sequence depends on the state sequence and the adjoint vector sequence , then, also uniformly converges to the optimal control law , that is, (30) Also, also uniformly converges to the optimal state trajectory of the system. The proof is complete.

Theorem 4.1 proves the convergence of the state sequence and the control sequence depending on the adjoint vector sequence, and the proof of Theorem 4.1 reveals the design process of AIA. Note that the closed-loop compensation term in the optimal control law (25(25) ) related to the adjoint vector will increase the robustness of the system as the disturbance effect is reflected in the adjoint vector. However, it is impractical to use the sequences as it contains infinite series. To apply the AIA in practice, we propose the following efficient algorithm in Algorithm 1 for solving the minimum-current optimal control problem. In this algorithm, the Mth iteration suboptimal control law is employed by replacing ∞ with a finite positive integer M in (30(30) ), i.e. (31) where M is determined by a concrete error criterion.

Remark 4.1

It is shown from the Practical Algorithm, during the iterative procedure, the parameter Q affects the value in the Riccati matrix differential equation, the parameter determines the boundary values and , and the parameter R affects the state sequence and further influences the optimal control law.

Remark 4.2

To compare with existing approximation iteration approaches for optimal control of nonlinear systems, we give a brief comparative analysis as follows.

• The idea of Galerkin approximation method (Beard et al., 1997; Kim et al., 2005) is to directly transform the HJB equation into a sequence of nonlinear vector differential equations and achieve suboptimal control by solving the limit of the sequence. Although the iterative process is fast, it takes a long time to calculate the inner product related to a cost-to-go function for iteration. In addition, this method depends on the selection of initial values and the iterative process will be slow and even divergent without appropriate selection of initial values. However, such a method is very suitable for solving optimal control problems of nonlinear systems with zero output.

• The power series expansion method (Cebubar & Costanza, 1984) constructs a control law by using a power series and obtains the approximate optimal solution in the form of sequence. However, it requires the system is analytical to the state vector so that the power series expansion can be carried out which is unrealistic in many practical systems.

• In the state-dependent Riccati equation (SDRE) approach (Pittner & Simaan, 2006), the Riccati matrix differential equation (RMDE) with state vector related to is transformed into an iterative form of constant-parameter RMDE and the solution sequence or series of the RMDE is used to approximate the solution of SDRE. This approach avoids solving the nonlinear HJB equation itself, but it depends on the approximate solution of and needs iterative solution of a series of matrix differential equations. Therefore, the computational requirements by using this approach are large. Such an issue also exits in the Riccati-equation approximation sequence method (Banks, 1986; Çimen & Banks, 2004), although this method has a faster convergence speed when the dimension of the system is not very large.

• The AIA in Gao (2008) is only applicable to nonlinear systems that can be decomposed into independent linear state parts and bilinear input parts. It has the advantage of simple calculation, but it is sensitive to the external weak disturbance and the parameter perturbations within the system.

• In contrast to above approximate methods, the proposed AIA avoids solving directly the nonlinear HJB equation or SDRE and provides a convenient way to obtain the approximate solutions for the suboptimal control problems of oscillatory neuron models. Since the affine nonlinear term is treated as the ‘parameter perturbation’ of a linear system, the proportion of the closed-loop feedback term has a much higher effect than the case of treating the nonlinear term in the system as an additional disturbance. Therefore, it is robust to the parameter perturbations within the system.

• However, one limitation of applying the AIA is that it only causes great positive effects for nonlinear systems that can be decomposed into independent linear parts (that is, ) and state-dependent linear parts (that is, ). Hence, it is not necessary to apply the AIA in neuron models with highly nonlinear functions, such as the Hodgkin–Huxley model. It remains an open problem in our further work.

5. Simulations

For purpose of illustration, let us consider the FitzHugh–Nagumo model (2(2) ) with the objective being to control the states of the neuron system to the phaseless point while maintaining the performance given by (3(3) ), where, without loss of generality, the parameters are chosen as , , Q=0 and R=2. Similar to the FitzHugh–Nagumo model in Lindner, García-Ojalvo, Neiman, and Schimansky-Geier (2004), we consider the external disturbance driven by the white Gaussian noise with intensity d=0.1. For simplicity, take to eliminate input and voltage scaling. Following the procedure given in Practical Algorithm, we can obtain the suboptimal control law for the neuron model (2(2) ) with initial values and the objective function index (3(3) ). The objective function values at different iterations are listed in Table 1. It can be found from Table 1 that, the greater the iteration gets, the higher the control precision will be. However, when the iteration increases up to a high value, the values of the objective function tend to a determinate constant.

Table 1. Performance index values.

k	1	2	3	4	5
	2.9726	2.9654	2.9613	2.9510	2.9507

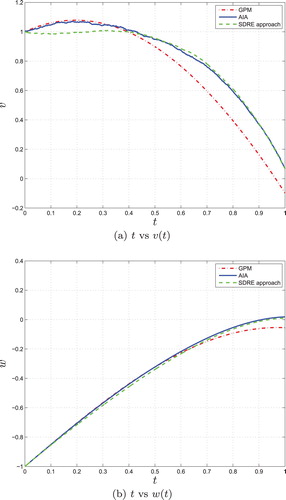
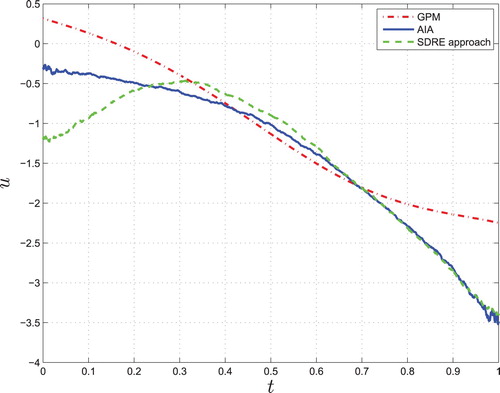
To obtain an accurate enough suboptimal trajectory, we set the tolerance error bound . In this case, convergence is achieved after 4 iterations, i.e. and a minimum of is obtained. It is worth to point out that, in the proposed algorithm, only a few iteration times are required in order to get a suboptimal control law. In order to verify whether the derived control achieves the objectives or not, it is applied to the neuron system to obtain controlled state trajectories. We compare the results of the AIA with the state trajectories and the optimal control trajectories obtained by using the SDRE approach (Pittner & Simaan, 2006) and the Gauss pseudospectral method (GPM) (Rao et al., 2010). As an orthogonal collocation method, GPM is an efficient optimization approach based on approximating the state and control trajectories using interpolating polynomials and has been used extensively throughout the world both in academia and industry https://en.wikipedia.org/wiki/GPOPS-II (Huntington & Rao, 2008). Figures 1 and 2 provide simulation results for minimum-current optimal control of the FitzHugh–Nagumo model using three different methods. Figure 1 shows the state trajectories of the solutions. It is seen from the terminal values of w that, the SDRE approach and our AIA perform better than the GPM, that is, the phaseless point are achieved by the SDRE approach and our AIA. This will be further illustrated by the error metric E in Table 2. Figure 2 shows the control trajectories of the solutions. It can be seen that among the three methods, the GPM needs the least energy. However, the AIA and the SDRE approach are comparable with the GPM for the needed energy. This is quantatively confirmed by the computational results listed in Table 2, where the iteration length, the computational time (CT) and the objective function value J for all methods are given. The error between the real and the desired terminal states, defined as is also given in Table 2. Obviously, the proposed AIA requires the least iterations and least computational time with tolerable control performance and good accuracy on the desired state. The SDRE approach takes the longest computational time although it achieves the best accuracy on the desired state.

Figure 1. The state solutions under different methods.

Figure 2. The optimal control solutions under different methods.

Table 2. Comparing computational efficiency.

Method	Number of iterations	CT (s)	J	E
SDRE approach	10	14.226	2.989	0.069
GPM	188	3.815	2.501	0.112
AIA	4	1.863	2.951	0.072

6. Conclusions

In this paper, we have studied the minimum-current optimal control of the FitzHugh–Nagumo model with external disturbance. By utilizing the Pontryagin's maximum principle, the optimal control problem has been transformed into solving a nonlinear two-point BVP. By solving the two-point BVP using iterative sequences of linear differential equations, the suboptimal control law has been designed through an approximation optimal iterative process. We have carried out simulations using the proposed method for the FitzHugh–Nagumo model. Comparisons of the results by using the SDRE approach, the GPM and the proposed AIA have also been revealed. An extension effort to more complicated neural systems such as the Hodgkin–Huxley model perturbed by general Lévy type noise is possible, which is left for future work.

Acknowledgments

We would like to thank the Editor and the anonymous reviewers for their very valuable comments and suggestions, which have helped in improving the quality of the paper.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work is partially supported by National Natural Science Foundation of China (NSFC) [61473136] and the Fundamental Research Funds for the Central Universities [JUSRP51322B].