Adaptive synchronization control for stochastic complex networks with derivative coupling

Abstract

In this paper, the problem of the adaptive synchronization control is studied for a class of stochastic complex networks with unknown nonlinear coupling strength and derivative coupling. First, in order to deal with the unknown nonlinear coupling strength, Takagi–Sugeno (T–S) fuzzy method is used to transform the network model into a T–S fuzzy complex network model. Then,a fuzzy adaptive controller and the corresponding adaptive parameter update rate are designed. Subsequently, a new Lyapunov function is constructed, which is related to the derivative coupling. By employing the stochastic analysis technique and Lyapunov stability theory, a sufficient condition is given for exponential stabilization in mean square of the synchronization error system. Finally, the effectiveness of the obtained theoretical results is verified through a simulation.

Keywords:

• Complex networks
• exponential synchronization
• adaptive control
• derivative coupling
• stochastic disturbance

1. Introduction

Due to the wide application of complex networks, such as Internet, communication network, electrical power grids and so on, the research of complex networks has attracted a lot of attention, including mathematics, biology and other fields. Synchronization is an important phenomenon in various dynamic behaviours of complex networks, i.e. the states of all nodes in the network approach the same trajectory. In the past decades, researchers have proposed different synchronization control methods, such as pinning control (Liu & Chen, 2015), sliding mode control (Chen et al., 2017), impulsive control (Dai et al., 2009), adaptive control (Ding & Li, 2016) and so on. Among many synchronization control methods, the adaptive control is an effective control method to achieve synchronization of complex networks due to the fact that the control parameters can be self-adjusted according to the characteristics of the system. To mention a few, the adaptive PI synchronization controller has been designed in Gu et al. (2020) for complex networks with stochastic coupled nonlinear dynamics. The design method of adaptive quantization finite-time synchronization controller has been provided in He et al. (2021) for the complex networks with time-varying delay coupling and adaptive coupling strength. In addition, in Hu et al. (2022) the quasi-synchronization problem has been investigated for uncertain complex networks based on the event triggering strategy, and the adaptive fuzzy controller has been designed to make the complex networks achieve quasi-synchronization.

However, the above adaptive synchronization control methods are suitable for complex networks with non-derivative coupling. In fact, because some networks often contain the past change rate information of state variables (i.e. the interconnected couplings have the form of derivative). Therefore, the complex networks with derivative coupling are often encountered in practical, such as coupled chaotic systems (Xu, Zhou, Fang, Sun & Pan, 2010), droop control inverters (Lombana & di Bernardo, 2015a) and linear or nonlinear oscillators (Lombana & di Bernardo, 2015b). Considering the practical application of the complex networks with derivative coupling, the synchronization problem of delay complex networks with derivative coupling has been studied in Yuan et al. (2018), and a fuzzy adaptive feedback controller has been designed to ensure the asymptotic stability of the synchronization error system. The adaptive synchronization control method has been given in Xu, Zhou, Fang and Sun (2010) for complex networks with derivative coupling by using LaSalle invariance principle. The pinning synchronization control method has been studied in Wang et al. (2020) for the complex networks with multi-order derivative coupling. In Tang et al. (2020), by using the parameter classification and mathematical induction methods, the sufficient condition to ensure the cluster synchronization of derivative coupled neural networks with time-delay and random disturbance has been derived.

On the other hand, most of the previous mentioned research results on the synchronization control of complex networks have mainly focussed on the synchronization control methods when the network dynamics model, coupling strength and the topology are known. In practical, due to the complexity of the network dynamic behaviour and network environment, some unknown situations of network dynamics, the coupling strength or topology are often encountered. In order to deal with this problem, considering the Takagi–Sugeno (T–S) fuzzy model as an effective method to approach nonlinear systems, some research results on the synchronization control of T–S fuzzy complex networks have been presented in recent years. The authors in Wu et al. (2013) used pinning control and adaptive feedback strategy to ensure the synchronization for T–S fuzzy complex networks with time-varying delay and adaptive coupling weight. Two chattering free quantized intermittent controllers have been designed in Zhou et al. (2020) for complex networks with nonlinear coupling strength and stochastic disturbance to solve the finite-time synchronization problem of T–S fuzzy complex networks. We also refer to Li et al. (2019, 2021) and Deng et al. (2019, 2020) for interesting results related to our study in different contexts.

In the existing research on synchronization control of complex networks, many published results assume that the coupling strength of complex networks is known and has linear properties. The problem of the synchronization control of complex networks with unknown nonlinear coupling strength has not been sufficiently studied. In this paper, we design the adaptive synchronization controller to ensure the mean square exponential stability of the synchronization error system for a class of stochastic complex networks with unknown nonlinear coupling strength and derivative coupling. The main contributions of this paper are presented as follows:

1. The derivative coupling, unknown nonlinear coupling strength and stochastic disturbance are considered simultaneously in complex networks. On the basis of the model characteristics of the complex networks, the network model is transformed into T–S fuzzy complex network model.

2. Based on the T–S fuzzy complex network model, the T–S fuzzy adaptive controller and corresponding adaptive parameter update rate are designed to realize the goal of synchronization control for the complex networks.

3. A new Lyapunov function related to derivative coupling is constructed. The mean square exponential stability of the synchronization error system is proved by using stochastic analysis technique and Lyapunov stability theory.

Notation

In this paper, ${\mathbb{N}}^{+}$ and ${\mathbb{R}}^{+}$ denote the sets of positive integers and positive real numbers, respectively. $\mathbb{R}$ is the space of real number, ${\mathbb{R}}^n$ denotes the n dimensional Euclidean space. $min\{\cdots \}$ and $max\{\cdots \}$ are the minimum and maximum values of this set. $A^T$ represents the transpose of the matrix A. ⊗ is the Kronecker product. $\mathrm{diag}\{\cdots \}$ stands for a block-diagonal matrix. $\Vert \cdot \Vert$ represents the Euclidean norm of the vector, $E(\cdot )$ represents mathematical expectation. $1_N$ represents the N-dimensional identity column vector.

2. Problem formulation and preliminaries

Consider a stochastic complex network composed of n nodes, and the dynamic model of node i is shown as follows: (1) $\begin{array}{rl}\mathrm{d}{x}_i(t)& =[A{x}_i(t)+f(x_i(t))+G(x(t))\sum _{j=1}^N{b}_{ij}\mathrm{\Gamma }{\dot{x}}_j(t)+u_i(t)]\mathrm{d}t\\ & +h(t,x_i(t))\mathrm{d}\omega (t),i=1,2,\dots ,N,\end{array}$(1) where $x_i(t)=[x_{i1}(t),x_{i2}(t),\dots ,x_{in}(t){]}^T\in {\mathbb{R}}^n$ represents the state vector of the ith node, $u_i(t)\in {\mathbb{R}}^n$ represents the control input of the ith node, $f(x_i(t))=[f_1(x_i(t)),f_1(x_i(t)),\dots ,f_n(x_i(t)){]}^T\in {\mathbb{R}}^n$ is a continuousnonlinear vector-valued function, $A\in {\mathbb{R}}^{n\times n}$ represents the constant matrix, $G(x(t))=G(x_1(t),x_2(t),\dots ,x_N(t))\in {\mathbb{R}}^{+}$ is the nonlinear coupling strength of the dynamic network, and it is an unknown positive bounded function. Assume that for all $x_i(t)\in {\mathbb{R}}^n$, $G(x(t))\in \{{\sigma }_1,{\sigma }_2,\dots ,{\sigma }_r\}$, where $r\in {\mathbb{N}}^{+}$, and ${\sigma }_s>0$, $s=1,2,\dots ,r$, are the known constants. $\mathrm{\Gamma }=\mathrm{diag}\{r_1,r_2,\dots ,r_n\}\in {\mathbb{R}}^{n\times n}$, where $r_j>0,j=1,2,\dots ,n$, is an inner-coupling matrix of the system. $B=(b_{ij}{)}_{N\times N}$ is the derivative coupling matrix. If there exists a link from node $j(j\ne i)$ to node i, then $b_{ij}=b_{ji}>0$, otherwise $b_{ij}=b_{ji}=0$, and $b_{ii}=-\sum _{j=1,j\ne i}^N{b}_{ij}$. $\omega (t)=[{\omega }_1(t),{\omega }_2(t),\dots ,{\omega }_n(t){]}^T\in {\mathbb{R}}^n$ is an n dimensional vector Weiner process defined on $(\mathbf{\Omega },\mathcal{F},P)$ with $E\{h(t,x_i(t))\mathrm{d}\omega (t)\}=0$, $E\{[h(t,x_i(t))\mathrm{d}\omega (t){]}^T[h(t,x_i(t))\mathrm{d}\omega (t)]\}=\mathrm{trace}[h(t,x_i(t){)}^{T}h(t,x_i(t))]\mathrm{d}t$. Here, the white noise ${\omega }_i(t)$ is independent of ${\omega }_j(t)$ for $i\ne j$. $h(t,x_i(t))\in {\mathbb{R}}^{n\times n}$ is the noise intensity function matrix.

Remark 2.1

Define the Laplacian matrix L = −B. For an undirected graph, the matrix L is symmetric. Since L has zero row sums, 0 is an eigenvalue of L with the associated eigenvector $1_N=[1,\dots ,1{]}^T$. According to Gershgorin's theorem, for an undirected graph all of the nonzero eigenvalues of L are positive. Therefore, all of the nonzero eigenvalues of B have negative. Then, the matrix B is a symmetric negative semi-definite matrix. And 0 is a simple eigenvalue of L if and only if the undirected graph is connected. Therefore, for the connected undirected graph, the eigenvalues of the matrix B are $0={\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_N$.

Since $G(x(t))$ is unknown, based on the fuzzy theory, the complex network (1(1) $\begin{array}{rl}\mathrm{d}{x}_i(t)& =[A{x}_i(t)+f(x_i(t))+G(x(t))\sum _{j=1}^N{b}_{ij}\mathrm{\Gamma }{\dot{x}}_j(t)+u_i(t)]\mathrm{d}t\\ & +h(t,x_i(t))\mathrm{d}\omega (t),i=1,2,\dots ,N,\end{array}$(1) ) can be expressed as the following T–S fuzzy model:

Rule s: IF$z_1(t)$ is $M_{s1}$, $z_2(t)$ is $M_{s2},\dots ,z_u(t)$ is $M_{su}$, THEN $\begin{array}{rl}\mathrm{d}{x}_i(t)& =[A{x}_i(t)+f(x_i(t))+{\sigma }_s\sum _{j=1}^N{b}_{ij}\mathrm{\Gamma }{\dot{x}}_j(t)+u_i(t)]\mathrm{d}t\\ & +h(t,x_i(t))\mathrm{d}\omega (t),i=1,2,\dots ,N,\end{array}$where $M_{s1},M_{s2},\dots ,M_{su}$, $s=1,2,\dots ,r$ are the fuzzy sets, $z(t)=[z_1(t),\dots ,z_u(t){]}^T$ is the premise variable vector.

By applying the standard fuzzy inference methods of single-ton fuzzification, product fuzzy and weighted average defuzzification, the T–S fuzzy complex network model can be obtained as follows: (2) $\begin{array}{rl}\mathrm{d}{x}_i(t)& =[\phantom{\sum _{s=1}^r{h}_s}A{x}_i(t)+f(x_i(t))\\ & +\sum _{s=1}^r{h}_s(z(t)){\sigma }_s\sum _{j=1}^N{b}_{ij}\mathrm{\Gamma }{\dot{x}}_j(t)+u_i(t)]\mathrm{d}t\\ & +h(t,x_i(t))\mathrm{d}\omega (t),i=1,2,\dots ,N,\end{array}$(2) where $h_s(z(t))=\frac{w_s(z(t))}{{\sum }_{s=1}^r{w}_s(z(t))},w_s(z(t))=\prod _{j=1}^u{M}_{sj}(z_j(t)).$$M_{sj}(z_j(t))$ denotes the membership function of the premise variable $z_j(t)$ corresponding to the fuzzy set $M_{sj}$. $w_s(z(t))$ indicates the membership of rule s, if $w_s(z(t))\ge 0$, $s=1,2,\dots ,r$, then for all $t\ge 0$, ${\sum }_{s=1}^r{w}_s(z(t))>0$. $h_s(z(t))$ represents the normalized membership function satisfying $\sum _{s=1}^r{h}_s(z(t))=1,h_s(z(t))\ge 0,s=1,2,\dots ,r.$Letting $s(t)\in {\mathbb{R}}^n$ be the solution of an isolated node and satisfying the following dynamic equation: (3) $\mathrm{d}s(t)=[As(t)+f(s(t))]\mathrm{d}t+h(t,s(t))\mathrm{d}\omega (t),$(3) where the matrix A, the functions $f(s(t))$, $h(t,s(t))$ and $\omega (t)$ are defined in the same way as in Equation (1(1) $\begin{array}{rl}\mathrm{d}{x}_i(t)& =[A{x}_i(t)+f(x_i(t))+G(x(t))\sum _{j=1}^N{b}_{ij}\mathrm{\Gamma }{\dot{x}}_j(t)+u_i(t)]\mathrm{d}t\\ & +h(t,x_i(t))\mathrm{d}\omega (t),i=1,2,\dots ,N,\end{array}$(1) ).

The synchronization error vectors can be defined as follows: $e_i(t)=x_i(t)-s(t),i=1,2,\dots ,N.$From (2(2) $\begin{array}{rl}\mathrm{d}{x}_i(t)& =[\phantom{\sum _{s=1}^r{h}_s}A{x}_i(t)+f(x_i(t))\\ & +\sum _{s=1}^r{h}_s(z(t)){\sigma }_s\sum _{j=1}^N{b}_{ij}\mathrm{\Gamma }{\dot{x}}_j(t)+u_i(t)]\mathrm{d}t\\ & +h(t,x_i(t))\mathrm{d}\omega (t),i=1,2,\dots ,N,\end{array}$(2) ) and (3(3) $\mathrm{d}s(t)=[As(t)+f(s(t))]\mathrm{d}t+h(t,s(t))\mathrm{d}\omega (t),$(3) ), we can obtain the following dynamic equation of synchronization error system: (4) $\begin{array}{rl}\mathrm{d}{e}_i(t)& =[\phantom{\sum _{s=1}^r{h}_s}A{e}_i(t)+\overline{f}(e_i(t))\\ & +\sum _{s=1}^r{h}_s(z(t)){\sigma }_s\sum _{j=1}^N{b}_{ij}\mathrm{\Gamma }{\dot{e}}_j(t)+u_i(t)]\mathrm{d}t\\ & +\overline{h}(t,e_i(t))\mathrm{d}\omega (t),\end{array}$(4) where $\overline{f}(e_i(t))=f(x_i(t))-f(s(t))$, $\overline{h}(t,e_i(t))=h(t,x_i(t))-h(t,s(t))$.

The following fuzzy adaptive controller is designed for the synchronization error system (4(4) $\begin{array}{rl}\mathrm{d}{e}_i(t)& =[\phantom{\sum _{s=1}^r{h}_s}A{e}_i(t)+\overline{f}(e_i(t))\\ & +\sum _{s=1}^r{h}_s(z(t)){\sigma }_s\sum _{j=1}^N{b}_{ij}\mathrm{\Gamma }{\dot{e}}_j(t)+u_i(t)]\mathrm{d}t\\ & +\overline{h}(t,e_i(t))\mathrm{d}\omega (t),\end{array}$(4) ):

Rule s: IF$z_1(t)$ is $M_{s1}$, $z_2(t)$ is $M_{s2},\dots ,z_u(t)$ is $M_{su}$, THEN (5) $u_i^s(t)=-k_i^s(t)P{e}_i(t),$(5) where $P\in {\mathbb{R}}^{n\times n}$ is the controller gain matrix, $k_i^s(t)$ is the adaptive gain parameter. Based on T–S fuzzy rules, the adaptive fuzzy controller is (6) $u_i(t)=-\sum _{s=1}^r{h}_s(z(t))k_i^s(t)P{e}_i(t),$(6) where the adaptive update law of $k_i^s(t)$ is designed as follows: (7) ${\dot{k}}_i^s(t)={\rho }_i^s{e}^{\mu t}{e}_i^T(t)P{e}_i(t).$(7) Based on the synchronization error system (4(4) $\begin{array}{rl}\mathrm{d}{e}_i(t)& =[\phantom{\sum _{s=1}^r{h}_s}A{e}_i(t)+\overline{f}(e_i(t))\\ & +\sum _{s=1}^r{h}_s(z(t)){\sigma }_s\sum _{j=1}^N{b}_{ij}\mathrm{\Gamma }{\dot{e}}_j(t)+u_i(t)]\mathrm{d}t\\ & +\overline{h}(t,e_i(t))\mathrm{d}\omega (t),\end{array}$(4) ) and the adaptive fuzzy controller (6(6) $u_i(t)=-\sum _{s=1}^r{h}_s(z(t))k_i^s(t)P{e}_i(t),$(6) ), by using the properties of Kronecker product of matrix, we can obtain the closed-loop synchronization error system as follows: (8) $\begin{array}{rl}\mathrm{d}e(t)& =\sum _{s=1}^r{h}_s(z(t))[(\mathcal{A}e(t)+\overline{f}(e(t))+({\sigma }_{s}B\otimes \mathrm{\Gamma })\dot{e}(t)\\ & -(K^s(t)\otimes P)e(t))\mathrm{d}t\\ & +H(t,e(t))\mathrm{d}\mathrm{\Omega }(t)\phantom{\overline{f}}],\end{array}$(8) where $\mathcal{A}=I_N\otimes A$, $e(t)=[e_1^T(t),e_2^T(t),\dots ,e_N^T(t){]}^T$,$\overline{f}(e(t))=[\overline{f}(e_1(t)),$ $\overline{f}(e_2(t)),\dots \overline{f}(e_N(t)){]}^T$, $K^s(t)=\mathrm{diag}\{k_1^s(t),k_2^s(t),\dots ,k_N^s(t)\}$, $H(t,e(t))=\mathrm{diag}\{\overline{h}(t,e_1(t)),\overline{h}(t,e_2(t)),\dots ,\overline{h}(t,e_N(t))\}$, $\mathrm{d}\mathrm{\Omega }(t)=1_N\otimes d\omega (t)$.

Definition 2.1

If there exist constants M>0 and $\alpha >0$, for any initial condition the following inequality is satisfied: $E\{\Vert e(t){\Vert }^2\}\le M{e}^{-\alpha t}.$Then, the synchronization error system (4(4) $\begin{array}{rl}\mathrm{d}{e}_i(t)& =[\phantom{\sum _{s=1}^r{h}_s}A{e}_i(t)+\overline{f}(e_i(t))\\ & +\sum _{s=1}^r{h}_s(z(t)){\sigma }_s\sum _{j=1}^N{b}_{ij}\mathrm{\Gamma }{\dot{e}}_j(t)+u_i(t)]\mathrm{d}t\\ & +\overline{h}(t,e_i(t))\mathrm{d}\omega (t),\end{array}$(4) ) is said to be mean square exponentially stable.

Assumption 2.2

For vector-valued function $f(\cdot )$ and vectors $x_i(t),s(t)\in {\mathbb{R}}^n$, there exists a constant d such that $\Vert f(x_i(t))-f(s(t))\Vert \le d\Vert x_i(t)-s(t)\Vert .$

Assumption 2.3

Tanaka et al., 2003

Assume that the derivative of functions $h_s(z(t))$ satisfies $|{\dot{h}}_s(z(t))|\le {\varphi }_s,{\varphi }_s\ge 0,s=1,2,\dots ,r.$

Assumption 2.4

There exists a non-negative constant ξ such that the noise intensity function matrix $\overline{h}(t,e_i(t))\in {\mathbb{R}}^{n\times n}$ satisfies $\mathrm{trace}\{\overline{h}(t,e_i(t){)}^T\overline{h}(t,e_i(t))\}\le \xi \Vert e_i(t){\Vert }^2.$

Lemma 2.5

Friedman, 1976

Consider the following nonlinear stochastic system: (9) $\mathrm{d}x(t)=f(t,x(t))\mathrm{d}t+\sigma (t,x(t))\mathrm{d}\omega (t),$(9) where $x(t)\in {\mathbb{R}}^n$is the state vector, $f(\cdot ):{\mathbb{R}}^{+}\times {\mathbb{R}}^n\to {\mathbb{R}}^n$ and $\sigma (\cdot ):{\mathbb{R}}^{+}\times {\mathbb{R}}^n\to {\mathbb{R}}^{n\times n}$ are continuous, $\omega (t)=[{\omega }_1(t),{\omega }_2(t),\dots ,{\omega }_n(t){]}^T\in {\mathbb{R}}^n$ is n-dimensional Weinerprocess. Suppose $V(t,x(t))$ are non-negative function, which are twice continuous differentiable in x and once in t, then $V(t,x(t))$ along the stochastic differential of the system (9(9) $\mathrm{d}x(t)=f(t,x(t))\mathrm{d}t+\sigma (t,x(t))\mathrm{d}\omega (t),$(9) ) is (10) $\begin{array}{r}\mathrm{d}V(t,x(t))=\mathcal{L}V(t,x(t))\mathrm{d}t+V_x(t,x(t))\sigma (t,x(t))\mathrm{d}\omega (t),\end{array}$(10) where the operator $\mathcal{L}V(t,x(t))$ is defined as $\begin{array}{rl}\mathcal{L}V(t,x(t))& =V_t(t,x(t))+V_x(t,x(t))f(t,x(t))\\ & +\frac{1}{2}\mathrm{trace}[\sigma (t,x(t){)}^T{V}_{xx}(t,x(t))\sigma (t,x(t))],\end{array}$where $V_t(t,x(t))=\frac{\mathrm{\partial }V(t,x(t))}{\mathrm{\partial }t}$, $V_x(t,x(t))=\{\frac{\mathrm{\partial }V(t,x(t))}{\mathrm{\partial }{x}_1},\frac{\mathrm{\partial }V(t,x(t))}{\mathrm{\partial }{x}_2},\dots ,\frac{\mathrm{\partial }V(t,x(t))}{\mathrm{\partial }{x}_n}\}$, $V_{xx}(t,x(t))=\{\frac{{\mathrm{\partial }}^{2}V(t,x(t))}{\mathrm{\partial }{x}_i\mathrm{\partial }{x}_j}{\}}_{n\times n}$. Then for any $0\le t_0<t<\mathrm{\infty }$, we have $E\{V(t,x(t))\}=E\{V(t_0,x(t_0))\}+E\{{\int }_{t_0}^t\mathcal{L}V(s,x(s))\mathrm{d}s\},$as long as the expectations of the integrals exist.

3. Main results

Theorem 3.1

For a stochastic complex network (1(1) $\begin{array}{rl}\mathrm{d}{x}_i(t)& =[A{x}_i(t)+f(x_i(t))+G(x(t))\sum _{j=1}^N{b}_{ij}\mathrm{\Gamma }{\dot{x}}_j(t)+u_i(t)]\mathrm{d}t\\ & +h(t,x_i(t))\mathrm{d}\omega (t),i=1,2,\dots ,N,\end{array}$(1) ) satisfying Assumptions 2.2, 2.3, 2.4, given the scalars $\xi >0,\epsilon >0$, if there exists a positive definite symmetric matrix P, such that the following linear matrix inequality holds: (11) $\begin{array}{r}\mathrm{\Pi }=\left[\begin{array}{cc}\mathrm{\Phi }& I_{nN}\\ I_{nN}& -\epsilon I_{nN}\end{array}\right]<0,\end{array}$(11) where $\mathrm{\Phi }=\mathcal{A}+{\mathcal{A}}^T+\mu (I_{Nn}-\sum _{s=1}^r{h}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma }))+(k_2\xi +\epsilon d^2)I_{Nn}-2(D\otimes P)-\sum _{s=1}^r{\varphi }_s({\sigma }_{s}B\otimes \mathrm{\Gamma })$,$D=d^{\ast }{I}_N$, $d^{\ast }$ is the given positive number, $k_2={\lambda }_{max}(I_{nN}-\sum _{s=1}^r{h}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma }))$, μ is an arbitrary positive constant. Then, the stochastic complex dynamic networks (1(1) $\begin{array}{rl}\mathrm{d}{x}_i(t)& =[A{x}_i(t)+f(x_i(t))+G(x(t))\sum _{j=1}^N{b}_{ij}\mathrm{\Gamma }{\dot{x}}_j(t)+u_i(t)]\mathrm{d}t\\ & +h(t,x_i(t))\mathrm{d}\omega (t),i=1,2,\dots ,N,\end{array}$(1) ) and (3(3) $\mathrm{d}s(t)=[As(t)+f(s(t))]\mathrm{d}t+h(t,s(t))\mathrm{d}\omega (t),$(3) ) can be synchronized with the mean square exponential stable by the fuzzy adaptive controller (6(6) $u_i(t)=-\sum _{s=1}^r{h}_s(z(t))k_i^s(t)P{e}_i(t),$(6) ) and the adaptive update law (7(7) ${\dot{k}}_i^s(t)={\rho }_i^s{e}^{\mu t}{e}_i^T(t)P{e}_i(t).$(7) ).

Proof.

The Lyapunov function is chosen as follows: (12) $\begin{array}{rl}V(t,e(t))& =e^{\mu t}{e}^T(t)(I_{nN}-\sum _{s=1}^r{h}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma }))e(t)\\ & +\sum _{s=1}^r{h}_s(z(t))\sum _{i=1}^N\frac{1}{{\rho }_i^s}(k_i^s(t)-d^{\ast }{)}^2,\end{array}$(12) where ${\rho }_s>0$ is a constant. Then, by using Lemma 2.5, the stochastic differential of $V(t,e(t))$ along the synchronization error system (8(8) $\begin{array}{rl}\mathrm{d}e(t)& =\sum _{s=1}^r{h}_s(z(t))[(\mathcal{A}e(t)+\overline{f}(e(t))+({\sigma }_{s}B\otimes \mathrm{\Gamma })\dot{e}(t)\\ & -(K^s(t)\otimes P)e(t))\mathrm{d}t\\ & +H(t,e(t))\mathrm{d}\mathrm{\Omega }(t)\phantom{\overline{f}}],\end{array}$(8) ) can be obtained as (13) $\begin{array}{rl}\mathrm{d}V(t,e(t))& =\mathcal{L}V(t,e(t))\mathrm{d}t\\ & +2e^{\mu t}{e}^T(t)(I_{nN}-\sum _{s=1}^r{h}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma }))\\ & \times H(t,e(t))\mathrm{d}\mathrm{\Omega }(t),\end{array}$(13) where (14) $\begin{array}{rl}\mathcal{L}V(t,e(t))& =2e^T(t)\left[e^{\mu t}(I_{nN}-\sum _{s=1}^r{h}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma }))\right]\dot{e}(t)\\ & +e^T(t)[\mu e^{\mu t}(I_{nN}-\sum _{s=1}^r{h}_s(z(t))\times ({\sigma }_{s}B\otimes \mathrm{\Gamma }))\\ & -e^{\mu t}\sum _{s=1}^r{\dot{h}}_s(z(t))\phantom{\sum _{s=1}^r}({\sigma }_{s}B\otimes \mathrm{\Gamma })]e(t)\\ & +e^{\mu t}\mathrm{trace}\{H^T(t,e(t))(I_{nN}-\sum _{s=1}^r{h}_s(z(t))\\ & \phantom{\sum _{s=1}^r}\times ({\sigma }_{s}B\otimes \mathrm{\Gamma }))H(t,e(t))\}\\ & +2\sum _{s=1}^r{h}_s(z(t))\sum _{i=1}^N\frac{1}{{\rho }_i^s}(k_i^s(t)-d^{\ast }){\dot{k}}_i^s(t)\\ & =2e^{\mu t}{e}^T(t)\dot{e}(t)-2e^{\mu t}{e}^T(t)\sum _{s=1}^r{h}_s(z(t))\\ & \times ({\sigma }_{s}B\otimes \mathrm{\Gamma })\dot{e}(t)+\mu e^{\mu t}{e}^T(t)\\ & (I_{nN}-\sum _{s=1}^r{h}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma }))e(t)\\ & -e^{\mu t}{e}^T(t)(\sum _{s=1}^r{\dot{h}}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma }))e(t)\\ & +e^{\mu t}\mathrm{trace}\{H^T(t,e(t))(I_{nN}-\sum _{s=1}^r{h}_s(z(t))\\ & \phantom{\sum _{s=1}^r}({\sigma }_{s}B\otimes \mathrm{\Gamma }))H(t,e(t))\}\\ & +2\sum _{s=1}^r{h}_s(z(t))\sum _{i=1}^N\frac{1}{{\rho }_i^s}(k_i^s(t)-d^{\ast })\\ & \times {\rho }_i^s{e}^{\mu t}{e}_i^T(t)P{e}_i(t)\\ & =2e^{\mu t}{e}^T(t)\sum _{s=1}^r{h}_s(z(t))(\mathcal{A}e(t)+\overline{f}(e(t))\\ & +({\sigma }_{s}B\otimes \mathrm{\Gamma })\dot{e}(t)-(K^s(t)\otimes P)e(t)\phantom{\mathcal{A}})\\ & -2e^{\mu t}{e}^T(t)\sum _{s=1}^r{h}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma })\dot{e}(t)\\ & +\mu e^{\mu t}{e}^T(t)e(t)\\ & -\mu e^{\mu t}\sum _{s=1}^r{h}_s(z(t))e^T(t)({\sigma }_{s}B\otimes \mathrm{\Gamma })e(t)\\ & -e^{\mu t}{e}^T(t)(\sum _{s=1}^r{\dot{h}}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma }))e(t)\\ & +e^{\mu t}\mathrm{trace}\{H^T(t,e(t))(I_{nN}-\sum _{s=1}^r{h}_s(z(t))\\ & \phantom{\sum _{s=1}^r}\times ({\sigma }_{s}B\otimes \mathrm{\Gamma }))H(t,e(t))\}\\ & +2e^{\mu t}\sum _{s=1}^r{h}_s(z(t))e^T(t)[(K^s(t)-D)\otimes P]e(t)\\ & =\sum _{s=1}^r{h}_s(z(t))e^{\mu t}\{e^T(t)(\mathcal{A}+{\mathcal{A}}^T)e(t)\\ & +2e^T(t)\overline{f}(e(t))\}+\mu e^{\mu t}{e}^T(t)e(t)\\ & -\mu e^{\mu t}\sum _{s=1}^r{h}_s(z(t))e^T(t)({\sigma }_{s}B\otimes \mathrm{\Gamma })e(t)\\ & -e^{\mu t}{e}^T(t)(\sum _{s=1}^r{\dot{h}}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma }))e(t)\\ & +e^{\mu t}\mathrm{trace}\{H^T(t,e(t))(I_{nN}-\sum _{s=1}^r{h}_s(z(t))\\ & \phantom{\sum _{s=1}^r}({\sigma }_{s}B\otimes \mathrm{\Gamma }))H(t,e(t))\}\\ & -2e^{\mu t}\sum _{s=1}^r{h}_s(z(t))e^T(t)(D\otimes P)e(t).\end{array}$(14) According to the definition of the derivative coupling matrix B and looking back Remark 2.1, we know that the eigenvalues of the matrix B are $0={\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_N$, then the matrix $I_{nN}-\sum _{s=1}^r{h}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma })$ is a positive definite matrix and its minimum eigenvalue $k_1={\lambda }_{min}(I_{nN}-\sum _{s=1}^r{h}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma }))=1$ and the maximum eigenvalue $k_2={\lambda }_{max}(I_{nN}-\sum _{s=1}^r{h}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma }))\ge 1$. Subsequently, from Assumption 2.4, we have (15) $\begin{array}{rl}& e^{\mu t}\mathrm{trace}\{H^T(t,e(t))(I_{nN}-\sum _{s=1}^r{h}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma }))H(t,e(t))\}\\ & \le e^{\mu t}{k}_2\mathrm{trace}\{H^T(t,e(t))H(t,e(t))\}\\ & =e^{\mu t}{k}_2\sum _{i=1}^N\mathrm{trace}\{{\overline{h}}^T(t,e_i(t))\overline{h}(t,e_i(t))\}\\ & \le e^{\mu t}{k}_2\xi \sum _{i=1}^N\Vert e_i(t){\Vert }^2.\end{array}$(15) From Assumption 2.2, we get $\Vert \overline{f}(e_i(t))\Vert =\Vert f(x_i(t))-f(s(t))\Vert \le d\Vert e_i(t)\Vert .$Therefore, we obtain (16) $d^2{e}^T(t)e(t)-{\overline{f}}^T(e(t))\overline{f}(e(t))\ge 0.$(16) For any scalar $\epsilon >0$, from (14(14) $\begin{array}{rl}\mathcal{L}V(t,e(t))& =2e^T(t)\left[e^{\mu t}(I_{nN}-\sum _{s=1}^r{h}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma }))\right]\dot{e}(t)\\ & +e^T(t)[\mu e^{\mu t}(I_{nN}-\sum _{s=1}^r{h}_s(z(t))\times ({\sigma }_{s}B\otimes \mathrm{\Gamma }))\\ & -e^{\mu t}\sum _{s=1}^r{\dot{h}}_s(z(t))\phantom{\sum _{s=1}^r}({\sigma }_{s}B\otimes \mathrm{\Gamma })]e(t)\\ & +e^{\mu t}\mathrm{trace}\{H^T(t,e(t))(I_{nN}-\sum _{s=1}^r{h}_s(z(t))\\ & \phantom{\sum _{s=1}^r}\times ({\sigma }_{s}B\otimes \mathrm{\Gamma }))H(t,e(t))\}\\ & +2\sum _{s=1}^r{h}_s(z(t))\sum _{i=1}^N\frac{1}{{\rho }_i^s}(k_i^s(t)-d^{\ast }){\dot{k}}_i^s(t)\\ & =2e^{\mu t}{e}^T(t)\dot{e}(t)-2e^{\mu t}{e}^T(t)\sum _{s=1}^r{h}_s(z(t))\\ & \times ({\sigma }_{s}B\otimes \mathrm{\Gamma })\dot{e}(t)+\mu e^{\mu t}{e}^T(t)\\ & (I_{nN}-\sum _{s=1}^r{h}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma }))e(t)\\ & -e^{\mu t}{e}^T(t)(\sum _{s=1}^r{\dot{h}}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma }))e(t)\\ & +e^{\mu t}\mathrm{trace}\{H^T(t,e(t))(I_{nN}-\sum _{s=1}^r{h}_s(z(t))\\ & \phantom{\sum _{s=1}^r}({\sigma }_{s}B\otimes \mathrm{\Gamma }))H(t,e(t))\}\\ & +2\sum _{s=1}^r{h}_s(z(t))\sum _{i=1}^N\frac{1}{{\rho }_i^s}(k_i^s(t)-d^{\ast })\\ & \times {\rho }_i^s{e}^{\mu t}{e}_i^T(t)P{e}_i(t)\\ & =2e^{\mu t}{e}^T(t)\sum _{s=1}^r{h}_s(z(t))(\mathcal{A}e(t)+\overline{f}(e(t))\\ & +({\sigma }_{s}B\otimes \mathrm{\Gamma })\dot{e}(t)-(K^s(t)\otimes P)e(t)\phantom{\mathcal{A}})\\ & -2e^{\mu t}{e}^T(t)\sum _{s=1}^r{h}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma })\dot{e}(t)\\ & +\mu e^{\mu t}{e}^T(t)e(t)\\ & -\mu e^{\mu t}\sum _{s=1}^r{h}_s(z(t))e^T(t)({\sigma }_{s}B\otimes \mathrm{\Gamma })e(t)\\ & -e^{\mu t}{e}^T(t)(\sum _{s=1}^r{\dot{h}}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma }))e(t)\\ & +e^{\mu t}\mathrm{trace}\{H^T(t,e(t))(I_{nN}-\sum _{s=1}^r{h}_s(z(t))\\ & \phantom{\sum _{s=1}^r}\times ({\sigma }_{s}B\otimes \mathrm{\Gamma }))H(t,e(t))\}\\ & +2e^{\mu t}\sum _{s=1}^r{h}_s(z(t))e^T(t)[(K^s(t)-D)\otimes P]e(t)\\ & =\sum _{s=1}^r{h}_s(z(t))e^{\mu t}\{e^T(t)(\mathcal{A}+{\mathcal{A}}^T)e(t)\\ & +2e^T(t)\overline{f}(e(t))\}+\mu e^{\mu t}{e}^T(t)e(t)\\ & -\mu e^{\mu t}\sum _{s=1}^r{h}_s(z(t))e^T(t)({\sigma }_{s}B\otimes \mathrm{\Gamma })e(t)\\ & -e^{\mu t}{e}^T(t)(\sum _{s=1}^r{\dot{h}}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma }))e(t)\\ & +e^{\mu t}\mathrm{trace}\{H^T(t,e(t))(I_{nN}-\sum _{s=1}^r{h}_s(z(t))\\ & \phantom{\sum _{s=1}^r}({\sigma }_{s}B\otimes \mathrm{\Gamma }))H(t,e(t))\}\\ & -2e^{\mu t}\sum _{s=1}^r{h}_s(z(t))e^T(t)(D\otimes P)e(t).\end{array}$(14) )–(16(16) $d^2{e}^T(t)e(t)-{\overline{f}}^T(e(t))\overline{f}(e(t))\ge 0.$(16) ), and Assumption 2.3, we have (17) $\begin{array}{rl}& \mathcal{L}V(t,e(t))\\ & \le e^{\mu t}\{e^T(t)[\mathcal{A}+{\mathcal{A}}^T+\mu I_{Nn}-\sum _{s=1}^r{h}_s(z(t))\mu ({\sigma }_{s}B\otimes \mathrm{\Gamma })\\ & \phantom{\sum _{s=1}^r}-2(D\otimes P)]e(t)+2e^T(t)\overline{f}(e(t))+\epsilon d^2{e}^T(t)e(t)\\ & -\epsilon {\overline{f}}^T(e(t))\overline{f}(e(t))+k_2\xi \sum _{i=1}^N\Vert e_i(t){\Vert }^2-\sum _{s=1}^r{\varphi }_s{e}^T(t)\\ & \phantom{\sum _{s=1}^r}\times ({\sigma }_{s}B\otimes \mathrm{\Gamma })e(t)\}\\ & =e^{\mu t}\{e^T(t)[\mathcal{A}+{\mathcal{A}}^T+\mu (I_{Nn}-\sum _{s=1}^r{h}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma }))\\ & +(k_2\xi +\epsilon d^2)I_{Nn}-2(D\otimes P)-\sum _{s=1}^r{\varphi }_s({\sigma }_{s}B\otimes \mathrm{\Gamma })]e(t)\\ & \phantom{\sum _{s=1}^r}+2e^T(t)\overline{f}(e(t))-\epsilon \overline{f}(e(t){)}^T\overline{f}(e(t))\}\\ & =e^{\mu t}{z}^T(t)\mathrm{\Pi }z(t),\end{array}$(17) where $z(t)=[e^T(t),{\overline{f}}^T(e(t)){]}^T$. On the basis of the theorem condition (11(11) $\begin{array}{r}\mathrm{\Pi }=\left[\begin{array}{cc}\mathrm{\Phi }& I_{nN}\\ I_{nN}& -\epsilon I_{nN}\end{array}\right]<0,\end{array}$(11) ), we get $\mathcal{L}V(t,e(t))<0$. Taking the expectation for both sides of (17(17) $\begin{array}{rl}& \mathcal{L}V(t,e(t))\\ & \le e^{\mu t}\{e^T(t)[\mathcal{A}+{\mathcal{A}}^T+\mu I_{Nn}-\sum _{s=1}^r{h}_s(z(t))\mu ({\sigma }_{s}B\otimes \mathrm{\Gamma })\\ & \phantom{\sum _{s=1}^r}-2(D\otimes P)]e(t)+2e^T(t)\overline{f}(e(t))+\epsilon d^2{e}^T(t)e(t)\\ & -\epsilon {\overline{f}}^T(e(t))\overline{f}(e(t))+k_2\xi \sum _{i=1}^N\Vert e_i(t){\Vert }^2-\sum _{s=1}^r{\varphi }_s{e}^T(t)\\ & \phantom{\sum _{s=1}^r}\times ({\sigma }_{s}B\otimes \mathrm{\Gamma })e(t)\}\\ & =e^{\mu t}\{e^T(t)[\mathcal{A}+{\mathcal{A}}^T+\mu (I_{Nn}-\sum _{s=1}^r{h}_s(z(t))({\sigma }_{s}B\otimes \mathrm{\Gamma }))\\ & +(k_2\xi +\epsilon d^2)I_{Nn}-2(D\otimes P)-\sum _{s=1}^r{\varphi }_s({\sigma }_{s}B\otimes \mathrm{\Gamma })]e(t)\\ & \phantom{\sum _{s=1}^r}+2e^T(t)\overline{f}(e(t))-\epsilon \overline{f}(e(t){)}^T\overline{f}(e(t))\}\\ & =e^{\mu t}{z}^T(t)\mathrm{\Pi }z(t),\end{array}$(17) ), we get (18) $E\{\mathcal{L}V(t,e(t))\}<0.$(18) For any $t\ge 0$, from Equation (18(18) $E\{\mathcal{L}V(t,e(t))\}<0.$(18) ) and Lemma 2.5, we have (19) $E\{V(t,e(t))\}=E\{V(0)\}+E\{{\int }_0^t\mathcal{L}V(s,e(s))\mathrm{d}s\}\le E\{V(0)\}.$(19) From the definition of $V(t)$ and Equation (19(19) $E\{V(t,e(t))\}=E\{V(0)\}+E\{{\int }_0^t\mathcal{L}V(s,e(s))\mathrm{d}s\}\le E\{V(0)\}.$(19) ), we have (20) $\begin{array}{rl}{k}_1{e}^{\mu t}E\{\Vert e(t){\Vert }^2\}& \le E\{V(t,e(t))\}\\ & \le E\{V(0)\}\\ & \le k_{2}E\{\Vert e(0){\Vert }^2\}\\ & +\sum _{s=1}^r{h}_s(z(0))\sum _{i=1}^N\frac{1}{{\rho }_i^s}(k_i^s(0)-d^{\ast }{)}^2.\end{array}$(20) From Equation (20(20) $\begin{array}{rl}{k}_1{e}^{\mu t}E\{\Vert e(t){\Vert }^2\}& \le E\{V(t,e(t))\}\\ & \le E\{V(0)\}\\ & \le k_{2}E\{\Vert e(0){\Vert }^2\}\\ & +\sum _{s=1}^r{h}_s(z(0))\sum _{i=1}^N\frac{1}{{\rho }_i^s}(k_i^s(0)-d^{\ast }{)}^2.\end{array}$(20) ), noting that $k_1=1$, we have (21) $E\{\Vert e(t){\Vert }^2\}\le M{e}^{-\mu t},$(21) where $M=k_{2}E\{\Vert e(0){\Vert }^2\}+\sum _{s=1}^r{h}_s(z(0))\sum _{i=1}^N\frac{1}{{\rho }_i^s}(k_i^s(0)-d^{\ast }{)}^2$.

According to Definition 2.1, the synchronization error system (8(8) $\begin{array}{rl}\mathrm{d}e(t)& =\sum _{s=1}^r{h}_s(z(t))[(\mathcal{A}e(t)+\overline{f}(e(t))+({\sigma }_{s}B\otimes \mathrm{\Gamma })\dot{e}(t)\\ & -(K^s(t)\otimes P)e(t))\mathrm{d}t\\ & +H(t,e(t))\mathrm{d}\mathrm{\Omega }(t)\phantom{\overline{f}}],\end{array}$(8) ) is mean square exponentially stable under the fuzzy adaptive controller (6(6) $u_i(t)=-\sum _{s=1}^r{h}_s(z(t))k_i^s(t)P{e}_i(t),$(6) )–(7(7) ${\dot{k}}_i^s(t)={\rho }_i^s{e}^{\mu t}{e}_i^T(t)P{e}_i(t).$(7) ).

4. Illustrative examples

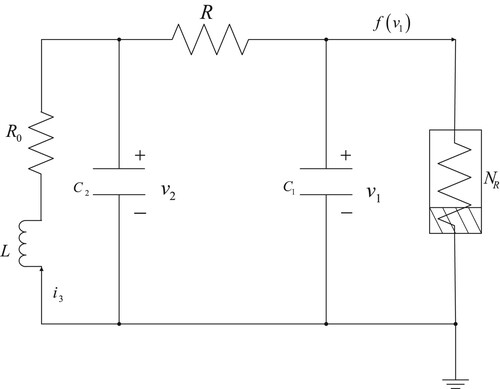
Consider a complex network of Chua's circuit with five nodes. A single Chua's circuit is shown in Figure 1 (Chua et al., 1993), which satisfied the following differential equation: (22) $\begin{array}{rl}{C}_1{\dot{v}}_1(t)& =\frac{1}{R}(-v_1+v_2)-f(v_1),\\ C_2{\dot{v}}_2(t)& =\frac{1}{R}(v_1-v_2)+i_3,\\ L{\dot{i}}_3(t)& =-(v_2+R_0{i}_3),\end{array}$(22) where $v_1$ and $v_2$ represent the voltage at both sides of capacitors $C_1$ and $C_2$, $i_3$ represents the current through the inductor L. $R_0$ and R are linear resistance. $f(v_1)$ represents the current through the nonlinear resistance $N_R$, and $f(v_1)=G_{b1}{v}_1+0.5(G_{a1}-G_{b1})(|v_1+1|-|v_1-1|)$. According to Hwang et al. (1997), the feedback controller and the inductor are connected in series to form the voltage $u_i(t)$. On the other hand, complex networks may be affected by noise. Therefore, the Chua's circuit network model can be expressed in the following form: (23) $\begin{array}{rl}\mathrm{d}{x}_i(t)& =[A{x}_i(t)+f(x_i(t))+G(x(t))\sum _{j=1}^N{b}_{ij}\mathrm{\Gamma }{\dot{x}}_j(t)+u_i(t)]\mathrm{d}t\\ & +h(t,x_i(t))\mathrm{d}\omega (t),i=1,2,3,4,5,\end{array}$(23) where $\begin{array}{rl}{x}_i(t)& =[x_{i1}(t),x_{i2}(t),x_{i3}(t){]}^T,x_{i1}=v_{i1},\\ x_{i2}& =v_{i2},x_{i3}=i_{i3},\\ A& =\left(\begin{array}{ccc}{\displaystyle -{\displaystyle \frac{1}{R{C}_1}}}& {\displaystyle \frac{1}{R{C}_1}}& 0\\ {\displaystyle {\displaystyle \frac{1}{R{C}_2}}}& -{\displaystyle \frac{1}{R{C}_2}}& {\displaystyle \frac{1}{C_2}}\\ {\displaystyle 0}& -{\displaystyle \frac{1}{L}}& -{\displaystyle \frac{R_0}{L}}\end{array}\right),\\ f(x_i(t))& =\left[\begin{array}{c}-wf(x_{i1}(t))\\ 0\\ 0\end{array}\right],\\ w& =\frac{1}{C_1},\mathrm{\Gamma }=\mathrm{diag}\{1,1,1\}.\end{array}$

Figure 1. Chua's circuit.

The external coupling matrix of the complex network is $B=\left(\begin{array}{ccccc}-2& 1& 0& 0& 1\\ 1& -3& 1& 1& 0\\ 0& 1& -3& 1& 1\\ 0& 1& 1& -4& 2\\ 1& 0& 1& 2& -4\end{array}\right).$Letting $z(t)=\sum _{i=2}^5\Vert x_i(t)-x_1(t){\Vert }_2$, we have $G(x(t))=\{\begin{array}{ll}0.05,& z(t)\le 1,\\ 0.1,& z(t)>1.\end{array}$Using the T–S fuzzy rule, the system (23(23) $\begin{array}{rl}\mathrm{d}{x}_i(t)& =[A{x}_i(t)+f(x_i(t))+G(x(t))\sum _{j=1}^N{b}_{ij}\mathrm{\Gamma }{\dot{x}}_j(t)+u_i(t)]\mathrm{d}t\\ & +h(t,x_i(t))\mathrm{d}\omega (t),i=1,2,3,4,5,\end{array}$(23) ) can be described as follows:

Rule 1: IF $z(t)$ is $M_1$, THEN $\begin{array}{rl}\mathrm{d}{x}_i(t)& =[A{x}_i(t)+f(x_i(t))+{\sigma }_1\sum _{j=1}^5{b}_{ij}\mathrm{\Gamma }{\dot{x}}_j(t)+u_i(t)]\mathrm{d}t\\ & +h(t,x_i(t))\mathrm{d}\omega (t),i=1,2,3,4,5.\end{array}$Rule 2: IF $z(t)$ is $M_2$, THEN $\begin{array}{rl}\mathrm{d}{x}_i(t)& =[A{x}_i(t)+f(x_i(t))+{\sigma }_2\sum _{j=1}^5{b}_{ij}\mathrm{\Gamma }{\dot{x}}_j(t)+u_i(t)]\mathrm{d}t\\ & +h(t,x_i(t))\mathrm{d}\omega (t),i=1,2,3,4,5,\end{array}$where $M_1$ is $z(t)\le 1$, $M_2$ is $z(t)>1$, ${\sigma }_1=0.05$, ${\sigma }_2=0.1$. As a result, the T–S fuzzy model of system (23(23) $\begin{array}{rl}\mathrm{d}{x}_i(t)& =[A{x}_i(t)+f(x_i(t))+G(x(t))\sum _{j=1}^N{b}_{ij}\mathrm{\Gamma }{\dot{x}}_j(t)+u_i(t)]\mathrm{d}t\\ & +h(t,x_i(t))\mathrm{d}\omega (t),i=1,2,3,4,5,\end{array}$(23) ) is (24) $\begin{array}{rl}\mathrm{d}{x}_i(t)& =[A{x}_i(t)+f(x_i(t))\\ & +\sum _{s=1}^2{h}_s(z(t)){\sigma }_s\sum _{j=1}^5{b}_{ij}\mathrm{\Gamma }{\dot{x}}_j(t)+u_i(t)]\mathrm{d}t\\ & +h(t,x_i(t))\mathrm{d}\omega (t),i=1,2,3,4,5,\end{array}$(24) where $h_1(z(t))=\{\begin{array}{ll}1,& z(t)\le 1,\\ 0,& z(t)>1,\end{array}{h}_2(z(t))=\{\begin{array}{ll}0,& z(t)\le 1,\\ 1,& z(t)>1.\end{array}$According to Liu et al. (2019), we choose R = 0.257, $C_1=0.4274$, $C_2=1$, L = 0.0603, $R_0=0.083$, $G_{a1}=-0.8$, $G_{b1}=-0.5$. The initial states of each node in the networks are $x_1(0)=[0.6,1.7,1.1{]}^T$, $x_2(0)=[0.6,2.5,-1.3{]}^T$, $x_3(0)=[0.5,-0.2,1.3{]}^T$, $x_4(0)=[1.1,2.3,-1.1{]}^T$, $x_5(0)=[0.6,2,-0.45{]}^T$, and the initial value of the isolated node is $s(0)=[3,-0.9,-0.2{]}^T$. It can be shown that there exists a positive constant d = 2, which satisfies Assumption 2.2. The selected noise intensity function matrix $\overline{h}(t,e_i(t))=0.002\mathrm{diag}\{e_{i1}(t),e_{i2}(t),e_{i3}(t)\}$, $\omega (t)$ is a three-dimensional Weiner process. 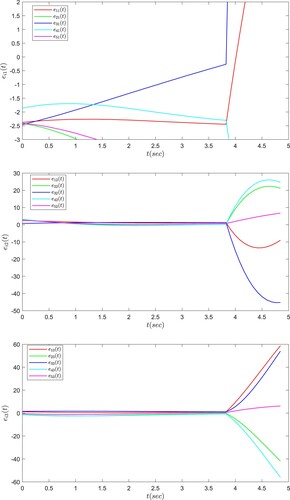Let $\xi =2$, such that $\mathrm{trace}(\overline{h}(t,e_i(t){)}^T\overline{h}(t,e_i(t)))\le 2\Vert e_i(t){\Vert }^2.$Simulation results are shown in Figures 2–5. Figure 2 plots the open-loop response trajectories of synchronization error systems without controllers. From Figure 2, we can see that states of complex networks are not synchronization with state of isolated node.

Figure 2. The trajectories of open-loop synchronization error systems.

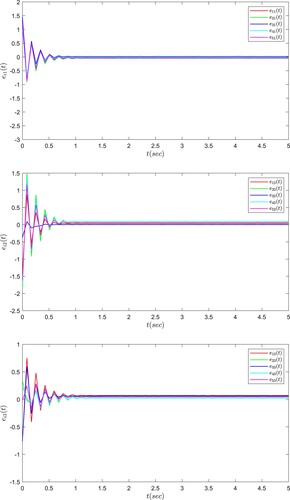
Taking $\mu =0.001$, ${\rho }_i^1=0.001$, ${\rho }_i^2=0.002$, $i=1,2,\dots ,5$, $\epsilon =1$, the linear matrix inequality (11(11) $\begin{array}{r}\mathrm{\Pi }=\left[\begin{array}{cc}\mathrm{\Phi }& I_{nN}\\ I_{nN}& -\epsilon I_{nN}\end{array}\right]<0,\end{array}$(11) ) has the feasible solution $P=\left(\begin{array}{ccc}36.1813& 0.1429& 0\\ 0.1429& 35.2384& 0\\ 0& 0& 36.1908\end{array}\right).$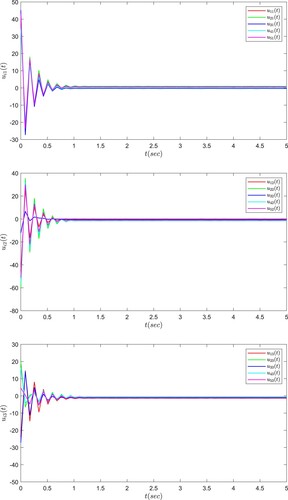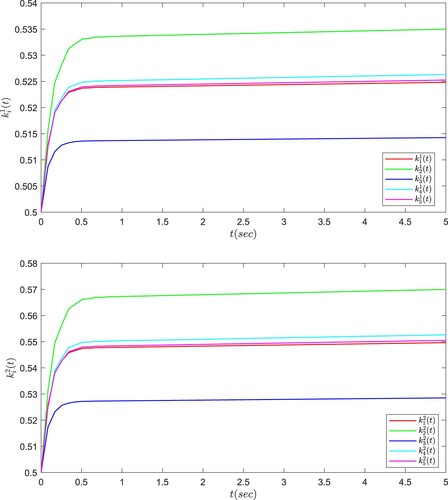The closed-loop response trajectories of the synchronization error systems are given in Figure 3. From Figure 3, it can be seen that the T–S fuzzy adaptive controller designed in this paper is effective and it can guarantee the synchronization performance of the stochastic complex networks. The trajectories of the control input are given in Figure 4. Figure 5 shows the time response curves of the adaptive controller parameters $k_i^s(t)$. From Figure 5, it can be seen that the controller adaptively adjusts the parameter $k_i^s(t)$ towards a constant when then states of synchronization error systems tend to zero.

Figure 3. The trajectories of closed-loop synchronization error systems.

Figure 4. The trajectories of control input.

Figure 5. The trajectories of adaptive parameters $k_i^s(t)$.

5. Conclusions

In this paper, the adaptive synchronization control problem is studied for stochastic complex networks with unknown nonlinear coupling strength and derivative coupling. First, a set of T–S fuzzy complex network models with constant coupling strength is obtained by using T–S fuzzy method. Then, in order to realize the synchronization of the above T–S fuzzy networks, a suitable T–S fuzzy adaptive controller and the corresponding adaptive parameter update rate are designed. Meanwhile, a new T–S fuzzy Lyapunov function closely related to the derivative coupling matrix and the derivative coupling strength is constructed. Using the Lyapunov stability theory and the Itô differential law, it is proved that the fuzzy adaptive synchronization control method designed in this paper can guarantee the mean square exponential stability of the synchronization error system of the stochastic complex network. Finally, the feasibility and effectiveness of the proposed control method are verified by the simulation of the complex network of Chua's circuit.

Disclosure statement

No potential conflict of interest was reported by the authors.

Data availability statement

Data sharing not applicable to this article as no datasets were generated or analysed during the current study.

Additional information

Funding

This article was supported by the National Natural Science Foundation of China [12171124] and the Scientific Research Foundation for Introduced Talents, Fujian Province of China [GY-Z21215, GY-Z21216].