Multiple-bipartite consensus for networked Lagrangian systems without using neighbours' velocity information in the directed graph

Abstract

This paper investigates the multiple-bipartite consensus problem without considering neighbours' velocity information in networked Lagrangian systems (NLSs). A distributed adaptive control algorithm without using neighbours' velocity information is proposed, which facilitates the practical configuration deployments in the coopetition networks. By borrowing a subtle vector composed of the eigenvector components associated with zero eigenvalue of Laplacian matrix, a novel reference estimated vector is introduced to conduct the stability analysis step-by-step in the coopetition networks. Finally, simulations are provided to show the effectiveness of the proposed algorithm.

Keywords:

• Multiple-bipartite consensus
• networked Lagrangian systems
• coopetition networks
• without relative velocity information

1. Introduction

In the last few decades, the mechanical system coordination control has received considerable attention for the extensive applications in the fields of rescue missions, scheduling of automated highway systems, handling of large objects, sensor networks (Cao et al., 2011; Cheah et al., 2009; Dimarogonas & Kyriakopoulos, 2007; Naserian et al., 2020; Ou et al., 2017; Ren, 2007; Zhu et al., 2013). Usually, coordination control is modelled as a consensus or synchronization problem. Many efforts have been devoted to studying a variety of the distributed control of coordinated behaviours for NLSs, such as rendezvous (Dong & Chen, 2019), distributed formation (Bechlioulis et al., 2018) and flocking (Ghapania et al., 2016). In Liu et al. (2015), three distributed adaptive group consensus schemes for NLSs were presented with parametric uncertainties. Recently, a novel distributed adaptive backstepping strategy was given in the finite-time containment control of NLSs with uncertain parameters in Zhao et al. (2022).

Notably, all the work mentioned above is about the consensus problem of NLSs in cooperation networks. However, coopetition networks, in which the widespread antagonistic interactions between agents are involved, should be considered. For example, social network is a classic coopetition network (Xia et al., 2016). Altafini (2013) first proposed the concept of bipartite consensus with first-order dynamics in the Altafini-type coopetition network, in which the agent states evolve a symmetric behaviour eventually. Since then, lots of work has been devoted to the studies of this topic. Valcher and Misra (2014) discussed bipartite consensus in high-order multi-agent dynamical systems with antagonistic interactions. Based on the sliding mode control theory, Wu et al. (2020) addressed bipartite tracking problem of networked robotic systems with external disturbances in the task space, exerting on two antagonistic subgroups to reach two arbitrarily small neighbourhoods of the leader state with opposite signs in a finite time. We refer the reader for more details (Hu & Wu, 2017; Hu et al., 2018; Hu & Zheng, 2014).

Nevertheless, the application scenario of bipartite consensus remains limited. There are a broad range of potential engineering backgrounds more than single bipartite consensus problem framework, such as in the applications of surveillance, monitoring for environmental protection, multi-mission rescue and disease diagnosis and treatment (Abrate et al., 2013; Chien et al., 2017; Durdu & Korkmaz, 2019; Xie et al., 2019). Thus it is natural and necessary to solve the consensus problem of multiple symmetrical characteristic, which facilitates the deployment of adaptations and applications for NLSs. Based on this, Zhang et al. (2021) proposed the concept of multiple-bipartite consensus in NLSs, integrating two emergent collective behaviours in cooperative-competitive networks.

It should be noted that the controllers designed in the aforementioned literature all utilize relative velocity information. Inspired by the above-mentioned literature, this paper investigates the multiple-bipartite consensus problem of NLSs without using relative velocity information. The contributions of this study are listed as follows. (1) Considering that the relative velocity information is difficult to measure directly in the actual situations, a multiple-bipartite consensus algorithm without using relative velocity information for NLSs is proposed in coopetition networks. (2) By utilizing the decomposition property of the Laplacian matrix in structurally balanced acyclic graph, a novel reference vector, composed of eigenvector components associated with zero eigenvalue of Laplacian matrix, is introduced to carry out stability analysis in each group by step.

The rest of this paper is organized as follows: the basic notations, problem formulation and the main results of multiple-bipartite consensus problem in our framework are introduced in Section 2, respectively. The validity of the main results is verified by numerical simulations in Section 3. Finally, Section 4 summarizes the contributions of this paper and outlines the future work.

2. Presentation of main results

2.1. Notations

$\mathbb{R}$, ${\mathbb{R}}^p$ and ${\mathbb{R}}^{s\times t}$ are the set of real numbers, the set of p-dimensional Euclidean space and the set of $s\times t$ real matrices, respectively. ${\mathbf{1}}_n$ and ${\mathbf{0}}_n$ are the column vectors with all elements 1 and 0, respectively. $I_p$ denotes the $p\times p$ identity matrix. Sgn(·) and ⊗ denote respectively the sign function and the Kronecker product.

2.2. Problem formulation

The network communication topology of multi-agent is represented by a directed graph. Let $\mathcal{G}=(\mathcal{V},\mathcal{E},\mathcal{A})$ be a weighted directed graph, $\mathcal{V}=\{1,2,\dots ,d\}$ is the agent set, $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$ is the edge set and $A=[a_{ij}]\in R^{d\times d}$ is the weighted adjacency matrix associated with $\mathcal{G}$, which is given by $a_{ij}=0$ if $(j,i)\notin \mathcal{E}$, otherwise, $a_{ij}\ne 0$ if $(j,i)\in \mathcal{E}$. A directed path from $i_1$ to $i_k$ in the graph is defined as the serial different edges of $(i_1,i_2),(i_2,i_3),\dots ,(i_{k-1},i_k)$, such that $(i_j,i_{j+1})\in \mathcal{E},j=1,2,\dots ,k-1.$ The directed graph is strongly connected, i.e. for any two nodes i and j in $\mathcal{G}$, $i\ne j$, there exists least a directed path from i to j. Furthermore, the graph $\mathcal{G}$ is said to be structurally balanced, if $\mathcal{V}$ can be divided into two subsets $\{{\mathcal{V}}^{(1)},{\mathcal{V}}^{(2)}\}$, of which the intersection is empty, and the union is $\mathcal{V}$. In addition, $a_{ij}\ge 0$ if i and j are in the same subset ${\mathcal{V}}^{(m)}$, m = 1, 2, and $a_{ij}\le 0$ if i and j are from different subsets.

It is said that the agent set $\mathcal{V}=\{1,2,\dots ,d\}$ has a partition $\{{\mathcal{V}}_1,{\mathcal{V}}_2,\dots ,{\mathcal{V}}_k\}$, such that ${\mathcal{V}}_l\ne \mathrm{\varnothing },\bigcup _{l=1}^k{\mathcal{V}}_l=\mathcal{V},{\mathcal{V}}_l\bigcap {\mathcal{V}}_m=\mathrm{\varnothing },l\ne m,l,m\in \{1,2,\dots ,k\}.$ ${\mathcal{V}}_l$ can be denoted as ${\mathcal{V}}_l=\{\sum _{j=0}^{l-1}{n}_j+1,\dots ,\sum _{j=0}^l{n}_j\},$ where $n_0=0,\sum _{l=1}^k{n}_l=d,n_l>0,l=1,2,\dots ,k$. For convenience, we denote $h_0=0,h_l=\sum _{j=1}^l{n}_j,l=1,2,\dots ,k$. If $i\in V_l$, the index set $\overline{i}$ represents $\overline{i}=l$. The subnetwork graph ${\mathcal{G}}_l$ of $\mathcal{G}$ associates with ${\mathcal{V}}_l$. In addition, two assumptions are listed as follows.

Assumption 2.1

Each ${\mathcal{G}}_l$ is structurally balanced.

Assumption 2.2

Each ${\mathcal{G}}_l$ is strongly connected.

By Assumption 2.1, ${\mathcal{V}}_l$ can be partitioned into two subsets, ${\mathcal{V}}_l^{(1)}$ and ${\mathcal{V}}_l^{(2)}$, such that ${\mathcal{V}}_l^{(1)}\bigcap {\mathcal{V}}_l^{(2)}=\mathrm{\varnothing }$, ${\mathcal{V}}_l^{(1)}\bigcup {\mathcal{V}}_l^{(2)}={\mathcal{V}}_l$. Define ${\varphi }_i\in \{-1,1\}$, if $i\in {\mathcal{V}}_l^{(1)}$, ${\varphi }_i=1$, and otherwise if $i\in {\mathcal{V}}_l^{(2)}$, ${\varphi }_i=-1$, and ${\mathrm{\Phi }}_l=diag\{{\varphi }_{h_{l-1}+1},{\varphi }_{h_{l-1}+2},\dots ,{\varphi }_{h_l}\}$, $i=1,2,\dots ,d,l=1,2,\dots ,k$. The Laplacian matrix of $\mathcal{G}$ is defined as $L=[l_{ij}]\in R^{d\times d}$, $l_{ii}=\sum _{j\notin {\mathcal{V}}_{\overline{i}}}{\varphi }_j{a}_{ij}+\sum _{j\in \overline{i}}|a_{ij}|,i=1,2,\dots ,d$, and $l_{ij}=-a_{ij},i\ne j$.

Considering NLSs consisting of d robots, for the ith robot, the dynamics equation can be written as the following Euler–Lagrange formulation: (1) $M_i(q_i){\ddot{q}}_i+C_i(q_i,{\dot{q}}_i){\dot{q}}_i+G_i(q_i)={\tau }_i,i=1,2,\dots ,d,$(1) where $q_i,{\dot{q}}_i\in {\mathbb{R}}^p$ are generalized coordinate and velocity vectors, respectively, $M_i(q_i)\in {\mathbb{R}}^{n\times p}$ is the symmetric positive inertial matrix, $C_i(q_i,{\dot{q}}_i)\in {\mathbb{R}}^{p\times p}$ is the Coriolis and centrifugal force matrix, $G_i(q_i)\in {\mathbb{R}}^p$ is the generalized potential force, ${\tau }_i\in {\mathbb{R}}^p$ is the input torque vector. Moreover, in the following discussion, three basic dynamics properties of system (1(1) $M_i(q_i){\ddot{q}}_i+C_i(q_i,{\dot{q}}_i){\dot{q}}_i+G_i(q_i)={\tau }_i,i=1,2,\dots ,d,$(1) ) are listed as follows:

Proposition 2.3

There exist positive constants $k_{i1},k_{i2},k_{i3}$, satisfying $0\le k_{i1}{I}_p\le M_i(q_i)\le k_{i2}{I}_p,||C_i(x,y)z||\le k_{i3}||y||||z||,\mathrm{\forall }x,y,z\in {\mathbb{R}}^p$.

Proposition 2.4

${\dot{M}}_i-2C_i$ is skew symmetric, i.e. for $\mathrm{\forall }X\in {\mathbb{R}}^p$, $X^{\mathrm{T}}(\dot{M_i}(q_i)-2C_i(q_i,{\dot{q}}_i))X=0$.

Proposition 2.5

System (1(1) $M_i(q_i){\ddot{q}}_i+C_i(q_i,{\dot{q}}_i){\dot{q}}_i+G_i(q_i)={\tau }_i,i=1,2,\dots ,d,$(1) ) is linearly parameterizable with respect to a constant dynamic parameter vector ${\theta }_i$ , that is (2) $M_i(q_i)x+C_i(q_i,{\dot{q}}_i)y+G_i(q_i)=Y_i(q_i,{\dot{q}}_i,x,y){\theta }_i,$(2) where $x,y\in {\mathbb{R}}^p$ are differentiable vectors and $Y_i(q_i,{\dot{q}}_i,x,y)$ is the regression matrix.

Definition 2.6

Under the partition $\{{\mathcal{V}}_1,{\mathcal{V}}_2,\dots ,{\mathcal{V}}_k\}$, system (1(1) $M_i(q_i){\ddot{q}}_i+C_i(q_i,{\dot{q}}_i){\dot{q}}_i+G_i(q_i)={\tau }_i,i=1,2,\dots ,d,$(1) ) is said to realize multiple-bipartite consensus if $(I)$ $q_i(t)\to q_j(t)$, ${\dot{q}}_i(t)\to {\dot{q}}_j(t)$, as $t\to \mathrm{\infty }$, for $i,j\in {\mathcal{V}}_l^{(1)}$ or $i,j\in {\mathcal{V}}_l^{(2)}$. $(II)$ $q_i(t)\to -q_j(t)$, ${\dot{q}}_i(t)\to -{\dot{q}}_j(t)$, as $t\to \mathrm{\infty }$, for $i\in {\mathcal{V}}_l^{(1)}$, $j\in {\mathcal{V}}_l^{(2)}$or $i\in {\mathcal{V}}_l^{(2)}$, $j\in {\mathcal{V}}_l^{(1)}$, where $i,j=1,2,\dots ,d$, $l=1,2,\dots ,k$.

Assume that the Laplacian matrix L has the form below (3) $L=\left[\begin{array}{ccc}{L}_{11}& \cdots & 0_{n_1\times n_k}\\ ⋮& \ddots & ⋮\\ L_{k1}& \cdots & L_{kk}\end{array}\right],$(3) where $L_{mm}$ and $L_{mn}$ describe the situation of information transmission in ${\mathcal{G}}_m$, and from ${\mathcal{G}}_n$ to ${\mathcal{G}}_m$, $m,n=1,2,\dots ,k$, respectively. In addition, we assume that the following assumption holds:

Assumption 2.7

The sum of each row in ${\mathrm{\Phi }}_m{L}_{mn}{\mathrm{\Phi }}_n$ is zero, $m\ne n,m,n=1,2,\dots ,k$.

Remark 2.1

The inequalities of Property 2.4 are commonly used in Lagrangian-type dynamics coordination problems, which ensures that $Y_i(q_i,{\dot{q}}_i,x,y)$ of Property 2.5 is bounded in the following stability analysis (Kelly et al., 2005). Additionally, ${\theta }_i$ and $Y_i$ in Equation (2(2) $M_i(q_i)x+C_i(q_i,{\dot{q}}_i)y+G_i(q_i)=Y_i(q_i,{\dot{q}}_i,x,y){\theta }_i,$(2) ) are not unique, whose formulations are determined by the dynamics Equation (1(1) $M_i(q_i){\ddot{q}}_i+C_i(q_i,{\dot{q}}_i){\dot{q}}_i+G_i(q_i)={\tau }_i,i=1,2,\dots ,d,$(1) ).

Remark 2.2

Equation (3(3) $L=\left[\begin{array}{ccc}{L}_{11}& \cdots & 0_{n_1\times n_k}\\ ⋮& \ddots & ⋮\\ L_{k1}& \cdots & L_{kk}\end{array}\right],$(3) ) shows that $\mathcal{V}=$ $\{{\mathcal{V}}_1,{\mathcal{V}}_2,\dots ,{\mathcal{V}}_k\}$ is an acyclic partition of $\mathcal{G}$. If the L does not have the form of Equation (3(3) $L=\left[\begin{array}{ccc}{L}_{11}& \cdots & 0_{n_1\times n_k}\\ ⋮& \ddots & ⋮\\ L_{k1}& \cdots & L_{kk}\end{array}\right],$(3) ), we can always rearrange the order of the agents to make the new Laplacian matrix have the normal form in Mei et al. (2012).

2.3. Main results

In this section, considering a consensus-based algorithm without using relative velocity information for NLSs, the main results of multiple-bipartite consensus problem of NLSs are presented in coopetition networks.

First, for the ith robot, define the following auxiliary variable as (4) ${\dot{q}}_{ri}=-{\mathrm{\Sigma }}_{j\in {\mathcal{V}}_{\hat{i}}}{a}_{ij}[\mathrm{sgn}(a_{ij})q_i-q_j]-{\mathrm{\Sigma }}_{j\notin {\mathcal{V}}_{\hat{i}}}{a}_{ij}({\varphi }_j{q}_i-q_j),$(4) where ${\dot{q}}_{ri}\in {\mathbb{R}}^p$.

A sliding vector ${\overline{s}}_i$ (${\overline{s}}_i\in {\mathbb{R}}^p$) is introduced by (5) ${\overline{s}}_i={\dot{q}}_i-{\dot{q}}_{ri}.$(5) Next, the torque control protocol is given by (6) ${\tau }_i=Y_i(q_i,{\dot{q}}_i,{\mathbf{0}}_p,{\dot{q}}_{ri}){\overline{\theta }}_i-K_i{\overline{s}}_i,$(6) where $K_i$ is the positive definite matrix, which is beneficial to construct the Lyapunov-like function in Equation (11(11) $V_1(t)={\mathrm{\Sigma }}_{i=1}^{n_1}(\frac{1}{2}{\overline{s}}_i^{\mathrm{T}}{M}_i(q_i){\overline{s}}_i+\frac{1}{2}{\tilde{\theta }}_i^{\mathrm{T}}{\mathrm{\Lambda }}_i^{-1}{\tilde{\theta }}_i+{\varphi }_i{\alpha }_{1i}{\tilde{q}}_i^{\mathrm{T}}{\tilde{q}}_i).$(11) ). ${\overline{\theta }}_i$ is the estimation of ${\theta }_i$. Here, we do not utilize the relative velocity information. Accordingly, the adaptive law of ${\overline{\theta }}_i$ is designed as (7) ${\dot{\overline{\theta }}}_i=-{\mathrm{\Lambda }}_i{Y}_i^{\mathrm{T}}(q_i,{\dot{q}}_i,{\mathbf{0}}_p,{\dot{q}}_{ri}){\overline{s}}_i,$(7) where ${\mathrm{\Lambda }}_i$ is a symmetric positive definite matrix.

Apply control protocol (6(6) ${\tau }_i=Y_i(q_i,{\dot{q}}_i,{\mathbf{0}}_p,{\dot{q}}_{ri}){\overline{\theta }}_i-K_i{\overline{s}}_i,$(6) ) and adaptive law (7(7) ${\dot{\overline{\theta }}}_i=-{\mathrm{\Lambda }}_i{Y}_i^{\mathrm{T}}(q_i,{\dot{q}}_i,{\mathbf{0}}_p,{\dot{q}}_{ri}){\overline{s}}_i,$(7) ) to system (1(1) $M_i(q_i){\ddot{q}}_i+C_i(q_i,{\dot{q}}_i){\dot{q}}_i+G_i(q_i)={\tau }_i,i=1,2,\dots ,d,$(1) ), yielding that (8) $M_i(q_i){\dot{\overline{s}}}_i=-C_i(q_i,{\dot{q}}_i){\overline{s}}_i-Y_i(q_i,{\dot{q}}_i,{\mathbf{0}}_p,{\dot{q}}_{ri}){\tilde{\theta }}_i-K_i{\overline{s}}_i.$(8) where ${\tilde{\theta }}_i={\theta }_i-{\overline{\theta }}_i$.

Assume that ${\mathrm{\Phi }}_l$ and ${\varphi }_i$ are defined the same as in Section 2.2. Under Assumptions 2.1, 2.2 and 2.7, the Laplacian matrix L has a zero eigenvalue with the algebraic multiplicity and geometric multiplicity being both k. Then the k linear independent left eigenvectors of the zero eigenvalue can be expressed as ${\overline{\xi }}_1=({\alpha }_{11},{\alpha }_{12},\dots ,{\alpha }_{1n_1},0,\dots ,0)$, ${\overline{\xi }}_2=({\beta }_{11}^{(2)},{\beta }_{12}^{(2)},\dots ,{\beta }_{1n_1}^{(2)},{\alpha }_{21},{\alpha }_{22},\dots ,{\alpha }_{2n_2},0,\dots ,0)$, ··· , ${\overline{\xi }}_k=({\beta }_{11}^{(k)},{\beta }_{12}^{(k)},\dots ,{\beta }_{1n_1}^{(k)},\dots ,{\beta }_{(k-1),1}^{(k)},{\beta }_{(k-1),2}^{(k)},\dots ,{\beta }_{(k-1),n_{k-1}}^{(k)},{\alpha }_{k1},{\alpha }_{k2},\cdots ,{\alpha }_{k{n}_k}),$ satisfying (9) ${\mathrm{\Sigma }}_{j=1}^{n_w}{\varphi }_{h_{w-1}+j}{\alpha }_{wj}=1,w=1,2,\dots ,k.$(9)

Lemma 2.8

Mei et al., 2016

Suppose that ${\hat{G}}_w$ is a directed graph of order $n_w$ in cooperative networks and is strongly connected, $w\in \{1,2,\dots ,k\}$. Define the matrix ${\hat{P}}^{(w)}$ as ${\hat{P}}^{(w)}\triangleq {\hat{P}}_w{\hat{L}}_{ww}+{\hat{L}}_{ww}^T{\hat{P}}_w$, where ${\hat{L}}_{ww}$ is the Laplacian matrix associated with ${\hat{G}}_w$, ${\hat{P}}_w=\mathrm{diag}\{{\hat{\alpha }}_{w1},{\hat{\alpha }}_{w2},\dots ,{\hat{\alpha }}_{w{n}_w}\}$, and ${\mathrm{\Sigma }}_{j=1}^{n_w}{\hat{\alpha }}_{wj}=1$. Then ${\hat{P}}^{(w)}$ is the symmetric Laplacian matrix associated with an undirected graph. Assume that ϵ be any positive vector, let ${\hat{\xi }}_w={({\hat{\alpha }}_{w1},{\hat{\alpha }}_{w2},\dots ,{\hat{\alpha }}_{w{n}_w})}^{\mathrm{T}}$, then the following formula holds: $a({\hat{L}}_{ww})=\underset{{ϵ}^{\mathrm{T}}ϵ=1,{\hat{\xi }}_w^{\mathrm{T}}ϵ=0}{min}{ϵ}^{\mathrm{T}}{\hat{P}}^{(w)}ϵ>0.$

Next, the major result of this paper is readily given below:

Theorem 2.9

Assume that $\mathcal{V}=$ $\{{\mathcal{V}}_1,{\mathcal{V}}_2,\dots ,{\mathcal{V}}_k\}$ is an acyclic partition of $\mathcal{G}$ and that 2.1, 2.2 and 2.7 hold. Under (6(6) ${\tau }_i=Y_i(q_i,{\dot{q}}_i,{\mathbf{0}}_p,{\dot{q}}_{ri}){\overline{\theta }}_i-K_i{\overline{s}}_i,$(6) ) and (7(7) ${\dot{\overline{\theta }}}_i=-{\mathrm{\Lambda }}_i{Y}_i^{\mathrm{T}}(q_i,{\dot{q}}_i,{\mathbf{0}}_p,{\dot{q}}_{ri}){\overline{s}}_i,$(7) ), select appropriate control gains, system (1(1) $M_i(q_i){\ddot{q}}_i+C_i(q_i,{\dot{q}}_i){\dot{q}}_i+G_i(q_i)={\tau }_i,i=1,2,\dots ,d,$(1) ) can realize multiple bipartite consensus in the sense of Definition 2.6.

Proof.

First consider the situation of the subgraph ${\mathcal{G}}_1$. By Assumption 2.2, as can be seen from Equation (3(3) $L=\left[\begin{array}{ccc}{L}_{11}& \cdots & 0_{n_1\times n_k}\\ ⋮& \ddots & ⋮\\ L_{k1}& \cdots & L_{kk}\end{array}\right],$(3) ), $G_1$ corresponding to $L_{11}$ is strongly connected. Combining Equation (9(9) ${\mathrm{\Sigma }}_{j=1}^{n_w}{\varphi }_{h_{w-1}+j}{\alpha }_{wj}=1,w=1,2,\dots ,k.$(9) ) and Lemma 2.8 shows that there exist a serial real numbers ${\alpha }_{1i}$,  $i=1,\dots ,n_1$, such that ${\mathrm{\Sigma }}_{i=1}^{n_1}{\varphi }_i{\alpha }_{1i}=1$. Denote $P_1=\mathrm{diag}\{{\alpha }_{11},{\alpha }_{12},\dots ,{\alpha }_{1n_1}\}$, and ${\xi }_1=({\alpha }_{11},{\alpha }_{12},\dots ,{\alpha }_{1n_1}{)}^{\mathrm{T}}$. Define the reference vector ${\check{q}}_1={\mathrm{\Sigma }}_{j=1}^{n_1}{\alpha }_{1j}{q}_j$, ${\tilde{q}}_i=q_i-{\varphi }_i{\check{q}}_1$, $i=1,\dots ,n_1$. Let $\mathbf{q}$ be the column stack vector of $q_i$, $i=1,\dots ,d$, i.e. $\mathbf{q}=[{\mathbf{q}}_1^{\mathrm{T}};\cdots ,{\mathbf{q}}_k^{\mathrm{T}}{]}^T$, where ${\mathbf{q}}_j$ is the column stack vector of state variables for all the agents in kth group, $j=1,\dots ,k$. Let ${\tilde{\mathbf{q}}}_1$, ${\mathbf{s}}_1$, ${\mathbf{q}}_{r1}$ be the column stack vector of ${\tilde{q}}_i$, ${\overline{s}}_i$, $q_{ri}$, respectively, $i=1,\dots ,n_1$.

Rewrite sliding vectors (5(5) ${\overline{s}}_i={\dot{q}}_i-{\dot{q}}_{ri}.$(5) ) as the compact form (10) ${\mathbf{s}}_1={\dot{\mathbf{q}}}_1+(L_{11}\otimes I_p){\tilde{\mathbf{q}}}_1.$(10) Building Lyapunov-like function (11) $V_1(t)={\mathrm{\Sigma }}_{i=1}^{n_1}(\frac{1}{2}{\overline{s}}_i^{\mathrm{T}}{M}_i(q_i){\overline{s}}_i+\frac{1}{2}{\tilde{\theta }}_i^{\mathrm{T}}{\mathrm{\Lambda }}_i^{-1}{\tilde{\theta }}_i+{\varphi }_i{\alpha }_{1i}{\tilde{q}}_i^{\mathrm{T}}{\tilde{q}}_i).$(11) Combining Equation (11(11) $V_1(t)={\mathrm{\Sigma }}_{i=1}^{n_1}(\frac{1}{2}{\overline{s}}_i^{\mathrm{T}}{M}_i(q_i){\overline{s}}_i+\frac{1}{2}{\tilde{\theta }}_i^{\mathrm{T}}{\mathrm{\Lambda }}_i^{-1}{\tilde{\theta }}_i+{\varphi }_i{\alpha }_{1i}{\tilde{q}}_i^{\mathrm{T}}{\tilde{q}}_i).$(11) ) with Equation (10(10) ${\mathbf{s}}_1={\dot{\mathbf{q}}}_1+(L_{11}\otimes I_p){\tilde{\mathbf{q}}}_1.$(10) ), the derivative of $V_1(t)$ with respect to t is given by ${\dot{V}}_1(t)=-{\mathbf{s}}_1^{\mathrm{T}}K{\mathbf{s}}_1+{\dot{\tilde{\mathbf{q}}}}_1^{\mathrm{T}}(P_1{\mathrm{\Phi }}_1\otimes I_p){\tilde{\mathbf{q}}}_1+{\tilde{\mathbf{q}}}_1^{\mathrm{T}}(P_1{\mathrm{\Phi }}_1\otimes I_p){\dot{\tilde{\mathbf{q}}}}_1.$where K is the control gain diagonal matrix of all agents.

Denoting ${\mathrm{\Xi }}_1=({\varphi }_1,{\varphi }_2,\dots ,{\varphi }_{n_1}{)}^{\mathrm{T}}$, by Equation (10(10) ${\mathbf{s}}_1={\dot{\mathbf{q}}}_1+(L_{11}\otimes I_p){\tilde{\mathbf{q}}}_1.$(10) ), note that (12) $\begin{array}{rl}{\dot{\tilde{\mathbf{q}}}}_1& ={\dot{\mathbf{\text{q}}}}_1-{\mathrm{\Xi }}_1\otimes {\dot{\check{q}}}_1\\ & ={\dot{\mathbf{\text{q}}}}_1-{\mathrm{\Xi }}_1\otimes ({\xi }_1^{\mathrm{T}}\otimes I_p){\dot{\mathbf{\text{q}}}}_1\\ & ={\mathbf{s}}_1-(L_{11}\otimes I_p){\tilde{\mathbf{q}}}_1-{\mathrm{\Xi }}_1\otimes ({\xi }_1^{\mathrm{T}}\otimes I_p){\mathbf{s}}_1,\end{array}$(12) and (13) $\begin{array}{rl}& (P_1{\mathrm{\Phi }}_1\otimes I_p)\{{\mathbf{s}}_1-{\mathrm{\Xi }}_1\otimes \left[({\xi }_1^{\mathrm{T}}\otimes I_p){\mathbf{s}}_1\right]\}\\ & =(P_1{\mathrm{\Phi }}_1\otimes I_p)\{{\mathbf{s}}_1-[(({\mathrm{\Xi }}_1\otimes {\xi }_1^{\mathrm{T}})\otimes I_p]{\mathbf{s}}_1\}\\ & =(P_1{\mathrm{\Phi }}_1\otimes I_p){\mathbf{s}}_1-\{[P_1{\mathrm{\Phi }}_1({\mathrm{\Xi }}_1\otimes {\xi }_1^{\mathrm{T}})]\otimes I_p\}{\mathbf{s}}_1\\ & =[(P_1{\mathrm{\Phi }}_1-{\xi }_1{\mathrm{\Phi }}_1{\mathrm{\Phi }}_1^{\mathrm{T}}{\xi }_1^{\mathrm{T}})\otimes I_p]{\mathbf{s}}_1\\ & =[(P_1{\mathrm{\Phi }}_1-{\xi }_1{\xi }_1^{\mathrm{T}})\otimes I_p]{\mathbf{s}}_1.\end{array}$(13) Applying Equations (12(12) $\begin{array}{rl}{\dot{\tilde{\mathbf{q}}}}_1& ={\dot{\mathbf{\text{q}}}}_1-{\mathrm{\Xi }}_1\otimes {\dot{\check{q}}}_1\\ & ={\dot{\mathbf{\text{q}}}}_1-{\mathrm{\Xi }}_1\otimes ({\xi }_1^{\mathrm{T}}\otimes I_p){\dot{\mathbf{\text{q}}}}_1\\ & ={\mathbf{s}}_1-(L_{11}\otimes I_p){\tilde{\mathbf{q}}}_1-{\mathrm{\Xi }}_1\otimes ({\xi }_1^{\mathrm{T}}\otimes I_p){\mathbf{s}}_1,\end{array}$(12) ) and (13(13) $\begin{array}{rl}& (P_1{\mathrm{\Phi }}_1\otimes I_p)\{{\mathbf{s}}_1-{\mathrm{\Xi }}_1\otimes \left[({\xi }_1^{\mathrm{T}}\otimes I_p){\mathbf{s}}_1\right]\}\\ & =(P_1{\mathrm{\Phi }}_1\otimes I_p)\{{\mathbf{s}}_1-[(({\mathrm{\Xi }}_1\otimes {\xi }_1^{\mathrm{T}})\otimes I_p]{\mathbf{s}}_1\}\\ & =(P_1{\mathrm{\Phi }}_1\otimes I_p){\mathbf{s}}_1-\{[P_1{\mathrm{\Phi }}_1({\mathrm{\Xi }}_1\otimes {\xi }_1^{\mathrm{T}})]\otimes I_p\}{\mathbf{s}}_1\\ & =[(P_1{\mathrm{\Phi }}_1-{\xi }_1{\mathrm{\Phi }}_1{\mathrm{\Phi }}_1^{\mathrm{T}}{\xi }_1^{\mathrm{T}})\otimes I_p]{\mathbf{s}}_1\\ & =[(P_1{\mathrm{\Phi }}_1-{\xi }_1{\xi }_1^{\mathrm{T}})\otimes I_p]{\mathbf{s}}_1.\end{array}$(13) ) to ${\dot{V}}_1(t)$, one derives (14) $\begin{array}{rl}{\dot{V}}_1(t)& =-{\mathbf{s}}_1^{\mathrm{T}}K{\mathbf{s}}_1+2{\tilde{\mathbf{q}}}_1^{\mathrm{T}}[(P_1{\mathrm{\Phi }}_1-{\xi }_1{\xi }_1^{\mathrm{T}})\otimes I_p]{\mathbf{s}}_1\\ & -{\tilde{\mathbf{q}}}_1^{\mathrm{T}}{\mathrm{\Phi }}_1(P^{(1)}\otimes I_p){{\mathrm{\Phi }}_1\tilde{\mathbf{q}}}_1.\end{array}$(14) where $P^{(1)}=({\mathrm{\Phi }}_1{P}_1){\mathrm{\Phi }}_1{L}_{11}{\mathrm{\Phi }}_1+{\mathrm{\Phi }}_1{L}_{11}^{\mathrm{T}}{\mathrm{\Phi }}_1({\mathrm{\Phi }}_1{P}_1)$.

Thanks to Lemma 2.8, one has (15) ${\tilde{\mathbf{q}}}_1^{\mathrm{T}}{\mathrm{\Phi }}_1(P^{(1)}\otimes I_p){{\mathrm{\Phi }}_1\tilde{\mathbf{q}}}_1\ge a(L_{11})\Vert {\tilde{\mathbf{q}}}_1{\Vert }^2.$(15) Indeed, since the matrix $(P_1{\mathrm{\Phi }}_1-{\xi }_1{\xi }_1^{\mathrm{T}})$ is diagonally dominant, it is symmetric positive semidefinite, yielding that (16) ${\sigma }_{max}(P_1{\mathrm{\Phi }}_1-{\xi }_1{\xi }_1^{\mathrm{T}})\le 1.$(16) Denote $\eta =\mathrm{m}in\{K\}$. From Equations (15(15) ${\tilde{\mathbf{q}}}_1^{\mathrm{T}}{\mathrm{\Phi }}_1(P^{(1)}\otimes I_p){{\mathrm{\Phi }}_1\tilde{\mathbf{q}}}_1\ge a(L_{11})\Vert {\tilde{\mathbf{q}}}_1{\Vert }^2.$(15) ) and (16(16) ${\sigma }_{max}(P_1{\mathrm{\Phi }}_1-{\xi }_1{\xi }_1^{\mathrm{T}})\le 1.$(16) ), it gives rise to $\begin{array}{rl}{\dot{V}}_1(t)& \le -\eta \Vert {\mathbf{s}}_1{\Vert }^2+2\Vert {\tilde{\mathbf{q}}}_1\Vert \Vert {\mathbf{s}}_1\Vert -a(L_{11})\Vert {\tilde{\mathbf{q}}}_1{\Vert }^2\\ & \le -\eta \Vert {\mathbf{s}}_1{\Vert }^2+\frac{4}{a(L_{11})}\Vert {\mathbf{s}}_1{\Vert }^2+\frac{a(L_{11})}{4}\Vert {\tilde{\mathbf{q}}}_1{\Vert }^2\\ & -a(L_{11})\Vert {\tilde{\mathbf{q}}}_1{\Vert }^2.\end{array}$If η is selected as $\eta >\frac{4}{a(L_{11})}+{\eta }_0,$ where ${\eta }_0$ is a positive constant. All of above give the fact that (17) ${\dot{V}}_1(t)\le -{\eta }_0\Vert {\mathbf{s}}_1{\Vert }^2-\frac{3a(L_{11})}{4}\Vert {\tilde{\mathbf{q}}}_1{\Vert }^2<0.$(17) From Equation (17(17) ${\dot{V}}_1(t)\le -{\eta }_0\Vert {\mathbf{s}}_1{\Vert }^2-\frac{3a(L_{11})}{4}\Vert {\tilde{\mathbf{q}}}_1{\Vert }^2<0.$(17) ), ${\mathbf{s}}_1,{\tilde{\mathbf{q}}}_1\in {\mathbb{L}}_{\mathrm{\infty }}$. And by Equation (12(12) $\begin{array}{rl}{\dot{\tilde{\mathbf{q}}}}_1& ={\dot{\mathbf{\text{q}}}}_1-{\mathrm{\Xi }}_1\otimes {\dot{\check{q}}}_1\\ & ={\dot{\mathbf{\text{q}}}}_1-{\mathrm{\Xi }}_1\otimes ({\xi }_1^{\mathrm{T}}\otimes I_p){\dot{\mathbf{\text{q}}}}_1\\ & ={\mathbf{s}}_1-(L_{11}\otimes I_p){\tilde{\mathbf{q}}}_1-{\mathrm{\Xi }}_1\otimes ({\xi }_1^{\mathrm{T}}\otimes I_p){\mathbf{s}}_1,\end{array}$(12) ), ${\dot{\tilde{\mathbf{q}}}}_1\in {\mathbb{L}}_{\mathrm{\infty }}$, ${\mathbf{s}}_1,{\tilde{\mathbf{q}}}_1\in {\mathbb{L}}_2$. Therefore, according to Barbalat's Lemma, one has ${\tilde{\mathbf{q}}}_1\to {\mathbf{0}}_{p{n}_1}$. Hence, $\mathrm{\exists }{T}_1>0,$ if $t>T_1,q_i\to {\varphi }_i{\check{q}}_1,i=1,2,\dots ,h_1.$

Second consider the consistency of group two. By Assumption 2.2, the subgraph $G_2$ corresponding to $L_{22}$ is strongly connected. Combining Equation (9(9) ${\mathrm{\Sigma }}_{j=1}^{n_w}{\varphi }_{h_{w-1}+j}{\alpha }_{wj}=1,w=1,2,\dots ,k.$(9) ) and Lemma 2.8 shows that there exist another serial real numbers ${\alpha }_{2i}$, , $i=1,\dots ,n_2$, such that ${\mathrm{\Sigma }}_{i=1}^{n_2}{\varphi }_{n_1+i}{\alpha }_{2i}=1$. Denote $P_2=\mathrm{diag}\{{\alpha }_{21},{\alpha }_{22},\dots ,{\alpha }_{2n_2}\},$ and ${\xi }_2=({\alpha }_{21},{\alpha }_{22},\dots ,{\alpha }_{2n_2}{)}^{\mathrm{T}}$. Define the reference vector ${\check{q}}_2={\mathrm{\Sigma }}_{j=1}^{n_2}{\alpha }_{2j}{q}_j$, ${\tilde{q}}_i=q_i-{\varphi }_i{\check{q}}_2$, $i=n_1+1,\dots ,h_2$. Let ${\tilde{\mathbf{q}}}_2$, ${\mathbf{s}}_2$, ${\mathbf{q}}_{r2}$ be the column stack vector of ${\tilde{q}}_i$, ${\overline{s}}_i$, $q_{ri}$, respectively, $i=n_1+1,\dots ,h_2$.

Rewrite sliding vectors (3(3) $L=\left[\begin{array}{ccc}{L}_{11}& \cdots & 0_{n_1\times n_k}\\ ⋮& \ddots & ⋮\\ L_{k1}& \cdots & L_{kk}\end{array}\right],$(3) ) as the compact form (18) ${\mathbf{s}}_2={\dot{\mathbf{q}}}_2+(L_{21}\otimes I_p){\tilde{\mathbf{q}}}_1+(L_{22}\otimes I_p){\tilde{\mathbf{q}}}_2.$(18) Building Lyapunov-like function $\begin{array}{rl}{V}_2(t)& ={\mathrm{\Sigma }}_{i=n_1+1}^{h_2}(\frac{1}{2}{\overline{s}}_i^{\mathrm{T}}{M}_i(q_i){\overline{s}}_i+\frac{1}{2}{\tilde{\theta }}_i^{\mathrm{T}}{\mathrm{\Lambda }}_i^{-1}{\tilde{\theta }}_i\\ & \phantom{\frac{1}{2}}+{\varphi }_i{\alpha }_{2(i-n_1)}{\tilde{q}}_i^{\mathrm{T}}{\tilde{q}}_i).\end{array}$The derivative of $V_2(t)$ with respect to t is given by ${\dot{V}}_2(t)=-{\mathbf{s}}_2^{\mathrm{T}}{K}_i{\mathbf{s}}_2+{\dot{\tilde{\mathbf{q}}}}_2^{\mathrm{T}}(P_2{\mathrm{\Phi }}_2\otimes I_p){\tilde{\mathbf{q}}}_2+{\tilde{\mathbf{q}}}_2^{\mathrm{T}}(P_2{\mathrm{\Phi }}_2\otimes I_p){\dot{\tilde{\mathbf{q}}}}_2.$Denoting ${\mathrm{\Xi }}_2=({\varphi }_{n_1+1},{\varphi }_{n_1+2},\dots ,{\varphi }_{h_2}{)}^{\mathrm{T}}$, from the expression of ${\dot{\tilde{\mathbf{q}}}}_2$, one has (19) $\begin{array}{rl}{\dot{\tilde{\mathbf{q}}}}_2& ={\dot{\mathbf{\text{q}}}}_2-{\mathrm{\Xi }}_2\otimes {\dot{\check{q}}}_i\\ & ={\dot{\mathbf{\text{q}}}}_2-{\mathrm{\Xi }}_2\otimes ({\xi }_2^{\mathrm{T}}\otimes I_p){\dot{\mathbf{\text{q}}}}_2\\ & ={\mathbf{s}}_2-(L_{21}\otimes I_p){\tilde{\mathbf{q}}}_1-(L_{22}\otimes I_p){\tilde{\mathbf{q}}}_2\\ & -{\mathrm{\Xi }}_2\otimes ({\xi }_2^{\mathrm{T}}\otimes I_p)({\mathbf{s}}_2-(L_{21}\otimes I_p){\tilde{\mathbf{q}}}_1),\end{array}$(19) and (20) $\begin{array}{rl}& (P_2{\mathrm{\Phi }}_2\otimes I_p)\{{\mathbf{s}}_2-{\mathrm{\Xi }}_2\otimes \left[({\xi }_2^{\mathrm{T}}\otimes I_p){\mathbf{s}}_2\right]\}\\ & =(P_2{\mathrm{\Phi }}_2\otimes I_p)\{{\mathbf{s}}_2-[(({\mathrm{\Xi }}_2\otimes {\xi }_2^{\mathrm{T}})\otimes I_p]{\mathbf{s}}_2\}\\ & =(P_2{\mathrm{\Phi }}_2\otimes I_p){\mathbf{s}}_2-\{[P_2{\mathrm{\Phi }}_2({\mathrm{\Xi }}_2\otimes {\xi }_2^{\mathrm{T}})]\otimes I_p\}{\mathbf{s}}_2\\ & =[(P_2{\mathrm{\Phi }}_2-{\xi }_2{\mathrm{\Phi }}_2{\mathrm{\Phi }}_2^{\mathrm{T}}{\xi }_2^{\mathrm{T}})\otimes I_p]{\mathbf{s}}_2\\ & =[(P_2{\mathrm{\Phi }}_2-{\xi }_2{\xi }_2^{\mathrm{T}})\otimes I_p]{\mathbf{s}}_2.\end{array}$(20) Combining Equations (19(19) $\begin{array}{rl}{\dot{\tilde{\mathbf{q}}}}_2& ={\dot{\mathbf{\text{q}}}}_2-{\mathrm{\Xi }}_2\otimes {\dot{\check{q}}}_i\\ & ={\dot{\mathbf{\text{q}}}}_2-{\mathrm{\Xi }}_2\otimes ({\xi }_2^{\mathrm{T}}\otimes I_p){\dot{\mathbf{\text{q}}}}_2\\ & ={\mathbf{s}}_2-(L_{21}\otimes I_p){\tilde{\mathbf{q}}}_1-(L_{22}\otimes I_p){\tilde{\mathbf{q}}}_2\\ & -{\mathrm{\Xi }}_2\otimes ({\xi }_2^{\mathrm{T}}\otimes I_p)({\mathbf{s}}_2-(L_{21}\otimes I_p){\tilde{\mathbf{q}}}_1),\end{array}$(19) ) and (20(20) $\begin{array}{rl}& (P_2{\mathrm{\Phi }}_2\otimes I_p)\{{\mathbf{s}}_2-{\mathrm{\Xi }}_2\otimes \left[({\xi }_2^{\mathrm{T}}\otimes I_p){\mathbf{s}}_2\right]\}\\ & =(P_2{\mathrm{\Phi }}_2\otimes I_p)\{{\mathbf{s}}_2-[(({\mathrm{\Xi }}_2\otimes {\xi }_2^{\mathrm{T}})\otimes I_p]{\mathbf{s}}_2\}\\ & =(P_2{\mathrm{\Phi }}_2\otimes I_p){\mathbf{s}}_2-\{[P_2{\mathrm{\Phi }}_2({\mathrm{\Xi }}_2\otimes {\xi }_2^{\mathrm{T}})]\otimes I_p\}{\mathbf{s}}_2\\ & =[(P_2{\mathrm{\Phi }}_2-{\xi }_2{\mathrm{\Phi }}_2{\mathrm{\Phi }}_2^{\mathrm{T}}{\xi }_2^{\mathrm{T}})\otimes I_p]{\mathbf{s}}_2\\ & =[(P_2{\mathrm{\Phi }}_2-{\xi }_2{\xi }_2^{\mathrm{T}})\otimes I_p]{\mathbf{s}}_2.\end{array}$(20) ), one has $\begin{array}{rl}{\dot{V}}_2(t)& =-{\mathbf{s}}_2^{\mathrm{T}}{K}_i{\mathbf{s}}_2+2{\tilde{\mathbf{q}}}_2^{\mathrm{T}}[(P_2{\mathrm{\Phi }}_2-{\xi }_2{\xi }_2^{\mathrm{T}})\otimes I_p]{\mathbf{s}}_2\\ & -{\tilde{\mathbf{q}}}_2^{\mathrm{T}}{\mathrm{\Phi }}_2(P^{(2)}\otimes I_p){\mathrm{\Phi }}_2{\tilde{\mathbf{q}}}_2,\end{array}$where $P^{(2)}=({\mathrm{\Phi }}_2{P}_2){\mathrm{\Phi }}_2{L}_{22}{\mathrm{\Phi }}_2+{\mathrm{\Phi }}_2{L}_{22}^{\mathrm{T}}{\mathrm{\Phi }}_2({\mathrm{\Phi }}_2{P}_2)$,

From Lemma 2.8, one has (21) ${\tilde{\mathbf{q}}}_2^{\mathrm{T}}{\mathrm{\Phi }}_2(P^{(2)}\otimes I_p){\mathrm{\Phi }}_2{\tilde{\mathbf{q}}}_2\ge a(L_{22})\Vert {\tilde{\mathbf{q}}}_2{\Vert }^2.$(21) The matrix $(P_2{\mathrm{\Phi }}_2-{\xi }_2{\xi }_2^{\mathrm{T}})$ is diagonally dominant and symmetric positive semidefinite, yielding that (22) ${\sigma }_{max}(P_2{\mathrm{\Phi }}_2-{\xi }_2{\xi }_2^{\mathrm{T}})\le 1.$(22) By Equations (21(21) ${\tilde{\mathbf{q}}}_2^{\mathrm{T}}{\mathrm{\Phi }}_2(P^{(2)}\otimes I_p){\mathrm{\Phi }}_2{\tilde{\mathbf{q}}}_2\ge a(L_{22})\Vert {\tilde{\mathbf{q}}}_2{\Vert }^2.$(21) ) and (22(22) ${\sigma }_{max}(P_2{\mathrm{\Phi }}_2-{\xi }_2{\xi }_2^{\mathrm{T}})\le 1.$(22) ), one obtains $\begin{array}{rl}{\dot{V}}_2(t)& \le -\eta \Vert {\mathbf{s}}_2{\Vert }^2+2\Vert {\tilde{\mathbf{q}}}_2\Vert \Vert {\mathbf{s}}_2\Vert -a(L_{22})\Vert {\tilde{\mathbf{q}}}_2{\Vert }^2\\ & \le -\eta \Vert {\mathbf{s}}_2{\Vert }^2+\frac{4}{a(L_{22})}\Vert {\mathbf{s}}_2{\Vert }^2+\frac{a(L_{22})}{4}\Vert {\tilde{\mathbf{q}}}_2{\Vert }^2\\ & -a(L_{22})\Vert {\tilde{\mathbf{q}}}_2{\Vert }^2.\end{array}$If η is selected as $\eta >\frac{4}{a(L_{22})}+{\eta }_0$, where ${\eta }_0$ is a positive constant.

All of above give the fact that (23) ${\dot{V}}_2(t)\le -{\eta }_0\Vert {\mathbf{s}}_2{\Vert }^2-\frac{3a(L_{22})}{4}\Vert {\tilde{\mathbf{q}}}_2{\Vert }^2<0.$(23) From Equation (23(23) ${\dot{V}}_2(t)\le -{\eta }_0\Vert {\mathbf{s}}_2{\Vert }^2-\frac{3a(L_{22})}{4}\Vert {\tilde{\mathbf{q}}}_2{\Vert }^2<0.$(23) ), ${\mathbf{s}}_2,{\tilde{\mathbf{q}}}_2\in {\mathbb{L}}_{\mathrm{\infty }}$. And by Equation (19(19) $\begin{array}{rl}{\dot{\tilde{\mathbf{q}}}}_2& ={\dot{\mathbf{\text{q}}}}_2-{\mathrm{\Xi }}_2\otimes {\dot{\check{q}}}_i\\ & ={\dot{\mathbf{\text{q}}}}_2-{\mathrm{\Xi }}_2\otimes ({\xi }_2^{\mathrm{T}}\otimes I_p){\dot{\mathbf{\text{q}}}}_2\\ & ={\mathbf{s}}_2-(L_{21}\otimes I_p){\tilde{\mathbf{q}}}_1-(L_{22}\otimes I_p){\tilde{\mathbf{q}}}_2\\ & -{\mathrm{\Xi }}_2\otimes ({\xi }_2^{\mathrm{T}}\otimes I_p)({\mathbf{s}}_2-(L_{21}\otimes I_p){\tilde{\mathbf{q}}}_1),\end{array}$(19) ), ${\dot{\tilde{\mathbf{q}}}}_2\in {\mathbb{L}}_{\mathrm{\infty }}$. Integrate both sides of Equation (23(23) ${\dot{V}}_2(t)\le -{\eta }_0\Vert {\mathbf{s}}_2{\Vert }^2-\frac{3a(L_{22})}{4}\Vert {\tilde{\mathbf{q}}}_2{\Vert }^2<0.$(23) ), yielding that ${\mathbf{s}}_2,{\tilde{\mathbf{q}}}_2\in {\mathbb{L}}_2$. Therefore, according to Barbalat's Lemma, one has ${\tilde{\mathbf{q}}}_2\to {\mathbf{0}}_{p{n}_2},t\to \mathrm{\infty }$. Therefore, $\mathrm{\exists }{T}_2>T_1,$ if $t>T_2,q_i\to {\varphi }_i{\check{q}}_1,i=1,2,\dots ,h_2.$

Analogously, repeating above processes derives that ${\tilde{\mathbf{q}}}_i\to {\mathbf{0}}_{p{n}_i},$ as $t\to \mathrm{\infty }$, $i=1,2,\dots ,k$, i.e. multiple bipartite consensus for NLSs can be achieved. Thus the designed algorithm can well realize our control objective.

Remark 2.3

In the process of analysis, we can see that, under the condition of the given geometrical assumptions in Theorem 2.9, due to the influence of the former subgroup on the latter subgroup, it will take a longer time for the latter subgroup to reach agreement with the acyclic partition structure.

Remark 2.4

The Lagrangian dynamics owns strong coupled inherent nonlinearity properties. To the authors' best knowledge, our work makes the first attempt to solve the problem of multiple-bipartite consensus without relative velocities in the context of this classical type. In the view of a more engineering standpoint, the interesting encoding–decoding approach deserves focus (Wang et al., 2019, 2022), which gives a hand for the possible discrete control of NLSs.

3. Simulations

This section will verify the effectiveness of the proposed protocol via simulation. Consider the system composed of seven two-link revolute joint manipulators. The dynamics of all manipulators are illustrated by the same Lagrange equation. For the specific form and parameters, please refer to  Liu et al. (2015).

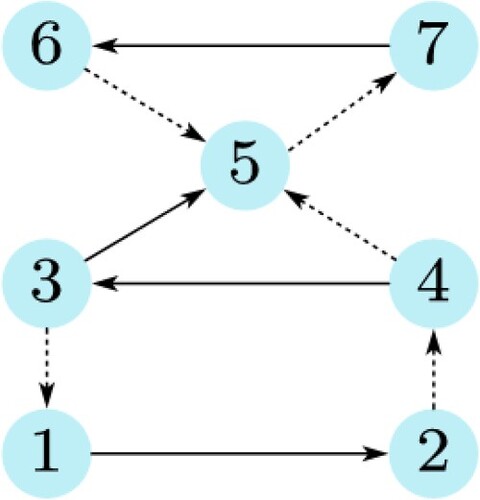
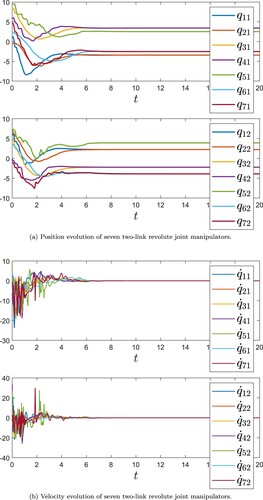
The initial rotation angle of each agent is selected randomly. Control parameters are selected as follows: $K_i=22\mathrm{diag}\{2.3,1.5\}$ and ${\mathrm{\Lambda }}_i=10I_2,i=1,2,\dots ,7$. The topological relationship is shown in Figure 1. It can be seen that, under the control of designed algorithm, the angles converge to symmetric values of two groups as shown in Figure 2(a). The rotational angular velocity revolution is shown as in Figure 2(b). Above-mentioned parameters in simulations are the ones which act on the real Lagrange dynamics equation (1(1) $M_i(q_i){\ddot{q}}_i+C_i(q_i,{\dot{q}}_i){\dot{q}}_i+G_i(q_i)={\tau }_i,i=1,2,\dots ,d,$(1) ) and adequate to solve multiple-bipartite consensus problem. Therefore, the simulation results live up to the requirement of multiple-bipartite consensus.

Figure 1. The network communication topology for seven two-link revolute joint manipulators.

Figure 2. Demonstration of simulation results of multiple-bipartite consensus: (a) position evolution and (b) velocity evolution.

4. Conclusion

In this paper, we addressed the multiple-bipartite consensus problem of NLSs without using neighbours velocity information. A novel reference vector was introduced to facilitate stability analysis and simulations were provided to show the effectiveness of the proposed algorithm. Under our theory, anticipative results are achieved and the collective behaviours of NLSs can be highly stable and reliable. In the future, the multiple bipartite containment control problem of NLSs will be discussed. It is also very challenging to consider more practical engineering thought, such as with the help of RRP communication (Luo et al., 2023, 2016).

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This study was funded in part by the National Natural Science Foundation of China under Grant 61703181, 62073209 and Grant 61991415, in part by the Shandong Provincial Natural Science Foundation of China under Grant ZR2020KA005, in part by the Shanghai Municipal of Science and Technology Commission under Grant 21SQBS00300, and in part by the Key Research and Development Project of Shandong Province of China (Soft Science) under Grant 2021RKY02033.