Uncovering the mechanism of dislocation interaction with nanoscale (<4 nm) interphase precipitates in microalloyed ferritic steels

ABSTRACT

Nanoscale interphase precipitation in microalloyed ferritic steels provides a remarkable (200–400 MPa) strengthening increment, however its origin is unclear. Scanning transmission electron microscopy revealed step formation at the matrix/precipitate interface after both macroscopic uniaxial tension and nanopillar compression testing. Supported by Density Functional Theory modelling, dislocation shearing of nano-sized (<4 nm) VC precipitates was identified as a strengthening mechanism. The findings suggest the operation of an unusual {001}<110> slip–system in the VC nanoparticles.

GRAPHICAL ABSTRACT

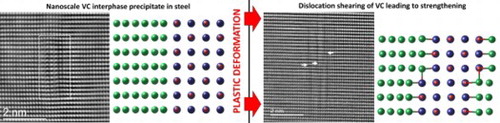
IMPACT STATEMENT

Shearing of VC nanoparticles by dislocations on a non-traditional slip–system was identified as a strengthening mechanism for steels with <4 nm nanoparticles.

KEYWORDS:

• Interphase precipitation
• precipitation strengthening
• high resolution STEM
• DFT modelling

Introduction

There is a continuous demand for the development of higher-strength steels without a significant loss in their formability, in particular bendability, and avoiding excessive expensive alloying. In this regard JFE, Japan [1,2], developed the first microalloyed steels with a ferritic matrix, strengthened by nanoscale interphase precipitation ((Ti,Mo) C) exhibiting an excellent combination of strength, ductility and bending characteristics. Fundamental understanding of the strengthening mechanisms of these steels is critical for future property optimisation. As the high density and fine size of interphase precipitates (IPs) produces a significant strength increment in this type of steels [1–13], better understanding of the associated strengthening mechanism is crucial. To date, the strength arising from IPs is generally estimated from several equations based on the assumption that dislocations loop around particles during plastic deformation. These are the Orowan and Ashby-Orowan equations [14,15] for randomly distributed particles and the modified equations for strengthening arising from IPs arranged in rows by Batte and Honeycombe [13], Chen et al. [3] and by Yen et al. [9]. Evidence of dislocation loops around >5 nm sized IPs in steels alloyed with Ti and Ti + Mo was reported by Kamikawa et al. [4], justifying their use of the Orowan equation. Even for (Ti,Mo)C precipitates as small as 3 nm in diameter, the Ashby-Orowan equation was applied by Funakawa et al. [1]. However, instead of forming a loop, dislocations may also shear the precipitates if these are coherent with the matrix, deformable and <5 nm in size [15]. For IPs, typically disc-shaped and <2-3 nm thick, the mechanism of dislocation–precipitate interaction remains unclear. The aim of this paper is to address this deficiency, as the recent progress made in the application of aberration–corrected scanning transmission electron microscopy to ferromagnetic materials provides the necessary tool for this task.

Material and methods

A new steel (0.08C, 1.5Mn, 0.3Si, 0.2Ni, 0.01N, 0.015P, 0.003S and 0.73 (Cr + V+Nb)(wt%)) was subjected to thermo-mechanical processing using a Gleeble 3500 simulator. The samples were heated to 1250°C at 5 K/s, held for 180 s, then cooled to 1175°C and subjected to a set of plane strain compressions to a total strain of 1.35 followed by accelerated cooling to a simulated coiling temperature of 600°C, held for 900 s and air cooled to ambient temperature. Mini-tensile samples were tested at room temperature and 1 × 10⁻³ s⁻¹ strain rate using a modified Kammrath and Weiss GmbH tensile stage.

Lamellae specimens and nanopillars were prepared using an FEI Helios NanoLab CX G3 focused ion beam (FIB) microscope following the methods described in Refs. [16,17]. A cold field emission gun JEOL ARM-200F probe-corrected high-resolution scanning transmission electron microscope (STEM) operating at 200 kV was used for STEM investigations. High-resolution images were simulated using QSTEM software. In-situ nanopillar compression testing was conducted with a Hysitron PI 95 holder.

Ab initio quantum mechanical calculations were performed utilising Density Functional Theory (DFT) using the plane augmented wave (PAW) formalism implemented in the Vienna Ab-initio Simulation Package (VASP) version 5.44 [18–20]. For the exchange–correlation function, the Generalized-Gradient Approximation using the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional was employed. The total number of atoms in the simulations was a large supercell consisting of up to 150 atoms, involving 54 Fe, 48 V and 48 carbon in a supercell. The energy cut-off and electronic convergence were 300 eV and 1.0 × 10⁻⁵ eV, respectively. Ionic relaxation was performed using a conjugate gradient method until the forces were converged within 0.02 eV/A. The output configurations were converted to the *.cif format which was used for visualisation [21].

Results

The steel displayed a yield strength of 862 ± 62 MPa, ultimate tensile strength of 1117 ± 52 MPa and total elongation of 0.19 ± 0.1. These are impressive mechanical properties for a ferritic microalloyed steel and are comparable to, or even exceed those, of some other IP-strengthened steels. Most ferrite grains (average grain size 4.1 ± 3.0 µm) were fully or partially strengthened by IPs (Figure 1a). It should be noted that different types of precipitates are present in this steel: carbonitrides and carbides formed in austenite (12-70 nm size), as well as IP and random precipitates in ferrite (1.4-6 nm size). Here, we focus only on nanosized (<4 nm) IP. STEM demonstrated IP arrangement in straight or curved rows with an average spacing of 16 ± 4 nm (Figure 1a and c). Energy–dispersive X–ray spectroscopy revealed a chemical composition of V_53±16Cr_28±7Nb_9±4. Thus, IPs are multi-component V-rich carbides with face-centred-cubic (fcc) lattice (Figure 1b and e) and a lattice parameter of 0.417 nm, which is very close to the theoretical one (0.4154 nm) for vanadium-carbide (VC) [22].

Figure 1. Interphase precipitation in the steel after thermo-mechanical processing: a. Bright field image and (b) associated selected area diffraction pattern with zone axis $[011{]}_{\alpha }||[010{]}_{\text{VC}}$. The additional unindexed diffraction spots originate from (Nb,V)C particles formed in austenite; c. Dark field image taken using the ${200}_{\text{VC}}$ reflection in b. d HR-STEM micrograph showing rows of interphase precipitates marked with red ovals; e. V EDS map showing two rows of VC marked with red ovals. f. A representative HAADF-STEM atomically resolved micrograph of carbide particle in bcc matrix down the $[011{]}_{\alpha }$ zone axis. Carbide particle is outlined by the dash lines.

The IPs were characterised as discs with their long axis (3.1 ± 1 nm) aligned with the $[0\overline{1}1{]}_{\alpha }$ of the body-centred-cubic (bcc) ferrite matrix (Figure 1e), having a habit plane (100)_α //(100)_VC and a typical Baker-Nutting orientation-relationship [23]: $\begin{array}{rl}& (\text{1}00{)}_{\alpha }//(\text{1}00{)}_{\text{VC}},[0\text{11}{]}_{\alpha }//[0\text{1}0{]}_{\text{VC}},[0\overline{1}\text{1}\left]{}_{\alpha }//\right[00\text{1}{]}_{\text{VC}}\end{array}$

The thickness of the discs was 1.4 ± 0.4 nm, i.e. 2–5 unit cells. The matrix/IP interfaces were planar as shown in the edge-on projection in the HAADF-STEM image with a $[011{]}_{\alpha }||[010{]}_{VC}$ zone axis (Figure 1f).

Using DFT, ab initio calculations were conducted to construct the (100)_α||(100)_VC, [011]_α||[010]_VC and (011)_α||(010)_VC, [100]_α||[100]_VC interfaces with periodic boundary conditions. Ionic relaxation was performed to minimise forces on the atoms and generate realistic interface configurations within the periodic superlattice (Figure 2).

Figure 2. DFT simulation of the a. (100)_α||(100)_VC, [011]_α||[010]_VC interface and b. (011)_α||(010)_VC, [100]_α||[100]_VC interface. c. Bright Field (BF)-STEM image with overlay $\left[011\right]$_α||[010]_VC zone axis view of the model (upper black box) and the corresponding simulated BF-STEM image from the DFT model in (b) (lower red box). The intensity profiles originate from the arrows within the images with their respective colour (bottom). Fe atoms- green, V- blue and C-red.

The DFT model revealed a strong C-Fe-C bond at the interface which corresponds to the low-energy coherent interface structure of C atoms adjoining Fe atoms (shown for an Fe-NbC interface in Ref. [24]). Using the atomic positions obtained from DFT for the interface (011)_α||(010)_VC, [100]_α||[100]_VC (Figure 2b) a high-resolution BF-STEM image was simulated along the [011]_α zone axis of the model, shown in Figure 2c with an excellent agreement between the simulation and the experiment. The line profile in Figure 2c depicts a difference in the relative intensities in the location of the columns of atoms marked by blue arrows between the experiment and the simulation; this is the result of the limited number of atoms used in the DFT model; instead of 4-to-3 V-to-Fe atomic ratio in each column, the real 50 nm thick foil had a 3-to-47 V-to-Fe thickness ratio. STEM and DFT consistently show a low ∼3% mismatch for the $(100{)}_{\alpha }||(100{)}_{\text{VC}}$_, [011]_α||[010]_VC interface (Figure 2a), whereas the $(011{)}_{\alpha }||(010{)}_{\text{VC}}$_, [100]_α||[100]_VC interface exhibits a mismatch of ∼32% along [100]_α and a ∼3% mismatch along [001]_α (Figure 2b).

Calculations performed following the approach in Ref. [25] and using theoretical lattice parameters for VC and Fe matrix predict that misfit edge dislocations should be introduced every 5.1 nm (∼25 atomic layers) at the $(100{)}_{\alpha }||(100{)}_{\text{VC}}$ interface and every 0.65 nm (∼5 atomic layers) at the $(011{)}_{\alpha }||(010{)}_{\text{VC}}$ interface along [100]_α to accommodate the associated elastic strain. As the particles have a < 5 nm disc-diameter, the presence of dislocations at the $(100{)}_{\alpha }||(100{)}_{\text{VC}}$ interface is not expected, rendering it coherent. At the $(011{)}_{\alpha }||(010{)}_{\text{VC}}$ interface many particles however contain >10 atomic layers, thus, dislocations must be present. However, due to a very small particle size relative to the lamellar thickness, there is an overlap between the particle and the matrix in the STEM images making it impossible to observe directly. Nevertheless, the projection of the matrix and the precipitate in the simulated STEM image match the experimental data indicating the presence of interface dislocations. A similar situation was reported for NbC precipitates in an fcc matrix [26] and for (Ti,Mo)C in a bcc matrix [27]; when carbides grew in size, the presence of dislocations was detected.

Figure 3 shows the HAADF images of IPs after ex-situ tensile deformation to 10% strain and after in–situ nanopillar compression. After the applied deformation the matrix/carbide interface is no longer planar, but displays monoatomic steps. Generally one step per interface was observed while some larger particles showed multiple steps at equal distance of 0.78 nm (Figure 3c). No remaining dislocation loops around IPs were detected.

Figure 3. STEM-HAADF images of VC after deformation: a., b. and c. Ex-situ uniaxial tensile test and d. In-situ compression of pillars. Arrows indicate the steps at the particle/matrix interfaces. The matrix is imaged down the $[011{]}_{\alpha }$ zone axis.

To better understand the observed monoatomic steps at coherent $(100{)}_{\alpha }||(100{)}_{\text{VC}}$ interfaces, the theoretical lattices obtained via DFT were translated to simulate shear associated with the after–effect of a dislocation. Figure 4a shows the $\alpha$ and VC lattices after an imposed shear corresponding to the magnitude and direction of the Burgers vector in ferrite ${\overrightarrow{b}}_{\alpha }:\frac{a_{\alpha }}{2}\left[\overline{1}11\right]$ as a setup for a DFT model. Two atomic displacements of opposite sign along the phase interface were introduced to comply with periodic boundary conditions in DFT. The in-plane component of shear ${\overrightarrow{b}}_{\alpha }$ $\mathrm{i}\mathrm{s}$ $\overrightarrow{b_{\alpha }^{\ast }}:\frac{a_{\alpha }}{2}$$\left[\overline{1}00\right]$ and the out-of-plane component is $\frac{a_{\alpha }}{2}\left[011\right]$. Imposing ${\overrightarrow{b}}_{\alpha }$ onto both Fe and VC leads to a mismatch after shear creating C-Fe-C bond-angles at 80.76°. After ionic relaxation, the C-Fe-C bonds shown in Figure 4b increase to 91° and the mismatch is accommodated elastically in the Fe matrix. The higher Fe-C-Fe bond angles are similar to those in iron carbides in the ICSD database, for example in Fe₂C [28]. The resulting configuration closely resembles the experimentally observed atomic displacement in Figure 3. Figure 4c depicts the electron density of the relaxed model, displaying the presence of the covalent bond formed by overlapping density for the V and C, which is important to the overall stability of the interface.

Figure 4. DFT simulation results of $(100{)}_{\alpha }||{\left(100\right)}_{\text{VC}},{\left[0\overline{1}1\right]}_{\alpha }||[001{]}_{\text{VC}}$ interfaces after imposed shear ${\overrightarrow{b}}_{\alpha }:\frac{a_{\alpha }}{2}\left[\overline{1}11\right]$ on the $\alpha$ matrix and VC precipitate: a. before relaxation, b. after relaxation and c. electron density state after relaxation. The in-plane component of the shear is $\overrightarrow{b_{\alpha }^{\ast }}:\frac{a_{\alpha }}{2}$$\left[\overline{1}00\right]$ and the out-of-plane component is $\frac{a_{\alpha }}{2}\left[011\right]$. Fe atoms- green, V atoms- blue and C atoms- red.

Discussion

Nano-sized IPs before deformation were found to be 1-2 nm thick discs. The parallel alignment of the coherent interface with this thinnest dimension (Figure 2a) enables dislocation-shearing of these particles during plastic deformation. The critical diameter of the particle for the shearable /non-shearable transition can be estimated by balancing the theoretical strength of the precipitate with the stress to support a dislocation loop [29]: $D_c=\frac{30b{G}_{\alpha }}{G_{VC}}$where G_α is the shear modulus of ferrite 81.6 GPa [30], G_VC is the shear modulus of the VC precipitate 175.7 GPa [31], and b is the magnitude of the Burgers vector of the bcc matrix $\frac{\sqrt{3}}{2}a$, which is 0.248 nm. The critical diameter was found to be ∼3.5 nm, which is slightly smaller than the approximation of 5 nm by Gladman [15]. The observed length of the precipitates in the $[011{]}_{\alpha }$ ||[010]_VC zone axis corresponds to the disc-diameter which was predominantly in the range of 2-3 nm and only on rare occasions >4 nm. Thus, both the thickness and diameter of the carbides satisfy the size condition for shearable particles.

Figure 4 illustrates the shearing of $\alpha$ and VC by a $\frac{a_{\alpha }}{2}\left[\overline{1}11\right]$ dislocation. The $(0\overline{1}1{)}_{\alpha }$ glide plane smoothly transits into the (001)_VC plane and the $[\overline{1}11{]}_{\alpha }$glide direction deviates by 7° from a $[\overline{1}10{]}_{VC}$ glide direction. The (001)_VC plane is not a classic glide plane for $\frac{a_{VC}}{2}$<110> dislocations in an fcc lattice. The active slip-system in the case of VC is however not unique: i) The critical resolved shear stress was found to strongly depend on the carbon-to-metal ratio in V carbide [32], which could vary depending on the number of vacancies and the C atom position arrangement and ii) Different slip–systems were found to be active in VC at different temperatures [33]. In the latter, Hannink et al. argued that at low temperatures the covalent bonding between V and C obstructs slip on {111}, leading to the operation of the, for fcc unusual, {110}<$1\overline{1}0$>slip system. At room temperature, the active slip system could not be uniquely identified. The magnitudes of the Burgers vectors are 0.304 and 0.248 nm in VC and in the ferrite matrix, respectively, giving 19% mismatch. This mismatch in magnitude and the misalignment by 7° of the Burgers vectors may lead to the formation of a residual defect (interfacial dislocation) at the interface, which is accommodated by the step. DFT modelling demonstrated that imposing the shear of ${\overrightarrow{b}}_{\alpha }$ onto both $\alpha$ and VC resulted in the step formation at the interface (Figure 4). The resulting shear in VC after relaxation corresponded to a $\frac{a_{VC}}{2}\left[\overline{1}10\right]$ dislocation and the height of the step was 0.19 nm (Figure 4b), agreeing well with the experimentally observed 0.16 nm (Figure 3). These findings consistently suggest that nanoscale VC particles were sheared by slip on the {001}<$110$> system, as it maintains the best slip continuity to the bcc matrix. The geometrical conditions for slip transition across the interface, including an angular limit between the Burgers vectors of two adjacent phases of <60° and for the angle between the slip traces with the interface of <15°, are satisfied [34]. Evidence of sheared particles having different lattice structure and slip systems from those of the matrix, were reported for semi-coherent Ω precipitate in an Al-Cu-Mg-Ag alloy [35] and for θ-Al₂Cu nanolayers in an Al matrix [36]. Shearing of nearly 1 μm size plate-like θ′-Al₂Cu was also reported due to the dislocations pile-up at particle/matrix interface in Al-2.5Cu alloy when operation of the Orowan mechanism was restricted [37]. The DFT model (Figure 4b) shows that imposing the shear of the dislocation in the Fe-matrix onto the VC precipitate leads to a stable configuration in which VC maintains its order and the interfacial strain is accommodated in the Fe matrix. The increase in interfacial energy caused by shearing of the particle and step formation is 540 mJ/m².

When coherent carbide particles are sheared by dislocations, a significant contribution to the yield strength could arise from the elastic coherency strain, modulus, chemical and order hardening [38]. The identified mechanism of particle-dislocation interaction will allow future design of high-strength metallic alloys strengthened by nanoscale precipitation.

Conclusion

For the first time, STEM provides evidence of dislocations cutting IPs with a thickness <2 nm and different from the ferrite matrix crystal structure both after uniaxial tensile testing and in-situ nanopillar compression. Our observations suggest the operation of an unusual for VC {001}<110> slip system which satisfies the slip plane continuity condition between the phases.

Acknowledgements

Financial support was provided by the Australian Research Council (ARC) through the ARC Research Hub for Australian Steel Manufacturing under the Industrial Transformation Research Hubs scheme (IH130100017) and by the Danish Council for Independent Research (DFF-8027-00009B). The microscopy was carried out using ARM 200F (LE120100104). The authors thank Prof. J. Wang, University of Nebraska-Lincoln, for discussion of results and suggestions.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

Financial support was provided by the Australian Research Council (ARC) through the ARC Research Hub for Australian Steel Manufacturing under the Industrial Transformation Research Hubs scheme (IH130100017) and by the Danish Council for Independent Research (DFF-8027-00009B). The microscopy was carried out using ARM 200F (LE120100104).