Synthesis, characterization and first principle modelling of the MAB phase solid solutions: (Mn_1-xCr_x)₂AlB₂ and (Mn_1-xCr_x)₃AlB₄

ABSTRACT

The MAB phases are a family of layered ternary transition metal borides, with atomically laminated crystal structures comprised of transition metal boride (M-B) layers interleaved by single, or double, Al (A) layers. Herein, density functional theory is implemented to evaluate the thermodynamic stability of disordered (Mn_1-xCr_x)₂AlB₂, and disordered and ordered (Mn_1-xCr_x)₃AlB₄ quaternaries. The (Mn_1-xCr_x)₂AlB₂ solid solutions were synthesized over the entire range of substitution. A (Mn_1-xCr_x)₃AlB₄ solid solution was produced, on the base of Cr₃AlB₄, to form (Mn_0.33Cr_0.66)₃AlB₄. Powder X-ray diffraction shows lattice parameter shifts and unit cell expansions indicative of successful solid solution formations.

GRAPHICAL ABSTRACT

IMPACT STATEMENT

In this work, first-principles calculations evaluate the stability of (Mn_1-xCr_x)₂AlB₂ and (Mn_1-xCr_x)₃AlB₄ solid solutions. Experimentally, MAB phase solid solutions of (Mn_1-xCr_x)₂AlB₂ and (Mn_0.33Cr_0.66)₃AlB₄ are synthesized for the first time.

KEYWORDS:

• Solid solutions
• transition metal borides
• Mn₂AlB₂
• Cr₂AlB₂
• Cr₃AlB₄

Introduction

The MAB phases are a family of atomically laminated, ternary, transition metal borides, wherein M is a transition metal, A is generally aluminium, Al, and B is boron. The first MAB phase, MoAlB, was synthesized in 1966 by Jeitschko et al. [1], followed by Mn₂AlB₂ [2] and Fe₂AlB₂ [3] later that same year. The ternaries, Cr₂AlB₂ and Cr₃AlB₄ were not synthesized until 1973 by Chaban and Kuz’ma [4]. Recently, there has been a renewed interest in these phases due to their unique magneto-caloric properties [5], high-temperature oxidation resistance [6] and their role as a precursor for 2-D, MXene-like borides [7,8]. A more complete history and summary of the MAB phases and their properties can be found in Ref. [9].

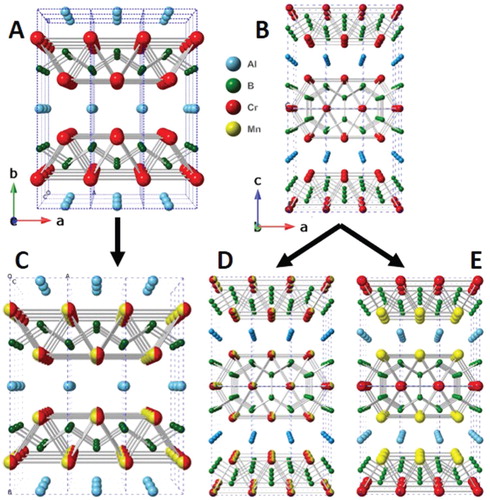
The MAB phase structure contains either single, or double, Al atomic layers sandwiched between two M-B layers (Figure 1(a–b)) [10]. All structures examined herein contain a single Al atomic layer. The 212 MABs, Mn₂AlB₂ and Cr₂AlB₂, are isostructural and crystallize in the Cmmm space group [11]. To date the only 314 MAB phase synthesized is Cr₃AlB₄ that crystallizes in the Pmmm space group. Density functional theory, DFT, calculations have shown that other 314 MAB phases, such as Mn₃AlB₄ and Fe₃AlB₄, to be thermodynamically unstable vis-à-vis other competing phases [12]. In the 212 MAB structures, the layers stack in the b-direction; in the 314 they stack in the c-direction.

Figure 1. Crystal structures of, a) M₂AlB₂, b) M₃AlB₄, c) disordered (Mn_1-xCr_x)₂AlB₂, d) disordered (Mn_1-xCr_x)₃AlB₄ and e) ordered Mn₂CrAlB₄. Note that in the 212 structure (a), the layers stack along the b-direction, while in the 314 (b) they stack along the c-direction.

Solid solutions on the M sites allow for tuning of material properties as a function of substitution. In the MAB phases, partial M-site substitutions have been successful for MoAlB, WAlB and Fe₂AlB₂. In 1995, Yu et al. were the first to synthesize single crystals of the solid solutio, (Mo_0.61Cr_0.39)AlB [13]. Okada et al. later expanded the doping range, as well as synthesizing a (Mo_1-xW_x)AlB quaternary [14]. Increasing the W content led to an increase in hardness, while increasing the Cr substitution lowered the resistivity of the material. Solid solutions of (Fe_1-xM′_x)₂AlB₂ have been synthesized wherein M′ = Mn [15] or Co [16] with substitutions up to x = 1 and x = 0.15, respectively. The solid solutions were shown to increase the magneto-caloric effect over a greater range of temperatures. DFT calculations suggest that ordered (M_1-xM′_x)₃AlB₄ compounds may be stable. However, since  these calculations do not take into account the formation of competing ordered 212 phases, these conclusions, as shown below, are incorrect  [17].

The purpose of this work was to expand the range of MAB solid solutions in the Mn-Cr-Al-B system. This endeavour has been fruitful in that we discovered that solid solutions in (Mn_1-xCr_x)₂AlB₂ exist for all x. We also discovered the existence of a (Mn_1-xCr_x)₃AlB₄ solid solution for x = 0.33.

Methods

Computational

All first-principles calculations were performed by means of DFT and the projector augmented wave method [18,19], as implemented within the Vienna ab-initio simulation package (VASP) version 5.4.1 [20,21,22], with a plane-wave energy cut-off of 400 eV. The spin-polarized version of the generalized gradient approximation (GGA), as parameterized by Perdew–Burke–Ernzerhof (PBE) [23], was used for treating the electron exchange and correlation effects. Multiple spin configurations were considered; the results presented are the ones for the lowest energy spin configuration. The Brillouin zone was integrated by Monkhorst–Pack special k-point sampling [24]. The total energy was minimized through relaxation of unit-cell shape and volume, and internal atomic positions until satisfying an energy convergence of 10⁻⁵ eV/atom and force convergence of 10⁻² eV/Å.

Chemical disorder of Mn and Cr in the (Mn_1-xCr_x)₂AlB₂ and (Mn_1-xCr_x)₃AlB₄ quaternaries were modelled on the M-sublattice using the special quasi-random structure (SQS) method [25]. Convergency tests show that supercells with 120 or more atoms give a qualitatively accurate representation and a quantitative convergency in terms of calculated formation enthalpies, equilibrium volumes and lattice parameters.

The thermodynamic stabilities of (Mn_1-xCr_x)₂AlB₂ and (Mn_1-xCr_x)₃AlB₄ were investigated at 0 K with respect to their decomposition into any combination of competing phases. The set of most competing phases, denoted the equilibrium simplex, is identified using a linear optimization procedure [26,27]. The stability of a phase is quantified in terms of the formation enthalpy, ΔH_cp, by comparing its energy to the energy of the equilibrium simplex according to (1) $\begin{array}{rl}\mathrm{\Delta }{H}_{\text{cp}}& =E\left[{\left(\text{M}{\text{n}}_{1-x}\text{C}{\text{r}}_x\right)}_2\text{Al}{\text{B}}_2\text{ or }{\left(\text{M}{\text{n}}_{1-x}\text{C}{\text{r}}_x\right)}_3\text{Al}{\text{B}}_4\right]\\ & -E\left(\text{equilibrium simplex}\right)\end{array}$(1) A phase is concluded to be stable when ΔH_cp < 0.

We approximate contributions from other temperature-dependent effects, e.g. lattice vibrations and electronic entropy, to the formation enthalpy to be negligible as such contributions from a phase, significant or not, tend to be cancelled out in the Gibbs free energy of formation terms [28]. However, since we are investigating solid solutions of Mn and Cr, approximated through modelled disorder (SQS), the contributions from configurational entropy to the Gibbs free energy of formation $\mathrm{\Delta }{G}_{\text{cp}}^{\text{disorder}}$, when T ≠ 0 K, are approximated by (2) $\mathrm{\Delta }{G}_{cp}^{disorder}\left[T\right]=\mathrm{\Delta }{H}_{cp}^{disorder}-T\mathrm{\Delta }S$(2) where the entropic contribution, ΔS, assuming an ideal solution of Mn and Cr on the M-site, is given by (3) $\mathrm{\Delta }S=-2{\text{k}}_{\text{B}}\left[x\text{ln}\left(x\right)+\left(1-x\right)\text{ ln}\left(1-x\right)\right]$(3) where k_B is the Boltzmann constant and x is the concentration of Cr on the M-sublattice.

The structure of each of the three phases modelled can be visualized such that that the disordered structure is a mixture of Mn and Cr atoms on the M lattice sites (Figure 1(c–d)), while in the ordered Mn₂CrAlB₄, the M site, nearest to the Al layer is replaced by Mn (Figure 1(e)).

Experimental details

Samples were prepared via a powder metallurgical route starting with elemental Mn (Alfa Aesar, 99.6%, <10 µm), Cr (Alfa Aesar, 99.2%, <10 µm), Al (Alfa Aesar, 99.5%, <44 µm), CrB (Grade B, H.C. Starck, 0.1–0.3% Fe impurities), amorphous B (B_a) (Alfa Aesar, 98%, <44 µm) and crystalline B (B_c) (Alfa Aesar, 98%, <44 µm) powders. For the 212 solid solutions, the synthesis was carried out in a two-step method wherein Mn, Cr and B_c were first reacted to form (Mn_1-xCr_x)B solid solutions. This was followed by reaction of the latter with Al to form the corresponding MAB phase. To form the initial (Mn_1-xCr_x)B solid solutions, a total of 2.5 g of powders were mixed, where x = 0.10, 0.25, 0.50, 0.75 and 0.9. These molar ratios were selected to cover the entire solid solution range. For the 314 solid solutions, powders were mixed in molar ratios of (Mn_1-xCrB_x)₃Al_1.15B_3(1-x)+1, where x = 0.33, 0.66 and 1. The powder mixtures were ball milled for 24 h in plastic jars using yttria-stabilized zirconia media. Green bodies were cold pressed at 300 MPa from the mixtures to form 13 mm diameter, ≈10 mm high cylinders. The (Mn_1-xCr_x)B pellets were reacted via pressureless sintering in a horizontal tube furnace, heated at a rate of 5°C/min and held at 1050°C for 5 h, before cooling to ambient temperatures at the same rate. The reaction was conducted in a flowing Ar atmosphere, with Ti powder upstream gettering oxygen. The reacted pellets were crushed to fine powders using an agate mortar and pestle, mixed with Al powder in the ratio of (Mn_1-xCr_x)₂Al_1.2B₂, ball milled and cold-pressed in the same method as above. The pellets were sintered at 1050°C for 5 h in a horizontal tube furnace under the same conditions as above.

The two-step reaction sintering for the M₃AlB₄ sample was slightly different. First, the green bodies were reacted at 970°C for 1 h, then crushed and re-pressed; followed by a second sintering at 1050°C for 10 h.

After reaction, the samples were ground into fine powders using an agate mortar and pestle. X-ray diffraction (XRD) was performed using a diffractometer (Rigaku SmartLab) using a Cu Kα source. The step size and dwell times were 0.02° and 1.8 s/step, respectively. A graphite monochromator was utilized to remove background fluorescence. Small amounts of Si powder were added to the powders as an internal reference to more accurately determine the lattice parameters, LPs. XRD analysis was conducted using Jade 6 software. The quantitative analysis for the 314 phase was performed with the Easy Quant package using the RIR method [29].

Results and discussion

Computational results

For the evaluation of the thermodynamic phase stability of (Mn_1-xCr_x)₂AlB₂ and (Mn_1-xCr_x)₃AlB₄, we compare their calculated energies to an identified set of most competing phases (equilibrium simplex) in terms of the formation enthalpy ΔH_cp using Equation 1. The identified equilibrium simplex for each composition is given in Table 1. Figure 2(a) shows the calculated phase stabilities at 0 K (ΔH_cp) and at elevated temperatures (ΔG_cp). In this system, both Mn₂AlB₂ and Cr₂AlB₂ are stable with calculated formation enthalpies of −67 and −30 meV/atom, respectively. In Figure 2(a), these values are used as reference points, i.e. are set to zero. The (Mn_1-xCr_x)₂AlB₂ solid solutions, with disorder on the M sites, are predicted to be stable at all x (Figure 2(a)). At elevated temperatures, the entropy contribution due to the disorder further stabilizes the solids solutions with respect to decomposition into Mn₂AlB₂ and Cr₂AlB₂ (Figure 2(a)).

Figure 2. Calculated formation enthalpies, ΔH, at 0 K and Gibbs free energies of formation, ΔG, at T > 0 K for, a) (Mn_1-xCr_x)₂AlB₂ and, b) (Mn_1-xCr_x)₃AlB₄ solid solutions. In (a), enthalpies of ternaries, viz. −67 and −30 meV/atom for Mn₂AlB₂ and Cr₂AlB₂ respectively, are used as reference points (zero).

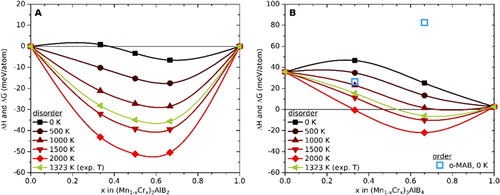
Table 1. Identified equilibrium simplex for (Mn_1-xCr_x)₂AlB₂ and (Mn_1-xCr_x)₃AlB₄ phases

x in (Mn1-xCrx)2AlB2	Equilibrium simplex	x in (Mn1-xCrx)3AlB4	Equilibrium simplex
0	Mn2AlB2	0	Mn2AlB2, MnB, MnB4
0.33	Mn2AlB2, Cr2AlB2	0.33	Mn2AlB2, CrB2
0.50	Mn2AlB2, Cr2AlB2
0.66	Cr2AlB2, Mn2AlB2	0.66	CrB2, Cr2AlB2, Mn2AlB2
1	Cr2AlB2	1	Cr2AlB2, CrB2

Figure 2(b) shows the calculated stability for the (Mn_1-xCr_x)₃AlB₄ quaternaries Both disorder of Mn and Cr on the M-sublattices (solid symbols) as well as an out-plane chemically ordered structures (open squares), here referred to as o-MAB, were considered. At 0 K, only Cr₃AlB₄ is found to be close to stable with ΔH = +3 meV/atom. None of the considered ordered o-MAB structures, viz. (MnCr₂)AlB₄ nor (Mn₂Cr)AlB₄, were found to be stable. Disorder of the Mn and Cr atoms, however, are stabilized with increasing temperatures, but only if the solid solutions are Cr-rich (Figure 2(b)). At 1323 K (1050°C), the experimental condition used herein, (Mn_0.33Cr_0.66)₃AlB is predicted to be stable, but (Mn_0.66Cr_0.33)₃AlB₄ is not.

The theoretical lattice parameters and unit cell volumes, V_uc, were calculated for both the (Mn_1-xCr_x)₂AlB₂ and (Mn_1-xCr_x)₃AlB₄ systems. As the entire (Mn_1-xCr_x)₂AlB₂ system was found to be stable in the disordered state, only this state was considered, with the calculated values presented in Table 2. For the (Mn_1-xCr_x)₃AlB₄ system, both disordered and ordered structures were evaluated, and the calculated values are listed in Table 3.

Table 2. Calculated and experimental LPs and V_uc of (Mn_1-xCr_x)₂AlB₂ solid solutions.

Calculated					Experimental
x	a (Å)	b (Å)	c (Å)	V (Å^3)	x	a (Å)	b (Å)	c (Å)	V (Å^3)
0	2.895	11.054	2.828	90.50	0	2.921	11.066	2.897	93.62
					0.10	2.921	11.049	2.906	93.78
0.33	2.895	10.972	2.886	91.68	0.25	2.921	11.011	2.932	94.29
0.50	2.895	10.968	2.910	92.38	0.50	2.921	10.985	2.950	94.65
0.66	2.899	10.968	2.923	92.96	0.75	2.924	11.004	2.964	95.37
					0.90	2.932	11.033	2.970	95.97
1.00	2.9231	11.042	2.931	94.61	1.00	2.937	11.047	2.968	96.30

Table 3. Experimental and calculated LPs and V_uc for (Mn_1-xCr_x)₃AlB₄ with disorder (D) and order (O) of Mn and Cr.

Calculated					Experimental
x	a (Å)	b (Å)	c (Å)	V (Å^3)	x	a (Å)	b (Å)	c (Å)	V (Å^3)
0.00	2.834	2.935	8.145	67.76
0.33 (O)	2.830	2.942	8.131	67.69
0.33 (D)	2.881	2.934	8.107	68.53
0.66 (O)	2.934	2.950	8.034	69.53	0.66	2.949	2.985	8.054	70.90
0.66 (D)	2.918	2.933	8.073	69.10
1.00	2.937	2.937	8.081	69.70	1.00	2.945	2.968	8.072	70.57

Experimental results

(Mn_1-xCr_x)₂AlB₂

XRD patterns of the (Mn_1-xCr_x)₂AlB₂ solid solutions, reacted at 1050°C for 5 h, are shown in Figure 3(a). The XRD patterns for the Cr-rich solid solutions show residual CrB peaks that increase in intensity as the Cr content increases. As shown in previous work [8,30], Cr₂AlB₂ may require a second sintering, or excess Al, to fully react. As these compositions approach Cr₂AlB₂, the 20% excess Al is insufficient to react with all the CrB in a single reaction step, resulting in some impurity phases.

Figure 3. a) XRD patterns of (Mn_1-xCr_x)₂AlB₂ sold solutions reacted at 1050°C for 5 h as a function of x. Si powder was added as a reference. b) Lattice parameters, and c) unit cell volumes of (Mn_1-xCr_x)₂AlB₂ solid solutions as a function x. Solid lines and symbols denote the experimental LPs; dashed lines and open symbols, denote calculated LPs.

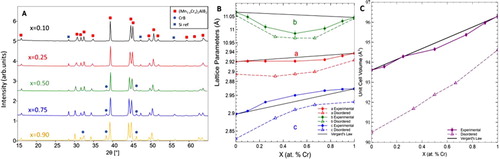
Figure 4. Structural characteristics of (Mn_1-xCr_x)₃AlB₄ solid solutions, a) XRD patterns of Cr₃AlB₄ and (Mn_0.33Cr_0.66)₃AlB₄ powders b) Lattice parameters, and c) unit cell volume as a function of Cr substitution. Solid lines and symbols denote experimental LPs; dashed lines and open symbols, denote calculated LPs.

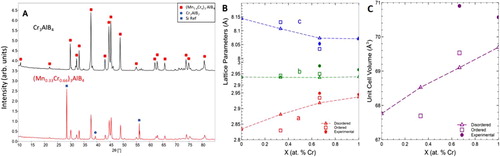
Table 2 lists the LP and V_uc changes in the (Mn_1-xCr_x)₂AlB₂ compositions as a function of x. The same results are plotted alongside the calculated values for the disordered structure as well as Vegard’s law estimations in Figure 3(b) and (c). Though the calculated values are slightly smaller than experimental, the trends are identical for both sets of LPs. Here the largest deviation is found for the c-LP of Mn₂AlB₂ being −2.4%. The deviations are even les (−1.2% to −1.5%) for x ≠ 0. The deviations for a- and b-LPs are in the range 0 to −0.9% as compared to experiment. This agreement could likely be improved through a much more detailed investigation that includes more intricate magnetic configurations and, maybe, through the use of other xc-functionals.

From these results, it is clear, that the a-LP and V_uc deviate little from those expected from Vegard’s law. In contradistinction, the b- and c-LPs deviate from Vegard’s law, with a negative deviation in the b-direction and a positive deviation in the c-direction. Given that these deviations are theoretically predicted, it follows that these trends are embedded in the intricacies of bonding [17]. Based on both the theoretical and experimental results, it is reasonable to assume that the solid solution range extends over all compositions. This is consistent with the fact that Mn₂AlB₂ and Cr₂AlB₂ both crystalize in the Cmmm space group.

(Mn_1-xCr_x)₃AlB₄

After reacting, the (Mn_1-xCr_x)₃AlB₄ composition did not densify, instead, the powders were loosely bound with a ‘burnt toast’ like consistency. XRD analysis of the powders showed that the mixture was fully reacted and indeed formed a 314 solid solution with 16.5 ± 2.6 wt. % of Cr₂AlB₂ impurities (Figure 4(a)). Compared to Cr₃AlB₄ synthesized in the same manner, there is evidence of peak shifting, indicating the successful formation of a solid solution [30]. Table 3 lists the LPs and the V_uc derived from these patterns. The experimental and calculated LP and V_uc values are shown for both the disordered and ordered (Mn_1-xCr_x)₃AlB₄ compositions in Figure 4(b) and (c), respectively Like in the (Mn_1-xCr_x)₂AlB₂ case, the calculated LPs are lower than the experimental, however trends from all three can be analysed. In the disordered model, as the Cr is substituted into the system, the b-LP remains mostly unchanged. Concomitantly there is expansion in the a-direction and contraction in the stacking, or c-direction. This trend parallels that of the 212 system, with regards to the contraction in the stacking direction and expansion perpendicular to the direction of the B chains.

Overall, the calculated values show a monatomic increase in V_uc as a function of Cr loading. The experimental results, however, show the opposite trend. At this time, the reasons for the discrepancy are not understood and more theoretical work is indicated. This comment notwithstanding the differences in the absolute values between theory and experiment are, at worst, <2%. As important, the fact that theory predicts the ordered phases to be unstable, suggests they are not ordered. More work, possibly neutron diffraction that can differentiate between Cr and Mn, is needed to resolve this important question.

On the other hand, attempts to synthesize the (Mn_0.66Cr_0.33)₃AlB₄ solid solutions resulted in a mixture of Mn₂AlB₂ and Cr₂AlB₂. Said otherwise, like theory predicts, (Mn_0.66Cr_0.33)₃AlB₄ is thermodynamically unstable at this stoichiometry at the processing temperature used, viz. 1050°C. Dai et al. [17] predicted Mn₂CrAlB₄ to be stable. This prediction is, as noted above and the results shown here, is incorrect because the authors did not include the M₂AlB₂ phases in their analysis.

Conclusions

Herein we show, for the first time, that in the (Mn_1-xCr_x)₂AlB₂ system, a continuous M-site substitution is possible, for all x values. First-principles studies of disordered solid solution thermodynamics and experimental synthesis both confirm the stability of the system across the entire range. While the experimental values for the lattice parameter and unit cell volume are slightly larger than the calculated values, both exhibit similar trends. Similarly, the shifts in the a- and UC volume follow Vegard’s law, but b- and c-LPs, do not, indicating a negative and positive deviation, respectively. Investigations of the magnetic and electronic behaviour of such MAB solid solutions, with full range M-site substitution, is a topic of future work.

In the (Mn_1-xCr_x)₃AlB₄ system, the expected stability was modelled for both a disordered and ordered structure across the entire range. Experimentally, a solid solution of (Mn_0.33Cr_0.66)₃AlB₄ phase was successfully synthesized, again for the first time, while attempts to make (Mn_0.66Cr_0.33)₃AlB₄ were unsuccessful, paralleling the findings of our DFT calculations. These results indicate that future solid solutions may be possible for 314 MAB phases (M ≠ Mn) with a base of Cr₃AlB₄.

Acknowledgements

The calculations were carried out using supercomputer resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Centre (NSC), the High Performance Computing Center North (HPC2N), and the PDC Center for High Performance Computing.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was funded by Knut och Alice Wallenbergs Stiftelse [grant number KAW 2015.0043].