Stress-dependent dislocation core structures leading to non-Schmid behavior

Abstract

The stress-dependent core structures of dislocations for basal slip in magnesium are calculated using ab initio generalized stacking fault energy surface and microscopic phase-field method. The dissociation of dislocation cores exhibits the dependence on the non-shear component in the stress tensor; the Peierls stress is found to either become virtually zero or increase by an order of magnitude, depending on the applied shear stress magnitude and direction. The results, in contrast to the classical Schmid's law for crystal plasticity, are explained using the Escaig stress concept and the resulting implication on plastic deformation is discussed.

GRAPHICAL ABSTRACT

IMPACT STATEMENT

Dependence of dislocation core structure on stress is predicted using a microscopic phase-field model with subatomic resolution, revealing non-Schmid behavior together with significant influence on the Peierls stress.

KEYWORDS:

• Magnesium
• basal dislocation
• Peierls stress
• phase-field
• Escaig stress

1. Introduction

Ductility is crucial to developing advanced alloys and processing techniques. For example, as a lightweight metal with promising potential for improving energy efficiency, magnesium is still excluded from applications in many energy-saving lightweight structures, owing to its low ductility. Mechanistic understanding of ductility relies on explaining how crystals deform plastically on several different length scales (i.e. from atomic to macroscopic scales). The multi-scale nature of crystal plasticity stems largely from its principal agents, i.e. dislocations, which possess a core structure localized within ∼1–10$a_0$ ($a_0$ is the lattice parameter) but produce an elastic field interacting with other dislocations over a long range of ∼ $r_0=1/\sqrt{\rho }$ (usually $r_0\gg a_0$). The motion of dislocations, which collectively gives rise to macroscopic plastic strain, is modeled typically using a viscous drag law $v=b\left(\tau -{\tau }_c\right)/B$, where $v$ is the dislocation velocity, $b$ is the magnitude of Burgers vector, $\tau$ is the resolved shear stress, ${\tau }_c$ is the critical resolved shear stress proposed by the Schmid's law, and $B$ is the dislocation drag coefficient. Elasticity theory has been successfully used to calculate the force term (i.e. $b\tau$) arising from external stresses applied far from the core, which, owing to the significant atomic distortion, is treated either as a one-dimensional (1D) singularity prescribed with an ad hoc cut-off [1] or a non-singular distribution using more advanced methods [2]. In contrast, determination of $B$ and ${\tau }_c$, which characterize dislocation motions such as glide, cross-slip, and climb and are crucial inputs to mesoscale dislocation dynamics [3,4], relies on the ability to resolve the dislocation core structure at microscale.

Atomistic methods, in particular, ab initio calculations based on density functional theory (DFT), have been largely used in recent years to predict dislocation core structures; the extreme diversity in terms of the structure configuration, energetics, and stability of dislocation cores in pure metals, alloys, and semiconductors have been investigated in the past few years [5]. While these ab initio calculations can offer predictions with high accuracy, a major limitation is the number of atoms that can be considered, which is particularly limited in metals [5]. The limited simulation size causes a severe theoretical challenge, as proper boundary conditions must be prescribed in a way to minimize the inconsistency between the intended single dislocation and the actual groups of dislocations simulated, especially in terms of the long-range elastic interactions. In general, the influence of elastic interaction on dislocation core structures, which is believed to relate to the widely reported non-Schmid effects in various crystals [6–8], can be a challenge to ab initio methods. This is again due to the fact that the localized dislocation core produces non-local distortion field. In addition, dislocation motion during plastic deformation is largely driven by the external far-field stress, whose effect on dislocation core structures is less studied by ab initio methods. Therefore, there is a strong need to study the stress-dependence of dislocation core structures both qualitatively and quantitatively, which may provide some new insight into plastic properties of many important crystalline metals and alloys.

In this paper we address this issue by employing a recently developed microscopic phase-field (MPF) model [9] that links ab initio calculations with phase-field descriptions of defects in continuum. The model possesses subatomic resolution and is predictive and quantitative, in the sense that it requires only the generalized stacking fault (GSF) energy surface and elastic stiffness tensors (delivered by ab initio calculations) as inputs and has no fitting parameters. As an example, we present the stress-dependent core structures of the basal slip dislocation $\frac{a_0}{3}〈2\overline{1}\overline{1}0〉/\left\{0001\right\}$ in magnesium, which shows a behavior different from the Schmid's law. Our results suggest that the applied stress can not only reduce the resistance to dislocation slip (Peierls stress) but also promote the propensity for basal dislocations to cross-slip, indicating the possibility of enhancing ductility of magnesium via controlling the transition and interaction between basal and non-basal dislocations with the aid of stress-dependent core structures.

2. Methods

The GSF energy surface for the basal plane of magnesium are calculated using DFT. Briefly, we use a planewave basis (138 eV cutoff), with a generalized gradient approximation (Perdew-Wang 91), and a Vanderbilt ultrasoft pseudopotential for magnesium (with a [Ne]3s² electronic configuration) that accurately reproduces experimental lattice [10] (less than 0.9% error) and elastic [11] (less than 5% error) constants, and phonon frequencies [12,13] (less than 3% error) of bulk Mg at room temperature. The corresponding elastic constants are $c_{11}=59.3\text{GPa}$, $c_{33}=61.5\text{GPa}$, $c_{44}=16.4\text{GPa}$, $c_{12}=25.7\text{GPa}$, $c_{13}=21.4\text{GPa}$ (Ref. [14]). The generalized stacking fault surface was computed using 18 layers of (0001) planes, with affine shears—over a grid of displacements in the (0001) plane—to form periodic layers of stacking fault, and with full relaxation perpendicular to the (0001) planes; 32×32×1 k-point meshes with 0.5 eV Methfessel-Paxton smearing was used for these geometries. (More details about the ab initio calculations can be found in Ref. [14].) In particular, the calculated GSF energy surface gives rise to a value of 34 mJ/m² for the intrinsic stacking fault energy, which plays an important role in determining the dislocation core structure and will be used in later analysis. The MPF methodology has been well documented in our previous works [9,15]. In the current study straight screw and edge dislocations of infinite length are considered for a basal dislocation with $\mathbf{b}=\left(a_0/3\right)\left[2\overline{1}\overline{1}0\right]$; the stress-controlled boundary condition is used in all simulations throughout this work.

3. Results

In the absence of any external applied stress, our MPF simulation predicts that both screw and edge dislocations will dissociate into two Shockley partials according to $\frac{1}{3}\left[2\overline{1}\overline{1}0\right]\to \frac{1}{3}\left[1\overline{1}00\right]+\frac{1}{3}\left[10\overline{1}0\right]$. The separation between these two partials defines the core width, which is $3.9a_0$ for screw dislocation and $6.3a_0$ for edge dislocation, as shown in Figure 1(a,b), respectively, by plotting the disregistry and dislocation density across the core region. These core widths predicted using MPF agree well with the original DFT calculations [14], suggesting that MPF combined with GSF is indeed able to replace the full atomistic simulation for predicting dislocation core structures without losing the accuracy. The difference between the core width of screw and edge dislocations can be rationalized based on their elastic energy difference. Since magnesium is close to elastic isotropy, the ratio between the elastic energy of screw and edge dislocations is simply $1-\nu$, where $\nu$ is the Poisson's ratio [1]. As a result, the screw dislocation has a lower elastic energy than that of the edge dislocation. According to the MPF model, the total energy $E^{\text{tot}}$ (in the absence of the work term) is a sum of the crystalline energy $E^{\text{m}}$ and the elastic energy $E^{\text{e}}$. The former is roughly the same for both the screw and edge dislocations as it is controlled by the same GSF energy surface. $E^{\text{m}}$ prefers a narrow core whereas $E^{\text{e}}$ prefers a wider core (similar to the sharp versus diffuse interface in conventional phase-field models [15,16]). In the current case, the ratio $E^{\text{e}}\left(\text{screw}\right)/E^{\text{e}}\left(\text{edge}\right)=1-\nu \approx 0.72$ (using the analytical solution for elastic isotropy), which is close to the ratio of 0.62 between their corresponding core widths.

Figure 1. Disregistry and density of Burgers vectors of screw and edge dislocations (a,b) in the principal direction (parallel to Burgers vector) without applied stress, (c,d) in the principal direction under 60 MPa shear stress with $\alpha ={270}^{\circ }$, (e,f) in the minor direction (perpendicular to Burgers vector) under 60 MPa shear stress with $\alpha ={270}^{\circ }.$

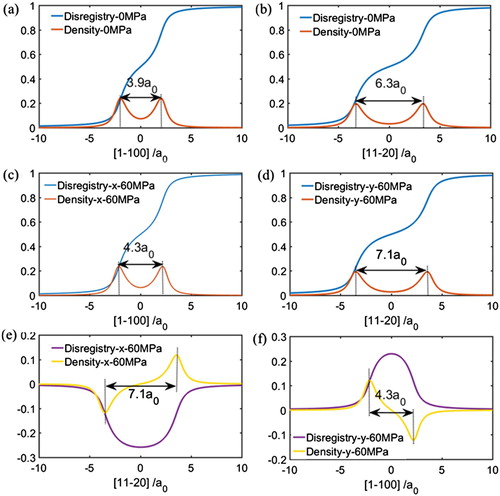
We then apply a shear stress of 60 MPa along the direction perpendicular to the Burgers vectors $\mathbf{b}$. To differentiate the cases of positive and negative shear stresses, we define the rotation angle $\alpha$ from the Burgers vector to the applied shear stress direction in a clockwise direction on the slip plane. The simulated disregistry and density of dislocations suggest that under the applied shear stress ($\alpha ={270}^{\circ }$) the dislocation cores are expanded to $4.3a_0$ and $7.1a_0$ for screw and edge dislocation, respectively, as shown in Figure 1(c,d). It should be noted that in the classical dislocation model (Volterra construction), the displacement experiences a sudden jump across the mathematically sharp dislocation line and only the component parallel to the Burgers vector (defined here as the ‘principal’ disregistry) is non-zero. In contrast, our MPF follows the Peierls model [17] and yields a smooth and finite core region that contains not only the principal disregistry but also a non-zero displacement component perpendicular to the Burgers vector, defined as ‘minor' disregistry (as shown in Figure 1(e,f)). In addition, the distance between the two peaks in the density profiles associated with the principal disregistry coincides exactly with that associated with the minor disregistry, suggesting that a unique core width can be defined here.

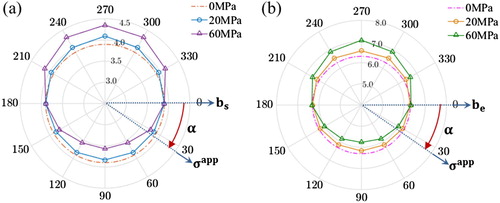
It is further confirmed that not only the magnitude of the applied stress can change the core width but also its direction can exhibit influences. A set of systematic simulations is carried out for both screw and edge dislocations under applied shear stresses of 20 and 60 MPa along different directions and the results on the core width are summarized in Figure 2. In these two polar plots, the dotted circles are the cases in the absence of an applied stress and the solid lines with markers correspond to results under different applied stresses. Note that for both screw and edge dislocations, when the shear stress is applied parallel to the Burgers vector ($\alpha =0^{\circ }$ or $\alpha ={180}^{\circ }$), the core width does not change regardless of the stress level. When the applied shear stress is not parallel to the Burgers vector, the core width will change for both screw and edge dislocations; in addition, the deviation in the core width from that under zero applied stress increases as the magnitude of the applied stress increases. These results and their implication on dislocation-mediated plasticity are certainly beyond the conventional Schmid's law and will be analyzed and explained in the following.

Figure 2. Core widths (in the unit of $a_0$) of (a) screw dislocation and (b) edge dislocation under 20 and 60 MPa in a function of applied shear directions ($\alpha =0\sim {360}^{\circ }$).

4. Discussion

The most striking results in Figure 2 are that (i) the core width changes mostly when a given applied shear stress is perpendicular to the Burgers vector, i.e. $\alpha ={90}^{\circ }$ and $\alpha ={270}^{\circ }$, and (ii) $\alpha ={90}^{\circ }$ and $\alpha ={270}^{\circ }$ lead to completely different changes, with the former leading to a decreased core width and the latter an increased one, namely, a polarized effect due to the applied stress. These can be explained based on the so-called Escaig stress [6] that can modify the width of the stacking fault ribbon between the two Shockley partials. The Escaig stress can be defined in general as the shear stress perpendicular to the Burgers vector [18]. Given an Escaig stress with a magnitude of $\tau$ and based on the dislocation dissociation $\frac{1}{3}\left[2\overline{1}\overline{1}0\right]\to \frac{1}{3}\left[1\overline{1}00\right]+\frac{1}{3}\left[10\overline{1}0\right]$ with the two Shockley partials denoted as ${\mathbf{b}}_1$ and ${\mathbf{b}}_2$, one can easily calculate the Peach-Koehler forces acted on ${\mathbf{b}}_1$ and ${\mathbf{b}}_2$, which are both perpendicular to the Burgers vector of the full dislocation but in opposite directions and have the same magnitude of $\tau b/2\sqrt{3}$. As a result, the applied Escaig stress can narrow or widen the width of this extended dislocation core, depending on the sign of $\tau$. It has been confirmed that our previous MPF results are consistent with the results from the Peach-Koehler force calculation.

The applied Escaig stress will enter the force equilibrium equation for determining the width of the stacking fault ribbon [1] and can thus be considered as modifying the intrinsic stacking fault (ISF) energy ${\gamma }_{\text{ISF}}$ (or, more precisely, I2 stacking fault for our HCP case) to an effective value of ${\gamma }_{\text{ISF}}^{\text{eff}}={\gamma }_{\text{ISF}}+\frac{\tau b}{2\sqrt{3}}$. We can plug this ${\gamma }_{\text{ISF}}^{\text{eff}}$ in the analytical expression for the ISF width, which can be found in [19], to give the estimated stress-dependent core width based on anisotropic elasticity (AE) theory. The results are shown in Figure 3, where the prediction form MPF is included. Note that for each method, there are two sets of data, one showing that the core width is widening as increasing the Escaig stress and the other showing the opposite. 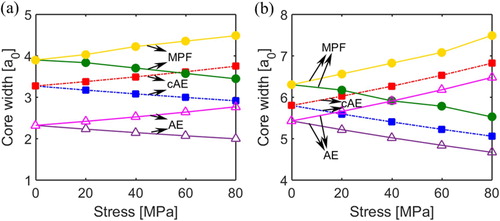Note that AE gives stress-dependence (the slope of the lines) very similar to that of the MPF prediction, which suggests that the idea of incorporating Escaig stress effect into ${\gamma }_{\text{ISF}}^{\text{eff}}$ can be an effective way of considering the stress-dependent core width based on the analytical expression. However, in both the screw and edge dislocation cases AE always underestimates the core width as compared to MPF for all the stress values considered. This trend has also been seen in the comparison between AE and ab initio calculation in predicting the core width of screw dislocations in Ni and Ni₃Al [19]. This underestimation is attributed to the ‘corner cutting' in the dislocation core configuration (see [9,20]), which means that the dislocation dissociation will never fully reach the ISF to reduce the total length of dislocations (and hence line tension). Tan et al. [19] proposed a correction to AE prediction (which is termed as ‘corrected AE' approach in the following) by replacing the geometrically expected edge (screw) component for screw (edge) dislocation with the actual value determined from atomistic calculation. This suggests that in our case we may use the maximum minor disregistry obtained from the MPF prediction to do a similar correction. Results from such a corrected AE (cAE) approach are shown in Figure 3, which suggests that the above correction can indeed reduce the difference between the AE and MPF predictions.

Figure 3. Comparison between the predicted core width using MPF, anisotropic elasticity (AE), and corrected anisotropic elasticity (cAE) approaches for (a) screw and (b) edge dislocation.

The predicted stress-dependent core width can be further used to provide a quantitative estimation on its influence on some material properties. In particular, the Peierls stress depends sensitively on the dislocation core structure. Accurate calculation of the Peierls stress requires explicit consideration of lattice discreteness and hence a reformulation of the energy [21]. To have a quick assessment of the influence of the previous result on the Peierls stress ${\sigma }^p$, we employ the well-known analytical expression (1) ${\sigma }^p=\frac{Kb}{a_s}\text{exp}\left(-\frac{2\pi \xi }{a_s}\right)$(1) where $b$ is the magnitude of the Burgers vector, $a_s$ is the spacing of atomistic planes along the glide direction (i.e. y-direction in Figure 1(b,c)), $\xi$ is the half-core width of the dislocation, $K=\mu \left(\frac{\text{si}{\text{n}}^2\theta }{1-\upsilon }+\text{co}{\text{s}}^2\theta \right)$ is a modulus-related ($\mu$: shear modulus) parameter with $\theta$ being the angle between the dislocation line and the Burgers vector [22]. 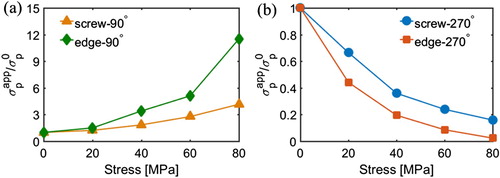In our case, $K_s=16.4$ GPa for a screw dislocation and $K_e=22.8$ GPa for an edge dislocation. Equation (1) is considered reliable when the core width is larger than the lattice parameter [23], which is well satisfied in our case. We plot in Figure 4 the change of Peierls stress as a function of the resolved shear stress for two different directions, i.e. $\alpha ={90}^{\circ }$ and $\alpha ={270}^{\circ }$. In the case of $\alpha ={90}^{\circ }$, the reduced core width (Figure 3) due to the applied stress increases the Peierls stress significantly. In particular, for the edge dislocation an order of magnitude increase in the Peierls stress is predicted when the applied shear stress is 80 MPa, whereas the corresponding increase for the screw dislocation is much smaller (but still reaches to ∼4 times of the value under zero stress). In the case of $\alpha ={270}^{\circ }$, the Peierls stress decreases and quickly reduces to virtually zero for the edge dislocation and down to 20% for the screw dislocation.

Figure 4. Relative magnitude of Peierls stresses as a function of applied shear stress in reversed directions: (a) $\alpha ={90}^{\circ }$ and (b) $\alpha ={270}^{\circ }$.

The implication of the stress-dependent core width is not limited to the Peierls stress for dislocation glide. As the core width is significantly reduced, the mode of dislocation motion may essentially change as well. In particular, as the core becomes more compact, the propensity for the basal dislocations to cross-slip onto other slip planes, e.g. prismatic and pyramidal planes, is expected to increase significantly. This can be of great importance, because the transition and interaction between basal and non-basal slip are believed to control the ductility of magnesium and magnesium-alloys [24,25]. As basal slip is the easiest slip mode for magnesium and as other slip modes and deformation twinning must involve non-basal slip, a primary question is where the non-basal dislocations come from. Several mechanisms have been proposed so far as discussed in [26]. Cross-slip of basal $\mathbf{a}$ dislocations may be involved in these mechanisms but is considered energetically unfavorable based purely on the line-tension model where the core energy is assumed constant. Our current prediction suggests that this may not be the case in the presence of the applied load and thus urges reconsideration of this unsolved issue. In addition, the atomistic simulations of Wu and Curtin [25] have also shown that the core structure ($\mathbf{c}+\mathbf{a}$ and $\mathbf{a}$) in Mg evolves with increasing the applied load, which agrees with our current conclusion.

Finally, the current findings may also shed light on the understanding of deformation twinning in magnesium. Since strong correlation between dislocation glide and deformation twinning has been proposed based on experiments and simulations [27], care must be given when considering the interaction between dislocations and deformation twins as many theories are motivated and/or based on pure crystallographic consideration. Indeed, MPF has recently been applied to studying dislocation dynamics during slip transmission across the $\alpha /\text{β}$ interfaces in Ti-alloys [28], which shows clearly that reactions that are geometrically unfavorable can actually occur with the aid of an applied external stress.

5. Conclusions

The core width of basal dislocations in Mg has been found to depend strongly on the resolved shear stress on the slip plane using an integrated microscopic phase-field model and ab initio calculations. Such a non-Schmid effect becomes more significant as the applied shear stress increases. For a given stress magnitude, the core can either expand or contract depending on the applied stress direction, revealing a polarization effect. The resulting influence on the material property is further quantified based on the predicted core width, which suggests that the Peierls stress can either become virtually zero or increase by an order of magnitude depending on the applied stress magnitude and direction. Further implication of the current findings on plastic deformation of Mg is also discussed.

Acknowledgements

DQ would like to acknowledge the support from China Postdoctoral Science Foundation under grant number 2018M630437, National Postdoctoral Program for Innovative Talents under grant number BX201600099, The National Key Research and Development Program of China under grant number 2020YFB0704503, and National Science Foundation of China under grant number 51801123. PZ would like to acknowledge the support from Shanghai Pujiang Program under grant number 20PJ1406500. PZ and YW would like to acknowledge the support from the US National Science Foundation under grant number DMR-1922239. DRT acknowledge the support from the US National Science Foundation under Grants No. 0825961 and 1410596. DQ and PZ jointly conceptualized the work and developed the model; DQ conducted the simulations and analysis; DRT provided the ab initio GSF energy surface data; YW organized the partnership and supervised the work; DQ and PZ took the lead in writing the manuscript, with contributions from all other authors.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by China Postdoctoral Science Foundation: [Grant Number 2018M630437]; National Science Foundation of China: [Grant Number 51801123]; Shanghai Pujiang Program: [Grant Number 20PJ1406500]; The National Key Research and Development Program of China: [Grant Number 2020YFB0704503]; US National Science Foundation: [Grant Number 0825961, 1410596,DMR-1922239]; National Postdoctoral Program for Innovative Talents: [Grant Number BX201600099].