Double transition metal-containing M₂TiAlC₂o-MAX phases as Li-ion batteries anodes: a theoretical screening

Abstract

Here, thermodynamic stability and lithium storage properties of double transition metal M₂TiAlC₂ o-MAX phases (M = Cr, V, Mo, Nb, Ta, Hf, Zr, Sc, Y, La) are theoretically investigated by density functional theory (DFT) calculation. M₂TiAlC₂ with a larger M atomic radius shows larger interlayer space that may benefit the Li-ion intercalation. A promising theoretical capacity of 276.87 mAh g^-1 is predicted for Sc₂TiAlC₂. The low Li-ion diffusion barriers (0.57–0.64 eV) for M₂TiAlC₂ indicate the possibility to achieve fast Li-ion diffusion that is crucial for designing high-power batteries. This work provides opportunities to explore MAX phases as promising Li-ion storage materials.

GRAPHICAL ABSTRACT

IMPACT STATEMENT

This work investigates the thermostability and lithium storage properties of double transition metal o-MAX phases by DFT calculation and provides a guideline for exploring MAX phases for lithium storage applications.

KEYWORDS:

• DFT calculation
• o-MAX phases
• Li-ion battery
• Li-ion diffusion

Introduction

MAX phases are hexagonal nanolaminated ternary metal/ceramics with the general formula M_n+1AX_n, where M is the transition metal, A is the main III to V group elements, X is C or N and typically n = 1, 2, 3, 4, etc. [1,2]. There are currently more than 150 MAX phases known, including solid solutions [3,4]. Due to the alternative stacking between the A layer and ceramic layer, MAX phases possess high conductivity and structural stability that is being considered for electrical contacts, sensors, protective coating, microelectromechanical systems, and high-temperature structural applications [5–8]. In recent years, MAX phases are receiving increasing attention as precursor materials of two-dimensional MXenes that are extensively investigated as electrochemical energy storage materials [9–13]. Although much less attention has been paid to MAX phases as lithium storage materials, several studies confirmed the promising potential of using MAX phases as lithium storage electrode materials. In 2016, Xu et al. [14] reported on the enhanced lithium storage performance of Ti₃SiC₂ and Ti₂SC MAX phases by reducing the particle size of the MAX phases, achieving a maximum capacity of 180 mAh g⁻¹. Zhao et al. [15] demonstrated Nb₂SnC MAX phases with a lithium storage capacity of 234 mAh g⁻¹ and proposed that the Sn atomic layer can contribute additional capacity through reversible Sn–Li alloying reaction. Recently, Wu et al. [16] showed the Ti₂SnC MAX phases are capable of delivering 735 mAh g⁻¹ and Li et al. [17] reported V₂SnC MAX phases could obtain high gravimetric capacity up to 490 mAh g⁻¹ and proposed a lithium storage mechanism with V₂C-Li and Sn–Li reactions.

To achieve high specific energy for Li-ion batteries, developing novel anode materials with a high specific capacity, low delithiation potential, high cycling stability, and reversibility are highly demanded [18–20]. MAX phases featured with layered structures and high electrical conductivities are believed to be promising lithium storage hosts. However, to the best of our knowledge, studies on MAX phases as an electrode for energy storage is scarce and the charge storage mechanism is not fully understood yet. Therefore, it is of great interest and significance to explore the lithium storage properties of MAX phases. DFT calculations are effective methods for theoretical investigation on materials’ properties. Zhu et al. [21] predicted by DFT calculation that the stress-enhanced V₂SC MAX phases could achieve good lithium storage properties and soft interlayer in MAX phases provide the possibility for lithium storage. However, other researchers found the interlayer space of MAX phases is too narrow to incorporate lithium and the lithiation formation energy is positive [22,23]. Therefore, more studies focused on the exfoliation or interlayer expansion to enhance the chances of lithium interaction [24,25].

Elemental doping and substitution, in many cases, are effective routes to tune the electronic properties of MAX phases [26,27]. Therefore, we speculate that the ordered M₂TiAlC₂ (M = Cr, V, Mo, Nb, Ta, Hf, Zr, Sc, Y, La) MAX phases with outer Ti atomic layers substitutional strategy may expand the interlayer space and achieve enhanced lithium storage properties. In the ceramic layer structure, the face-centered cubic (fcc) transition metal carbides are more stable. Thus, the Ti located inside of the ceramic layer can usually stabilize the structure [28]. Combining the M element substitution and the stability of Ti carbide layer, it can be expected that the M₂TiAlC₂ may achieve high lithium storage properties and structural stability.

In this work, the structural stability and electronic properties of the M₂TiAlC₂ MAX phases (M = Cr, V, Mo, Nb, Ta, Hf, Zr, Sc, Y, La) with or without lithium intercalation are investigated by DFT calculations. The phonon density of states is employed to predict the lithium storage capacity by checking the stabilities of M₂TiAlC₂ containing the different numbers of Li-ions. The kinetic properties are evaluated for M₂TiAlC₂ by analyzing the migration pathways of Li-ion.

Results and discussion

For selecting MAX phases as promising electrode materials, the thermodynamic stability, lithiation formation energy$\mathrm{\Delta }{E}_{Li}$, theoretical capacity, and Li-ion diffusion barrier are vital criteria and will be carefully screened step by step.

Stability of M₂TiAlC₂

The calculated lattice constants and formation energies of M₂TiAlC₂ are listed in Table 1, in which the values of Ti₃AlC₂ matched well with the previous works [29]. With the outer M atomic size increasing, the a and c lattice constants increase from 2.904 to 3.460 Å and 17.793 to 22.704 Å, respectively. With the atom size differences of substitutional M and Ti increase, the formation energies of M₂TiAlC₂ correspondingly increase, leading to the enhancement of instability. However, according to the formation energies, substitutions of Zr, Hf, Sc, and Y not only have less influence on the thermodynamics but also expand their interlayer space effectively. The substitutions of Cr, V, Mo, Nb, and Ta result in the decrease of interlayer space, and these M₂TiAlC₂ MAX phases are not considered for further investigation due to the difficulty for lithium intercalation. Unstable (∼ −0.05 eV) La₂TiAlC₂ is not further discussed as well.

Table 1. Lattice constants, cell volume, and formation energies, $\mathrm{\Delta }{E}_{M_{2}TiAl{C}_2}$, of M₂TiAlC₂ MAX phases (M = Cr, V, Mo, Ti, Nb, Ta, Hf, Zr, Sc, Y, and La).

M2TiAlC2	a (Å)	c (Å)	V (Å^3)	$\mathrm{\Delta }{E}_{M_{2}TiAl{C}_2}$ (eV/atom)
Cr2TiAlC2	2.904	17.793	519.659	−0.447
V2TiAlC2	2.965	18.077	550.494	−0.691
Mo2TiAlC2	3.002	18.743	584.885	−0.526
Ti3AlC2	3.072	18.730	612.781	−0.841
Nb2TiAlC2	3.105	18.896	630.824	−0.732
Ta2TiAlC2	3.131	18.904	641.779	−0.641
Hf2TiAlC2	3.250	19.314	706.742	−0.695
Zr2TiAlC2	3.259	19.565	719.659	−0.779
Sc2TiAlC2	3.190	20.173	712.566	−0.623
Y2TiAlC2	3.403	21.258	852.427	−0.260
La2TiAlC2	3.460	22.704	940.866	−0.050

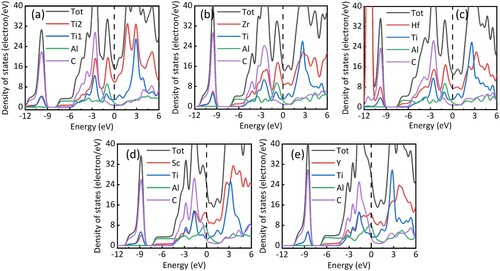
The density of states (DOS) of Ti₃AlC₂, Zr₂TiAlC₂, Hf₂TiAlC₂, Sc₂TiAlC₂, and Y₂TiAlC₂ phases are calculated as shown in Figure 1. Similar to Ti₃AlC₂, the DOS of M₂TiAlC₂ has similar hybridization characteristics, including the covalent bonding of M and C and the metallic properties dominated by transition elements [30]. Since the insufficient number of valence electrons for filling the bonding states, the hybridization peaks of Sc₂TiAlC₂ and Y₂TiAlC₂ will shift toward a higher energy level. The DOS in higher energy levels tend to fill nonbonding/antibonding states, which reduces the stability of the structure. It is in good agreement with the calculated formation energies. Since Ti, Zr, and Hf have the same number of valence electrons, the bonding states of M₂TiAlC₂ MAX phases are filled and their corresponding antibonding states remain unfilled, separating by a pseudogap in the Fermi level [31]. Thus, the substitution of Sc and Y would be less stable than Zr, and Hf substitution. Besides, the order of phase stability is Ti₃AlC₂ > Zr₂TiAlC₂ > Hf₂TiAlC₂, which conforms to the order of M atomic size (Hf > Zr > Ti), indicating the M atom size is opposite to thermodynamic stability.

Figure 1. The density of states of (a) Ti₃AlC₂, (b) Zr₂TiAlC₂, (c) Hf₂TiAlC₂, (d) Sc₂TiAlC₂ and (e) Y₂TiAlC₂.

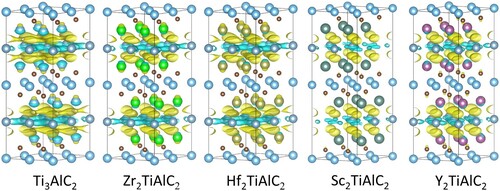
As shown in Figure 2, the charge differences between Al and ceramic layers are calculated to obtain insight into the structural changes. The degree of the charge transfer represents bonding strength. Compared with Ti₃AlC₂, the M₂TiAlC₂ MAX phases show similar electronic distributions but less charge transfer, suggesting weaker M–Al bonding. The relatively weakening M–Al bonds represent the longer M–Al bonding length, further generating an expanding interlayer space [32]. Besides, the weaker bonding strength can also be explained by overlapped states shifting toward higher energy levels as shown in Figure 1. Combining the analysis of electronic structure and thermodynamics (formation energy), we reach the conclusion that the larger difference between the atomic sizes of M and Ti results in the larger interlayer space and the less structural stability, which agrees well with previous studies[31,33].

Figure 2. The charge differences of Ti₃AlC₂ and M₂TiAlC₂ MAX phases at the same isosurface with isovalue are 0.05 electrons/bohr³.

Lithium storage properties of M₂TiAlC₂

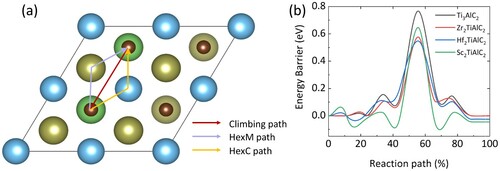
Characterized by the expanded interlayer space, M₂TiAlC₂ MAX phases are interesting to be explored as electrode materials for LIBs. To figure out the energetically favorable sites of Li-ion in M₂TiAlC₂, five configurations are considered as follows: (1) M3Al tetrahedron (T_M), (2) Al3Ti tetrahedron (T_Al), (3) M3Al3 octahedron (O), (4) C hexahedron (H_C), (5) M hexahedron (H_M), as shown in Figure 3. The more negative value of formation energy is, the more energetically stable configuration is. The lithiation formation energies of T_M, H_M, and H_c are positive, indicating the Li-ion in these sites are unfavorable. Noticeably, Li in O sites are all moved to the surrounding H_C after full optimizations, indicating the inserted Li should firstly be stored in the Al layer. Besides, the formation energy values of O and H_C sites are considerably close, as listed in Table S1, which indicates H_C is the most energetic favorable lithiation site.

Figure 3. Structure of M₂TiAlC₂ MAX phases and initial lithium storage sites, where the black dotted line represents different interstices.

To obtain insight into the lithiation process, the Bader charge and charge difference analyses are performed. In Table 2, the charge transfer of Li in M₂TiAlC₂ is around −0.72 |e| that loses more electrons than in Ti₃AlC₂ (−0.69 |e|), which indicates Li will be more ionic states in the large interlayer spaces. Meanwhile, Al gains more electrons that explain the increasing degree of Li–Al alloy reaction. The charge transfer of Ti remains almost unchanged, reflecting that lithiation has slight influences on the interior of the ceramic layer. Besides, charge differences show the interaction between Li and host material, as shown in Figure S1. The Coulomb force between Li and M elements is weaker with the interlayer space enlarging because the smaller positive electron cloud generates less repulsion.

Table 2. Charge transfer with reference to isolated atoms (in electrons; calculated by the Bader approach) for lithiation of M₂TiAlC₂ MAX phases.

Type	Elements	Hf2TiAlC2	Sc2TiAlC2	Y2TiAlC2	Zr2TiAlC2	Ti3AlC2
Lithiation	Ti	−1.46	−1.49	−1.49	−1.45	−1.46
	C	1.73	1.8	1.81	1.81	1.64
	Al	0.82	0.95	0.93	0.86	0.69
	Outsides M	−1.37	−1.48	−1.49	−1.47	−1.22
	Li	−0.72	−0.72	−0.74	−0.72	−0.69

Specific capacity is a crucial parameter that determines the energy density of LIBs. To confirm the theoretical specific capacities of M₂TiAlC₂, the lithiation formation energy $\mathrm{\Delta }{E}_{Li}$ for each continually inserting Li is calculated via Eq (S2) and presented in Figure 4(a). Obviously, Ti₃AlC₂ shows the lowest $\mathrm{\Delta }{E}_{Li}$, indicating less thermodynamic stable for Li insertion. Once the value of $\mathrm{\Delta }{E}_{Li}$ tends to be zero or positive, no more lithium can be inserted, which corresponds to the maximum saturation of Li storage. Base on the Eq (S3), the theoretical capacities of Ti₃AlC₂, Zr₂TiAlC₂, Hf₂TiAlC₂, Sc₂TiAlC₂, and Y₂TiAlC₂ are calculated to be 243.54, 252.55, 105.03, 411.22, and 256.7 mAh g⁻¹, respectively. Furthermore, the dynamical stability of maximal Li insertions is investigated by performing lattice phonon calculations, as shown in Figure S2. Imaginary frequency demonstrates the structure is dynamically unstable and the partial phonon density of stats of ceramic layer and Al layer with Li-ions are calculated. Among all M₂TiAlC₂ MAX phases, the ceramic layer is calculated without imaginary frequency, suggesting the dynamically stable and the optical and acoustical branches are well-separated, presenting a phonon dispersion characteristic of layered material [34]. Ti₃AlC₂ phases can maintain only one Li atom per Al layer in a supercell with an imaginary frequency value of 100 THz, which indicates the theoretical capacity would be lower than ∼122.84 mAh g⁻¹ calculated via Eq (S3). However, the Sc₂TiAlC₂ could maintain two Li atoms per Al layer in a supercell without any imaginary frequency, and the theoretical capacity could be 276.87 mAh g⁻¹ that is twice larger than Ti₃AlC₂. With the same Li storage number but different molar weights, the theoretical capacities of Zr₂TiAlC₂ and Hf₂TiAlC₂ are 169.39 and 105.03 mAh g⁻¹, respectively. After lithiation, as shown in Figure S3, the conductivities of M₂TiAlC₂ have no significant change because the metallic property is contributed mainly by M elements’ d orbital.

Figure 4. (a) The lithiation formation energy for M₂TiAlC₂ for every inserting Li. The bonding length between the (b) M and Li, (c) Al and Al, (d) Al and Li as the function with the inserted Li number.

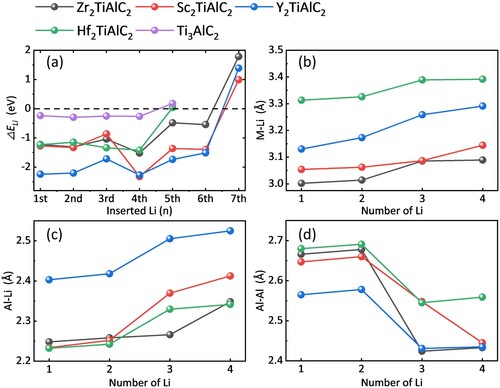
To clarify the effect of interlayer space on lithium storage, the M–Li, Al–Li, and Al–Al bonding lengths (representing different directions of interlayer space) are calculated, as shown in Figure 4(b–d). The sudden change of the Al–Li and Al–Al bonding lengths happens at the third Li insertion. On the one hand, the M–Li bonding length changes slightly, reflecting that lithiation hardly influences the ceramic layer. On the other hand, the Al–Li boding length increases, and Al–Al bonding length decreases as the inserted Li number increases, indicating the Al layer atoms will rearrange during lithiation/delithiation. Al can rearrange in M₂TiAlC₂ easier because of the larger interlayer space that produces less Coulomb force and weaker M–Al bonding.

The charge/discharge rate capability of rechargeable LIBs is mainly determined by the ion diffusion kinetic. The intrinsic metallic behavior of M₂TiAlC₂ has been demonstrated by DOS [35]. The NEB method is performed to estimate the Li diffusion. Three diffusion pathways along the high symmetry line between the two neighboring favorable sites (H_C) are designed to find the minimum energy barrier, as shown in Figure 5(a). However, the diffusion barrier of the HexM path is around 1.2 eV, which implicates M repulsive force hinders this diffusion path. Besides, the climbing path could not be realized because the ceramic layer’s repulsive force is larger than the Al layer. The diffusion energy barriers of the HexC path are relatively low, as presented in Figure 5(b). The minimum energy barrier is 0.57 eV in Hf₂TiAlC₂. It is worth noting that along the HexC path, the diffusion trajectory of Li-ion passes through an Al position, resulting in the position derivation of the Al atom. Hence, if there is enough space for Al to move, the Li-ion would diffuse more easily. As demonstrated above, M substitution expands the interlayer space that facilitates the easy rearrangement of Al, thereby reducing the Li-ion diffusion barriers in M₂TiAlC₂.

Figure 5. (a) The three types of Li diffusion pathways and (b) the diffusion energy barrier for M₂TiAlC₂.

Conclusions

We performed a computational investigation on the structural and lithium storage properties of M₂TiAlC₂ MAX phases. DFT calculations demonstrate that M₂TiAlC₂ MAX phases are thermally stable. M elements substituting expands the interlayer space expands and thus reduces lithiation formation energy, and the charge difference shows that the strong repulsion force decreases, suggesting the great potential for lithium storage. Next, the maximum theoretical capacities of the M₂TiAlC₂ MAX phases are calculated. Zr₂TiAlC₂ and Sc₂TiAlC₂ are predicted with the maximum specific capacities of 169.39 and 276.87 mAh g⁻¹ respectively. Finally, the different diffusion pathways were screened for investigating the diffusion barriers of Li-ion into M₂TiAlC₂ MAX phases. The lowest diffusion energy barrier (∼0.57 eV) is obtained for Hf₂TiAlC₂.

In this work, the M elements substitution strategy was proposed for fine-tuning the interlayer space and electronic structure of MAX phases as promising lithium storage materials. The guideline to improve the lithium storage properties of MAX phases are summarized as following: (1) enlarge the interlayer space by larger radii elements substitution; (2) select proper A elements to make inserted Li in more ionic states.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This study was supported by the National Natural Science Foundation of China [grant number 51902215] and Sichuan Science and Technology Program [Project No. 2021YFGZ0092].