Universal Trend in the dynamic relaxations of tilted metastable grain boundaries during ultrafast thermal cycle

Abstract

Nonequilibrium relaxations in a multiplicity of tilted grain boundaries (GBs) subjected to ultrafast thermal driving forces are investigated by atomistic modeling. By scrutinizing the intermediate metastable microstates and their assessable activation barriers in the underlying energy landscape, we demonstrate the energetics and atomic diffusions in tilted metastable GBs are disorder-driven rather than free volume-driven. A critical transition temperature is identified, separating the nonequilibrium GBs’ evolution into a fast-varying stage, and a tuning-ineffective stage, respectively. We further discover a universal correlation between such critical temperature and GBs’ inherent structure energy, which enables predicting the tunability of metastable GBs’ kinetic and mechanical properties.

GRAPHICAL ABSTRACT

IMPACT STATEMENT

We report a universal correlation between tilted GBs’ metastable microstates and kinetic properties during extreme thermal processing, suggesting a new strategy of manipulating interface-rich materials’ performance without changing their macroscopic textures.

KEYWORDS:

• Metastable tilted grain boundaries
• nonequilibrium processing
• activation energy spectra in energy landscape
• tunability prediction on kinetics and mechanics

1. Introduction

Grain boundaries (GBs), as one of the most common solid–solid interfaces, determine many important properties of poly-/nano-crystalline materials [1–4]. In terms of the macroscopic degrees of freedom, GBs are usually characterized by 5 independent angular parameters representing the misorientation between neighboring grains. In the past, extensive efforts have been made on probing the thermodynamic equilibrium atomic structures and properties of GBs at different misorientations [5–7]. Consequently, the conventional wisdom of GB-engineering strategy has been focused on creating and controlling the relative fraction of GBs with special coincident site lattice structures (e.g. twin or other low-Σ boundaries) [8].

Recent theoretical studies [9] have demonstrated that a given GB, even with its macroscopic misorientation angle fixed, can possess essentially infinite number of metastable microstates. This marks the insufficiency of traditional focus on the equilibrium structures, and such an issue becomes more critical when extreme environments are imposed. For example, recent experiments demonstrate non-equilibrium processing can remarkably change GBs’ behaviors without affecting their macroscopic features. Specifically, pulse fs-laser irradiation can significantly change the nano-crystals’ hardness with negligible variations in grain sizes [10]. Recent additive manufacturing experiments [11] also suggest that, the very rapid heating/cooling cycle can create non-equilibrium states of GBs with remarkably high diffusivity (10^4∼8 times faster than usual) without discernible changes in grain sizes and orientations. These studies collectively envisage a new school of thought on GB engineering—a way to manipulate the metastable microstates of GBs without changing their macroscopic textures. In the meantime, such a prospect also prompts fundamentally new challenges on understanding the behavior of metastable GBs at extremes.

Here we investigate the responses of a multiplicity of bicrystal tilted GBs subjected to ultrafast thermal cycles comparable with the selective laser melting or fs-laser irradiation environments. A universal hysteresis on energy evolution is observed in both symmetrically tilted GBs (STGBs) along different axes and asymmetrically tilted GBs. By probing the atomic configurations and energy landscape of metastable GBs at various intermediate stages and resolving the activation energy spectra for collective atom rearrangements, we demonstrate a strong sensitivity of GBs’ kinetic behavior to their processing histories. Most notably, in the rapid cooling stage we discover a scaling relationship between GBs’ inherent structure energies and their critical structural transition temperatures. These findings provide a foundation to assess the tunability of different tilted metastable GBs and predict their most effective processing windows. It may hold the promise for a new route to harness the properties of interface-dominant systems.

2. Materials and methods

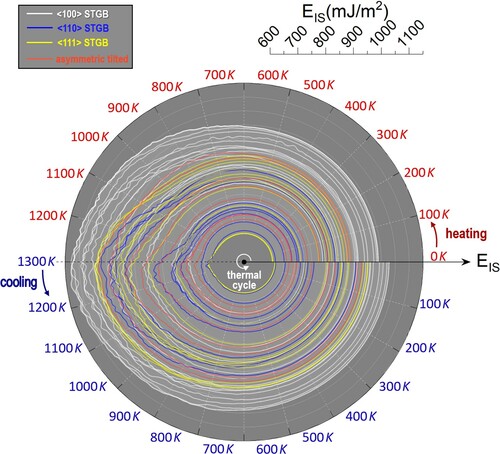
We first create a variety of ‘ground-state’ GBs in Cu with EAM potential [12] via the bicrystal set-up protocol [13–16]. Mis-oriented upper and lower crystals are combined through rigid in-plane translations and occasional atom deletions to identify the lowest energy states and configurations. Note that our ground-state structures and energetics calculations at different misorientation angles are well consistent with earlier studies [13,14]. Fast heating and cooling (0K→1300K→0K at 10K/ps) are then imposed to the so-constructed static GBs, and their energetics and structural evolutions are consequently scrutinized. Note that the temperature changing rate here is not unrealistic in scope of non-equilibrium processing [17–19]. The upper bound of temperature is set deliberately below the bulk melting point (∼1350 K), because we would like to keep the constraints of macroscopic textures while focusing on the evolution of GBs’ metastable microstates. Also note that the atoms number in the simulation box keeps fixed, because the ultrafast stimuli will drive the system out of equilibrium, and one should not assume a grand canonical ensemble. Figure 1 shows the evolution of inherent structure (IS) energy during the thermal cycle over different types of GBs (details of tilting axes and misorientation angles, as well as the controls of MD simulations, are shown in Supplementary Materials, Table.S1 & Fig. S1). Despite of a wide range distribution of energetics across various GBs, there clearly exhibit some universal features: (1) At low temperatures the curves are almost in perfect arches with invariant radii (i.e. E_IS), reflecting the kinetically arrested stage; (2) At high temperatures there present significant energy fluctuations while the radii are ramping up, yielding a cluster of skewed curves. As will be discussed below, this reflects the ISs of GBs are becoming increasingly more disordered via atomic rearrangements near interfaces; (3) Most notably, the curves are not closed loops after the thermal cycle; instead, the upper and lower halves in Figure 1 are off from mirror symmetry. More specifically, a universal hysteretic behavior exhibits, and the E_IS of GBs shift to higher values after cooling than they were initially located, corroborating the rejuvenating responses of nanocrystals under pulse fs-laser processing [10]. It is also worth noting that, in high temperature regime there exist frequent crossovers among various curves, indicating very complex and diverse relaxation behaviors of different GBs at extreme conditions. In what follows, we report the discovery of a scaling relationship that can delineate these complex relaxations.

Figure 1. Inherent structure energy evolution under rapid thermal cycling (0K→1300K→0K at 10K/ps) for various types of GBs.

3. Results and discussion

Figure 2(a-b) presents a case study on the ∑5 (310) <100> STGB. Its hysteretic E_IS evolution is clearly seen in Figure 2(a1). There are only limited overlaps between the heating and cooling stages around 1100∼1300 K, because at such high temperatures equilibrated GB structures can be achieved even within very short timescales. Beyond that regime the cooling curve significantly deviates from its heating counterpart, and the system eventually freezes at a higher energy level after the processing. We also did a benchmark study in a single Cu crystal at the same condition and found its E_IS stays constant throughout entire cycle, and the heating/cooling process is completely reversible. Such a benchmark therefore verifies the hereby observed hysteresis is not an artifact in MD simulation; instead, it reflects the strong coupling between the extreme stimuli and the accessible metastable states of a GB.

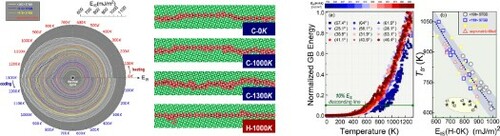
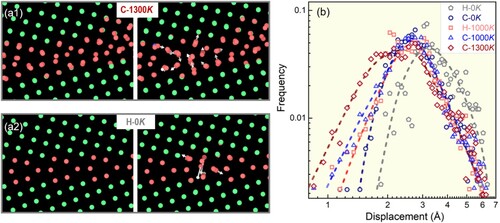
Figure 2. (a1) E_IS evolution for ∑5 (310) <100> STGB. (a2) The average atomic square displacement (normalized by nearest neighbor distance) of non-FCC atoms during the cooling process. Inset: selected ISs at different temperatures during the heating-cooling process. Non-FCC atoms (red) are distinguished by the common neighbor analysis. (b) Activation energy spectra for the selected ISs. (c) Variations of E_IS for all <100> STGBs considered in the present study. The green circles represent the E_IS at Lindemann threshold, namely $\surd (\mathrm{\Delta }{d}^2)/$r_NN= 0.08. The orange crosses represent the 10% descending energy illustrated in (a1). Inset: strong overlap between the Lindemann extraction and 10% E_IS descending line.

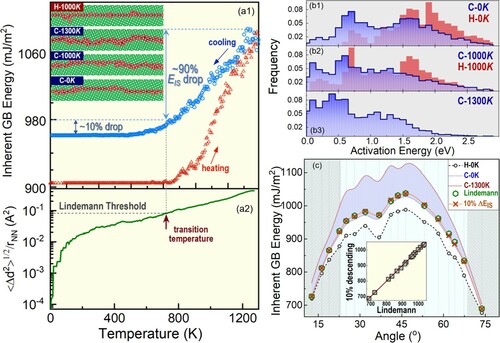
Along with energetics variation the GB's atomic structure also keeps evolving, and a higher E_IS state is usually associated with a more disordered configuration. To quantify the microstructural evolution, Figure 2(a2) shows the average atomic square displacement of non-FCC atoms to be discussed below. Figure 2(a1)’s inset shows a few selected ISs at various heating/cooling stages. The very initial ground-state configuration (denoted as H-0 K below) is not presented here, because it is a well-known structure made of repeating kite units [13,20,21]. When the system is heated to 1000 K, some dispersed fluctuations emerge while the overall GB remains thin and straight (H-1000 K). At 1300 K, where heating ends and cooling starts, the IS becomes thicker and distorted (C-1300 K). Apparently, disorders are accumulated and the repeating kite units at low temperatures no longer exist, corroborating the ‘smooth-to-rough’ transition [22–24]. When the system is cooled to 1000 K (C-1000 K), the GB’s thickness is reduced while the curvature and disorder remain elevated. When the system is eventually cooled back to 0 K (C-0 K) the GB turns thin and smooth again but leaving behind a kink structure. The reason that the system does not recover the ground-state configuration is due to the mismatch between two timescales: namely the intrinsic relaxation timescale for a given GB to reach its thermodynamics equilibrium structure through atomic reconfigurations, and the extrinsic timescale imposed by the processing condition (e.g. the rapid cooling). More specifically, the GB tries to find its ground state (i.e. the repeating kite units) during the cooling stage but cannot fully achieve so because of the exceedingly longer intrinsic relaxation timescales at low temperatures and subsequently its mismatch with the permissible extrinsic timescales.

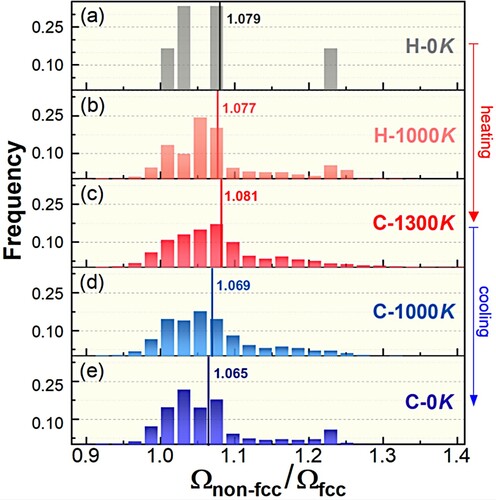
Earlier studies demonstrate that, for ground-state GBs with different misorientation angles, their energetics positively correlate with excess free volumes [7,25]. However, we found such a free volume sensitivity no longer holds in the present study under extreme stimuli. More specifically, Figure 3 shows the free volume distributions of GB atoms (defined as Voronoi volumes ratio between non-FCC and FCC particles) at different processing stages. There are only 4 distinct local environments in the initial state (H-0 K), due to the above-mentioned repeating kites. Under fast thermal cycling the free volume distributions become much broadened, indicating more disordered configurations. However, the average ${\mathrm{\Omega }}_{non-fcc}/{\mathrm{\Omega }}_{fcc}$ values (i.e. vertical lines) only change little, in stark contrast to Figure 2(a)’s significant energetics variations. Note that the previous studies [7,25] primarily focused on the equilibrium states of GBs. Therefore, the present study indicates a qualitatively different behavior at far-from-equilibrium conditions, that is, the metastability of non-equilibrium GBs are disorder-driven rather than free volume-driven. Interestingly, such a disorder-driven mechanism aligns with recent studies of ceramic nanocrystals under ion irradiations [26].

Figure 3. The distributions of Voronoi volume ratios between non-FCC particles (GBs) and FCC particles (bulk) at different processing stages.

Many important properties of GBs—including diffusion, migration, and strength—are controlled by activation barriers of collective atomic rearrangements inside the boundaries [27–33]. Therefore, we probe the distributions of accessible activation barriers for the above-selected ISs using an energy landscape sampling algorithm [34–38], as shown in Figure 2(b). At first, the activation barriers show broad spectra rather than explicit values. This can be attributed to the break of translational symmetry in single crystals and/or the disorders at GBs, which is not surprising. Secondly, by comparing through Figure 2(b1–b3), it is clear that the activation energy spectra vary significantly at different stages, and that a metastable state with higher E_IS yields a smaller effective activation barrier. This is understandable because, as shown by the configurations in Figure 2(a), higher-energy metastable GBs are more random and disordered, where the emergence of easily accessible activation pathways can be expected.

To quantify the kinetic boost factor between the post-processing and pre-processing states (C-0 K vs. H-0 K), one can compute the Boltzmann factor-weighted integral of the two activation barriers spectra in Figure 2(b1) as: (1) $\alpha (T)=\frac{\int P(E_A|C-0K)\cdot e^{-\frac{E_A}{k_{B}T}}d{E}_A}{\int P(E_A|H-0K)\cdot e^{-\frac{E_A}{k_{B}T}}d{E}_A}$(1) Note that very recent isotope diffusion measurements demonstrate non-equilibrium states of GBs in rapidly cooled alloys can exhibit diffusivity 10^4∼8 times faster than that in regularly annealed GBs [11]. Markedly, plugging the same measurement temperature (500 K) into Equation (1) yields a boost factor of 6.5*10⁵, which is in line with experiments. It is also worth noting that the diffusions in GBs are believed to be mediated by free volumes [39,40]; however, the negligible free volume variations seen in Figure 3 indicate a different picture for non-equilibrium GBs. To unravel the underlying physics, we examine the displacement fields for the elementary atomic rearrangements retrieved from energy landscape sampling (details in Supplementary Materials, Fig. S2). It is found that the unit processes of particle reconfigurations are in general more collective and accompanied with smaller magnitude of displacements in a higher-energy metastable state than that in a lower-energy state (Figure 4(a1) vs. (a2)). Figure 4(b) shows the Euclidean norm distributions for the atomic displacements at different processing stages. It is evident that a higher-energy metastable GB exhibits a more extended tail distribution on the left side, indicating a rougher energy landscape with higher fraction of easily accessible and low-cost reconfiguration processes. Such a free volume-insensitive and energy landscape-driven picture closely resembles the excitations in metallic glasses [41,42].

Figure 4. (a1-a2) Displacement fields (white arrows) of two exemplified elementary atomic rearrangements events inside GBs in a high energy state (C-1300 K), and a low energy state (H-0 K), respectively. (b) Euclidean norm distributions of GBs’ atomic rearrangements at different processing stages.

In addition to the elementary atomic reconfigurations discussed above, we further quantify the overall microstructural evolution of GBs during the cooling stage. Specifically, we calculate the average square atomic displacement between two successive ISs on the fly as: (2) $\begin{array}{rl}⟨d^2⟩& \equiv \frac{1}{N_{non-FCC}}\sum _{i=1}^{N_{non-FCC}}[{(x_i^n-x_i^{n-1})}^2\\ & +{(y_i^n-y_i^{n-1})}^2+{(z_i^n-z_i^{n-1})}^2]\end{array}$(2) where $(x_i^n,y_i^n,z_i^n)$ represents the atom #i's Cartesian coordinate in the current frame of IS, while where $(x_i^{n-1},y_i^{n-1},z_i^{n-1})$ represents its coordinate in the previous IS frame. $N_{non-FCC}$ represents non-FCC atom numbers, as an effective measure of particles in GB. As seen in Figure 2(a2), the average atomic displacement at high T is comparable with nearest neighbor distance ($r_{NN}$), suggesting a drastic structural variation; while at low T its value is rapidly decaying. Here we borrow the spirit of Lindemann criterion as a characteristic threshold of structural change. The Lindemann criterion can vary between 0.05∼0.20 [43,44] across different systems, and here we adopt the value of 0.08 retrieved from a recent systematic study on both 2D and 3D systems [45]. The corresponding temperature at $\sqrt{⟨d^2⟩}$/$r_{NN}$ = 0.08 can thus be regarded as a critical structural transition temperature T_tr, above which the GB's configurations and properties are dynamically evolving, while below which they would present an enhanced metastability. This is consistent with the energetics inspection in Figure 2(a1), where E_IS descends mostly (∼90%) above T_tr, compared with only 10% further drop below it. Such a measure can also robustly apply to other GBs, as supported by Figure 2(c) and the inset plot, where the Lindemann extraction and the 10% E_IS descending line are almost always overlapping.

To probe the correlation between a given GB and its T_tr during the fast-cooling stage, and to better contrast the relaxations in different GBs, in Figure 5(a) we plot the rescaled IS energy variations of the group of <100> STGBs, ${\hat{E}}_{IS}(C-T)$, which is defined as: (3) ${\hat{E}}_{IS}(C-T)=\frac{E_{IS}(C-T)-E_{IS}(C-0K)}{E_{IS}(C-1300K)-E_{IS}(C-0K)}$(3) where ‘C’ refers to cooling and ‘T’ represents the temperature. Note that a few low-angle GBs are excluded in Figure 5(a), and it will be discussed later.

Figure 5. (a) ${\hat{E}}_{IS}(C-T)$ for different <100> STGBs. The data for each GB is colored according to its pre-processing energy at H-0 K. T_tr is measured when ${\hat{E}}_{IS}(C-T)$ reaches 10%, as marked by the green line.(b) The correlation between E_IS(H-0 K) and T_tr for various GBs. A few outlier points labeled by the gray filled stars correspond to low angle GBs shown in c1-c5 (H-0 K configurations), whose misorientation angles are 12.7°, 16.3°, 18.9°, 22.6°, and 73.7°, respectively.

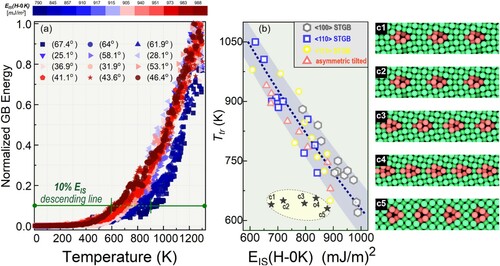
As seen in Figure 5(a), in general the curves are rather steep at high temperatures and become much flatter at low temperatures. However, different GBs show different energy variation rates and the entire cluster of curves span into a crescent-shaped region. If one colors the curves according to the GBs’ pre-processing energy $E_{IS}(H-0K)$, then a clear trend reveals by itself: the curves associated with lower $E_{IS}(H-0K)$ values (more blue) tend to be leaning toward the right edge, suggesting narrower windows for the changes of atomic structures and properties during the fast cooling stage. To be more quantitative, the T_tr of a GB is measured by the intersecting point between its ${\hat{E}}_{IS}(C-T)$ curve and the afore-mentioned 10% energy descending line (green line in Figure 5(a)). Figure 5(b) shows the correlations between $E_{IS}(H-0K)$ and T_tr, where a clear monotonic correlation exhibits. This notable finding indicates that, as long as a GB’s ground-state energy is known, one can then predict the tunability of its metastable states when subjected to ultrafast thermal cycle.

We would like to emphasize that, due to the non-equilibrium nature, in principle there could be various ways of defining the T_tr (e.g. cooling stage extraction vs. heating stage extraction) and correlating it with differently assessed $E_{IS}$ (e.g. ground state H-0 K vs. post-processing state C-0 K). More details are shown in Supplemental Materials, Fig. S3. Here we focus on the cooling stage and the $E_{IS}$ at H-0 K state for the following considerations: (i) In many non-equilibrium processing techniques, such as ultra-fast laser irradiation or additive manufacturing, the final step and arguably the most properties-determining step is the rapid cooling stage. Therefore, we believe the cooling stage should be more meaningful than the heating stage; (ii) Compared with any other non-equilibrium states during or after the extreme thermal stimuli, H-0 K samples represent the ground states that can be unambiguously obtained both in experiments by slow annealing and in atomistic modeling by well-defined protocols [13], making them as good reference states.

To further examine the universality of such correlation, in Figure 5(b) we also add other GBs considered in the present study, including a number of <110> and <111> STGBs, as well as some asymmetrically tilted GBs. Evidently most data points fall into a narrow band, indicating a strong and universal correlation between the two variables. It is known that Cu has a medium-to-low stacking fault energy, and to further assess the applicability of the hereby obtained results we also investigate a group of GBs in Ni [46], a system with relatively higher stacking fault energy. A similar correlation persists there (Fig. S4 in Supplementary Materials), which gives reason to expect the present study may apply to other materials as well.

4. Conclusion

We have demonstrated that the energetics and kinetics evolution of metastable GBs under extremes are very different from those in equilibrium or near-equilibrium states. Free volume only plays a minor role here, and the evolution is mainly driven by disorder and rough energy landscape. Importantly, a universal scaling is observed between the GBs’ inherent structure energies and their T_tr during the rapid cooling stage. The discovery herein is noteworthy, not only because it enables an increased control over how the metastable microstates and properties of GBs can be effectively tuned in advanced processing such as additive manufacturing and fs-laser irradiation, but more critically it suggests the importance of E_IS as a robust parameter to delineate the complex relaxation behaviors of GBs under non-equilibrium environments. There is already evidence that the energetics of GBs are more effective than their detailed morphologies in determining the system’s strength [47,48] and mobility [47]. Our present study therefore lends further credence to such a notion. Note that the significance of E_IS is well appreciated in amorphous materials [42,48,49]. It has been quantified that, regardless of the samples’ processing histories and detailed configurations, as long as they exhibit similar E_IS then their mechanical and kinetic properties are close to each other [50]. Considering many similarities between GBs and glasses [10,51,52], one may believe E_IS would play a decisive role in the performance of metastable GBs.

Admittedly, there are new questions prompted. Figure 5(b) contains a few outliers (filled stars), whose T_tr do not exhibit strong dependence on $E_{IS}(H-0K)$. This may indicate the low-angle GBs consisting of dislocation arrays (Figure 5(c)) would present qualitatively distinct responses to extreme stimuli compared with those high-angle 2D planar GBs. The underlying physics for such fundamental difference, however, yet remains to be explored. In addition, to highlight the impact of microstructural metastability, this work does not present complications resulting from chemical complexity. While single-element model can well capture many important physics relevant to real alloys [51,53,54], we also realize that solutes may largely impact GBs’ metastability [55,56] and impose complex chemo-thermo-mechanical coupling. Last but not least, in the present study we only focused on extreme thermal stimuli but did not introduce any global mechanical driving forces introduced in the simulations. This sets a distinction both from the conventional grain coarsening behaviors, where the capillary force often serves as the main driver to the motion of curved GBs; and from many previous atomistic modeling studies [21,22,57,58], where an artificial bias/driving force is applied to the simulation to extract the structures and velocity/mobility of GBs when a steady state is reached. In other words, the thermo-mechanical coupling effects on the metastable GBs still remain unknown. These challenges would warrant future studies.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This project was funded by National Science Foundation (NSF), Division of Materials Research (DMR), with the grant number of 1944879.