First-principles core energies of isolated basal and prism screw dislocations in magnesium

Abstract

We use first-principles energy density method (EDM) to calculate atomic energies for isolated $〈a〉$-type basal and prism screw dislocation cores in Mg and compute line energies and core energy differences. The atomic energy distribution in the dislocations reflect the slip in the cores and the elastic energy further afield. Line energies are computed by summing up atomic energies, from which core energies and energy differences are straightforward to determine. We compare our results with two different classical potentials.

GRAPHICAL ABSTRACT

IMPACT STATEMENT

This work is the first exact, direct calculation of core energies of isolated dislocations using density functional theory via atomic energies, applied to core energy differences in magnesium.

Keywords:

• Dislocation core
• line energy
• density-functional theory
• energy density method

Dislocations are important line defects in crystalline materials that impact a wide variety of material phenomena such as mechanical strength and plastic deformation in metals [1,2], gate leakage and carrier mobility in semiconductors and electronic devices [3–5], embrittlement resistance and hydrogen trapping in electrochemical processes [6,7], and atomic diffusion and segregation [1,8,9]. Dislocations have a long-range displacement field and a core with local abrupt change in lattice structure which controls how the dislocation behaves and interacts with other defects. The energy per length of a dislocation $E_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{l}\mathrm{o}\mathrm{c}}$ is defined in a cylinder of radius r, as the sum of the logarithmic elastic energy and core energy $E_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}$ (1) $E_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{l}\mathrm{o}\mathrm{c}}=\frac{K{b}^2}{4\pi }\ln \frac{r}{r_0}+E_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}},$(1) where $r_0$ is the estimated size of the core, b is the Burgers vector, and K is the ‘energy factor’, a function of the elastic constants.¹ The core energy $E_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}$ is difficult to compute analytically due to the failure of elasticity theory in the core region, however.

The core energy $E_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}$ contains information essential to understanding dislocation core structure and line tension, as well as stability, dissociation or splitting, motion and interactions of the core. The unusual cross-slip of $〈c+a〉$ dislocations between pyramidal planes in Mg is controlled by the core energy difference in pyramidal I and II planes as the elastic energies are the same [10]. In situ straining experiments of BCC Fe found that dislocation shapes in the material deviate from theoretical predictions based on elastic calculations, suggesting that dislocation core energies can refine prediction of dislocation shapes at the vicinity of the screw orientation [11,12]. The STEM-HAADF observation of Mg-doped GaN suggests that the $〈c+a〉$ dislocation dissociation is influenced by the core energy [13]. In addition, the core energy makes important contributions to the line energy, which explains a variety of phenomena like dislocation bowing [10], the formation of junctions [14] and the shape of dislocation loops [15]. Dislocation core energies also provides inputs and insights for other models or simulations, such as discrete dislocation dynamics (DDD) [16–18] and phase field dislocation dynamics (PFDD) [19–21].

There has been a decades-long interest in building models that predict dislocation energies both efficiently and accurately in various systems. The computationally simplest approach is an analytical model for dislocation line energies derived from linear elasticity, which has been applied to graphite [22], polyethylene crystals [23], and Ni-based alloys [24]. In order to correct for nonlinear displacements in the core of the dislocation, Peierls–Nabarro (PN) models assume sinusoidal interactions between neighboring planes of atoms in the core region, which has been applied to Ni [25], Ag [25], Cu [25,26], Au [26], Mo [27], Zn [26], Be [26], and Cu-Al alloys [25]. However, classical PN models are inaccurate for narrow dislocation cores, leading to the development of semidiscrete variational generalized PN models [28], as applied to Al [29,30], Si [28], and Mg alloys [31]. To account for nonlinear displacements more generally, all-atom methods, such as empirical potentials, are used to compute core energies for a variety of systems: Al [32], W [33], Fe [17], Ta [34], Nb [35], Ti [36,37], Mg [38–41], Si [42], MgO [43], GaN [44] and Ni-Ti alloy [45]. Monte Carlo models are also used to model dislocation core energy numerically, for example, by assessing the dislocation pair formation probability in the case of hard disks [46], or the effect of hydrogen on dislocation line energies in bcc Fe [47]. Increasing the accuracy of the interatomic interactions from empirical potentials requires electronic structure-based methods, but at the expense of increased computational complexity. Tight-binding models have been applied to study dislocation core energies in Mo [48] and GaN [49]. First-principle approaches based on density functional theory (DFT) have been used to investigate screw dislocations in Ti [37] and GaN [50], but core energy differences have to be compared using classical potentials in the first case. Orbital-free DFT can compute Al [51,52] and Mg [53,54] core energies at the expense of accuracy. Dislocation dipoles in DFT are used to study compact screw dislocation cores in bcc Fe [55–57] as well as other bcc transition metals (V, Nb, Ta, Cr, Mo, and W) [58], in which the core energies are deduced using a method combining with DFT and anisotropic elasticity.

Although many ways have been proposed to calculate dislocation energies as listed above, several issues remain to be solved. First, non-ab initio methods lack accuracy or universality, and the complexity of dislocation cores exacerbates this. However, standard ab initio methods that model isolated dislocation cores nominally only have access to the total energy of the supercell, and the core energy is difficult to separate from spurious contributions from the supercell boundary or free surfaces. Alternately, ab initio methods for non-isolated dislocation cores require dislocation dipoles or quadrupoles periodically in a supercell to cancel long-range displacement fields and boundary effects, a technique that risks dislocation annihilation during geometry relaxation, and conditional convergence issues with image interactions [59] requiring corrections and finite-size error studies [55]. In principle, dislocation core properties are localized and should only be determined by the atoms in the vicinity of the core, which suggests that a spatial partitioning of the energy would allow for computation of dislocation line energies for arbitrary dislocations.

Here, we use a DFT-based energy density method (EDM) proposed by Chetty and Martin [60] and developed by Yu et al. [61] to study energies of isolated basal and prism screw dislocation cores in magnesium. With their light weight and high specific strength, Mg alloys are good candidates for structural materials, but their poor ductility and formability [62–65] limit their application. The core energy difference between basal and prism screw dislocations controls cross-slip and influences the ductility of Mg [66]. The EDM decomposes the total DFT energy into atomic contributions, where uniqueness of the decomposition is ensured by integration of DFT energy density components over volumes that preserve gauge independence. With EDM, the investigation of energies of dislocation cores or other defects becomes straightforward as the defect energy is simply the sum of the atomic energies within the defect. We find line energies and core energy differences, and compare with an EAM interatomic potential by Sun et al. [67] and a MEAM interactomic potential by Wu et al. [68]. As our method relies only on DFT without empirical data or external assumptions, it is applicable to other defects that DFT can model.

In order to handle the long-range displacement field of isolated screw dislocations in Mg, the dislocation geometries were relaxed using flexible boundary conditions (FBC) [69] with the lattice Green's function (LGF) [70,71]. The DFT supercell contains a single dislocation, divided into three regions: region I surrounding the dislocation core, region III atoms near the supercell boundaries, and an intermediate region II in between. With FBC, the system is relaxed iteratively: (1) relax forces in region I while regions II and III atoms are fixed, and (2) update all atom positions from the LGF based on forces from region II atoms, until atomic forces in region I and II are less than 5 meV/Å. The screw dislocation can be placed inside a periodic cell without adding vacuum, and by using partial supercell vectors ($\frac{25}{2}a\left[1\overline{1}00\right]\times \frac{21}{2}c\left[0001\right]\times \frac{a}{3}\left[11\overline{2}0\right]$ for 525 atoms) the periodic boundaries are more ‘bulklike’ with the largest deviations at the corners; this ‘domain boundary’ approach ensures that regions I and II accurately represent the dislocation core environment. In our study, we use EDM energies for atoms in regions I and II, and use elasticity theory for energies of atoms outside the range of the DFT supercell. In this way, we acquire full knowledge of dislocation line energy characterized by Equation (1(1) $E_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{l}\mathrm{o}\mathrm{c}}=\frac{K{b}^2}{4\pi }\ln \frac{r}{r_0}+E_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}},$(1) ), and eliminate any contributions from region III, which extends out to the supercell domain boundaries.

The EDM calculations are performed using the EDM code by M. Yu et al. [61], which is implemented under the framework of the Vienna ab initio simulation package (VASP, version 4.6.36) [72–75], a DFT-based code using a plane-wave basis. The projector augmented-wave (PAW) method and the generalized-gradient approximation of Perdew and Wang [76] are used for the exchange-correlation potential. The $2p$ and $3s$ electrons are treated as valence while other electrons are treated as frozen in the core. A plane-wave cut-off energy of 370 eV is used throughout the calculations which ensures energy convergence of 0.1 meV/atom. Gamma-centered k-point meshes of $1\times 1\times 16$ are employed with 16 k-points along the dislocation line, along with an order-1 Methfessel–Paxton smearing [77] of 0.5 eV to represent electronic density of states. We compute the charge densities and energy densities in the EDM calculations on a real-space grid of $896\times 700\times 40$ and $700\times 896\times 40$ for basal and prism cores, respectively.

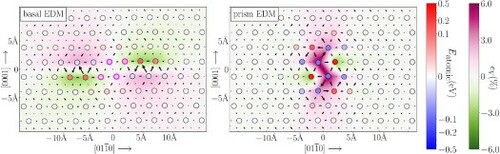
The atomic energy distribution in the Mg basal screw dislocation core from EDM in Figure 1 shows defect energies arising from volumetric strain and local slip. The length of arrows show differential displacements along the line direction (perpendicular to the page) between neighboring atoms in the dislocated lattice compared to those in the bulk. The differential displacements are modulo b/2 to identify atoms in the partial cores, separated by stacking fault. In the core, atoms with energies significantly higher or lower than the bulk atomic energy appear in two separated clusters spread along the $\left[1\overline{1}00\right]$ direction symmetric to the center, where the magnitudes of volumetric strains and differential displacements also reach maxima, as the basal core dissociates into partials [38]. In these partials, our data reveal that volumetric compression leads to an increase in atomic energies while tension leads to a decrease. The components of EDM atomic energies (Figure S3) show that compression decreases classical Coulomb and exchange-correlation energies while increasing kinetic energies. Compressed volumes increase energy densities as electrons are closer, leading to stronger Coulombic and exchange-correlation interactions, and increasing the electron momenta and kinetic energy; however, it also shrinks the integration volume. The net change in each EDM energy component depends on which factor dominates; the reverse is true for tension. Between the partials, four atoms—marked with magenta in Figure 1—correspond to the stacking fault area. Our EDM calculation shows that these atoms have energies of $-19$, 32, 23 and $-21$ meV, respectively, from left to right and top to bottom in the figure; if these are scaled by the planar area of 11.75 Å${}^2$, the ‘stacking fault energy’ of 21.4 mJ/m${}^2$ is consistent with the basal fault energy of 34 mJ/m${}^2$ reported in [38]. Away from the core, atomic energies decrease as distance from the core region increases.

Figure 1. Geometries of basal screw $\frac{1}{3}〈11\overline{2}0〉$ (left) and prism screw $\frac{1}{3}〈11\overline{2}0〉$ (right) dislocation cores in Mg computed from first principles (top) and two classical potentials Wu MEAM [68] (middle) and Sun EAM [67] (bottom). The dislocation line is perpendicular to the page, and atomic columns have blue-to-red face shading for their atomic energies. Volumetric strains are shown in green-to-purple color contours around atoms, and differential displacements (modulo b/2) between columns are shown with arrows to reveal the partial core structures, showing large distortion near cores and that the core splits into partials separated by stacking fault. In the top left figure, magenta circles mark the atoms in the stacking fault region between dissociated partials.

Alternately, the Mg prism core in Figure 1 shows a complex environment where atoms see mixed energy contributions from different stacking fault components. The prism core is metastable [38], corrugated and spreads rather than completely splitting; differential displacements show leading and trailing partials that are centrosymmetric about the dislocation center. EDM data show atomic energies that are lower than the bulk atomic energy in the corrugated tensile area connecting the two partials due to the sharp decrease in EDM kinetic energies, which matches the basal core (Figure S4). Adjacent to the tensile area, each partial contains four core sites: two with low energies (near and far from center, called sites 1 and 3 in [66]) and two with high energies (near and far from center, called sites 2 and 4 in [66]). There are two types of stacking faults in the prism core: ‘easy’ and ‘hard’ that differ by the choice of slip planes. Density of states overlap calculations [66] reveal that the low energy core sites are correlated with stacking fault sites near the easy fault plane, and the high energy core sites are correlated with stacking fault sites near the hard fault plane. Hence, the low energies in the core sites come from an easy fault, while the high energies in the core sites from a hard fault. Similar to the basal core, the atomic energies decrease when moving away from the core region.

Figure 1 also shows that Wu MEAM [68] better reproduces the geometry and energy distributions of the dislocation cores compared with Sun EAM [67]. In the basal core, similar to results in DFT geometries, both potentials predict core splitting, along with high atomic energies in the partials and lower energies in the stacking fault between the partials, as well as decaying energies moving away from the core region. Wu MEAM predicts a larger distance between the partials compared with Sun EAM and DFT geometries, while Sun EAM predicts a more compact core with smaller volumetric strains and atomic energies. For the prism core, both Wu MEAM and EDM predict low energy sites in the corrugated core despite the differences in spreading, but the Sun EAM does not produce low energy sites in the core. Generally, the Wu MEAM results show a closer match with DFT and EDM results.

Figure 2 compares EDM atomic energies with elastic energies, showing consistency between EDM and anisotropic elasticity in region II. Anisotropic elastic atomic energies are computed from the local atomic strain after FBC relaxation using the DFT stiffness constants. Both basal and prism cores show small disagreements between EDM and elastic atomic energies in region II, with average of $\sim 0.2$ meV/atom and standard deviation of $\sim 1.6$ meV/atom in both cases. However, the energy differences increase in region I, due to failure of elasticity theory in dislocation cores. The negative values in region I are atoms on the basal stacking fault or the low energy prism core sites, while the positive values are atoms on the dislocation partials or the high energy prism core sites. Region III also shows larger differences, as the EDM atomic energies are spuriously large at the edges of the supercell where the dislocation displacement produces domain boundaries. As we plot distance from the partials, regions I and II and regions II and III show overlaps, which have similar deviations from elasticity. This confirms that our choices for regions I, II and III in FBC method lead to sufficient separation and are not corrupting the final results.

Figure 2. Difference between EDM and anisotropic elastic atomic energies $E_{\mathrm{a}\mathrm{t}\mathrm{o}\mathrm{m}\mathrm{i}\mathrm{c}}^{\mathrm{E}\mathrm{D}\mathrm{M}}-E_{\mathrm{a}\mathrm{t}\mathrm{o}\mathrm{m}\mathrm{i}\mathrm{c}}^{\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{s}}$ of basal and prism screw dislocations as a function of minimal distance from dislocation partials (left) and the perspective with narrower energy range (right). Data points corresponding to atoms in regions I, II and III in both geometries are shown in blue, black and green symbols, respectively. The averages of $E_{\mathrm{a}\mathrm{t}\mathrm{o}\mathrm{m}\mathrm{i}\mathrm{c}}^{\mathrm{E}\mathrm{D}\mathrm{M}}-E_{\mathrm{a}\mathrm{t}\mathrm{o}\mathrm{m}\mathrm{i}\mathrm{c}}^{\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{s}}$ of region II atoms are marked with black dashed lines in each zoomed-in figure, and the areas spanning over one standard deviation from the average are shown with a light gray background. The energy differences fluctuate near zero in region II while diverging in regions I and III in both geometries, indicating good agreement between EDM and anisotropic elasticity theory in elastic regions.

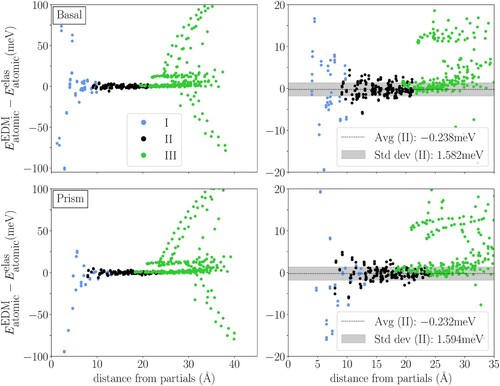
Figure 3 compares the line energies $E_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{l}\mathrm{o}\mathrm{c}}\left(r\right)$ of basal and prism screw dislocations computed using EDM, Wu MEAM and Sun EAM atomic energies, showing consistency with the elastic part of Equation (1(1) $E_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{l}\mathrm{o}\mathrm{c}}=\frac{K{b}^2}{4\pi }\ln \frac{r}{r_0}+E_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}},$(1) ) far from the center, and deviation from that near the center. Atomic energies are summed within a cylindrical space of radius r centered at the dislocation line to calculate line energy $E_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{l}\mathrm{o}\mathrm{c}}\left(r\right)$ as a function of logarithmic radius $\ln \left(r/b\right)$ from Equation (1(1) $E_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{l}\mathrm{o}\mathrm{c}}=\frac{K{b}^2}{4\pi }\ln \frac{r}{r_0}+E_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}},$(1) ). We use EDM atomic energies for atoms in regions I and II and anisotropic elastic energies for region III which goes beyond the EDM supercell. The line energies are linear with logarithmic radius $\ln \left(r/b\right)$ for $\ln \left(r/b\right)>2$, and we do least squares fitting to the data with $\ln \left(r/b\right)$ between 2.5 and 4.5 for the slopes and vertical intercepts, as listed in Table 1. Theoretical slopes $K{b}^2/4\pi$ can be calculated from anisotropic elasticity theory using elastic constants; for $〈a〉$-type screw dislocations in an HCP lattice [2], $K=\sqrt{C_{44}{C}_{66}}$. Note that slopes are different for the same core calculated with different methods because of differences in elastic constants, but within the same method slopes are the same for basal and prism cores because they have the same Burgers vector and line direction. The fitted slopes agree well with theoretical slopes, indicating consistency with the elastic part of Equation (1(1) $E_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{l}\mathrm{o}\mathrm{c}}=\frac{K{b}^2}{4\pi }\ln \frac{r}{r_0}+E_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}},$(1) ).

Figure 3. Line energy ($E_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{l}\mathrm{o}\mathrm{c}}$) of basal and prism screw dislocations in Mg, calculated using EDM and anisotropic elasticity theory (EDM, elas) (left), Wu MEAM (middle) and Sun EAM (right) interatomic potentials. The energies are shown as a function of logarithmic distance from the center r in units of Burgers vector b. For (EDM, elas), atomic energies in regions I and II are determined using EDM while those in region III are determined using anisotropic elasticity. The overlapping parts of regions I and II, as well as regions II and III are highlighted with cyan backgrounds. For large r, the energies for both basal and prism screw dislocations have linear relationships with $\ln \left(r/b\right)$ and the slopes are the same. The core energy difference $\mathrm{\Delta }{E}_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}$ between the two dislocations can be found from the difference in vertical intercepts (Table 1).

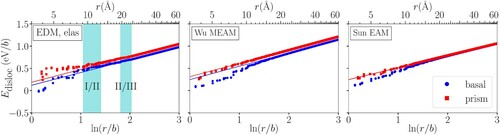
Table 1. Properties associated with line energies of basal and prism screw dislocations in Mg computed using EDM (top two rows) and interatomic potentials and orbital-free DFT (bottom rows) as shown in Figure 3. For EDM, we compare using EDM energies for regions I and II [EDM (I,II)] and using EDM only for region I [EDM (I)]. Dislocation energies grow as $\ln \left(r/b\right)$ far from the core, with a $K{b}^2/4\pi$ prefactor and a constant core energy $E_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}$, c.f. Equation (1(1) $E_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{l}\mathrm{o}\mathrm{c}}=\frac{K{b}^2}{4\pi }\ln \frac{r}{r_0}+E_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}},$(1) ). Difference in core energies per unit length $\mathrm{\Delta }{E}_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}$ is estimated by taking the difference between vertical intercepts of prism and basal curve extrapolations.

	$K{b}^2/4\pi$ (eV/b)			$E_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}$ (eV/b)		$\mathrm{\Delta }{E}_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}$ (eV/b)
	Elasticity theory	Basal	Prism	Basal	Prism	(Prism − Basal)
EDM (I,II)	0.2851	0.2860	0.2860	0.1199	0.1883	0.0684
EDM (I)	0.2851	0.2860	0.2860	0.1632	0.2268	0.0637
Wu MEAM	0.3004	0.3004	0.3005	0.2461	0.3120	0.0659
Sun EAM	0.2707	0.2695	0.2695	0.2457	0.2464	0.0006
OFDFT [54]	0.361	–	–	0.425	–	–
DFT-drag [78]	–	–	–	–	–	<0.0614
DFT-NEB [79]	–	–	–	–	–	$<$0.075

Table 1 gives the dislocation line energies and core energy differences $\mathrm{\Delta }{E}_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}$ from EDM, Wu MEAM, and Sun EAM. The elastic contributions to the line energies are the same for basal and prism dislocations, thus the difference in vertical intercepts is the difference in core energies. We confirm that the prism core is less stable than the basal core. For the EDM $\mathrm{\Delta }{E}_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}$, we calculate both EDM and anisotropic elastic energies for region II atoms and compute the core energy differences separately, getting close results of 0.0684 eV/b and 0.0637 eV/b respectively, which shows that the EDM core energy difference is insensitive to whether EDM or elastic atomic energies are used for region II atoms. Had we chosen to instead simply subtract the total energy of the two supercells—as in this case they are the same size—we get 0.1178 eV/b, which is nearly double the EDM value due to region III differences. Orbital-free density-functional theory [54] gives a significantly higher core energy for the basal dislocation of 0.425 eV/b, which suggests that while the core geometry may be similar to that of standard density-functional theory, orbital-free methods can have difficulty producing accurate energetics. Itakura et al. [78] used a ‘drag method’ to change basal into prismatic cores in quadrupole supercells; fitting three different sized supercells to infinite separation produces a closer, but still inaccurate energy barrier of 0.0614 eV/b, as it is supposed to be no less than the core energy difference. Tsuru and Chrzan [79] used nudged-elastic band to examine the barrier for basal slip along the prismatic plane; after correcting for periodic image effects, they compute a barrier of 0.075 eV/b. The differences in the periodic calculation may be caused by dislocation interactions on the core fields as the cores are neither fully compact nor have the same size. For the interatomic potentials, Wu MEAM predicts $\mathrm{\Delta }{E}_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}$ of 0.0659 eV/b which agrees well with the EDM 0.0684 or 0.0637 eV/b, while Sun EAM potential predicts a much smaller 0.0006 eV/b.

First-principles EDM calculations of isolated $〈a〉$-type basal and prism screw dislocation core geometries in Mg are able to compute accurate core energy differences, which can be used to model screw dislocation motion by cross-slip. It provides a simple approach for computing dislocation energies from first principles for arbitrary dislocation types, in a wide range of materials using standard DFT methods. Furthermore, it can check for possible spurious effects of boundary conditions by comparison with elasticity. EDM can provide more accurate dislocation core energies for DDD simulations, which is essential for predicting critical stresses that determine several phenomena such as how dislocations loop or cut precipitates, or how dislocation junctions form and break. Also, EDM data can improve atomistic potential development for modeling complex defects. Lastly, using the energy distribution calculated by EDM helps simulate more complex systems involving multiple defects as well, for example, solute-core interaction or alloys, through only one single calculation.

Acknowledgments

The authors thank Vikram Gavini and Sambit Das for helpful discussions of their orbital-free density functional theory work. This work made use of the Illinois Campus Cluster, a computing resource that is operated by the Illinois Campus Cluster Program (ICCP) in conjunction with the National Center for Supercomputing Applications (NCSA) and which is supported by funds from the University of Illinois at Urbana-Champaign.

Disclosure statement

The authors declare no competing financial or non-financial interests.

Additional information

Funding

This work is sponsored by the NSF program [grant number MPS-1940303].

Notes

1 In isotropic systems, for screw dislocations $K=K_s=G$ while for edge dislocations $K=K_e=G/(1-\nu )$, where G is the shear modulus and ν is the Poisson ratio.