Evaluation of phase stability and diffusion kinetics in novel BCC-structured high entropy alloys

Abstract

The diffusion kinetics of the BCC-structured high-entropy alloys (HEAs) is studied experimentally for the first time. First, the literature data regarding the transition-metal based, single-phase, BCC-structured HEAs is re-evaluated using the state-of-the-art, HEAs-dedicated TCHEA4 thermodynamic database, signalizing the need for further reassessment of the literature data accumulated during the last decade. The selected Al-Cr-Fe-Mn-V system was used for the interdiffusion experiments. The concentration profiles were evaluated using the numerical combinatorial approach, revealing surprisingly fast diffusion kinetics. The comparison with the available diffusion data for conventional BCC alloys supports recent findings regarding the lack of the ‘sluggish diffusion’ in HEAs.

IMPACT STATEMENT

The first-ever experimental study of interdiffusion in BCC-structured high-entropy alloys is conducted, revealing fast diffusion kinetics and providing a further argument against the presence of sluggish diffusion effect in HEAs.

GRAPHICAL ABSTRACT

KEYWORDS:

• Diffusion
• CALPHAD
• phase diagram
• thermodynamics
• high-entropy alloys

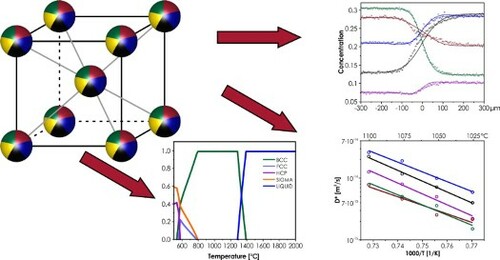
1. Introduction

The high-entropy alloys (HEAs), initially developed back in 2004 [1,2], have become one of the most extensively researched directions of studies in materials science, carrying a promise of obtaining next-generation, structural materials for high-temperature applications. For years believed to possess a number of unique features [3,4], regardless of the actual extent of high-entropy effects [5,6], over the years they have proved to be a viable alternative to state-of-the-art, conventional alloys, with multiple compositions displaying excellent high-temperature corrosion behavior [7–9], good fatigue-resistance [10], complex and tailorable deformation mechanism [11], and most importantly, an excellent thermomechanical behavior [5,12–14]. The common denominator for these latter compositions, especially with regard to transition metal-based HEAs (TM-HEAs), is the presence of a multiphase structure [5,12–16], with body-centered cubic phases (BCC) being of especially crucial importance. However, despite these observations, our understanding of the high-temperature behavior of BCC-structured HEAs, especially in terms of phase stability and diffusion kinetics, remains extremely limited. While the diffusion in FCC-structured HEAs (face-centered cubic) has been relatively thoroughly investigated during last few years [17–27], even allowing for negative verification of the so-called ‘sluggish diffusion effect’ theorem [20,28], which turned out to be associated primarily with the presence of the particular elements in the system e.g. Mn rather than a high number of elements, the diffusion in BCC structure, much more relevant from the application point of view, has never been previously studied on the experimental grounds. The main limiting factor there was likely the fact that most of the early BCC, solid solution-structured HEAs systems had been based mainly on the refractory elements (RF HEAs), characterized by prohibitively high Tamman and melting temperatures [29], rendering the diffusion studies with the use of conventional techniques highly problematic. This has changed with the studies of Senkov et al. [30,31] and Tazuddin et al. [32], who carried out extensive screening procedures with the use of CALPHAD approach (CALculated PHAse Diagrams), revealing a number of stable, non-refractory, BCC-structured HEAs. However, despite their comprehensive nature, both these studies were limited by the quality of early thermodynamic databases, which in turn led to a relatively low level of agreement between theoretical and experimental data [32], bringing questions regarding the overall value of such an approach.

The presented study is intended to address the above-mentioned unknowns, both in terms of our ability to predict the formation of single-phase BCC solid solutions and their transport properties. These objectives are achieved by re-evaluating the single-phase, BCC-structured system suggested by the earlier works [30–32], with the use of the most up-to-date thermodynamic databases, followed by the very first experimental evaluation of the diffusion behavior in body-centered cubic HEAs.

2. Theoretical assessment of phase stability

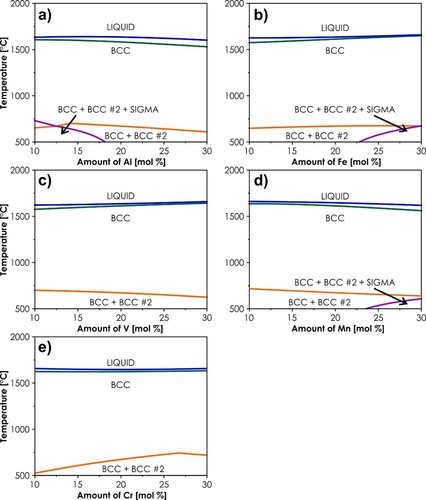
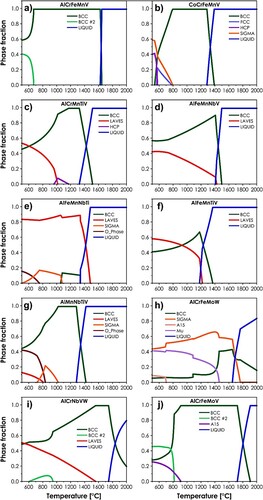
Firstly, the temperature-dependent phase stabilities of a total of 10 equimolar systems classified by both Senkov et al. [30,31] and Tazuddin et al. [32] as single-phase, BCC ones, were examined with the use of Thermo-Calc software, utilizing the latest HEA-dedicated TCHEA4 database [33]. The results are presented in Figure 1. As can be seen, only 3 out of 10 evaluated alloys are predicted to be characterized by the single-phase, BCC structure at temperatures exceeding 1000°C, namely AlCrFeMnV, CoCrFeMnV, and AlCrFeMoV, with additional 2 systems exhibiting single-phase, solid-solution structure in a much more limited range: AlCrMnTiV and AlCrNbVW. The comparison with the available experimental data yields nearly perfect agreement, as both AlCrFeMnV and CoCrFeMnV alloys have been proved to form single-phase structures [32] (also in agreement with our results, see Supplementary Figure S1), while the AlCrMnTiV alloy was found by Tazzudin et al. to exhibit the presence of BCC + HCP (hexagonal dense-packed) phases at 900°C [32], almost matching the predictions from Figure 1c. On the other hand, using the TCHEA4 database, one can arrive at the conclusion that the other five systems, previously predicted in literature to provide single-phase structures, are now expected to form multiphase ones. This shows how drastic progress had been made in terms of the HEAs’ thermodynamic description during the last few years, also indicating the need for a systematic re-evaluation of the previous literature data. In this case, however, the agreement with available experimental data is rather qualitative than quantitative, as for example, the AlMnNbTiV was found in [32] to exhibit multiphase, mainly HCP structure at 900°C, rather than the BCC one predicted in Figure 1g. Therefore, it can be stated that even with the evident, significant progress in predicting capabilities of the state-of-the-art thermodynamic databases, they still exhibit major deficiencies, which should be addressed in the future.

Figure 1. Temperature vs. phase fraction results calculated by the Thermo-Calc for equimolar alloys: (a) AlCrFeMnV; (b) CoCrFeMnV; (c) AlCrMnTiV; (d) AlFeMnNbV; (e) AlFeMnNbTi; (f) AlFeMnTiV; (g) AlMnNbTiV; (h) AlCrFeMoW; (i) AlCrNbVW; (j) AlCrFeMoV.

Thanks to by far the most extensive single-phase region, the Al-Cr-Fe-Mn-V system was selected for the experimental investigation of the interdiffusion behavior with the use of diffusion couple method. The design of the diffusion couples end-members was supported by further thermodynamic considerations, with the isopleth-type phase diagrams clearly indicating the possibility of obtaining single-phase materials within a wide compositional range, Figure 2.

Figure 2. Isopleths of the Al-Cr-Fe-Mn-V phase diagram for: (a) Al; (b) Fe; (c) V; (d) Mn; (e) Cr. In all cases, all other elements are assumed to be in an equimolar ratio.

3. Materials and methods

To avoid substantial chemical differences between end-members, and therefore minimize effects connected with the composition dependence of tracer diffusion coefficients values, as well as to keep all materials within the HEAs definition, all elements were assumed to vary within a relatively narrow compositional range of 10–30 at.%: The selected end-members are presented in Table 1.

Table 1. Nominal and EDS measured compositions for the alloys used in the experiments. The melting (T_m, solidus) and Tamman (T_T) temperatures were calculated with use of Thermo-Calc software.

	Nominal composition [at.%]					Measured composition [at.%]					Temp [°C]
	Al	Cr	Fe	Mn	V	Al	Cr	Fe	Mn*	V	Tm	TT
A	20	20	20	20	20	20.7	20.5	20.3	18.4	20.1	1628	994
B	12	28	28	12	20	12.8	30.5	28.2	7.3	21.2	1668	1021
C	28	12	20	12	28	28.8	12.4	20.4	9.9	28.4	1632	997
D	20	12	28	12	28	20.6	12.9	27.7	11.0	27.9	1668	1021

*The differences between nominal and experimental content of Mn originate from the its relatively low T_m, leading to evaporation.

All studied alloys were obtained from high-purity metals (Alfa Aesar, minimum purity of 99.95% except for V: 99.7%) with the use of the induction melting method, combined with casting into copper molds to form cylindrical ingots of 6 mm diameter. All ingots were remelted 3 times to assure their homogeneity and further subjected to the homogenizing annealing at 1100°C for 48 h, under vacuum conditions, followed by fast removing of the materials from the heating zone to preserve the high-temperature phase structure. Then, from each ingot, a piece was cut and polished to metallographic quality. The prepared samples were investigated using the Scanning electron microscopy (SEM) combined with the Energy-dispersive X-ray spectroscopy (EDS) (ThermoFisher Scientific Phenom XL Desktop SEM equipped with a silicon drift detector). After confirming the single-phase character, the alloys were cut with EDM (Electrical discharge machining method) into 1 mm slices, ground, and polished. The diffusion couples were prepared by assembling together two end-members in the molybdenum holders. For studying the Kirkendall effect, small particles of thorium dioxide were placed on the surface of the initial joint of alloy samples, by using their acetone suspension. Based on the calculated melting and estimated Tamman temperatures (see Table 1), the following experimental temperatures were established: 1025, 1050, 1075, and 1100°C, with the annealing duration of 72, 48, 24, and 24 h, respectively. All experiments were carried out under vacuum conditions (10⁻⁶ Tr provided by Pfeiffer Vacuum HiPace^® 80 turbomolecular pump), with fast removal of the samples from the heating zone after the experiment’s end. The annealed couples were cut into halves and polished. The prepared samples were analyzed using SEM + EDS method (apparatus: FEI VERSA 3D with EDS analyzer), allowing extracting the concentration profiles.

Firstly, the positions of Matano and Kirkendall planes were assessed, see Table S1. For the exemplary cross-sections of the diffusion couples see Figure S2. However, it turned out that the values of Kirkendall shifts did not exceed 6 µm in all cases, making the examination of interdiffusion with the application of analytical methods, such as [34,35], extremely problematic. Therefore, the numerical approach similar as in [28] was utilized.

The theoretical model used in the analysis of the data obtained from the diffusion couples was based on the Darken formalism [36,37] and its extension by Manning [38–40], which provides a direct connection to Onsager's theory of irreversible thermodynamics [41,42]. The solved set of diffusion equations in the closed, one-dimensional system (zero flux at the boundary) was as follows: (1) $\{\begin{array}{c}{\displaystyle \frac{\mathrm{\partial }{n}_i}{\mathrm{\partial }t}}=-\frac{\mathrm{\partial }{\tilde{J}}_i}{\mathrm{\partial }x}\\ {\tilde{J}}_i\left(x^{-},t\right)={\tilde{J}}_i\left(x^{+},t\right)=0\end{array}\left(i=1,\dots ,r\right),$(1) where (2) $\begin{array}{rl}& {\tilde{J}}_i=J_i+n_i{\upsilon }^D,\\ & \sum _{i=1}^r{\tilde{J}}_i=0,\\ & J_i=-\sum _j{L}_{ij}\frac{\mathrm{\partial }{\mu }_j}{\mathrm{\partial }x},\\ & L_{ii}=\frac{n_i{D}_i^{\ast }}{RT}\left(1+\frac{2n_i{D}_i^{\ast }}{M_0\sum _k{n}_k{D}_k^{\ast }}\right),\\ & L_{ij}=\frac{2n_i{n}_j{D}_i^{\ast }{D}_j^{\ast }}{RT{M}_0\sum _k{n}_k{D}_k^{\ast }},\end{array}$(2) where x⁻ and x⁺ correspond to the left and right boundary of the system, respectively, r is a total number of elements in the system, $\widetilde{J_i}$ is the volume flux of the i-th element in the laboratory reference frame, J_i is the volume flux of the i-th element in the material's reference frame, n_i is the molar fraction of the i-th element, ${\upsilon }^D$ is the drift velocity, common for all components, $D_i^{\ast }$ is the tracer diffusion coefficient of i-th element, μ_i is the chemical potential of the i-th component, L_ij are Onsager’s phenomenological coefficients, R is the gas constant, T is temperature, and M₀ denotes the geometrical factor in Manning’s theory, equal to 5.33 for BCC structures. The thermodynamics of the system was described within the framework of the regular solid solution model: (3) $\begin{array}{rl}{G}_{mix}& =\sum _{i=1,i\ne j}^{r}4\mathrm{\Delta }{H}_{ij}^{mix}{n}_i{n}_j+RT\sum _{i=1}^r{n}_i\ln n_i\\ & =\sum _{i=1,j\ne i}^r{\mathrm{\Omega }}_{ij}{n}_i{n}_j+RT\sum _{i=1}^r{n}_i\ln n_i,\end{array}$(3) where $G_{mix}$ is Gibbs energy of a solid solution phase, $\mathrm{\Delta }{H}_{ij}^{mix}$ denotes the mixing enthalpy of equimolar binary system i and j, and ${\mathrm{\Omega }}_{ij}$ is the interaction parameter. The chemical potential can be calculated according to the formula: (4) ${\mu }_i=G+\frac{\mathrm{\partial }G}{\mathrm{\partial }{n}_i}-\sum _{j=1}^{r-1}\frac{\mathrm{\partial }G}{\mathrm{\partial }{n}_j}{n}_j.$(4)

The interaction parameters values were determined based on the modified Miedema’s scheme [43,44], optimized towards the solid solution structures (Table S2) [45]. The determination of the diffusion coefficients was possible thanks to the numerical procedure, conducted in a ‘global’ manner for each temperature i.e. all profiles from a given temperature were optimized simultaneously using the same set of diffusivities, allowing for averaging of the values and minimizing the error of determination. Further details regarding the diffusion model and numerical procedure can be found elsewhere [28].

4. Results and discussion

The exemplary profiles, both measured and fitted, are presented in Figure 3. The rest of the data can be found in Supplementary Figures S3–S6. As can be seen, the utilized procedure allows obtaining good quality of the fit, including the directions and magnitude of the up-hill effects, which further supports the correctness of the applied thermodynamic description. The determined values of tracer diffusion coefficients for each considered element and temperature are summarized in Table 2.

Figure 3. The exemplary diffusion profiles determined for the Al-Cr-Fe-Mn-V diffusion couples, both experimental and theoretical values are presented: (a) couple A-C, T = 1100°C, t = 24 h; (b) couple A-D, T = 1075°C, t = 24 h; (c) couple B-C, T = 1050°C, t = 46 h; (d) couple B-D, T = 1025°C, t = 72 h.

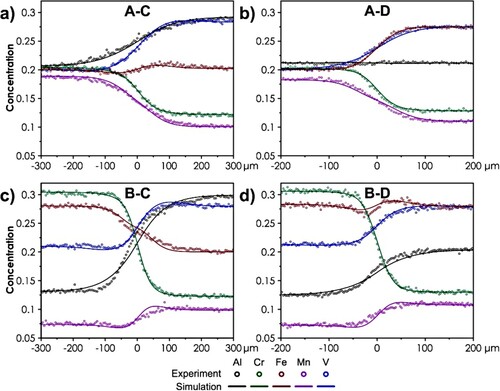
Table 2. The determined values of tracer diffusion coefficients $D_i^{\ast }$ for each experimental temperature. The values of $D_{i,0}^{\ast }$ and E_a are also provided.

		Tracer diffusion coefficients $D_i^{\ast }$ [m/s^2]
T [°C]	Time [h]	Al	Cr	Fe	Mn	V
1025	72	3.99·10^−15	1.51·10^−15	2.15·10^−15	2.22·10^−15	5.91·10^−15
1050	48	7.15·10^−15	3.59·10^−15	2.53·10^−15	5.00·10^−15	9.96·10^−15
1075	24	1.17·10^−14	5.02·10^−15	4.61·10^−15	8.01·10^−15	1.90·10^−14
1100	24	2.24·10^−14	7.76·10^−15	7.84·10^−15	1.25·10^−14	2.61·10^−14
$D_{i,0}^{\ast }$	[m/s^2]	${1.3}_{-0.3}^{+5.0}\cdot {10}^{-1}$	${9.3}_{-8.3}^{+78}\cdot {10}^{-3}$	${6.1}_{-6.0}^{+345}\cdot {10}^{-3}$	${8.6}_{-8.2}^{+159}\cdot {10}^{-2}$	${8.4}_{-8.2}^{+407}\cdot {10}^{-1}$
Ea	[kJ/mol]	336.0 ± 15.1	311.9 ± 24.9	264.5 ± 45.0	336.7 ± 32.9	302.9 ± 43.3

In order to check whether the obtained results can be considered unambiguous, and, consequently, if they represent the actual global minimum of the target function, the optimization procedure was carried out for a number of different sets of initial estimates, see Table S3. In all cases the determined values were independent on the algorithm’s starting point, proving the correctness of the utilized approach.

Based on the Arrhenius relation: (5) $D_i^{\ast }=D_{i,0}^{\ast }\exp \left(-\frac{E_a}{RT}\right),$(5) the pre-exponential factors $D_{i,0}^{\ast }$ and energies of activation E_a were also determined, see Table 2. The resulting Arrhenius-type plot is presented in Figure 4, together with the values of intrinsic diffusion coefficients determined for the respective elements. It is worth noting that the profiles from each temperature were optimized separately, and therefore the fact that the temperature dependence is well preserved, further confirms the physical soundness of the results.

Figure 4. Arrhenius plot for the Al-Cr-Fe-Mn-V system: (a) tracer diffusion coefficients; (b) intrinsic diffusion coefficients. The open points correspond to the values determined for each considered temperature, while the lines represent the linear fits.

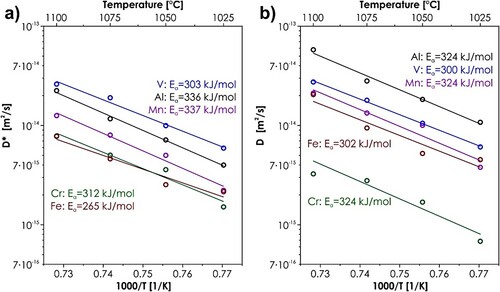
As visible, the kinetics in the Al-Cr-Fe-Mn-V can be considered relatively fast, with the values of tracer diffusivities exceeding 10⁻¹⁴ m²/s at 1100°C, being similar or slightly higher than the values reported for FCC-structured HEAs [19,20,28]. What is especially worth noticing, are the differences between tracer and intrinsic diffusion coefficients, which show how prominent the effects of thermodynamics are in this system. It can be clearly seen that while for the tracer diffusivities vanadium appears to be a faster diffusing element than aluminum, the exact opposite is true for the intrinsic ones. It explains why Al behaves like a faster diffusing species on multiple diffusion profiles in Figure 3, despite the apparently lower value of the tracer diffusion coefficient. Such behavior can be easily understood, when one compares the values of mixing enthalpies in the typical FCC-structured HEAs system, such as Co-Cr-Fe-Mn-Ni, with the values for Al-Cr-Fe-Mn-V (see Table S4). As visible, the average values of ΔH_mix in our system are several times higher than in the reference FCC composition, as a consequence leading to much higher values of thermodynamic factors, introducing much more profound differences when converting between tracer and intrinsic diffusivities.

Considering the history of HEAs development, the question of the biggest importance in terms of diffusion in HEAs, is whether the transport of mass is actually sluggish. What should give a better overview of the actual rate of diffusion, is the comparison among the systems with the temperature scale normalized with respect to the melting point, which is more likely to show actual anomalies in the transport behavior than comparison in the absolute temperature scale [28,46,47]. It should be noted here that between the FCC and BCC structures in HEAs, the latter ones are actually much more likely to exhibit the ‘sluggish diffusion effect’, at least from the viewpoint of the original theory used to support its existence. Such a notion stems from the fact that BCC-structured HEAs are by definition characterized by a much higher atomic size mismatch, described by the δ parameter [48], which in turn should result in a much higher level of lattice distortion, originally believed by Yeh to be hindering the atomic movement in HEAs [3]. Combined with the typical for HEAs, complex and random nature of the nearest-neighbor surroundings of each lattice site, which may lead to the presence of ‘atomic traps’—regions of unfavorable energy landscape [46], it may seem that the BCC-structured HEAs are much closer to the originally envisioned origins of the ‘sluggish diffusion’ [3] than their FCC-structured counterparts. To settle this matter, in Figure 5 the comparison of the Al-Cr-Fe-Mn-V system with the available data for BCC elements and conventional alloys is presented. Additionally, to provide some general idea regarding the rate of mass transport in the studied materials, the values for the FCC-structured Co-Cr-Fe-Mn-Ni reference system are also included [28].

Figure 5. The values of tracer diffusion coefficients of different elements, in different BCC-structured metals and alloys [34,49–53]: (a) Al; (b) Cr; (c) Fe; (d) Mn; (e) V. All plots are presented in the temperature scale normalized with respect to the melting point value T_m of respective materials. The Tamman temperature, corresponding to the 2/3 of the absolute T_m value of is denoted by the vertical gray line. The open circles for the Al-Cr-Fe-Mn-V system correspond to the experimental points determined in this study, while the violet line shows the respective linear fit. Data for Co-Cr-Fe-Mn-Ni, FCC-structured system is also shown for reference [28,34,49–53].

As can be noticed, despite the presence of Mn [28], the diffusion kinetics in the studied system cannot be considered anomalous - for most of the elements it is neither particularly slow nor fast when compared with more conventional systems, and in the case of V, and to a lesser extend Cr, the diffusion kinetics can be even considered to be relatively swift. As a result, it can be stated that despite a number of factors believed to be potentially favoring the occurrence of sluggish diffusion behavior, the Al-Cr-Fe-Mn-V system is yet another evidence of its non-existence in the high-entropy alloys. Of course, a thorough examination of other BCC systems will be necessary before the general conclusions can be drawn, nevertheless, the obtained results strongly support the increasingly popular notion that the diffusion in HEAs is not anomalous in any meaningful way [5,19,20,28].

5. Conclusions

To conclude, the presented study describes the thermodynamic reassessment of the phase stability in BCC-structured TM-HEA systems, and, most importantly, the very first experimental assessment of the diffusion coefficients in such materials, on the example of Al-Cr-Fe-Mn-V system. The thermodynamic analysis documents significant progress in terms of predicting capability between the state-of-the-art TCHEA 4 database and its previous generation predecessors, also signalizing a need for a re-evaluation of the literature data, to fully exploit these improvements. The diffusion kinetics of the selected Al-Cr-Fe-Mn-V system appears to follow the behavior of typical, conventional, BCC-structured systems, showing no sign of diffusion retardation, despite the presence of Mn in the system, and despite the expected higher level of lattice distortion in comparison to high-entropy FCC systems, which in theory should contribute to more sluggish kinetics. As a result, the obtained results strongly support the notion that the ‘sluggish diffusion effect’ does not occur in HEAs and cannot be considered their inherent characteristic.

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work has been supported by the National Science Centre (Poland) DEC-2020/39/D/ST8/03072 and DEC-2019/03/X/ST5/00914.