Twinning-mediated plasticity by a novel multistage twinning mode in an Mg-Al-Gd alloy

Abstract

Twinning-mediated plasticity has great potential for enhancing the strength and plasticity of Mg alloys, which is limited due to the lack of twin types. Here, we report a novel multistage twinning mode, i.e. the dominant twinning mode changes from single $\left\{10\overline{1}2\right\}$ twins to the co-existence of $\left\{10\overline{1}2\right\}$ and $\left\{11\overline{2}6\right\}$ twins, in a deformed Mg-Al-Gd alloy. Introducing novel multistage twinning mode to accommodate strains appreciably along c-axes, combined with the interactions of high-density dislocations and dense twin boundaries, guarantees the high strain hardening of Mg alloys. These findings provide new insights into deformation mechanisms and mechanical properties of Mg-alloys.

GRAPHICAL ABSTRACT

IMPACT STATEMENT

Introducing novel multistage twinning mode to accommodate strains appreciably along c-axes, combined with the interactions of high-density dislocations and dense twin boundaries, guarantees the high strain hardening of Mg alloys.

KEYWORDS:

• Deformation twins
• magnesium alloy
• strain accommodation
• plasticity

1. Introduction

Mg-Al based alloys are widely studied and used in high-end applications, such as the aerospace and communications industries [1,2]. However, high-strength Mg-Al-based alloys often exhibit poor plasticity. The limited number of independent slip systems, and the difficulty in activating pyramidal-$〈c+a〉$ slips due to the higher critical resolved shear stress (CRSS) lead to difficulties in accommodating the strain along c-axes of hexagonal close-packed (HCP) Mg alloys [3,4]. In addition to dislocation slips, mechanical twinning plays a crucial role in accommodating the strain along c-axes of Mg alloys through the lattice reorientation [5,6]. Therefore, it may be feasible to enhance the plasticity of Mg alloys by manipulating the twinning behavior, on the premise of ensuring strength.

For Mg alloys, although a few twinning modes, such as $\left\{10\overline{1}2\right\}〈\overline{1}011〉$, $\left\{\overline{2}112\right\}〈2\overline{1}\overline{1}3〉$ and $\left\{1\overline{1}01\right\}〈\overline{1}102〉$, have been predicted in theory and relevant experimental data have been reported in literature at present [7,8], only $\left\{10\overline{1}2\right\}$ extension twins have been widely observed experimentally [9–11]. Essentially, the $\left\{10\overline{1}2\right\}$ twinning is associated with a lattice rotation of 86° about $〈11\overline{2}0〉$ axes, resulting in a strong crystallographic texture with the c-axes aligned close to the loading direction during compression. As a consequence, dislocation plasticity becomes unfavorable upon further compression, which leads to reduced plasticity and premature failure. This inherent dilemma that only one extension twinning mode cannot accommodate complex strains along c-axes has propelled numerous studies of new twinning modes, such as $\left\{11\overline{2}1\right\}〈\overline{1}\overline{1}26〉$ twins in Mg-14 wt.% Gd alloys [12], as well as twin-like $\left\{33\overline{6}4\right\}$ tilt boundaries in a high strain rate deformed Mg-9 wt.% Y alloy [13]. Nevertheless, it is still unclear whether the $\left\{33\overline{6}4\right\}$ twins are extension or contraction twins. Furthermore, the effect of twins on mechanical properties of Mg alloys remains underexplored. Recently, through theoretical analysis and atomic simulations, Cayron [14], Ostapovets [15] and Gao et al. [16] suggest a new extension twinning mode of $\left\{11\overline{2}6\right\}〈11\overline{2}1〉$ that is not predicted by the classical theory of twinning [17,18]. Ostapovets et al. [15] speculate that the $\left\{11\overline{2}6\right\}$ twin may impede dislocation movement, which contributes to the strength of pure Mg. However, up till now, the effect of $\left\{11\overline{2}6\right\}$ twinning on the mechanical behavior of Mg alloys has not been studied and experimentally verified. Therefore, it is necessary to explore the underlying mechanism of the $\left\{11\overline{2}6\right\}$ twinning mode on the plastic deformation behavior of Mg alloys.

Here, we report a novel multistage twinning mode, i.e. the dominant twinning mode changes from single $\left\{10\overline{1}2\right\}$ twins to the co-existence of $\left\{10\overline{1}2\right\}$ and $\left\{11\overline{2}6\right\}$ twins. $\left\{11\overline{2}6\right\}$ twins have been identified in an Mg-Al-Gd alloy using delicate microstructure characterizations. Simultaneously, multiple slip systems are activated within $\left\{11\overline{2}6\right\}$ twins, where the mean free path of dislocations is confined by $\left\{11\overline{2}6\right\}$ twin boundaries, which contributes to large work hardening. Additionally, the selection of $\left\{11\overline{2}6\right\}$ twinning mode and resultant maximum theoretical strain induced by $\left\{11\overline{2}6\right\}$ twinning have been determined by calculating the Schmid factor (SF) and lattice distortion. Introducing the multistage twinning mode can break the dilemma that the single $\left\{10\overline{1}2\right\}$ twinning is inadequate to accommodate the plastic deformation along c-axes, which guarantees a high plasticity (∼18%) in the present Mg-Al-Gd alloy upon compression. These findings can provide new perspectives for designing and preparing high-performance Mg alloys by tailoring multiple twinning modes.

2. Materials and methods

The Mg-1Al-1.8Gd (wt.%) alloy was fabricated via melting high-purity Mg (99.99 wt.%), high-purity Al (99.99 wt.%) and Mg-73.49 wt.%Gd alloy, followed by casting under a protective atmosphere. The as-cast ingot was preheated at 450°C for 2 h and subsequently hot-extruded with an extrusion ratio of 20:1. Cylindrical compression samples with dimensions of Ø 8 mm × 12 mm were subjected to compression testing at room temperature. The tests were conducted using an AGS-X-100 kN testing machine at a strain rate of 10⁻³s⁻¹, with loading applied along the extrusion direction. The microstructure of the compression samples was characterized using a Zeiss Field Emission Scanning Electron Microscope (Sigma 500) equipped with an EBSD detector. Transmission electron microscopy (TEM) samples were mechanically polished followed by ion-milling using Gatan PIPS691 at −120°C. TEM was performed in a FEI Tecnai G2 using an accelerating voltage of 200 kV. TEM samples were also analyzed by transmission Kikuchi diffraction (TKD) in a field-emission gun scanning electron microscope (SEM) operating at 30 kV, with a step size of 0.2 µm. To provide a more comprehensive background, we have included additional analyses on the tensile deformation of as-extruded Mg-1Al-1.8Gd (wt.%) alloy in Appendix A.

3. Results and discussion

Figure 1 shows the representative compressive engineering stress–strain curve of the as-extruded Mg-Al-Gd alloy. The compressive yield strength (CYS) and ultimate compressive strength (UCS) of the as-extruded alloy are ∼160 MPa and ∼400 MPa, respectively. Notably, the UCS of the low-alloyed Mg-Al-Gd alloy closely rivals that of the high-alloyed WE43 alloy [19]. Moreover, the plasticity of the Mg-Al-Gd alloy reaches ∼18%, which is much higher in comparison to other Mg alloys either containing RE elements or not, e.g. AZ31 (wt.%) alloy (∼14%) [20], AZ80-3(Y, Gd) (wt.%, AEZ830) alloy (∼13%) [21], Mg-3Al-5Bi (wt.%, BA53) alloy (∼13.5%) [22] and Mg-8Gd-4Y-1Zn-Mn (wt.%, E128N) alloy (∼13.2%) [23] reported in literature. To reveal the underlying mechanisms for the high plasticity, compression testing was interrupted at various strains, i.e. 0%, ∼8% and ∼14%, for microstructure observation using EBSD, as indicated by blue pentagonal markers. The representative inverse pole figure (IPF) maps (Figure 1(a–c)) and corresponding kernel average misorientation (KAM) maps (Figure 1(d and f)) are presented. The as-extruded alloy exhibits a heterogeneous grain structure, including elongated grains along the ED and equiaxed grains. Extension and contraction twins are seldom discovered (Figure 1(a and d)). After compressed by ∼8%, multiple lenticular-shaped twins with a boundary misorientation angle of ∼86° (highlighted in red) have formed, which are identified as $\left\{10\overline{1}2\right\}$ extension twins (Figure 1(b and e)) that are similar to the observations in previous studies [24,25]. Moreover, a few twins with a boundary misorientation angle of ∼56° about $〈1\overline{1}00〉$ axes (highlighted in orange-yellow) are observed in several grains of the 8%-strained sample. It is interesting that these boundaries with a misorientation angle of ∼56° about $〈1\overline{1}00〉$ axes have developed in addition to the frequently observed $\left\{10\overline{1}2\right\}$ twin boundaries, which is inferred to be a new type of twins (Figure 1(c and f)). A detailed statistical analysis of the area fraction and grain boundary length occupancy of uncommon twins shows that they are ∼6.8% and ∼13%, respectively.

Figure 1. Typical compressive stress-strain curve of the as-extruded Mg-Al-Gd alloy. IPF maps, KAM maps (overlaid with special boundaries by red and orange-yellow lines) and pole figures of the as-extruded alloy with various compression strains: (a, d and g) 0%, (b, e and h) ∼8% and (c, f and i) ∼14%.

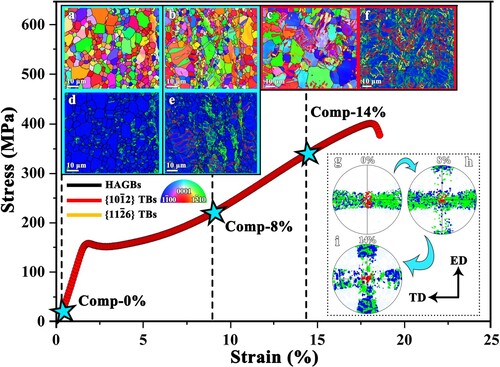
Moreover, the main texture component in pole figures (PFs) under the strain of 0∼14% reflects the orientation dependence of the deformation mechanisms (Figure 1(g–i)). At ϵ = 0 (Figure 1(g)), fairly strong preferred orientations, i.e. the $〈1\overline{1}00〉$ (green) and $〈11\overline{2}0〉$ (blue), are nearly perpendicular to ED. As the strain increases (ϵ = ∼8% and ϵ = ∼14%), the formation of ED texture components is mainly attributed to the twinning [26,27] (Figure 1(h and i)).

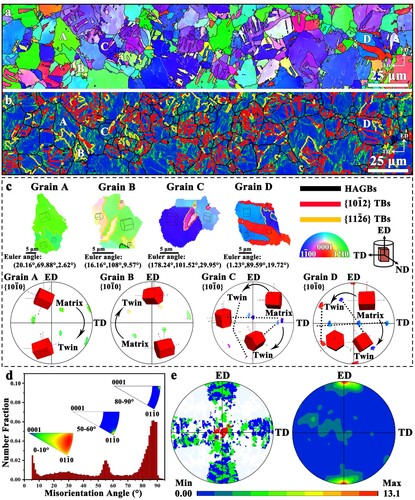
An enlarged view of a representative region from Figure 1(c) is shown in Figure 2, which indicates that twins can be classified into two types based on boundary misorientation angles: (i) ∼86° (highlighted in red) and (ii) ∼56° (highlighted in orange-yellow) in the IPF and KAM maps (Figure 2(a and b)). Several grains containing twins, such as A, B, C and D in Figure 2(b), are depicted in Figure 2(c) together with their corresponding PFs. Within grains A and B, twin boundaries (TBs) delineated by ∼56° about $〈1\overline{1}00〉$ axes are identified; whereas grains C and D display two characteristic misorientation relationships: one at ∼86° about $〈11\overline{2}0〉$ axes and the other at ∼56° about $〈1\overline{1}00〉$ axes. Additionally, the misorientation angle (θ) distributions derived from Figure 2(a) are shown in Figure 2(d), where the presence of a peak at ∼86° about $〈11\overline{2}0〉$ axes are attributed to $\left\{10\overline{1}2\right\}$ TBs [28]. The concentration of misorientation angles at ∼56° forms mainly owing to the ∼56° $〈1\overline{1}00〉$ twins. Also, the changes in crystal orientations during compression can be macroscopically reflected on the PFs (Figure 2(e)).

Figure 2. Typical EBSD result of the as-extruded Mg-Al-Gd alloy compressed by ∼14%: (a) IPF map. (b) Corresponding grain boundary map. (c) Enlarged IPF maps for grains A, B, C, and D with corresponding PFs. (d) Misorientation angle distribution maps corresponding to (a) and (e) Pole figures corresponding to (a): $〈0002〉$ (red), $〈1\overline{1}00〉$ (green) and $〈11\overline{2}0〉$ (blue).

We also analyzed the two twin types using TKD and TEM (Figure 3). The IPF (Figure 3(a)) and SEM (Figure 3(b)) micrographs accurately correlate the crystallographic orientations with the microscale morphology of the TKD sample. TEM micrographs (Figure 3(e–k)) reveal two characteristic twin boundaries with misorientation angles of ∼86° (red) and ∼56° (orange-yellow). Figure 3(e) shows the bright-field TEM (BF-TEM) image of twin lamella structures. The inset is the selected area electron diffraction (SAED) pattern from both the matrix and twin. Based on the SAED pattern (Figure 3(e)) and the high-resolution TEM (HRTEM) image with the fast Fourier transform (FFT) patterns (Figure 3(f)) taken around the twin boundary along the $〈11\overline{2}0〉$ zone axes, the twins are identified as $\left\{10\overline{1}2\right\}$ twins. The crystallographic characteristic of $\left\{10\overline{1}2\right\}$ twin agrees well with previous works [29,30]. Figure 3(g) demonstrates a low-magnification image of the twin lamella viewed slightly off the $〈1\overline{1}00〉$ zone axes. The enlarged BF-TEM image in Figure 3(h), highlights the interface between the twin and the matrix. The corresponding SAED pattern in Figure 3(i) is derived from the twin boundary in Figure 3(h). Further analysis reveals that the net reorientation of the basal plane is ∼56° about $〈1\overline{1}00〉$ axes, and the twin boundary plane belongs to $\left\{11\overline{2}6\right\}$ planes (Figure 3(j)). Figure 3(k) shows an HRTEM image from the twin boundary in Figure 3(h), viewed along the $〈1\overline{1}00〉$ zone axes. The insets in Figure 3(k) show the FFT pattern from the matrix and twin, respectively. Combining the results in Figure 3(i–k), the twin is identified to be $\left\{11\overline{2}6\right\}$ twins. Correspondingly, the multistage twinning mode is unambiguously determined, i.e. from a single $\left\{10\overline{1}2\right\}$ twinning mode at a lower strain level (∼8%) to the co-existence of $\left\{10\overline{1}2\right\}$ and $\left\{11\overline{2}6\right\}$ twins at a higher strain level (∼14%).

Figure 3. TEM and TKD results of two types of twins in the Mg-Al-Gd alloy compressed by ∼14%: (a) TKD orientation map with special boundary misorientation angles: ∼86° (red) and ∼56° (orange-yellow). (b) SEM image corresponding to (a). (c, d) Enlarged images corresponding to the rectangle in (a, b). (e) BF-TEM image of the $\left\{10\overline{1}2\right\}$ twin. (f) HRTEM image showing the $\left\{10\overline{1}2\right\}$ TB. (g) BF-TEM image of the $\left\{11\overline{2}6\right\}$ twin. (h) BF-TEM image corresponding to the rectangle in (g). (i) The SAED pattern from both the matrix and $\left\{11\overline{2}6\right\}$ twin. (j) Schematic diagram of the SEAD pattern in (i). (k) HRTEM image showing the $\left\{11\overline{2}6\right\}$ TB.

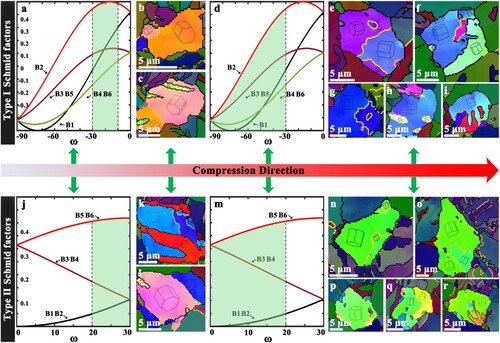
The selection of $\left\{11\overline{2}6\right\}$ twinning mode can be determined by Schmid factors (SF) calculations. A continuous loading is assumed to be applied in crystals, where the loading directions of type I and II are along $〈0001〉$ and $〈1\overline{1}00〉$, respectively. The angle ω (the angle between the loading direction and the crystal orientation) was measured to evaluate the variation of SF values for twins. The SF values of $\left\{10\overline{1}2\right\}$ and $\left\{11\overline{2}6\right\}$ twin variants were calculated. Details of SF calculations are described in Supplementary Appendix B & Figure S3.

For Type I, $\left\{10\overline{1}2\right\}$ twin variants are more likely to be activated, as the SF values for such twins are larger than 0.3. Note that the maximum SF values of $\left\{11\overline{2}6\right\}$ twin variants are as high as 0.499 in certain ω ranges (−20° < ω < −15°) (Figure 4(a and b)). For Type II, both $\left\{10\overline{1}2\right\}$ twin variants, and $\left\{11\overline{2}6\right\}$ twin variants (B5 and B6, as shown in Figure 4(j)) have higher SF values (0.4 < SF < 0.5). Considering that certain deviations could exist between the applied stress and the actual stress states, it is also feasible that the $\left\{11\overline{2}6\right\}$ twins with relatively low SF values could be activated.

Figure 4. Schmid-factor (SF) determined twinning mode selection. The Schmid-factor maps and corresponding orientation maps of $\left\{11\overline{2}6\right\}$ twins: (a to c) Higher SF values (0.441–0.499) in Type I. (d to i) Lower SF values in Type I. (j to l) Higher SF values (0.399–0.409) in Type II. (m to r) Lower SF values in Type II.

It has been reported that, in HCP Mg alloys, the easily activated $\left\{10\overline{1}2\right\}$ twin with the Burgers vector ${\text{b}}_{tw}^{\left\{10\overline{1}2\right\}}=\frac{3-r^2}{3+r^2}\left[\overline{1}011\right]$ and the shear strain $\left(\text{s}=\frac{c^2-3a^2}{c\sqrt{3}}\right)$ of 0.129 $\left(r=c/a=1.624\right)$ [31] can provide a lattice strain of ∼6.65%. In the present work, a maximum lattice strain along c-axes due to the $\left\{11\overline{2}6\right\}$ twins with the Burgers vector ${\text{b}}_{tw}^{\left\{11\overline{2}6\right\}}=\frac{r^2-2}{3\left(1+r^2\right)}\left[11\overline{2}1\right]$, is estimated to be ∼5.2%. Theoretically, the coexistence of $\left\{10\overline{1}2\right\}$ and $\left\{11\overline{2}6\right\}$ twins can provide a maximum strain higher than that provided by either the single $\left\{10\overline{1}2\right\}$ or $\left\{11\overline{2}6\right\}$ twinning mode. Thereby, the co-existence of $\left\{10\overline{1}2\right\}$ or $\left\{11\overline{2}6\right\}$ twinning could play an essential role in strain accommodation along c-axes.

From TKD characterizations (Figure 5(a)), we can observe that a typical grain contains a $\left\{11\overline{2}6\right\}$ twin. This facilitates the accommodation of deformation incompatibilities at grain boundaries [32] and leads to a redistribution of local stresses [33,34]. To further elaborate the influence of the $\left\{11\overline{2}6\right\}$ twins on dislocation slips, the theoretical SFs of slip systems (SS) are considered for both matrix and $\left\{11\overline{2}6\right\}$ twins. As shown in Table 1, the maximum SF value of dislocation slip systems in the parent grain belongs to basal-$〈a〉$ slips ($\text{S}{\text{F}}_{\left(0001\right)\left[2\overline{1}\overline{1}0\right]}$ = 0.45, SS1), whereas the maximum SF value in the $\left\{11\overline{2}6\right\}$ twin belongs to pyramidal-$〈c+a〉$ dislocations ($\text{S}{\text{F}}_{\left(21\overline{1}2\right)\left[2\overline{1}\overline{1}\overline{3}\right]}$ = 0.48, SS13). Therefore, it is reasonable to hypothesize that non-basal slip might be activated within $\left\{11\overline{2}6\right\}$ twins.

Figure 5. TEM images illustrating the dislocations and cross-slips in the $\left\{11\overline{2}6\right\}$ twin.

Table 1. Calculated Schmid factors of the eighteen slip systems in Parent grain (Euler angle: 125°, 86°, 17°) and the $\left\{11\overline{2}6\right\}$ twin (Euler angle: 84°, 121°, 8°).

				Schmid factor
Slip mode	SS.	Slip plane	Slip direction	Matrix	Twin
Basal- slip	1	$\left(0001\right)$	$\left[2\overline{1}\overline{1}0\right]$	0.45	0.08
	2	$\left(0001\right)$	$\left[\overline{1}2\overline{1}0\right]$	0.09	0.41
	3	$\left(0001\right)$	$\left[\overline{1}\overline{1}20\right]$	0.35	0.33
Prismatic- slip	4	$\left(01\overline{1}0\right)$	$\left[2\overline{1}\overline{1}0\right]$	0.10	0.04
	5	$\left(10\overline{1}0\right)$	$\left[\overline{1}2\overline{1}0\right]$	0.06	0.08
	6	$\left(\overline{1}100\right)$	$\left[\overline{1}\overline{1}20\right]$	0.16	0.13
Pyramidal- slip	7	$\left(01\overline{1}1\right)$	$\left[2\overline{1}\overline{1}0\right]$	0.12	0.08
	8	$\left(\overline{1}011\right)$	$\left[\overline{1}2\overline{1}0\right]$	0.09	0.12
	9	$\left(1\overline{1}01\right)$	$\left[\overline{1}\overline{1}20\right]$	0.02	0.04
	10	$\left(10\overline{1}1\right)$	$\left[\overline{1}2\overline{1}0\right]$	0.01	0.27
	11	$\left(\overline{1}101\right)$	$\left[\overline{1}\overline{1}20\right]$	0.30	0.28
	12	$\left(0\overline{1}11\right)$	$\left[2\overline{1}\overline{1}0\right]$	0.29	0.00
Pyramidal-<c + a> slip	13	$\left(21\overline{1}2\right)$	$\left[2\overline{1}\overline{1}\overline{3}\right]$	0.15	0.48
	14	$\left(11\overline{2}2\right)$	$\left[11\overline{2}\overline{3}\right]$	0.06	0.41
	15	$\left(\overline{1}2\overline{1}2\right)$	$\left[\overline{1}2\overline{1}\overline{3}\right]$	0.33	0.41
	16	$\left(\overline{2}112\right)$	$\left[\overline{2}11\overline{3}\right]$	0.36	0.36
	17	$\left(\overline{1}\overline{1}22\right)$	$\left[\overline{1}\overline{1}2\overline{3}\right]$	0.37	0.10
	18	$\left(1\overline{2}12\right)$	$\left[1\overline{2}1\overline{3}\right]$	0.25	0.03

Note: SFs of the activated slip system(s) are bolded for each grain.

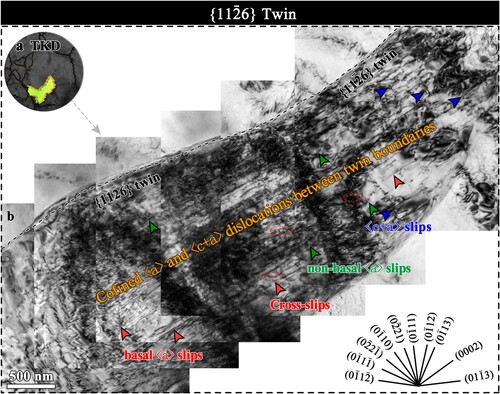
The $\left\{11\overline{2}6\right\}$ twins have been further investigated by TEM. Figure 5(b) presents a BF-TEM image showing a $\left\{11\overline{2}6\right\}$ twin, viewed along the $\left[11\overline{2}0\right]$ zone axes. Based on the invisibility criterion, dislocation analysis reveals the activation of multiple slip systems, including high-density basal-$〈a〉$ (red arrow), non-basal-$〈a〉$ (green arrow) and pyramidal-$〈c+a〉$ (blue arrow) dislocations within the $\left\{11\overline{2}6\right\}$ twin. Herein, the $〈c+a〉$ dislocations can be determined by analyzing various two-beam conditions, i.e. g = $\left(10\overline{1}0\right)$ and g = $\left(0002\right)$, as shown in Supplementary Figure S4. High density of $〈a〉$ dislocations is observed under g = $\left(10\overline{1}0\right)$, while dislocations with $〈c〉$-type Burgers vectors are clearly discerned at the same location under the g = $\left(0002\right)$ condition. Cross-slips between basal and non-basal planes are also observed (Figure 5(b)), evidenced by wavy slip lines [35,36]. Generally, the activation of non-basal slips is much more difficult than the basal-$〈a〉$ slips in Mg alloys due to the higher CRSS [37,38]. The activated non-basal-$〈a〉$ slip systems with lower SF values (m < 0.3) and pyramidal-$〈c+a〉$ slips inside the $\left\{11\overline{2}6\right\}$ twins are mainly attributed to (i) the stacking-fault energy reduction caused by the Gd addition [39,40] and (ii) the changed parent grain orientation by twinning to a favorable orientation for activating non-basal slips.

The activated multiple slip systems within $\left\{11\overline{2}6\right\}$ twins that satisfy the Von Mises criteria [41], enable to coordinate the complex plastic deformation along both the a and c-axes, effectively promoting isotropic deformation and reducing the likelihood of premature fracture at grain boundaries [42]. Additionally, the mean free paths of dislocations are confined by the $\left\{11\overline{2}6\right\}$ twin boundaries, leading to a strong tendency for tangling of dislocations inside the twin and long-range back stresses [43,44] at twin boundaries (Figure 5(b)). These factors contribute to sustained strain hardening and enhanced plasticity. The formation mechanisms associated with the $\left\{11\overline{2}6\right\}$ twin are detailed in Appendix C.

4. Conclusions

In summary, a novel multistage twinning mode has been identified in a Mg-Al-Gd alloy subjected to compressive deformation at room temperature. Correlative EBSD and TEM analysis reveal that the dominant twinning mode changes from $\left\{10\overline{1}2\right\}$ twins to the co-existence of $\left\{10\overline{1}2\right\}$ and $\left\{11\overline{2}6\right\}$ twins. Furthermore, the interactions of high-density pyramidal-$〈c+a〉$ and non-basal-$〈a〉$ dislocations and dense twin boundaries contribute to the high strain hardening. These findings are expected to shed some new insights into deformation mechanisms of Mg alloys, which are useful for designing high-performance Mg alloys.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was primarily supported by National Natural Science Foundation of China under Grant Nos. 52234009 and 52271103. Partial financial support came from the Program for the Central University Youth Innovation Team and Jilin Scientific and Technological Development Program (Nos. 20210201115GX and 20220301026GX).