A comparison of parameter covariance estimation methods for item response models in an expectation-maximization framework

Abstract

The Expectation-Maximization (EM) algorithm is a method for finding the maximum likelihood estimate of a model in the presence of missing data. Unfortunately, EM does not produce a parameter covariance matrix for standard errors. Both Oakes and Supplemented EM are methods for obtaining the parameter covariance matrix. SEM was discovered in 1991 and is implemented in both open-source and commercial item response model estimation software. Oakes, a more recent method discovered in 1999, had not been implemented in item response model software until now. Convergence properties, accuracy, and elapsed time of Oakes and Supplemental EM family algorithms are compared for a diverse selection IFA models. Oakes exhibits the best accuracy and elapsed time among algorithms compared. We recommend that Oakes be made available in item response model estimation software.

Keywords:

• parameter covariance matrix
• Oakes direct method
• supplemented EM algorithm
• item factor analysis
• Monte Carlo
• standard errors

Public Interest Statement

Item models are a family of a statistical models frequently used for high stakes testing (SAT, GRE, or MCAT) and for data obtained from psychological questionnaires (like personality assessments). For any statistical model, an important consideration is how precisely the model parameters are determined by the data. For these particular kind of item models, obtaining the information about parameter precision is difficult. This report runs the leading methods against each other, ranking them in terms of accuracy and performance. The method described by Oakes, which is also the simplest, outperforms all the other methods in both accuracy and performance. We recommend that Oakes be made available more widely in statistical software that deals with item models.

1. Introduction

Once a model is fit to data, it is routine practice to examine the degree of confidence we ought to have in the parameter estimates. One approximation of this information is found in the parameter covariance matrix V, and in summary form, as standard errors (SEs), . The Expectation-Maximization (EM) algorithm (Dempster, Laird, & Rubin, 1977) is a method for finding the maximum likelihood estimate (MLE, ) of a model in the presence of missing data. For example, one EM algorithm of importance to psychologists and educators is for implementation of Item Factor Analysis (IFA) (Bock & Aitkin, 1981). Unfortunately, the parameter covariance matrix is not an immediate output of the EM algorithm. Before exploring methods to obtain the parameter covariance matrix, the EM approach will be informally outlined.

Following traditional notation, let be the observed data. We want to find the MLE of parameter vector for model . Unfortunately, is intractable or cumbersome to optimize. The EM approach is to start with initial parameter vector and fill in missing data as the expectation of (E-step). In the case of Bock and Aitkin (1981), the missing data are the examinee latent scores (as determined by item parameters). Together, the observed and made-up data constitute completed data . With the parameter vector at iteration t, we can use a complete data method to optimize and find (M-step). With an improved parameter vector , the process is repeated until . As a memory aid, the reader may prefer to associate the m in with made up (not missing).

In exponential family models, the parameter covariance matrix V is often estimated using the observed information matrix. The negative M-step Hessian(1)

is usually easy to evaluate but asymtotically underestimates the variability of .

A better estimate is the negative Hessian of only the observed data ,(2)

Usually is difficult to evaluate; One benefit of the EM method is the ability to optimize efficiently without evaluation of Equation (2).

To estimate the parameter covariance matrix in an EM context, many methods have been proposed. Some methods require problem specific apparatus such as the covariance of the row-wise gradients (Mislevy, 1984) or a sandwich estimate (e.g. Louis, 1982; Yuan, Cheng, & Patton, 2013). For IFA models, the Fisher information matrix can be computed analytically. However, a sum is required over all possible patterns (Bock & Aitkin, 1981). Since such a sum is impractical for as few as 20 dichotomous items, no further consideration of this method will be given. Here we will focus on methods that are less reliant on problem specific features.

Finite differences with Richardson extrapolation has been advocated (Jamshidian & Jennrich, 2000). This method evaluates the observed data log-likelihood at a grid of points in the space to approximate the Hessian. For example, for a single parameter function f, the Hessian can be approximated by(3)

for some small . For Richardson extrapolation, the perturbation distance is reduced on every iteration. Precision is enhanced by extrapolating the change in curvature between iterations (Richardson, 1911). Unfortunately, the number of points required to approximate the Hessian is where r is the number of iterations and N is the number of parameters in vector (Gilbert & Varadhan, 2012). This limits the practical applicability of Richardson extrapolation to models with a modest number of parameters.

We are aware of only two algorithms that offer performance that scales linearly with the number of parameters and require little problem specific apparatus: Supplemented EM (SEM) (Meng & Rubin, 1991) and the direct method (Oakes, 1999). Although the direct method is simpler than SEM, Oakes has not been implemented in IFA software until recently (Pritikin, 2015) and has not been compared with parameter covariance estimation methods for IFA models. We describe SEM in some detail so that the reader may appreciate its relationship with Oakes.

In IFA software, SEM grew to popularity because it was superior to the methods commonly available at the time (Cai, 2008). SEM is based on the observation that the information matrix of the completed data is the sum of the information matrices of the observed and made-up data (Orchard & Woodbury, 1972). With some algebraic manipulation we can rearrange the terms,(4) (5)

Intuitively, represents the fraction of information that contributes to in excess of (Dempster et al., 1977). One cycle of the EM algorithm can be regarded as a mapping . In this notation, the EM algorithm is(6)

If converges to some point and is continuous then must satisfy . In the neighborhood of , by Taylor series expansion, where is the Jacobian of M evaluated at the MLE ,(7)

Dempster et al. (1977) showed that the rate of convergence is determined by the fraction of information that contributes to . In particular, in the neighborhood of ,(8)

Combining Equations (5) and (8), we obtain . Therefore, the inverse observed data parameter covariance matrix .

The rate matrix from Equation (7) can be approximated using a forward difference method. Let d be the number of elements in vector so we can refer to it as . Column j of is approximated by(9)

That is, we run 1 cycle of EM with set to the MLE except for the jth parameter of which is set to where (Note that indices i and j are interchangeable on the diagonal). Then we subtract from the result and divide by the scalar . This amounts to numerically differentiating the EM map M.

Theoretically, accuracy improves as . In practice, however, this is arithmetic on a computer using a floating-point representation. We cannot take but must pick a particular . The original formulation proposed to use the EM convergence history (where is the parameter vector at iteration t) and compute the series of columns , until is “stable” from t to . This procedure may initially seem appealing, but note that the history of is a function of the starting parameter vector and no guidance was provided about appropriate starting values. Regardless of starting values, Meng and Rubin (1991) suggested that could be declared stable if no element changed by more than the square root of the tolerance of an EM cycle. For example, if the EM tolerance for absolute change in log-likelihood is then the SEM tolerance would be . Hence, the jth column of is converged when(10)

But they remarked that the stopping criterion deserved further investigation.

SEM as originally described does not perform well in some circumstances. Its disappointing performance prompted at least two refinements. One refinement proposed a heuristic for the search of the parameter trajectory history (Tian-SEM; Tian, Cai, Thissen, & Xin, 2013) and was reinforced by a report of promising performance in unidimensional and multidimensional item response models simulation studies (Paek & Cai, 2014). The idea of Tian-SEM is that parameter estimates typically start far from the MLE and approach closely only after a number of EM cycles. Starting SEM from is usually wasteful because does not stabilize until with t close to convergence. During an EM run, the log-likelihood typically changes rapidly and then slowly as the parameter values are fine tuned. The quantity was proposed as a standardized measure of closeness to convergence and suggested that the best opportunity for SEM is history subset corresponding to . This refinement helps in many cases. However, lingering weaknesses in Tian-SEM prompted another more drastic refinement (Agile-SEM; Pritikin, 2016). Agile-SEM will be shown to perform better than other SEM family algorithms, but not as well as the best method. A full description of Agile-SEM is lengthy and beyond the scope of this article. We include the original algorithm (MR-SEM) and these two refinements in our comparison.

Recall that the goal of SEM family algorithms is to estimate in Equation (4). Oakes gave a remarkably direct way to obtain this quantity,(11)

This is the Jacobian of the completed data gradient of the vector in with respect to the made up data (Oakes, 1999). We are not aware of an analytic expression for this quantity for an item response model, but little additional computer programming is needed to estimate it using finite differences.

2. Method

2.1. Models

We introduce a set of conditions designed to present a challenge to parameter covariance matrix estimators. We included underidentified models, models with bounds, and latent distribution parameters. Underidentified models do not contain enough data to uniquely identify the most likely model parameters. IFA models consist of a collection of response models, each item response model associated with a single item. To some extent, the number of possible response outcomes determines the choice of item model. The dichotomous or graded response model is suitable for items with only two possible outcomes (e.g. correct/incorrect). In contrast, the graded response or nominal model is suitable for items with more than two possible outcomes. Many other response models are available, but we focus on these three because of their enduring popularity. The definitions of these item response models are given in Appendix and detailed in the rpf package (Pritikin, 2015). The structure of Models m2pl5, m3pl15, grm20, and cyh1 will be described.

Model m2pl5 contained 5 2PL items. Slopes were 0.5, 1.4, 2.2, 3.1, and 4. Intercepts were , , 0, 0.75, and 1.5. Data were generated with a sample size of 1000 and all parameters were estimated. Model m2pl5 is not always identified at this sample size. This allowed us to examine the extent to which algorithms agreed on whether a given model was identified or not.

Model m3pl15 contained 15 3PL items. Slopes were set to 2 and items were divided into 3 groups of 5. Each group had the intercepts set as in Model m2pl5 and the lower bound parameters set to with g as the group number (1–3). A sample size of 250 was used. For estimation, all slopes were equated to a single slope parameter. To stabilize the model, a Gaussian Bayesian prior on the lower bound (in logit units) with a standard deviation of 0.5 was used (see, Cai, Yang, & Hansen, 2011, Appendix ).

Model grm20 contained 20 graded response items with 3 outcomes. Slopes were equally spaced from 0.5 to 4. The first intercept was equally spaced from to 1.5 every 5 items. The second intercept was 0.1 less than the first intercept. A sample size of 2,000 was used and all parameters were estimated. In the graded model, intercepts must be strictly ordered (Samejima, 1969). The placement of intercepts so close together should boost curvature in the information matrix.

Table 1. Data generating parameters for Model cyh1. Group 2 did not contain items 13-16

Item	a1	a2	a3	a4	a5	c
1	1.00	0.80				1.00
2	1.40	1.50				0.25
3	1.70	1.20
4	2.00	1.00
5	1.40		1.00			1.00
6	1.70		0.80			0.25
7	2.00		1.50
8	1.00		1.20
9	1.70			1.20		1.00
10	2.00			1.00		0.25
11	1.00			0.80
12	1.40			1.50
13	2.00				1.50	1.00
14	1.00				1.20	0.25
15	1.40				1.00
16	1.70				0.80

Note: Nonzero parameters were estimated.

The first simulation study from Cai et al. (2011) was included. Model cyh1 was a bifactor model with 2 groups of 1,000 samples each. Group 1 had 16 2PL items with the latent distribution fixed to standard Normal. Group 2 had the first 12 of the items from Group 1. All item parameters appearing in both groups were constrained equal. Data generating parameters for the items are given in Table 1. The latent distribution of Group 2 was estimated. Latent distribution generating parameters were 1, , 0, 0.5 and 0.8, 1.2, 1.5, 1, for means and variances respectively.

In addition, a 20 item 2PL model and the model from the second simulation study of Cai et al. (2011) were examined. Little additional insight was gained from these models and we do not report them here in detail. However, this work indicated that our results generalize to the nominal response model (see Appendix ).

All item response models used a multidimensional parameterization (slope intercept form instead of discrimination difficulty). Hence, intercepts were multiplied by slopes in Models m2pl5, m3pl15, and grm20. Both MR-SEM and Tian-SEM strongly depend on the parameter convergence trajectory. Therefore, it is crucial to report optimization starting values. In general, all slopes were started at 1, intercepts at 0, means at 0, and variances at 1. For Model m3pl15, all lower bounds were started at their true value. Since the intercepts of the graded model cannot be set equal, for Model grm20, intercepts were started at 0.5 and respectively.

2.2. Ground truth

All models were subjected to 500 Monte Carlo trials to obtain the ground truth for the parameter covariance matrix. For each trial, data were generated with the rpf.sample function from the rpf package (Pritikin, 2015). Models were fit with (Bock & Aitkin, 1981) as implemented in the IFA module of OpenMx with EM acceleration enabled (Pritikin, 2015, Varadhan & Roland, 2008). For the multidimensional model, Cai (2010b) was used for analytic dimension reduction. The EM and M-step tolerance for relative change in log-likelihood,(12)

were set to and , respectively. The use of relative change removes the influence of the magnitude of on the precision of . In models where the latent distribution was fixed, numerical integration was performed using a standard Normal prior. Single dimensional models used an equal interval quadrature of 49 points from Z score to 6. The multidimensional model used an equal interval quadrature of 21 points from Z score to 5. The computer used was running GNU/Linux with a 2.40 GHz Intel i7-3630QM CPU and ample RAM. Table 2 summarizes the results.

Table 2. Descriptive summary of the Monte Carlo simulation studies

		Unidentified
m2pl5	10	13	16.1	0.665	0.84	35
m3pl15	31	6	8.5	0.306	0.55	90
grm20	60	0	16.1	0.111	0.22	369
cyh1	56	1	8.5	0.055	0.14	281

Notes: The first column is the number of free parameters in the model. Where the Unidentified column is 0, all trials were included. Trials were considered unidentified if the iteration limit was reached or the log condition number using the covariance of the gradients was greater than log(CondNum). V is the Monte Carlo parameter covariance matrix.

The condition number of the information matrix is the maximum singular value divided by the minimum singular value and provides a rough gauge of the stability of a solution (Luenberger & Ye, 2008, p. 239). For example, models that are amply overspecified have a condition number close to 0 whereas slightly overspecified models will have a large positive condition number. When the information matrix is not positive definite then the MLE is unstable and may be a saddle point (Luenberger & Ye, 2008, p. 190). For reference, bias is defined as (columns 4 and 5) and the Monte Carlo parameter covariance matrix is simply the covariance of each trial’s MLE as the rows of data (column 6).

2.3. Measures of quality

In theory, SEs approach 0 proportional to . In practice, however, each additional participant does not contribute exactly 1 unit of information. Relative difference (RD) is a way to transform SEs into comparable units across conditions,

To summarize RDs for a set of parameters, the Euclidean or -norm is used, .

SEs are an incomplete measure of information matrix estimation quality because they only reflect parameter variance. Accurate parameter covariances can be regarded as evidence that the estimation algorithm will generalize to other models. Kullback-Leibler (KL) divergence was used to assess the quality of the variance covariance matrix as a whole. For a 0 mean multivariate Normal distribution, KL divergence was defined as

where K is the dimension of .

2.4. Procedure

We evaluated convergence properties, accuracy, and elapsed time of Oakes, MR-SEM, Tian-SEM, and Agile-SEM with 500 Monte Carlo replications. The completed data information matrix (Equation (1)) and central difference Richardson extrapolation with an initial step size of and 2 iterations were included as low and high accuracy benchmarks, respectively. A relative EM tolerance of was used without EM acceleration. This relative tolerance roughly corresponds to an absolute tolerance of for the models of interest. The quantity required by Oakes (Equation (11)), was estimated by forward difference with a step size of . Richardson extrapolation was not used so only evaluations of the M-step gradient were required.

Since both MR-SEM and Tian-SEM depend on the parameter convergence trajectory, EM acceleration was disabled for trials of these algorithms. Without EM acceleration, the EM iteration limit was raised to 750 from the default of 500 to protect many replications of Model cyh1 from early termination. SEM tolerance was set to the square root of the nominal absolute EM tolerance, (Meng & Rubin, 1991, p. 907). Other EM and SEM tolerances could have been selected, but would involve a trade-off. Either accuracy would be improved at the cost of speed or vice versa. As will be seen, Oakes outperforms all SEM family algorithms in both accuracy and speed.

Table 3. Percentage of trials that failed to converge by model and algorithm

	RE	Oakes	Agile	Tian	MR SEM
m2pl5	2.6	2.6	3.6	3.8	4.8
m3pl15	1.0	1.0	1.0	1.0	1.2
grm20	0.0	0.0	0.4	0.0	95.4
cyh1	0.0	0.0	0.0	20.0	70.2

Notes: Failure was due to either iteration limit or a non-positive definite covariance matrix. Since some trials were genuinely unidentified, these trials failed to converge for all algorithms. Compare with the unidentified column in Table 2.

Table 4. Mean elapsed time and accuracy of parameter covariance matrix estimators

	RE	Oakes	Agile	Tian	MR SEM	M-step
m2pl5
Seconds	0.015	0.015	0.019	0.035	0.08	0.012
	3.225	3.225	3.232	4.537	4.364	4.532
	1.428	1.402	1.369	1.758	1.685	1.751
m3pl15
Seconds	0.275	0.056	0.111	0.094	0.177	0.048
	11.893	11.893	11.893	12.014	11.944	12.014
	5.273	3.408	5.271	4.772	5.07	4.771
grm20
Seconds	8.039	0.143	0.478	0.515	0.247	0.026
	0.862	0.862	0.899	1.326	2.159	2.15
	0.675	0.675	0.687	0.859	1.55	1.532
cyh1
Seconds	46.358	0.829	2.953	9.657	12.18	0.072
	1.406	1.395	1.395	1.482	1.626	4.919
	1.286	1.243	1.26	2.028	4.216	3.772

Notes: RE is central difference with Richardson extrapolation and Mstep is the completed data information matrix (Equation (1)). Since unconveraged trials were excluded, the performance of MR-SEM and Tian are shown in a most positive light. The scales of and are model specific and should not be compared between models.

3. Results

Table 3 exhibits the percentage of models for which each algorithm converged. MR-SEM and Tian-SEM failed to converge for a substantial number of trials. For these algorithms, a failure to converge does not only squander the time spent due to SEM, but if SEM is to be reattempted then the model must be re-fit from starting values. Although Agile-SEM performs well, Oakes exhibits the best performance. Table 4 exhibits mean elapsed time and accuracy of parameter covariance matrix estimators. Oakes matches or outperforms all other algorithms in both accuracy and time, with the exception of the quick to estimate, low accuracy Mstep benchmark.

4. Application

A subset of data from the 2009 Program for International Student Assessment (Bryer, 2012, Organisation for Economic Co-operation and Development, 2009) were used to illustrate the performance of Oakes. Responses to 35 mathematics items by students in the United States were analyzed. A total of 2,981 examinees were represented, but non-missing responses per item ranged from 1,040 to 1,618. The items were scored in 2 and 3 outcomes. Item calibration used the graded response model, consisting of 73 parameters. IFA Model Builder for OpenMx (Pritikin, 2016) was used to create the analysis script.

Figure 1. Scatterplot of Oakes vs. Richardson extrapolation derived standard errors.

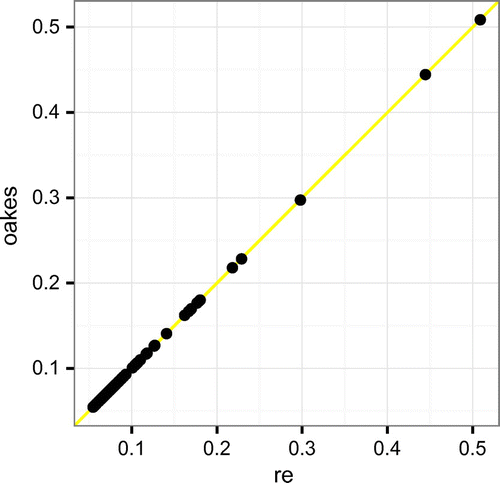
Both Oakes and Richardson extrapolation were used to estimate standard errors of the item parameters. As before, Richardson extrapolation used central difference with an initial step size of and 2 iterations, and Oakes used forward difference with a step size of . The EM algorithm converged with a maximum absolute gradient of . For both algorithms, condition number of the information matrix was estimated at about 28. The maximum absolute difference between SE estimates was . The SEs are plotted in Figure 1. Richardson extrapolation took 20.08 s and Oakes took 0.17 s.

5. Discussion and conclusion

We compared the convergence properties, accuracy, and elapsed time of Oakes and Supplemental EM family algorithms for a diverse selection IFA models. Oakes exhibited superior accuracy and speed. In the present article, only four models were examined. More research is needed to firmly establish whether the superior accuracy of Oakes generalizes. However, we argue that the evidence is already persuasive. When an algorithm is implemented optimally according to theoretical considerations, the deciding factor between algorithms may be the parsimony of the theory. By virtue of its theoretical simplicity, we suggest that the accuracy of Oakes cannot be surpassed by other numerical approaches.

Although SEs are a useful tool, they are not the most accurate way to assess the variability of estimated parameters. If any parameters are close to a boundary of the feasible set then likelihood-based confidence intervals should be used instead (e.g. Pek & Wu, 2015). Likelihood-based confidence intervals are comparatively slow to compute, but offer higher accuracy than a Wald test and are well supported by OpenMx.

Complete source code for all algorithms discussed is part of the OpenMx source distribution available from http://openmx.psyc.virginia.edu/. The OpenMx website additionally contains documentation and user support to assist users in analysis of their own data using item response models. OpenMx is a package for the R statistical programming environment (R Core Team, 2014).

Additional information

Funding

The author received no direct funding for this research.

Notes on contributors

Joshua N. Pritikin

Joshua N. Pritikin is a postdoctoral fellow at Virginia Commonwealth University in Richmond, Virginia. Joshua is interested in developing software for the applied statistician. He has made contributions at all levels from the layout of user interface elements that are directly manipulated by applied researchers to the underlying mathematics and algorithms that implement a statistical idea.

Appendix 1

Item models

labelapp:models IFA models involve a set of response probability functions to appropriately model the ordinal data. The response models used in the present article are defined here. The logistic function,

is the basis of the response functions considered here. Due to the limits of IEEE 754 double-precision binary floating-point, the maximum absolute logit was set to 35. That is, was clamped to |35|.

Dichotomous model

The dichotomous response probability can model items when there are exactly two possible outcomes. It is defined as,

where is the slope, c is the intercept, g is the pseudo-guessing lower asymptote expressed in logit units, and is the latent ability of the examinee (Birnbaum, 1968). A #PL naming shorthand has developed to refer to versions of the dichotomous model with different numbers of free parameters. Model nPL refers to the model obtained by freeing the first n of parameters b, a, and g.

Graded response model

The graded response model is a response probability function for two or more outcomes (Cai, 2010a; Samejima, 1969). For outcomes k in 0 to K, slope vector , intercept vector , and latent ability vector , it is defined as,

Nominal model

The nominal model is a response probability function for three or more outcomes (e.g. Thissen, Cai, & Bock, 2010). It can be defined as,

where and are the result of multiplying two vectors of free parameters and by fixed matrices and , respectively; and are fixed to 0 for identification; and C is a normalizing constant to ensure that .