Is order creation through disorder in additive manufacturing possible?

Abstract

Additive manufacturing is based on a deterministic principle of spatially localized material transformation. By using spatial energy resolution modes, it is thus possible to produce an object that meets a set of specifications in a step-by-step manner. This paper attempts to take the opposite view by examining whether it is interesting to use knowledge on “morphogenesis” (cf. Alan Turing) and other conceptual ideas of spontaneous self-organization to achieve a desired shape. This new and more systemic form of 3D/4D printing enables the self-assembly and establishment of elements (voxels) in various environments through the use of programmable or smart matter. The necessary convergence of interacting elements requires a related decisive activity, however, to the sign of unknown, indecision, complexity, unpredictable bifurcations, in short of scientific promise that cannot be robustly kept. Beyond this frame of generalized non-decidability—a form of abandonment of self-organization paradigm in favour of deterministic doctrines—, there are paths to partial success where desired spatial transformations can be created through (mastered?) disorder. The paper presents the conceptual bases of 3D self-organization with some illustrative examples. The objective is to highlight the interests of this disruptive vision with its realistic limits.

Keywords:

• Additive manufacturing
• self-organization
• morphogenesis
• self-assembly
• voxel
• programmable matter
• determinism

PUBLIC INTEREST STATEMENT

With the development of additive manufacturing technology, complexity in terms of shape and structure is becoming free. It is based on a deterministic principle of transforming material at a specific location using spatial energy resolution modes to build objects in a layer-by-layer manner. The paper addresses an opposite discourse which consists in studying the morphogenesis principle—initially introduced by Alan Turing and its related conceptual theories of spontaneous self-organization—to achieve a desired shape. Such discussions lead to the consideration of the emerging technology of 4D printing. It enables the self-assembly and the establishment of volumes elements (called voxels) of active and inert materials stimulated in their usage environment. Beyond this frame of generalized non-decidability—a form of abandonment of self-organization paradigm in favour of deterministic doctrines—, there are paths to partial success where desired spatial transformations can be created through (mastered?) disorder.

1. Introduction

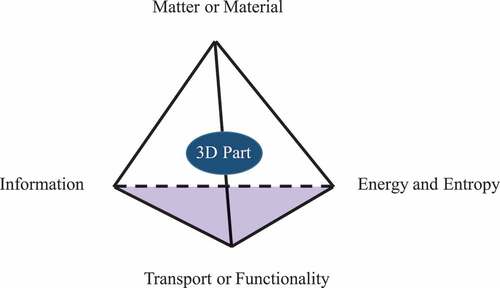
The object of this proactive reflection deals with an analysis of a field of stimulated self-organization considering the possibilities of local manipulation of matter by different forms of energy, this matter being “programmable” (according to the denomination proposed more than 30 years ago by Alain Le Méhauté) with the ultimate goal of realizing 3D shapes meeting industrial specifications. This field is called “morphogenetic engineering” (Doursat et al., 2013). It “explores the design, implementation and control (directly, by programming, and/or indirectly, by learning or evolution) of complex system agents capable of giving rise, in an autonomous and reproducible manner, to large heterogeneous architectures that will support a set of desired functionalities, without relying on central planning or external control”. In fact, it is necessary to control the parameters presented in Figure 1 in order to achieve an operating efficiency that allows the realization of a 3D object.

Figure 1. Key parameters to be considered in the realization of a 3D object

One of the objectives of this paper is to try to get out of this opposition between the morphology of an artificial structure desired by the designer—designed numerically in advance and then physically manufactured in a step-by-step manner (current case of additive manufacturing)—and a system that can be physically developed over time through the interactions between the different parts made of informed materials of the structure, which is known to generally lead to weakly structured forms. But is this way possible? Yet, trapped in the certainties of their scientific paradigms, many researchers are constantly ploughing the same furrow. What the authors actually intend in this article is to get closer to the thinking of the detective or explorer by examining (no doubt with great naivety) whether it is possible to discover exceptions to accepted laws, to go to the limits of accepted theories (Lévy-Leblond, 2020).

2. Context elements

“I don’t understand why one wouldn’t also think that the twenty-one letters of the alphabet […], if gathered together in some place and then thrown on the ground, can produce the ‘Annals of Ennius’ as a continuous reading; I doubt for my part that chance can succeed in forming a single verse” (Cicero, 2002). “Engineers hate complexity. I hate emergent properties. I don’t want the plane I’m going to take tomorrow to have any emergent properties in flight” (Drew, 2010).

In 1871, Auguste Blanqui, a French theorist of revolutionary socialism, was imprisoned and wrote in prison “L’éternité par les astres” (Eternity through the stars). For him, if the universe is vast enough, there is a chance that any object can be reproduced identically somewhere. It is thus only necessary to look in the universe for the desired object! But what do we do if time is running out? Probably Blanqui did not know Maxwell and his demons? In these same periods, with the development of automata and the exploitation of new forms of energy, the fantasy of an ideal mutation will arise, where Man would have another almost human being, an artificial clone, who would act with limitless speed, precision, regulation and strength to produce the material goods he thinks he needs. Indeed, the world of technology has undergone a major transformation over the recent decades. Elements that previously existed in purely mechanical or electrical (i.e. physical) form, and in particular elements describing logic, control and decision-making, are increasingly taking the form of integrated systems and software (i.e. cyber-elements). There is no manufacturing without digital support. “Then appears the image of a moment when everything would be transferred, transposed, gesture, force, thought, in a perfect double” (Guièze, 1983). The engineer, in charge of the efficient, economical and robust realization of the products and objects, is the intermediary in reaching the objective.

An intentional artifact (related to the work of the engineer and/or designer) can be considered as a means of linking an “internal” environment, the substance, functioning and organization of the object itself, and an external environment, the surroundings in which it is implemented. If the two environments are compatible, the artifact meets the specifications. As pointed out by Simon (Simon, 2004) in another context, knowledge of an artifact as a machine “has an advantage over knowledge of nature, because it is based on valid prior bases, whose purposes will be diverted with a certain amount of new intention to give projects intelligibility and openings to society”.

“The job of the engineer is to gather the technical knowledge at his/her disposal to imagine innovations that represent a compromise acceptable to all stakeholders. Technical perfection is the poison of the economy! You have to be ready to tinker so as to satisfy the greatest number. The resources of technology are such that you cannot believe an engineer who assures you without batting an eyelid that there is only one efficient and cost-effective technical solution and that you have to choose it” (Callon & Lacoste, 2011). Thus, in the cultural approach in engineering sciences, the search for understanding reality is largely based on “detour strategies, in other words, on the construction of models or the production of virtual facts” (Granger, 1995). But these possible detours exploit the knowledge of a robust possible and, as far as possible, the simplest possible by imposing majority causalities and the greatest possible determinism.

It is on these bases that additive manufacturing emerged in 1984 (André et al., 1984). The idea consists in placing precisely “in the right place” and “at the right time” of the material so that the organization leads by addition to the object sought (and not something close to it).… To reach this objective, it is advisable to look for situations where it is possible to take control of the complexity of the global by choosing specific processes: polymerization induced by light or electromagnetic waves, localized fusion of fusible wires, powders, etc. … (André, 2017). The notion of voxel (transformed elementary volume) is involved in this process: an object is thus defined by the addition/aggregation of n voxels (n≫1).

At the same time, volumetric processes are beginning to emerge (a single voxel with n sources) more, for the time being, out of a concern for scientific elegance and curiosity than out of actual need (André, 2020; De Beer et al., 2019; Kelly et al., 2019). Indeed, with a growth rate of around 20% a year (publications, patents and industrial market), economic pressure is more aimed at deepening than disruption. So, why try to envisage the realization of objects based on disorder, like cell growth?

Thermodynamics describes the change of a system from an initial state to a final state of equilibrium, without taking transitions into account. In fact, it is the path and the “distance” of the system from its final equilibrium that generates and maintains the structural complexity that is found in living organisms and that we seek to reproduce with “non-living” matter (Monteiro, 2018). To design a set of components that will self-assemble in solution to form a desired thermodynamically stable structure, the interactions between the components must be strong enough that an assembled structure has less free energy than its unassembled components. They must also be “specific” so that the desired shape is lower in free energy than other possible assembled structures … However, these strength and specificity requirements that may apply to a modest number of diluted elements (lack of shielding effect) may be inapplicable to a large number of systems and the “meeting” time between elements may be very long, preventing timely fabrication (Whitelam & Jack, 2015).

Dissipative structures are processes in which a fluctuation stabilizes to form a dynamic macroscopic configuration permitted by the energy flow through the system under construction. These macroscopic structures require a continuous supply of energy of an amplitude adapted to its coherence in order to grow. “The term `self-organization’ rather implies a spontaneous creation of order or organization than it refers to an agential identity capable of determining or constituting itself in a sense that implies a functional plasticity” (Alvaro, 2004). It is basically to respect the words of Bruter (1976) who wrote: “Events shape the object over time, it is above all to have pierced the secrets of its history, of the lineage of which it is both the culmination and a projection … ” (Alvaro, 2004).

A classic example is that of living systems that demonstrate behaviours and capacities for autonomy: growth, differentiation, self-repair (at least partial), etc. They are capable of modifying their behaviour and structure according to external parameters (e.g., nutrients, temperature, gravity, etc.).

Heinz Von Foerster (,1960) introduced the apparently paradoxical main idea on the principle of creating “order from noise principle”, formulated as early as 1960, which was taken up in particular by Henri Atlan in his theory of self-organization (Atlan, 2006, 2011). The thesis consists in maintaining that the noise introduced into self-organizing systems ultimately generates less entropy than a reorganization of the system that is oriented towards new purposes (the contemporary revival of this idea in the cognitive sciences appears in the form of “stochastic resonances” (Varela, 1983)). It is thus a direction envisaged in this article by imagining how, by means of a disorder (more or less organized), forms can be created responding to a user’s expectations.

Self-organization: The term refers to a spontaneous/stimulated formation of a dynamic nature leading to forms of organization resulting from a set of homogeneous or non-interacting units. Self-organization results from large-scale structures based on microscopic chaotic movement and small-scale random fluctuations (Lebedev, 2012). After having placed energy in the right place and at the right time, in a given environment, the initial random (or non-random) system organizes itself to reach a form, if possible sought by the experimenter (Moreno, 2004). From a thermodynamic point of view, this “shaping” supposes that the transport of matter and energy between the system being created must be under functional constraint in the absence of external energy input. As the object is constructed, there is an appearance of causality (universal physical laws), which can be represented by a sort of selection between several possible alternatives (Campbell, 1974).

After a cybernetics of observed systems (first-order cybernetics), a cybernetics of systems that observe (second-order cybernetics) emerged with Von Foerster (1960), i.e. an approach that takes into account the observer included in the organization process with feedback and logical and epistemological consequences of the behaviours of this category of systems that can act on themselves (Von Foerster, 1981). This kind of approach obliges the observer to formulate paradoxes and to resort to self-referential concepts, which leads to a real epistemological leap with regard to classical logic.

In addition, everyone knows the “programmed” growth of living cells, whose development exploits their environment, up to the precise creation of living beings. So why not try to master this program to achieve the less natural, roundabout objectives of creating three-dimensional objects? In order to achieve this objective, it would be necessary to exploit the processes of self-organization in natural systems by investigating whether models of collective behaviour can emerge from relatively simple rules of agents (a situation present in many complex systems). However, in the case of the spots studied by Turing (1952), the patterns are essentially stochastic and seem not to be easily guided except by external conditions (from spontaneous generation to stimulation). These stains do not normally have an intrinsic structured shape, unlike what is sought in 3D objects resulting from additive manufacturing processes where precision is required. However, Doursat et al. (2013) consider that there are exceptions that blur this apparent dichotomy and show a possible path towards the alliance of pure self-organization and 3D architecture.

2.1. Note: the interdisciplinary mission of the two authors in this paper

Within a paradigm, everyone knows that specialization is a factor in reducing errors; but, at the same time, it can be a way of some confinement. In environments requiring creativity to express itself, the disciplinary autonomy of the actors is major because it is impossible to mobilize them to make them responsible and creative, knowing that they can deviate from the mono-disciplinary criteria of evaluation and judgment. This work is part of an epistemological paradigm that we can position schematically between positivism and constructivism. However, this interaction is delicate because it associates different stakes between the natural sciences which tries to understand reality (self-organization) and the engineering sciences (3D/4D printing) which tries to create artifacts that serve human purposes.

It is true that the sought autonomy, trust and self-organization present a risk of possible dispersion by not encountering in-depth focus. For the authors, this work consists in associating at least two pillars that are today strongly disjointed, one centered on self-organization processes, the other aiming at its possible mastery in order to define new 3D/4D printing processes. Our approach has been to try to evolve and bring together these two important themes and to modestly translate them for debate and possible research action. That is to say to make evolve, by collective commitment, the representations which are normally in the scientific game, by generating as much as possible more flexible visions to open the actors of additive manufacturing towards new perspectives, because the approach can bring new ideas and new ways in advanced research, resulting directly and indirectly from this reflection. Then, along the way, this opens the door to new ways of make things in problem conceptualization, problem solving and solution building, particularly with regard to modes of thinking, collective work and its richness.

3. Framing elements associated with additive manufacturing

As expressed by Thomas-Seale et al. (2019): “Efficient design for additive manufacturing requires increased creativity, something that is currently constrained by the psychological inertia imposed by a history of subtractive manufacturing”. Of course, manufacturing strategies differ in the way they store and use assembly information. For Cademartiri and Bishop (2015), in top-down approaches, information is stored in a centralized location (a computer), and executed one by one. For researchers involved in bio-printing activities, information is possibly located in the cells and their environment … The complexity of the assembled structure (i.e., the amount of information required to describe its characteristics) stems from the capabilities of the machine rather than from the basic elements, which may be simple voxels. In contrast, in bottom-up approaches—i.e. based on self-assembly principles—information is distributed among the components (e.g., in their interactions), and is executed by spontaneous physical and/or chemical processes with little or no external guidance. Relative to the top-down approach, the massive parallelism inherent in self-assembly is one of its most attractive attributes for the idea of “autonomous”, or even spontaneous construction (Bhalla et al., 2015). The paragraph only concerned the latter approach.

3.1. System with two cubic voxels

Technology does not have to mimic nature because there can be multiple ways of assembling elements to make an object. Let us remember, however, that the embryonic development already mentioned is a practically universal reality of self-assembly. In this context, morphogenesis refers to the embryological processes that create a three-dimensional shape in the body (Doursat et al., 2013). According to these authors, it results from the behaviour of individual cells, a behaviour that is governed by their genetic regulatory circuits, which itself governs their communication and coordination with the environment (see for example (MacLennan, 2010, 2012; Murata & Kurokawa, 2007)).

But before tackling these questions, which concern a very large number of elements, it seemed interesting to us to return to the construction of an elementary set composed of two homogeneous cubes of identical size and mass. This operation also allows us in this paragraph to introduce some definitions that will be useful to the reader. Initially positioned randomly in a flat-bottomed tank, they have a certain probability of touching each other (without constituting a perfect cylinder). If one wishes to increase the chance of seeing a structure appear that is close to the desired cylinder, it is possible, by applying the first principle of thermodynamics, to favor an approximation by having a curved bottom, but also to shake the tank so that the cubes move. These elementary considerations bring to light thermodynamic aspects that will be involved in the whole body of this reflection.

Self-organization is defined by Hermann Haken (2008) as the spontaneous formation, often with apparent purpose, of spatial, temporal or functional structures in systems consisting of several components. In physics and biology, self-organization appears in open systems far from thermodynamic equilibrium. It is a phenomenon in which interacting elements cooperate to produce large-scale coordinated behaviour and structures (such as the configurations created by dissipative structures). The appearance of a higher-level structure is produced without the need for an organizing principle by demonstrating a certain autonomy and robustness (Bar-Yam, 2003; Fromm, 2004; Di Marzo Serugendo et al., 2006; Ottino, 2004); let us recall that for Ashby (1962), self-organization is normally impossible: “a system cannot self-organize because it would mean changing its law of organization according to another law that should itself be its organization … ”. This is a debate that will not be engaged here …

The development of this artificial system of self-assembly then exploits the energy transferred during these stimulated processes to perhaps achieve the goal (see Monteiro (2018)). The self-assembly of both voxels is a process of non-equilibrium in which the system evolves from an initial disordered state to a stable state that is generally more orderly. For this system, the driving force of this process is of thermodynamic nature (the assembled structures having a lower free energy than their unassembled components) (Whitelam & Jack, 2015).

If one intends to increase the probability of the formation of the cubic cylinder, it is possible, for example, with the aid of magnets included in each cube, to attract the two voxels at a short distance to form the small cylinder. Thus, the external agitation must allow the displacement of at least one or both cubes (the equivalent of an energy higher than k_BT where k_B is the Boltzman constant and T is the absolute temperature), the local attraction potentials bringing them closer together until the formation of the cylinder of the two cubes.

If now, one wishes to associate a specific face of cube no. 1 with another specific face of cube no. 2, it would be advisable to number the faces and eliminate the “bad” cylinders by repeating the operation until the objective is reached. Another way is to use specific “coders” or attractors that will increase the probability of the desired achievement. We thus highlight the importance of spatial recognition in the easy realization of a simple object.

By increasing the number of voxels, the probability of realization of an object decreases, which leads to a situation reminiscent of the one not treated by Auguste Blanqui: the non-control of time (unless each voxel is conditioned to connect at the right place and at the right time with the object under construction). In terms of fabrication, this is what Campbell et al. (2014) have achieved with specialized voxels of this type, which allow the construction of a sphere by agitating the elements.

Daniela Rus’s team at MIT worked on the creation of “catomes”, which can be magnetically assembled to produce any object (Gilpin et al., 2012; Knaian, 2010). As early as 2007, researchers from the same university created prototypes from cylinders of about 5 cm in diameter, which have since become somewhat miniaturized. Their programmable cubes move to create true three-dimensional structures, but with a still very limited number of voxels as shown in Figure 2 (Gilpin et al., 2012; Rus & Vona, 2001).

Figure 2. Example of programmable matter using cubes (Rus & Vona, 2001)

In this project, a new intelligent system made from hardware and software components allows the creation of a set of programmable objects (a form of externalized collective intelligence). The hardware component is a mass-producible micro-robot that uses the same computing device, energy, communication mean, adhesion and locomotion distributions. The software part allows a set of micro-robots to be reconfigured for a given purpose (André, 2017).

Note: Traditional approaches in creating an arbitrary shape from a group of robots involve motion planning. With a large set of robots (>106, for example) it is unlikely that programming is possible with communication and exchange times that could be very long. Goldstein et al. (2005) also remind us that manufacturing would be stopped if a single robot failed. This situation, coupled with the difficulty of building small robots that are compatible with the resolution sought in additive manufacturing (0.1 mm typically), limits the interest in pursuing work on this topic for additive manufacturing. This opinion does not correspond to the optimistic vision of Derakhshandeh et al. (2016) who proposed a universal algorithm for arbitrary shape formation (see also Arroyo et al., 2018; Daymude et al., 2017).

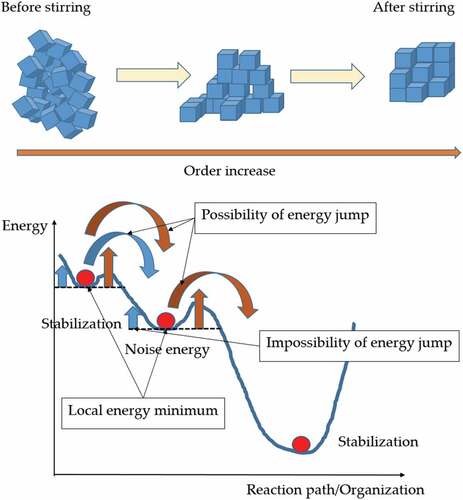
With less constrained systems, with several degrees of freedom, all attractors are not equal: some aim for greater stability, others for greater growth potential. However, the dynamics involved do not necessarily lead to the most stable state: the system following the fastest route may reach local zones of stability. This path will generally end with a local minimum of potential, not the global minimum (see Figure 3).

Figure 3. Principle of a self-organizing system

One way to take the system out of a local minimum is to add a degree of indeterminism to the dynamic, i.e. to give the system the possibility of making transitions to states other than the one that is most locally “fit”. This can be seen as the injection of “noise” or random disturbances into the system, allowing new trajectories. Physically, it is usually the effect of external disturbances (e.g., vibrations or jolts in the system) or intrinsic indeterminacy (e.g., thermal or quantum fluctuations, or simply unknown factors that have not been integrated into the description of the state).

The deeper the “valley” representing free energy, the more difficult it will be for a disturbance to move a system out of that valley. Therefore, noise will generally move the system out of the shallower valleys and into the deeper valleys (a form of determinism). However, a system undergoing noise will never really be able to settle in a local or global minimum, because whatever energy level it reaches, it can always be disturbed with the risk of reaching more energetic metastable states. So, would not it be advantageous to use an energetic noise adapted to the maximization of self-organization, starting with high amplitude noises and then decreasing them until they stop, in order to avoid the achievement of several organizational results? (Heylighen, 2000).

Determinism: It reflects the following definition: “Two experiments with exactly the same initial and boundary conditions must give exactly the same results” and the mathematical model of a phenomenon will be considered deterministic if the conditions of existence and uniqueness of the solutions are satisfied, which is generally the case for models using systems of differential equations (Dalmedico et al., 1992; Gleick, 2008; Da Silva, E., 2011).

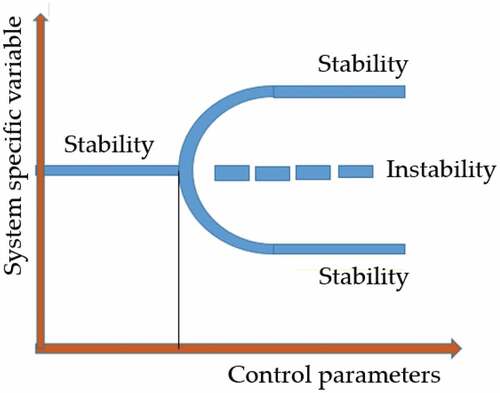
Recall that in linear systems, changes in parameters lead to quantitative changes, but do not change the behaviour (steady state) of the system. In Non-Linear Dynamic Systems (NLDS), a small variation of certain parameters, known as control parameters, can under well-defined conditions, near a critical value, cause a complete change in the equilibrium behaviour of the system. This is called a bifurcation. Figure 4 shows such a “fork bifurcation”.

Figure 4. Fork bifurcation

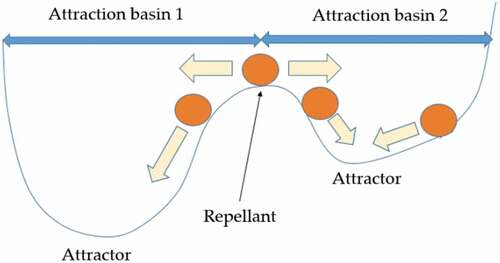
“So what seems ‘simple’ at first glance is in fact the result of a concerted evolution of various characters, moving towards a real optimization of means. It is therefore, from a biological point of view, something very complex, and the original vision of the simple ancestral disappears by this reversal due to evolutionary reasoning” (Le Guyader, 2008). Figure 5 from Delignières (2015) recalls, in a two-dimensional representation, situations associated with possible bifurcations (reaching different states from the same law of behaviour with multi-stable states).

Figure 5. Schematic representation of a landscape of attractors

In this figure, the levels of stability are in pools of attraction while the “repellents” correspond to the zones of maximum instability; the ball can go either to the right or to the left according to the very low amplitude impulse it receives (noise stimulation). The essential characteristic of the attractor is the stability of the order parameter with a strong tendency to reproducibility. According to Delignières (2015), bifurcations are announced by critical fluctuations, i.e. a significant evolution of the order parameter in the vicinity of the transition (as in a change of orientation of molecules in an organized system as soon as a transition temperature is exceeded). Ultimately, it would be possible to find an applicable approach if, during these evolutions, the number of attraction basins and their qualities are little disturbed. Or in other words, is it possible to show the possibility of having, as Thomas et al. (2004) propose, “Chaotic labyrinths” that constrain complexity?

Order of a system (Shannon’s redundancy function R): R is defined by R = 1 − H/H_max where H_max is the amount of information that corresponds to a diversity system in the absence of redundancy. The organization would play on a kind of compromise between the quantity of information and redundancy … (Yue et al., 2015). Self-organization would be associated with an increase in the quantity of information (internal programming? (cf., for example, (Kaern et al., 2005)). For Rothstein (1962), the order of the system would be defined by R$\times$H_max, R being dependent on the constraints of the system and H_max on the potential diversity of the system (see also (Atlan, 2006)). Under the influence of disturbances, for high values of R, the system can continue to operate as long as a certain redundancy can remedy communication losses according to the principle of order through noise (Von Foerster, 1960).

However, it is easy to imagine that the proposal made above to control the energy amplitude of the random stimulations (or not) will not be enough to create an organization similar to a 3D object as long as there is no attractive potential between the particles constituting it. This is indeed what Campbell et al. (Ashby, 1962) sought to do in their spectacular experiment (and as von Foerster had envisaged in 1960).

3.2. Morphogenesis

The example of morphogenesis (D’Arcy Thompson, 1917)—a set of laws that determine the shape and structure of tissues, organs and living organisms with extensions in other fields such as 3D/4D printing, architecture, etc.—is a good example. By considering the following statement: “form as a diagram of forces” of D’Arcy Thompson (1917), one can identify a symmetry of the `form-context’ system (Alexander, 1964), which supposes a mutual relationship/phenomenon between the form and the environment (Henderson, 1913, 1917). This paradigm illustrates the relevance of the non-linear approach (a simple, deterministic, local dynamic model that explains how nature globally constructs stable, reproducible, and robust forms, at the macroscopic level), but also the margin of scientific progress that exists in understanding, and then in mastering and exploiting, the associated mechanisms for concrete applications (André, 2017). Morphogenesis deals with the evolution of forms, i.e. any subsets, which are not necessarily regular (Aubin & Lesne, 2016; Thom, 1972, 1980).

The interaction between the voxels constituting a system is central to the problem of self-organization, as it is the means of capturing and transmitting the information that influences each voxel (Atlan, 2006; Oxman, 2010). We generally distinguish two modalities for the transfer of information: direct from voxel to voxel, or indirect by modification of the environment itself. The question of the nature of interactions is therefore fundamental and a prerequisite for any modeling of self-organization.

Note: Stigmergy. Indirect interactions are associated with the phenomenon of stigmergy (Charrier, 2009; Grassé, 1959) where the construction of an object has an amplifying effect on the subsequent construction of the object. The object that emerges from collective fabrication thus participates in its own development, since it participates passively in the construction (Michener, 1974).

Turing (1952) proposed the concept of “morphogen” and integrates, in a mathematical model, in the form of non-linear differential equations, biochemical data, more particularly from enzymology and solution physics (Harrington, 2016; Lesne, 2012; Szalai et al., 2012). Turing demonstrates that, starting from a homogeneous medium, one can arrive at a periodic spatial distribution of the concentration of these morphogens. In Turing’s model, an instability resulting from the intrinsic properties of the reaction system breaks the initial symmetry of the medium, spontaneously generating its structuring, and its “self-organization”. To understand morphogenesis, we need access to these pre-patterns, which are the result of two simple mechanisms of physico-chemistry, the chemical reaction and the diffusion of matter. Processes that are biological are almost secondary, since they correspond to a stereotyped response of the threshold effect type (Le Guyader, 2008; Koch & Meinhardt, 1994).

It is generally not possible to predict the evolution of forms by inferring them only from the application of simple laws that could have been identified (non-deterministic evolution by interaction of systems with each other and with their environment). However, as an example, Prigogine (Szalai et al., 2012) recalls this experiment: If sodium chlorate is cooled at rest, the crystals produced are optically inactive. If, at the same time, the solution is stirred, one obtains either levorotatory or dextrorotatory crystals … It is a bifurcation; the first gives either a left or a right form and the initial germs that will participate in the crystallization are either left or right. The symmetry of the reactive system is thus broken. This example serves to show that irreversible phenomena do not necessarily reduce to an increase in disorder, but that there can be constructive roles to this irreversibility of time, as in the case of life. Hawking (1989) reminds us on this subject: “A strong thermodynamic arrow is necessary for intelligent life to be able to act”.

Under these conditions, Turing (1952) showed, by using other examples, how reactions between chemical or morphogenic substances—coupled with a process of diffusion of these substances through living tissues—could give rise to the appearance of specific structures or regularities (spots on a coat, the shape of a crystal, a shell, etc.). In his seminal article, he introduced a mathematical model called “reaction-diffusion equations” as well as the study of this model in some relatively simple cases. The dynamics of this basic model, which it makes explicit, results from the coupling between chemical reactions and the diffusion of reagents, in a continuously fed system. Turing structures correspond to spatially periodic variations in the concentrations of chemical species (Joshi & Davidson, 2012; Lesne, 2013; Shalygo, 2015; Zenil, 2013) that compete with molecular transport mechanisms. Thus, to observe spatial variations in concentrations, other mechanisms have to be considered. He introduces a scenario involving two species denoted A and B, “morphogenic” and the conjunction of the following properties:

• Species A is able of inducing its own production;

• Species A can produce the second species B;

• Species B inhibits the production of A;

• B diffuses faster than A.

It is thus sufficient that a small local fluctuation at a point in space induces a slight excess of A so that the production of A and B is higher than the average at that point. B, diffusing faster than the excess of A, creates an inhibitory crown around the initial point, isolating the peak of A by a zone richer in B. These random evolutions may occur at other points in space with other peaks of A. “These activator peaks result from the selective amplification of the minute but innumerable fluctuations that spontaneously affect the state of homogeneous mixing. The most dynamically stable distribution of these peaks forms a periodic pattern, like the spots that can be observed on the cheetah” (Chossat, 2015).

James Clerk Maxwell wrote in 1876 (cited by Thom (1983)): “When the state of things is such that an infinitely small variation in the present state will alter the future state only by an infinitely small amount, the state of the system, at rest or in motion, is said to be stable: but, when an infinitely small variation in the present state can cause a finite difference in a finite time, the condition of the system is said to be unstable. It is obvious that the existence of unstable conditions makes it impossible to predict future events, if our knowledge of the present state is only approximate and not exact “ … The question of the control of the “good” main parameters influencing stability or instability is therefore primordial, but may not be sufficient.

3.2.1. Inverse problem

The shape of an object, designed in advance, thanks to the knowledge of the interactions between the different parts of the structure, its manufacture must take into account the global and local effects of the environment during morphogenesis (Zahadat et al., 2017). One question is how to organize the initial structure of voxels to reach a given shape. In living organisms, morphogenesis processes adapt the structure to the environment, both at the individual and evolutionary scales. However, according to Beal et al. (2011), no clear framework has been developed to exploit morphogenetic principles in the creation of artificial systems.

From a modeling point of view, we can consider a system that evolves over time from a given form to reach another form (dynamic approach) or to impose on a stable form constraints of different natures (chemical, energetic, etc.) that will lead to deformation (thermodynamic approach). In the first case, it may be useful to introduce temporal elements U_i to define the evolution at a given time; in the second case, thermodynamic and chemical potential elements S_j are introduced. This being the case, starting from a given set U_i, it is possible to define in principle the S_j, as long as all the influencing factors are known. U_i is defined from its spatial coordinates, its time-dependent functionality while the S_j define the interactions between the different U_i. Then, the U_i can be defined by a relation f of the type: U_i = f(U_i, S_i, N) where N represents random noise and/or bifurcations.

The inverse problem aims at defining, if possible, the S_j defining a set point and to find the U_i that meet the objective. This is a classical problem which is always difficult in the case of generally ill conditioned linear systems (cf. de-convolution if only because of noise and measurement errors (Mugnier, 2008)); it will be all the more difficult in non-linear approaches with noisy signals. This being the case, the stakes are high because the control of the inverse problem can constitute an integral means of realizing an object from a matrix that is easily realized and whose deformation as a function of time or energy supplied could allow the realization of an object with a complex shape.

Morphogenetic engineering: This sub-discipline explores the design, implementation and control (directly, by programming, and/or indirectly, by learning or evolution) of complex system agents capable of giving rise, in an autonomous and reproducible manner, to large heterogeneous architectures that will support a set of desired functionalities, without relying on central planning or external steering (Doursat et al., 2013).

3.3. General considerations

An element of any kind can be defined from its ontology (what it is), its functionality (what the object does), and its genetics (what the object becomes). This systemic introduction made by Le Moigne in 1994 (Le Moigne, 1994) in fact implies a triple knowledge. In a causal logic, the knowledge of interactions between the different elements of an object can explain how this object evolves in time to a stable structure from a thermodynamic point of view. On the other hand, when these interactions are not precisely known and/or when recursive effects are to be taken into consideration, especially when different elements are included in the object, the situation of the final fate can become inextricable and one must often be satisfied with trends. But the precision sought in additive manufacturing cannot be achieved.

For the researcher studying the behaviours associated with the intrusion of time and functionality aspects in additive manufacturing, systems are for times sufficiently long, fully determined. But, as “self-organizing” phenomena, they can become sensitive, far from equilibrium, to factors considered negligible near equilibrium. It is the intrinsic activity of the increasingly complex system, increasingly non-linearly behaving, that determines how it is possible to describe its relationship to the environment, and thus generates the kind of intelligibility that would be relevant to understanding its possible histories. It is therefore not only an application field with its constraints, but also a theoretical field to be addressed in order to robustly solve the equation finality/means to achieve it.

“The work of an engineer is to gather the technical knowledge he or she has at his or her disposal to imagine innovations that represent a compromise acceptable to all stakeholders. Technical perfection is the poison of the economy! You have to be ready to tinker to satisfy the greatest number. The resources of technology are such that you cannot believe an engineer who assures you without batting an eyelid that there is only one efficient and cost-effective technical solution and that you have to choose it” (Callon & Lacoste, 2011). On reading these sentences, the failure to master the inverse problems in the morphogenesis aspects presented in this reflection could (should?) have closed the debate. There is still no realistic solution today! In the cultural approach in engineering sciences, the search for the understanding of reality is largely based on the construction of models or the production of virtual facts (Granger, 1995). But these detours exploit the knowledge of the possible, the known and as far as possible the simple by imposing causalities … These simple elements do not appear in a very clear or obvious way! Moreover, as soon as bifurcations, autonomous systems are brought into play, apparently non-causal approaches, conservatisms (associated, however, with a distant disruption in 1984 (André et al., 1984)) are reinforced. So, apart from a few timid attempts, the field of the theme is rather unexplored. It is not possible, for example, to know whether bottom-up/top-down couplings generate possible gains (in machine time, functionality, etc.). With the success of current technologies and the difficulty of supporting risk-taking in research, it is possible that this exciting field will remain fallow.

The change in the focus of research towards a more systemic approach does not wish to be an indication of a field of scientific disciplines that, wishing to retain its power, is losing its authority, even if current societal concerns still do not bear well with constructive forms of insubordination (even in research). It aims at a real responsible integration of exploration, of deepened curiosity, of activities open to society, carrying meaning, and allowing new research in additive manufacturing to emerge as possible credible scientific carriers of the movements that are taking shape or that could take shape.

The evocation of the different attractors of disruptive innovation in manufacturing seeking to exploit principles of massive parallelism is an integral part of our quest in this article. Transposing the reality as experienced by the authors with its possible biases of understanding, is to redo a bit the history of new additive manufacturing processes and techniques that could, if successful, populate, or even invade our daily life in a few years. It is in the spirit, to make a story, to internalize it by trying with the means and time available to restore them with a vision of a duo accomplice, with the risk of making mistakes, of having missed the fertile idea … But this is the price to pay … remembering however this sentence by Simone Weil (2020): “The negligible is not anything else than what must be neglected to build physics; it is by no means what is of little importance, for what is neglected is always an infinite error” …

Figure 6 reminds us of the modes of operation necessary in a systemic approach … Interdisciplinarity, which is indispensable in this type of operation (after defining the project framework), is a process in which one develops a capacity for analysis and synthesis from the perspectives of several disciplines. Its objective is to deal with a problem as a whole (principle of integration in organizational engineering), by identifying and integrating the relationships between the different involved elements. It attempts to synthesize and link disciplinary knowledge and to place it in a broader systemic framework, while engaging each member from a discipline in the relationship to his or her own identity and without forgetting the relationship between scientific practices and identity constructions.

Figure 6. The “virtuous” circle of the systemic approach (simulation also includes experimentation in connection with)

4. The role of chemistry and/or digital technology to the organization

It is of course possible to keep the spirit of Dr Skylar Tibbits or Prof. Daniela Rus in programming the material, it is also envisaged to keep the principle of a less “stimulated” self-organization; this section is structured towards this aim.

4.1. “Strict” material programming

From a historical point of view, DNA origami makes arbitrary shapes from pieces of DNA. It was developed by Paul Rothemund of Caltech, USA, in 2006. The chemical properties of the molecules that make up DNA, the nucleic bases, are well known. Built upon the principle of “Watson–Crick” bonds, it is possible to model two- or three-dimensional structures. Rothemund’s technique uses a long chain of virus DNA with a linear and relatively uncomplicated structure, the sequence of which is known exactly. Then, by using a computer, the precise places where the DNA molecule must be bent to reach the desired shape is specified and located. Small “pieces” are then synthesized that will bind themselves exactly where they are needed to “bind” the viral genome.

Only these “staples” need to be synthesized, as the basic material is borrowed from nature, and the operations are therefore both less expensive and less time consuming. These small staples will then, by the role of chemical bonds, cling to the scaffolding chain. In addition, since these staples will also attract other molecules, they will bend the central DNA strand and give it a particular shape. This is from this bending that the original name DNA origami comes from. In Rothemund’s publication (Rothemund, 2006), images of constructions in various forms that he has made were presented. The most original are undoubtedly the world map, the snowflake and the smiling man. Of course, it is not only drawings that can be reproduced with DNA. Hao Yan’s team managed to create closed three-dimensional shapes as illustrated in Figure 7 (Han et al., 2011; Sawyer, 2011).

Figure 7. DNA origamis

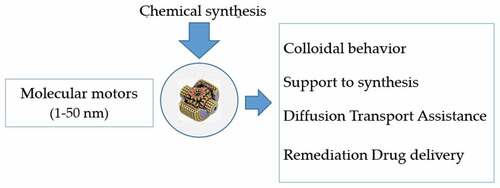
Since then, nano-motors of a few nanometres have been developed with controlled direction of rotation (Dureuil, 2013). “The rotor is made of five ferrocenes connected to a central phenyl, while a ruthenium in the center acts as the axis of rotation. Finally, the assembly is lifted by three feet and tiols to grip the molecule on the surface” (Dureuil, 2013). These spectacular molecular machines are animated by movements under the action of an external stimulus (nano-motors, nano-elevators, nano-pincers and nano-transporters). Their use, due to their extreme small size, raises the question of energy input (stimulus) and its mechanical recovery. However, there are applications in drug delivery (Bandari et al., 2020; Medina-Sanchez et al., 2018). Other applications, presented in Figure 8, of these nano-metric entities are considered by Novotný et al. (2020).

Figure 8. Application areas of nano-machines

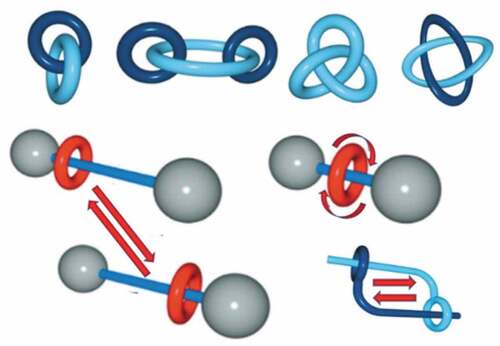
Once science begins to understand how nature has selected some forms and not others, both in the physical and biological world, it can seek to apply/transpose the corresponding mechanisms to solve engineering problems, i.e. those related to the manufacture of artifacts, tools or final objects. The wide variety of applications given to a generic form such as the fabrication of a functional object is not inspired by what nature does, and it is interesting to examine whether “morphogenesis” knowledge can be used to achieve the desired form through self-organization (rather stimulated) (Baquiast, 2004). Figure 9 from Sauvage (2017) presents some examples of such systems.

Figure 9. Examples of molecular machines and their displacements

According to Vilain (Prix, 2016), Richard Feynman had envisaged the development of nanotechnologies around 1960 and in 1984 evoked the possibility of building machines on a molecular scale. Sauvage, among others, showed that it was possible to design and synthesize these “molecular machines” by assembling distinct molecular components, designed to perform movements like a classical engine, under the effect of an external stimulus and via an energy input (Sauvage’s work aimed at the synthesis of contractile and extensible molecular systems by analogy to the functioning of a muscle).

It is a matter of entangling molecules within each other, via mechanical and non-covalent bonds: for example, two ring-shaped molecules (cf. Figure 8) can be nested within each other, or a ring-shaped molecule can be “threaded” onto an axis-shaped molecule, like a pearl onto a wire. The molecular “wire” is provided with bulky groups at its ends to prevent the ring-shaped molecule from escaping. The different elements move relatively independently. These nano-objects are mainly directed towards the transformation of external energy into internal energy (mechanical), with potential application in drug delivery and information processing (molecular electronics).

This is a problem that is always difficult in the case of generally poorly conditioned linear systems (Mugnier, 2008), especially in the presence of noise. This being the case, the stakes are high, because the control of the inverse problem can constitute an integral means of realizing an object from a matrix that is easily realizable and whose deformation as a function of time or energy supplied could allow the realization of an object of complex shape. Thus, according to (2014), it is now possible to create DNA Origami by computer. But this is already less satisfactory when we are interested in larger elements since the number of chemical bonds to be taken into consideration increases with the power of three of the size (see, for example, Kotov, (2017); Sanchez (2011) and Zentel (2020)). It therefore does not yet seem possible to develop systems in which the object would be entrusted with a form of intentionality, thus, at the limit, leaving it the choice of searching itself for what it needs to make itself, and thus moving to self-organization with selection of the necessary elements that it would extract from a “bank” for the construction of the final object?

4.2. Programmable matter

Programmable material is a material whose properties can be programmed to achieve specific shape or stiffness to order (Cuellar et al., 2018; Derakhshandeh et al., 2016; Kenyon, 2009; Mirzaali et al., 2019). This concept requires that the constituent elements interact and rearrange themselves “intelligently” in order to achieve the goal (techniques for programming materials and materials to assemble or deform themselves, perform a function, or even disassemble afterwards). Other examples of metamaterials than those presented in the previous paragraph have been developed; examples include logic systems based on Belousov–Zhabotinsky reactions (Alba (DARPA), 2017), logic sensors (Abadal et al., 2020; Liu et al., 2019), actuators (Giltinan et al., 2016), etc. We have an organization composed of multiple materials, designed by engineers, leading to particular functionalities. Other metamaterials of programmable matter have shape-changing capabilities; in the target domain, the idea is to use them in 4D printing, an emerging field combining additive manufacturing and stimulus-responsive materials (Ge, Sakhaei et al., 2016; Hamel et al., 2019; Lin et al., 2018; Maeda et al., 2011; Pinho et al., 2020; Sossou, Demoly, Belkebir, Qi, Gomes, Montavon et al., 2019a, 2019b). Figure 10 presents an example of the potentialities of 4D printing. However, unlike what the Portuguese man-of-war (Physalia physalis) is able to do in nature (Munro et al., 2019), one of the difficulties consists in assembling the individual voxels to form an efficient and robust tool/machine.

Figure 10. Thermally excited actuator made of shape memory polymer and 3D printed with stereo-lithography technique (image provided by Ge, Qi et al. (2016) and Ge, Sakhaei et al. (2016))

Belousov–Zhabotinsky reaction: It illustrates the fact that non-linear differential equations controlling a set of chemical reactions can make structures and patterns appear in space and time in a chemical system. In a thin layer (thickness of the order of mm) one can observe the emergence from points in space, called centers, of concentration fronts propagating radially in an isotropic manner at a speed of the order of a few millimeters per minute (Guespin-Michel, 2016a; Vanag & Epstein, 2001; Vidal et al., 1986).

In any case, imposing the structure and functionality of the constituent elements of an adaptive system is far from the spirit of publication. Nevertheless, considering the proximal aspect and the development of the theme, it seemed necessary to the authors to clarify this notion.

4.3. “Programmed” matter—bio-mimicry

Morphogenesis is the set of processes that will give shape to an organism. Perhaps we should examine the movements of a certain number of social insects (e.g., bees, ants, termites), fishes, birds, etc. that know how to move in a complex environment and for some of them build habitats that are themselves complex according to specific forms: “why is the group coherent while each individual seems autonomous? How are the activities of all individuals coordinated without supervision? Ethologists who study the behaviour of social insects observe that cooperation within colonies is self-organized: it often results from interactions between individuals” (Bonabeau et al., 1999; Bonabeau & Théraulaz, 2000). What Nature knows how to do with ants or termites, Man is beginning to understand and do, but the application stage in additive manufacturing is at best only in its infancy. Nevertheless, if we can be satisfied with shapes that are not very precise, it is not impossible to envisage a very flexible process for making intelligent objects …

In 3D systems to be designed based on “network swarm” type principles, voxels randomly interact (but with probabilities linked to supposedly known interaction laws) on a three-dimensional network, and have no global representation of the architecture they build; they can only perceive the local configurations of matter surrounding them, and perhaps a small number of these configurations will lead to an organized structure fulfilling the specifications (Mirzaali et al., 2020; Théraulaz & Bonabeau, 1995).

Swarm: a large group of identical organisms, natural or artificial, each with limited intelligence, that work together to achieve a higher goal beyond their individual capacities (Li et al., 2016; Marshall, 2020a; Sharkey, 2007).

With simple laws, different applications can be envisaged:

Reconfigurable cellular robotics (La boîte verte. Des recherches de forme pour des essaims robotiques collaboratifs, 2020; Fiévet, 2004; Firat et al., 2020; Goldstein et al., 2005; Hornyak, 2019; Jin & Meng, 2012; Mathews et al., 2017). Competitive behaviour is the opposite of cooperative behaviour. However, in such a case, difficulties of convergence towards a consensus for the resolution of a task—in which at least two robots are involved—must be mastered (Kancir, 2018); Slavkov et al. (Slavkov et al., 2018) showed how hundreds of mini-robots could use the genetic and cellular mechanisms governing early biological morphogenesis. The spontaneous organization process emanates from local interactions of elementary robots under the control of genetic circuits identical in each voxel, resistant to intrinsic noise, and able to adapt to changing environments. Swarm programming may seem quite simple, as it involves only a few identical lines of code for each robot. The difficulty lies in making sure that the few simple rules that govern the interaction of each robot with its neighbor generate the swarm behaviour required to perform the task. The goal is that a robot can be programmed to respond predictably to its sensory inputs, but the inputs themselves cannot be predicted with certainty (Marshall, 2020b);

Bio-printing (André, 2017; Landau et al., 2018; Okuda et al., 2016; Richards et al., 2017; Skylar-Scott et al., 2019; Tamay et al., 2019): Bio-printing from additive manufacturing technologies is developing in terms of scientific research. It indeed becomes possible, with stem cells from people (with serious diseases), to one day recreate deficient organs without rejection from sick patients since these organs would be recreated from compatible healthy cells. On these bases, the engineer’s initial vision was to make it simple, if possible within a causal thinking, with the tools at his disposal. Living matter can be ordered, meaning that its shape can be, at least in first approximation, geometrically described. It may be thought that structures, more or less self-organized, must be associated with certain types of physical or physico-chemical conditions. Placed in a broader evolutionary perspective, it is however impossible to predict the evolution of shapes by inferring them from the application of simple laws that we could have identified. More precisely, with experience, if these laws are necessary, they are probably not sufficient. They form the inescapable background of an evolution that develops in a non-apparently deterministic way by interaction of natural systems with each other and with their environment. The sciences of “morphogenesis” would thus have validity only within the limits of ordinary or macroscopic physics. However, this one is only an approximation imposing to chase away linear determinism …

“Human life starts from just a single cell. Cells proliferate, differentiate, lay down extracellular matrix which eventually forms tissues and organs, which all grow and function in synergy” (Thomas-Seale et al., 2019). Recently, the understanding of cell self-organization processes in three-dimensional multicellular structures has opened perspectives for tissue engineering (Laurent et al., 2017). Micro-engineering approaches for the construction of functional tissues are being developed with a better understanding of morphogenetic processes and in the ability to direct them in vitro without being able to build robust organs. Numerous challenges remain to associate micro-engineering, morphogenesis and cellular self-organization (Martin et al., 2019; Zhu & Yang, 2018).

Attractors and initial conditions: Non-linear differential equations in general are non-integrable: Either one calculates numerically the evolution of each variable over time by numerical methods, or one is interested in the solutions towards which the system converges after a certain time. However, non-linear systems can have several possible states, the system arriving in one of them depending on the initial conditions. Each solution is an attractor. For a given dynamic system, the solution towards which it will tend, therefore, depends on the values of the variables at the moment when the movement begins (Guespin-Michel, 2016b).

In this logic of progress, in an attempt to simulate the fate of cell growth with differentiation, Danzo and André (2020) used a model of the “cellular automaton” connectionist type, characterized by three basic components: a network, an activation rule and a learning rule (Collectif, 1995; Neagu et al., 2006; Wang & Sun, 2013). The network is composed of a set of cells initially placed at a given point in two-dimensional space. On this basis, cell proliferation and migration can occur as long as nutrient and oxygen supply criteria are met (MacCune et al., 2014; Sun et al., 2017). After many generations, the system must tend towards a dynamic equilibrium, with the cells present (if any) being those that respond to the “biological” programming sought. As long as the cells retain their nature (no differentiation in this stage), it must be possible to demonstrate that a stationary state is indeed reached.

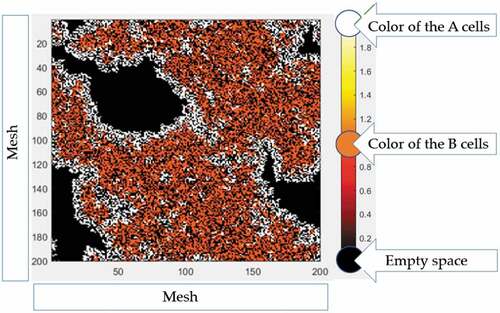
With A cells that can transform into B cells (and vice versa), it is possible to find conditions where one obtains areas preferentially populated by A cells with B cells surrounding empty spaces (which could anticipate the formation of blood vessels) as shown in Figure 11.

Figure 11. Growth with cell differentiation and location

What the simulations show is that with a very limited number of parameters, it is possible to observe bio-buildings with functionalities that can mimic natural cellular behaviour. If this is indeed the case in real conditions, it would be conceivable to try to orient cellular behaviours towards forms likely to build elements of what could be a real biological tissue. However, whatever the parameters (such as for tiger spots or zebra stripes), it was not possible to foresee a manufacturing process that would strictly comply with a set of specifications. Some orientations are therefore conceivable, but not precise locations.

4.4. Crystalline self-organization

Cited by Thuillier (1980), Stéphane Leduc, more than a century ago, wrote: “The elementary act of life is diffusion and osmosis”. It was this professor of medical physics who fabricated forms and structures “similar to those of living beings”. In 1910, he published a work entitled: “Physico-chemical theory of life and spontaneous generations”. Figure 12 represents one of Leduc’s osmotic productions (Haudin et al., 2018; Thuillier, 1980). “When we have come to know the physical mechanism of the production of an object or a phenomenon, […] it becomes possible […] to reproduce the object or the phenomenon, science has become synthetic. Biology is a science like any other, […] it must be successively descriptive, analytical and synthetic” (Leduc, 1912) …

Figure 12. Leduc’s osmotic productions (copy of Thuillier (1980); see also Eastes et al., (2009); Haudin et al. (2018); Leduc (1912, 1910); Whitesides & Grzybowski (2002))

This causal theory and the resulting methods to be applied to these constructs aim at obtaining finished and optimized products after “their start-up”, especially with regard to the consumption of matter and energy, the notion of voxel which can then reach the size of a molecule, or even a cation or an atom … With such an idea, as for all (or most) engineering sciences, these methods are still often thought of as deterministic: Phenomena are controlled by laws, which must be discovered and applied as faithfully as possible … There would therefore be (too) little room for randomness.

On this basis, it is possible to think that one will be able to master matter, in its most intimate elements, so that it transforms itself to reach a given form and functionality. This is what we find in the science fiction film “Terminator 2”. The generic idea is based on the concept of self-organization, where a system composed of elementary components assembles and organizes itself spontaneously and autonomously, following specific and local interactions between these components. Molecular self-assembly occurs when the components are molecules or supramolecular elements. The transformation of matter to reach a given shape is possible if the number of operations to be performed on it is as limited as possible, hence the exemplary realization of nanometric objects. Indeed, stimulated “self-organization” phenomena can become sensitive, far from equilibrium, to factors considered negligible near equilibrium. It is the intrinsic activity of the increasingly complex system, increasingly non-linear in its behaviour, that determines how it is possible to describe its relationship to the environment, thus generating the type of intelligibility that will be relevant to understand its possible histories.

Crystal growth as introduced by Leduc (1910) is a form of self-assembly (Bowden et al., 1997; Singh et al., 2014; Whitesides & Grzybowski, 2002), where individual objects (i.e. atoms and molecules) arrange themselves in regular arrays. According to Abelmann et al. (2020), crystal formation has been extensively studied (Beatty & Jackson, 2000; Goodsell & Olson, 2000; Langer, 1980). The growth of crystals occurs through a mechanism of nucleation and growth, the former starting on well-defined matrices (epitaxy) (Goodsell & Olson, 2000) or random imperfections. Thus, apart from crystalline shapes corresponding by chance exactly to the size and shape of the 3D object, it does not seem possible to envisage the direct use of such spontaneous technology to make 3D objects. Moreover, for objects of industrial size (several cm), the molecular transport mechanisms associated with the thermodynamics of crystallization will probably impose a time-consuming construction of the object.

However, if it were possible to orient the crystallization in certain privileged directions, would it be possible to hope for the realization of a shape by coupling self-organizing top-down and bottom-up approaches?

5. Can we associate order and disorder?

Following the research initiative of Lipson and Pollack (2000) on 3D printing autonomous (in terms of power, behaviour and even of design and fabrication) robotic systems based on structure and control building blocks, Kheifetz (2018) considers that it is necessary to use 3D machines to produce objects and that self-organization processes cannot meet this objective. The previous paragraphs seem to prove him right because it seems difficult, on reading the bibliography, to master precisely a shape that meets a prior instruction. Indeed, Tolley, Krishnan, Erickson et al. (2008); Tolley, Krishnan, Lipson et al. (2008) and Krishnan et al. (2009) have built an indirect assembly technique of regular objects exhibiting interlocking faces at the 2D level by controlling fluidic forces and fluid flow conditions at the local and global scales. Such work overcomes limitations of stochastic agitation and rail-fixed systems. It is during the self-assembly of elements from the beginning of manufacturing that the object acquires its final shape (Jakab et al., 2004) and the difficulty is to solve the opposite problem (provided that at least one solution exists and is known). In this paragraph on self-assembly processes, we find the dream of having the universal assembler that could make any object (or organism) from atoms/molecules/voxels taken from the environment. We are far from this, but this does not prevent us from trying to build less ambitious models of self-assemblers. To put it simply, what the engineer is looking for is to place the matter “in the right place” and “at the right time” so that the organization leads to the desired object (and not something close to it) … As we are dealing with an insufficient mastery of systems, the designer must look for situations where he can regain control over the complexity of the global by informing the matter. It is these efforts that are presented below.

The morphology of a 3D object is thought and designed in advance or it can be developed over time thanks to the interactions between the different elements that will participate in the creation of the shape. A successful generation process must consider the global and local effects of the environment during morphogenesis (Zahadat et al., 2017). The evolution of many systems here is governed by the external environment. For synergistics, this is mathematically translated by the variation of the order (or control) parameters of the system by the environment. The system thus sees its stability disturbed, which can lead to other motives, other regularities and, consequently, to the achievement of desired objectives (Firat et al., 2020). The creation of transformative novelty is thus possible because of this break in the logical sequence by bifurcating between a set of interacting elements (Schwarz, 1977).

A morphogenetic approach to programmable matter can be organized around two main classes of objects: active assemblers and passive components; together they fulfil roles similar to those of cells and their products in embryonic morphogenesis. The components include structural elements and physical signal carriers (e.g., chemical morphogens). These components are passive to the assembly process, but may be active in the assembled system. For example, components could include objects that will be used as sensors, actuators, or amplifiers in a robot, but are passively manipulated during assembly and reconfiguration (D.J. MacLennan, 2015).

5.1. Constraints to bring in free self-organizing systems

Programmed assembly of structures from their components requires instructions to direct reproducible fabrication of a particular structure from a set of possibilities (some of which are not known). This “fabrication information” must specify the location and connectivity of the building elements within the assembled structure and, often, the order and manner in which they are added (Cademartiri & Bishop, 2015). These authors propose in an unstimulated constructive dynamic to constrain space through spatially resolved self-organizing processes (puzzle, folding, dynamically switchable affinities between assembly components for Tolley, Krishnan, Lipson et al. (2008); reaction envelope for Labrot et al. (2006)). The question of spatial resolution is thus solved using a hybrid fabrication mode (see also (Alben et al., 2019; Bende, 2017)).

The dynamics that Turing (Von Foerster, 1981) explained in his model results from the coupling between chemical reactions and the diffusion of reagents. Turing structures corresponding to spatially periodic variations in the concentrations of chemical species could be localized by localized energy inputs and/or by molecular diffusions in an artificially bounded space (Szalai et al., 2012). Apart from a 3D bio-manufacturing process (Zhu & Yang, 2018), we found only a limited number of scientific references for the exploitation of this idea of realizing “pixelized” polymers with specific properties.

One of the reasons may be the non-existence of reactive/diffusion associations or the time required to perform a transformation which, given the classical spatial constraints of additive manufacturing (0.1 mm) and molecular diffusion coefficients (between 10⁻⁵ and 10⁻⁷ cm².s⁻¹) imply processing times of approximately 10 seconds to 10 minutes per voxel. While the evolutions may be independent of each other, this time may not be prohibitive. However, as suggested by Bhalla et al. (2015), it is conceivable to consider the design of self-assembled voxels produced by different stimuli, time savings during the manufacture of the object as a whole may occur.

5.2. Stimulated self-organizing systems: bottom-up/top-down coupling

To illustrate the point, Rajasekharan et al. (2017) have shown that it is possible to make bio-inspired composites based on a combination of bottom-up molecular self-assembly and top-down additive fabrication (see also Vincent et al. (2006)). This association allows to adjust the properties of the materials from bottom to top resulting in mechanical behaviours similar to those observed in natural mineralized composites. The general idea is to have acceptable self-organization conditions without affecting the spatial resolution, one of the fundamental constraints of 3D printing. There are several ways to achieve this goal, the main way being to achieve self-organization in a voxel of a size close to the desired resolution. This compromise moves away from the sought-after principle of exploiting the massive parallelism inherent to self-assembly, which was a particularly attractive promise.

5.3. Chemical robots

Richard Feynman had predicted the development of molecular nano-machines as early as the 1950s, such as those developed by Jean-Pierre Sauvage in 1983 when he invented a chemical method allowing two molecules to be intertwined in the form of rings, thus forming a chain called catenane (CNRS, 2016; Collin et al., 2001). Through electrical or light stimulation it has been widely shown that it is possible to rotate a molecule in a controlled motor-like manner. The cooperative behaviour that is exploited is characterized by a situation where different agents interact to solve a task or situation.

Maeda et al. (2011) have shown that self-oscillating gel actuators can be realized for chemical robotics. The gel has a cyclic reaction network as a metabolic process. During the reaction, the gel shows a small but significant change in volume by chemical energy. The periodic self-oscillating motion of the gel is produced by the dissipation of chemical energy from the Belousov–Zhabotinsky oscillatory reaction. Other systems where chemistry is absent have been proposed in Section 1.1 (see also (Mathews et al., 2017)). The final question is to control, not the displacement, but its stoppage (obligation to eliminate a chemical reagent).

Generally speaking, the collective behaviour that could be exploited in additive manufacturing is not sufficient on its own. It would be necessary to find ways to increase the capacities of voxels alone with a control mean … This is, moreover, the whole scientific debate opened in this article.

5.4. Results of self-organization stimulated or under constraint

In the field of additive manufacturing, one seeks to provide a form of an object responding to a preliminary instruction; one also seeks to provide the object with other performances of functionality, evolution (such as currently addressed in 4D printing and bio-printing), etc. (André, 2017). Table 1 brings together some (non-biological) results based on the different items in Section 3.

Table 1. Examples of linkages between top-down and bottom-up approaches

Title	Comments	Reference(s)
Self-organization of environmentally sensitive nanoparticles	3D inkjet printing of the self-organization of aqueous colloidal suspensions containing mono-dispersed silica particles and/or polystyrene nanoparticles as a function of solvent evaporation.	(Sowade et al. (2015)
Colloidal self-assembly	Direct write colloidal assembly is a process combining the bottom-up principle of colloidal sel-assembly with the versatility of direct ink writing.	(Tan et al. (2018)
Deposition under magnetic field	Non-contact handling and deposition of particles from a colloidal solution (guided electrophoresis) followed (or not) by relaxation.	Pritchet et al. (2020); Grzelczak et al. (2010); Abelmann et al. (2020)
Deposition under electric field	Construction of hierarchical structures inspired by mother-of-pearl with three-dimensional (3D) shapes.	Yang et al. (2019); Yadav et al. (2017); Grzelczak et al. (2010)
Orientation in shear	Particle/filler alignment under shear stresses applied to concentrated inks during writing in additive manufacturing.	Hausmann et al. (2018)
Phase orientation	Use of an inhomogeneous reception surface.	Palacin (2017)
Directed self-assembly in additive manufacturing (stereo-lithography)	Ultrasound-directed self-assembly to organize a user-specified particle model to fabricate 3D materials at the macro scale with a user-specified microstructure consisting of particles of any material.	Greenhall & Raeymaekers (2017);Niendorf & Raeymaekers (2020); Wadsworth et al. (2020)
Self-organization of polymers in additive manufacturing	Self-assembly of photonic crystal polymers with colour change.	Patel et al. (2020)
Pixelized voxels	Directed self-assembly of liquid crystal monomers to give cross-linked polymer networks with stimuli induced property variations .	Kowalski et al. (2017)
Polymer-ceramic composite	Macroscopic alignment of a self-assembled nanostructure of lyotropic liquid crystals polymerizable by 3D printing.	Rajasekharan et al. (2017)
Thermal-graded pixelization	Method that optimizes synthesis with initial heating rates up to 100°/min generating a rich family of nanoscale building blocks with distinct morphologies.	Ye et al. (2010)
Adhesive properties change	pH control is used to increase adhesion when handling and to cancel it when releasing into a micro forceps.	Dejeu et al. (2009)
Rheological properties change in additive manufacturing	Application of self-assembly principles to change the rheology of “non-printable” materials, while providing the possibility of having key properties of supramolecular and stimulus-sensitive materials.	Manning et al. (2019)

It is a question, it will have been understood, essentially to define situations where materials are sensitive to an artificially created environment which allows them to see modified their physical properties, such as for example, the shape, the electrical conductivity, the colour or the reflection, according to an external stimulation. But these few examples represent only a modest contribution to the total number of publications in additive manufacturing (160,000 on the CNRS website) which increases by about 20% a year …

5.5. Programming

If the future prospects of additive manufacturing associated with self-organizational aspects, presented here, can be envisaged in the physical domain, within the constraints expressed, their integration in manufacturing software will constitute an additional level of complication. Software intended to support design and manufacturing changes is outside the scope of the present reflection. Let us recall, in agreement with the writings of Thomas-Seale et al., (2019), that current design methods are deterministic where the voxel located in space at a point x, y, z is univocally related to its numerical position with the possibility of additivity. If self-organization processes develop locally during the manufacturing process, this “simple” situation resulting from “classical” additive manufacturing is no longer suitable, which imposes either prior prevention of deformations during manufacturing by avoiding stimuli or by their knowledge and effects a programming of manufacturing that would take them into account. One can then imagine the difficulty of this programming. In any case, the non-interference between stimuli and fabrication must be validated before the realization of a 4D object (Bowyer, 1983; Party-Barwick & Bowyer, 1995). Jones et al. (2012) proposed a kinematic replicator through a rapid assembler, capable of positioning and bonding pre-manufactured voxels. In such conditions, independent self-organizational voxels can be used according to the fact that the manufacturing would be achieved using traditional manufacturing technologies (including robotics) (Cuellar et al., 2018; Hiller & Lipson, 2009).

6. Conclusion

For academic research, it is undoubtedly a means of trying to “decipher”, on the occasion of the development of a theme as intellectually attractive as the inclusion of massively parallel additive manufacturing, the “mysteries” of an integrating field of study, ensuring it, if successful, a real legitimacy, rather than solving “local” problems and seizing opportunities. It is necessary to go a little further by no longer relying on classic inertial foundations (because they have proven their worth (Morange, 2012)), and by proposing that we break out of the following conservative spiral: rather than producing knowledge adapted to situations as they emerge, we adapt it to existing knowledge or as planned!

In doing so, those who do can naturally develop technologies and/or methods that will partially address the issue. Could we then find, as in artificial intelligence relative to “natural” intelligence, an original construction, subject to what Nature knows how to do … This could open new fields of research, capacities to change the world at our small level, for good or for bad. This is the object that aims at a real support to the exploration of complexity for the redeployment of additive manufacturing on new niches. First of all, it will already be a question of getting out of simple proofs-of-concept by verifying the reproducibility of experiments (which is indispensable). Secondly, it will be a question of investing in the risk-taking aspects, interdisciplinary and inter-disciplinary convergences and inter-professional technological areas, which everyone acknowledges as being difficult and poorly recognized by the hierarchy and the financial backers. The first controlled self-organization is still to be hoped for, hence the need to build operational machines!

If the possible revolution, into which the theme of self-organization could plunge us, consists in applying knowledge to knowledge itself, it is probably appropriate to leave the final word to Jean Staune (Staune, 2015) to conclude with this paradoxical and pessimistic sentence: “Why study problems that have no solution or whose solution is too complex to be found?” … Remember that, in such domains, disciplinary competence can be destructive while general incompetence (or agnotology, the “science” of non-knowledge) can be creative, under certain conditions. Four factors can favor the emergence of a “productive” incompetence:

• The identification of a relatively well-defined problem, a determination to understand and solve it;

• A willingness to pool our respective insights, and thus to share our skills and incompetence. This process can be a tool for overcoming difficulties, particularly epistemological ones;

• The implementation of the proposed solutions must be made possible (organization, finance, hierarchical support, etc.);

• Then, we must confront the reflection with reality.

So, let’s try to get out from underneath the difficulties presented in this paper by trying to find ways of fruitful alliances between spontaneous or stimulated self-organization and additive manufacturing responding to new applicative challenges … For the moment, a promising approach consists in the realization of voxels of a size close to the desired 3D spatial resolution made of self-organizing constituents that can be locally stimulated. The experiments and the associated mathematical modeling will then be likely to allow applications, but also a possible generalization, step by step, towards more global systems and consequently closer to the initial purpose of this reflection.

Acknowledgments

If in 1984, Alain Le Mehaute had not submitted the question of how to manufacture objects by laser to JCA, additive manufacturing would have been invented a few weeks later. JCA would have continued to work on light–matter interactions. Many patents and publications came out of this fruitful meeting. We would like to thank him warmly for his creativity, support and communicative enthusiasm.

Conflicts of Interest

The authors declare no conflict of interest.

Additional information

Funding

The two authors did not use specific funding for the present work of reflection and analysis which uses conceptual bases corresponding to their research activities in the field of additive manufacturing.

Notes on contributors

Jean-Claude André

Frederic Demoly is currently leading a research group on formalism, methods and tools for proactive design of adaptable and transformable products. His interests include design for assembly, additive manufacturing and 4D printing, knowledge formalization and representation, advanced computer-aided design, formal ontology, multi-material 3D printing and voxel-based modeling.

Jean-Claude André is involved in light–matter interactions research. He is in 1984 at the origin of (probably) the first patent in 3D printing (i.e. stereo-lithography) and since this starting date involved in the fields of 3D and 4D printing. Current research concerns the development of new 3D Printing processes without going through the additivity step in 3D printing (with 3 patents on non-linear optic use for the 3D process), 4D printing (process, materials and software with the Frederic Demoly’s teams as principal partner), the epistemology of bio-printing (with an exploration of the complexity associated with biological processes).