Key statistical assumptions and methods in one-arm meta-analyses with binary endpoints and low event rates, including a real-life example in the area of endoscopic colonic stenting

Abstract

There are relatively few publications on the methodology of one-arm meta-analyses, especially when the outcome is binary and has low probability of occurring. We will discuss a few of the important assumptions underlying one-arm meta-analyses, including publication bias, fixed effect versus random-effects models, and raw event incidence rate transformations required when the event frequency is low. Finally, we will provide a real-life example taken from the endoscopic colonic stenting literature to illustrate the consequences of failure to thoroughly investigate these assumptions. In this example, we find arcsine transformation provides more appropriate results than logit transformation.

Keywords:

• one-arm meta-analysis
• low event rates
• publication bias
• random-effects model
• colonic stenting
• endoscopy

Public Interest Statement

Meta-analyses are incredibly useful tools for researchers that can be utilized to explore what the overall literature is showing about a particular topic. However, similar to using any statistical analysis method, there are assumptions that need to be understood prior to performing the analysis. In this paper, we look at the key statistical assumptions underlying one-arm meta-analyses with binary endpoints and low event rates. We also provide an example from the literature of the consequences of not understanding these assumptions.

Competing Interests

The authors declare no competing interest.

1. Introduction

Meta-analyses or systematic reviews are commonly used to estimate what the true effect of a particular treatment is, based on what has been published in the literature. Meta-analysis is defined as the statistical analysis of a combination of studies. Meta-analyses are used in many different ways, but two of the most common are, to attempt to resolve disagreement regarding a particular treatment’s true effect size in the literature, and to determine the assumptions that will be used when designing study hypotheses.

The most common types of studies that are used for meta-analysis are randomized controlled trials (RCTs). There is an abundance of literature on performing meta-analysis on RCTs. However, for some types of treatments, RCTs are not very common due to ethical, logistical, or economic reasons. Single-arm studies are either retrospective or prospective, but many are observational in nature and many include small sample sizes. Performing a meta-analysis is an excellent way to determine the true effect or risk of the treatment in these instances. Such meta-analyses are commonly referred to as a “one-arm meta-analysis.” There is a paucity of research on the methods used to perform these types of analyses, unlike on the meta-analysis methods for RCTs. In addition, a number of one-arm meta-analyses study the risk of adverse events (AEs) and not necessarily the treatment effect. The rates of these AEs can be small and can cause problems when performing the meta-analysis. In this article we will explore the assumptions, methods, and some potential problems that can occur when performing a one-arm meta-analysis with binary data and small event rates.

2. Motivating example

We consider a real-life motivating example taken from the endoscopic colonic stenting literature, to illustrate the consequences of failure to thoroughly investigate the assumptions underlying one-arm meta-analyses, especially when there are studies that are small and have binary outcomes with zero event rates.

This example in the area of gastrointestinal endoscopy reports on a meta-analysis of outcomes of colonic stenting. The example is a paper entitled Perforation in colorectal stenting: a meta-analysis and a search for risk factors reporting one-arm meta-analyses with low event rates and published in Gastrointestinal Endoscopy in 2014 by van Halsema et al. (2014). This meta-analysis looked at the perforation rate in colorectal stenting with self-expanding metal stents (SEMS) in patients with a colorectal obstruction. The use of SEMS for colorectal obstructions has been controversial for years. A safety concern has been colonic perforation, which can lead to the need for risky surgery and even death. The paper (van Halsema et al., 2014) concluded that the overall perforation rate of colonic stenting is 7.4% and that stent design, benign etiology of the colonic stricture, and concomitant use of chemotherapeutic agent bevacizumab were risk factors for colonic perforation.

However, this perforation rate of 7.4% was surprisingly high, for several reasons. First, there have been other reviews performed on this subject that have typically found perforation rates around 4% (Khot, Lang, Murali, & Parker, 2002; Sebastian, Johnston, Geoghegan, Torreggiani, & Buckley, 2004; Watt, Faragher, Griffin, Rieger, & Maddern, 2007). In addition, we were involved in the analysis of one of the larger registries published in this area. Our analysis determined that, in this registry, the perforation rate was 3.9% (Meisner et al., 2011). Second, the raw perforation rate is only 5.0%.

Failure to use appropriate methods may create the wrong conclusions about the risk of a treatment and could cause physicians to receive biased information on which to base selection of optimal methods of treatment. In addition, it could lead to economic consequences as choices of one over another treatment option can be associated with cost implications which should be assessed in the context of comparative outcomes.

In the Example section later, we will further consider this example of a published one-arm meta-analysis, for which we will perform alternative analysis methods, to explore their consequences. We examine the robustness of that article’s conclusions as impacted by meta-analytic methodology. We investigate various assumptions underlying one-arm meta-analyses and consider their impact on reported colonic perforation rate, namely that of publication bias, fixed effect model versus random-effects model, and different transformations of raw event incidence rates.

3. Publication bias

Publication bias is possible when performing any meta-analysis and could lead to erroneous conclusions. The most significant source of potential bias lies in the selection criteria used to identify the publications which will be included in the meta-analysis. However, several techniques have been reported to minimize risk of bias or at a minimum to provide an assessment of the degree to which the meta-analysis addresses publication bias. Such techniques include funnel plots (Light & Pillemer, 1984), Rosenthal’s (1979) Fail Safe N, and Orwin’s (1983) Fail Safe N. A shortcoming of these techniques is that they do not necessarily adequately capture bias problems if studies have been omitted from the meta-analyses.

4. Fixed effect versus random-effects models

Two of the most popular methods for performing a meta-analysis are a fixed effect model, which assumes that the effect size across studies is constant, and a random-effects model which assumes that there is heterogeneity of the treatment effect sizes across the studies.

The major differences between fixed effect and random-effects models lie in the presumed homogeneity of the studies used in the meta-analysis and in the weight given to each study. Both may impact the conclusions of a meta-analysis.

First, in a fixed effect model, since the effect is assumed to be homogeneous, the variability between the studies is ignored. This typically leads to tighter confidence intervals (CIs) than a random-effects method.

Second, the weight each study is given in the analysis is different between the two methods. In a fixed effect analysis, the weight given to each study is only determined by the sample size of each study, similar to a simple weighted average. In a random-effects model, the weight is not only determined by the sample size, but it is also based on the effect size itself. Therefore, a study that is an outlier, but has a high N, will not have as much influence on the analysis in a random-effects model compared to a fixed effect model.

Given the nature of medical research, in which studies are typically conducted under different protocols and in different parts of the world, and given the complex nature of human anatomy and the natural history of diseases, the effect across studies will likely be heterogeneous. Therefore, a fixed effect model will tend to be inferior to a random-effects model when estimating effects in most studies in this area (DerSimonian & Laird, 1986).

5. Transformations

Another assumption in one-arm meta-analyses that needs to be understood is that, for binary rates, a transformation of raw event incidence rates usually occurs before the analysis is performed. The most common transformation is the log or logit transformation, taking the log of the risk or odds. Since in one-arm meta-analyses, there is no control group, as with an RCT, this is equivalent to taking the log or logit of the estimate, whereas in RCTs the log of the risk ratio or odds ratio is taken. This leads to an interesting distinction between one-arm and multi-arm meta-analyses in that the odds ratio or risk ratio in RCTs with multiple arms, are likely not to be zero, even with low event rates, since RCTs tend to have larger sample sizes than one-arm trials. However, in meta-analyses of one-arm trials, the trials are often retrospective with no reported events, given that retrospective trials typically capture data less rigorously than prospective trials. As a result, since the log of zero does not exist, a continuity correction must be made. The most common type of continuity correction used is to add one-half to the numerator and one to the denominator and then do the transformation and subsequently the analysis. For example, if a trial included 1,000 patients with no events, then 0 out of 1,000 would become 0.5 out 1,001, effectively increasing the risk of an event from 0% to about 0.05%. In this example, the increase is not particularly significant; however, oftentimes these retrospective trials have far fewer patients than RCTs, with many including fewer than 100 patients and some even including fewer than 10 patients. In these cases, performing the same transformation increases the risk of an event from 0% to about 0.5% and from 0% to almost 4.5%, respectively. Using these examples, it can be easily seen that such transformations can lead to significant overestimations of the risk of an event.

Unfortunately, most of the statistical software that is used today typically uses this method as the default method for transformation and in addition, the software performs these transformations automatically without a warning. Most packages do not offer an option for a different transformation. However, in the R software, using the “meta” package, there is a function that allows one to use other transformation methods including Freeman-Tukey Double arcsine (Freeman & Tukey, 1950) transformation and arcsine transformation. Neither of these methods requires a transformation from zero since the arcsine of zero exists and is in fact still zero.

6. Example

Based on the article discussed in the Motivating Example section earlier, we will further consider this example of a published one-arm meta-analysis, for which we will perform alternative analysis methods, to explore their consequences. The paper (van Halsema et al., 2014) concluded that the overall perforation rate of colonic stenting is 7.4% and that stent design, benign etiology of the colonic stricture, and concomitant use of chemotherapeutic agent bevacizumab were risk factors for colonic perforation. We examine the robustness of that article’s conclusions as impacted by meta-analytic methodology. We investigate various assumptions underlying one-arm meta-analyses and consider their impact on reported colonic perforation rate, namely that of publication bias, fixed effect model versus random-effects model, and different transformations of raw event incidence rates.

6.1. Publication bias

The paper (van Halsema et al., 2014) published 2014 after initial submission in the middle of 2013 on individual publications between 2005 and 2011. It does mention apparent differences between the reported colonic perforation rate established by its meta-analysis compared to four more recent publications from 2011 (Jimenez-Perez et al., 2011); Meisner et al., 2011 and 2012 (Cheung et al., 2012; Meisner et al., 2012). These four publications were discussed in the paper but were not included in the meta-analysis, based on the date for the literature search but not based on publication selection criteria. It might have been useful to identify this potential publication bias in the section on limitations of the paper, but it was clearly mentioned at the beginning of the discussion section of the paper.

6.2. Fixed effect versus random-effects models

The authors of this meta-analysis included 86 articles, with a total of 4,086 patients and 207 instances of perforation. The meta-analysis produced a perforation rate of 7.4% with a 95% CI of (6.5, 8.5%). This was surprising for several reasons. First, there have been other reviews performed on this subject that have typically found perforation rates around 4% (Khot et al., 2002; Sebastian et al., 2004; Watt et al., 2007). These three articles did not use a meta-analysis to determine perforation rates; instead the perforation rate was reported as the number of perforations that occurred divided by the number of patients in the review. In addition, we were involved in the analysis of one of the larger registries published in this area. Our analysis determined that, in this registry, the perforation rate was 3.9% (Meisner et al., 2011). Second, the raw perforation rate resulting from 207 out of 4,086 patients is only 5.0% with an exact 95% CI of (4.4, 5.7%). This is significantly lower than the reported meta-analytic rate of 7.4%, with a non-overlapping 95% CI of (6.5, 8.5%), and led us to examine the cause of this apparent discrepancy. The article does not include a clear and detailed description of the statistical methods used. The perforation rates for each of the individual articles, however, were provided in an appendix which was essential to our independent analysis.

van Halsema et al. (2014) used a fixed effect model and not a random-effects model. For reasons outlined above, we felt that this may have contributed to the higher-than-expected perforation rate as established by the meta-analysis of the publication (van Halsema et al., 2014). The perforation rate across all studies is not homogeneous, given the large number of studies and the diverse nature of these studies, e.g. retrospective versus prospective, one arm versus randomized, single center versus multi center. In fact, the authors do multiple analyses of I², which is a statistic used to assess heterogeneity of the meta-analysis, and also state that their analysis displays “high heterogeneity (I² = 52%)”. In addition, the publication states that “aggregated data presented in this review are based on heterogeneous patient populations.” Despite this the authors elected to use a fixed effect model. If the studies are indeed heterogeneous, a random-effects model should be used.

6.3. Transformations

The authors (van Halsema et al., 2014) used a logit transformation to perform their meta-analysis. As stated earlier, this comes with a continuity correction consisting of adding 1 to both the numerator and the denominator of raw rates of zero for applicable individual studies. In van Halsema et al. (2014), 23 of 86 (27%) of studies used in the published meta-analysis reported zero perforations. Ten of these studies involved fewer than twenty patients and the largest study with zero perforations included 151 patients. As discussed earlier, continuity corrections of zero rates from studies with small numbers of patients can lead to an artificial inflation of the corrected rate.

6.4. Revised meta-analysis

The findings described above led us to re-analyze the data using different methods. We re-analyzed the data using a random-effects model. Figure 1 shows a graphical comparison of the analyses. The raw perforation rate of 5.0% is lower than the estimate of 5.7% with 95% CI (4.6, 7.1%), but lies inside of the 95% CI and hence seems insignificantly different and probably does not substantiate a different assessment of perforation risk of the treatment. However, when we revise the method of transformation we see that the results are very different. When we use the Freeman-Tukey double arcsine transformation we find that the perforation rate is 3.3% with 95% CI (2.3, 4.6%) using a random-effects model and 3.1% with 95% CI (2.4, 3.7%) with a fixed effect model. Using the arcsine transformation we find that the perforation rate is 3.5% with 95% CI (2.4, 4.7%) using a random-effects model and 3.5% with 95% CI (3.0, 4.1%) using a fixed effect model. These point estimates of the perforation rate should be compared to the reported value of 7.4% with 95% CI (6.5, 8.5%) in the example publication (van Halsema et al., 2014). The estimates are reduced to about half and the CIs do not overlap. Since the two arcsine transformations appear to be consistent and closer to what is expected from previous literature Khot et al. (2002), Sebastian et al. (2004) and Watt et al. (2007), the arcsine transformation appears more appropriate than the logit transformation.

Figure 1. Forest plot showing analysis with different transformations.

Notes: Reference line shown is van Halsema lower CI bound which illustrates that the arcsine transformations are well below the lower bound of the logit transformation.

6.5. Risk factors

The paper (van Halsema et al., 2014) also discusses the risk of perforation in four different subgroupings: stent type, stricture etiology, stricture dilation prior to placement of the colonic stent, and concomitant chemotherapy. While we were able to re-analyze the overall results, we were not able to re-create these subgroup analyses because the publication did not disclose enough information to determine what the perforation rates were in the subgroups and we did not have the resources to attempt to gather all of this data. However, given what we mentioned above regarding the continuity correction and the fixed effect model, the perforation risk in the subgroups would likely have been overestimated as well. This overestimation could be even higher in the “stent type” subgroup analyses because this variable had seven different values or stent types, whereas the other three subgroupings had only two values, namely presence or absence of stricture dilation prior to placement of the colonic stent, stricture etiology (benign or malignant) and use of concomitant chemotherapy. For example, if there were only a few stents of one type used and there were zero perforations reported with that type, then using the logit transformation method could increase the overestimation of the perforation risk in the small subgroup.

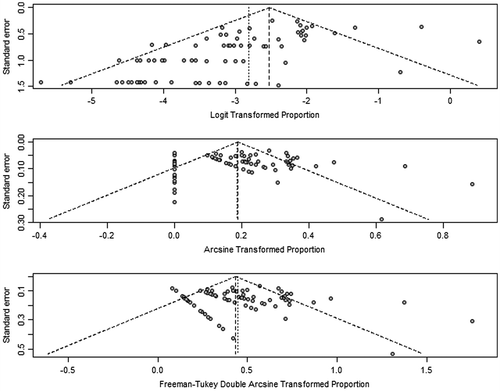
To better illustrate the impact of different transformation techniques, we created funnel plots provided in Figure 2. The funnel plots show there is likely asymmetry but it is difficult to attribute this solely to publication bias, as asymmetry can be compounded by heterogeneity between studies. These plots also show that the arcsine methods of transformation are more appropriate as the studies are more evenly spread across the graph, whereas the logit transformation shows that many more studies fall below the mid-point of the graph.

Figure 2. Funnel plots of the three different transformations. Since the arcsine plots are generally distributed more evenly across the graphs this shows that the arcsine transformation is more appropriate.

7. Conclusion

Meta-analyses are incredibly useful tools to broaden our research capabilities and give us the ability to quantitatively summarize the literature in a certain disease or treatment. However, like any other statistical method, the underlying assumptions to such an analysis must be understood and different methods should be explored, so that the most appropriate analytical method can be selected.

Here, we have shown that using an arcsine transformation instead of a logit transformation was the more appropriate method to use for a meta-analysis of literature in the area of colonic stenting as it pertains to a low incidence metric, namely colonic perforation risk. Use of the arcsine transformations substantially lowered the estimate for risk of colonic perforation. Failure to use appropriate methods may create the wrong conclusions about the risk of a treatment and could cause physicians to receive biased information on which to base selection of optimal methods of treatment. In addition, it could lead to economic consequences as choices of one over another treatment option can be associated with cost implications which should be assessed in the context of comparative outcomes.

This problem does not only occur in meta-analysis or in medicine. It can occur throughout the entire scientific community. The statistical methods for every paper need to be thoroughly understood and vetted so that the risk or treatment effect is not over- or underestimated. All research needs to be collaborative, and the responsibility for this lies not only with those performing the research, but also with those performing statistical analyses and those reviewing manuscripts for publication in peer-reviewed scientific journals.

Funding

This work was supported by Boston Scientific Corporation.

Additional information

Notes on contributors

Matthew J. Rousseau

Matthew Rousseau is a biostatistician who has been researching medical devices for the past 8 years. Primarily his work has been in the field of gastrointestinal endoscopy and he has extensive experience in clinical trial design and data analysis, along with performing meta-analyses for both study design and publication purposes. This work represents the authors’ hope to improve knowledge and understanding of assumptions underlying statistical analyses that appear in the literature, especially among non-statisticians.