On Solution Regularity of the Two-Dimensional Radiation Transfer Equation and Its Implication on Numerical Convergence

Abstract

In this paper, we deal with the differential properties of the scalar flux $\varphi (x)$ defined over a two-dimensional bounded convex domain, as a solution to the integral radiation transfer equation. Estimates for the derivatives of $\varphi (x)$ near the boundary of the domain are given based on Vainikko’s regularity theorem. The optimal pointwise error estimates in terms of the scalar flux are presented for the two classic finite difference methods: diamond difference (DD) and step difference (SD). Numerical results indicate the implication of the solution smoothness on the numerical convergence behavior.

Keywords:

• Integral radiation transfer equation
• solution regularity
• numerical convergence

1. Introduction

The one-group radiation transfer problem in a three-dimensional (3D) convex domain reads as follows: find an angular flux function $\psi :$ $\overline{\mathrm{G}}\times {\mathrm{S}}^2\to {\mathbb{R}}_{+}$ such as (1) $$\sum _{j=1}^3{\mathrm{\Omega }}_j\frac{\partial \psi \left(x,\mathrm{\Omega }\right)}{\partial x_j}+\sigma \left(x\right)\psi \left(x,\mathrm{\Omega }\right)=\frac{{\sigma }_s\left(x\right)}{4\pi }\underset{\mathrm{\Omega }}{\int }s(x,\mathrm{\Omega },\mathrm{\Omega }\prime )\psi \left(x,{\mathrm{\Omega }}^{\prime }\right)d\mathrm{\Omega }\prime +q\left(x,\mathrm{\Omega }\right),\mathrm{ }x\in \mathrm{G},$$(1) (2) $$\psi \left(x,\mathrm{\Omega }\right)={\psi }_{\partial \mathrm{G}}\left(x,\mathrm{\Omega }\right),\mathrm{ }x\in \partial \mathrm{G},\mathrm{ }\mathrm{\Omega }·\widehat{n}\left(x\right)<0,$$(2) where $\overline{\mathrm{G}}$ is the closure of the domain $\mathrm{G}\subset {\mathbb{R}}^3$ with the boundary $\partial \mathrm{G},$ ${\mathrm{S}}^2$ is the unit sphere of ${\mathbb{R}}^3,$ $\mathrm{\Omega }$ denotes the direction of radiation transfer, $\sigma$ is the extinction coefficient (or macroscopic total cross section in neutron transport), ${\sigma }_s$ is the scattering coefficient (or macroscopic scattering cross section), $s$ is the phase function of scattering with $\underset{\mathrm{\Omega }}{\int }s(x,\mathrm{\Omega },\mathrm{\Omega }\prime )d\mathrm{\Omega }\prime =4\pi ,$ $q$ is the external source function, and $\widehat{n}$ is the unit normal vector of the domain surface. Note that ${\sigma }_s\left(x\right)<\sigma \left(x\right)$ under the subcritical condition, and $s\left(x,\mathrm{\Omega },{\mathrm{\Omega }}^{\prime }\right)=s(x,\mathrm{\Omega }\prime ,\mathrm{\Omega }).$

Assuming the isotropic scattering $s\left(x,\mathrm{\Omega },{\mathrm{\Omega }}^{\prime }\right)=1,$ isotropic source $q\left(x,\mathrm{\Omega }\right)=\frac{Q\left(x\right)}{4\pi },$ and isotropic boundary condition ${\psi }_{\partial \mathrm{G}}\left(x,\mathrm{\Omega }\right)=\frac{{\varphi }_{\partial \mathrm{G}}\left(x\right)}{4\pi },$ we can obtain the so-called Peierls integral equation of radiation transfer for the scalar flux $\varphi \left(x\right)$ as follows: (3) $$\begin{array}{c}\varphi \left(x\right)=\frac{1}{4\pi }{\int }_{\mathrm{G}}\frac{{\sigma }_s\left(y\right){\mathrm{e}}^{–\tau \left(x,y\right)}}{{\left|x–y\right|}^2}\varphi \left(y\right)dy+\frac{1}{4\pi }{\int }_{\mathrm{G}}\frac{{\mathrm{e}}^{–\tau \left(x,y\right)}}{{\left|x–y\right|}^2}Q\left(y\right)dy\\ +\frac{1}{4\pi }{\int }_{\partial \mathrm{G}}\frac{{\mathrm{e}}^{–\tau \left(x,y\right)}}{{\left|x–y\right|}^2}\left|\frac{x–y}{\left|x–y\right|}·n\left(x\right)\right|{\varphi }_{\partial \mathrm{G}}\left(y\right)d{S}_y,\end{array}$$(3) (4) $$\tau \left(x,y\right)={\int }_0^{\left|x–y\right|}\sigma \left(r–\xi \mathrm{\Omega }\right)d\xi ,$$(4) where $dS$ is the differential element of the domain surface, $\tau \left(x,y\right)$ is the optical path between $x$ and $y.$ One can find detailed derivation in Vainikko (1993).

For simplicity, we assume $\sigma$ and ${\sigma }_s$ are constant over the domain. Then Equation (3)(3) $$\begin{array}{c}\varphi \left(x\right)=\frac{1}{4\pi }{\int }_{\mathrm{G}}\frac{{\sigma }_s\left(y\right){\mathrm{e}}^{–\tau \left(x,y\right)}}{{\left|x–y\right|}^2}\varphi \left(y\right)dy+\frac{1}{4\pi }{\int }_{\mathrm{G}}\frac{{\mathrm{e}}^{–\tau \left(x,y\right)}}{{\left|x–y\right|}^2}Q\left(y\right)dy\\ +\frac{1}{4\pi }{\int }_{\partial \mathrm{G}}\frac{{\mathrm{e}}^{–\tau \left(x,y\right)}}{{\left|x–y\right|}^2}\left|\frac{x–y}{\left|x–y\right|}·n\left(x\right)\right|{\varphi }_{\partial \mathrm{G}}\left(y\right)d{S}_y,\end{array}$$(3) can be simplified as (5) $$\begin{array}{c}\varphi \left(x\right)={\int }_{\mathrm{G}}\mathrm{K}\left(x,y\right)\varphi \left(y\right)dy+\frac{1}{{\sigma }_s}{\int }_{\mathrm{G}}\mathrm{K}\left(x,y\right)Q\left(y\right)dy\\ +\frac{1}{{\sigma }_s}{\int }_{\partial \mathrm{G}}\mathrm{K}\left(x,y\right)\left|\frac{x–y}{\left|x–y\right|}·n\left(x\right)\right|{\varphi }_{\partial \mathrm{G}}\left(y\right)d{S}_y\end{array}$$(5) where the 3D radiation kernel is given as (6) $$\mathrm{K}\left(x,y\right)=\frac{{\sigma }_s{\mathrm{e}}^{–\sigma \left|x–y\right|}}{4\pi {\left|x–y\right|}^2}.$$(6)

The boundary integral term in the above equation can produce singularities in the solution. We omit its discussion in this paper. In other words, here we only consider the problem with the vacuum boundary condition, i.e., ${\varphi }_{\partial \mathrm{G}}=0.$ Thus, Equation (6)(6) $$\mathrm{K}\left(x,y\right)=\frac{{\sigma }_s{\mathrm{e}}^{–\sigma \left|x–y\right|}}{4\pi {\left|x–y\right|}^2}.$$(6) can be treated as the weakly integral equation of the second kind: (7) $$\varphi \left(x\right)=\underset{\mathrm{G}}{\int }\mathrm{K}\left(x,y\right)\varphi \left(y\right)dy+f\left(x\right), x\in \mathrm{G}$$(7) where $\mathrm{G}\subset {\mathbb{R}}^n,$ $n\ge 1,$ is an open bounded domain and the kernel $\mathrm{K}\left(x,y\right)$ is weakly singular, i.e., $\left|\mathrm{K}\left(x,y\right)\right|\le C{\left|x-y\right|}^{-\nu },$ $0\le \nu \le n.$ Note that $f\left(x\right)=\frac{1}{{\sigma }_s}{\int }_{\mathrm{G}}\mathrm{K}\left(x,y\right)Q\left(y\right)dy$ for radiation transfer. Weakly singular integral equations arise in many physical applications such as elliptic boundary problems and particle transport.

Since $\mathrm{K}\left(x,y\right)$ has a singularity at $x=y,$ the solution of a weakly integral equation is generally not a smooth function and its derivatives at the boundary would become unbounded from a certain order. There was extensive research on the smoothness (regularity) properties of the solutions to weakly integral equations (Mikhlin 1965; Mikhlin and Prossdorf 1986), especially those early work in neutron transport theory done in the former Soviet Union (Vladimirov 1963; Germogenova 1969). It is believed that Vladimirov first proved that the scalar flux $\varphi \left(x\right)$ possesses the property $\left|\varphi \left(x+h\right)-\varphi \left(x\right)\right|\sim h\log h$ for the one-group transport problem with isotropic scattering in a bounded domain (Vladimirov 1963). Germogenova analyzed the local regularity of the angular flux $\psi (x,\mathrm{\Omega })$ in a neighborhood of the discontinuity interface and obtained an estimate of the first derivative, which has the singularity near the interface (Germogenova 1969). Pitkäranta (1980) derived a local singular resolution showing explicitly the behavior of $\varphi \left(x\right)$ near the smooth portion of the boundary. Vainikko (1993) introduced weighted spaces and obtained sharp estimates of pointwise derivatives near the smooth boundary for multidimensional weakly singular integral equations.

There exists some previous research work on the regularity of the integral radiation transfer solutions (Johnson and Pitkaranta 1983; Hennebach, Junghanns, and Vainikko 1995). However, the 2D kernel treated in those studies bears no physical meaning since it does not model the scattering correctly. A physically relevant 2D kernel can be found in Lewis and Miller (1993). In this paper, we rederive the 2D kernel by directly integrating the 3D kernel with respect to the third dimension. We examine the differential properties of the new 2D kernel and provide estimates of pointwise derivatives of the scalar flux according to Vainikko’s regularity theorem for the weakly integral equation of the second kind.

The remainder of the paper is organized as follows. In Sect. 2, we derive the 2D kernel for the integral radiation transfer equation. We examine the derivatives of the kernel and show that they satisfy the boundedness condition of Vainikko’s regularity theorem in Sect. 3. Then the estimates of local regularity of the scalar flux near the boundary of the domain are given. In Sect. 4, we derive local estimates for the spatial discretization error in terms of the scalar flux for the two classical numerical methods, diamond difference (DD) and step difference (SD). Sect. 5 presents numerical results of DD and SD to demonstrate how the asymptotic convergence behavior of the spatial discretization error is affected by the smoothness of the exact solution. Concluding remarks are given in Sect. 6.

2. Two-dimensional radiation transfer equation

In this section, we derive the 2D integral radiation transfer equation from its 3D form, Eqs. (5)(5) $$\begin{array}{c}\varphi \left(x\right)={\int }_{\mathrm{G}}\mathrm{K}\left(x,y\right)\varphi \left(y\right)dy+\frac{1}{{\sigma }_s}{\int }_{\mathrm{G}}\mathrm{K}\left(x,y\right)Q\left(y\right)dy\\ +\frac{1}{{\sigma }_s}{\int }_{\partial \mathrm{G}}\mathrm{K}\left(x,y\right)\left|\frac{x–y}{\left|x–y\right|}·n\left(x\right)\right|{\varphi }_{\partial \mathrm{G}}\left(y\right)d{S}_y\end{array}$$(5) and (6)(6) $$\mathrm{K}\left(x,y\right)=\frac{{\sigma }_s{\mathrm{e}}^{–\sigma \left|x–y\right|}}{4\pi {\left|x–y\right|}^2}.$$(6) . In 3D, $dy=d{y}_{1}d{y}_{2}d{y}_3$ and $\left|x–y\right|=\sqrt{{\left(x_1–y_1\right)}^2+{\left(x_2–y_2\right)}^2+{\left(x_3–y_3\right)}^2}.$ Let $\rho =\sqrt{{\left(x_1–y_1\right)}^2+{\left(x_2–y_2\right)}^2},$ then $\left|x–y\right|=\sqrt{{\rho }^2+{\left(x_3–y_3\right)}^2}.$ In a 2D domain $\mathrm{G}\subset {\mathbb{R}}^2,$ the solution function $\varphi \left(x\right)$ only depends on $x_1$ and $x_2$ in Cartesian coordinates. Therefore, we only need to find the 2D radiation kernel, which can be obtained by integrating out $y_3$ as follows: (8) $$\begin{array}{c}\mathrm{K}\left(x,y\right)={\int }_{\text{-}\mathrm{\infty }}^{\mathrm{\infty }}\frac{{\sigma }_s{\mathrm{e}}^{–\sigma \left|x–y\right|}}{4\pi {\left|x–y\right|}^2}d{y}_3\\ =\frac{{\sigma }_s}{4\pi }{\int }_{\text{-}\mathrm{\infty }}^{\mathrm{\infty }}\frac{{\mathrm{e}}^{-\sigma \sqrt{{\rho }^2+{\left(x_3–y_3\right)}^2}}}{{\rho }^2+{\left(x_3–y_3\right)}^2}d{y}_3.\end{array}$$(8)

To proceed, we introduce the variables $t=\sigma \sqrt{{\rho }^2+{\left(x_3–y_3\right)}^2}$ and $z=y_3-x_3.$ Then we substitute $d{y}_3=d\mathrm{z}=\frac{t}{\sigma \sqrt{t^2–{\sigma }^2{\rho }^2}}dt$ into the above equation to have (9) $$\begin{array}{c}\mathrm{K}\left(x,y\right)=\frac{{\sigma }_s}{4\pi }{\int }_{\text{-}\mathrm{\infty }}^{\mathrm{\infty }}\frac{{\mathrm{e}}^{-t}}{\frac{t^2}{{\sigma }^2}}d\mathrm{z}=\frac{{\sigma }_s}{2\pi }{\int }_0^{\mathrm{\infty }}\frac{{\mathrm{e}}^{-t}}{\frac{t^2}{{\sigma }^2}}d\mathrm{z}\\ =\frac{{\sigma }_s}{2\pi }{\int }_{\sigma \rho }^{\mathrm{\infty }}\frac{{\mathrm{e}}^{-t}}{\frac{t^2}{{\sigma }^2}}\frac{t}{\sigma \sqrt{t^2–{\sigma }^2{\rho }^2}}dt\\ \begin{array}{c}=\frac{{\sigma }_s\sigma }{2\pi }{\int }_{\sigma \rho }^{\mathrm{\infty }}\frac{{\mathrm{e}}^{-t}}{t\sqrt{t^2–{\sigma }^2{\rho }^2}}dt\\ =\frac{{\sigma }_s}{2\pi \rho }{\int }_0^1\frac{{\mathrm{e}}^{-\frac{\sigma \rho }{t}}}{\sqrt{1–t^2}}dt.\end{array}\end{array}$$(9)

The above derivation of the 2D kernel is much simpler than the process given in Lewis and Miller (1993), where the integral form is obtained by the projection of the particle flight path on the 2D plane. Note that the last integral is the first Bickley-Naylor function ${\mathrm{Ki}}_1\left(r\right)={\int }_0^1\frac{{\mathrm{e}}^{-\frac{r}{t}}}{\sqrt{1–t^2}}dt$ (Abramowitz and Stegun 1970; Altaç 2007).

Now we show that the 2D kernel $\mathrm{K}\left(x,y\right)$ has a singularity at $\rho =0$ (i.e., $x=y)$ as follows. As $\rho$ is sufficiently small, we can have $\sigma \rho <1$ and (10) $$\mathrm{K}\left(x,y\right)=\frac{{\sigma }_s}{2\pi \rho }{\int }_0^1\frac{{\mathrm{e}}^{-\frac{\sigma \rho }{t}}}{\sqrt{1–t^2}}dt>\frac{{\sigma }_s}{2\pi \rho }{\int }_0^1\frac{{\mathrm{e}}^{-\frac{1}{t}}}{\sqrt{1–t^2}}dt>\frac{0.3{\sigma }_s}{2\pi \rho }.$$(10)

Thus, it can be seen that $\mathrm{K}\left(x,y\right)$ becomes unbounded at $\rho =0.$

By replacing the 3D kernel as defined by Equation (6)(6) $$\mathrm{K}\left(x,y\right)=\frac{{\sigma }_s{\mathrm{e}}^{–\sigma \left|x–y\right|}}{4\pi {\left|x–y\right|}^2}.$$(6) with the above one, Equation (5)(5) $$\begin{array}{c}\varphi \left(x\right)={\int }_{\mathrm{G}}\mathrm{K}\left(x,y\right)\varphi \left(y\right)dy+\frac{1}{{\sigma }_s}{\int }_{\mathrm{G}}\mathrm{K}\left(x,y\right)Q\left(y\right)dy\\ +\frac{1}{{\sigma }_s}{\int }_{\partial \mathrm{G}}\mathrm{K}\left(x,y\right)\left|\frac{x–y}{\left|x–y\right|}·n\left(x\right)\right|{\varphi }_{\partial \mathrm{G}}\left(y\right)d{S}_y\end{array}$$(5) becomes the 2D integral radiation transfer equation. Notice that the surface integral in the last term on the right-hand side of Equation (5)(5) $$\begin{array}{c}\varphi \left(x\right)={\int }_{\mathrm{G}}\mathrm{K}\left(x,y\right)\varphi \left(y\right)dy+\frac{1}{{\sigma }_s}{\int }_{\mathrm{G}}\mathrm{K}\left(x,y\right)Q\left(y\right)dy\\ +\frac{1}{{\sigma }_s}{\int }_{\partial \mathrm{G}}\mathrm{K}\left(x,y\right)\left|\frac{x–y}{\left|x–y\right|}·n\left(x\right)\right|{\varphi }_{\partial \mathrm{G}}\left(y\right)d{S}_y\end{array}$$(5) should be replaced with a line integral in the 2D domain.

Remark 2.1.

By simply assuming a 2D scattering, Johnson and Pitkaranta derived a 2D kernel, i.e., $\mathrm{K}\left(x,y\right)=\frac{{\mathrm{e}}^{–\left|x–y\right|}}{\left|x–y\right|}$ (where $\sigma =1$), which is however physically incorrect since the scattering is essentially a 3D phenomenon (Johnson and Pitkaranta 1983). Hennebach, Junghanns, and Vainikko (1995) also used the same 2D kernel for analyzing the radiation transfer solutions. In addition, the integral equations in other geometries such as slab or sphere can be obtained by following the same approach, and they can be found in Bell and Glasstone (1970).

Applying Banach’s fixed-point theorem, we can prove the existence and uniqueness of the solution in the 2D domain by showing that ${\int }_G\mathrm{K}\left(x,y\right)dy$ is bounded below unity as follows. (11) $$\begin{array}{c}{\int }_{\mathrm{G}}\mathrm{K}\left(x,y\right)dy={\int }_{\mathrm{G}}\left(\frac{{\sigma }_s\sigma }{2\pi }{\int }_{\sigma \rho }^{\mathrm{\infty }}\frac{{\mathrm{e}}^{-t}}{t\sqrt{t^2–{\sigma }^2{\rho }^2}}dt\right)dy\\ =\frac{{\sigma }_s\sigma }{2\pi }{\int }_{\mathrm{G}}dy{\int }_{\sigma \rho }^{\mathrm{\infty }}\frac{{\mathrm{e}}^{-t}}{t\sqrt{t^2–{\sigma }^2{\rho }^2}}dt\\ =\frac{{\sigma }_s\sigma }{2\pi }{\int }_{\mathrm{G}}\mathit{\text{ρdφdρ}}{\int }_{\sigma \rho }^{\mathrm{\infty }}\frac{{\mathrm{e}}^{-t}}{t\sqrt{t^2-{\sigma }^2{\rho }^2}}dt\end{array}$$(11) where $\phi$ is the azimuthal angle. By extending the above bounded domain to the whole space, we have (12) $$\begin{array}{c}{\int }_{\mathrm{G}}\mathrm{K}\left(x,y\right)dy<\frac{{\sigma }_s\sigma }{2\pi }{\int }_0^{\mathrm{\infty }}2\mathit{\text{πρdρ}}{\int }_{\sigma \rho }^{\mathrm{\infty }}\frac{{\mathrm{e}}^{-t}}{t\sqrt{t^2–{\sigma }^2{\rho }^2}}dt\\ ={\sigma }_s\sigma {\int }_0^{\mathrm{\infty }}\rho d\rho {\int }_{\sigma \rho }^{\mathrm{\infty }}\frac{{\mathrm{e}}^{-t}}{t\sqrt{t^2–{\sigma }^2{\rho }^2}}dt\end{array}$$(12)

Denoting $\zeta =\sigma \rho ,$ Equation (12)(12) $$\begin{array}{c}{\int }_{\mathrm{G}}\mathrm{K}\left(x,y\right)dy<\frac{{\sigma }_s\sigma }{2\pi }{\int }_0^{\mathrm{\infty }}2\mathit{\text{πρdρ}}{\int }_{\sigma \rho }^{\mathrm{\infty }}\frac{{\mathrm{e}}^{-t}}{t\sqrt{t^2–{\sigma }^2{\rho }^2}}dt\\ ={\sigma }_s\sigma {\int }_0^{\mathrm{\infty }}\rho d\rho {\int }_{\sigma \rho }^{\mathrm{\infty }}\frac{{\mathrm{e}}^{-t}}{t\sqrt{t^2–{\sigma }^2{\rho }^2}}dt\end{array}$$(12) is simplified as (13) $$\begin{array}{c}{\int }_{\mathrm{G}}\mathrm{K}\left(x,y\right)dy<\frac{{\sigma }_s}{\sigma }{\int }_0^{\mathrm{\infty }}\zeta d\zeta {\int }_{\zeta }^{\mathrm{\infty }}\frac{{\mathrm{e}}^{-t}}{t\sqrt{t^2–{\zeta }^2}}dt\\ =\frac{{\sigma }_s}{\sigma }{\int }_0^{\mathrm{\infty }}{\int }_{\zeta }^{\mathrm{\infty }}\frac{{\mathrm{e}}^{-t}}{t}\frac{\zeta }{\sqrt{t^2-{\zeta }^2}}\mathit{\text{dtdζ}}\mathrm{ }=\frac{{\sigma }_s}{\sigma }{\int }_0^{\mathrm{\infty }}\frac{{\mathrm{e}}^{-t}}{t}dt{\int }_0^t\frac{\zeta }{\sqrt{t^2–{\zeta }^2}}d\zeta \\ \begin{array}{c}=\frac{{\sigma }_s}{\sigma }{\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-t}dt\\ =\frac{{\sigma }_s}{\sigma }<1.\end{array}\end{array}$$(13)

Notice we have changed the order of integration to solve the integral. It is apparent that for there exists a unique solution, the subcritical condition, ${\sigma }_s<\sigma ,$ must be satisfied.

Remark 2.2.

A similar proof can be found for the 2D kernel in terms of the Bickley-Naylor function (de Azevedo et al. 2018). Existence of the unique solution to the general neutron transport equation in $L^1$ and $L^{\infty }$ has been long established in Case and Zweifel (1967). Corresponding results in $L^p$ for $1 \le p \le \infty$ can be found in (Agoshkov 1998; Latrach 2001; Latrach and Zeghal 2012; Egger and Schlottbom 2014).

3. Solution regularity

We first introduce Vainikko’s regularity theorem (Vainikko 1993), which provides a sharp characterization of singularities for the general weakly integral equation of the second kind. Then we analyze the differential properties of the 2D radiation kernel and show that the derivatives are properly bounded. Finally, Vainikko’s theorem is used to give the estimates of pointwise derivatives of the radiation transfer solution.

3.1. Vainikko’s regularity theorem

Before we state the theorem, we introduce the definition of weighted spaces ${\mathbb{C}}^{m,\nu }(\mathrm{G}).$

Weighted space ${\mathbb{C}}^{\mathit{m},\mathit{\nu }}(\mathbf{G}).$ For a $\lambda \in \mathbb{R},$ introduce a weight function (14) $$w_{\lambda }=\{\begin{array}{c}1, \lambda <0\\ {\left(1+\left|\log \varrho \left(x\right)\right|\right)}^{-1}, \lambda =0\\ \varrho {\left(x\right)}^{\lambda }, \lambda >0\end{array},\mathrm{ }x\in \mathrm{G}$$(14) where $\mathrm{G}\subset {\mathbb{R}}^n$ is an open bounded domain and $\varrho \left(x\right)=\underset{y\in \partial \mathrm{G}}{\inf }\left|x-y\right|$ is the distance from $x$ to the boundary $\partial \mathrm{G}.$ Let $m\in \mathbb{N},$ $\nu \in \mathbb{R}$ and $\nu <n.$ Define the space ${\mathbb{C}}^{m,\nu }(\mathrm{G})$ as the set of all $m$ times continuously differentiable functions $\varphi :\mathrm{G}\to \mathbb{ }\mathbb{R}$ such that (15) $${\Vert \varphi \Vert }_{m,\nu }=\sum _{\alpha \le m}\underset{x\in \mathrm{G}}{\sup }\left(w_{\alpha –\left(n–\nu \right)}\left|D^{\alpha }\varphi \left(x\right)\right|\right)<\mathrm{\infty }.$$(15)

In other words, a $m$ times continuously differentiable function $\varphi$ on $\mathrm{G}$ belongs to ${\mathbb{C}}^{m,\nu }(\mathrm{G})$ if the growth of its derivatives near the boundary can be estimated as follows: (16) $$\left|D^{\alpha }\varphi \left(x\right)\right|\le c\{\begin{array}{c}1, \alpha <n–\nu \\ 1+\left|\log \varrho \left(x\right)\right|, \alpha =n–\nu \\ \varrho {\left(x\right)}^{n-\nu -\alpha }, \alpha >n–\nu \end{array},\mathrm{ }x\in \mathrm{G},\mathrm{ }\alpha \le m$$(16) where $c$ is a constant. The space ${\mathbb{C}}^{m,\nu }(\mathrm{G}),$ equipped with the norm ${\Vert ·\Vert }_{m,\nu },$ is a complete Banach space.

After defining the weighted space, we introduce the smoothness assumption about the kernel in the following form: the kernel $\mathrm{K}\left(x,y\right)$ is $m$ times continuously differentiable on $\left(\mathrm{G}\times \mathrm{G}\right)\backslash \left\{x=y\right\}$ and there exists a real number $\nu \in \left(-\infty ,n\right)$ such that the estimate (17) $$\left|D_x^{\alpha }{D}_{x+y}^{\beta }\mathrm{K}\left(x,y\right)\right|\le c\{\begin{array}{c}1, \nu +\alpha <0\\ 1+\left|\log \left|x-y\right|\right|, \nu +\alpha =0\\ {\left|x-y\right|}^{-\nu -\alpha }, \nu +\alpha >0\end{array},\mathrm{ }x,y\in \mathrm{G}$$(17) where (18) $$D_x^{\alpha }={\left(\frac{\partial }{\partial x_1}\right)}^{{\alpha }_1}\cdots {\left(\frac{\partial }{\partial x_n}\right)}^{{\alpha }_n},$$(18) (19) $$D_{x+y}^{\beta }={\left(\frac{\partial }{\partial x_1}+\frac{\partial }{\partial y_1}\right)}^{{\beta }_1}\cdots {\left(\frac{\partial }{\partial x_n}+\frac{\partial }{\partial y_n}\right)}^{{\beta }_n}$$(19) holds for all multi-indices $\alpha =\left({\alpha }_1,\dots ,{\alpha }_n\right)\in {\mathbb{Z}}_{+}^n$ and $\beta =\left({\beta }_1,\dots ,{\beta }_n\right)\in {\mathbb{Z}}_{+}^n$ with $\alpha +\beta \le m.$ Here the following usual conventions are adopted: $\alpha ={\alpha }_1+\cdots +{\alpha }_n,$ and $\left|x\right|=\sqrt{x_1^2+\cdots +x_n^2}.$

Now we present Vainikko’s theorem in characterizing the regularity properties of a solution to the weakly integral equation of the second kind (Vainikko 1993).

Theorem 3.1.

Let $\mathrm{G}\subset {\mathbb{R}}^n$ be an open bounded domain, $f\in {\mathbb{C}}^{m,\nu }(\mathrm{G})$ and let the kernel $\mathrm{K}\left(x,y\right)$ satisfy the condition (17)(17) $$\left|D_x^{\alpha }{D}_{x+y}^{\beta }\mathrm{K}\left(x,y\right)\right|\le c\{\begin{array}{c}1, \nu +\alpha <0\\ 1+\left|\log \left|x-y\right|\right|, \nu +\alpha =0\\ {\left|x-y\right|}^{-\nu -\alpha }, \nu +\alpha >0\end{array},\mathrm{ }x,y\in \mathrm{G}$$(17) . If the integral equation (7)(7) $$\varphi \left(x\right)=\underset{\mathrm{G}}{\int }\mathrm{K}\left(x,y\right)\varphi \left(y\right)dy+f\left(x\right), x\in \mathrm{G}$$(7) has a solution, $\varphi \in {\mathrm{L}}^{\infty }\left(\mathrm{G}\right)$ then $\varphi \in {\mathbb{C}}^{m,\nu }(\mathrm{G}).$

Remark 3.1.

The solution does not improve its properties near the boundary $\partial \mathrm{G},$ remaining only in ${\mathbb{C}}^{m,\nu }(\mathrm{G}),$ even if $\partial \mathrm{G}$ is of class ${\mathbb{C}}^{\mathit{\infty }},$ and $f\in {\mathbb{C}}^{\infty }\left(\mathrm{G}\right).$ A proof can be found in Vainikko (1993). More precisely, for any $n$ and $\nu$ ($\nu <n$) there are kernels $\mathrm{K}\left(x,y\right)$ satisfying (17)(17) $$\left|D_x^{\alpha }{D}_{x+y}^{\beta }\mathrm{K}\left(x,y\right)\right|\le c\{\begin{array}{c}1, \nu +\alpha <0\\ 1+\left|\log \left|x-y\right|\right|, \nu +\alpha =0\\ {\left|x-y\right|}^{-\nu -\alpha }, \nu +\alpha >0\end{array},\mathrm{ }x,y\in \mathrm{G}$$(17) and such that Equation (7)(7) $$\varphi \left(x\right)=\underset{\mathrm{G}}{\int }\mathrm{K}\left(x,y\right)\varphi \left(y\right)dy+f\left(x\right), x\in \mathrm{G}$$(7) is uniquely solvable and, for a suitable $f\in {\mathbb{C}}^{\infty }\left(\mathrm{G}\right),$ the normal derivatives of order $k$ of the solution behave near $\partial \mathrm{G}$ as $\log \varrho \left(x\right)$ if $k=n–\nu ,$ and as $\varrho {\left(x\right)}^{n-\nu -k}$ for $k>n–\nu .$

3.2. Regularity of the radiation transfer solution

To apply the results of Theorem 3.1 to the 2D integral radiation transfer equation, we need to analyze the kernel $\mathrm{K}\left(x,y\right)$ and show that it satisfies the condition (17)(17) $$\left|D_x^{\alpha }{D}_{x+y}^{\beta }\mathrm{K}\left(x,y\right)\right|\le c\{\begin{array}{c}1, \nu +\alpha <0\\ 1+\left|\log \left|x-y\right|\right|, \nu +\alpha =0\\ {\left|x-y\right|}^{-\nu -\alpha }, \nu +\alpha >0\end{array},\mathrm{ }x,y\in \mathrm{G}$$(17) , i.e., $\left|D_x^{\alpha }{D}_{x+y}^{\beta }\mathrm{K}\left(x,y\right)\right|\le {c\left|x-y\right|}^{-1-\alpha }.$ We can simply set $\left|\beta \right|=0$ without loss of generality for our problem. $$\mathit{\alpha }=0:$$ (20) $$\begin{array}{c}\mathrm{K}\left(x,y\right)=\frac{{\sigma }_s}{2\pi \rho }{\int }_0^1\frac{{\mathrm{e}}^{-\frac{\sigma \rho }{t}}}{\sqrt{1–t^2}}dt<\frac{{\sigma }_s}{2\pi \rho }{\int }_0^1\frac{1}{\sqrt{1–t^2}}dt\\ =\frac{{\sigma }_s}{2\pi \rho }\frac{\pi }{2}\mathrm{ }=\frac{{\sigma }_s}{4\rho }\\ \le c{\left|x–y\right|}^{-1}.\end{array}$$(20) $\mathit{\alpha }>1:$ Let $\zeta =\sigma \rho =\sigma \left|x–y\right|=\sigma \sqrt{{\left(x_1–y_1\right)}^2+{\left(x_2–y_2\right)}^2},$ then $\mathrm{K}\left(x,y\right)=\frac{{\sigma }_s}{2\pi \zeta }{\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt.$ By the chain rule, $D_x^{\alpha }$ can be written as (21) $$D_x^{\alpha }={\left(\frac{\partial }{\partial x_1}\right)}^{{\alpha }_1}{\left(\frac{\partial }{\partial x_2}\right)}^{{\alpha }_2}={\left(\frac{\partial }{\partial \zeta }\frac{\partial \zeta }{{\partial x}_1}\right)}^{{\alpha }_1}{\left(\frac{\partial }{\partial \zeta }\frac{\partial \zeta }{{\partial x}_2}\right)}^{{\alpha }_2}=\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}{\left(\frac{\partial \zeta }{{\partial x}_1}\right)}^{{\alpha }_1}{\left(\frac{\partial \zeta }{{\partial x}_2}\right)}^{{\alpha }_2}.$$(21)

Then we have (22) $$\begin{array}{c}\left|D_x^{\alpha }\mathrm{K}\left(x,y\right)\right|=\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}{\left(\frac{\partial \zeta }{{\partial x}_1}\right)}^{{\alpha }_1}{\left(\frac{\partial \zeta }{{\partial x}_2}\right)}^{{\alpha }_2}\mathrm{K}\left(x,y\right)\right|\\ =\left|{\left(\frac{\partial \zeta }{{\partial x}_1}\right)}^{{\alpha }_1}{\left(\frac{\partial \zeta }{{\partial x}_2}\right)}^{{\alpha }_2}\right|\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\mathrm{K}\left(x,y\right)\right|\end{array}$$(22) where (23a) $$\left|\frac{\partial \zeta }{\partial x_1}\right|=\sigma \left|\frac{\left(x_1–y_1\right)}{\sqrt{{\left(x_1–y_1\right)}^2+{\left(x_2–y_2\right)}^2}}\right|\le \sigma ,$$(23a) (23b) $$\left|\frac{\partial \zeta }{\partial x_2}\right|=\sigma \left|\frac{\left(x_2–y_2\right)}{\sqrt{{\left(x_1–y_1\right)}^2+{\left(x_2–y_2\right)}^2}}\right|\le \sigma .$$(23b)

Substituting Eqs. (23a)(23a) $$\left|\frac{\partial \zeta }{\partial x_1}\right|=\sigma \left|\frac{\left(x_1–y_1\right)}{\sqrt{{\left(x_1–y_1\right)}^2+{\left(x_2–y_2\right)}^2}}\right|\le \sigma ,$$(23a) and (23b)(23b) $$\left|\frac{\partial \zeta }{\partial x_2}\right|=\sigma \left|\frac{\left(x_2–y_2\right)}{\sqrt{{\left(x_1–y_1\right)}^2+{\left(x_2–y_2\right)}^2}}\right|\le \sigma .$$(23b) into (22)(22) $$\begin{array}{c}\left|D_x^{\alpha }\mathrm{K}\left(x,y\right)\right|=\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}{\left(\frac{\partial \zeta }{{\partial x}_1}\right)}^{{\alpha }_1}{\left(\frac{\partial \zeta }{{\partial x}_2}\right)}^{{\alpha }_2}\mathrm{K}\left(x,y\right)\right|\\ =\left|{\left(\frac{\partial \zeta }{{\partial x}_1}\right)}^{{\alpha }_1}{\left(\frac{\partial \zeta }{{\partial x}_2}\right)}^{{\alpha }_2}\right|\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\mathrm{K}\left(x,y\right)\right|\end{array}$$(22) , we obtain (24) $$\left|D_x^{\alpha }\mathrm{K}\left(x,y\right)\right|\le {\sigma }^{\alpha }\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\mathrm{K}\left(x,y\right)\right|.$$(24)

Apparently, we only need to find the upper bound of $\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\mathrm{K}\left(x,y\right)\right|\le {c\zeta }^{-(\alpha +1)},$ which is shown as follows. (25) $$\begin{array}{c}\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\mathrm{K}\left(x,y\right)\right|=\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\left(\frac{{\sigma }_s}{2\pi \zeta }{\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt\right)\right|=\frac{{\sigma }_s}{2\pi }\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\left(\frac{1}{\zeta }{\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt\right)\right|\\ =\frac{{\sigma }_s}{2\pi }\left|\frac{{\left(-1\right)}^{\alpha }}{{\zeta }^{\alpha +1}}{\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt+\frac{1}{\zeta }\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\left({\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt\right)\right|\\ \begin{array}{c}\le \frac{{\sigma }_s}{2\pi }\frac{1}{{\zeta }^{\alpha +1}}\left|{\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt\right|+\frac{{\sigma }_s}{2\pi }\frac{1}{\zeta }\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\left({\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt\right)\right|\\ <\frac{{\sigma }_s}{2\pi }\frac{1}{{\zeta }^{\alpha +1}}\left|{\int }_0^1\frac{1}{\sqrt{1–t^2}}dt\right|+\frac{{\sigma }_s}{2\pi }\frac{1}{\zeta }\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\left({\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt\right)\right|\\ =\frac{{\sigma }_s}{4}\frac{1}{{\zeta }^{\alpha +1}}+\frac{{\sigma }_s}{2\pi }\frac{1}{\zeta }\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\left({\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt\right)\right|.\end{array}\end{array}$$(25)

Now we need to find the bound for $\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\left({\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt\right)\right|$ in the above equation, which is analyzed as follows. (26) $$\begin{array}{c}\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\left({\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt\right)\right|=\left|{\int }_0^1\frac{\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\left({\mathrm{e}}^{-\frac{\zeta }{t}}\right)}{\sqrt{1–t^2}}dt\right|=\left|{\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{t^{\alpha }\sqrt{1–t^2}}dt\right|=\left|{\int }_0^{\zeta }\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{t^{\alpha }\sqrt{1–t^2}}dt+{\int }_{\zeta }^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{t^{\alpha }\sqrt{1–{\mathrm{t}}^2}}dt\right|\\ <\left|{\int }_0^{\zeta }\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{t^{\alpha }\sqrt{1–t^2}}dt+\frac{1}{{\zeta }^{\alpha }}{\int }_{\zeta }^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt\right|\mathrm{ }<\left|{\int }_0^{\zeta }\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{t^{\alpha }\sqrt{1–t^2}}dt\right|+\frac{1}{{\zeta }^{\alpha }}\left|{\int }_0^1\frac{1}{\sqrt{1–t^2}}dt\right|\\ \begin{array}{c}=\left|{\int }_0^{\zeta }\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{t^{\alpha }\sqrt{1–t^2}}dt\right|+\frac{\pi }{2{\zeta }^{\alpha }}\\ =\frac{1}{{\zeta }^{\alpha }}\left|{\int }_1^{\mathrm{\infty }}\frac{t^{\alpha }{\mathrm{e}}^{-t}}{\sqrt{{\left(\frac{t}{\zeta }\right)}^2–1}}dt\right|+\frac{\pi }{2{\zeta }^{\alpha }}\\ <c{\zeta }^{-\alpha }\mathrm{ }.\end{array}\end{array}\mathrm{ }$$(26)

Note that in the above equation, $0<\zeta <1$ and $\left|{\int }_1^{\infty }\frac{t^{\alpha }{\mathrm{e}}^{-t}}{\sqrt{{\left(\frac{t}{\zeta }\right)}^2–1}}dt\right|<\infty ,$ i.e., it is bounded. Substituting Equation (26)(26) $$\begin{array}{c}\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\left({\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt\right)\right|=\left|{\int }_0^1\frac{\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\left({\mathrm{e}}^{-\frac{\zeta }{t}}\right)}{\sqrt{1–t^2}}dt\right|=\left|{\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{t^{\alpha }\sqrt{1–t^2}}dt\right|=\left|{\int }_0^{\zeta }\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{t^{\alpha }\sqrt{1–t^2}}dt+{\int }_{\zeta }^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{t^{\alpha }\sqrt{1–{\mathrm{t}}^2}}dt\right|\\ <\left|{\int }_0^{\zeta }\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{t^{\alpha }\sqrt{1–t^2}}dt+\frac{1}{{\zeta }^{\alpha }}{\int }_{\zeta }^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt\right|\mathrm{ }<\left|{\int }_0^{\zeta }\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{t^{\alpha }\sqrt{1–t^2}}dt\right|+\frac{1}{{\zeta }^{\alpha }}\left|{\int }_0^1\frac{1}{\sqrt{1–t^2}}dt\right|\\ \begin{array}{c}=\left|{\int }_0^{\zeta }\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{t^{\alpha }\sqrt{1–t^2}}dt\right|+\frac{\pi }{2{\zeta }^{\alpha }}\\ =\frac{1}{{\zeta }^{\alpha }}\left|{\int }_1^{\mathrm{\infty }}\frac{t^{\alpha }{\mathrm{e}}^{-t}}{\sqrt{{\left(\frac{t}{\zeta }\right)}^2–1}}dt\right|+\frac{\pi }{2{\zeta }^{\alpha }}\\ <c{\zeta }^{-\alpha }\mathrm{ }.\end{array}\end{array}\mathrm{ }$$(26) into (25)(25) $$\begin{array}{c}\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\mathrm{K}\left(x,y\right)\right|=\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\left(\frac{{\sigma }_s}{2\pi \zeta }{\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt\right)\right|=\frac{{\sigma }_s}{2\pi }\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\left(\frac{1}{\zeta }{\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt\right)\right|\\ =\frac{{\sigma }_s}{2\pi }\left|\frac{{\left(-1\right)}^{\alpha }}{{\zeta }^{\alpha +1}}{\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt+\frac{1}{\zeta }\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\left({\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt\right)\right|\\ \begin{array}{c}\le \frac{{\sigma }_s}{2\pi }\frac{1}{{\zeta }^{\alpha +1}}\left|{\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt\right|+\frac{{\sigma }_s}{2\pi }\frac{1}{\zeta }\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\left({\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt\right)\right|\\ <\frac{{\sigma }_s}{2\pi }\frac{1}{{\zeta }^{\alpha +1}}\left|{\int }_0^1\frac{1}{\sqrt{1–t^2}}dt\right|+\frac{{\sigma }_s}{2\pi }\frac{1}{\zeta }\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\left({\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt\right)\right|\\ =\frac{{\sigma }_s}{4}\frac{1}{{\zeta }^{\alpha +1}}+\frac{{\sigma }_s}{2\pi }\frac{1}{\zeta }\left|\frac{{\partial }^{\alpha }}{\partial {\zeta }^{\alpha }}\left({\int }_0^1\frac{{\mathrm{e}}^{-\frac{\zeta }{t}}}{\sqrt{1–t^2}}dt\right)\right|.\end{array}\end{array}$$(25) and noting that $\zeta =\sigma \left|x–y\right|,$ we obtain (27) $$\left|D_x^{\alpha }\mathrm{K}\left(x,y\right)\right|<c{\left|x–y\right|}^{-\alpha -1}.$$(27)

Finally, we conclude that the 2D radiation kernel satisfies the condition (17)(17) $$\left|D_x^{\alpha }{D}_{x+y}^{\beta }\mathrm{K}\left(x,y\right)\right|\le c\{\begin{array}{c}1, \nu +\alpha <0\\ 1+\left|\log \left|x-y\right|\right|, \nu +\alpha =0\\ {\left|x-y\right|}^{-\nu -\alpha }, \nu +\alpha >0\end{array},\mathrm{ }x,y\in \mathrm{G}$$(17) . Therefore, by Theorem 3.1, the estimates of derivatives of the scalar flux $\varphi \left(x\right)$ for radiation transfer are the same as those for the general weakly integral equation of the second kind: (28) $$\left|D^{\alpha }\varphi \left(x\right)\right|\le c\{\begin{array}{c}1, \alpha <1\\ 1+\left|\log \varrho \left(x\right)\right|, \alpha =1\\ \varrho {\left(x\right)}^{1-\alpha }, \alpha >1\end{array},\mathrm{ }x\in \mathrm{G}.$$(28)

It should be noted that in radiation transfer $f\left(x\right)=\frac{1}{{\sigma }_s}{\int }_{\mathrm{G}}\mathrm{K}\left(x,y\right)Q\left(y\right)dy,$ where $Q$ is the external source. If the function $Q$ is bounded, then $f\in {\mathbb{C}}^{m,\nu }\left(\mathrm{G}\right)$ (Vainikko 1993).

Remark 3.2.

The first derivative of the solution $\varphi \left(x\right)$ behaves as $\log \varrho \left(x\right)$ and becomes unbounded as approaching the boundary. The derivatives of order $k$ behave as $\varrho {\left(x\right)}^{1-k}$ for $k>1.$ These pointwise estimates cannot be improved by adding more strong smoothness on the data and domain boundary. Here, we only deal with the solution regularity in the normal direction near the boundary. It is noted that the tangential derivatives behave essentially better than the normal derivatives (Vainikko 1993). In other words, the solution is smoother (or less singular) in the tangential direction than the normal direction near the boundary. The obtained pointwise bounds on the derivatives are strong results, which imply bounds in other norms such as Sobolev norms. Golse et al. (1988) studied the regularity of the mean value (with respect to velocity) of the solution of transport equations in terms of fractional Sobolev space.

Remark 3.3.

These sharp error estimates are needed to analyze numerical methods. The lack of smoothness in the exact solution could adversely affect the convergence rate of spatial discretization schemes for solving the radiation transfer equation (Madsen 1972; Larsen 1982; Wang and Ragusa 2009). The spatial discretization error of a numerical method can be expressed as $\left|{\varphi }_j-{\varphi }_j^N\right|\le C{h}_j^p{\Vert {\varphi }^{(k)}\Vert }_{\infty },$ where ${\varphi }_j$ is the exact solution, ${\varphi }_j^N$ is its numerical result, $h_j$ is the mesh size, $p$ is the order of accuracy, and ${\varphi }^{(k)}$ is the $k$-th derivative of the scalar flux. According to the above regularity results, we have ${\Vert {\varphi }^{(k)}\Vert }_{\infty }\le c{h}_j^{1-k},$ then $\left|{\varphi }_j-{\varphi }_j^N\right|\le C{h}_j^{p+1-k}.$ However, for any numerical methods, we would generally have $k\ge p$ and thus the spatial convergence rate would asymptotically reduce to the first order of accuracy or even worse as the mesh is refined.

4. Error analysis of DD and SD

In this section, we present the optimal error estimates in terms of the scalar flux for the two classic numerical methods: DD and SD. The DD method is a second-order central finite difference method, while the SD method is a first-order upwind method. In the next section, numerical results of a homogeneous unit-square problem are presented for both DD and SD to show how the convergence behavior of numerical solutions are impeded by the underlying regularity of the exact transport solution. The derivation follows our previous analysis (Wang 2022) using the discrete maximum principle (Miller, O’Riordan, and Shishkin 2012; Stynes and Stynes 2018). Although the optimal error estimates are obtained for the 1D slab geometry, it is applicable for 2D problems since we are only concerned with the smoothness in the normal direction to the boundary in this work.

4.1. Error estimate for DD

The monoenergetic S_N equation in slab geometry with the assumption of isotropic scattering and constant external neutron source is written as (29) $${\mu }_m\frac{d{\psi }_m}{dx}+\mathrm{\sigma }{\psi }_m=\frac{{\mathrm{\sigma }}_s}{2}\sum _{m^{\prime }=1}^M{\psi }_{m\prime }{w}_{m\prime }+\frac{Q}{2},$$(29) where ${\mu }_m,$ $m=1,\dots ,M,$ is the neutron direction cosine with respect to the $x$-axis, ${\psi }_m$ is the angular flux, $w_{m\prime }$ is the quadrature weight, $\mathrm{\sigma }$ is the total macroscopic cross section, ${\mathrm{\sigma }}_s$ is the macroscopic scattering cross section, and $Q$ is the external neutron source.

The mesh gird employed for discretizing DD and SD is shown in Figure 1. The index $j$ denotes the center of cell $j,$ $j-1/2$ is the left edge, and $j+1/2$ is the right edge.

Figure 1. One-dimensional mesh.

The DD discretization for the S_N equation on the one-dimensional mesh can be written as (30) $$\begin{array}{c}\frac{{\mu }_m}{h_j}\left({\psi }_{m,j+\frac{1}{2}}^N-{\psi }_{m,j-\frac{1}{2}}^N\right)+{\mathrm{\sigma }}_j\left(\frac{{\psi }_{m,j-\frac{1}{2}}^N+{\psi }_{m,j+\frac{1}{2}}^N}{2}\right)\\ =\frac{1}{2}{\mathrm{\sigma }}_{s,j}\sum _{m^{\prime }=1}^M\left(\frac{{\psi }_{m\prime ,j-1/2}^N+{\psi }_{m\prime ,j+1/2}^N}{2}\right)w_{m^{\prime }}+\frac{Q_j}{2}\text{ for }j\mathrm{ }=\mathrm{ }1,\dots ,N,\end{array}$$(30) where (31a) $$h_j=x_{j+1/2}-x_{j-1/2},$$(31a) (31b) $${\psi }_{m,0}^N=f\left({\mu }_m\right),$$(31b) (31c) $${\psi }_{m,N}^N=g\left({\mu }_m\right).$$(31c) ${\mathrm{\sigma }}_j\mathrm{ }{\mathrm{\sigma }}_{s,j},$ and $Q_j$ are assumed to be piecewise constant in each cell. The superscript "$N$" denotes the numerical solution.

We introduce the linear discrete operator ${\mathit{L}}_{\psi ,DD}^N\left({\psi }_{m,j}^N\right)$ for the DD discretization as (32) $${\mathit{L}}_{\psi ,DD}^N\left({\psi }_{m,j}^N\right)=\frac{Q_j}{2},$$(32) where (33) $$\begin{array}{c}{\mathit{L}}_{\psi ,DD}^N\left({\psi }_{m,j}^N\right)=\frac{{\mu }_m}{h_j}\left({\psi }_{m,j+\frac{1}{2}}^N-{\psi }_{m,j-\frac{1}{2}}^N\right)+{\mathrm{\sigma }}_j\left(\frac{{\psi }_{m,j-\frac{1}{2}}^N+{\psi }_{m,j+\frac{1}{2}}^N}{2}\right)\\ -\frac{1}{2}{\mathrm{\sigma }}_{s,j}\sum _{m^{\prime }=1}^M\left(\frac{{\psi }_{m\prime ,j-1/2}^N+{\psi }_{m\prime ,j+1/2}^N}{2}\right)w_{m^{\prime }}.\end{array}$$(33)

By multiplying ${\mathit{L}}_{\psi ,DD}^N\left({\psi }_{m,j}^N\right)$ with each quadrature weight $w_m$ and summing them from $m=1$ to $M,$ we can obtain the DD discrete operator for the scalar flux: (34) $${\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j^N\right)=\sum _{m=1}^M{\mathit{L}}_{\psi ,DD}^N\left({\psi }_{m,j}^N\right)w_m\mathrm{ }=Q_j,$$(34) where (35) $$\begin{array}{c}{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j^N\right)=\sum _{m=1}^M\left[\frac{{\mu }_m}{h_j}\left({\psi }_{m,j+\frac{1}{2}}^N-{\psi }_{m,j-\frac{1}{2}}^N\right)+{\mathrm{\sigma }}_j\left(\frac{{\psi }_{m,j-\frac{1}{2}}^N+{\psi }_{m,j+\frac{1}{2}}^N}{2}\right)\right]w_m\\ -\sum _{m=1}^M\left[\frac{1}{2}{\mathrm{\sigma }}_{s,j}\sum _{m^{\prime }=1}^M\left(\frac{{\psi }_{m\prime ,j-1/2}^N+{\psi }_{m\prime ,j+1/2}^N}{2}\right)w_{m^{\prime }}\right]w_m\\ =\frac{1}{h_j}\left(J_{j+1/2}^N-J_{j-1/2}^N\right)+{\mathrm{\sigma }}_{a,j}\left(\frac{{\varphi }_{j-1/2}^N+{\varphi }_{j+1/2}^N}{2}\right),\end{array}$$(35) with (36a) $${\varphi }_{j-1/2}^N=\sum _{m=1}^M{\psi }_{m,j-1/2}^N{w}_m,$$(36a) (36b) $$J_{j-1/2}^N=\sum _{m=1}^M{\mu }_m{\psi }_{m,j-1/2}^N{w}_m,$$(36b) (36c) $${\mathrm{\sigma }}_{a,j}={\mathrm{\sigma }}_j-{\mathrm{\sigma }}_{s,j}.$$(36c)

The local truncation error for the scalar flux is calculated as (37) $$\begin{array}{c}\left|{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j-{\varphi }_j^N\right)\right|=\left|{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j\right)-{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j^N\right)\right|=\left|{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j\right)-Q_j\right|\\ =\left|\begin{array}{c}\frac{1}{h_j}\left(J_{j+1/2}-J_{j-1/2}\right)+{\mathrm{\sigma }}_{a,j}\left(\frac{{\varphi }_{j-1/2}+{\varphi }_{j+1/2}}{2}\right)-Q_j\end{array}\right|,\end{array}$$(37) where ${\varphi }_j$ denotes the exact solution. Note that in deriving Equation (37)(37) $$\begin{array}{c}\left|{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j-{\varphi }_j^N\right)\right|=\left|{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j\right)-{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j^N\right)\right|=\left|{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j\right)-Q_j\right|\\ =\left|\begin{array}{c}\frac{1}{h_j}\left(J_{j+1/2}-J_{j-1/2}\right)+{\mathrm{\sigma }}_{a,j}\left(\frac{{\varphi }_{j-1/2}+{\varphi }_{j+1/2}}{2}\right)-Q_j\end{array}\right|,\end{array}$$(37) , we have used Eqs. (34)(34) $${\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j^N\right)=\sum _{m=1}^M{\mathit{L}}_{\psi ,DD}^N\left({\psi }_{m,j}^N\right)w_m\mathrm{ }=Q_j,$$(34) and (35)(35) $$\begin{array}{c}{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j^N\right)=\sum _{m=1}^M\left[\frac{{\mu }_m}{h_j}\left({\psi }_{m,j+\frac{1}{2}}^N-{\psi }_{m,j-\frac{1}{2}}^N\right)+{\mathrm{\sigma }}_j\left(\frac{{\psi }_{m,j-\frac{1}{2}}^N+{\psi }_{m,j+\frac{1}{2}}^N}{2}\right)\right]w_m\\ -\sum _{m=1}^M\left[\frac{1}{2}{\mathrm{\sigma }}_{s,j}\sum _{m^{\prime }=1}^M\left(\frac{{\psi }_{m\prime ,j-1/2}^N+{\psi }_{m\prime ,j+1/2}^N}{2}\right)w_{m^{\prime }}\right]w_m\\ =\frac{1}{h_j}\left(J_{j+1/2}^N-J_{j-1/2}^N\right)+{\mathrm{\sigma }}_{a,j}\left(\frac{{\varphi }_{j-1/2}^N+{\varphi }_{j+1/2}^N}{2}\right),\end{array}$$(35) .

Now we introduce the linear operator $\mathit{L}$ for the continuous neutron balance equation as (38) $$\mathit{L}\varphi =\frac{d}{dx}J+{\mathrm{\sigma }}_a\varphi =Q.$$(38)

From Equation (38)(38) $$\mathit{L}\varphi =\frac{d}{dx}J+{\mathrm{\sigma }}_a\varphi =Q.$$(38) , we can have (39) $$\frac{1}{2}\left(J_{j-1/2}^{\prime }+J_{j+1/2}^{\prime }\right)+{\mathrm{\sigma }}_{a,j}\left(\frac{{\varphi }_{j-1/2}+{\varphi }_{j+1/2}}{2}\right)=Q_j.$$(39)

We substitute Equation (39)(39) $$\frac{1}{2}\left(J_{j-1/2}^{\prime }+J_{j+1/2}^{\prime }\right)+{\mathrm{\sigma }}_{a,j}\left(\frac{{\varphi }_{j-1/2}+{\varphi }_{j+1/2}}{2}\right)=Q_j.$$(39) into (37)(37) $$\begin{array}{c}\left|{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j-{\varphi }_j^N\right)\right|=\left|{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j\right)-{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j^N\right)\right|=\left|{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j\right)-Q_j\right|\\ =\left|\begin{array}{c}\frac{1}{h_j}\left(J_{j+1/2}-J_{j-1/2}\right)+{\mathrm{\sigma }}_{a,j}\left(\frac{{\varphi }_{j-1/2}+{\varphi }_{j+1/2}}{2}\right)-Q_j\end{array}\right|,\end{array}$$(37) to obtain (40) $$\left|{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j-{\varphi }_j^N\right)\right|=\left|\begin{array}{c}\frac{1}{h_j}\left(J_{j+1/2}-J_{j-1/2}\right)-\frac{1}{2}\left(J_{j-1/2}^{\prime }+J_{j+1/2}^{\prime }\right)\end{array}\right|.$$(40)

By Taylor series expansion at $x_j,$ we obtain (41) $$\left|{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j-{\varphi }_j^N\right)\right|\le C{h}_j^2\max \hspace{0.17em}\left|\begin{array}{c}{J}_j^{″\prime }\left({\xi }_j\right)\end{array}\right|,$$(41) where ${\xi }_j\in \left[x_{j-1/2}, x_{j+1/2}\right],$ and $C$ is a sufficiently large constant.

Differentiating Equation (38)(38) $$\mathit{L}\varphi =\frac{d}{dx}J+{\mathrm{\sigma }}_a\varphi =Q.$$(38) twice with respect to $x,$ we obtain (42) $$J_j^{″\prime }\left({\xi }_j\right)=-{\mathrm{\sigma }}_a\varphi ″\left({\xi }_j\right).$$(42)

Note that we have assumed that $Q$ is piecewise constant in each cell. Plugging Equation (42)(42) $$J_j^{″\prime }\left({\xi }_j\right)=-{\mathrm{\sigma }}_a\varphi ″\left({\xi }_j\right).$$(42) into (41)(41) $$\left|{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j-{\varphi }_j^N\right)\right|\le C{h}_j^2\max \hspace{0.17em}\left|\begin{array}{c}{J}_j^{″\prime }\left({\xi }_j\right)\end{array}\right|,$$(41) , the local truncation error is to satisfy (43) $$\left|{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j-{\varphi }_j^N\right)\right|\le C{\mathrm{\sigma }}_a{h}_j^2\mathrm{m}\mathrm{ax}\left|\begin{array}{c}\varphi ″\left({\xi }_j\right)\end{array}\right|,$$(43)

Next, we use the discrete maximum principle to find the local bound of $\left({\varphi }_j-{\varphi }_j^N\right).$ We define (44) $$\mathcal{M}=\frac{1}{{\mathrm{\sigma }}_{a,j}}\underset{1\le j\le N}{\max }\left|{\mathit{L}}_{\varphi ,DD}^N({\varphi }_j-{\varphi }_j^N)\right|,$$(44) and (45) $${\mathrm{\Phi }}_j=\mathcal{M}\pm \left({\varphi }_j-{\varphi }_j^N\right).$$(45)

Then for $1\le j\le N,$ we have (46) $${\mathit{L}}_{\varphi ,DD}^N\left({\mathrm{\Phi }}_j\right)={\mathit{L}}_{\varphi ,DD}^N\left(\mathcal{M}\right)\pm {\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j-{\varphi }_j^N\right).$$(46)

Since $\mathcal{M}$ is a constant, we find from Equation (35)(35) $$\begin{array}{c}{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j^N\right)=\sum _{m=1}^M\left[\frac{{\mu }_m}{h_j}\left({\psi }_{m,j+\frac{1}{2}}^N-{\psi }_{m,j-\frac{1}{2}}^N\right)+{\mathrm{\sigma }}_j\left(\frac{{\psi }_{m,j-\frac{1}{2}}^N+{\psi }_{m,j+\frac{1}{2}}^N}{2}\right)\right]w_m\\ -\sum _{m=1}^M\left[\frac{1}{2}{\mathrm{\sigma }}_{s,j}\sum _{m^{\prime }=1}^M\left(\frac{{\psi }_{m\prime ,j-1/2}^N+{\psi }_{m\prime ,j+1/2}^N}{2}\right)w_{m^{\prime }}\right]w_m\\ =\frac{1}{h_j}\left(J_{j+1/2}^N-J_{j-1/2}^N\right)+{\mathrm{\sigma }}_{a,j}\left(\frac{{\varphi }_{j-1/2}^N+{\varphi }_{j+1/2}^N}{2}\right),\end{array}$$(35) (47) $${\mathit{L}}_{\varphi ,DD}^N\left(\mathcal{M}\right)={\mathrm{\sigma }}_{a,j}\mathcal{M}.$$(47)

Substituting Equation (44)(44) $$\mathcal{M}=\frac{1}{{\mathrm{\sigma }}_{a,j}}\underset{1\le j\le N}{\max }\left|{\mathit{L}}_{\varphi ,DD}^N({\varphi }_j-{\varphi }_j^N)\right|,$$(44) into Equation (47)(47) $${\mathit{L}}_{\varphi ,DD}^N\left(\mathcal{M}\right)={\mathrm{\sigma }}_{a,j}\mathcal{M}.$$(47) , we obtain (48) $${\mathit{L}}_{\varphi ,DD}^N\left(\mathcal{M}\right)=\underset{1\le j\le N}{\max }\left|{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j-{\varphi }_j^N\right)\right|.$$(48)

Then using Equation (48)(48) $${\mathit{L}}_{\varphi ,DD}^N\left(\mathcal{M}\right)=\underset{1\le j\le N}{\max }\left|{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j-{\varphi }_j^N\right)\right|.$$(48) in Equation (46)(46) $${\mathit{L}}_{\varphi ,DD}^N\left({\mathrm{\Phi }}_j\right)={\mathit{L}}_{\varphi ,DD}^N\left(\mathcal{M}\right)\pm {\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j-{\varphi }_j^N\right).$$(46) , we can have (49) $${\mathit{L}}_{\varphi ,DD}^N\left({\mathrm{\Phi }}_j\right)\ge 0.$$(49)

However, the above result does not warrant a positive solution ${\mathrm{\Phi }}_j\ge 0$ since the matrix form of ${\mathit{L}}_{DD}^N$ is not always an M-matrix. It is known that the DD method is strictly positive when the mesh size $h_j\le \frac{2{\mu }_n}{{\mathrm{\sigma }}_j},$ which is for the most limiting pure absorbing case (i.e., the scattering ratio $c=0$). Nevertheless, this condition can be relaxed as the problem becomes more diffusive (i.e., $c>0$). In this work, we are only interested in the asymptotic convergence behavior. We can have ${\mathrm{\Phi }}_j\ge 0$ when the mesh is sufficiently fine. Then from Equation (45)(45) $${\mathrm{\Phi }}_j=\mathcal{M}\pm \left({\varphi }_j-{\varphi }_j^N\right).$$(45) we obtain by using Equation (43)(43) $$\left|{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j-{\varphi }_j^N\right)\right|\le C{\mathrm{\sigma }}_a{h}_j^2\mathrm{m}\mathrm{ax}\left|\begin{array}{c}\varphi ″\left({\xi }_j\right)\end{array}\right|,$$(43) (50) $$\left|{\varphi }_j-{\varphi }_j^N\right|\le \mathcal{M}=\frac{1}{{\mathrm{\sigma }}_{a,j}}\underset{1\le j\le N}{\max }\left|{\mathit{L}}_{\varphi ,DD}^N\left({\varphi }_j-{\varphi }_j^N\right)\right|\le C{h}_j^2\underset{1\le j\le N}{\max }\left|\varphi ″\left({\xi }_j\right)\right|.$$(50)

Therefore, the DD has the second order convergence rate in spatial discretization if $\varphi ″$ is bounded. It is the case for 1D geometry, but for multi-dimensional geometry the derivatives of the exact solution become unbounded near the boundary as shown in the previous section.

4.2. Step difference (SD)

The SD discretization for the S_N transport equation can be written as (51a) $$\frac{{\mu }_m}{h_j}\left({\psi }_{m,j+1/2}^N-{\psi }_{m,j-1/2}^N\right)+{\mathrm{\sigma }}_j{\psi }_{m,j+1/2}^N=\frac{1}{2}{\mathrm{\sigma }}_{s,j}\sum _{m^{\prime }=1}^M{\psi }_{m\prime ,j+1/2}^N{w}_{m^{\prime }}+\frac{Q_j}{2},\mathrm{ }{\mu }_m>0,$$(51a) (51b) $$\frac{{\mu }_m}{h_j}\left({\psi }_{m,j+1/2}^N-{\psi }_{m,j-1/2}^N\right)+{\mathrm{\sigma }}_j{\psi }_{m,j-1/2}^N=\frac{1}{2}{\mathrm{\sigma }}_{s,j}\sum _{m^{\prime }=1}^M{\psi }_{m\prime ,j-1/2}^N{w}_{m^{\prime }}+\frac{Q_j}{2},\mathrm{ }{\mu }_m<0.$$(51b)

Unlike DD, the SD method employs an upwind stencil instead of the symmetric one. More care should be taken to carry out the error analysis for the SD method.

We introduce the SD discrete operator (52) $${\mathit{L}}_{\varphi ,SD}^N\left({\varphi }_j^N\right)=Q_j,$$(52) where (53) $$\begin{array}{c}{\mathit{L}}_{\varphi ,SD}^N\left({\varphi }_j^N\right)=\sum _{m=1}^{\frac{M}{2}}\left[\begin{array}{c}\frac{{\mu }_m}{h_j}\left({\psi }_{m,j+1/2}^N-{\psi }_{m,j-1/2}^N\right)+{\mathrm{\sigma }}_j{\psi }_{m,j+1/2}^N-\frac{1}{2}{\mathrm{\sigma }}_{s,j}{\varphi }_{j+1/2}^N\end{array}\right]w_m\\ +\sum _{m=M/2+1}^M\left[\begin{array}{c}\frac{{\mu }_m}{h_j}\left({\psi }_{m,j+1/2}^N-{\psi }_{m,j-1/2}^N\right)+{\mathrm{\sigma }}_{\mathrm{j}}{\psi }_{m,j-1/2}^N-\frac{1}{2}{\mathrm{\sigma }}_{s,j}{\varphi }_{j-1/2}^N\end{array}\right]w_m\\ \begin{array}{c}=\frac{1}{h_j}\left(J_{j+\frac{1}{2}}^N-J_{j-\frac{1}{2}}^N\right)+{\mathrm{\sigma }}_j\sum _{m=1}^{\frac{M}{2}}{\psi }_{m,j+\frac{1}{2}}^N{w}_m-\frac{1}{2}{\mathrm{\sigma }}_{s,j}{\varphi }_{j+\frac{1}{2}}^N\\ +{\mathrm{\sigma }}_j\sum _{m=\frac{M}{2}+1}^M{\psi }_{m,j-\frac{1}{2}}^N{w}_m-\frac{1}{2}{\mathrm{\sigma }}_{s,j}{\varphi }_{j-1/2}^N\end{array}\end{array}$$(53)

The local truncation error for the scalar flux is calculated as (54) $$\left|{\mathit{L}}_{\varphi ,SD}^N\left({\varphi }_j-{\varphi }_j^N\right)\right|=\left|{\mathit{L}}_{\varphi ,SD}^N\left({\varphi }_j\right)-{\mathit{L}}_{\varphi ,SD}^N\left({\varphi }_j^N\right)\right|=\left|{\mathit{L}}_{\varphi ,SD}^N\left({\varphi }_j\right)-Q_j\right|,$$(54)

By Taylor series expansion of ${\mathit{L}}_{\varphi ,SD}^N\left({\varphi }_j\right)$ at $x_j,$ we have (55) $$\begin{array}{c}\left|{\mathit{L}}_{\varphi ,SD}^N\left({\varphi }_j-{\varphi }_j^N\right)\right|\le C{h}_j{\mathrm{\sigma }}_j\left|\begin{array}{c}\sum _{m=1}^{\frac{M}{2}}{\psi }_{m,j}^{\prime }{w}_m-\sum _{m=\frac{M}{2}+1}^M{\psi }_{m,j}^{\prime }{w}_m\end{array}\right|\\ \le C{h}_j{\mathrm{\sigma }}_j\left|\begin{array}{c}\sum _{m=1}^{\frac{M}{2}}{\psi }_{m,j}^{\prime }{w}_m-\sum _{m=\frac{M}{2}+1}^M{\psi }_{m,j}^{\prime }{w}_m\end{array}\right|\\ \begin{array}{c}\le C{h}_j{\mathrm{\sigma }}_j\max \hspace{0.17em}\left|\begin{array}{c}\sum _{m=1}^M{\psi }_{m,j}^{\prime }\left({\xi }_j\right)w_m\end{array}\right|\\ =C{h}_j{\mathrm{\sigma }}_j\max \hspace{0.17em}\left|\begin{array}{c}\varphi \prime \left({\xi }_j\right)\end{array}\right|.\end{array}\end{array}$$(55) where ${\xi }_j\in \left[x_{j-1/2},\mathrm{ }{x}_{j+1/2}\right],$ and $C$ is a sufficiently large constant. In the above derivation, we have used the inequality, $\left|\begin{array}{c}{\sum }_{m=1}^{\frac{M}{2}}{\psi }_{m,j}^{\prime }{w}_m-{\sum }_{m=\frac{M}{2}+1}^M{\psi }_{m,j}^{\prime }{w}_m\end{array}\right|\le C·\max \left|\begin{array}{c}{\sum }_{m=1}^{\frac{M}{2}}{\psi }^{\prime }\left({\xi }_j\right)w_m+{\sum }_{m=\frac{M}{2}+1}^M{\psi }^{\prime }\left({\xi }_j\right)w_m\end{array}\right|,$ which can be always found to hold for some ${\xi }_j\in \left[x_{j-1/2},\mathrm{ }{x}_{j+1/2}\right]$ when $C$ is sufficiently large. If $\begin{array}{c}\varphi \prime \end{array}=0,$ then the solution is constant, and the inequality holds trivially. It should be noted that the bound on $\left|\begin{array}{c}{\sum }_{m=1}^{\frac{M}{2}}{\psi }_{m,j}^{\prime }{w}_m-{\sum }_{m=\frac{M}{2}+1}^M{\psi }_{m,j}^{\prime }{w}_m\end{array}\right|$ can be further improved for the thick diffusive problem (Wang 2022).

Like DD, we use the discrete maximum principle to find the local bound of $\left({\varphi }_j-{\varphi }_j^N\right).$ We define (56) $$\mathcal{M}=\frac{1}{{\mathrm{\sigma }}_{a,j}}\underset{1\le j\le N}{\max }\left|{\mathit{L}}_{\varphi ,SD}^N\left({\varphi }_j-{\varphi }_j^N\right)\right|,$$(56) and (57) $${\mathrm{\Phi }}_j=\mathcal{M}\pm \left({\varphi }_j-{\varphi }_j^N\right).$$(57)

Then for $1\le j\le N,$ we have (58) $${\mathit{L}}_{\varphi ,SD}^N\left({\mathrm{\Phi }}_j\right)={\mathit{L}}_{\varphi ,SD}^N\left(\mathcal{M}\right)\pm {\mathit{L}}_{\varphi ,SD}^N\left({\varphi }_j-{\varphi }_j^N\right),$$(58)

Since $\mathcal{M}$ is a constant, we find from Equation (53)(53) $$\begin{array}{c}{\mathit{L}}_{\varphi ,SD}^N\left({\varphi }_j^N\right)=\sum _{m=1}^{\frac{M}{2}}\left[\begin{array}{c}\frac{{\mu }_m}{h_j}\left({\psi }_{m,j+1/2}^N-{\psi }_{m,j-1/2}^N\right)+{\mathrm{\sigma }}_j{\psi }_{m,j+1/2}^N-\frac{1}{2}{\mathrm{\sigma }}_{s,j}{\varphi }_{j+1/2}^N\end{array}\right]w_m\\ +\sum _{m=M/2+1}^M\left[\begin{array}{c}\frac{{\mu }_m}{h_j}\left({\psi }_{m,j+1/2}^N-{\psi }_{m,j-1/2}^N\right)+{\mathrm{\sigma }}_{\mathrm{j}}{\psi }_{m,j-1/2}^N-\frac{1}{2}{\mathrm{\sigma }}_{s,j}{\varphi }_{j-1/2}^N\end{array}\right]w_m\\ \begin{array}{c}=\frac{1}{h_j}\left(J_{j+\frac{1}{2}}^N-J_{j-\frac{1}{2}}^N\right)+{\mathrm{\sigma }}_j\sum _{m=1}^{\frac{M}{2}}{\psi }_{m,j+\frac{1}{2}}^N{w}_m-\frac{1}{2}{\mathrm{\sigma }}_{s,j}{\varphi }_{j+\frac{1}{2}}^N\\ +{\mathrm{\sigma }}_j\sum _{m=\frac{M}{2}+1}^M{\psi }_{m,j-\frac{1}{2}}^N{w}_m-\frac{1}{2}{\mathrm{\sigma }}_{s,j}{\varphi }_{j-1/2}^N\end{array}\end{array}$$(53) (59) $${\mathit{L}}_{\varphi ,SD}^N\left(\mathcal{M}\right)={\mathrm{\sigma }}_{a,j}\mathcal{M}.$$(59)

Substituting Equation (56)(56) $$\mathcal{M}=\frac{1}{{\mathrm{\sigma }}_{a,j}}\underset{1\le j\le N}{\max }\left|{\mathit{L}}_{\varphi ,SD}^N\left({\varphi }_j-{\varphi }_j^N\right)\right|,$$(56) into Equation (59)(59) $${\mathit{L}}_{\varphi ,SD}^N\left(\mathcal{M}\right)={\mathrm{\sigma }}_{a,j}\mathcal{M}.$$(59) , we obtain (60) $${\mathit{L}}_{\varphi ,SD}^N\left(\mathcal{M}\right)=\underset{1\le j\le N-1}{\max }\left|{\mathit{L}}_{\varphi ,SD}^N\left({\varphi }_j-{\varphi }_j^N\right)\right|.$$(60)

Then using Equation (60)(60) $${\mathit{L}}_{\varphi ,SD}^N\left(\mathcal{M}\right)=\underset{1\le j\le N-1}{\max }\left|{\mathit{L}}_{\varphi ,SD}^N\left({\varphi }_j-{\varphi }_j^N\right)\right|.$$(60) in Equation (58)(58) $${\mathit{L}}_{\varphi ,SD}^N\left({\mathrm{\Phi }}_j\right)={\mathit{L}}_{\varphi ,SD}^N\left(\mathcal{M}\right)\pm {\mathit{L}}_{\varphi ,SD}^N\left({\varphi }_j-{\varphi }_j^N\right),$$(58) , we obtain (61) $${\mathit{L}}_{\varphi ,SD}^N\left({\mathrm{\Phi }}_j\right)\ge 0.$$(61)

Since the SD method is strictly positive, we always have ${\mathrm{\Phi }}_j\ge 0,$ and then we can obtain $\left|{\varphi }_j-{\varphi }_j^N\right|\le \mathcal{M}$ from Equation (57)(57) $${\mathrm{\Phi }}_j=\mathcal{M}\pm \left({\varphi }_j-{\varphi }_j^N\right).$$(57) . Using Equation (55)(55) $$\begin{array}{c}\left|{\mathit{L}}_{\varphi ,SD}^N\left({\varphi }_j-{\varphi }_j^N\right)\right|\le C{h}_j{\mathrm{\sigma }}_j\left|\begin{array}{c}\sum _{m=1}^{\frac{M}{2}}{\psi }_{m,j}^{\prime }{w}_m-\sum _{m=\frac{M}{2}+1}^M{\psi }_{m,j}^{\prime }{w}_m\end{array}\right|\\ \le C{h}_j{\mathrm{\sigma }}_j\left|\begin{array}{c}\sum _{m=1}^{\frac{M}{2}}{\psi }_{m,j}^{\prime }{w}_m-\sum _{m=\frac{M}{2}+1}^M{\psi }_{m,j}^{\prime }{w}_m\end{array}\right|\\ \begin{array}{c}\le C{h}_j{\mathrm{\sigma }}_j\max \hspace{0.17em}\left|\begin{array}{c}\sum _{m=1}^M{\psi }_{m,j}^{\prime }\left({\xi }_j\right)w_m\end{array}\right|\\ =C{h}_j{\mathrm{\sigma }}_j\max \hspace{0.17em}\left|\begin{array}{c}\varphi \prime \left({\xi }_j\right)\end{array}\right|.\end{array}\end{array}$$(55) , we obtain the local error estimate as (62) $$\left|{\varphi }_j-{\varphi }_j^N\right|\le \mathcal{M}=\frac{1}{{\mathrm{\sigma }}_{a,j}}\underset{1\le j\le N}{\max }\left|{\mathit{L}}_{\varphi ,SD}^N\left({\varphi }_j-{\varphi }_j^N\right)\right|=C{h}_j\frac{{\mathrm{\sigma }}_j}{{\mathrm{\sigma }}_{a,j}}\underset{1\le j\le N}{\max }\left|\varphi \prime \left({\xi }_j\right)\right|.$$(62)

Thus, the SD method is only first-order accurate, i.e., $O(h).$

Remark 4.1.

To derive the error estimate for the DD method, we have assumed the positivity of the numerical solution, which is however only true on sufficiently fine meshes. The SD method does not require such assumption since it is strictly positive. It should be noted that the error estimates obtained are sharp. There exist some previous results on the error estimates of finite difference methods for solving the S_N neutron transport equation (Madsen 1972; Larsen and Miller 1980). Madsen performed truncation error analysis in terms of the angular flux by assuming that the exact solution has bounded third partial derivatives, and obtained the error estimate for the DD method, i.e., $|{\psi }_{m,j}-{\psi }_{m,j}^N|\le C{h}_j^2\Vert \psi ‴\Vert .$ In the work of Larsen and Miller, they obtained the same error estimate for the 1D slab problem, of which the solution is infinitely differentiable. In our analysis, we are only concerned with the scalar flux. With the help of the discrete maximum principle, we can show that the error estimate of the scalar flux only requires the second derivatives to be bounded.

Remark 4.2.

The error estimate indicates that the accuracy of DD is not affected by the physical properties of the problem, which means that the method is an asymptotic preserving scheme (Larsen, Morel, and Miller 1987; Wang 2019). However, the SD method is not asymptotic preserving since its accuracy will deteriorate as the problem becomes thick and diffusive (i.e., $\mathrm{\sigma }\to \mathrm{\infty }$ and ${\mathrm{\sigma }}_{\mathrm{a}}\to 0$) due to the factor $\mathrm{\sigma }/{\mathrm{\sigma }}_a$ in the error estimate.

5. Numerical results

In this section, we demonstrate how the regularity of the exact solution will impact the numerical convergence rate by solving the S_N neutron transport equation in its original integro-differential form, using the classic DD and SD methods. The model problem is a 1 cm $\times$ 1 cm square with the vacuum boundary condition. Thus, there will be no complication from the boundary condition. The S12 level-symmetric quadrature set is used for angular discretization.

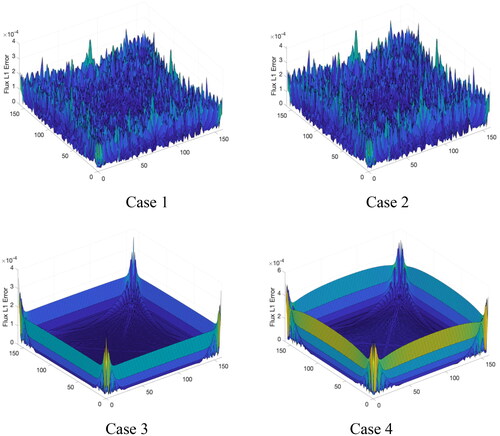
We analyze the following four cases: Case 1: $\sigma =1,$ ${\mathrm{\sigma }}_s=0;$ Case 2: $\sigma =1,$ ${\mathrm{\sigma }}_s=0.8;$ Case 3: $\sigma =10,$ ${\mathrm{\sigma }}_s=0,$ and Case 4: $\sigma =10,$ ${\mathrm{\sigma }}_s=0.9.$ For all the cases, the external source $Q=1.$ Cases 1 and 3 are pure absorption problems, while Case 3 is optically thicker. It is worth noting that the solutions are only determined by the external source for these two cases. Cases 2 and 4 include the scattering effects, while Case 4 is optically thicker and more diffusive. Both the scattering and external source contribute to the solution. The flux distribution calculated with DD for each case is shown in Figure 2.

Figure 2. Flux distribution on the mesh $160\times 160.$

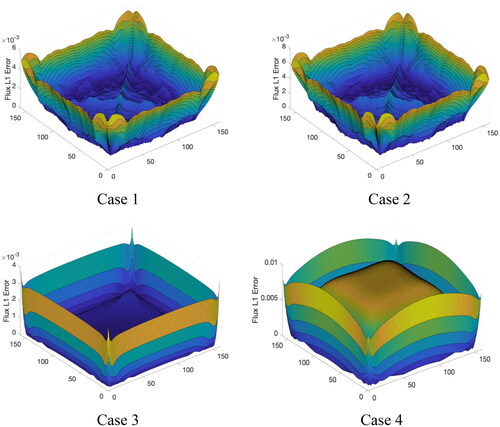
The flux $L^1$ errors as a function of mesh size and the rates of convergence are summarized in Tables 1 and 2 for DD and SD, respectively. In Figures 3 and 4 are depicted the error distributions of DD and SD on the mesh $160\times 160.$ The reference solutions for all the cases are obtained on a very fine mesh ($5120\times 5120$) using the DD method.

Figure 3. Flux error distribution on the mesh $160\times 160$ (DD).

Figure 4. Flux error distribution on the mesh $160\times 160$ (SD).

Table 1. Scalar flux $L^1$ errors and convergence rates of DD.

Mesh ($\mathit{N}\times \mathit{N}$)	Case 1		Case 2		Case 3		Case 4
	Error^1	Rate^2	Error	Rate	Error	Rate	Error	Rate
$10\times 10$	2.87E-03		3.59E-03		2.31E-03		9.29E-03
$20\times 20$	7.95E-04	1.85	1.01E-03	1.83	8.12E-04	1.51	2.56E-03	1.86
$40\times 40$	2.90E-04	1.45	3.73E-04	1.44	2.31E-04	1.82	5.89E-04	2.12
$80\times 80$	1.14E-04	1.35	1.44E-04	1.37	5.19E-05	2.15	1.37E-04	2.10
$160\times 160$	5.04E-05	1.17	6.32E-05	1.19	1.32E-05	1.97	3.53E-05	1.96
$320\times 320$	2.46E-05	1.03	3.06E-05	1.04	3.61E-06	1.87	9.39E-06	1.91
$640\times 640$	1.31E-05	0.91	1.63E-05	0.91	1.11E-06	1.71	2.70E-06	1.80
$1280\times 1280$	6.26E-06	1.07	7.76E-06	1.07	3.87E-07	1.51	8.51E-07	1.66

1. The $L^1$ error on each mesh grid is defined by averaging the absolute differences between the numerical scalar flux and reference solution on each cell.

2. The convergence rate $=\ln \left(\frac{\mathrm{Error}\left(N\times N\right)}{\mathrm{Error}\left(2N\times 2N\right)}\right)/\ln 2.$

Table 2. Scalar flux $L^1$ errors and convergence rates of SD.

Mesh ($\mathit{N}\times \mathit{N}$)	Case 1		Case 2		Case 3		Case 4
	Error^1	Rate^2	Error	Rate	Error	Rate	Error	Rate
$10\times 10$	1.40E-02		2.24E-02		2.58E-03		5.74E-02
$20\times 20$	7.83E-03	0.84	1.19E-02	0.92	1.88E-03	0.45	3.92E-02	0.55
$40\times 40$	4.18E-03	0.91	6.20E-03	0.94	1.08E-03	0.81	2.17E-02	0.85
$80\times 80$	2.20E-03	0.93	3.20E-03	0.96	5.95E-04	0.85	1.16E-02	0.90
$160\times 160$	1.14E-03	0.95	1.65E-03	0.96	3.14E-04	0.92	5.99E-03	0.95
$320\times 320$	5.90E-04	0.95	8.50E-04	0.95	1.62E-04	0.96	3.05E-03	0.98
$640\times 640$	3.06E-04	0.95	4.40E-04	0.95	8.23E-05	0.98	1.54E-03	0.99
$1280\times 1280$	1.60E-04	0.94	2.29E-04	0.94	4.15E-05	0.99	7.71E-04	0.99

For the DD, it is evident that the convergence rate decreases as the mesh is refined, and the errors are much larger at the boundary. The “noisier” distributions in Cases 1 and 2 are due to the ray effects of the discrete ordinates (S_N) method, which are more pronounced in the optically thin problem. The convergence behavior is similar between the cases with and without the scattering, indicating that the source term plays a significant role in defining the irregularity of the solution. Cases 3 and 4 show the improved convergence rate as compared to Cases 1 and 2 because the exponential function ${\mathrm{e}}^{–\sigma \left|x–y\right|}$ in the solution makes the kernel less singular for larger total cross section $\sigma .$ In addition, Case 4 has a slightly better rate of convergence than Case 3 on fine meshes (e.g., 1.80 vs. 1.71 on $640\times 640$), because the transport problem in Case 4 becomes more like an elliptic diffusion problem (Wang and Byambaakhuu 2021), which usually has better regularity. It is noted that that in Case 3 the convergence rate is only 1.51 on the coarse mesh. It is because for the pure absorption case, the DD becomes unstable when the mesh size is larger than $\frac{2{\mu }_j}{\sigma }.$ While for the SD method, the convergence rate is the first order for all the cases. By comparing Cases 4 and 3, the SD method has relatively large error for thick diffusive problems because of the factor $\mathrm{\sigma }/{\mathrm{\sigma }}_a$ in the error estimate.

Remark 5.1.

The optimal error derived for the DD method is $\left|{\varphi }_j-{\varphi }_j^N\right|\le C{h}_j^2{\Vert \varphi ″\Vert }_{\infty }.$ As given by Equation (28)(28) $$\left|D^{\alpha }\varphi \left(x\right)\right|\le c\{\begin{array}{c}1, \alpha <1\\ 1+\left|\log \varrho \left(x\right)\right|, \alpha =1\\ \varrho {\left(x\right)}^{1-\alpha }, \alpha >1\end{array},\mathrm{ }x\in \mathrm{G}.$$(28) , the second derivative ${\varphi }^{″}$ is bounded in the interior of the domain, while it behaves as ${\varphi }^{″}\sim O(h_j^{-1})$ near the boundary. Therefore, it is expected that the convergence rate of the DD would decrease with refining the mesh, and asymptotically tend to $O\left(h_j\right).$ It is interesting to note that if the solution were sufficiently smooth (e.g., a manufactured smooth solution), the DD would maintain its second-order accuracy on any mesh size (Wang et al. 2019). While for the SD method, $\left|{\varphi }_j-{\varphi }_j^N\right|\le C{h}_j{\Vert \varphi \prime \Vert }_{\infty },$ where $\varphi \prime \sim O(1)$ or at most $O\left(1+\left|\log h_j\right|\right)$ based on the theoretical results given by Equation (28)(28) $$\left|D^{\alpha }\varphi \left(x\right)\right|\le c\{\begin{array}{c}1, \alpha <1\\ 1+\left|\log \varrho \left(x\right)\right|, \alpha =1\\ \varrho {\left(x\right)}^{1-\alpha }, \alpha >1\end{array},\mathrm{ }x\in \mathrm{G}.$$(28) . From the numerical results, we observe that the SD has maintained the first-order convergence on all the meshes.

Remark 5.2.

The scattering does not appear to play a role in defining the smoothness of the solution. For the problem without the external source, if there exists a nonsmooth or anisotropic incoming flux on the boundary, the scattering may not be able to regularize the solution either, since the irregularity caused by the incoming flux, which is defined by the surface integral term of Equation (3)(3) $$\begin{array}{c}\varphi \left(x\right)=\frac{1}{4\pi }{\int }_{\mathrm{G}}\frac{{\sigma }_s\left(y\right){\mathrm{e}}^{–\tau \left(x,y\right)}}{{\left|x–y\right|}^2}\varphi \left(y\right)dy+\frac{1}{4\pi }{\int }_{\mathrm{G}}\frac{{\mathrm{e}}^{–\tau \left(x,y\right)}}{{\left|x–y\right|}^2}Q\left(y\right)dy\\ +\frac{1}{4\pi }{\int }_{\partial \mathrm{G}}\frac{{\mathrm{e}}^{–\tau \left(x,y\right)}}{{\left|x–y\right|}^2}\left|\frac{x–y}{\left|x–y\right|}·n\left(x\right)\right|{\varphi }_{\partial \mathrm{G}}\left(y\right)d{S}_y,\end{array}$$(3) , has nothing to do with the scattering and the solution flux $\varphi .$

6. Conclusions

We have derived the integral kernel for the two-dimensional integral radiation transfer equation, and examined the differential properties of the integral kernel for fulfilling the boundedness conditions of Vainikko’s theorem. We applied the theorem to estimate the derivatives of the radiation transfer solution near the boundary of the domain. It is noted that the first derivative of the scalar flux $\varphi \left(x\right)$ becomes unbounded when approaching the boundary. The derivatives of order $k$ behave as $\varrho {\left(x\right)}^{1-k}$ for $k>1,$ where $\varrho \left(x\right)$ is the distance to the boundary. We have derived the optimal error estimates in terms of the scalar flux for the DD and SD methods. The numerical results demonstrate that the irregularity of the exact transport solution will adversely reduce the rate of convergence of numerical methods. We are currently extending the analysis to the boundary integral transport problem in considering nonzero incoming boundary conditions and corner effects. In addition, it would be interesting to study the convergence behavior of weak numerical solutions.

Disclosure statement

No potential conflict of interest was reported by the authors.