Topological nodal line semimetals in graphene network structures

ABSTRACT

Topological semimetals are a fascinating class of quantum materials that possess extraordinary electronic and transport properties. These materials have attracted great interests in recent years for their fundamental significance and potential device applications. There have been intensive studies suggested that three-dimensional graphene networks support topological semimetals with two types of continuous nodal lines: one is to form closed nodal rings in Brillouin zone and the other ones traversing the whole Brillouin zone to be periodically connected. Carbon has negligible spin-orbit coupling, non-magnetism and great diversity of allotropes, which makes it very promising in realizing topological nodal line semimetals. Here we review recent efforts in proposing various carbon allotropes to realize these two types of nodal line semimetals. The nodal rings or lines are protected by the coexistence of time reversal and spatial inversion symmetries. When projecting these nodal lines or rings onto the certain surface, drumhead like surface flat bands will appear. Based on these flat bands, Chern insulator and high-temperature superconductor will be induced by electron-electron correlation effects. The recent discoveries of Mott insulator and superconductor in twisted bilayer graphene-related with flat bands have made these reviewed efforts very important and meaningful.

Graphic Abstract

KEYWORDS:

• Carbon
• nodal line semimetal
• Ab initio calculations

1. Introduction

Carbon exhibits an extremely rich variety of allotropic forms [1] that possess a wide range of properties with numerous applications in many areas of science and technology. Despite the existence of a large number of known carbon allotropes, the quest for new carbon structures has been a very active research field. The valence electrons of the carbon atom are capable of forming $s{p}^3$-, $s{p}^2$-, and $s{p}^1$-hybridized states that support four basic types of single, double, triple, and aromatic C-C bonds, which are closely related to the bonding configurations in ethane, ethene, ethyne, and benzene-type hydrocarbon structures [2–6]. At ambient conditions, graphite, which is structurally related to polycyclic benzenoid aromatic hydrocarbon, is the most thermodynamically stable carbon configuration. The polycyclic carbon atoms form a two-dimensional three-connected benzenoid $s{p}^2$ bonding network with bond angles of 120${ }^o$ and bond lengths of 0.142 nm. Diamond, which is related to polycyclic-saturated hydrocarbon, is the second most stable allotrope of carbon with all the carbon atoms in a methane-like tetrahedral $s{p}^3$ bonding with bond angles of 109.47${ }^o$ and bond lengths of 0.1544 nm as in alkanes, forming a very rigid three-dimensional four-connected carbon network with a larger band gap of 5.47 eV [4]. Under static pressure, the highly crystalline varieties of graphite can be transformed to diamond via slipping, buckling, and cross-linking of the carbon sheets with an $s{p}^2\to s{p}^3$ bonding transition [7–16]. Moreover, a rich variety of carbon phases have been synthesized under laboratory conditions, including, most notably, carbon nanotubes [17], fullerenes [18], graphene [19], graphyne (or graphdiyne) [20–24], and the simplest polyyne-like carbyne chains [5].

In addition to these well-characterized carbon allotropes, a new type of stable chiral framework structures comprising threefold, fourfold [2] and sixfold [6] helical chains have been identified in all-$s{p}^2$ bonding networks connected by ethene-type planar $\pi$ conjugation. By inserting acetylenic or diacetylenic bonds into the all $s{p}^2$-hybridized polybenzene lattice, the three-dimensional (3D) polybenzene-ynes in $sp+s{p}^2$ hybridized bonds with phenylic rings and acetylenic chains have been reported [25]. Also, 3D $sp$+$s{p}^3$-yne-diamond was suggested by inserting acetylenic linkers into the C-C bonds in cubic diamond and supercubane [26–29]. Meanwhile, a family of hypothetical graphitic foams with mixed $s{p}^2$-$s{p}^3$ hybridized bonding networks have been proposed theoretically [30–32] and investigated in experiments [33–36] by inserting a phenyl ring into each C-C bond of the diamond lattice.

Topological semimetals are a fascinating class of quantum materials that possess extraordinary electronic and transport properties [37–57]. These materials have attracted great interest in recent years for their fundamental significance and potential device applications. In this paper, we review the topological semimetals found in 3D graphene network structures [58–68]. According to the classification of topological nodal-line semimetals suggested by Hyart et al. [69], topological semimetals in 3D graphene networks can be divided into two types: type A has closed nodal rings in the Brillouin zone (BZ), while type B has continuous nodal lines that traverse the whole BZ to be periodically connected. The topological semimetals with nodal rings have been found in all-$s{p}^2$ carbon network structures such as Mackay-Terrones carbon crystal [59], body-centered orthorhombic C${ }_{16}$ [62], and body-centered tetragonal C${ }_{16}$ [64]; meanwhile, the topological semimetals with nodal lines have been found in $s{p}^2$-$s{p}^3$ hybrid network structures such as interpenetrated graphene network C${ }_6$ [60], orthorhombic C${ }_{24}$ [65], monoclinic mC${ }_{16}$ [66], simple orthorhombic C${ }_{12}$ [67], and body-centered tetragonal C${ }_{40}$ [68]. These topological nodal lines or nodal rings are protected by the coexistence of time reversal and spatial inversion symmetry in bulk and form drumhead-like surface flat bands either inside or outside of the nodal lines when the nodal lines are projected onto certain surfaces.

2. Nodal points in 2D graphene and graphyne sheets

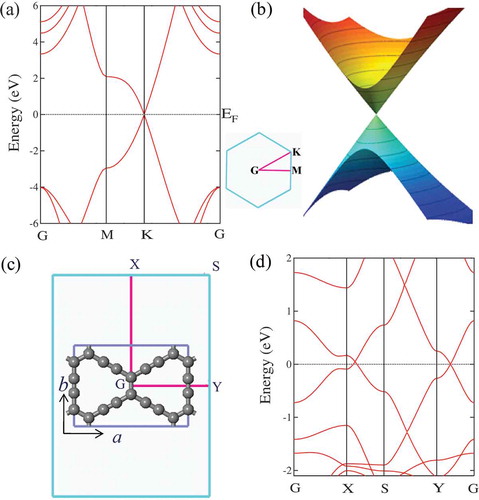
To get the best understanding on the electronic property of 3D graphene network structures, we first introduce the typical electronic property of graphene. As a typical example of topological semimetal of carbon, graphene [70] possesses more superior comprehensive properties, such as high thermal conductivity [71], high strength [72], high chemistry stability [73], and giant intrinsic charge mobility [74]. The electronic property of graphene can be described by a Dirac-like equation, $H=v\vec{k}\cdot \vec{\sigma }$, where $v$ is the velocity, $\vec{k}=(k_x,k_y)$ is the momentum, and $\vec{\sigma }$ is the Pauli matrix [75]. In the 2D BZ, the valence and conduction bands meet in a single point $K$ at the Fermi level [see Figure 1(a)] and yield a Dirac cone [see Figure 1(b)]. Around Dirac points the valence and conduction bands exhibit a linear dispersion. To protect the 2D Dirac cone, two conditions are required: (i) the absence of spin-orbit coupling (SOC) and (ii) the presence of inversion symmetry. The first condition is naturally satisfied in graphene, because its SOC strength is negligible small (${10}^{-3}$ meV). The second requirement is satisfied in the presence of A-B sublattice symmetry in the honeycomb structure [75]. The similar Dirac cone is also found in the honeycomb-like $\alpha$-graphyne structure [76]. The hexagonal lattice symmetry ($p6m$) like graphene is commonly considered a necessary precondition for the presence of Dirac cones. However, the existence of Dirac cone-like features in the band structure of 2D materials does neither depend on a honeycomb structure nor on hexagonal symmetry [76]. One of these materials, 6,6,12-graphyne, has a rectangular ($pmm$) [see Figure 1(c)] instead of a hexagonal symmetry and exhibits two distorted Dirac points along the G-Y and S-X direction [see Figure 1(d)] in its 2D BZ. Such 2D graphene and graphyne sheets with one or two Dirac point are characterized as a nodal-point semimetal [37]. When the dimension is extended from 2D to 3D, the Dirac point at $K$-point in graphene has been found to be kept along the $z$-direction to form a nodal line near the $H$-$K$-$H$ edge in the hexagonal BZ of graphite [58].

Figure 1. (a) Electronic band structure of 2D graphene along several high-symmetry directions of G-M-K-G. (b) Dirac cone formed by the valence and conduction band in the vicinity of the Dirac point $K$. (c) Rectangular 6,6,12-graphyne in $pmm$ symmetry with lattice parameters $a$ = 9.4980 Å, $b$ = 6.7323 Å, and its 2D BZ. (d) Electronic band structure of 2D 6,6,12-graphyne along with the high-symmetry directions of G-X-S-Y-G.

3. Nodal rings in all-$s{p}^{\mathbf{2}}$ 3D carbon network structures

In this section, we introduce two type-A topological nodal line semimetals found in all-$s{p}^2$ Mackay-Terrones carbon crystal [59] and body-centered orthorhombic C${ }_{16}$ [62].

3.1. Nodal rings in cubic mackay-terrones crystal

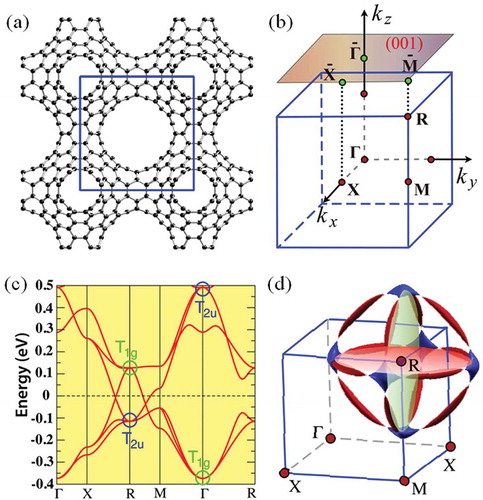
Based on first-principles calculations and tight-binding (TB) analyses, Weng et al. [59] have predicted that a family of all-carbon 3D allotrope, Mackay-Terrones crystals, can have topological node-line semimetal state that has three nodal rings, protected by both time reversal and spacial inversion symmetry.

Figure 2(a) shows a cubic symmetric Mackay-Terrones crystal (MTC) of carbon. It comprises a characteristic all-$s{p}^2$ six-membered-ring bonding network with a 176 atom unit cell in $Pm\bar{3}m$ ($O_h^1$, No. 221) symmetry [77]. The lattice parameters are estimated to be $a=$ 14.557 Å, occupying six nonequivalent atomic Wyckoff positions of 8$g$ (0.2279, 0.2279, 0.2279), 24$m$ (0.1864, 0.1864, 0.3073), 24$m$ (0.2809, 0.0492, 0.2809), 24$l$ (0.1591, 0.0928, 0.5), 48$n$ (0.2178, 0.0979, 0.3367), and 48$n$ (0.1879, 0.0480, 0.4156). The bond lengths are between 1.36$-$1.44 Å, which are on average close to 1.42 Å in graphene. Detailed analysis of the band structure reveals the following: (i) The occupied and unoccupied low-energy bands [see Figure 2(b,c)] are triply degenerate at $\mathrm{\Gamma }$, and they have $T_{1g}$ and $T_{2u}$ symmetry, respectively. Those of $T_{1g}$ are even while those of $T_{2u}$ are odd under spatial inversion symmetry. Moving away from the $\mathrm{\Gamma }$ point their degeneracy is lifted, but upon arriving at the R point their degeneracy is recovered again. However, their energy ordering exchanges, leading to the so-called band inversion, which is one of the key ingredients for the topological insulators [78]. Due to the band inversion, the band crossings happen along both X-R and R-M paths, as seen from Figure 2(c); (ii) Including SOC in the first-principles calculation, a gap will open up around the band crossings, leading to a 3D strong topological insulator. However, similar to graphene, the computed SOC splitting is small (around 0.13 meV or 1.5 K), and it can be neglected in cases with a temperature higher than 1.5 K. Moreover, the detailed tight-binding analyses show that the band crossings exist along certain-closed loops in 3D BZ, and they generate three ring-like nodal lines around the R point [see Figure 2(d)]. These nodal rings are protected by the coexistence of time reversal ($T$) and spacial inversion ($P$) symmetry.

Figure 2. (a) Schematic depiction of the structure of MTC. (b) Bulk and (001)-surface BZ, as well as the highly symmetrical $k$ points. (c) Band structure from the first-principles calculation. The two triply degenerate eigenstates at $\mathrm{\Gamma }$ and R with $T_{1g}$ and $T_{2u}$ symmetrical representation are marked. The band inversion between them can be easily seen. (d) The Fermi surface consists of three lotus-root-like rings from the tight-binding calculation. These rings are center the R point and are parallel to the $k_x=\pi a$, $k_y=\pi a$, and $k_z=\pi a$ plane, respectively. They are formed by the electron pockets (blue) and hole pockets (red) connected by nodal points at the Fermi energy.

With the coexistence of $P$ and $T$ symmetries, there exists a certain gauge choice under which the spineless Hamiltonian is completely real-valued [59]. For this system, if there is an energy level-crossing of two bands at a momentum ${\mathbf{k}}_0$, a stable node-line will unavoidably appear. Around the crossing point, the two-level 2$\times$2 Hamiltonian can be written in the following general form:

(1) $\mathcal{H}=d_0(\vec{k})+d_x(\vec{k})\cdot {\sigma }_x+d_y(\vec{k})\cdot {\sigma }_y+d_z(\vec{k})\cdot {\sigma }_z,$(1)

where the Pauli matrices ${\sigma }_i$ ($i$ = $x,y,z$) denote the two-band space. Without loss of generality, $d_i(\vec{k})$($i$ = $0,x,y,z$) are all real function of $\vec{k}$. The eigen energy of $\mathcal{H}$ being

(2) $E(\vec{k})=\pm \sqrt{d_x^2(\vec{k})+d_y^2(\vec{k})+d_z^2(\vec{k})}+d_0(\vec{k}),$(2)

and the energy degeneracy can be obtained when the three conditions $d_i(\vec{k})$ = 0 ($i$ = $x,y,z$) are satisfied with three parameters $\vec{k}(k_x,k_y,k_z)$ in the 3D momentum space. As mentioned above, the Hamiltonian can be chosen to be real-valued leading to $d_y=0$. The rest $d_0(\vec{k})$, $d_x(\vec{k})$ and $d_z(\vec{k})$ can be expanded around $k_0$ and the location of the crossing points can be determined by $d_x({\vec{k}}_0)\approx {\delta }_x+{\vec{v}}_x(\vec{k}-k_0)=0$ and $d_z({\vec{k}}_0)\approx {\delta }_z+{\vec{v}}_z(\vec{k}-k_0)=0$, where ${\vec{v}}_i={\vec{\mathrm{\nabla }}}_{\vec{k}}{d}_i(\vec{k})$ and ${\delta }_i$ denote the small perturbative terms with both $T$ and $P$ symmetries. In the generic case, the above two equations give a line in the vicinity of $k_0$ with its direction determined by ${\vec{v}}_x\times {\vec{v}}_z$. Therefore, the generic solution of the band crossing point in 3D k-space is a closed rings. Any external perturbations that keep $T$, $P$ and translational symmetry can only shift or distort but not eliminate the nodal rings.

Since the two crossing bands have opposite mirror eigenvalue when they are in the mirror plane of $k_z$ (or $k_x$,$k_y$) $=\pi a$, the topologically stable nodal line in MTC can be looked as to be protected by $P$ and $T$ or by the mirror symmetry of the above planes. The cubic symmetry leads to three in-plane nodal rings, as was found from the tight-binding calculations in Figure 2(d). The nodal rings are not necessarily flat in energy, and they can have energy dispersion in the $k$ space determined by the $d_0$(k) term (which breaks the particle-hole symmetry). The situation becomes even more interesting if $P$ symmetry is broken further. In such a case, from the above discussions, we will generally expect three conditions $d_0$(k) $=0$ with three parameters for the band crossing points, leading to isolated points in the 3D $k$ space. In fact, although the calculated perfect structure has inversion symmetry, most of the known real samples of MTC have strong defects and orientation disorder, which should break inversion symmetry. The plausible existence of these stable 3D Dirac points has been indicated by the density of states [79].

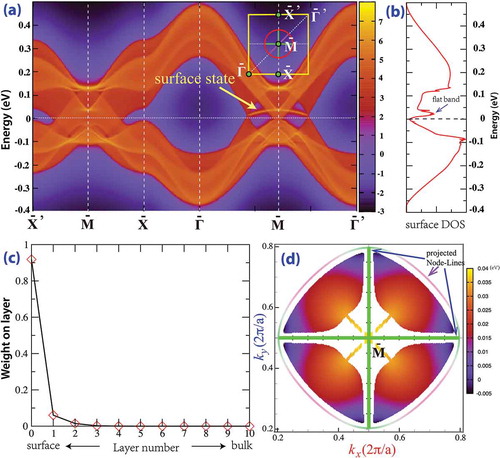
Such topologically stable node-line semimetal state can have nontrivial surface states. For the (001) surface, the three node-line rings are projected to be a ring and two orthogonal diameter segments inside of it, as shown in Figure 3(a). The (001) surface state is calculated based on the six-band TB model using both the Green’s function method and the slab-model method. There is a nearly flat surface band nestled inside of the projected node-line ring with its bandwidth being about 40 meV due to the particle-hole asymmetry. The peak-like surface density of states contributed by this nearly flat band is clearly shown in Figure 3(b), which is proposed to be an important route to high-temperature surface superconductivity [80]. The layer-resolved weight of the wave function for the surface flat band is shown in Figure 3(c). It penetrates just three layers into the bulk with most of the weight on the surface layer. The surface localization of these flat bands is well resolved for those separated from bulk bands. The nestled flat surface states have small dispersion, and their eigenenergy distribution in the surface BZ is shown in Figure 3(d), which looks like some vibrational mode of a drumhead. Such drumhead-like states are readily detected by angle-resolved photoelectron spectroscopy or scanning tunneling microscopy [49].

Figure 3. The (001)-surface state of MTC. (a) The nearly flat surface band is nestled between two solid Dirac cones, which are the projection of one of the node-line circles as indicated in the inset (red circle). The other two node-line rings are projected as two orthogonal diameters (green line). (b) The surface density of state. (c) The wave function of the surface state indicated by the arrow decays rapidly into bulk. (d) The eigenenergy distribution of a surface flat band nestled inside of a projected node-line circle, which looks like a vibration model of a drumhead. The mixing of surface and bulk states leads to discontinuity in this plot.

3.2. Nodal ring in body-centered orthorhombic C₁₆

Distinct from the cubic symmetric MTC that has three nodal rings in its bulk BZ [59], Wang et al. reported a new type of nodal line semimetal that has one nodal ring in body-centered orthorhombic C${ }_{16}$ (termed bco-C${ }_{16}$) [62].

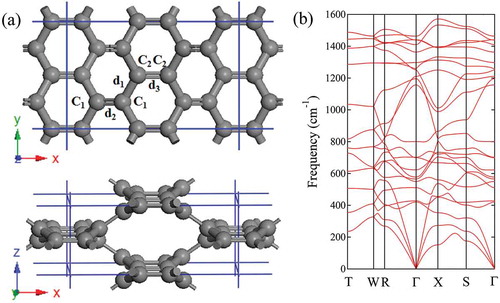
The bco-C${ }_{16}$ carbon has a 16-atom body-centered orthorhombic unit cell in $Imma$ ($D_{2h}^{28}$, No. 74) symmetry [see Figure 4(a)]. The lattice parameters are estimated to be $a$ = 7.8061 Å, $b$ = 4.8772 Å, and $c$ = 3.2372 Å with the carbon atoms occupying two nonequivalent atomic Wyckoff positions of 8i (0.3231, 0.25, 0.1258) and 8f (0.0885, 0.5, 0.5), denoted by C${ }_1$ and C${ }_2$, respectively. This structure topologically corresponds to a 2D (2$\sqrt{3}$ $\times$ 2) graphene-like lattice with one-third double and two-thirds single C-C bonds. Therefore, it also can be regarded as a 3D modification of graphite in AA stacking consisting of benzene linear chains connected by ethene-type planar $\pi$-conjugation. However, in contrast to the uniform bond length of 1.42 Å in graphite, there are three distinct C-C bond lengths, a longer bond of 1.459 Å ($d_1$) associated with a butadiene-type C${ }_1$($s{p}^2$)$-$C${ }_2$($s{p}^2$) single bond and two shorter bonds of 1.396 Å ($d_2$) and 1.382 Å ($d_3$) associated with ethene-type planar C${ }_1$($s{p}^2$)$=$C${ }_1$($s{p}^2$) and C${ }_2$($s{p}^2$)$=$C${ }_2$($s{p}^2$) double bonds, respectively. There are also three different bond angles, $\mathrm{\angle }$C${ }_1$$=$C${ }_1$$-$C${ }_2$ = 123.19${ }^o$ out of the benzene rings, $\mathrm{\angle }$C${ }_2$$-$C${ }_1$$-$C${ }_2$ = 113.38${ }^o$ and $\mathrm{\angle }$C${ }_1$$-$C${ }_2$$=$C${ }_2$ = 118.23${ }^o$ in the benzene rings. Figure 4(b) shows the calculated the phonon dispersion of bco-C${ }_{16}$, no imaginary frequency in the entire BZ, confirming its dynamical stability.

Figure 4. Structure of bco-C${ }_{16}$ and its phonon dispersion. (a) Top and side view of the all-$s{p}^2$ bco-C${ }_{16}$ in $Imma$ ($D_{2h}^{28}$) symmetry with one-third double ($d_2$, $d_3$) and two-thirds single ($d_1$) C-C bonds. It has a 16-atom body-centered orthorhombic structure with lattice parameters $a$ = 7.8061 Å, $b$ = 4.8772 Å, $c$ = 3.2372 Å, occupying the $8i$ (0.3231, 0.25, 0.1258) and $8f$ (0.0885, 0.5, 0.5) Wyckoff positions, denoted by C${ }_1$ and C${ }_2$, respectively. (b) Calculated phonon dispersion curves of bco-C${ }_{16}$ at zero pressure.

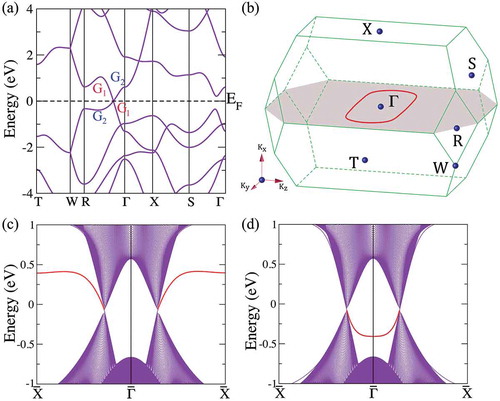
Figure 5 present the calculated bulk and surface band structures of bco-C${ }_{16}$ at equilibrium lattice parameters. It is shown that the valence and conduction bands of bco-C${ }_{16}$ exhibit linear dispersion near the Fermi energy and cross at the Fermi level along the $\mathrm{\Gamma }$-R direction [see Figure 5(a)], and further analysis of the band structure in the full BZ indicates that the band crossing points (or nodal points) of the valence and conduction bands in bco-C${ }_{16}$ form a continuous nodal ring inside a mirror plane [the shaded region in Figure 5(b)]. Moreover, the states near the crossing points around the nodal ring are formed by the inversion of the valence and conduction bands and protected by the coexistence of the time-reversal and inversion symmetry. These electronic properties characterize bco-C${ }_{16}$ as a topological node-line semimetal. When the nodal ring is projected onto the (100) surface, it produces topologically protected surface flat bands either inside or outside of the ring, depending on the termination of the surface, as shown in Figure 5(c,d). The SOC may open up a gap at the band crossing points, but the SOC in bco-C${ }_{16}$, estimated to be 0.74 meV, is negligibly weak at all but extremely low temperatures, thus not expected to alter the semimetal phase.

Figure 5. Calculated bulk and surface band structures of bco-C${ }_{16}$ at equilibrium lattice parameters. (a) The bulk band structure along several high-symmetry directions. G${ }_1$ and G${ }_2$ indicate the irreducible representation of the two crossing bands, respectively. (b) The BZ with several high-symmetry momenta indicated. The nodal ring (red circle), formed by the band crossing points, is in the shaded mirror plane. (c) and (d) show the surface states for different zigzag-like (c) and beard-like (d) terminations of the (100) surface. The surface flat band (red line) can be outside or inside the surface-projected nodal ring.

To establish the experimental connection of bco-C${ }_{16}$, we compare its simulated x-ray diffraction (XRD) spectra, along with those of graphite, diamond, rh6 [6], cT8 [2], cR6 [2], fcc-C${ }_{60}$ [81], to the experimental data from detonation soot of TNT/diesel oil [82] and chimney soot [83] as shown in Figure 6. The measured XRD spectra reveals a considerable amount of amorphous carbon and provide clear evidence for several crystalline phases in the recovered specimen. The prominent peak around 26.5${ }^o$ is attributed to the graphite (002) diffraction, and the weak peak around 43.7${ }^o$, matching that of the diamond (111) diffraction, indicates the presence of a small amount of cubic diamond. The most distinct feature of the measured XRD spectra is a strong peak at ${30}^o$ that does not match any previously known carbon phases [82–84]; the high intensity and sharpness of this peak along with its consistent presence in different experiments suggest that a new crystalline carbon phase has been produced. Our simulated XRD results show that the main (101) diffraction peak of bco-C${ }_{16}$ perfectly matches this previously unexplained peak. It is noted that the main peak of rh6 carbon is also close to 30${ }^o$ because it also comprises sixfold helices (or benzene rings) [6], but bco-C${ }_{16}$ is energetically more stable with a substantial energy gain of 0.12 eV per carbon atom [62] (see Figure 13) due to its complementary chirality. These structural and energetic results suggest that bco-C${ }_{16}$ is a likely candidate of the intriguing new carbon phase observed in the detonation and chimney soot [82–84].

Figure 6. X-ray diffraction (XRD) patterns. (a) Simulated XRD patterns for graphite, diamond, rh6, cT8, cR6, fcc-C${ }_{60}$, and bco-C${ }_{16}$. (b) Experimental XRD patterns for detonation soot of TNT/diesel oil [82] and chimney soot [83]. X-ray wavelength is 1.5406 Å with a copper source.

Similar nodal ring was also reported by Cheng et al. [64] in an all-$s{p}^2$ body-centered tetragonal C${ }_{16}$. This new carbon phase has a 16-atom unit cell in $I{4}_1/amd$ symmetry with space group No. 141, thus termed bct-C${ }_{16}$. It is consisting of two eightfold handed chains with same chirality, topologically corresponding to the 2D square lattice-like as cT8 [2], but less stable than cT8 (see Figure 13) with two fourfold left-handed and two fourfold right-handed chains connected by ethene-type $\pi$-conjugation. Due to the tetragonal symmetry, there is only one nodal ring in the BZ of bct-C${ }_{16}$ like as that in bco-C${ }_{16}$ [62], but distinct from the cubic symmetric MTCs [59] that has three nodal ring in the bulk BZ. Note that the tetragonal symmetric $s{p}^2$-$s{p}^3$ hybrid carbon network structures favor to form a nodal-net [68] as shown in the following section.

4. Nodal lines in $s{p}^{\mathbf{2}}$-$s{p}^{\mathbf{3}}$ hybrid 3D carbon network structures

The type-B topological nodal line semimetal was firstly found in the interpenetrated graphene network C${ }_6$ (termed ign-C${ }_6$) [60]. Electronic band calculations revealed that ign-C${ }_6$ is a topological node-line semimetal with two mirror-inversion symmetric nodal lines that go through the whole BZ in bulk and a projected surface flat band around the Fermi level. Similar electronic property was also found in orthorhombic oC${ }_{24}$ [65] and monoclinic mC${ }_{16}$ [66]. Here we introduce two typical carbon network structures, a simple orthorhombic C${ }_{12}$ [67] which has two mirror-inversion symmetric nodal lines as well as ign-C${ }_6$ and a body-centered tetragonal C${ }_{40}$ [68] which has two mirror-inversion symmetric nodal nets consisting of multiple nodal lines in its bulk BZ.

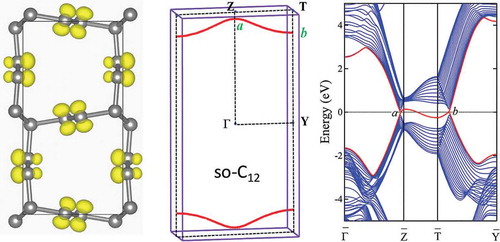
4.1. Nodal lines in the simple orthorhombic C${ }_{\mathbf{12}}$

The simple orthorhombic C${ }_{12}$ phase contains 12 atoms in its unit cell, thus termed so-C${ }_{12}$. It can be constructed by inserting zigzag carbon chains between the graphene layers in AA stacking along the $x$ direction or AB stacking along the $y$ direction [see Figure 7(a)]. The calculated equilibrium lattice parameters are $a$ = 4.313 Å, $b$ = 8.604 Å, and $c$ = 2.461 Å, occupying the 4$d_1$ (0.0507, 0.2104, 0.25), 4$d_2$ (0.0763, 0.0351, 0.25), and 4$d_3$ (0.5783, 0.5052, 0.25) Wyckoff positions denoted by C${ }_1$, C${ }_2$ and C${ }_3$, respectively. The carbon atoms on the 4$d_1$ and 4$d_3$ sites form four zigzag carbon chains with aromatic $s{p}^2$ hybridization, while the carbon atoms on the 4$d_2$ sites form two zigzag carbon chains with diamond-like $s{p}^3$ hybridization. Thus, there are three sets of distinct carbon-carbon bonds in this structure, namely two $s{p}^3$ single longer bonds of 1.512 Å (C${ }_2$-C${ }_3$ and C${ }_2$-C${ }_1$) and 1.520 Å (C${ }_2$-C${ }_2$), and a shorter $s{p}^2$ aromatic bond of 1.406 Å (C${ }_1$-C${ }_1$ and C${ }_3$-C${ }_3$). There are also two sets of distinct bond angles: 108.04${ }^o$ for $\mathrm{\angle }$C${ }_2$-C${ }_2$-C${ }_2$, 111.38${ }^o$ for $\mathrm{\angle }$C${ }_2$-C${ }_2$-C${ }_1$, and 111.04${ }^o$ for $\mathrm{\angle }$C${ }_2$-C${ }_2$-C${ }_3$, which are on average close to the 109.5${ }^o$ angle in diamond; 118.95${ }^o$ for $\mathrm{\angle }$C${ }_2$-C${ }_3$-C${ }_3$, 118.90${ }^o$ for $\mathrm{\angle }$C${ }_2$-C${ }_1$-C${ }_1$, and 122.05${ }^o$ for $\mathrm{\angle }$C${ }_3$-C${ }_3$-C${ }_3$, which are on average close to the 120${ }^o$ angle in graphene.

Figure 7. (a) The crystal structure of so-C${ }_{12}$ in $Pbcm$ ($D_{2h}^{11}$) symmetry with lattice parameters $a$ = 4.313 Å, $b$ = 8.604 Å, and $c$ = 2.461 Å, occupying the 4$d_1$ (0.0507, 0.2104, 0.25), 4$d_2$ (0.0763, 0.0351, 0.25), and 4$d_3$ (0.5783, 0.5052, 0.25) Wyckoff positions denoted by C${ }_1$, C${ }_2$ and C${ }_3$, respectively. (b) Phonon band structures and partial density of states (PDOS) for so-C${ }_{12}$. The peaks around 1443 cm${ }^{-1}$ and 1268 cm${ }^{-1}$ are related to $s{p}^2$ and $s{p}^3$ bonding, respectively.

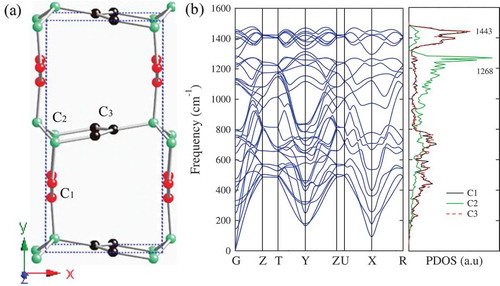
To assess the dynamical stability, we have calculated phonon dispersion and partial density of states (PDOS), and the obtained results are shown in Figure 7(b). It is seen that there are two main peaks around 1443 cm${ }^{-1}$ and 1268 cm${ }^{-1}$ in the PDOS. The peak around 1443 cm${ }^{-1}$ is related to the C${ }_1$ and C${ }_3$ carbon atoms in $s{p}^2$ bonding similar to the finding in all-$s{p}^2$ bco-C${ }_{16}$ [62], while the peak around 1268 cm${ }^{-1}$ is related to the C${ }_2$ carbon atoms in $s{p}^3$ bonding similar to the finding in diamond [85]. There are also some peaks below 800 cm${ }^{-1}$ related to the C${ }_1$, C${ }_2$, and C${ }_3$ carbon atoms in $s{p}^2$-$s{p}^3$ hybrid bonds. No imaginary frequency exists in the entire BZ and PDOS, confirming the dynamical stability of so-C${ }_{12}$.

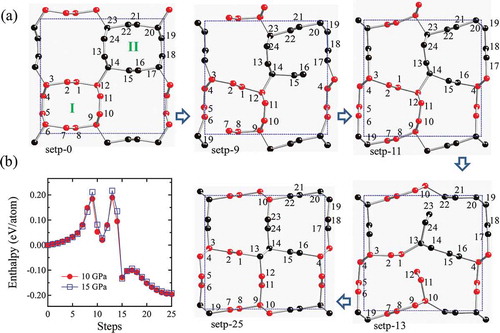
It is noted that so-C${ }_{12}$ can be produced by a crystalline modification of (3,3) CNT. A double cell reconstruction pathway from polymeric (3,3) CNT [86,87] toward so-C${ }_{12}$ is showed in Figure 8(a) and the enthalpy versus pathway is plotted in Figure 8(b) at 10 and 15 GPa. There are two sharp enthalpy peaks in Figure 8(b). The first peak corresponds to the bond breaking between atoms 6–7 and 16–17 at step-9, followed by the enthalpy decrease with the rebonding between atoms 7–19 and 16–4 around step-11; the second peak corresponds to the bond breaking between atoms 1–12 and 22–23 at step-13, followed by the rebonding with atoms 12–13 and 10–23 with the bond rotation of atoms 13–14 and 9–10, respectively, to form the final so-C${ }_{12}$ structure. Throughout this bond rotation assisted two-stage reconstruction pathway, the enthalpy barriers are estimated to be 0.19$-$0.22 eV [see Figure 8(b)], which is similar to the findings in cold-compressed graphite phase transformations [11].

Figure 8. (a) A double cell reconstruction pathway from polymeric (3,3) CNT toward so-C${ }_{12}$ with bond breaking between atoms 6–7 and 16–17 at step-9 and between atoms 1–12 and 22–23 at step-13. The atoms are marked as red in tube-I and black in tube-II, respectively. (b) Enthalpy versus pathway from polymeric (3,3) CNT toward so-C${ }_{12}$ at 10 and 15 GPa.

Figure 9(a) shows the calculated bulk band structure at equilibrium lattice parameters. It is seen that the valence and conduction bands exhibit linear dispersion near the Fermi energy and cross at the Fermi level to form several nodal points along with the high symmetric directions of G-Z, T-Y, and Y-Z in the bulk BZ. Further analysis of the band structure in the full BZ indicates that the band crossing points of the valence and conduction bands in so-C${ }_{12}$ form two discrete saddle nodal lines inside a mirror plane G-Z-T-Y [see Figure 9(b)] with an inversion symmetry about the center of $G$ in the bulk BZ. The states near the crossing points around the nodal lines are formed by the inversion of the valence and conduction bands. To clarify this point, we have calculated the band decomposed charge density near the nodal point $b$ on the high symmetric direction T-Y in BZ [see Figure 9(c)]. One can see that the charge around the nodal points near the Fermi level are located on the C${ }_1$ and C${ }_3$ atoms and show the $\pi$-band character related to the $p$ orbitals. The charge distributions for $b_1$ (and $b_4$) are 53.3$\mathrm{\%}$ from C${ }_1$-$p_x$ and 45.1$\mathrm{\%}$ from C${ }_3$-$p_y$, while for $b_2$ (and $b_3$) the values are 49.3$\mathrm{\%}$ from C${ }_1$-$p_x$ and 49.3$\mathrm{\%}$ from C${ }_3$-$p_y$ orbitals. The obvious difference between the charge distributions of $b_1$($b_4$) and $b_2$($b_3$) reveal that the inversion of the valence and conduction bands on both the left and right side of the nodal point. This band inversion can be described by two crossing $\pi$ bands of G${ }_1$ and G${ }_2$ throughout the full BZ around the nodal lines. Furthermore, these node lines are protected by the coexistence of time reversal ($T$) and spatial inversion ($P$) symmetry [59].

Figure 9. Calculated bulk and surface band structures of so-C${ }_{12}$ at equilibrium lattice parameters. (a) The bulk band structure along several high-symmetry directions. G${ }_1$ and G${ }_2$ indicate the irreducible representations of the two crossing bands, respectively. (b) The BZ with several high-symmetry momenta indicated, and the nodal lines (red), formed by the band crossing points, in the G-Z-T-Y mirror plane. The $a$ and $b$ points represent the nodal point located along G-Z and T-Y line, respectively. (c) The band-decomposed charge density isosurfaces (0.07 $e$/Å${ }^3$) around the nodal point $b$ along T-Y direction in BZ. (d,e) The (010) surface states obtained using a ten-layer-thick slab geometry along the [010] direction. The surface flat band (red line) can be inside or outside the surface projected nodal lines, depending on the termination of the surface without (d) or with (e) saturation by hydrogen atoms. The projected surface BZ $\bar{G}$-$\bar{Z}$-$\bar{T}$-$\bar{Y}$ is marked relative to G-Z-T-Y in bulk in (b). (f) Partial charge density isosurfaces (0.05 $e$/Å${ }^3$) related to the (red) surface bands in (d) at the $\bar{G}$ point. The outermost atoms are C${ }_2$ and C${ }_3$ with dangling bonds on C${ }_2$ sites.

Figure 9(d,e) show the surface band structures calculated using a ten-layer thick slab geometry along the [010] crystalline direction [see Figure 9(f)]. The surface dangling bonds in Figure 9(e) are saturated with hydrogen atoms. The projected surface BZ $\bar{G}$-$\bar{Z}$-$\bar{T}$-$\bar{Y}$ is marked corresponding to G-Z-T-Y in bulk as shown in Figure 9(b). It is seen that when the resulted nodal lines are projected onto the surface BZ, they can produce one topologically protected surface flat band around the Fermi level, either outside [region containing the BZ boundaries in Figure 9(e)] or inside [region containing the $\bar{G}$ point in Figure 9(d)] of two symmetric (up and down) nodal lines, depending on the termination of the surface with or without saturation by hydrogen atoms. In the Figure 9(f) the partial charge density isosurfaces related to the energy bands around the Fermi level in Figure 9(d) at $\bar{G}$ point are plotted. The electronic charges are located on the topmost surface carbon layers, confirming that the surface flat band is indeed deriving from the surface atoms.

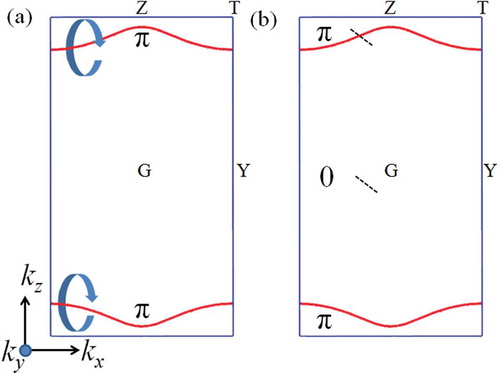
As a topological nodal line semimetal, the nodal line structure is usually protected by the topological invariant, i.e. the Berry phase (a ${\mathbb{Z}}_2$-type invariant) along a closed path encircling the nodal line [69]. To clarify this point, we have calculated the Berry phase using the Wannier Tools package [88] based on a Wannier tight-binding model constructed by Wannier90 [89]. The Berry phase with a closed loop surrounding the nodal lines [see Figure 10(a)] is calculated to be $\pi$. Further, the Berry phase (or Zak phase) along the line passing through the BZ parallel to the $k_y$ axis are calculated. If the line is inside the area between two separated nodal lines [see Figure 10(b)], the result is either $0$ or $\pi$. The nonzero quantized Berry phase further confirms the nodal-line feature in so-C${ }_{12}$ carbon. The appearance of surface states at the surface of nodal line semimetal arises from a quantized Berry phase. Since the Berry phase is equal to $\pi$ for any closed path that interlinks with the nodal line, the surface states should connect the $a$ and $b$ points on the projected nodal loop in the 2D momentum space in Figure 9(d,e) since the surface states and the nodal line in bulk are at the same energy level.

Figure 10. (a) Berry phase with a closed loop surrounding one of the nodal lines. (b) Berry phase using two lines (the black dash lines) in $k_y$ direction passing through the BZ inside or outside between two separated nodal lines. The result is either $0$ or $\pi$.

By carefully comparing the structure of so-C${ }_{12}$ with that in ign-C${ }_6$ [60], mC16 [66], and bct-C${ }_{12}$ [61], we found that the all these graphene network structures can be constructed by inserting zigzag carbon chains between the graphene layers in graphite. Specifically, the so-C${ }_{12}$ is very similar to ign-C${ }_6$ with the similar crystal structures (so-C${ }_{12}$ in $D_{2h}^{11}$ and ign-C${ }_6$ in $D_{2h}^{17}$ symmetry) and electronic band structures. The difference between these structures might be simply due to a slight difference in the stacking of graphene layers. To understand the reconstruction process and kinetics, the pathways from polymeric (3,3) CNT toward bct-C${ }_{12}$ [61] and ign-C${ }_6$ [60] are also simulated at 10 GPa [67]. The enthalpy barriers are estimated to be 0.30 eV toward bct-C${ }_{12}$ and 0.34 eV toward ign-C${ }_6$. These enthalpy barriers are larger than the values of 0.19$-$0.22 eV for the pathway toward so-C${ }_{12}$. These results suggest that so-C${ }_{12}$ is more preferred than bct-C${ }_{12}$ and ign-C${ }_6$ based on kinetics [67].

4.2. Nodal nets comprising multiple-interconnected nodal lines in body-centered tetragonal C₄₀

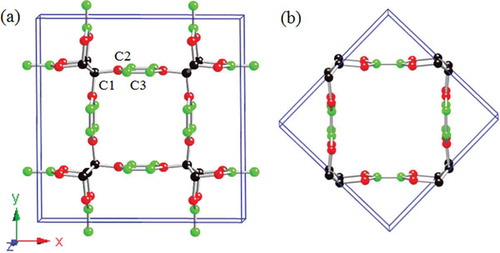
The body-centered tetragonal C${ }_{40}$ carbon allotrope can be constructed by inserting a benzene ring into each C-C bond in a previously established all-$s{p}^3$ bct-C${ }_4$ carbon lattice [9]. The resulted $s{p}^2$-$s{p}^3$ interconnected graphene network structure contains fourty atoms in one unit cell, thus termed bct-C${ }_{40}$. Electronic band structure calculations reveal that bct-C${ }_{40}$ belongs to a new class of topological nodal net semimetal that exhibits nodal nets comprising multiple interconnected nodal lines in bulk and have two coupled drumhead-like flat bands around the Fermi level on its surface [68].

Figure 11(a) shows the body-centered tetragonal network structure of bct-C${ }_{40}$ in $I4/mmm$ ($D_{4h}^{17}$, No. 139) symmetry. The calculated equilibrium lattice parameters are $a$ = 12.901 Å and $c$ = 2.46 Å with three inequivalent crystallographic sites C${ }_1$, C${ }_2$ and C${ }_3$, occupying the 8$h$ (0.7257, 0.7257, 0.5), 16$l_1$ (0.7370, 0.6096, 0.5), and 16$l_2$ (0.7615, 0.0558, 0.5) Wyckoff positions, respectively. The carbon atoms on the 16$l_1$ and 16$l_2$ sites form eight benzene rings with aromatic $s{p}^2$ hybridization, while the carbon atoms on the 8$h$ sites form four zigzag carbon chains as in bct-C${ }_4$ [9]. There are two sets of distinct C-C bonds in this structure, namely two $s{p}^3$ single longer bonds of 1.516 Å (C${ }_1$-C${ }_1$) and 1.505 Å (C${ }_1$-C${ }_2$), and two shorter $s{p}^2$ aromatic bonds of 1.412 Å (C${ }_2$-C${ }_3$) and 1.440 Å (C${ }_3$-C${ }_3$). There are also two sets of distinct bond angles: 109.49${ }^o$ for $\mathrm{\angle }$C${ }_1$-C${ }_1$-C${ }_1$, 111.80${ }^o$ for $\mathrm{\angle }$C${ }_1$-C${ }_1$-C${ }_2$, and 101.09${ }^o$ for $\mathrm{\angle }$C${ }_2$-C${ }_1$-C${ }_2$, which are close to the 109.5${ }^o$ angle in diamond; 119.37${ }^o$ for $\mathrm{\angle }$C${ }_1$-C${ }_2$-C${ }_3$, 121.11${ }^o$ for $\mathrm{\angle }$C${ }_3$-C${ }_2$-C${ }_3$, and 119.43${ }^o$ for $\mathrm{\angle }$C${ }_3$-C${ }_3$-C${ }_2$, which are close to the 120${ }^o$ angle in graphene. Note that bct-C${ }_{40}$ has a 20-atom primitive cell [see Figure 11(b)], and it can be regarded as a crystalline modification of (5,5) CNT [31].

Figure 11. (a) The 40-atom unit cell of bct-C${ }_{40}$ with lattice parameters a = 12.9012 Å, c = 2.4599 Å, occupying the 8$h$ (0.7257, 0.7257, 0.5), 16$l_1$ (0.7370, 0.6096, 0.5), and 16$l_2$ (0.7615, 0.0558, 0.5) Wyckoff positions denoted by C${ }_1$, C${ }_2$ and C${ }_3$, respectively. (b) A 20-atom primitive cell of bct-C${ }_{40}$ viewed as a crystalline modification of the (5,5) CNT.

Figure 12 show the calculated bulk and surface band structures of bct-C${ }_{40}$. It is found that bct-C${ }_{40}$ has interconnected nodal lines forming two nearly 2D nodal nets in BZ [Figure 12(c)], which is distinct from all existing, both nodal point and nodal line, topological semimetals shown above [90]. The crossing bands forming these nodal lines belong to two different irreducible representations $G_1$ and $G_2$ [Figure 12(a)] distinguished by opposite mirror eigenvalues. The resulted nodal lines go through the whole BZ instead of forming a closed ring found in all-$s{p}^2$ carbon network structures [59,62,64]. They are topologically robust protected by the coexisting time-reversal and inversion symmetries without considering the spin-orbit coupling [59] and are constrained on the mirror planes [91]. The nodal lines form two boxed-asterisk shaped nets and the connecting points are on the intersecting lines of different mirror planes.

Figure 12. Calculated bulk and surface band structures of bct-C${ }_{40}$. (a) The bulk band structure along several high-symmetry directions. $G_1$ and $G_2$ indicate the irreducible representations of the two crossing bands, respectively. (b) The bulk BZ with several high-symmetry points indicated at G(0.00, 0.00, 0.00); X(0.00, 0.00, 0.50); P(0.25, 0.25, 0.25); N(0.00, 0.50, 0.00); Z(−0.50, 0.50, 0.50); L(0.26, 0.26, −0.26), and A(−0.26, 0.74, 0.26). (c) Two symmetric-boxed-asterisk shaped nodal nets (red lines) formed by several nodal lines is in the high symmetric mirror plane. (d) and (e) show the (100) surface band states. In (e), the surface dangling bonds are saturated with hydrogen atoms. There are two coupled surface flat bands with one occupied and the other unoccupied around the Fermi level.

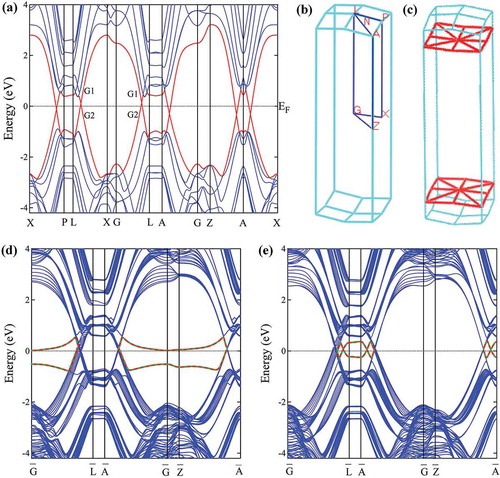
Note that the nodal nets discussed by Bzdusek et al. in [92] are different from bct-C${ }_{40}$ in the following aspects: (1) the nodal net in bct-C${ }_{40}$ is formed by type-B nodal lines going through the whole BZ, while that in the work by Bzdusek et al. is formed by type-A nodal rings traversing only part of the BZ; (2) in bct-C${ }_{40}$, nonsymmorphic symmetry is not required but inversion symmetry is necessary, while in the work by Bzdusek et al. more than one glide mirrors and noncentrosymmetric symmetry are needed; (3) the nodal net in bct-C${ }_{40}$ is nearly 2D, rather than 3D reported by Bzdusek et al.; (4) in bct-C${ }_{40}$, the mirror symmetry constrains the nodal lines inside the mirror plane but its existence is topologically protected by inversion, time-reversal and spin rotation symmetries. Therefore, the crossing points of different nodal lines naturally appear on the intersection lines of different mirror planes. However, in the work by Bzdusek et al., the nodal lines must appear on the glide mirror plane, which also constrains the location of the tangent point of the two nodal rings.

Figure 12(d) and 12(e) show the calculated (100) surface states of bct-C${ }_{40}$ using a slab geometry along the [93] crystalline direction, where the surface dangling bonds are saturated with hydrogen atoms in Figure 12(e). The top and bottom surface bands are marked in red solid and green dotted lines, respectively. They are degenerate due to the inversion symmetric slab model used in the calculation. The surface bands can be inside (region containing the $\bar{G}$ point) or outside (region containing the BZ boundaries) of the momentum space divided by the two symmetric nodal nets depending on the details of the surface termination. When the surface dangling bonds are (not) saturated with hydrogen atoms, the surface bands are outside (inside), which are similar to the results obtained in other nodal line systems [62]. A distinct property of bct-C${ }_{40}$ is that it hosts two surface flat bands, which is different from the previously proposed nodal line semimetals with only a single flat surface band inside or outside the projected nodal line or ring [58–64]. Similar surface states were also found on the (110) surface of bct-C${ }_{40}$ [68]. This distinct property is due to the superposition of the projection regions from the multiple nodal lines in the nodal net. Recently, Bzdusek et al. [92] and Hyart et al. [94] have studied this situation and found that it is possible to have multiple zero-energy flat surface bands if chiral symmetry is assumed. In the case of bct-C${ }_{40}$, the chiral symmetry is absent, and the coupling of the two surface states opens a gap with two bands located below and above the Fermi level, respectively. This finding provides a multiband rather than a single-band-based flat-band platform to study possible novel-correlated effects.

Figure 13. Calculated energy versus volume per atom for various carbon allotropes in all-$s{p}^2$ or mixed $s{p}^2$-$s{p}^3$ bonding networks. The detailed structures are described in text.

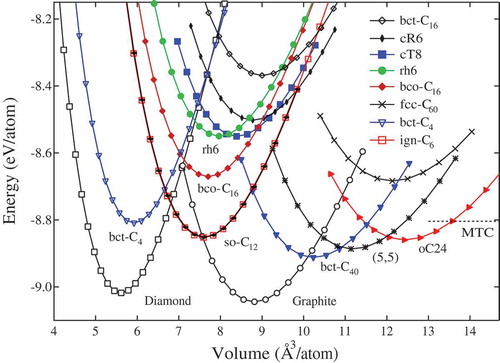
5. Relative stability for the new carbon allotropes

Finally, we discuss the relative structural stability. The total energies are calculated using the density functional theory as implemented in the Vienna ab initio simulation package (VASP) [95]. The generalized gradient approximation (GGA) developed by Armiento-Mattsson (AM05) [96] was adopted for the exchange-correlation function for the structural relaxation. The all-electron projector augmented wave (PAW) method [97] was adopted with 2$s^2$2$p^2$ treated as valence electrons. A plane-wave basis set with a large energy cutoff of 800 eV was used. Convergence criteria employed for both the electronic self-consistent relaxation and the ionic relaxation were set to 10${ }^{-8}$ eV and 0.01 eV/Å for energy and force, respectively. The electronic band structures and related properties are obtained using the standard GGA-PBE method [98], while the band gaps are corrected using a hybrid density functional based on the Heyd-Scuseria-Ernzerhof scheme (HSE06) [99]. The calculated equilibrium structural parameters, total energy, bulk modulus, and electronic band gap are list in Table 1.

Table 1. Calculated equilibrium structural parameters (space group, volume $V_0$, total energy $E_{tot}$, bulk modulus $B_0$, and HSE06 electronic band gap $E_g$ for MTC [59], bco-C${ }_{16}$ [62], bct-C${ }_{16}$ [64], ign-C${ }_6$ [60], oC24 [65], so-C${ }_{12}$ [67] and bct-C${ }_{40}$ [68] in all-$s{p}^2$ or $s{p}^2$-$s{p}^3$ hybrid networks compared to diamond, and other all-$s{p}^2$ carbon phases including graphite, fcc-C${ }_{60}$ [81], and three chiral framework structures cR6 [2], cT8 [2], rh6 [6] at zero pressure, compared to available experimental data [4].

Structure	Method	$V_0$(Å${ }^3$)	$E_{tot}$ (eV)	$B_0$ (GPa)	$E_g$ (eV)
Diamond ($Fd\bar{3}m$)	AM05	5.60	−9.018	451	5.36
	Exp [4]	5.67		446	5.47
cR6 ($R\bar{3}m$)	AM05	8.78	−8.502	268	2.95
cT8 ($I{4}_1/amd$)	AM05	8.40	−8.551	283	2.41
rh6 ($R\bar{3}m$)	AM05	7.96	−8.550	299	0.47
MTC ($Pm\bar{3}m$)	AM05	17.55	−8.804	138	semimetal
bco-C${ }_{16}$ ($Imma$)	AM05	7.70	−8.671	315	semimetal
bct-C${ }_{16}$ ($I{4}_1/amd$)	AM05	9.00	−8.369	257	semimetal
ign-C${ }_6$ ($Cmcm$)	AM05	7.60	−8.852	323	semimetal
oC24 ($Cmmm$)	AM05	12.43	−8.858	192	semimetal
so-C${ }_{12}$ ($Pbcm$)	AM05	7.61	−8.851	322	semimetal
bct-C${ }_{40}$ ($I4/mmm$)	AM05	10.23	−8.912	239	semimetal
fcc-C${ }_{60}$ ($Fm\bar{3}$)	AM05	12.14	−8.684	198
Graphite ($P{6}_3/mmc$)	AM05	8.81	−9.045	280
	Exp [4]	8.78		286

Figure 13 shows the calculated total energy versus volume per atom for the nodal line semimetals in all-$s{p}^2$ or $s{p}^2$-$s{p}^3$ hybrid networks compared to the all-$s{p}^3$ bct-C${ }_4$ [9] and diamond, and other all-$s{p}^2$ carbon phases including graphite, fcc-C${ }_{60}$ fullerene [81], and the recently reported chiral framework structures cR6 [2], cT8 [2] and rh6 carbon [6]. For all-$s{p}^2$ carbon phases, the MTC [59] is more stable than bco-C${ }_{16}$ [62] and bct-C${ }_{16}$ [64] with a large equilibrium volume of 17.55 Å${ }^3$/atom (see Table 1); the stability of bco-C${ }_{16}$ is comparable to that of fcc-C${ }_{60}$, and more favorable than rh6 carbon phase with a substantial energy gain of 0.12 eV per carbon atom due to its complementary chirality [62]; Meanwhile, bct-C${ }_{16}$ [64] is topologically corresponding to the 2D square lattice as well as cT8 [6], but it is less stable than cT8, due to the structure of bct-C${ }_{16}$ is consisting of two eightfold handed chains with same chirality; On the other hand, for the $s{p}^2$-$s{p}^3$ hybrid network structures such as ign-C${ }_6$ [60], oC24 [65], so-C${ }_{12}$ [67], and bct-C${ }_{40}$ [68], they are all energetically stable comparable with (5,5)-CNT, and more favorable than C${ }_{60}$, bco-C${ }_{16}$, and the chiral framework structures cR6, cT8 [2] and rh6 carbon [6] in all-$s{p}^2$ bonding networks. Especially, bct-C${ }_{40}$ is slightly (0.11$\sim$0.13 eV/atom) higher in energy than diamond and graphite, but more stable than all the other carbon phases examined here.

6. Conclusions and outlook

As discussed through several examples in the preceding text, the all-$s{p}^2$ carbon network structures such as Mackay-Terrones carbon crystal [59], body-centered orthorhombic C${ }_{16}$ [62], and a body-centered tetragonal C${ }_{16}$ [64], like to form type-A nodal rings that reside inside a mirror plane of the BZ, while the $s{p}^2$-$s{p}^3$ hybrid network structures such as interpenetrated graphene network C${ }_6$ [60], orthorhombic oC24 [65], simple orthorhombic C${ }_{12}$ [67], and body-centered tetragonal C${ }_{40}$ [68], like to form type-B nodal lines that go through the whole BZ. Especially, body-centered tetragonal C${ }_{40}$ belongs to a new class of topological nodal net semimetal that exhibits nodal nets comprising multiple-interconnected nodal lines in bulk and have two coupled drumhead-like flat bands around the Fermi level on its surface [68].

Beside these nodal lines or nodal net semimetals, the 3D Weyl-surface semimetals are also reported in triangular graphene network TGN(2,2) [93], quadrilateral graphene network QGN(2,2) [93], and hexagonal graphene network HGN(2,2) [93], respectively. Noted that such Weyl surfaces are closely related to an additional sublattice-symmetry operator in the tight-binding model [93], in contrast to the nodal nets reported in bct-C${ }_{40}$ [68]. A similar Dirac surface was also reported in the high symmetric bct-C${ }_{12}$ [61], but it should decay to type-B nodal lines in the low symmetric phase such as so-C${ }_{12}$ reported here [67]. Recently, a new metastable 3D carbon allotrope entirely composed of pentagon rings [100] is also reported. The unique structure of this Pentagon carbon leads to extraordinary electronic properties, making it a cornucopia of emergent topological fermions. All of these results expand the realm of nodal manifolds in topological semimetals.

These carbons based topological nodal line semimetals can support topological surface flat bands, which are fascinating for generating new quantum states. For example, Kopnin et al. [80] have proposed to realize high-temperature superconductor by introducing pairing interaction into these flat bands. Chen et al. [101] proposed that if electron–electron interaction is taken into account, the surface flat bands will lead to Stoner ferromagnetic instability and even 2D Chern insulator at the surface. These expectation seems to be very promising since the recent remarkable experimental observation of Mott insulator and superconductor in twisted bilayer graphene. These have been widely believed to be related with flat bands that arises at a ‘magic’ twist angle [102,103].

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This study was supported by the National Natural Science Foundation of China (Grants No. 11274356, No. 11674364 and No.11674369) and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grants No. XDB28000000 and XXH13506-202). H.W. acknowledge the support from the National Key Research and Development Program of China (Grants No. 2016YFA0300600 and 2018YFA0305700), the Science Challenge Project (TZ2016004), the K. C. Wong Education Foundation (GJTD-2018-01), the Beijing Natural Science Foundation (Z180008), and the Beijing Municipal Science and Technology Commission (Z181100004218001).