A first step in finite-element simulation of a grasping task

Abstract

This paper investigates a biomechanical aspect of human hand during grasping, using the finite-element method. A realistic three-dimensional finite–element (FE) model of a human hand is developed, including wrist bones, phalanges, soft tissues and skin, reconstructed from medical computed tomography (CT) scan images. Material laws of the literature have been implemented in the model, in order to be able to simulate a simple activity of grasping. In a human design context, this model allows an interesting biomechanical study, which simulates the grasping task in a biofidelic manner. This model is a first step in the modeling of the human hand that can lead to future studies dealing with the interaction of the hand with its environment for the improvement of safety requirements of future products development.

Keywords:

• Model
• grasp simulation
• finite-element method
• biomechanics

1. Introduction

Hands are used to grasp, hold, and manipulate an object. This is an organ that is widely used in interaction with human environment in multiple ways, which makes of its behavior a complex mechanism to understand. In an industrial context, a proper design of work objects and work space that considers the properties of the hand can be necessary to increase workers ‘productivity, safety of workers, and efficiency.[1] The integration of ergonomic analyses of hand function in an industrial environment goes through the comprehension of human structures, and a consideration of both mechanical and biomedical factors. Numerical biomechanics could be an interesting tool with the possibility to investigate local stress of biological tissues under loading, and by developing a numerical-based method to improve mechanical design for a powerful ‘human-centered modeling and design.’

In summary, development of a model of a human hand is fundamental and necessary to estimate its mechanical behavior. To date, many biomechanical models of the hand have been developed. Most of them, which are based on the human skeleton, and which were developed for predicting grip posture, focus only on the kinematic structure of the human hand.[2–8] In these models, the deformable aspect of the hand and its real mechanical behavior are not taken into account.

To model such a deformable hand, it is appropriate to deploy proven methods and tools such as finite-element (FE) method to integrate biomechanical knowledge into the existing design process. The precise pressure map of the contacts is a critical focal point of the study as an accurate computer simulated representation would provide a powerful tool to study contacts for many ergonomic centered studies for product, system, and process development. In these applications, it is very important and interesting to evaluate the magnitudes and to determine the locations of these pressure peaks that require realistic modeling of the deformation of soft tissues.

Many studies have already investigated specific motion or loads of the hand via the FE method. Anderson et al. developed in 1995 a plane strain FE model of the radiocarpal joint.[9] Improvements of this model were performed by the same authors in 2005 [10], with an enhanced geometry and contacts between lunate, scaphoid, and radius. Ulrich et al. [11] developed a highly detailed micro-FE model with the aim of studying the load transfer in the trabecular part of the scaphoid, the distal radius, and the lunate with a voxel size of 165 μm. Oda et al. [12] studied the influence of wrist joint model and of the replacement of lunate bone using two-dimensional FE simulation. Ledoux et al. [13] investigated the influence of the scaphoid on the global behavior of the wrist using a two-dimensional model of the wrist. Simulation of several scaphoid bone fracture were performed, which could explain the clinical evolution of the behavior of the wrist. He also developed a more realistic three-dimensional FE model of lunate bone to investigate the specific Kienbock's disease [14]. Carrigan et al. [15] developed a FE model to study the load transmission into the carpus under static load and concluded to the importance of the cartilage and the rotational degree of freedom of the carpal in the pressure distribution into the wrist. Tarnita et al. [16] investigated mechanical parameters (stress and displacements) of a hand phalanx with the FE method under compression, torsion and bending loading, and a comparison with clinical observations of a number of real world hand trauma. A simplified model of the hand has been created by Zadpoor,[17] coupled to a simplified model of the arm in order to study the response of this structure under vibrations, describing the influence of the boundary conditions on the calculated natural frequencies. Richmond et al. [18] studied the phalanges' curvature during grasping with a FE model and concluded to the great influence of the curvature on the computed strain. Ezquerro et al. [19] developed a FE model of the carpal scaphoid and its joints to study the most efficient configuration of scaphoid fractures fixation devices (Kirschner wires). Recommendations of the positioning of such device are evaluated with FE models, in order to improve the scaphoid fracture fixation. Guo et al. [20] created a three-dimensional model of the wrist including carpal bones, radius, ulna, metacarpal bones, and also interosseous wrist ligaments and the transverse carpal ligament with the objective of investigating the influence of dividing the transverse carpal ligament (TCL) on the contact stress distribution and location in the midcarpal joints. Wu et al. [21] used a nonlinear FE model of the distal phalanx in contact with a probe in order to investigate the influence of the contact locations, the different angles of contact, and different preindentation on a vibration simulation, in the well-known context of hand-arm vibration syndrome. Javanmardian et al. [22] investigate influence of the division of ligaments on the contact stress distribution with a three-dimensional FE model of the wrist including carpal bones. Gislason et al. [23] studied the stability of the human wrist and the influence of additional constraints on the response of a FE model. Chamoret et al. [24] explain the development of a three-dimensional FE model of the human hand and with a modeling of the contact between hand and a deformable object with complex constitutive anisotropic hyperelastic laws. The developed hand model is considered as biofidelic in terms of geometry which is based on three-dimensional reconstruction of CT scan images. This model is also an improvement of a previous developed model.[25] Others FE model have also been developed in order to study the interaction of the hand, more specially the fingertip, with objects.[26–31] Finally, many FE models have been developed in different context and for different type of loading. Many have been developed in the context of loading transmission into the wrist, or in order to investigate the behavior of a bone after its fracture fixation, or also to investigate vibration's transmission. To the author's knowledge, no FE analysis concerning the act of grasping have been performed. Indeed, this paper explains the development of a new complete FE model of the hand including all the wrist bones, the different phalanges of the five fingers, and the soft tissues. Based on CT scan images, the complex digital geometry of the human hand is created and meshed in order to perform a dynamical simulation of the act of grasping. In addition to previous studies concerning the grasp motion,[2,32,33] this study combines a kinematic analysis of the prehension and also a local analysis of the contact stress on the biomechanical model but also on the deformable object.

This paper is structured as follows. In Section 2, different steps concerning the generation of the three-dimensional FE model are presented. This model is then used to interact with a deformable object and the results are shown in Section 3. The results are compared with experimental results from literature.

2. Materials and methods

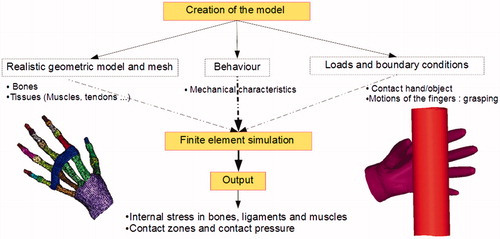
It appears clearly that the grasping task of a deformable object can lead to both geometrical and mechanical interactions. Indeed when a deformable object is grasped, the contact forces on it and on the fingertips can generate a deformation of both the object and of the fingertips. Until now, most models of the hand have focused on appropriately modeling of the different hand components and on some kinematics aspects. Little efforts have been made on the numerical simulation of grasping problem using a numerical biomechanical model and contact interfaces. The main limitations of these models come from the lack of reachable mechanical information such as stress and strain: they do not allow the estimation of the contact force/pressure and the knowledge of stress and strains in the hand. The use and the benefit of finite-element analysis (FEA) is to be able to study stress and strain and to be able to take into contact interactions. One of the objectives of this study is to achieve a first FE simulation of grasping of deformable objects and the second one is to validate this model. A study of the literature provides experimental results.[7] To compare our numerical results with experimental ones, the object is a rigid cylinder of 64 mm diameter. This process is illustrated as a flowchart in Figure 1. In this paper, the FEA is managed by an explicit scheme to cut down computational cost by using the software Radioss, Altair Hyperworks 11 ©. This choice is justified by the highly nonlinear feature of the case, as it deals with the dynamic contact. The explicit resolution of contact problem is much more efficient than the implicit one because it is well adapted to speed and acceleration discontinuities when a sudden contact status change occurs.

Figure 1. Flow chart of the creation of the grasping finite element model.

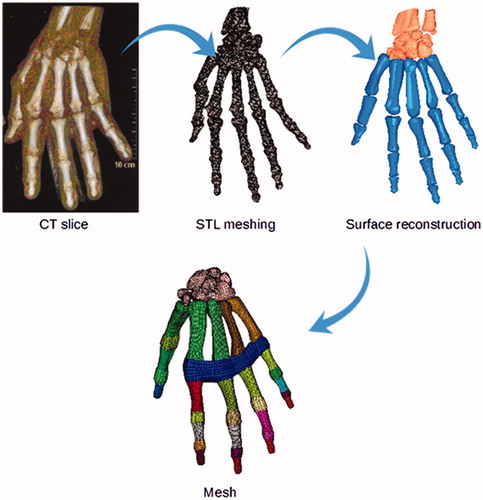
As shown in Figure 1, the starting point in the development of a biomechanical FE model is the three-dimensional reconstruction of the geometry. This geometrical representation is based on a three-dimensional reconstruction of CT scan images.

A tomodensitometry examination of the hand was performed on an adult subject for medical purposes with no relation with the present study. No abnormalities of the hand were found by the medical staff. Using Scan2Mesh software (Altair HyperWorks ©), a tool dedicated to the generation of a mesh from medical data, 300 slices separated by a thickness of 0.7 mm were processed using an automatic detection method based on thresholding. Once the contours of the hand and of its components were detected, a reconstruction method leads three-dimensional surface meshed model. Then, this mesh was imported in Hypermesh software (Altair ©) for a step of surface reconstructions and converted into solid meshes. An anatomically detailed three-dimensional FE mesh of hand was developed, involving bones of the different phalanges of every fingers and wrist bones. Considering the anatomy of the hand, the mechanical joints (Synovial Capsule) were modelled at the junction of each phalanges. Finally, the meshed model of the hand consists of 20,000 8-nodes brick elements for the bone components (including carpal, meta-carpal and phalanges), 18,000 8-nodes brick elements for flesh around bone components, and 9000 4-nodes shell elements with 2 mm thickness for the skin, and 3400 4-nodes shell elements were also used to simulate the synovial capsule between phalanges, and between wrist bones. The general work flow of this work is given in Figure 2.

Figure 2. Mesh generation workflow.

In order to define a numerical model of the grasp, a contact model must be defined. It is necessary to determine the forces or torques that the hand must exert on the contact areas. Contact model involves two fundamental conditions on the common interface between the bodies: the principle of impenetrability and the friction law. These conditions are mathematical described through the normal and frictional contact constraints, which are imposed on the contacting body surfaces. A key issue in the treatment of contact constraints in explicit dynamics is the choice of contact constraints to enforce at contacting nodes. The contact constraints evaluation has significant effect on the accuracy and efficiency of the analysis. A variety of numerical methods have been proposed in the literature to enforce the contact constraints: Lagrange multiplier methods, penalty,[34] augmented Lagrangian approach and bipotential method [35] are the most popular. The penalty method which is the most commonly used in explicit codes (such as Radioss, Altair Hyperworks), has been used for the modelling of the interface for our grasping problem.

The contact definition is a key point of our model. Two kinds of contact were distinguished as follows:

• An external contact. Understanding the behavior of contact is crucial to be able to conduct a correct grasping analysis. So, general contact interfaces were modeled between the object and the hand.

• Anatomic contact. Contact must be taken into account to model accurately the components of the hand. Contact between elements of the anatomy of the hand was defined by creating contact interfaces. The key point of the model is that the contact interactions joints were prescribed to allow relative bone movements and define the good kinematics of the hand. Friction surface-to-surface contact behavior was defined between the contacting bony structures and the synovial capsule. This allows all the components to slide over one another with friction.

As mentioned in Figure 1, during grasp simulation, the surface of the hand is deformed when making contact with the object. In general, this deformation has a nonlinear behavior. Complex constitutive anisotropic hyperelastic laws could be used to model the skin and the subcutaneous tissue. However, complex constitutive laws, such as anisotropic hyperelastic laws, coupled to the modeling of the contact would lead to high nonlinearities, and then, a very small time pitch and a long computational time. For that reason, it was decided to simplify the constitutive laws, in order to first define and validate the grasp motion. So, linear elastic isotropic materials were chosen in a first step to represent all the components of the hand. Discrepancies exist concerning the elasticity of cortical bones. Age dependency has been demonstrated varying between 10 and 15 GPa.[36–39] All the constitutive laws used in our model are listed in Table 1.

Table 1. Material data.

Component	Constitutive law	Youngmodulus(MPa)	Poisson'sratio	Density(kg/m^3)
Bones	Linear elastic	15,000	0.2	2150
Flesh	Linear elastic	0.5	0.3	900
Skin	Linear elastic	16.7	0.4	1200
Synovial membrane [40]	Linear elastic	10	0.4	1000

In order to simulate the motion of the hand to grasp the object, a system of virtual linear and torsional spring-damper (linking the phalanges and the object) [41] is defined taking into account all the DOF of the hand. They produced forces and torques necessary for virtual hand motion using dynamic simulation and for physically based response of grasped objects via collision response.

3. Results and discussion

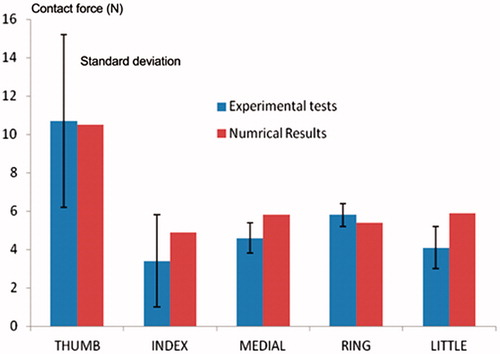
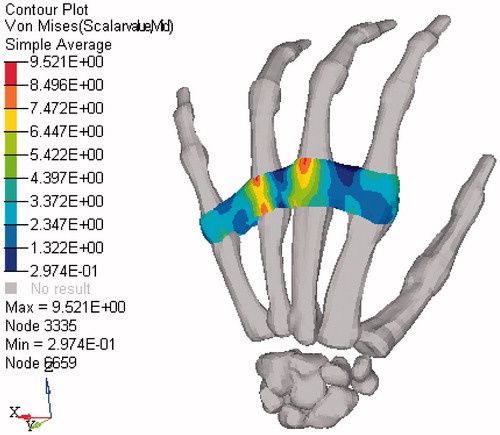
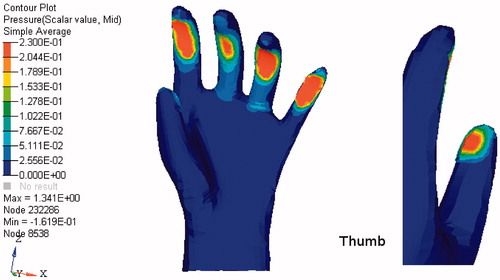
In reference, [7] the finger force patterns were registered during an experiment process of grasping. In order to compare the present results to experimental data from the literature, the contact force was calculated with our numerical model for each finger. Figure 3 shows the contact force in Newton obtained by our simulation and the reference experimental values from.[7] If we have a look in details on this comparison and the standard deviation, our numerical results agreed well agreed well with the experimental results. This is a crucial point to the validation of our numerical model. The contact between hand and objects results in contact force but also in contact area and contact pressure distribution. Especially, pressure distribution is essential in the evaluation of grasp stability, comfort and safety. The contact pressure distribution evaluated by our numerical hand model can be seen in Figure 5. The finite element simulation also allows investigating mechanical parameters such as stress. Von Mises stress in the mechanical joints (Synovial Capsule) was evaluated as illustrated in Figure 4.

Figure 3. Contact forces - comparison numerical results and experimental data.

Figure 4. Simulated Von Mises stress distribution (MPa).

Figure 5. Simulated contact pressure distribution (MPa).

Simulation performed in this study is a first step in the modeling of the task of grasping. The aim of the present work was to create a FE hand model as biofidelic as possible to be able to perform a grasping simulation. To this end, it was necessary to validate our model. The validity of the model was analyzed through the comparison with experimental results from the literature. Although this first step in the understanding of hand motion and related stresses have shown encouraging results, some explanations can be given to explain the observed differences and some limitations can be evoked.

Many parameters can influence the task of grasping. Configurations and interaction between the hand and an object can be very different according to the positioning of the fingers and the anthropometry of the hand. It is important to notice at the finite element model of the hand has been developed from the hand of a male whereas the experimental test were obtained with the hand of a female subject. The FE model of the human hand presented in this paper is biofidelic in terms of shape, anatomy but lots of internal soft tissues have not been modeled.

Preponderant effects of material properties of the soft tissues, of the bones must be underlined. The elasticity of the soft tissues of the hand can contribute to dexterity and also to help to stabilize the objects in manipulation task. In the FE model of the hand presented in this paper, simple elastic laws have been implemented for skin and soft tissues. Implementing more complex material definitions (anisotropic hyperelastic three-dimensional materials) would be a straightforward extension of the present FE model. Although attempts have already been made,[24,42,43] it is still a big challenge.

Friction effects play a key role in grasping task. Friction causes deformation of the skin and underlying tissues and both resist the external load. In terms of interaction between the hand and the material being grasped, it should be noticed that no friction coefficient has been implemented in the model for the modeling of the interface. Incorporating friction coefficient, between fingers and object, seems to be essential to understand the way to grasp an object.

Finally, even if further investigations are needed to improve the model, the simulation performed in the present work show encouraging results in terms of interaction between an object and the human body, and specifically the task of grasping at a numerical level, which provide interesting information and which could not be assessed with experimental protocol: indeed, the Von Mises stress has been evaluated with our model (Figure 4).

4. Conclusion and future works

In this study, a three-dimensional finite element model of the hand was established, with structural components. The model allows computation of contact forces, contact pressures and Von Mises stress during a case of grasping task.

Many grasping models have been already developed but none of them use a three-dimensional total deformable hand model, which means there are limitations to these models in terms of modeling deformity during contacts. In this research, the FE method has been chosen to model these phenomena to overcome the above deficiency. This approach has presented a big challenge for two main reasons. From a mechanical point of view, multiple nonlinearities must be taking into account in geometrical, frictional contact and impact modelling. From a biomechanical point of view, a much better knowledge of the hand's biomechanical capability as well as limitation must be understood in order to develop a closer representation of a real hand. The improved FE hand model could be used in the future for the optimization of the human–product interaction during the product development phase.

Disclosure statement

The authors report no conflicts of interest. The authors alone are responsible for the content and writing of this article.