Digital core reconstruction research: challenges and prospects

ABSTRACT

In this review we have briefly reviewed the state of the art of “digital core” technology. In particular, we reviewed the main artefacts that can occur in the analysis of rocks by computed X-ray microtomography. Next, we highlighted the existing approaches of direct mathematical modelling of core filtration characteristics using digital model and poroset models. Literature analysis has shown that the most justified in the ratio of required technical resources (computer power) and reliability of results is the integrated approach. Unfortunately, when calculating phase permeabilities using digital core models, it is necessary to calibrate simulation results using standard laboratory methods. We also analysed some approaches to modelling enhanced oil recovery methods such as hydrochloric acid and hydraulic fracturing, as well as thermal stimulation of oil matrix rocks. In conclusion, we noted that the main challenge of today’s “digital core” technology is reliable calculation of phase permeabilities, and further development of the technology should be towards 4D modelling of EOR methods using digital core models.

KEYWORDS:

• Digital petrophysics
• digital core
• X-ray microtomography
• filtration properties

Introduction

At present, due to the commissioning of oil and gas reservoirs with hard-to-recover reserves (Gajica et al., 2022; Sun et al., 2022; G. Wang et al., 2022), there is a need to improve the quality of petrophysical studies (Brailovskaya & Oks, 2021; D. Wang et al., 2020). This applies first of all to reservoirs represented by poorly consolidated rocks, clay-bituminous rocks and rocks with a complex lithological structure. The problem in this case is that when working with these rocks there are difficulties when preparing samples for analysis and their subsequent study by standard petrophysical methods: the core of poorly consolidated rocks – crumbles (Peixoto Filho et al., 2021), clay-bituminous rocks after extraction with organic solvents crack, and samples of rocks with complex lithological structure due to a complex combination of permeable and impermeable interlayers can show understated relative to the formation values of permeability and permeability properties

With the development of scientific and technical support of petrophysical laboratories and the need for reliable determination of filtration-volume properties in the above rock types, a new trend “digital petrophysics” or “digital core” has been actively developing over the last decade (Kadyrov et al., 2022; Pal et al., 2022; Payton et al., 2022). This trend implies obtaining a digital core model by means of computer X-ray microtomography and its mathematical processing in specialized software for calculating filtration-volume properties.

In this review, we will highlight the current state of research in the field of “digital petrophysics”: consider the main problems that may arise in obtaining a digital model (scanning artifacts), the state of research on the determination of filtration-volume properties by digital core model and assess the prospects for the development of this field.

Problems of computed X-ray core microtomography

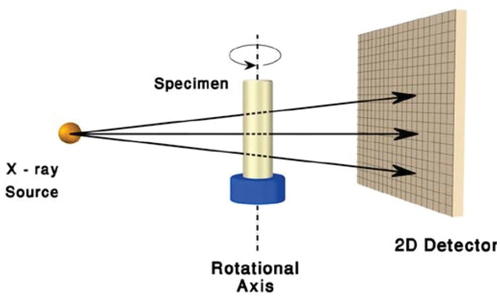
Before it was possible to examine rock samples at a high resolution by computed X-ray microtomography (A. A. Ponomarev et al., 2022; Ibrahim et al., 2021), first geologists were studying rocks by conventional computed X-ray tomography (Mees et al., 2003), the principle of which was identical as in medicine. Before turning to the problems encountered when examining cores by computed X-ray microtomography, we present the principle of operation of X-ray microtomography, Figure 1. X-rays pass through the object under study, hit the detector, which captures the shadow projection. The sample is then rotated by a certain angle and the procedure is repeated. Scanning results in a database of shadow projections of the sample from different angles. Further during reconstruction special mathematical algorithms are used to present the shadow projections in the form of tomographic slices of 1 pixel thickness. This makes it possible to work with a digital model, which is a set of consecutive tomographic slices that can be handled both in 3D and in 2D.

Figure 1. Principle of the computed micro-tomography system (Soltani et al., 2015).

There is probably little point in listing all the possible types of artefacts that can arise from tomographic scanning, as they are known and already well described (Stock, 2019). We want to highlight some of them that are characteristic of working with rocks. In particular, we should highlight artifacts that can occur when very heavy (dense) minerals are present in rocks. These artifacts can create a distortion of the real rock structure, which in turn leads to errors in further numerical modeling of filtration-volume properties. An example of such an artifact will be found in medicine, but similar artifacts are also found in rocks, see, Figure 2.

Figure 2. Trabecular bone with metal implants of different diameters: (a) No visible artefacts, (b) With small visible artefacts, (c) With large artefacts, (d) With very large artefacts (arrows indicate artefacts; Grandmougin et al., 2020).

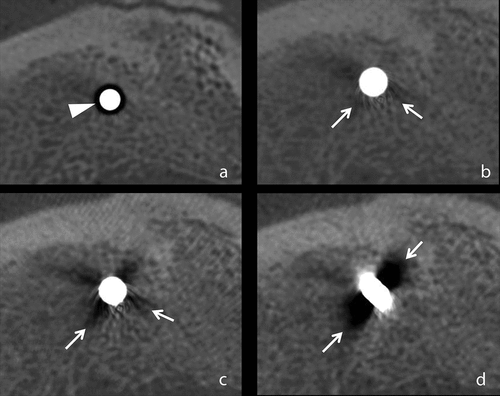
The artifacts shown in Figure 2 occur when the X-ray source is not powerful enough to sufficiently illuminate a dense object with X-rays. When examining rocks, similar scanning artefacts can occur when large, heavy (dense) minerals are present in the rock. In such cases, as shown in Figure 2(c,d), these artifacts distort the structure of the void space. Those areas in the vicinity of which such distortions are observed cannot be used for modeling and calculating rock filtration-volume properties. This is due to the fact that the mineral framework of the rock is segmented as a void space and causes overestimation of the defined properties.

Circular artefacts can also occur on tomographic images when working with rocks. These should be avoided and, if possible, eliminated. An example of circular artefacts is shown in Figure 3.

Figure 3. Example of circular artefacts (Kornilov et al., 2020).

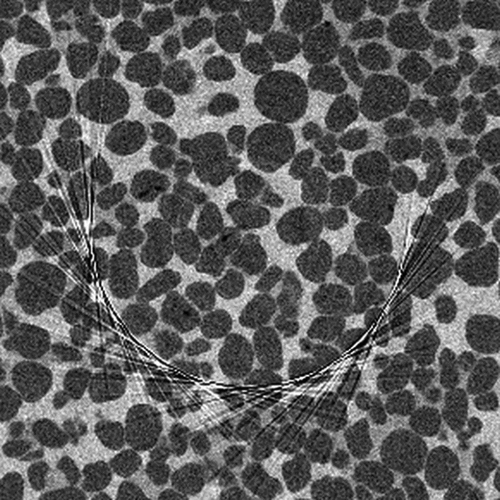
To combat ring artifacts, the following recommendations should be considered: 1. Fix the specimen securely on the slide so that the specimen does not move during scanning; 2. Increase the number of random frames in scanning settings; 3. Optimize reconstruction parameters.

Also in this section we briefly highlight a problem in the segmentation of void space or minerals in a rock. This is very important because an incorrectly chosen X-ray density or colour interval in a tomographic image can greatly affect the results of mathematical calculations of filtration-volume properties. Figure 4 shows a classic example of uncertainty in the selection of the boundary between the void space and the mineral skeleton of a rock.

Figure 4. Example of an enlarged image of a “pore space”-”mineral skeleton” rock interface (Perez et al., 2022).

In tomographic images the boundary between media “pore space” – “mineral skeleton” or “mineral” – “mineral” is a step-by-step colour transition – gradual intensity gradients. Firstly, it is due to the fact that the actual media interface in the tomographic image is represented as several voxels, whose colour intensity corresponds to the average value of neighbouring voxels from it. This is the so-called partial volume effect, resulting in unresolved morphological features, including pore space wall roughness. Secondly, the finite resolution of the imaging blurs the material interface by several voxels in width (Schlüter et al., 2014). In addition, the abrupt density transitions of the materials produce different refractive indices on either side of the interface, leading to so-called edge enhancement, which manifests as an over and under gray level immediately adjacent to the interface (Banhart, 2008). Based on this, the morphology of the void space in tomographic images is somewhat different from the real morphology in the material specimen (Soulaine et al., 2016). Although these effects can be minimized, they cannot be excluded from the imaging process (Perez et al., 2022).

All of the artefacts listed above can greatly influence further mathematical modelling and calculation of key petrophysical characteristics, so researchers need to keep artefacts to a minimum. Where this cannot be done, an “area of interest” in the sample volume that is free of artifacts should be selected for modeling. When selecting direct filtration-capacitance modeling approaches, proper void space segmentation greatly influences simulation results.

The main approaches to modelling filtration-capacitance properties

Currently, there are two main approaches for modelling filtration-capacitative properties from a digital core model: 1. direct numerical modelling based on the numerical solution of the Navier-Stokes equation and its simplification/modification, or using the Boltzmann lattice method and 2. modelling based on mesh models (Gerke et al., 2021).

The easiest in terms of mathematical modelling is to calculate absolute permeability from a digital core model. Typically, this involves solving the Navier-Stokes equation for a single fluid whose flow obeys Darcy’s law. Most often the following approaches are used for modeling and absolute permeability calculation: 1) LBM (Khirevich et al., 2015); 2) finite element and volume methods (FVM/FEM; Sedaghat et al., 2016); 3) smoothed particle methods (SPH; Holmes et al., 2016); 4) finite difference scheme (FDM) based calculation codes (Eichheimer et al., 2019). Usually, to solve the problem at hand and use the listed approaches, the computer power is sufficient to perform the calculation in a sufficiently representative sample volume.

When relative phase permeabilities need to be calculated, the use of direct calculation methods is greatly complicated by the need to use supercomputers for the calculations. However, even in this case, the calculation time can be excessively long. This is due to the fact that when multiphase filtration is simulated on a pore scale (two, three or more phases), in addition to solving the flow problem itself, it is also necessary to describe in time the evolution of the interface of the filtering fluids. In this case, different approaches are used for direct numerical simulation because it is necessary to describe the interaction of phases with the rock solid skeleton. In this case, the most common approaches are as follows: 1) Boltzmann lattice method (Zakirov & Khramchenkov, 2020); 2) fluid volume method (VoF; Bilger et al., 2017); 3) phasefield method (Rokhforouz & Akhlaghi Amiri, 2017); 4) density functional (Dinariev & Evseev, 2010).

Due to the fact that “digital core” technology implies high-quality and fast calculation of filtration characteristics, the use of direct calculation methods in multiphase filtration is inefficient in these technological possibilities. In this regard, scientists most often use poroset modelling to solve the set problems (Bembel et al., 2019; Kohanpur & Valocchi, 2020; X. Wang et al., 2021; H. Zhang et al., 2021; W. Zhang et al., 2022). In contrast to direct modelling, the main advantage of grid-based modelling is the speed of calculation, the possibility of working with representative numerical models and the absence of the requirement to carry out the calculation on a supercomputer. A standard, modern personal computer will be sufficient for calculations on the basis of grid models. Despite rather high calculation speed, grid computing has a lower accuracy in comparison to direct mathematical modelling. This is due to a large number of simplifications in reconstruction of poroset models from digital core model. To improve the quality of calculations of filtration-capacitative properties from digital core models, the use of an integrated modeling approach is considered to be the most modern approach. This approach implies the use of direct modelling methods to estimate filtration-volume properties in elementary filtration channels with a certain structural characteristic; then, using machine learning, pores with known structure and filtration-volume properties are segmented from tomography data and the properties of the sample as a whole are calculated using them (Miao et al., 2017). This approach reduces the time required for direct modelling by evaluating the filtration properties of individual pores, and further improves the accuracy of porosity modelling. An example of pore network topology extraction in a particular pore-network simulation for calculating filtration-capacitative properties is shown in Figure 5.

Figure 5. Identification of the pore throat network topology by the “maximum balloon” method: (a) pore bodies filled with spheres of different sizes, (b) schematic of the pore-throat-pore structure (L. Wang et al., 2020).

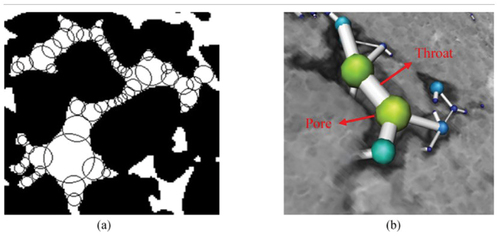
Figure 5 shows a particular case of poroset modelling, where the void space of a rock is broken up into large pores in the form of spheres and throats. In practice, there are various approaches to porous mesh modelling, where the void space can be transformed into shapes of different geometries.

It is important to remember that the computed X-ray microtomography method has limitations in imaging resolution, which entails an inaccurate digital core model. As a rule, when working with low-permeability reservoirs, some of the pores that are involved in filtration are beyond the resolution of the micro-CT. In such cases, the results of focused ion beam scanning electron microscopy (FIP-SEM) are used in conjunction with X-ray microtomography data (Jacob et al., 2021). This is necessary to obtain information on the morphology of the void space, which cannot be seen by microtomography. As a result of this integrated approach, it is possible to complement the porosette model in order to improve the determination of core filtration properties (Gerke et al., 2017).

Modelling of enhanced oil recovery methods and other properties

We would like to point out that the digital core technology, in addition to calculating the filtration-volume properties of rocks, also allows calculating the mechanical properties (Shulakova et al., 2013). In this review, we will not dwell on the problem of determining the mechanical properties of rocks, but will talk in more detail about the capabilities of the technology in modelling enhanced oil recovery methods.

There are papers in the literature on the use of digital core technology for fracture modelling, mainly focused on determining mechanical properties of the core using digital modelling (Lin et al., 2022; Rassouli & Lisabeth, 2021). It is also noted that computed X-ray microtomography can be used to improve the efficiency of hydraulic fracturing in terms of the most optimal proppant selection (Ramandi et al., 2021).

In a generalised sense, the use of computed X-ray microtomography in conjunction with digital core technology can be used to conduct experiments before and after core exposure using various methods. For example, thermal treatment of oil-bearing rocks (Gafurova et al., 2021) or hydrochloric acid core treatment (Ivanov et al., 2020, 2021). The results of these kinds of laboratory experiments on the core can be extrapolated to the reservoir as a whole to optimise pilot testing. Figure 6 shows 3D models of the void space of oil-bearing rocks as a result of heating to 100, 200, 300 and 400°C. In the presented models, the colouring corresponds to the pore size (red are the smallest, green and blue are the largest).

Figure 6. 3D models of the void space structure of heated samples with colour differentiation by the size of the pore channels (cubes with 1 mm edge): 1 – “nodules” of voids, 2 – crack (A. Ponomarev et al., 2021).

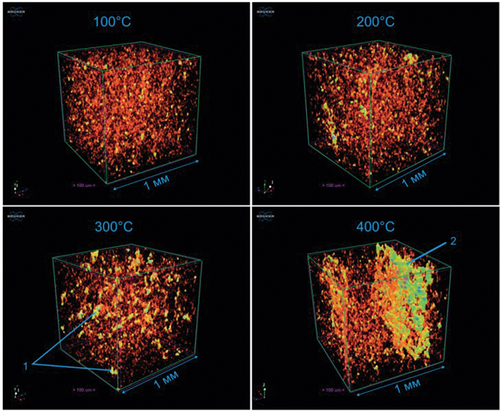
Analysis of Figure 6 indicates that the transformation of the void space occurs as a result of heat exposure of organic-rich oil-bearing rocks: new, larger pores and fractures are formed. This example does not simulate filtration properties, but given that permeability is a function of pore size distribution, we can infer an increase in the filtration properties of the samples as a result of heating. This laboratory experiment suggests that heat treatment of an oil-bearing reservoir should be used to increase its filtration characteristics and shale oil production.

Prospects for the development of digital core technology

A comprehensive review of the “digital core” study showed that the current technology allows to determine absolute permeability with high accuracy, as for relative phase permeability – the main problem is imperfect mathematical modelling methods. In the first case, in direct calculations of phase permeability – insufficient computing power of computers, and in the second case, when using porosity modeling approach – there is an oversimplification of the real structure of the void space of rocks, which leads to inaccuracies in the calculations. A promising direction in this case is the use of an integrated approach of direct and porous modeling, but this technology requires further development and is currently imperfect. In our opinion, the situation in calculations of phase permeabilities to the present time is as follows: modern mathematical models cannot provide sufficient accuracy of calculations, without calibration of the obtained data by standard laboratory experiments. Obviously, in the nearest decade the digital core technology will be improved by means of statistical data accumulation of digital core models characterized by standard laboratory methods. This will allow the use of neural network machine learning to extract the types of structural features of voids in the core pore space and improve the accuracy of pore-network modeling.

At present, the main priority of digital core technology is the reliable determination of petrophysical properties from a digital core model. Further development of the technology should include simulation of various kinds of influences on the rock without carrying out in-situ laboratory experiments. In this case, we mean, for example, estimating structural-textural changes and changes in petrophysical properties over time as a result of thermal or mechanical stress – the direction of 4D modelling without carrying out laboratory experiments. A kind of crash-testing of rocks digitally, similar to digital modelling of accidents in the automotive industry.

Highlights

• Describes the current state of the art of “Digital Core” technology

• To optimise the calculation of filtration-volume properties from a digital core model, it is advisable to use a combined approach of direct mathematical modelling and poroset models

• At present, without standard laboratory tests to determine phase permeabilities, mathematical calculations are not very accurate

Acknowledgments

This article was prepared as part of the Digital Core technology project at the West Siberian Interregional World-class Science and Education Centre

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by the West Siberian Interregional World-class Science and Education Centre;