Stability analysis of Gauss-type proximal point method for metrically regular mappings

Abstract

In this article, we study the stability properties of a Gauss-type proximal point algorithm for solving the inclusion y ϵ T (x), where T is a set-valued mapping acting on a Banach space X with locally closed graph that is not necessarily monotone and y is a parameter. Consider a sequence of bounded constants {λ_k} which are away from zero. Under this consideration, we present the semi-local and local convergence of the sequence generated by an iterative method in the sense that it is stable under small variation in perturbation parameter y whenever the set-valued mapping T is metrically regular at a given point. As a result, the uniform convergence of the Gauss-type proximal point method will be established. A numerical experiment is given which illustrates the theoretical result.

Keywords:

• set-valued mappings
• metrically regular mappings
• Lipschitz-like mappings
• Gauss-type proximal point algorithm
• semi-local convergence

AMS (MOS) Mathematics Subject classifications:

• 47H04
• 49J53
• 65K10

PUBLIC INTEREST STATEMENT

A large number of problems in engineering, optimization, economics and other disciplines can be brought in the form of equations. The unknowns of engineering equations can be differential equations, integral equations, systems of linear and nonlinear algebraic equations. The computational technique gives a lot of opportunity to researchers to solve these equations. The most commonly used solution methods for these equations are iterative and such iteration methods are applied for solving optimization problems. The generalized equation is an abstract model of a wide variety of variational problems including systems of inequalities, linear and nonlinear complementarity problems, system of nonlinear equations and first-order necessary conditions for nonlinear programming, equilibrium problems, etc. They have also plenty of applications in engineering and economics. In this communication, we have studied an iterative technique, namely Gauss-type proximal point method, to show the stability of the convergence of this method for solving generalized equation.

1. Introduction

This article is about to study the stability of the Gauss-type proximal point method for solving the perturbed inclusions involving set-valued mappings and parameters. We consider the perturbed inclusion of the following form:

(3.1) $\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{d}x\in X\mathrm{s}\mathrm{u}\mathrm{c}\mathrm{h}\mathrm{t}\mathrm{h}\mathrm{a}\mathrm{t}y\in T(x),$(3.1)

where $T:X\overrightarrow{\to \phantom{{ }_{\text{vbox}to.5ex\text{vss}}}}{2}^X$ is a set-valued mapping with closed graph acting on a Banach space $X$ and $y$ is a parameter.

This type of inclusion is an abstract model for a wide variety of variational problems including complementary problems, systems of nonlinear equations and variational inequalities. In particular, it may characterize optimality or equilibrium. The classical proximal point algorithm (see Algorithm 5.1 in Section 3), whose origins can be traced back to (Krasnoselskii, 1955), was born in the 1960s (see, e.g. (Martinet, 1970; Moreau, 1965)).

Rockfellar (1976a) presented a general convergence and rate of convergence analysis of the classical proximal point algorithm (see Algorithm 5.1 in Section 3) for solving $0\in T(x)$ (i.e. when y = 0) in the case when $X$ is a Hilbert space and $T$ is maximal monotone operator.

Furthermore, in his subsequent paper (Rockafellar, 1976b), he established its connection with the augmented Lagrangian method of constrained nonlinear optimization. In particular, Rockafellar (Rockafellar, 1976a, Theorem 1) showed that when $x_{k+1}$ is an approximate solution of $0\in T(x)$ and $T$ is maximal monotone, then the Algorithm 5.1 generates a sequence $\left\{x_k\right\}$ which is weakly convergent to a solution of $0\in T(x)$ for any starting point $x_0\in X$.

For solving the inclusion $0\in T(x)$, Aragón Artacho, Dontchev, and Geoffroy (2007) presented the following general version of the proximal point algorithm by considering a set-valued mapping $T$ acting Banach spaces $X$ and $Y$ for the nonmonotone case and choosing a sequence of functions $g_k:X\to Y$ with $g_k(0)=0$ which are Lipschitz continuous

(3.2) $0\in g_k(x_{k+1}-x_k)+T(x_{k+1}),\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}k=0,1,2,\dots ,$(3.2)

and proved the sequence obtained by (3.2) converges linearly. The uniform convergence analysis of the method (3.2) is given by Aragón Artacho and Geoffroy in (Aragón Artacho & Geoffroy, 2007). Many authors have been studied on proximal point algorithm and have also found applications of this method to specific variational problems. Most of the rapidly growing study on this subject has been concentrated on various versions of the algorithm for solving inclusions involving monotone mappings, and specially, on monotone variational inequalities (see (Anh, Muu, Nguyen, & Strodiot, 2005; Auslender & Teboulle, 2000; Bauschke, Burke, Deutsch, Hundal, & Vanderwerff, 2005; Solodov & Svaiter, 1999; Yang & He, 2005)). In recent work, Rashid et al. (Rashid, Jinhua, & Li, 2013) introduced the Gauss-type proximal point method and studied the semilocal and local convergence of the sequence generated by this method for solving the inclusion (3.1) when $y=0$. Moreover, by comparing with the results in Rockafellar (Rockafellar, 1976a, Theorem 1), these authors showed that the sequence generated by Gauss-type proximal point algorithm is more precise than the sequence generated by Algorithm 5.1. To see the further developments on perturbed generalized equations dealing with metrically regular mappings, one can refer to (Alom, Rashid, & Dey, 2016; Dontchev & Rockafellar, 2013; Rashid & Yuan, 2017).

Inspired by the works of Dontchev (Dontchev, 1996b) (or Aragón Artacho and Geoffroy (2007)), we propose the restricted proximal point method (see Algorithm 5.2 in Section 3) and study the convergence analysis of this method for solving (3.1), which will imply the uniform convergence of the Gauss-type proximal point method introduced in (Rashid et al., 2013).

In this article, our approach is to study the semilocal and local convergence of the sequence generated by Algorithm 5.2 under the assumption that $T$ is metrically regular, which means the uniform convergence of the Gauss-type proximal point method in Rashid et al. (2013) will be established. Indeed, we present a kind of convergence of the sequence generated by Algorithm 5.2 which is uniform in the sense that the attraction region (i.e. the ball in which the initial guess $x_0$ can be taken arbitrarily) does not depend on small variations in the perturbation parameter $y$ near $y_0$ and for such values of $y$ this method finds a solution $x$ of (3.1) whenever T is metrically regular.

The main tools, we use in this study, are metric regularity and Lipschitz-like properties for set-valued mappings. Based on the information around the initial point, we establish convergence criteria in Section 3, which provides some sufficient conditions ensuring the convergence to a solution of any sequence generated by Algorithm 5.2. As a consequence, uniformity of the local convergence result for Gauss-type proximal point method is obtained.

The content of this article is organized as follows. In Section 2, we present some notations, notions and some preliminary results. In Section 3, we introduce the restricted proximal point method defined by Algorithm 5.2. Utilizing the concept of Lipchitz-like and metric regular property, we show the existence and the convergence of the sequence generated by Algorithm 5.2. As a result, stability properties of the Gauss-type proximal point method will be justified. In Section 4, a numerical experiment is provided to illustrate the theoretical result. In the last section, we give a summary of the major results presented in this article.

2. Notations and preliminary results

Let $X$ be a real Banach space and $F$ be a set-valued mapping on $X$, indicated by $F:X\overrightarrow{\to \phantom{{ }_{\text{vbox}to.5ex\text{vss}}}}{2}^X$. The domain $\mathrm{d}\mathrm{o}\mathrm{m}F$, the inverse $F^{-1}$ and the graph $\mathrm{g}\mathrm{p}\mathrm{h}F$ of $F$ are, respectively, defined by

$\mathrm{d}\mathrm{o}\mathrm{m}F:=\{x\in X:F(x)\ne \text{O}\},F^{-1}(y):=\{x\in X:y\in F(x)\},$

and

$\mathrm{g}\mathrm{p}\mathrm{h}F:=\left\{(x,y)\in X\times X:y\in F(x)\right\}.$

Let $x\in X$ and $r>0$. The closed ball centered at $x$ with radius $r$ is denoted by ${\mathbb{B}}_r(x)$. All the norms are denoted by $\parallel \cdot \parallel$. Let $A\subseteq X$. The distance function of $A$ is defined by

$d(x,A)=inf\left\{\parallel x-a\parallel :a\in A\right\},\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}x\in X,$

while the excess from the set $A$ to the set $C\subseteq X$ is defined by

$e(C,A)=sup\left\{d(x,A):x\in C\right\}.$

We begin with the definition of metric regularity and pseudo-Lipschitz mappings for a set-valued mappings. The following concept of metric regularity for a set-valued mapping is extracted from Dontchev & Rockafellar (2004), whereas the notion of pseudo-Lipschitz property was introduced by Aubin (Aubin, 1984; Aubin & Frankowska, 1990). In particular, connection to linear rate of openness, pseudo-Lipschitz continuty, coderivative and metric regularity of set-valued mappings were established by Penot (Penot, 1989) and Mordukhovich (Mordukhovich, 1992). To see more details on these topics, one can refer to Dontchev & Rockafellar (2004, 2001), Ioffe (2000), Mordukhovich (1993) and books (Mordukhovich, 2006; Rockafellar & Wets, 1997).

Definition 4.1. Let $F:X\overrightarrow{\to \phantom{{ }_{\text{vbox}to.5ex\text{vss}}}}{2}^X$ be a set-valued mapping, and let $(x_0,y_0)\in \mathrm{g}\mathrm{p}\mathrm{h}F$. Let $r_{x_0}>0,r_{y_0}>0$ and $M>0$. Then

1. $F$ is said to be

   1. metrically regular at $(x_0,y_0)$ on ${\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0)$ with constant $M$ if the following inequality holds:

      (4.1) $\mathrm{d}(x,F^{-1}(y))\le M\mathrm{d}(y,F(x))\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}x\in {\mathbb{B}}_{r_{x_0}}(x_0),y\in {\mathbb{B}}_{r_{y_0}}(y_0).$(4.1)

   2. metrically regular at $x_0$ for $y_0$ if there exist constants $r_{x_0}^{\prime }>0,r_{y_0}^{\prime }>0and{M}^{\prime }>0$ such that $F$ is metrically regular at $(x_0,y_0)$ on ${\mathbb{B}}_{{r^{\prime }}_{x_0}}(x_0)\times {\mathbb{B}}_{{r^{\prime }}_{y_0}}(y_0)$ with constant $M^{\prime }$.

2. $F^{-1}$ is said to be

   1. (i) Lipchitz-like at $(y_0,x_0)$ on ${\mathbb{B}}_{r_{y_0}}(y_0)\times {\mathbb{B}}_{r_{x_0}}(x_0)$ with constant $M$ if the following inequality holds:

      (4.2) $\text{quade}(F^{-1}(y_1)\cap {\mathbb{B}}_{r_{x_0}}(x_0),F^{-1}(y_2))\le M\parallel y_1-y_2\parallel \mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{y}{y}_1,y_2\in {\mathbb{B}}_{r_{y_0}}(y_0).$(4.2)

   2. pseudo-Lipchitz around $(y_0,x_0)$ if there exist constants $r_{y_0}^{\prime }>0,r_{x_0}^{\prime }>0$ and $M^{\prime }>0$ such that $F^{-1}$ is Lipschitz-like at $(y_0,x_0)$ on ${\mathbb{B}}_{{r^{\prime }}_{y_0}}(y_0)\times {\mathbb{B}}_{{r^{\prime }}_{x_0}}(x_0)$ with constant $M^{\prime }$.

Remark 4.1. The infimum of the set of values $M$ for which (4.1) holds is the modulus of metric regularity, denoted by $\mathrm{r}\mathrm{e}\mathrm{g}F(\bar{x}|\bar{y})$. The absence of metric regularity at $\bar{x}$ for $\bar{y}$ corresponds to $\mathrm{r}\mathrm{e}\mathrm{g}F(\bar{x}|\bar{y})=\mathrm{\infty }$. The inequality (4.1) has direct use in providing an estimate for how far a point $x$ is from being a solution to the generalized equation $y\in F(x)$ and the expression $\mathrm{d}(y,F(x))$ measures the residual when $F(x)∍y$.

Remark 4.2. Equivalently, for the property (b–i) we can say that $F^{-1}$ is Lipschitz-like at $(y_0,x_0)\in \mathrm{g}\mathrm{p}\mathrm{h}{F}^{-1}$ on ${\mathbb{B}}_{r_{y_0}}(y_0)\times {\mathbb{B}}_{r_{x_0}}(x_0)$ with constant $M$ if for every $x_1,x_2\in {\mathbb{B}}_{r_{x_0}}(x_0)$ and for every $x_1\in F^{-1}(y_1)\cap {\mathbb{B}}_{r_{x_0}}(x_0)$, there exists $x_2\in F^{-1}(y_2)$ such that

$\parallel x_1-x_2\parallel \le M\parallel y_1-y_2\parallel ,forevery{y}_1,y_2\in {\mathbb{B}}_{r_{y_0}}(y_0).$

The following lemma plays an important role to prove our main result. This lemma establishes the connection between the metric regularity and the Lipchitz-like property. To see the proof of this lemma, one can refer to Rashid et al. (2013) or monogram (Dontchev & Rockafellar, 2009, Theorem 3E.6).

Lemma 4.1. Let $F:X\overrightarrow{\to \phantom{{ }_{\text{vbox}to.5ex\text{vss}}}}{2}^X$ be a set-valued mapping and let $(x_0,y_0)\in \mathrm{g}\mathrm{p}\mathrm{h}F$. Then $F$ is metrically regular at $(x_0,y_0)$ on ${\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0)$ with constant $M$ if and only if $F^{-1}$ is Lipschitz-like at $(y_0,x_0)$ on ${\mathbb{B}}_{r_{y_0}}(y_0)\times {\mathbb{B}}_{r_{x_0}}(x_0)$ with the same constant $M$, that is, the latter condition satisfies the following inequality:

(4.3) $e(F^{-1}(y)\cap {\mathbb{B}}_{r_{x_0}}(x_0),F^{-1}(y^{\prime }))\le M\parallel y-y^{\prime }\parallel \mathrm{h}\mathrm{o}\mathrm{l}\mathrm{d}\mathrm{s}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}y,y^{\prime }\in {\mathbb{B}}_{r_{y_0}}(y_0).$(4.3)

Recall the following statement which is a refinement of the Lyusternik-Graves theorem for metrically regular mapping taken from Dontchev, Lewis, & Rockafellar (2002), Theorem 3.3). Analogue developments on this result appear in Dontchev (1996a), Theorem 1.4) or Section 1 in Ioffe (2000). This theorem plays an important role in the theory of metric regularity. This theorem proves the stability of metric regularity of a generalized equation under perturbations. Roughly says that a generalized equation $\bar{y}\in F(x)$ with solution $x=\bar{x}$ can be perturbed by adding a to $F$ a single-valued mapping $g$ which is Lipschitz continuous with $g(\bar{x})=0$, by fundamental estimate so as to get a generalized equation $\bar{y}\in (g+F)(x)$ still having solution $x=\bar{x}$. For its statement, we recall that a set $C\subset X$ is locally closed at $z\in C$ if there exists $a>0$ such that the set $C\cap {\mathbb{B}}_a(z)$ is closed.

Proposition 4.1. Let $F:X\overrightarrow{\to \phantom{{ }_{\text{vbox}to.5ex\text{vss}}}}{2}^X$ be a set-valued mapping and let $(x_0,y_0)\in \mathrm{g}\mathrm{p}\mathrm{h}F$. Let $F$ be a metrically regular at $x_0,y_0)$ on ${\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0)$ with constant $\kappa >0$ and $\mathrm{g}\mathrm{p}\mathrm{h}F\cap ({\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0))$ be closed. Consider a function $g:X\to X$ which is Lipschitz continuous at $x_0$ with Lipschitz constant $\lambda$ such that $\lambda <{\kappa }^{-1}$. Then the mapping $g+F$ is metrically regular at $(x_0,y_0+g(x_0))$ on ${\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0+g(x_0))$ with constant $\frac{\kappa }{1-\kappa \lambda }.$

We end this section with the following fixed point lemma for set-valued mappings, which was proved in Dontchev & Hager (1994), Lemma (fixed point), is a generalization of the fixed point theorem (Ioffe & Tikhomirov, 1979).

Lemma 4.2. Let $\mathrm{\Phi }:X\overrightarrow{\to \phantom{{ }_{\text{vbox}to.5ex\text{vss}}}}{2}^X$ be a set-valued mapping. Let ${\eta }_0\in X$, $r>0$ and $0<\alpha <1$ be such that

(4.4) $d({\eta }_0,\mathrm{\Phi }({\eta }_0))<r(1-\alpha )$(4.4)

and

(4.5) $e(\mathrm{\Phi }(x_1)\cap {\mathbb{B}}_r({\eta }_0),\mathrm{\Phi }(x_2))\le \alpha \parallel x_1-x_2\parallel forany{x}_1,x_2\in {\mathbb{B}}_r({\eta }_0).$(4.5)

Then $\mathrm{\Phi }$ has a fixed point in ${\mathbb{B}}_r({\eta }_0)$, that is, there exists $x\in {\mathbb{B}}_r({\eta }_0)$ such that $x\in \mathrm{\Phi }(x)$. If $\mathrm{\Phi }$ is additionally single-valued, then the fixed point of $\mathrm{\Phi }$ in ${\mathbb{B}}_r({\eta }_0)$ is unique.

3. Stability of convergence analysis

Throughout, we suppose that $X$ is a Banach space and let $T:X\overrightarrow{\to \phantom{{ }_{\text{vbox}to.5ex\text{vss}}}}{2}^X$ be a set-valued mapping. Let $(x_0,y_0)\in \mathrm{g}\mathrm{p}\mathrm{h}T$ and $r_{x_0}>0,r_{y_0}>0$ be such that ${\mathbb{B}}_{r_{x_0}}(x_0)\subseteq \mathrm{d}\mathrm{o}\mathrm{m}T$ and ${\mathbb{B}}_{r_{y_0}}(y_0)\subseteq T(X)$, the image of $T$. Assume that $T$ is metrically regular at $(x_0,y_0)$ on ${\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0)$ with constant $\kappa >0$ and $g\mathrm{p}\mathrm{h}T\cap ({\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0))$ is closed.

Let $0<\mathrm{\Delta }\le \mathrm{\infty },\lambda >0$ and $\left\{{\lambda }_k\right\}\subseteq (0,\lambda )$. For any $x\in X$, we define ${\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_k,x)$ by

${\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_k,x):=\left\{v\in X:y\in {\lambda }_{k}v+T(x+v)\right\}.$

Recall the classical proximal point method, introduced in Rockafellar (1976a), which is defined as follows:

Algorithm 5.1. (The Proximal Point Method (PPM))

Step 1. Initialize $y=0,\lambda >0$, $\left\{{\lambda }_k\right\}\subseteq (0,\lambda )$, $x_0\in X$, and put $k:=0$.

Step 2. If $0\in {\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_k,x_k)$ then stop; otherwise go to Step $3$.

Step 3. If $0\notin {\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_k,x_k)$,choose $v_k$ such that $v_k\in {\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_k,x_k)$.

Step 4. Set $x_{k+1}:=x_k+v_k$.

Step 5. Update $k:=k+1$ and go to Step $2$.

The restricted proximal point method we propose here is given in the following:

Algorithm 5.2. (The Restricted Proximal Point Method (RPPM))

Step 1. Given $\eta \in [1,\mathrm{\infty })$, $\lambda >0$, $\left\{{\lambda }_k\right\}\subseteq (0,\lambda )$, $0<\mathrm{\Delta }\le \mathrm{\infty }$, $x_0\in X$,and put $k:=0$.

Step 2. If $0\in {\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_k,x_k)$ then stop; otherwise go to Step $3$.

Step 3. If $0\notin {\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_k,x_k)$,choose $v_k\in {\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_k,x_k)$ such that there exists $\bar{v}\in {\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_k,x_k)$ and

$\parallel v_k\parallel \le \eta mi{n}_{\bar{v}\in {\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_k,x_k)}\parallel \bar{v}\parallel .$

Step 4. Set $x_{k+1}:=x_k+v_k$.

Step 5. Update $k:=k+1$ and go to Step $2$.

We remarked that if $y=0$ and the set ${\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_k,x_k)$ is singleton for each $k=0,1,2,\dots$, Algorithm 5.1 and Algorithm 5.2 are coincident. However, when ${\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_k,x_k)$ is not singleton, Algorithm 5.2 is a restricted version of Algorithm 5.1 since it imposes a restriction on the length of $v_k$, $\parallel v_k\parallel :=\eta mi{n}_{\bar{v}\in {\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_k,x_k)}\parallel \bar{v}\parallel$. Moreover, if $y=0$, the Algorithm 5.2 coincides with the Gauss-type proximal point algorithm introduced in Rashid et al. (2013).

This section is intended to prove that whenever $T$ is metrically regular at $(x_0,y_0)$ on ${\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0)$ with constant $\kappa$, then, for starting point $x_0$ and for every element $y\in {\mathbb{B}}_{r_{y_0}}(y_0)$, there is a sequence $\left\{x_k\right\}$ generated by Algorithm 5.2 which is convergent to a solution $x$ of (3.1) for $y$.

In order to proceed, let $\gamma >0$ and $x\in X$. For our convenience, define a mapping $P_{(\gamma ,x)}:X\overrightarrow{\to \phantom{{ }_{\text{vbox}to.5ex\text{vss}}}}{2}^X$ by

(5.1) $P_{(\gamma ,x)}(\cdot ):=\gamma (\cdot -x)+T(\cdot ),$(5.1)

and $I:X\to X$ is an identity Lipschitz continuous function on ${\mathbb{B}}_{r_{x_0}}(0)$.

Then, we obtain the following equivalence

(5.2) $z\in P_{(\gamma ,x)}^{-1}(y)\iff y\in \gamma (z-x)+T(z)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{y}z\in X\mathrm{a}\mathrm{n}\mathrm{d}y\in T(x).$(5.2)

In particular,

(5.3) $x_0\in P_{(\gamma ,x_0)}^{-1}(y_0)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}(x_0,y_0)\in \mathrm{g}\mathrm{p}\mathrm{h}T.$(5.3)

Note that

(3.1); $T(x)∍\left\{\begin{array}{cc}{y}_0,& \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}x=x_0\mathrm{a}\mathrm{n}\mathrm{d}(x_0,y_0)\in \mathrm{g}\mathrm{p}\mathrm{h}T;\\ 0,& \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}x=x^{\ast }\mathrm{a}\mathrm{n}\mathrm{d}{x}^{\ast }\mathrm{i}\mathrm{s}\mathrm{a}\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{o}\mathrm{f};\\ y,& \mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{y}x\mathrm{e}\mathrm{x}\mathrm{c}\mathrm{e}\mathrm{p}\mathrm{t}{x}^{\ast }.\end{array}\right.$(3.1);

It is obvious that the mapping $\gamma I(\cdot -x_0)$ is Lipschitz continuous on ${\mathbb{B}}_{r_{x_0}}(0)+x_0$. Since $T$ is metrically regular at $(x_0,y_0)$ on ${\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0)$ with constant $\kappa >0$ and $\mathrm{g}\mathrm{p}\mathrm{h}T\cap ({\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0))$ is closed, by applying Lyusternik-Graves theorem (see Proposition 4.1) we have that the mapping $P_{(\gamma ,x_0)}$ is metrically regular at $(x_0,y_0)$ on ${\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0)$ with constant $\frac{\kappa }{1-\kappa }$. Setting

(5.4) $r^{\ast }:=\mathrm{m}\mathrm{i}\mathrm{n}\left\{\frac{2r_{y_0}-5\gamma r_{x_0}}{2},\frac{r_{x_0}(1-\kappa (1+2\gamma ))}{4\kappa }\right\}.$(5.4)

Then

(5.5) $r^{\ast }>0\iff \gamma <\mathrm{m}\mathrm{i}\mathrm{n}\left\{\frac{1-\kappa }{2\kappa },\frac{2r_{y_0}}{5r_{x_0}}\right\}.$(5.5)

To prove an important result in this section, we need the following lemma. This lemma plays an important role for convergence analysis of the restricted proximal point method. Up to some minor adjustment and simplifications of (Aragón Artacho & Geoffroy, 2007, Lemma 3.1), we state the modified result as follows:

Lemma 5.1. Let $\gamma >0$. Assume that the mapping $P_{(\gamma ,x_0)}$ is metrically regular at $(x_0,y_0)$ on ${\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0)$ with constant $\frac{\kappa }{1-\kappa }$ so that

(5.6) $\gamma <\mathrm{m}\mathrm{i}\mathrm{n}\left\{\frac{1-\kappa }{2\kappa },\frac{2r_{y_0}}{5r_{x_0}}\right\}.$(5.6)

Let $x\in {\mathbb{B}}_{\frac{r_{x_0}}{2}}(x_0)$. Then $P_{(\gamma ,x)}^{-1}(\cdot )$ is Lipschitz-like at $(y_0,x_0)$ on ${\mathbb{B}}_{r^{\ast }}(y_0)\times {\mathbb{B}}_{\frac{r_{x_0}}{2}}(x_0)$ with constant $\frac{\kappa }{1-\kappa (1+2\gamma )}$, that is,

(5.7) $e(P_{(\gamma ,x)}^{-1}(y_1)\cap {\mathbb{B}}_{\frac{r_{x_0}}{2}}(x_0),P_{(\gamma ,x)}^{-1}(y_2))\le \frac{\kappa }{1-\kappa (1+2\gamma )}\parallel y_1-y_2\parallel forany{y}_1,y_2\in {\mathbb{B}}_{r^{\ast }}(y_0).$(5.7)

Proof. According to our assumption on $P_{(\gamma ,x_0)}$, we obtain through Lemma 4.1 that the mapping $P_{(\gamma ,x_0)}^{-1}$ is Lipschitz-like at $(y_0,x_0)$ on ${\mathbb{B}}_{r_{y_0}}(y_0)\times {\mathbb{B}}_{r_{x_0}}(x_0)$ with $\frac{\kappa }{1-\kappa }$, that is, the following inequality holds:

(5.8) $e(P_{(\gamma ,x_0)}^{-1}(y)\cap {\mathbb{B}}_{r_{x_0}}(x_0),P_{(\gamma ,x_0)}^{-1}(y^{\prime }))\le \frac{\kappa }{1-\kappa }\parallel y-y^{\prime }\parallel \mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}y,y^{\prime }\in {\mathbb{B}}_{r_{y_0}}(y_0).$(5.8)

Note, by (5.5) and (5.6), that $r^{\ast }>0.$ Take

(5.9) $\mu :=\frac{\kappa }{1-\kappa }.$(5.9)

Then it is clear by (5.6) and (5.9)) that $2\gamma \mu <1$. Let

(5.10) $y_1,y_2\in {\mathbb{B}}_{r^{\ast }}(y_0)and{x}^{\prime }\in P_{(\gamma ,x)}^{-1}(y_1)\cap {\mathbb{B}}_{\frac{r_{x_0}}{2}}(x_0).$(5.10)

It suffices to show that there exists $x^{\prime \prime }\in P_{(\gamma ,x)}^{-1}(y_2)$ such that

$\parallel x^{\prime }-{x^{\prime }}^{\mathrm{\prime }}\parallel \le \frac{\mu }{1-2\gamma \mu }\parallel y_1-y_2\parallel .$

To complete this, we will proceed by mathematical induction on $k$ and verify that there exists a sequence $\left\{x_k\right\}\subset {\mathbb{B}}_{r_{x_0}}(x_0)$ such that

(5.11) $y_2\in \gamma (x_k-x_0)+\gamma (x_{k-1}-x)-\gamma (x_{k-1}-x_0)+T(x_k),$(5.11)

and

(5.12) $\parallel x_k-x_{k-1}\parallel \le \mu \parallel y_1-y_2\parallel (2\gamma \mu {)}^{k-2}$(5.12)

hold for each $k=2,3,4,\dots$. Define

(5.13) $z_i:=y_i-\gamma (x^{\prime }-x)+\gamma (x^{\prime }-x_0)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}i=1,2.$(5.13)

By (5.10), we obtain

(5.14) $\parallel x-x^{\prime }\parallel \le \parallel x-x_0\parallel +\parallel x_0-x^{\prime }\parallel \le r_{x_0}.$(5.14)

Now, we obtain that

$\parallel z_i-y_0\parallel =\parallel y_i-\gamma (x^{\prime }-x)+\gamma (x^{\prime }-x_0)-y_0\parallel \le \parallel y_i-y_0\parallel +\gamma \parallel x-x_0\parallel$

(5.15) $\le \parallel y_i-y_0\parallel +\gamma (\parallel x-x^{\prime }\parallel +\parallel x^{\prime }-x_0\parallel ).$(5.15)

Then by $2r^{\ast }\le 2r_{y_0}-5\gamma r_{x_0}$ in (5.4) together with (5.10) and (5.14), (5.15) yields that

(5.16) $\parallel z_i-y_0\parallel \le r^{\ast }+\frac{3\gamma r_{x_0}}{2}\le r_{y_0}.$(5.16)

This means that $z_i\in {\mathbb{B}}_{r_{y_0}}(y_0)$ for each $i=1,2$. Denote $x_1:=x^{\prime }$. Noting that $x_1-x\in {\mathbb{B}}_{r_{x_0}}(0)$ by (5.14). Then, we obtain $x_1\in P_{(\gamma ,x)}^{-1}(y_1)$ by (5.10), that is,

(5.17) $y_1\in \gamma (x_1-x)+T(x_1).$(5.17)

Inclusion (5.17) can be written as

$y_1-\gamma (x_1-x)+\gamma (x_1-x_0)\in \gamma (x_1-x_0)+T(x_1).$

This, by the definition of $z_1$, implies that $z_1\in \gamma (x_1-x_0)+T(x_1).$ Hence, we get $x_1\in P_{(\gamma ,x_0)}^{-1}(z_1)$. This together with (5.10) gives that

$x_1\in P_{(\gamma ,x_0)}^{-1}(z_1)\cap {\mathbb{B}}_{r_{x_0}}(x_0).$

From the Lipschitz-like property of $P_{(\gamma ,x_0)}^{-1}$ and noting that $z_1,z_2\in {\mathbb{B}}_{r_{y_0}}(y_0)$ by (5.16), it follows from (5.8) that there exists $x_2\in P_{(\gamma ,x_0)}^{-1}(z_2)$ such that

(5.18) $\parallel x_2-x_1\parallel \le \frac{\kappa }{1-\kappa }\parallel z_1-z_2\parallel =\mu \parallel y_1-y_2\parallel .$(5.18)

Moreover, for $x_1=x^{\prime }$ and by the definition of $z_2$, we have

$x_2\in P_{(\gamma ,x_0)}^{-1}(z_2)=P_{(\gamma ,x_0)}^{-1}(y_2-\gamma (x_1-x)+\gamma (x_1-x_0)).$

This implies that

(5.19) $y_2\in \gamma (x_2-x_0)+\gamma (x_1-x)-\gamma (x_1-x_0)+T(x_2).$(5.19)

Therefore, (5.18) and (5.19) are ensuring us that (5.11) and (5.12) are true with constructed points $x_1,x_2.$

Assume that $x_1,x_2,...,x_n$ are constructed such that (5.11) and (5.12) are true for $k=2,3,\dots ,n$. We have to construct $x_{n+1}$ such that (5.11) and (5.12) are also true for $k=n+1$. Write

$z_i^n:=y_2-\gamma (x_{n+i-1}-x)+\gamma (x_{n+i-1}-{\mathrm{x}}_0)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}i=0,1.$

Then, we have from the inductional assumption,

$\parallel z_1^n-z_0^n\parallel =\parallel -\gamma (x_n-x)+\gamma (x_n-x_0)+\gamma (x_{n-1}-x)-\gamma (x_{n-1}-x_0)\parallel$

$\le \parallel \gamma (x_n-x)-\gamma (x_{n-1}-x)\parallel +\parallel \gamma (x_n-x_0)-\gamma (x_{n-1}-x_0)\parallel$

$\le \gamma \parallel x_n-x_{n-1}\parallel +\gamma \parallel x_n-x_{n-1}\parallel$

(5.20) $=2\gamma \parallel x_n-x_{n-1}\parallel \le \parallel y_1-y_2\parallel (2\gamma \mu {)}^{n-1}.$(5.20)

Since $2\gamma \mu <1$, $\parallel x_1-x_0\parallel \le \frac{r_{x_0}}{2}$ by (17) and $\parallel y_1-y_2\parallel \le 2r^{\ast }$ by (5.10), it follows from (5.12) that

$\parallel x_n-x_0\parallel \le \sum _{k=2}^n\parallel x_k-x_{k-1}\parallel +\parallel x_1-x_0\parallel$

$\le 2\mu r^{\ast }\sum _{k=2}^n(2\gamma \mu {)}^{k-2}+\frac{r_{x_0}}{2}$

(5.21) $\le \frac{2\mu r^{\ast }}{1-2\gamma \mu }+\frac{r_{x_0}}{2}.$(5.21)

Utilizing the fact $4\kappa r^{\ast }\le r_{x_0}(1-\kappa (1+2\gamma ))$ from (5.4) together with (5.9) in (5.21), we have

(5.22) $\parallel x_n-x_0\parallel \le \frac{2\kappa r^{\ast }}{1-(1+2\gamma )\kappa }+\frac{r_{x_0}}{2}\le r_{x_0}.$(5.22)

Moreover, taking into account that

(5.23) $\parallel x_n-x\parallel \le \parallel x_n-x_0\parallel +\parallel x_0-x\parallel \le \frac{3}{2}{r}_{x_0}.$(5.23)

Furthermore, using (5.22) and (5.23), one has that, for each $i=0,1$,

$\parallel z_i^n-y_0\parallel \le \parallel y_2-y_0\parallel +\gamma \parallel x-x_0\parallel \le r^{\ast }+\gamma (\parallel x-x_n\parallel +\parallel x_n-x_0\parallel )$

$\le r^{\ast }+\frac{5\gamma r_{x_0}}{2}.$

By (5.4), the fact $2r^{\ast }\le 2r_{y_0}-5\gamma r_{x_0}$ reduces the above inequality that

(5.24) $\parallel z_i^n-y_0\parallel \le r_{y_0}.$(5.24)

Inequality (5.24) shows that $z_i^n\in {\mathbb{B}}_{r_{y_0}}(y_0)$ for each $i=0,1$.

By our assumption (5.11) holds for $k=n$, so we have

(5.25) $y_2\in \gamma (x_n-x_0)+\gamma (x_{n-1}-x)-\gamma (x_{n-1}-x_0)+T(x_n).$(5.25)

This can be written as

$y_2-\gamma (x_{n-1}-x)+\gamma (x_{n-1}-x_0)\in \gamma (x_n-x_0)+T(x_n)$

Then by the definition of $z_0^n$, we have $z_0^n\in \gamma (x_n-x_0)+T(x_n).$ This, together with (5.22), yields that

$x_n\in P_{(\gamma ,x_0)}^{-1}(z_0^n)\cap {\mathbb{B}}_{r_{x_0}}(x_0).$

Now, by (5.8), there exists an element $x_{n+1}\in P_{(\gamma ,x_0)}^{-1}(z_1^n)$ such that

(5.26) $\parallel x_{n+1}-x_n\parallel \le \frac{\kappa }{1-\kappa }\parallel z_1^n-z_0^n\parallel =\mu \parallel z_1^n-z_0^n\parallel .$(5.26)

Then by (5.20), we have

(5.27) $\parallel x_{n+1}-x_n\parallel \le \mu \parallel y_1-y_2\parallel (2\gamma \mu {)}^{n-1}.$(5.27)

Since $x_{n+1}\in P_{(\gamma ,x_0)}^{-1}(z_1^n)$, by definition of $z_1^n$ it follows that

(5.28) $y_2\in \gamma (x_{n+1}-x_0)+\gamma (x_n-x)-\gamma (x_n-x_0)+T(x_{n+1}).$(5.28)

Therefore, the inclusion (5.28) together with (5.27) completes the induction step and ensure the existence of the sequence $\left\{x_k\right\}$ satisfying (5.11) and (5.12).

Since $2\gamma \mu <1$, we see from (5.12) that $\left\{x_k\right\}$ is a Cauchy sequence and hence there exists ${x^{\prime }}^{\mathrm{\prime }}\in {\mathbb{B}}_{r_{x_0}}(x_0)$ such that $x^{\prime \prime }:=\underset{k\to \mathrm{\infty }}{lim}{x}_k$. From the previous proof, we have that $(x_{n+1},y_2-\gamma (x_n-x)+\gamma (x_n-x_0))\in \mathrm{g}\mathrm{p}\mathrm{h}T\cap ({\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0))$ for each $n=0,1,\dots$. Taking limit $n\to \mathrm{\infty }$ to (5.11) and since $\mathrm{g}\mathrm{p}\mathrm{h}T\cap ({\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0))$ is closed, we obtain that

$y_2\in \gamma (x^{\prime \prime }-x)+T(x^{\prime \prime }),$

that is, $x^{\prime \prime }\in P_{(\gamma ,x)}^{-1}(y_2).$ Moreover,

$\parallel x^{\prime }-x^{\prime \prime }\parallel \le \underset{n\to \mathrm{\infty }}{\mathrm{l}\mathrm{i}\mathrm{m}\mathrm{s}\mathrm{u}\mathrm{p}}\sum _{k=2}^n\parallel x_k-x_{k-1}\parallel \le \underset{n\to \mathrm{\infty }}{lim}\sum _{k=2}^n\mu \parallel y_1-y_2\parallel (2\gamma \mu {)}^{k-2}$

$=\frac{\mu }{1-2\gamma \mu }\parallel y_1-y_2\parallel =\frac{\kappa }{1-\kappa (1+2\gamma )}\parallel y_1-y_2\parallel .$

This completes the proof of the Lemma 5.1.

Remark 5.1. Let $y\in {\mathbb{B}}_{r^{\ast }-\frac{\gamma r_{x_0}}{2}}(y_0+\gamma (x_0-x))$. Then, for every $x\in {\mathbb{B}}_{\frac{r_{x_0}}{2}}(x_0)$, we have that

$\parallel y-y_0\parallel \le \parallel y-y_0-\gamma (x_0-x)\parallel +\parallel \gamma (x_0-x)\parallel \le r^{\ast }-\frac{\gamma r_{x_0}}{2}+\frac{\gamma r_{x_0}}{2}\le r^{\ast }.$

It follows that ${\mathbb{B}}_{r^{\ast }-\frac{\gamma r_{x_0}}{2}}(y_0+\gamma (x_0-x))\subseteq {\mathbb{B}}_{r^{\ast }}(y_0)$. Therefore, $P_{(\gamma ,x)}^{-1}(\cdot )$ is Lipschitz-like at $(y_0+\gamma (x_0-x),x_0)$ on ${\mathbb{B}}_{r^{\ast }-\frac{\gamma r_{x_0}}{2}}(y_0+\gamma (x_0-x))\times {\mathbb{B}}_{\frac{r_{x_0}}{2}}(x_0)$ with constant $\frac{\kappa }{1-\kappa (1+2\gamma )}$.

Before going to demonstrate the main result in this section, we need to introduce some notation. Let $x\in X$ and $\lambda >0$. Choose a sequence of scalars $\left\{{\lambda }_k\right\}$ such that $\left\{{\lambda }_k\right\}\subseteq (0,\lambda )$. Set $\gamma :={\lambda }_k$ in (5.1) for every $k$ . Then the set-valued mapping $P_{(\gamma ,x)}$ can be rewritten as follows:

(5.29) $P_{({\lambda }_k,x)}(\cdot ):={\lambda }_k(\cdot -x)+T(\cdot ).$(5.29)

Then, by Algorithm 5.2, we have that

(5.30) ${\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_k,x)=\left\{v\in X:x+v\in P_{({\lambda }_k,x)}^{-1}(y)\right\}.$(5.30)

and we obtain the following equivalence

(5.31) $z\in P_{({\lambda }_k,x)}^{-1}(y)\iff y\in {\lambda }_k(z-x)+T(z)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{y}z\in X\mathrm{a}\mathrm{n}\mathrm{d}y\in T(z).$(5.31)

In particular,

(5.32) $x_0\in P_{({\lambda }_k,x_0)}^{-1}(y_0)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}(x_0,y_0)\in \mathrm{g}\mathrm{p}\mathrm{h}T.$(5.32)

Also, we can rewrite (5.4) as follows:

(5.33) $\bar{r}:=\mathrm{m}\mathrm{i}\mathrm{n}\left\{\frac{2r_{y_0}-5{\lambda }_k{r}_{x_0}}{2},\frac{r_{x_0}(1-\kappa (1+2{\lambda }_k))}{4\kappa }\right\}.$(5.33)

Then

(5.34) $\bar{r}>0\iff {\lambda }_k<\mathrm{m}\mathrm{i}\mathrm{n}\left\{\frac{1-\kappa }{2\kappa },\frac{2r_{y_0}}{5r_{x_0}}\right\}.$(5.34)

Moreover, the mapping $P_{({\lambda }_k,x_0)}$ is metrically regular at $(x_0,y_0)$ on ${\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0)$ with constant $\frac{\kappa }{1-\kappa }$ by Lyusternik-Graves theorem (see Proposition 4.1). Then by Lemma 4.1, we have $P_{({\lambda }_k,x_0)}^{-1}$ is Lipschitz-like at $(y_0,x_0)$ on ${\mathbb{B}}_{r_{y_0}}(y_0)\times {\mathbb{B}}_{r_{x_0}}(x_0)$ with constant $\frac{\kappa }{1-\kappa }$, that is, the following inequality holds:

(5.35) $e(P_{({\lambda }_k,x_0)}^{-1}(y_1)\cap {\mathbb{B}}_{r_{x_0}}(x_0),P_{({\lambda }_k,x_0)}^{-1}(y_2))\le \frac{\kappa }{1-\kappa }\parallel y_1-y_2\parallel \mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}{y}_1,y_2\in {\mathbb{B}}_{r_{y_0}}(y_0).$(5.35)

For our convenience, we define for each $x\in X$ and $y\in T(X)$, the mapping $Z_{({\lambda }_k,x)}:X\to X$ by

(5.36) $Z_{({\lambda }_k,x)}(\cdot ):=y+{\lambda }_k(\cdot -x_0)-{\lambda }_k(\cdot -x),$(5.36)

and the set-valued mapping ${\mathrm{\Phi }}_{({\lambda }_k,x)}:X\overrightarrow{\to \phantom{{ }_{\text{vbox}to.5ex\text{vss}}}}{2}^X$ by

(5.37) ${\mathrm{\Phi }}_{({\lambda }_k,x)}(\cdot )=P_{({\lambda }_k,x_0)}^{-1}[Z_{({\lambda }_k,x)}(\cdot )].$(5.37)

Then

$\parallel Z_{({\lambda }_k,x)}(x^{\prime })-Z_{({\lambda }_k,x)}(x^{\prime \prime })\parallel =\parallel {\lambda }_k(x^{\prime }-x_0)-{\lambda }_k(x^{\prime }-x)-{\lambda }_k(x^{\prime \prime }-x_0)+{\lambda }_k(x^{\prime \prime }-x)\parallel$

$\le \parallel {\lambda }_k(x^{\prime }-x_0)-{\lambda }_k(x^{\prime \prime }-x_0)\parallel +\parallel {\lambda }_k(x^{\prime }-x)-{\lambda }_k(x^{\prime \prime }-x)\parallel$

$\le {\lambda }_k\parallel x^{\prime }-x^{\prime \prime }\parallel +{\lambda }_k\parallel x^{\prime }-x^{\prime \prime }\parallel$

(5.38) $=2{\lambda }_k\parallel x^{\prime }-x^{\prime \prime }\parallel \mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}{x}^{\prime },x^{\prime \prime }\in X.$(5.38)

We are now able to prove the semilocal convergence of the sequence generated by Algorithm 5.2 for solving (3.1) when $T$ is metrically regular.

Theorem 5.1. Suppose that $\eta >1$, $\lambda >0$ and let $x_0\in X$. Let $\left\{{\lambda }_k\right\}$ be a sequence of scalars such that $\left\{{\lambda }_k\right\}\subseteq (0,\lambda )$. Assume that the mapping $P_{({\lambda }_k,x_0)}$ is metrically regular at $(x_0,y_0)$ on ${\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0)$ with constant $\frac{\kappa }{1-\kappa }$ so that the following inequality holds:

(5.39) $\lambda :=\frac{1-\kappa }{2(\eta +2)\kappa }.$(5.39)

Let $\bar{r}$ be defined in (5.33) and let $\delta >0$ and $\sigma >0$ be such that

• $\delta \le \mathrm{m}\mathrm{i}\mathrm{n}\{\frac{r_{x_0}}{2},\frac{\bar{r}}{3\lambda },\frac{r_{y_0}}{(2\eta +1)\lambda },1\}$;

• $\sigma <\lambda \delta$.

Then, for every $y\in {\mathbb{B}}_{\sigma }(y_0)$, any sequence $\left\{x_k\right\}$ generated by Algorithm 5.2 with initial point $x_0$ converges to a solution $x$ of (3.1) for $y$.

Proof. Since $\eta >1$ and $\left\{{\lambda }_k\right\}\subseteq (0,\lambda )$, we have from (46) that

(5.40) ${\lambda }_k<\lambda =\frac{1-\kappa }{2(\eta +2)\kappa }<\frac{1-\kappa }{2\kappa }.$(5.40)

Let $M:=\frac{\kappa }{1-\kappa (1+2{\lambda }_k)}$. Thus, Lemma 5.1 is applicable with constants $\frac{r_{x_0}}{2}$, $\bar{r}$ and $M$. Moreover, inasmuch as $\left\{{\lambda }_k\right\}\subseteq (0,\lambda )$, we have that

(5.41) $M:=\frac{\kappa }{1-\kappa (1+2{\lambda }_k)}<\frac{\kappa }{1-\kappa (1+2\lambda )}.$(5.41)

It follows, for $\lambda =\frac{1-\kappa }{2(\eta +2)\kappa }$, that

$M\eta \lambda \le \frac{\eta \lambda \kappa }{1-\kappa (1+2\lambda )}=\frac{\eta (1-\kappa )}{2(1-\kappa )(\eta +2)-2(1-\kappa )}$

$=\frac{\eta }{2(\eta +1)}\le \frac{1}{2}.$

Note that the metric regularity of the mapping $P_{({\lambda }_k,x_0)}$ at $(x_0,y_0)$ on ${\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0)$ with constant $\frac{\kappa }{1-\kappa }$ implies through Lemma 4.1 that $P_{({\lambda }_k,x_0)}^{-1}$ is Lipschitz-like at $(y_0,x_0)$ on ${\mathbb{B}}_{r_{y_0}}(y_0)\times {\mathbb{B}}_{r_{x_0}}(x_0)$ with constant $\frac{\kappa }{1-\kappa }$, that is, (5.35) holds.

Let $y\in {\mathbb{B}}_{\sigma }(y_0)$. Since $(x_0,y_0)\in \mathrm{g}\mathrm{p}\mathrm{h}T$, then for $\parallel \sigma \parallel <\lambda \delta$ in assumption (b), we have that

(5.42) $\mathrm{d}(y,T(x_0))\le \parallel y-y_0\parallel \le \sigma <\lambda \delta .$(5.42)

To complete the proof, we will proceed by mathematical induction. It suffices to show that the Algorithm 5.2 generates at least one sequence and any generated sequence $\left\{x_k\right\}$ satisfies

(5.43) $x_{k+1}\in P_{({\lambda }_k,x_k)}^{-1}(y)\cap {\mathbb{B}}_{r_{x_0}}(x_0)$(5.43)

and

(5.44) $\parallel x_{k+1}-x_k\parallel \le (M\eta \lambda {)}^{k+1}\delta$(5.44)

for each $k=0,1,2,\dots .$ To this end, define

(5.45) ${\hat{r}}_x:=\frac{2\kappa }{1-\kappa }(\lambda \parallel x-x_0\parallel +\parallel y-y_0\parallel )\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}x\in X.$(5.45)

Since $\eta >1$, by using (5.39) and the fact $\sigma <\lambda \delta$ in assumption (b) we have from (5.45) that

(5.46) ${\hat{r}}_x\le \frac{2\kappa }{1-\kappa }(\lambda \delta +\sigma )<\frac{4\kappa \lambda }{1-\kappa }\delta <\frac{2}{\eta +2}\delta <\delta \mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}x\in {\mathbb{B}}_{\delta }(x_0).$(5.46)

First, we will prove that

(5.47) ${\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_0,x_0)\cap {\hat{r}}_{x_0}(0)\ne \text{O}.$(5.47)

To do this, we will consider the mapping ${\mathrm{\Phi }}_{({\lambda }_0,x_0)}$ defined by (5.37) and apply Lemma 4.2 to ${\mathrm{\Phi }}_{({\lambda }_0,x_0)}$ with ${\eta }_0:=x_0$, $r:={\hat{r}}_{x_0}$ and $\alpha :=\frac{1}{2}$. It’s sufficient to show that assertions (4.4) and (4.5) of Lemma 4.2 hold for ${\mathrm{\Phi }}_{({\lambda }_0,x_0)}$ with ${\eta }_0:=x_0$, $r:={\hat{r}}_{x_0}$ and $\alpha :=\frac{1}{2}$. To proceed, we note that $x_0\in P_{({\lambda }_0,x_0)}^{-1}(y_0)\cap {\mathbb{B}}_{{\hat{r}}_{x_0}}(x_0)$. Then by the definition of ${\mathrm{\Phi }}_{({\lambda }_0,x_0)}$ and excess $e$, we have

$d(x_0,{\mathrm{\Phi }}_{({\lambda }_0,x_0)}(x_0))\le e(P_{({\lambda }_0,x_0)}^{-1}(y_0)\cap {\mathbb{B}}_{{\hat{r}}_{x_0}}(x_0),{\mathrm{\Phi }}_{({\lambda }_0,x_0)}(x_0))$

(5.48) $\le e(P_{({\lambda }_0,x_0)}^{-1}(y_0)\cap {\mathbb{B}}_{r_{x_0}}(x_0),P_{({\lambda }_0,x_0)}^{-1}[Z_{({\lambda }_0,x_0)}(x_0)]).$(5.48)

(noting that ${\mathbb{B}}_{{\hat{r}}_{x_0}}(x_0)\subseteq {\mathbb{B}}_{\delta }(x_0)\subseteq {\mathbb{B}}_{r_{x_0}}(x_0)$). For each $x\in {\mathbb{B}}_{\delta }(x_0)$, we have that

(5.49) $\parallel Z_{({\lambda }_0,x_0)}(x)-y_0\parallel =\parallel y+{\lambda }_0(x-x_0)-{\lambda }_0(x-x_0)-y_0\parallel$(5.49)

$\le \parallel y-y_0\parallel \le \sigma .$

Then by the relations $\sigma <\lambda \delta$ and $(2\eta +1)\lambda \delta \le r_{y_0}$ in assumptions (b) and (a), respectively, we obtain that

(5.50) $\parallel Z_{({\lambda }_0,x_0)}(x)-y_0\parallel \le \lambda \delta \le \frac{r_{y_0}}{2\eta +1}\le r_{y_0},$(5.50)

that is, for each $x\in {\mathbb{B}}_{\delta }(x_0)$, $Z_{({\lambda }_0,x_0)}(x)\in {\mathbb{B}}_{r_{y_0}}(y_0)$. In particular, letting $x=x_0$ in (5.49), then we obtain that

(5.51) $\parallel Z_{({\lambda }_0,x_0)}(x_0)-y_0\parallel =\parallel y-y_0\parallel$(5.51)

$\le \sigma \le \lambda \delta .$

This yields that $Z_{({\lambda }_0,x_0)}(x_0)\in {\mathbb{B}}_{r_{y_0}}(y_0).$ Hence, by using (5.51) and Lipschitz-like property of $P_{({\lambda }_0,x_0)}^{-1}(\cdot )$ in (5.48), we obtain that

$d(x_0,{\mathrm{\Phi }}_{({\lambda }_0,x_0)}(x_0))\le \frac{\kappa }{1-\kappa }\parallel y_0-Z_{({\lambda }_0,x_0)}(x_0)\parallel \le \frac{\kappa }{1-\kappa }\parallel y-y_0\parallel$

$=(1-\frac{1}{2}){\hat{r}}_{x_0}=(1-\alpha )r.$

This implies that assertion (4.4) of Lemma 4.2 is satisfied. Below, we will show that the assertion (4.5) of Lemma 4.2 is also hold. To show this, let $x^{\prime },x^{\prime \prime }\in {\mathbb{B}}_{{\hat{r}}_{x_0}}(x_0)$. Then, by the fact $2\delta \le r_{x_0}$ in assumption (a) and (4.46), we have $x^{\prime },x^{\prime \prime }\in {\mathbb{B}}_{{\hat{r}}_{x_0}}(x_0)\subseteq {\mathbb{B}}_{\delta }(x_0)\subseteq {\mathbb{B}}_{r_{x_0}}(x_0)$. Moreover, we have from (4.50) that $Z_{({\lambda }_0,x_0)}(x^{\prime }),Z_{({\lambda }_0,x_0)}(x^{\prime \prime })\in {\mathbb{B}}_{r_{y_0}}(y_0)$. Then, by Lipschitz-like property of $P_{({\lambda }_0,x_0)}^{-1}(\cdot )$, we have

$e({\mathrm{\Phi }}_{({\lambda }_0,x_0)}(x^{\prime })\cap {\mathbb{B}}_{{\hat{r}}_{x_0}}(x_0),{\mathrm{\Phi }}_{({\lambda }_0,x_0)}(x^{\prime \prime }))$

$\le e({\mathrm{\Phi }}_{({\lambda }_0,x_0)}(x^{\prime })\cap {\mathbb{B}}_{r_{x_0}}(x_0),{\mathrm{\Phi }}_{({\lambda }_0,x_0)}(x^{\prime \prime }))$

$=e(P_{({\lambda }_0,x_0)}^{-1}[Z_{({\lambda }_0,x_0)}(x^{\prime })]\cap {\mathbb{B}}_{r_{x_0}}(x_0),P_{({\lambda }_0,x_0)}^{-1}[Z_{({\lambda }_0,x_0)}(x^{\prime \prime })])$

(5.52) $\le \frac{\kappa }{1-\kappa }\parallel Z_{({\lambda }_0,x_0)}(x^{\prime })-Z_{({\lambda }_0,x_0)}(x^{\prime \prime })\parallel .$(5.52)

Applying (5.38) and (5.39) in (5.52), we obtain

$e({\mathrm{\Phi }}_{({\lambda }_0,x_0)}(x^{\prime })\cap {\mathbb{B}}_{{\hat{r}}_{x_0}}(x_0),{\mathrm{\Phi }}_{({\lambda }_0,x_0)}(x^{\prime \prime }))$

$\le \frac{2\kappa {\lambda }_0}{1-\kappa }\parallel x^{\prime }-x^{\prime \prime }\parallel \le \frac{2\lambda \kappa }{1-\kappa }\parallel x^{\prime }-x^{\prime \prime }\parallel <\frac{1}{\eta +2}\parallel x^{\prime }-x^{\prime \prime }\parallel$

(5.53) $<\frac{1}{2}\parallel x^{\prime }-x^{\prime \prime }\parallel =\alpha \parallel x^{\prime }-x^{\prime \prime }\parallel .$(5.53)

Therefore, the assertion (4.5) of Lemma 4.2 is also satisfied. Since both assertions (4.4) and (4.5) of Lemma 4.2 are fulfilled, there exists a fixed point

(5.54) ${\hat{x}}_1\in {\mathbb{B}}_{{\hat{r}}_{x_0}}(x_0)\mathrm{s}\mathrm{u}\mathrm{c}\mathrm{h}\mathrm{t}\mathrm{h}\mathrm{a}\mathrm{t}{\hat{x}}_1\in {\mathrm{\Phi }}_{({\lambda }_0,x_0)}({\hat{x}}_1),$(5.54)

which translates to $Z_{({\lambda }_0,x_0)}({\hat{x}}_1)\in P_{({\lambda }_0,x_0)}({\hat{x}}_1)$, that is, $y\in {\lambda }_0({\hat{x}}_1-x_0)+T({\hat{x}}_1)$. This shows that ${\hat{x}}_1-x_0\in {\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_0,x_0)$ and hence (5.47) is hold. Consequently, inasmuch as $\eta >1$, we can choose $v_0\in {\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_0,x_0)$ such that there exists $\bar{v}\in {\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_0,x_0)$ and

(5.55) $\parallel v_0\parallel \le \eta \mathrm{m}\mathrm{i}{\mathrm{n}}_{\bar{v}\in {\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_0,x_0)}\parallel \bar{v}\parallel .$(5.55)

By Algorithm 5.2, $x_1:=x_0+v_0$ is defined. Hence, the point $x_1$ is generated by Algorithm 5.2. Furthermore, by the definition of ${\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_0,x_0)$, from (5.30) we can write

${\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_0,x_0):=\left\{v_0\in X:x_0+v_0\in P_{({\lambda }_0,x_0)}^{-1}(y)\right\}$

$=\left\{v_0\in X:x_1\in P_{({\lambda }_0,x_0)}^{-1}(y)\right\},$

and since there exists $\bar{v}\in {\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_0,x_0)$, we have

(5.56) $\mathrm{m}\mathrm{i}{\mathrm{n}}_{\bar{v}\in {\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_0,x_0)}\parallel \bar{v}\parallel =\mathrm{d}(0,{\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_0,x_0))=\mathrm{d}(x_0,P_{({\lambda }_0,x_0)}^{-1}(y)).$(5.56)

Thus, from (5.55) we have $\parallel v_0\parallel \le \eta \mathrm{d}(0,{\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_0,x_0))$. This implies that

$\parallel v_0\parallel \le \eta {\hat{r}}_{x_0}\le \eta \delta .$

Then by assumptions (a) and (b), we get that

$\parallel y-{\lambda }_0{v}_0-y_0\parallel \le \parallel y-y_0\parallel +{\lambda }_0\parallel v_0\parallel \le \sigma +\lambda \eta \delta \le \lambda (\eta +1)\delta \le r_{y_0},$

and so $y-{\lambda }_0{v}_0\in {\mathbb{B}}_{r_{y_0}}(y_0)$. This, together with the closedness of $gphT\cap ({\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0))$ and the fact $v_0\in {\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_0,x_0)$, implies that $y-{\lambda }_0{v}_0\in T(x_1)$. Then, by (5.31) we have that $x_1\in P_{({\lambda }_0,x_0)}^{-1}(y)$. Because of $v_0\in {\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_0,x_0)$, by (61) it follows that (5.54) holds for $k=0$.

Since (5.40) holds and $P_{({\lambda }_k,x_0)}(\cdot )$ is metrically regular at $(x_0,y_0)$ on ${\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0)$ with constant $\frac{\kappa }{1-\kappa }$, it follows from Lemma 5.1 that the mapping $P_{({\lambda }_k,x)}^{-1}(\cdot )$ is Lipschitz-like at $(y_0,x_0)$ on ${\mathbb{B}}_{\bar{r}}(y_0)\times {\mathbb{B}}_{\frac{r_{x_0}}{2}}(x_0)$ with constant $M$ for each $x\in {\mathbb{B}}_{\frac{r_{x_0}}{2}}(x_0)$. In particular, $P_{({\lambda }_0,x_0)}^{-1}(\cdot )$ is Lipschitz-like at $(y_0,x_0)$ on ${\mathbb{B}}_{\bar{r}}(y_0)\times {\mathbb{B}}_{\frac{r_{x_0}}{2}}(x_0)$ with constant $M$ as the ball ${\mathbb{B}}_{\frac{r_{x_0}}{2}}(x_0)$ contains the point $x_0$. Furthermore, the facts $3\lambda \delta \le \bar{r}$ and $\sigma <\lambda \delta$ in assumptions (a) and (b), respectively, imply that

$\sigma <\lambda \delta \le \frac{\bar{r}}{3}<\bar{r},$

and hence we have that $y\in {\mathbb{B}}_{\sigma }(y_0)\subseteq {\mathbb{B}}_{\bar{r}}(y_0)$. Applying Lemma 4.1, we have that the mapping $P_{({\lambda }_0,x_0)}(\cdot )$ is metrically regular at $(x_0,y_0)$ on ${\mathbb{B}}_{\frac{r_{x_0}}{2}}(x_0)\times {\mathbb{B}}_{\bar{r}}(y_0)$ with constant $M$ such that

(5.57) $\mathrm{d}(x_0,P_{({\lambda }_0,x_0)}^{-1}(y))\le M\mathrm{d}(y,P_{({\lambda }_0,x_0)}(x_0))\mathrm{f}\mathrm{o}\mathrm{r}{x}_0\in {\mathbb{B}}_{\frac{r_{x_0}}{2}}(x_0)\mathrm{a}\mathrm{n}\mathrm{d}y\in {\mathbb{B}}_{\bar{r}}(y_0).$(5.57)

Using (5.56), (5.57) and (5.42) in (5.55), we obtain that

$\parallel x_1-x_0\parallel =\parallel v_0\parallel \le \eta \mathrm{d}(0,{\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_0,x_0))=\eta \mathrm{d}(x_0,P_{({\lambda }_0,x_0)}^{-1}(y))$

$\le \eta M\mathrm{d}(y,P_{({\lambda }_0,x_0)}(x_0))=\eta M\mathrm{d}(y,T(x_0))$

(5.58) $\le (M\eta \lambda )\delta .$(5.58)

This shows that (5.44) holds for $k=0$.

We assume that the points $x_1,\dots ,x_n$ are generated by Algorithm 5.2 such that (5.43) and (5.44) are true for $k=0,1,2,\dots ,n-1$. We show that there exists $x_{n+1}$ such that (5.43) and (5.44) hold for $k=n$. Because (5.43) and (51) hold for $k\le n-1$, we have, for $M\eta \lambda \le \frac{1}{2}$, that

(5.59) $\parallel x_n-x_0\parallel \le \sum _{i=1}^n\parallel d_{i-1}\parallel \le \delta \sum _{i=1}^n(M\eta \lambda {)}^i\le \frac{M\eta \lambda }{1-M\eta \lambda }\delta \le \delta ,$(5.59)

and so $x_n\in {\mathbb{B}}_{\delta }(x_0)$. Now with almost same arguments as we used for the case when $k=0$, we can show that (5.43) and (5.44) hold for $k=n$. Hence, (5.43) and (5.44) hold for each $k$. This implies that $\left\{x_n\right\}$ is a Cauchy sequence which is generated by Algorithm 5.2 and there exists $x^{\ast }\in {\mathbb{B}}_{r_{x_0}}(x_0)$ such that $x_n\to x^{\ast }$. Thus, passing to the limit $x_{n+1}\in P_{({\lambda }_n,x_n)}^{-1}(y)$ and since $gphT\cap ({\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0))$ is closed, it follows that $y\in T(x^{\ast })$. Hence, the proof is complete.

The special case is that when $x_0$ is a solution of (1) for $y=0$, Theorem 5.1 can be reduced to the following corollary which gives the local convergence result for restricted proximal point method defined by Algorithm 5.2.

Corollary 5.1. Suppose that $\eta >1$, $\lambda >0$ and $\bar{x}$ is a solution of (1) for $y=0$. Let $\left\{{\lambda }_k\right\}$ be a sequence of scalars such that $\left\{{\lambda }_k\right\}\subseteq (0,\lambda )$. Let $T$ be metrically regular at $(\bar{x},0)$ which have locally closed graph at $(\bar{x},0)$. Let $\lambda <\frac{1-M}{2(\eta +2)M}$, where $M:=\mathrm{r}\mathrm{e}\mathrm{g}T(\bar{x}|0)$. Suppose that

(5.60) $\underset{x\to \bar{x}}{lim}d(0,T(x))=0.$(5.60)

Then there exist constants $\hat{\delta }>0$ and $\sigma >0$ such that for every $y\in {\mathbb{B}}_{\sigma }(0)$ there exists any sequence $\left\{x_k\right\}$ generated by Algorithm 5.2 with initial point $x_0\in {\mathbb{B}}_{\hat{\delta }}(\bar{x})$, which is convergent to a solution $x$ of (1) for $y$.

Proof. Let $\kappa >M$ be such that $\lambda =\frac{1-\kappa }{2(\eta +2)\kappa }$. Since $\mathrm{g}\mathrm{p}\mathrm{h}T$ is locally closed at $(\bar{x},0)$ and $T$ is metrically regular at $(\bar{x},0)$, there exist constants $r_{\bar{x}},r_0>0$ such that $T$ is metrically regular at $(\bar{x},0)$ on ${\mathbb{B}}_{r_{\bar{x}}}(\bar{x})\times {\mathbb{B}}_{r_0}(0)$ with constant $\kappa$ and $\mathrm{g}\mathrm{p}\mathrm{h}T\cap ({\mathbb{B}}_{r_{\bar{x}}}(\bar{x})\times {\mathbb{B}}_{r_0}(0))$ is closed. Since ${\lambda }_{k}I(\cdot -\bar{x})$ is Lipschitz continuous on ${\mathbb{B}}_{r_{\bar{x}}}(0)+\bar{x}$, by Proposition 4.1 we have that $P_{({\lambda }_k,\bar{x})}$ is metrically regular at $(\bar{x},0)$ on ${\mathbb{B}}_{r_{\bar{x}}}(\bar{x})\times {\mathbb{B}}_{r_0}(0)$ with constant $\frac{\kappa }{1-\kappa }$.

Choose $r_{x_0}\in (0,r_{\bar{x}})$ and $r_{y_0}\in (0,r_0)$ be such that $2r_{y_0}-5{\lambda }_k{r}_{x_0}>0$. Since $\eta >1$ and $\left\{{\lambda }_k\right\}\subseteq (0,\lambda )$, we have that

${\lambda }_k<\lambda =\frac{1-\kappa }{2(\eta +2)\kappa }<\frac{1-\kappa }{2\kappa }.$

This yields that $1-\kappa (1+2{\lambda }_k)>0$. Then define

$\bar{r}:=min\left\{\frac{2r_{y_0}-5{\lambda }_k{r}_{x_0}}{2},\frac{r_{x_0}(1-\kappa (1+2{\lambda }_k))}{4\kappa }\right\}>0.$

It follows that

${\lambda }_k<min\left\{\frac{2r_{y_0}}{5r_{x_0}},\frac{1-\kappa }{2\kappa }\right\}.$

Let $\delta >0$ be such that

$\delta \le min\{\frac{r_{x_0}}{2},\frac{\bar{r}}{3\lambda },\frac{r_{y_0}}{(2\eta +1)\lambda },1\}.$

Let $y\in {\mathbb{B}}_{\sigma }(0)$. Since (5.60) holds, we can take $0<\hat{\delta }\le \delta$ so that for each $x_0\in {\mathbb{B}}_{\hat{\delta }}(\bar{x})$ there exists $y_0$ near 0 such that $y_0\in T(x_0)$, that is, $y_0\in P_{({\lambda }_k,x_0)}(x_0)$. Then for such $y_0$ we have that $y\in {\mathbb{B}}_{\sigma }(y_0)$ so that

(5.61) $\parallel \sigma \parallel \le \lambda \delta .$(5.61)

It follows that ${\mathbb{B}}_{r_{x_0}}(x_0)\subset {\mathbb{B}}_{r_{\bar{x}}}(\bar{x})$ and ${\mathbb{B}}_{r_{y_0}}(y_0)\subset {\mathbb{B}}_{r_0}(0)$ and hence $\mathrm{g}\mathrm{p}\mathrm{h}T\cap ({\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0))$ is closed. Thus, by the property of $P_{({\lambda }_k,\bar{x})}$, we conclude that $P_{({\lambda }_k,x_0)}$ is metrically regular at $(x_0,y_0)$ on ${\mathbb{B}}_{r_{x_0}}(x_0)\times {\mathbb{B}}_{r_{y_0}}(y_0)$ with constant $\frac{\kappa }{1-\kappa }$. Now, it is routine to check that all assumptions in Theorem 5.1 hold. Thus, Theorem 5.1 is applicable to complete the proof of the Corollary 5.1.

4. Numerical experiment

In this section, a numerical experiment is given to validate the stability of convergence of Gauss-type proximal point method.

Example 6.1. Let $X=Y=\mathbb{R},y=1,x_0=-1.5,\eta =3,\kappa =0.2and\lambda =0.4$. Define a set-valued mapping $T$ on $\mathbb{R}$ by $T(x)=\left\{5x-2,3x-1\right\}$. Then Algorithm 5.2 generates a sequence for solving (3.1), which is converges to $x^{\ast }=0.6667$.

Solution: Let us consider $T(x)=5x-2$. It is obvious from the statement that $T$ has a closed graph at $(-1.5,-9.5)\in gphT$. From the definition of ${\mathrm{\Lambda }}_{\mathrm{\Delta }}(\lambda ,x_k)$, we have that

${\mathrm{\Lambda }}_{\mathrm{\Delta }}(\lambda ,x_k)=\left\{v_k\in \mathbb{R}:y\in \lambda v_k+T(x_k+v_k)\right\}$

$=\left\{v_k\in \mathbb{R}:v_k=\frac{y-5x_k+2}{\lambda +5}\right\}.$

On the other hand, the nonemptyness of ${\mathrm{\Lambda }}_{\mathrm{\Delta }}(\lambda ,x_k)$ implies that

$y\in \lambda (x_{k+1}-x_k)+T(x_{k+1})$

$\Rightarrow x_{k+1}=\frac{y+\lambda x_k+2}{\lambda +5},$

and we have, Theorem 5.1, that

$\parallel v_k\parallel =\parallel x_{k+1}-x_k\parallel \le \eta \mathrm{d}(0,{\mathrm{\Lambda }}_{\mathrm{\Delta }}(\lambda ,x_k))=\eta \mathrm{d}(x_k,P_{(\lambda ,x_k)}^{-1}(y))$

$\le \eta M\mathrm{d}(y,P_{(\lambda ,x_k)}(x_k))=\eta M\mathrm{d}(y,T(x_k))$

(6.1) $\le M\eta \lambda \parallel x_k-x_{k-1}\parallel =M\eta \lambda \parallel v_{k-1}\parallel .$(6.1)

Then by the definition of $M$, we obtain that $M<\frac{5}{16}\approx 0.31$, and hence for given values of $\eta ,\kappa$ and $\lambda$, we see that $M\eta \lambda <\frac{3}{8}<1$. Thus, this implies that the sequence generated by Algorithm 5.2 converges linearly. Using Mat lab program, we present the solution of (3.1), which is $0.6667$, when the number of iterations are $k=7$. Similarly, we can use the same approach for finding the solution of (3.1) when $T(x)=3x-1$. 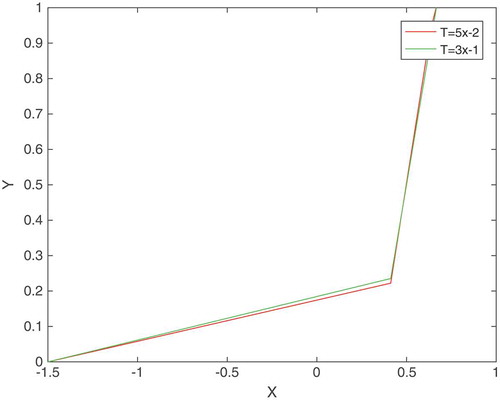The Table 1 shows the numerical results and Figure 1 gives the graphical representation of $T(x)=\left\{5x-2,3x-1\right\}$.

Table 1. Finding a solution of generalized equation

	$T(x)=5x-2$
x	−1.5000	0.4118	0.6367	0.6631	0.6663	0.6666	0.6667
T(x)	0	0.2222	0.9424	0.9957	0.9997	1.0000	1.0000
	$T(x)=3x-1$
x	−1.5000	0.4118	0.6367	0.6631	0.6663	0.6666	0.6667
T(x)	0	0.2353	0.9100	0.9894	0.9988	0.9999	1.0000

 Figure 1. The figure for set-valued mappings $\mathit{T}(x)=\left\{\mathbf{5}\mathit{x}\mathbf{-}\mathbf{2}\mathbf{,}\mathbf{3}\mathit{x}\mathbf{-}\mathbf{1}\right\}$.

5. Concluding remarks

When $\eta >1$, we have established the semilocal and local convergence of the restricted proximal point method defined by Algorithm 5.2 under the assumption that $T$ is metrically regular. Our proposed method coincides with the Gauss-type proximal point algorithm introduced by Rashid et al. in Rashid et al. (2013) when $y=0$. Moreover, when $y=0$, $\eta =1$ and the set ${\mathrm{\Lambda }}_{\mathrm{\Delta }}({\lambda }_k,x_k)$ is singleton, the Algorithm 5.2 reduces to the classical proximal point algorithm defined by Algorithm 5.1. The convergence result established in the present article is ensuring the validity of the Gauss-type proximal point method, introduced by Rashid et al. in Rashid et al. (2013), in the sense that the convergence result is uniform. Therefore, this study improves and extends the result corresponding to (Rashid et al., 2013). Finally, we have presented a numerical experiment that illustrated the theoretical result.

Acknowledgements

The author thanks the anonymous referees for their insightful comments and constructive suggestions, which contribute to the improvement of the initial versions of this manuscript. The author is also grateful to the associate editor for his constructive suggestions which have improved the presentation of this manuscript.

Additional information

Funding

This work was supported by the Ministry of Education, Bangladesh [37.20.0000.004.033.013.2015].

Notes on contributors

M.H. Rashid

Mohammed Harunor Rashid is an Associate Professor in the Department of Mathematics, University of Rajshahi, Bangladesh, where he teaches calculus, geometry, real analysis, numerical analysis, vector and tensor analysis, operations research, functional analysis and other courses in both undergraduate and graduate level. Presently, he is a Postdoctoral Fellow at the Institute of Computational Mathematics and Scientific/Engineering Computing, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, China. He has completed his PhD from Zhejiang University, China. His research interests focus on fuzzy Mathematics, nonlinear numerical functional analysis and nonlinear optimization, especially on generalized equations. In his investigation, he has shown how to solve generalized equations using an iterative method under some suitable conditions. He has published his research contributions in some internationally renowned journals whose publishers are Springer, Taylor & Francis, Yokohama and other journals.